Refined Admissible Analysis and Design Conditions for Discrete Fuzzy Singular Systems with Multiple Difference Matrices

ABSTRACT

This study mainly discusses extended admissibility and fuzzy parallel distributed compensation (PDC) control issues for discrete singular fuzzy systems with multiple difference matrices existing in the rules. By the overall system associated with the discrete singular models with multiple difference matrices, we first propose an extended admissibility analysis criteria, where the new results not only involve some slack matrices but also have a less number of linear matrix inequalities’ (LMIs) constraints. Furthermore, by hiring the fuzzy PDC, explicit design criteria are further developed for the regarded system. Noticeably, the new design method can cope with controller synthesis of the admissibility and D-admissibility issues. Due to all the presented criteria are formed by the strict LMIs, we can readily evaluate them via some existing LMI solvers. Finally, two numerical examples are involved to demonstrate the applicability and the feasibility of the developed results.

Introduction

Many physical systems and industrial processes can be intrinsically formulated by nonlinear systems. But, the corresponding control issues are stubborn and hard to be treated (see, e.g., Liu, Xia, Wang, and Hao (2021); Wang, Xia, Shen, Xing, and Park (2021); Wang, Yang, Xia, Wu, and Shen (2022); and the references therein). Based on fuzzy control with T-S fuzzy models (Tanaka and Sugeno 1992), we can well approximate nonlinear systems or uncertain systems by the extended formulation (Baumann and Rugh 1986; Tanaka and Sano 1994; Wang, Tanaka, and Griffin 1996; Chen, Wang, and Lee 2011; Askari and Markazi 2012). It can characterize the whole system by a set of fuzzy if-then rules with the consequent parts depicted by linear state models. Afterward, a lot of studies devoted to the stability analysis and stabilization for T-S fuzzy models (see, e.g., Ma, Sun, and He 1998; Chang and Sun 2003; Guerra, Kruszewski, Vermeiren, and Tirmant 2006; Hien 2010; Lam and Leung 2010; Liu, Gu, Tian, and Yan 2012; and the references therein).

Singular systems are used to describe complex systems, which can merge dynamic behaviors with algebraic dependent restrictions into a single system (Dai 1989; Duan 2010). They are also named as descriptor systems or generalized state-space systems. They have many comprehensive applications, such as electrical networks, chemical industrial processes, aerospace engineering, and social economic model (Luenberger 1977; Lewis 1986; Dai 1989; Jódar and Merello 2010; Duan 2010), and so on. However, the study of singular systems is more complicated than regular state-space ones, because besides the stability, we have to extra take the regularity and the causality (impulse-free for continue ones) into account (Xu and Yang 1999; Xu and Lam 2004). Furthermore, poles’ location in a specific region can directly dominate the systems’ states temporary responses and system’s performance (Juang, Hong, and Wang 1989; Chilali and Gahinet 1996; Chilali, Gahinet, and Apkarian 1999). Recently, some works had dealt with the D-admissibility issues for the singular systems, and proposed many applicable analysis and synthesis results (Bavafa-Toosi, Ohmori, and Labibi 2006; Rejichi, Bachelier, Chaabane, and Mehdi 2008; Huang 2011; Zhang 2013).

Accordingly, by comprising T-S fuzzy model and singular system, fuzzy singular systems are aroused in miscellaneous fields and reveal the appreciating advantage over past few years, where their consequent parts are replaced by singular systems’ models. They afford to represent an larger class of physical systems and engineering processes (Taniguchi, Tanaka, and Wang 2000). For discrete-time fuzzy singular systems (DFSs), many studies have achievements of admissibility analysis and controller synthesis. The DFSs with common E is firstly presented (Huang 2005), and less conservative result is then developed (Xu, Song, Lu, and Lam 2007). But, both the results need to impose a restriction $E^{T}PE\ge 0$ in the criteria, where it usually is a nonstrict linear matrix inequality (LMI) constraint with insufficient rank and cannot be directly treated via current LMI solvers (Gahinet, Nemirovski, Jaub, and Chilali 1995). And, some works further addressed the DFSs subject to state delays and/or uncertainties (Li, Shi, Wu, and Zhang 2014; Kchaou and El-Hajjaji 2017; Chen and Yu 2021; Chen, Yu, and Jam, 2022). For the DFSs with multiple difference term matrices E_i, some results (Estrada-Manzo, Lendek, Guerra, and Pudlo 2015; Lendek, Nagy, and Lauber 2018; Gonzalez and Guerra 2019; Qiao, Li, and Lu 2021) needed to beforehand transfer the original systems into augmented systems’ forms with a common difference term matrix with enlarged dimensions. By imposing assumption on E_i to satisfy some prescribed forms, the proposed augmented systems thus could be equivalent to the original ones for admissibility issues. However, it needs to stress that the more restriction on difference term matrices may reduce the applicability for system modeling from physical systems. Furthermore, the past work (Huang 2014) could directly deal with the original DFSs with multiple difference term matrices E_i in the rules. But, the proposed admissible and design criteria needed to involve a considerable number of LMIs’ constraints, where there may bring on the conservatism for numerical evaluation.

Motivated from the above analytic contentions, this work mainly addresses extended admissibility analysis and parallel distributed compensation (PDC) control law (Tanaka and Sugeno 1992) for DFSs subjected to distinct difference matrices. Based on matrix algebraic and LMI approach (Boyd et al., 1994), we first propose extended admissibility analysis criteria for the unforced system. The proposed new results not only involve some slack matrices but also can sharply reduce the number of LMIs’ constraints, where they both are helpful to reduce the conservatism of the analysis criteria. Furthermore, by employing the fuzzy PDC, design criteria for the resulting closed-loop system are further investigated. Prominently, the proposed design approach can conduct the controller design associated with the admissible and D-admissible assurance. Due to all the developed criteria can be formulated by strict LMIs, they can readily be verified via existing LMI solvers. Two illustrative examples are involved to demonstrate the efficiency and feasibility of the presented method.

Compared with previous works, the main contribution of this work is highlighted as follows:

1. This work mainly proposes a fuzzy descriptor system with the perturbed derivative matrices in the rules. It can suitably transfers nonlinear and/or uncertain systems into fuzzy inference control framework.

2. All the presented admissibility analysis and controller design criteria can be explicitly expressed in terms of LMIs or parametric LMIs. Accordingly, we can handily verify them by current LMI solvers for the admissibility analysis or implement a fuzzy PDC control for closed-loop systems associated with the admissible assurance or the admissibility with specific decay rate of states’ responses.

The rest of this work is arranged as follows. Systems formulation and some preliminaries are described in Section 2. In Section 3, the admissibility analysis for the regarded systems is addressed. And, the PDC control with admissible and D-admissible assurance are studied in Section 4. Two numerical example are given in Section 5 to verify the validity and the applicability. Finally, we give some concluding remarks in Section 6.

Notations: The notations used in this work are fairly standard. Rⁿ denotes the n-dimensional real Euclidean space. R^m×n denotes the sets of the m×n matrices. For a matrix M^T (M^-1) represents the transpose (inverse) of the matrix M. For a symmetric matrix P, P > 0 (P ≥0) represents the positive definite matrix (positive semi-definite matrix), P < 0 (P ≤0) represents the negative definite matrix (negative semi-definite matrix). det(P) means the determinant of P . deg(f(x)) means the degree of the polynomial f(x).

Systems Formulation and Preliminaries

Consider DFSs embracing multiple difference matrices E_i in the rules. The regarded fuzzy system can be represented by a set of fuzzy rules with T-S fuzzy singular systems, and the consequent parts of rules can characterize the local behaviors from a physical system. An overall system can be expressed by fuzzy reasoning with integrating all the individual models. The r rules of the fuzzy inference system can be denoted by

Rule i: If ${\phi }_1\left(k\right)$ is $F_1^i$ and ${\phi }_2\left(k\right)$ is $F_2^i$ and … ${\phi }_n\left(k\right)$ is $F_n^i$

Then $E_{i}x(k+1)=A_{i}x(k)+B_{i}u(k)$, i = 1, 2, … , r,

where $x(k)\in R^n$ stands for the state vector, $u(k)\in R^m$ stands for the control input, and ${\phi }_j(k)$, j = 1, 2, …, n, is the jth premise variable, $F_j^i$ is a fuzzy set, $E_i\in R^{n\times n}$ is a difference term matrix and may be singular, that is, $rank(E_i)=m\le n$, $A_i\in R^{n\times n}$ and $B_i\in R^{n\times m}$ stand for the individual system and input matrices in each rule.

An whole system can thus be integrated by

(1) $\begin{array}{rl}& \sum _{i=1}^r{h}_i(\phi (k))E_{i}x(k+1)=\frac{\sum _{i=1}^r{\omega }_i(\phi (k))(A_{i}x(k)+B_{i}u(k))}{\sum _{i=1}^r{\omega }_i(\phi (k))}\\ & =\sum _{i=1}^r{h}_i(\phi (k))(A_{i}x(k)+B_{i}u(k))\hspace{0.17em}\end{array}$(1)

where

$\left\{\begin{array}{c}{\omega }_i(\phi (k))=\prod _{j=1}^n{F}_j^i({\phi }_j(k))\ge 0\\ \sum _{i=1}^r{\omega }_i(\phi (k))>0\end{array}i=1,2,\cdots ,r\right.,$

$\left\{\begin{array}{c}{h}_i(\phi (k))=\frac{{\omega }_i(\phi (k))}{\sum _{i=1}^r{\omega }_i(\phi (k))}\ge 0\\ \sum _{i=1}^r{h}_i(\phi (k))=1\end{array}i=1,2,\cdots ,r\right.$

and $F_j^i({\phi }_j(k))$ is the firing rate of ${\phi }_j(k)$ in$F_j^i$.

To cope with the analysis and controller design issues for DFSs (1), we must beforehand involve some necessary definitions for the nominal system $Ex(k+1)=Ax(k)$ in the following.

Definition 2.1

(Dai, 1989, Huang, 2011):

1. The matrices pair $\left(E,A\right)$ is referred to be regular such that $det(sE-A)\ne 0$ holds.

2. The matrices pair $\left(E,A\right)$ is referred to be causal, if it is regular and deg[det($zE-A$)]=$rank(E)$.

3. The nominal system $Ex(k+1)=Ax(k)$ is referred to be admissible, if it is regular, causal, and all of its finite poles are within the unit disk $D(0,1)$.

4. The nominal system $Ex(k+1)=Ax(k)$ is referred to be D-admissible, if it is regular, causal, and all of its finite poles are within a disk $D(0,\alpha )\subset D(0,1)$, $\alpha <1$.

Some previous works are involved for deriving the main results as follows.

Lemma 1

(Xu and Yang, 1999): The nominal singular system $Ex(k+1)=Ax(k)$ is asserted to be admissible iff there exist a positive definite matrix $P$ and a compatible matrix Q satisfying

(2) $A^{T}PA-E^{T}PE+Q{S}^{T}A+A^{T}SQ{\hspace{0.17em}}^T<0,$(2)

where $S\in R^{n\times (n-m)}$ satisfying $E^{T}S=0$ is of full-column rank.

Based on Lemma 2 associated with the previous symmetric equivalent issues of singular system (Sun, Zhang, Yang, and Su 2011), a symmetric form can be presented in the following.

Corollary 1:

The nominal singular system $Ex(k+1)=Ax(k)$ is asserted to be admissible if there exist a positive definite matrix $P$ and a compatible matrix Q satisfying

(3) $AP{A}^T-EP{E}^T+ASQ{\hspace{0.17em}}_{\hspace{0.17em}}^T+Q{S}^T{A}^T<0$(3)

where $S\in R^{n\times (n-m)}$ satisfying $ES$ = 0 is of full-column rank.

For the design issues, by the nonsingularity of matrix P, we can replace the matrix $S$ by PS and the following result can be directly attained.

Corollary 2:

The nominal singular system $Ex(k+1)=Ax(k)$ is asserted to be admissible iff there exist a positive definite matrix $P$ and a compatible matrix Q satisfying

(4) $AP{A}^T-EP{E}^T+APSQ{\hspace{0.17em}}_{\hspace{0.17em}}^T+QP{S}^T{A}^T<0$(4)

where $S\in R^{n\times (n-m)}$ satisfying $EPS=0$ is of full-column rank.

The following result is introduced for the D-admissibility issues.

Lemma 2: (Huang 2011): The nominal singular system $Ex(k+1)=Ax(k)$ is asserted to be D-admissible iff there exist a positive definite matrix $P$ and a compatible matrix Q satisfying

(5) $\frac{1}{{\alpha }^2}{A}^{T}PA-E^{T}PE+Q{S}^{T}A+A^{T}SQ{\hspace{0.17em}}_{\hspace{0.17em}}^T<0,$(5)

where $S\in R^{n\times (n-m)}$ satisfying $E^{T}S=0$ is of full-column rank.

Admissibility Analysis

For the unforced DFSs (1), that is, $u(k)\equiv 0$in (1), the admissibility analysis condition is first derived in the following.

Theorem 1:

The unforced DFSs (1), $u(k)=0$in (1), is asserted to be admissible, if there exists a positive definite matrix $P>0$ and compatible matrices Q_i , $\mathrm{\forall }i$, satisfying

(6) $A_i^{T}P{A}_j+A_j^{T}P{A}_i-E_i^{T}P{E}_j-E_j^{T}P{E}_i+A_i^{T}S{Q}_j^T+Q_j{S}^T{A}_i+A_j^{T}S{Q}_i^T+Q_i{S}^T{A}_j<0\mathrm{\forall }i\le j,i,j=1,\hspace{0.17em}2,\hspace{0.17em}\dots ,r$(6)

where $S\in R^{n\times (n-m)}$ satisfying $E_i^{T}S=0$, $\mathrm{\forall }i$, is of full-column rank.

Proof:

Deducing from Lemma 1 for the unforced DFSs (1) with $\bar{A}\equiv \left(\sum _i{h}_i{A}_i\right)$ and $\bar{E}\equiv \left(\sum _i{h}_i{E}_i\right)$, and letting matrices $P>0$ and $\bar{Q}\equiv \sum _i{h}_i{Q}_i$ lead to

$\begin{array}{rl}& {\bar{A}}^{T}P\bar{A}-{\bar{E}}^{T}P\bar{E}+{\bar{A}}^{T}S{\bar{Q}}^T+\bar{Q}{S}^T\bar{A}\\ & \left(\sum _i{h}_i{A}_i^T\right)P\left(\sum _i{h}_i{A}_i\right)-\left(\sum _i{h}_i{E}_i^T\right)P\left(\sum _i{h}_i{E}_i\right)+\left(\sum _i{h}_i{A}_i^T\right)S\left(\sum _i{h}_i{Q}_i^T\right)\\ & +\left(\sum _i{h}_i{Q}_i\right)S^T\left(\sum _i{h}_i{A}_i\right)\\ & =\sum _i{h}_i^2\left(A_i^{T}P{A}_i-E_i^{T}P{E}_i+A_i^{T}S{Q}_i^T+Q_i{S}^T{A}_i\right)\\ & +\sum _{i<j}{h}_i{h}_j(A_i^{T}P{A}_j+A_j^{T}P{A}_i-E_i^{T}P{E}_j-E_j^{T}P{E}_i+A_i^{T}S{Q}_j^T+Q_{j}S{A}_i+A_j^{T}S{Q}_i^T+Q_i{S}^T{A}_j)\end{array}$

By Eq (6(6) $A_i^{T}P{A}_j+A_j^{T}P{A}_i-E_i^{T}P{E}_j-E_j^{T}P{E}_i+A_i^{T}S{Q}_j^T+Q_j{S}^T{A}_i+A_j^{T}S{Q}_i^T+Q_i{S}^T{A}_j<0\mathrm{\forall }i\le j,i,j=1,\hspace{0.17em}2,\hspace{0.17em}\dots ,r$(6) ), we can attain that the above is negative definite and the regarded unforced DFSs (1) is thus ensured to be admissible from Lemma 1.

Based on Theorem 1 associated with Corollary 1, we present a symmetric form of $\left(E^T,A^T\right)$ in the following.

Corollary 3:

The unforced DFSs (1), $u(k)=0$in (1), is asserted to be admissible, if there exist a positive definite matrix $P>0$ and compatible matrices Q_i , $\mathrm{\forall }i$, satisfying

(7) $A_{i}P{A}_j^T+A_{j}P{A}_i^T-E_i^{\hspace{0.17em}}P{E}_j^T-E_j^{\hspace{0.17em}}P{E}_i^T+A_{i}S{Q}_j^T+Q_j{S}^T{A}_i^T+A_{j}S{Q}_i^T+Q_i{S}^T{A}_j^T<0,\mathrm{\forall }i\le j,i,j=\hspace{0.17em}1,\hspace{0.17em}2,\hspace{0.17em}\dots ,r$(7)

where $S\in R^{n\times (n-m)}$ satisfying$E_{i}S=0$, $\mathrm{\forall }i$, is of full-column rank.

Based on Theorem 1 associated with Lemma 2, the D-admissible criteria can be presented as follows.

Corollary 4:

The unforced DFSs (1), $u(k)=0$in (1), is asserted to be D-admissible, if there exist a positive definite matrix $P$ and compatible matrices Q_i , $\mathrm{\forall }i$, satisfying

(8) $\frac{1}{{\alpha }^2}{A}_{i}P{A}_j^T+\frac{1}{{\alpha }^2}{A}_{j}P{A}_i^T-E_i^{\hspace{0.17em}}P{E}_j^T-E_j^{\hspace{0.17em}}P{E}_i^T+A_{i}S{Q}_j^T+Q_j{S}^T{A}_i^T+A_{j}S{Q}_i^T+Q_i{S}^T{A}_j^T<0,\mathrm{\forall }i\le j,i,j=\hspace{0.17em}1,\hspace{0.17em}2,\hspace{0.17em}\dots ,r$(8)

where $S\in R^{n\times (n-m)}$ satisfying $E_{i}S=0$, $\mathrm{\forall }i$, is of full-column rank.

Remark 1 In contraction to the previous results (Huang 2014; Qiao, Li, and Lu 2021), the LMIs numbers constraints are $r\times (r+C_r^2)$ (Huang 2014) and $r+2r^2+(r+1)C_r^2$ (Qiao, Li, and Lu 2021), respectively. However, the new method in Theorem 1 not only has less LMIs, where the LMIs’ constraints number severely reduce down to$(r+C_r^2)$, but also introduces multiple slack matrices $Q_i$ in the conditions, where there both are beneficial to reduce the conservatism of admissibility conditions.

PDC Controller Design

By involving fuzzy PDC control law (Tanaka and Sugeno 1992), the same fuzzy sets in system (1) are employed in the PDC rules and can be represented as

Rule i: If ${\phi }_1\left(k\right)$ is $F_1^i$ and ${\phi }_2\left(k\right)$ is $F_2^i$ and … ${\phi }_j\left(k\right)$ is $F_j^i$

If ${\phi }_1(k)$ is $F_1^i$ and ${\phi }_2(k)$ is $F_2^i$ and … ${\phi }_j(k)$ is$F_j^i$,

Then $u(k)=K_{i}x(k)$, i = 1, 2, … , r,

and the overall controller is integrated as

(9) $u(k)=\frac{\sum _{i=1}^r{\omega }_i(\phi (k))K_{i}x(k)}{{\omega }_i(\phi (k))}=\sum _{i=1}^r{h}_i(\phi (k))K_{i}x(k).$(9)

Substituting (9) into (1) leads to

(10) $\sum _{i=1}^r{h}_i(\phi (k))E_{i}x(k+1)=\sum _{i=1}^r\sum _{j=1}^r{h}_i(\phi (k))h_j(\phi (k))\left(A_i+B_i{K}_j\right)x(k).$(10)

Deducing from Theorem 1, the design criteria can be presented for the resulting closed-loop fuzzy singular system (10) in the sequel.

Theorem 2:

The discrete fuzzy closed-loop system (10) with the PDC control (9) is asserted to be admissible, if there exist a positive definite matrix $P$, and matrices Q, X_j , $\mathrm{\forall }j$, with appropriate dimensions satisfying

(11) $\left[\begin{array}{cc}{\mathrm{\Psi }}_1& A_{i}P+B_i{X}_i\\ P{A}_i^T+X_i^T{B}_i^T& -P\end{array}\right]<0,\mathrm{\forall }i,$(11)

(12) $\left[\begin{array}{cc}{\mathrm{\Psi }}_2& (A_i+A_j)P+B_i{X}_j+B_j{X}_i\\ P{(A_i+A_j)}^T+X_j^T{B}_i^T+X_i^T{B}_j^T& -P\end{array}\right]<0,\mathrm{\forall }i<j,$(12)

where

${\mathrm{\Psi }}_1=A_{i}PS{Q}^T+Q{S}^{T}P{A}_i^T+B_i{X}_{i}S{Q}^T+Q{S}^T{X}_i^T{B}_i^T-E_{i}P{E}_i^T,$

${\mathrm{\Psi }}_2=(A_i+A_j)PS{Q}^T+Q{S}^{T}P(A_i+A_j{)}^T+(B_i{X}_j+B_j{X}_i)S{Q}^T+QS{\hspace{0.17em}}_{\hspace{0.17em}}^T(B_i{X}_j+B_j{X}_i{)}^T-E_{i}P{E}_j^T-E_{j}P{E}_i^T,$

the matrix $S\in R^{n\times (n-m)}$ satisfying $E_{i}PS=0$, $\mathrm{\forall }i$, is of full-column rank. Then, a set of admissibilizing state feedback gains in (9) can be determined as $K_j=X_j{P}^{-1}$,$\mathrm{\forall }j$.

Proof:

Deducing from Corollary 2 for the fuzzy control system (10) with $A_C\equiv \sum _{i,j}{h}_i{h}_j(A_i+B_i{K}_j)$ and $E_C\equiv \sum _i{h}_i{E}_i$, we can ensure the admissibility for the resulting closed-loop system by that there exist matrices $P>0$, Q, and $S$ with compatible dimensions satisfying

$A_{C}P{A}_C^T-E_{C}P{E}_C^T+A_{C}PSQ{\hspace{0.17em}}_{\hspace{0.17em}}^T+Q{S}^{T}P{A}_C^T<0$

By Schur complement, the above is identical to

$\left[\begin{array}{cc}{A}_{C}PSQ{\hspace{0.17em}}_{\hspace{0.17em}}^T+QP{S}^T{A}_C^T-E_{C}P{E}_C^T& A_{C}P\\ P{A}_C^T& -P\end{array}\right]<0.$

By $A_C=\sum _{i,j}{h}_i{h}_j(A_i+B_i{K}_j)$ and $E_C=\sum _i{h}_i{E}_i$, the above leads to

$\begin{array}{rl}& \left[\begin{array}{cc}\sum _{i,j}{h}_i{h}_j(A_i+B_i{K}_j)PSQ{\hspace{0.17em}}^T+Q{S}^{T}P\sum _{i,j}{h}_i{h}_j{(A_i+B_i{K}_j)}^T-\left(\sum _i{h}_i{E}_i\right)P\left(\sum _i{h}_i{E}_i^T\right)& \sum _{i,j}{h}_i{h}_j(A_i+B_i{K}_j)P\\ P\sum _{i,j}{h}_i{h}_j(A_i+B_i{K}_j){\hspace{0.17em}}^T& -P\end{array}\right]\\ & =\sum _i{h}_i^2\left(\left[\begin{array}{cc}(A_i+B_i{K}_j)PSQ{\hspace{0.17em}}^T+Q{S}^{T}P{(A_i+B_i{K}_j)}^T-E_{i}P{E}_i^T& (A_i+B_i{K}_i)P\\ P{(A_i+B_i{K}_i)}^T& -P\end{array}\right]\right)\\ & +\sum _{i<j}{h}_i{h}_j\left(\left[\begin{array}{cc}\begin{array}{c}(A_i+B_i{K}_j)PSQ{\hspace{0.17em}}^T+(A_j+B_j{K}_i)PSQ{\hspace{0.17em}}^T\\ +Q{S}^{T}P(A_i+B_i{K}_j{)}^T+Q{S}^{T}P(A_j+B_j{K}_i{)}^T-E_{i}P{E}_j^T-E_{j}P{E}_i^T\end{array}& (A_i+B_i{K}_j)P+(A_j+B_j{K}_i)P\\ P{(A_i+B_i{K}_j)}^T+P{(A_j+B_j{K}_i)}^T& -2P\end{array}\right]\right)\\ & <0\end{array}$

By letting $X_j\equiv K_{j}P$, if the inequalities (11) and (12) is hold, the fuzzy control system (10) is ensured to be admissible from Corollary 2.

Furthermore, the PDC control law associated with D-admissibility is introduced in the sequel.

Theorem 3:

The discrete fuzzy closed-loop system (10) with PDC control (9) is asserted to be D-admissible, if there exist positive definite matrix $P$, and matrices Q, X_j , $\mathrm{\forall }j$, with appropriate dimensions satisfying

(13) $\left[\begin{array}{cc}{\mathrm{\Psi }}_1& A_{i}P+B_i{X}_i\\ P{A}_i^T+X_i^T{B}_i^T& -{\alpha }^{2}P\end{array}\right]<0,\mathrm{\forall }i,$(13)

(14) $\left[\begin{array}{cc}{\mathrm{\Psi }}_2& (A_i+A_j)P+B_i{X}_j+B_j{X}_i\\ P{(A_i+A_j)}^T+X_j^T{B}_i^T+X_i^T{B}_j^T& -2{\alpha }^{2}P\end{array}\right]<0,\mathrm{\forall }i<j,$(14)

where

${\mathrm{\Psi }}_1=A_{i}PS{Q}^T+Q{S}^{T}P{A}_i^T+B_i{X}_{i}S{Q}^T+Q{S}^T{X}_i^T{B}_i^T-E_{i}P{E}_i^T,$

${\mathrm{\Psi }}_2=(A_i+A_j)PS{Q}^T+Q{S}^{T}P(A_i+A_j{)}^T+(B_i{X}_j+B_j{X}_i)S{Q}^T+QS{\hspace{0.17em}}_{\hspace{0.17em}}^T(B_i{X}_j+B_j{X}_i{)}^T-E_{i}P{E}_j^T-E_{j}P{E}_i^T,$

the matrix $S\in R^{n\times (n-m)}$ satisfying $E_{i}PS=0$, $\mathrm{\forall }i$, is of full-column rank. Then, a set of admissibilizing state feedback gains with D-admissibility $\alpha <1$ in (9) can be determined as $K_j=X_j{P}^{-1}$, $\mathrm{\forall }j$.

Proof:

Based on Lemma 2 and following the same line in Theorem 2, the proof can be similarly attained.

Remark 2: In contraction to the previous result in (Huang, 2014), the proposed new design approach in Theorem 2 can provide more searchable parameters’ dimensions in $X_j$ , $\mathrm{\forall }j$, which is helpful to attain a set of feasible gains of $K_j=X_j{P}^{-1}$ for the closed-loop DFSs (10). Furthermore, the new result can severely reduce the LMIs’ constraints from $(r+C_r^2{)}^2$ to $(r+C_r^2)$.

Remark 3: For coping with the multiple difference term $E_i$, the previous work (Qiao, Li, and Lu 2021) has to transfer the primitive system to an augment system model with a common E with extended dimensions, where the augment system not only may loose some physical behaviors in connection with the original system but also need to satisfy some extra constraints. Furthermore, the LMIs’ constraints reach a large number $r+2r^2+(r+1)C_r^2$, which may cause the handicap to implement a feasible controller for the considered system with numerous rules.

Remark 4. For comparing with some other works (Huang 2005; Xu, Song, Lu, and Lam 2007; Li, Shi, Wu, and Zhang 2014; Kchaou and El-Hajjaji 2017; Chen and Yu 2021; Chen, Yu, and Jam 2022), they cannot directly deal with the considered systems embracing multiple difference matrices, or need to put some extra restriction on $E_i$ and transfer the original system to a new system with a common E. However, by the developed design method in Theorem 2 and Theorem 3, we not only can directly cope the considered system with multiple difference terms $E_i$ but also competently cope with the controller design with admissibility and D-admissibility issues. Furthermore, the proposed design conditions in Eq (11(11) $\left[\begin{array}{cc}{\mathrm{\Psi }}_1& A_{i}P+B_i{X}_i\\ P{A}_i^T+X_i^T{B}_i^T& -P\end{array}\right]<0,\mathrm{\forall }i,$(11) )-(14(14) $\left[\begin{array}{cc}{\mathrm{\Psi }}_2& (A_i+A_j)P+B_i{X}_j+B_j{X}_i\\ P{(A_i+A_j)}^T+X_j^T{B}_i^T+X_i^T{B}_j^T& -2{\alpha }^{2}P\end{array}\right]<0,\mathrm{\forall }i<j,$(14) ) all are formulated by the strict LMIs, where we can facilitate evaluating them via the existing LMI solvers for implementing the fuzzy systems with PDC control.

Illustrative Examples

For Verifying the Applicability of the Developed Results, We Give Two Illustrative Examples in the Following.

Example 1:

Consider the DFSs (1) with free input with a five fuzzy rules and three order singular models. The systems’ matrices are denoted as

$\begin{array}{rl}& E_1=\left[\begin{array}{ccc}1& 0& 1\\ 0& 1& 0\\ 0& 0& 0\end{array}\right],E_2=\left[\begin{array}{ccc}1& 0& 1\\ 1& 1& 0\\ 0& 0& 0\end{array}\right],E_3=\left[\begin{array}{ccc}1& 0& 2\\ 0& 1& 0\\ 0& 0& 0\end{array}\right],E_4=\left[\begin{array}{ccc}1& 0& 1\\ 2& 1& 0\\ 0& 0& 0\end{array}\right],E_5=\left[\begin{array}{ccc}1& 0& 2\\ 0& 2& 0\\ 0& 0& 0\end{array}\right]\\ & A_1=\left[\begin{array}{ccc}-1& 1& 0\\ -1& -0.4& 0.3\\ 0& -0.3& 0.2\end{array}\right],A_2=\left[\begin{array}{ccc}0.7& -0.5& 0\\ 1& 0.8& 1\\ 0.4& 0.3& 0.6\end{array}\right],A_3=\left[\begin{array}{ccc}0.8& 0.6& -1\\ -0.2& 0.4& 0.6\\ -0.7& 0.5& 0.5\end{array}\right]\\ & A_4=\left[\begin{array}{ccc}0.4& -0.3& 0.2\\ 0.5& 0.3& 1\\ 0.3& 0.4& 0.5\end{array}\right],A_5=\left[\begin{array}{ccc}1& -0.5& 0\\ -0.4& -1& 0.5\\ 0.3& -1& 0.6\end{array}\right].\end{array}$

Due to the considered DFSs embraces the distinct difference terms $E_i$ in the rules, some previous results with common difference terms are inapplicable (Huang 2005; Xu, Song, Lu, and Lam 2007; Li, Shi, Wu, and Zhang 2014; Kchaou and El-Hajjaji 2017; Chen and Yu 2021; Chen, Yu, and Jam 2022). Since the integrating difference matrices’ term is insufficient rank and cannot satisfy the prescribed form $E_i=Q_{i}E$, the previous result (Qiao, Li, and Lu 2021) also cannot be applicable. Furthermore, by the previous result in Theorem 1 (Huang 2014), we denote a matrix $S={\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}^T$ satisfying $E_i^{T}S=0$, $\mathrm{\forall }i$, and construct a set of LMIs according to Theorem 1. By hiring the current LMI solver (Gahinet, Nemirovski, Jaub, and Chilali 1995) for verification, we cannot attain a set of feasible solutions.

However, from Theorem 1 with a given matrix $S={\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}^T$ satisfying $E_i^{T}S=0$, $\mathrm{\forall }i$, we can construct fifteen LMI constraints by Eq (6(6) $A_i^{T}P{A}_j+A_j^{T}P{A}_i-E_i^{T}P{E}_j-E_j^{T}P{E}_i+A_i^{T}S{Q}_j^T+Q_j{S}^T{A}_i+A_j^{T}S{Q}_i^T+Q_i{S}^T{A}_j<0\mathrm{\forall }i\le j,i,j=1,\hspace{0.17em}2,\hspace{0.17em}\dots ,r$(6) ). By hiring the LMI solver for verification, a set of feasible solutions can be attained as

$P=\left[\begin{array}{ccc}7.4742& 9.5031& 8.7931\\ 9.5031& 18.7877& 23.5037\\ 8.7931& 23.5037& 67.0064\end{array}\right]\times {10}^{-1}>0,$

$Q_1=\left[\begin{array}{c}3.2041\\ -1.9406\\ -0.9908\end{array}\right],Q_2=\left[\begin{array}{c}3.3649\\ -7.9282\\ -3.5648\end{array}\right],Q_3=\left[\begin{array}{c}5.8484\\ -5.0914\\ -3.3251\end{array}\right],Q_4=\left[\begin{array}{c}1.9990\\ -8.9949\\ -5.3552\end{array}\right],Q_5=\left[\begin{array}{c}1.9537\\ 0.9761\\ -0.6783\end{array}\right]$

Thus, the considered system is ensured to be admissible according to Theorem 1.

Example 2:

Consider a two rules fuzzy control system together with three order singular model as

Rule 1: If $x_1(k)$ is $F_1^{\hspace{0.17em}}$

Then $E_{1}x(k+1)=A_{1}x(k)+B_{1}u(k)$,

Rule 2: If $x_1(k)$ is $F_2^{\hspace{0.17em}}$

Then $E_{2}x(k+1)=A_{2}x(k)+B_{2}u(k)$,

where $F_1^{\hspace{0.17em}}$and $F_2^{\hspace{0.17em}}$ are given membership functions, shown in Figure 1. The systems’ matrices in each rules can be individual depicted as

$\begin{array}{rl}& E_1=\left[\begin{array}{ccc}1& 1& 0\\ 0& 2& 0\\ 0& 0& 0\end{array}\right],E_2=\left[\begin{array}{ccc}2& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array}\right],\\ & A_1=\left[\begin{array}{ccc}1& 1& 0.5\\ 0.5& 1.5& 0.4\\ -1& 0.5& 1\end{array}\right],A_2=\left[\begin{array}{ccc}-1& -1& 1\\ -1& -1& 0.5\\ 0.5& 0.7& 1\end{array}\right],B_1=\left[\begin{array}{c}1\\ 1\\ 0\end{array}\right],B_2=\left[\begin{array}{c}1\\ 2\\ 0\end{array}\right]\end{array}$

Figure 1. Membership functions $F_1$ and $F_2$ of example 2.

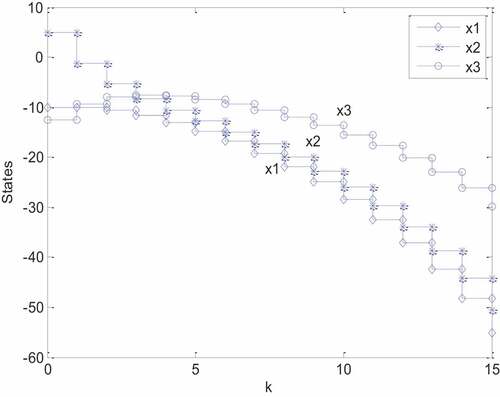
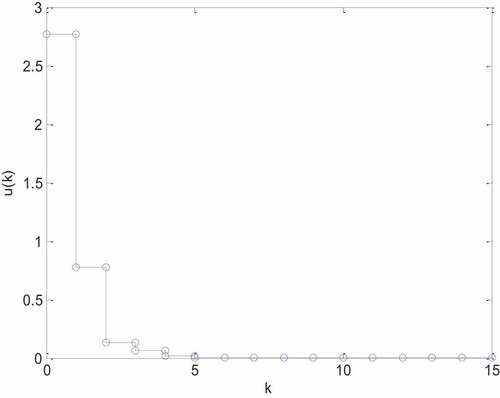
In this example, the free input system, that is, the system with $u(t)=0$, is unstable. When given an initial condition $x(0)=[\begin{array}{ccc}-10& 5& -12.5\end{array}{]}^T$, we firstly simulate the unforced system. The states’ behaviors are depicted in Figure 2. It’s show that the original system with free input is unstable, and a controller need to be involved. Since the considered system embraces multiple difference matrices $E_i$, some existing results (Huang 2005; Xu, Song, Lu, and Lam 2007; Li, Shi, Wu, and Zhang 2014; Kchaou and El-Hajjaji 2017; Chen and Yu 2021; Qiao, Li, and Lu 2021; Chen, Yu, and Jam 2022) cannot be applicable for systematically conducting the PDC control. Furthermore, by the previous result in Theorem 3 (Huang 2014), we can form a set of LMIs with a matrix $S={\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}^T$ satisfying $E_{i}S=0$. But, from the LMI solver for evaluating the parameters’ intervals $a_1\in \left[-10,10\right]$ and $a_2\in \left[-10,10\right]$, we cannot acquire existing feasible solutions.

Figure 2. States’ responses with free input of example 2.

However, based on Theorem 2 for controller design object, we then construct three LMIs’ constraints by (11) and (12) and denote $S={\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}^T$, $Q={\left[\begin{array}{ccc}-1& -1& -1\end{array}\right]}^T$, and

$P=\left[\begin{array}{cc}{P}_1& 0\\ 0& P_3\end{array}\right],$

where LMI variables P with $P_1\in R^{2\times 2}$, $P_3\in R^{1\times 1}$ satisfying $E_{i}PS=0$, $\mathrm{\forall }i$. By the LMI solver for evaluating, a set of feasible solutions thus are obtained as

$P=\left[\begin{array}{ccc}24.5760& -0.5987& 0\\ -0.5987& 47.8118& 0\\ 0& 0& 373.7504\end{array}\right]\times {10}^{-2}>0,$

$X_1=\left[\begin{array}{ccc}-21.4154& -5.7502& 99.4576\end{array}\right]\times {10}^{-2},$

$X_2=\left[\begin{array}{ccc}32.0670& 36.9098& 110.5853\end{array}\right]\times {10}^{-2}.$

And, the admissible PDC gains can be determined by

$K_1=X_1{P}^{-1}=\left[\begin{array}{ccc}-0.8746& -0.1312& 0.2661\end{array}\right],$

$K_2=X_2{P}^{-1}=\left[\begin{array}{ccc}1.3240& 0.7886& 0.2959\end{array}\right].$

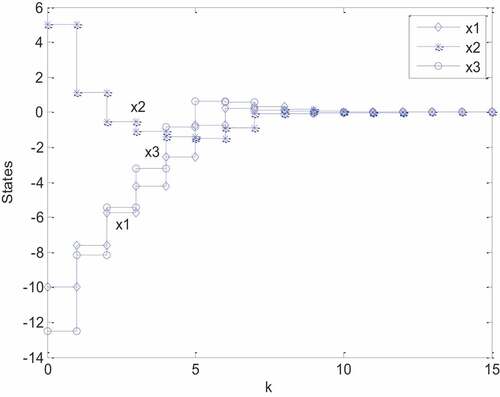
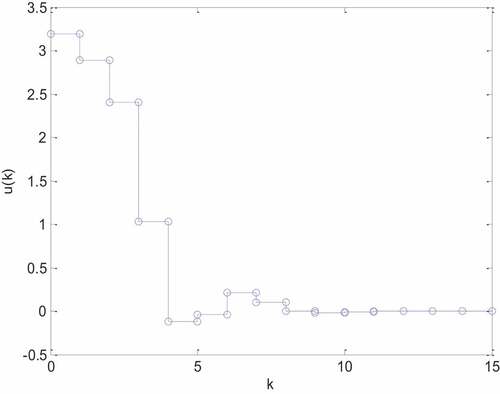
By the identical initial condition $x(0)=[\begin{array}{ccc}-10& 5& -12.5\end{array}{]}^T$, the considered system equipped with the PDC control with admissible assurance is simulated again. The states’ responses $x(k)$ and the input signal $u(k)$ are depicted in Figures 3 and 4, respectively. By observing on Figure 3, it shows that all the states’ trajectories have well convergent behaviors. According to Theorem 2 and the simulation result, the considered system associated with PDC control law are experimentally demonstrated to be admissible.

Figure 3. States’ responses by PDC control with admissibility of example 2.

Figure 4. The control input trajectory with admissibility of example 2.

Furthermore, in practical control system, we need to implement the control law to satisfy some specific performance requirements. Based on Theorem 3, we can implement the PDC control law with D-admissibility for specific stability performance. Thus, by Theorem 3 for PDC control with D-admissibility ($\alpha =0.6$), we can construct three LMIs’ constraints by (13) and (14). Let $S={\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}^T$, $Q={\left[\begin{array}{ccc}-1& -1& -1\end{array}\right]}^T\times {10}^1$, and

$P=\left[\begin{array}{cc}{P}_1& 0\\ 0& P_3\end{array}\right],$

where LMI variables P with $P_1\in R^{2\times 2}$, $P_3\in R^{1\times 1}$ satisfying $E_{i}PS=0$, $\mathrm{\forall }i$. By the LMI solver for evaluating, a set of feasible solutions can be attained as

$P=\left[\begin{array}{ccc}3.3070& -1.7737& 0\\ -1.7737& 6.4219& 0\\ 0& 0& 5.4931\end{array}\right]\times {10}^4>0,$

$X_1=\left[\begin{array}{ccc}-4.7809& 1.9445& 1.6161\end{array}\right]\times {10}^4,$

$X_2=\left[\begin{array}{ccc}1.7288& 4.3142& 0.9940\end{array}\right]\times {10}^4.$

And, the PDC gains with D-admissible assurance ($\alpha =0.6$) can be determined by

$K_1=X_1{P}^{-1}=\left[\begin{array}{ccc}-1.5065& -0.1133& 0.2942\end{array}\right],$

$K_2=X_2{P}^{-1}=\left[\begin{array}{ccc}1.0366& 0.9581& 0.1810\end{array}\right].$

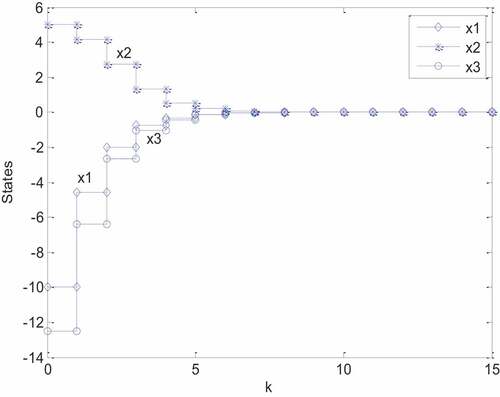
For comparison, the considered system equipped with the PDC control satisfying the D-admissibility ($\alpha =0.6$) is simulated once more. The states’ responses $x(k)$ and the input signal $u(k)$ are individually depicted in Figures 5 and 6. By observing on Figure 5, it reveals that the states’ trajectories with D-admissibility ($\alpha =0.6$) have more swiftly convergent behaviors than those with admissibility.

Figure 5. States’ responses by PDC control with D-admissibility ($\alpha =0.6$) of example 2.

Figure 6. The control input trajectory with D-admissibility ($\alpha =0.6$) of example 2.

Conclusions

In this study, we have coped with the admissible analysis and the PDC control for DFSs subjected to multiple difference matrices. Based on the matrix manipulation and the LMI technique, we first proposed the refined admissible analysis criteria, where the developed conditions not only involved some slack matrices but also severely reduced the number of LMIs’ constraints, where they both may be beneficial to reduce the conservatism of the analysis criteria. Moreover, by involving the fuzzy PDC control, the explicit design criteria were further presented for the resulting closed-loop system. Noticeably, the new design method can treat controller design with admissibility and D-admissibility for the regarded systems. Due to all the presented conditions were formed by the strict LMIs, they could directly be evaluated via the LMI solver. Finally, the illustrative examples were hired to demonstrate the efficiency and applicability of the proposed methods. Nevertheless, in many physical systems, state’s delays are inevitably needed to be embraced. Future work will dedicate to the analysis and design methods by simultaneously involving the state’s delays and uncertainties.

Disclosure statement

No potential conflict of interest was reported by the author(s).