Analyses of coarse graining procedure for mesoscale simulation

Abstract

In order to meet great progress in multi-scale modelling, one of the important issues is to know about detailed process of coarse graining. The coarse graining is a standard technique of statistical mechanics to extract specific degree(s) of freedom from a many component system. Many kinds of coarse-graining simulation methods have already been proposed. Because most of them were constructed based on a priori assumptions, making detailed analyses has been difficult from the microscopic points of view. Recently, a generalised coarse-grained (CG) equation of motion has been reported for many particle centre of mass systems straightforwardly derived from the explicit information about all the degrees of freedom at the microscopic level. This equation is mostly exact for the dynamics of CG particles defined in classical many particle systems. Therefore, making discussions about characteristics of this CG equation of motion is useful for obtaining detailed knowledge on the coarse graining from the microscopic points of view. In the present article, a review on recent discussions about characteristics of this generalised CG equation of motion is given. Previous conventional coarse-graining particle dynamics simulations can be categorised as some special cases. Generalisation, confirmation and progress of the fundamental knowledge of coarse graining are partly realised from the present discussions.

Keywords:

• coarse graining
• equation of motion
• molecular assembly
• projection operation of molecular motions
• particle dynamics simulation

1. Introduction

One of the most important bases for realising multi-scale modelling containing many particle expressions is a construction of a coarse-grained (CG) equation of motion having explicit relation with bare expressions at a finer level in the system. In the case that the coarser expression can be sufficiently described via equations having some parameters expressing finer level properties, the finer level equation of motion can be solved to just deduce such parameters. No explicit relation between coarser and finer level equations is required in such a case. At a point or on an area in the space expressed at the coarser scale, properties at a finer level must be completely expressed by statistically averaged ones. In other words, the coarser level in multi-scale expression must be constructed by points or areas having complete homogeneous properties. This restriction makes a wide gap between coarser and finer levels in a multi-scale modelling in general.

The equation of motion for the CG particles was derived via the projection operator method by several authors 1-5. The essential idea of coarse graining was that the total molecules were divided into groups of molecules (or clusters), and each molecular group was regarded as a CG particle. To derive the equation of motion for the CG particles, we introduced the projection operator [4] and applied to divide the Liouville equation for the phase space density for CG particles. In the recent publication by the present author's group [5], the derived expression was found to be constructed from the mean force, the friction force and the microscopic fluctuating force terms. In the next section, the explicit expression is given as Equation (8), with a brief explanation of its derivation. The resultant CG equation of motion has similar form to the generalised Langevin equations, but has explicit relationship with the information at the finer level in a multi-scale expression. We can, therefore, deduce all the terms in the resultant CG equation of motion via particle dynamics method at the finer level as molecular dynamics simulation. The mean forces for simple Lennard-Jones fluids via molecular dynamics simulations were calculated with the holonomic constraints, and the universality of the calculated mean forces was confirmed in these systems [6]. By analysing the fluctuating force term, we also derived correspondences of the present CG equation of motion to conventional CG particle dynamics methods, i.e. Brownian dynamics (BD) and dissipative particle dynamics (DPD), [5]. The difference in these simulation methods was found to appear in a characteristic of the model of the random force on an identical basis. We can conclude that the present CG equation of motion has some availability to describe explicit relations between coarser and finer levels in multi-scale modelling and generality.

The projection operator method is known as a useful tool for coarse graining as an elimination of fast variables 1-3. Although a general formulation is given for the coarse graining by the projection operator, there seems to be a lack of linkage between these formulations and conventional coarse-graining simulation methods. Kampen and Oppenheim [7] derived the equation for Brownian motion for single Brownian particle from first principles. CG equations for single chain in polymer melt [8], a 1D harmonic chain [9] and 3D harmonic lattices [10] were also derived using the projection operator method. These derivations are for specific systems and a part of them focus on a local system without explicit information on the correlation between different CG particles. Although these previous investigations give physically meaningful information on some explicit systems, further investigations based on a general formula of CG equation of motion are still needed.

Some comments on the characteristics of the resultant CG equation of motion can be found in reference [5]. They were rather restricted within that related to showing correspondences to the conventional coarse-graining simulation methods. In this paper, further remarks are provided, especially on analyses of the equation of motion as a generalised Langevin equation. Brief introductions for the derivation and the basic characteristics of the present CG equation of motion are reviewed in the next section. Reading the fluctuating force term as a random force term, we can see that the resultant equation of motion corresponds to a generalised Langevin equation, of which analyses have been mostly restricted to the system having periodic external forces [11]. After a brief introduction, we make several remarks in a more general sense rather than the point of view adopted in the previous contributions [5,6]. The discussion will be related to a generalised Langevin equation, the comparison of the determination procedure of the mean force with the conventional CG method, the role of friction and fluctuating force terms in conventional coarse-graining simulations, an extension to coarse-graining for arbitrary degrees of freedom (DOFs) and coarse-graining dynamics described by continuous distribution functions as another candidate. The aim of the present paper is to give basic information about the resultant CG equation of motion in more detail through reviewing and discussing the above several topics.

2. Outline for derivation of the present CG equation of motion

In this section, the derivation of the present CG equation of motion via the projection operator method is briefly reviewed. Details of the derivation are given in reference [5]. The idea of coarse graining adopted here is to divide the total N _t molecules into N groups (or clusters) which consist of n _α molecules, and regard a molecular group as a CG particle. For classical systems, trajectories of the total phase variables are determined completely by Hamilton's equation of motion, where and are the position and the momentum of a molecule i of α-th CG particle, respectively. If the full atomistic information is not required, we may use a description of the system by coordinates and momenta of the centre of mass (COM) of the CG particles. The phase space density for these variables is as follows:

where and are the position and momentum of the COM, respectively, is a phase point in the phase space of the COM, is a ‘relevant field variable’ [4,12] and is the Dirac's delta function. The phase space of the atomistic coordinates and the COM coordinates are referred to as Γ-space and Γ _s -space, respectively. The time evolution of along the trajectory in the Γ-space is written as

In this form, the Liouville operator in the Γ _s -space is defined as

where

is the sum of the forces acting on atoms belonging to the CG particle α. Here, U is the potential energy of the total system described in the Γ-space.

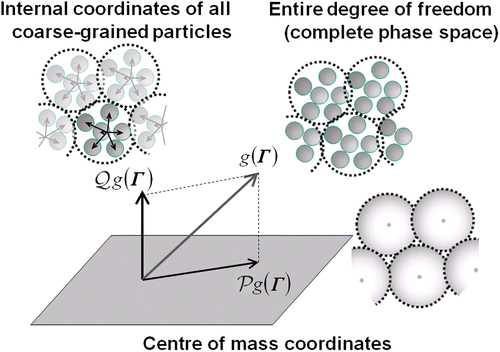
Figure 1 shows a schematic view of the present projection operation. An arbitrary configuration in the N _t molecule system can be defined at a point in the entire phase space of Γ. The Γ _s -space of CG particles' COM variables is a partial phase space in Γ, and the shadow of an arbitrary function in Γ can be defined by a projection operation onto the Γ _S -space. Trajectories of every possible configuration in the entire phase space can be monitored through the movements on the COM phase space (Γ _s -space). The probability to find the state at an arbitrary point on the COM phase space should depend on the number of the density of states having the same COM configurations. The projection operator 𝒫 of a phase function onto the Γ _S -space is in the form [4,12]:

Here, the assumption that the parts of a phase function out of the Γ _S -space, , are orthogonal to ‘basis functions’ defined in the Γ _S -space made to derive Equation (5). The right-hand side of Equation (2) of time evolution was divided by 𝒫 and , where I is the identity operator

Note that 𝒫 is the projection onto a functional space which consists of the ‘basis functions’ f _S at time t. Straightforward arithmetic yields the time evolution equation for the phase space density f _S (t). The result is in the form [5]

where , and are the frequency matrix, the memory function and the generalised fluctuating force, respectively.

Figure 1 Schematic view of projection operation (𝒫) of an arbitrary function g(Γ), which is defined in the entire phase space Γ onto the COM phase space.

The equation of motion for the CG particles is obtained by integration of Equation (7) with multiplying P _σ

where

and β = 1/k _B T (k _B, Boltzmann constant, T, absolute temperature). denotes an average with fixed Γ _s . In the above equations, we use notations and . In the CG equation of motion (8), the first, second and third terms of the right-hand side are the mean force, friction force and fluctuating force, respectively.

In the case where the effective mean force term is zero, the formula corresponds to the standard Langevin equation but includes correlation between fluctuating forces in different CG particles. The inclusion of such a correlation is capable of maintaining the effects such as the so-called hydrodynamic correlations in dynamics of Brownian particles, because all the correlations between every microscopic particle can be basically expressed in this term. Note that randomness still has not been introduced here onto fluctuating force term. Importance of hydrodynamic effects on polymer solution was studied [13,14] as an extension of Rouse model [15], which is a famous fundamental theoretical basis on investigation of polymer solutions. Equation (8) includes the correlation between microscopic particles even though the mean force term is assumed to be zero; therefore, it can be an extension to dynamics in polymer solutions with a general formulation. Schweizer's theory on dynamics in polymer solutions [4] was derived via the projection operator method as the present treatment. The theory corresponds to the case without effective mean force and focuses on dynamics within a region of one CG polymer. It can be assigned as a generalised extensive theory of Rouse model to investigate microscopic dynamics in a CG environment. Because the focused DOF is different from Equation (8), it is accepted as another type of the generalised Langevin equations.

3. Remarks on Equation (8) as a stochastic equation

The second term of Equation (8) is expressed as proportional to velocity and inverse to kinetic energy (k _B T) with the temporal correlation function of fluctuating forces. This can be acceptable as friction force term and seems to naturally correspond to generalised relation of the fluctuation–dissipation theorem. Although the fluctuating force of is random as in standard description is not necessary, this term formally shows a similar relation with the fluctuation–dissipation theorem. This characteristic would support an expectation that Equation (8), and other expressions derived from it, could naturally satisfy the fluctuation–dissipation theorem. Explicit commentary can be found in the previous paper on the correspondence to BD and DPD [5]. The point about the second term of Equation (8) would be discussed in more detail later.

A standard procedure on the analysis of equation of motion for a CG particle is started from phenomenological introduction of a friction force, which is proportional to the mass and the velocity of the particle under consideration, and a random force, which has no explicit correlation with the motion of the particle, into the Newtonian equation of motion of the CG particle:

where m is the mass of the CG particle, u is the velocity of the CG particle, t is the time, F is the force acting on the CG particle, γ is the friction coefficient and is the random force acting on the CG particle at time t. Here, γ is just introduced as a coefficient of m and u in the expression of the friction force. Depending on the system under consideration, the external force as gravity force or elastic force is frequently added to the equation of motion (11). This type of equation is called the Langevin equation and is a typical model of the stochastic differential equations.

Fourier transformations of u and ℛ teach us the relation between γ and ℛ which satisfies the equation of motion (11). After applying Wiener–Khinchin's theorem to the Fourier transformed formula of Equation (11), we can find the relation

where the time-scale on varying is assumed to be sufficiently faster than that of u (t) as a stochastic process. This relation is a kind of the fluctuation–dissipation theorem. Because the friction coefficient γ and the random force are phenomenologically introduced in Equation (11), the relation of the fluctuation–dissipation theorem (12) must be required for γ and after making definitions or modelling about them.

On the other hand, Equation (8) naturally satisfies the fluctuation–dissipation theorem in its derivation. When we either calculate based on atomistic processes via Equations (4) and (10) or assume some process on fluctuating forces, the fluctuation–dissipation theorem can be satisfied as long as Equation (8) is adopted. Because only one assumption, which is described just after Equation (5), is made in the derivation of Equation (8), there is no restriction in the application of the present CG equation of motion even in different in time-scales. The origin of the fluctuation–dissipation theorem is the energy or momentum exchange between different microscopic particles. It is understandable that the energy dissipation processes, which originate from microscopic inter-particle interactions, are naturally included in the description of Equation (8). Defining random forces that are assigned to each CG particle or to each pair of CG particles and substituting them to the fluctuating force term, we can find the correspondences of Equation (8) to the conventional CG simulation methods such as BD or DPD, respectively. In their foundations of BD and DPD, the fluctuation–dissipation theorem was introduced as a requirement to keep the proper condition in statistical systems. Contrary to this situation, the fluctuation–dissipation theorem is naturally satisfied in Equation (8), and it is not necessary to introduce it as an a priori requirement. The equipartition law of energy is also expected at thermal equilibrium condition here.

The second term of Equation (8) is actually not exactly identical to the friction term of the standard Langevin Equation (11). The formula of this term is expressed by a temporal integration to reflect all the previous processes occurring before time t. This means that Equation (8) is applicable also to non-Markovian processes. This fact is easily understood because no assumption is made in the derivation of Equation (8), besides that there is no statistical correlation between physical properties defined in and out of Γ _S -space. This assumption does not restrict the time-scales of varying to be faster than those of u (t). This type of equation of motion is called as the generalised Langevin equation, which was originally introduced by Mori for general cases [1]. Following the Mori's theory, many interesting investigations were reported, especially, on the analyses of molecular spectra related to dynamics of molecules in homogeneous condensed phases [16,17]. Experimental spectral intensities, band widths and/or band shapes were analysed according to Mori's theory to relate to intermolecular interactions and/or dynamics of molecules in condensed phases. Most of them were based on some phenomenological assumption to describe time-correlation functions of molecular properties. Contrary to such progresses in applications of Mori's theory, Equation (8) can be understood as a more definite formulation to perform explicit simulations for dynamics of COMs of CG particles without a priori assumptions.

4. On the determination of mean force term

The equation of motion for CG particles, Equation (8), has a similar formula to the standard Langevin-type equation having an external force term. Here, the external force should be considered as the mean force acting on a CG particle under every possible configuration of microscopic particles. Equation (9) assures the existence of an explicit procedure for reproducing such CG mean forces based on detailed microscopic expression. In order to make quantitative analyses, however, it is needed to assume some explicit formula of inter-particle potential at the microscopic level. Therefore, a distinct discussion may depend on a practical choice of microscopic interaction potential.

The DPD is estimated as one useful simulation technique to reproduce mesoscale structure formations. Simultaneously, several artefacts were also indicated on its temporal development and were ascribed to the nature of assemblies constructed by soft repulsive potentials 18-20. Several methods to overcome the artefacts originating from time integration have been recently proposed 21-23. The equation of motion of the DPD was found as a special case of Equation (11) with mean force term or Equation (8) for the case in which the fluctuation forces damp much faster than the movements of CG particles [5]. For the DPD, the correlation of randomness in the fluctuating force must be modelled as pairwise and the fluctuation–dissipation theorem be adopted to its equation of motion. Therefore, more fundamental discussions about the characteristics of the mean force could be made based on the general formula of the CG equation of motion. The mean force is commonly called the conservative force in the description of the DPD.

The Groot and Warren procedure [24] is one of the standard procedures of the DPD simulations. The interaction parameter of each DPD particle can be constructed by interatomic interaction parameters based on explicit molecular structures. According to the Groot and Warren procedure, the cohesive energy between two DPD particles derived via atomistic simulations should be mapped onto the relation between the Flory–Huggins χ-parameters and the conservative force parameters of DPD, which are calculated beforehand using hypothetical DPD simulations. Such an indirect way of determination of the mean force parameters seems to be unavoidable because the equation of motion of DPD is not constructed based on microscopic point of view. Equation (9), on the other hand, informs us of an existence of direct procedure to determine the mean force parameters based on microscopic points of view.

Because the mean force depends on the COM coordinates {R _α}, it is a multi-body force expressed in the COM coordinates. In the particle-based simulation, calculation of multi-body forces is very time consuming; therefore, effective two-body forces are usually adopted. In this context, we assumed that the mean force is decomposed to pairwise additive terms as follows:

where

is a statistical average with fixed R _ασ . With this assumption, we can calculate the mean force directly by molecular dynamics or Monte Carlo simulation. To estimate the mean force, we employed the constraints that the square of the distance between each microscopic particle and the COM of the corresponding CG particle and that between two different CG particles be constant. The mean forces for simple Lennard-Jones fluids were calculated via molecular dynamics simulations with the holonomic constraints [6]. The results of these calculations showed the mean forces have each peaked at some distance and did not diverge even in closer distance. This softness of potential mean forces is quite different from interatomic forces, which have a hard repulsive core. We also found the universality of the calculated mean forces in these systems by introducing a scale transformation based on the number of microscopic particles and the gyration radius of each CG particle. Of course, it is necessary to take a sufficiently large number of sampling to meet a sufficient statistics, but such a direct estimation is effective to keep accuracy, despite the procedure with additional time-consuming simulations. We found that the mean forces, estimated via the present procedure for simple Lennard-Jones fluid, have each peaked at some distance and do not diverge even in closer distances. This result is comparable to, though somewhat different from the conventional conservative force term of the DPD. On the basis of the above and the previously reported more detailed discussion [6], it can be said that the definition of Equation (14) is useful to confirm the determination procedure of the mean force terms, even in a conventional coarse-graining dynamics simulation.

5. Requirement of friction and fluctuating force terms for general coarse-graining simulations

In contrast to the above discussions, coarse-graining simulations only using mean force terms are frequently adopted to investigate condensed systems with large number of molecules, such as a rigid molecule model or the united atom model [25]. Such treatments can omit tracing faster varying DOF in simulation of the system which contains several DOFs with different time-scales. This is useful to keep computation time reasonable for large and complicate systems. A justification for using only mean force term is based on the expectation that higher frequency mode does not affect the statistically most probable processes of dynamics in such systems. Considering the fact that the Brownian particle can be moved by higher frequency modes of light particles, however, it is easy to find that such an expectation is not fulfilled for proper stochastic processes. For the case in which the dynamics is following a very simple reaction coordinate or that around near equilibrium configuration, the final results obtained by dynamics simulations with and without the friction and fluctuating terms might be identical to each other. In such cases, the explicit processes on dynamics are not important to find equilibrium configurations. For the cases of very complicated potential energy surfaces, the situation must be different. An explicit equation of motion for arbitrary DOFs in many CG particle systems is analysed and discussed in the next section.

It has been reported that introducing a Langevin-type thermostat is effective to keep the simulations with larger time intervals stable [26]. Most of thermostats in molecular dynamics techniques are based on introducing implicit DOF as the reservoir of energy dissipation to keep the kinetic energy constant [27]. Equation (8) is mostly exact and contains not only the dissipative (friction) but also fluctuating force terms. Introducing only the dissipative part seems to be unbalanced; therefore, it might be rather difficult to keep stabilities of the system. Successive results of Langevin-type thermostats can be accepted following this consideration.

Based on the above two points of discussions, we can see that both the friction and fluctuating force terms are required for general coarse-graining dynamics simulations. Indeed, the united atom model was augmented by phenomenologically introducing the DPD model as a Langevin type thermostat to describe the diffusion properties of bulk water [28]. By comparison with the united atom model without the thermostat and SPC (simple point charge) model, the united atom model with a DPD thermostat was found to reproduce well the proper results by the SPC model, while the original united atom model showed a result significantly different from that of SPC water. Since the friction and fluctuating terms were introduced into the united atom model in a phenomenological way, the effects of coarsening explicit molecular structures should be analysed in more detail. By treating the effects of molecular structures as dividing all the DOF of the molecule, a coarse-graining equation of motion for molecular assembly systems is analysed in the next section.

6. Coarse-graining for arbitrary degrees of freedom

Although the Langevin equation can be derived from an atomistic equation of motion, most of these derivations are limited within the equation of COM motions. A microscopic description for arbitrarily extracted DOF should be, therefore, obtained. In order to describe internal DOFs for each CG particle, the system should be restricted to an assembly of CG particles constructed by tightly bounded finer particles, such as polyatomic molecules. The derived equation of motion must have applicability to dynamics simulation of reorientational and/or internal vibrational motions of CG-particle systems by analyses of the equation for realistic conditions.

On the basis of the well-known analyses for the molecular theory of infrared and Raman spectra, we can express the total Hamiltonian of an isolated molecule by summation of COM motion, rotation (ROT), internal vibration (VIB) and VIB–ROT interaction terms [29,30]. As usually assumed, the VIB–ROT interaction term of a molecular Hamiltonian can be omitted if the amplitudes of internal vibrational modes are small enough so that angular velocity can be treated constant along with the internal vibrational motions. Under such an approximation, the Hamiltonian of an isolated molecule can be separately expressed by terms of the COM motion, the pure ROT and the individual internal VIBs. Such an expression of Hamiltonian could be accepted as a basic one to begin an analysis of more complicate problems. According to this approximate Hamiltonian, the Liouville operator can be also expressed by summation of each corresponding term.

The total Hamiltonian of a molecular assembly should be the summation of the isolated molecule Hamiltonians of component molecules and inter-atomic potentials between atoms (i and j) belonging to different molecules. Here, each DOF can be separately extracted from the other DOFs in the identical molecule and correlates to every DOF in the other molecules through the inter-atomic potential. The Liouville operator of the entire system is

where the contributions of COM motion, ROT and internal VIB in the Liouville operator of each molecule are indicated by the superscripts COM, ROT and VIB, respectively. R _Cξ is the position of the COM of molecule ξ, P _Cξ is the momentum of the COM of molecule ξ, Θ _ξη is the angular displacement along with direction η (η = x, y or z of Cartesian coordinate), J _ξη is the angular momentum corresponding to Θ _ξη , Q _k is k-th normal coordinate for expressing molecular internal VIBs and P _k is the momentum corresponding to Q _k . The phase space density for the entire system is a product of densities of all individual phase variables:

Here, the subscripts of and Γ in the last row of Equation (16) indicate that the variables are separately expressed by each component, i.e. COM motion, ROT and internal VIB.

Following the procedure for deriving the CG equation of motion, Equation (8), we can obtain the expression of the time evolution of phase space density defined on the partial phase space Ω, which is expanded by DOFs that are chosen for arbitrary ones. Multiplying a suitable term of momentum to this, we derived a general form of the time evolution of the phase space density on Ω [31] as

where is the momentum with respect to a DOF X _ξ of molecule ξ and is a generalised mass of inertia corresponding to the moment of inertia of rotational motion, the effective mass of the entire molecule or that of internal VIBs. Equation (8) has a term containing a summation over fluctuating forces acting on all CG particles, which corresponds to the second term in the right-hand side of Equation (17). By dividing the Liouville operator by orthogonal variables and collecting the corresponding terms, such terms of cross correlations in fluctuating forces at different points vanished in the present formulation. is one of the first three terms in Equation (15) which corresponds to tagged DOF X _ξ of molecule ξ. is defined by the triple summation in Equation (15) and it does not affect the forces, because the operations are respect to momentum onto the functions of positions. Therefore, the later equality in Equation (19) of fluctuating force is fulfilled.

It would be very useful if the resultant equation of motion, Equation (17), have a form in which some specific DOFs can be naturally extracted from the other ones. Such a characteristic is very appropriate for temporally wide-range dynamics simulations of complicated molecular assembly systems. Analyses reported here were mostly concentrated in the roles of internal VIBs acting as fluctuating forces. Higher frequency modes can be omitted from explicit treatments but without complete extinguishment of their information, via the present expression of CG equation of motion.

Incidentally, it is well known that the ROT and internal VIBs are strongly coupled in a free rotor having internal DOFs. The centrifugal distortion occurs so as to change the equilibrium positions in a steadily rotating coordinate system. The Coriolis force also appears as the origin of distortion of internal vibrational motions. Considering these facts, we can naturally understand that the rotational and internal vibrational motions cannot be separated in steadily rotating systems. Indeed the centrifugal distortion constant and Coriolis force constant are important properties that characterise the dynamical structure of small molecules [29,30]. To turn our notice to the condensed systems, on the other hand, the steady ROT cannot hold even in a cycle of rotational motion because of the frequent collisions among neighbouring molecules. Description by reorientation or libration seems to be more natural in this situation rather than the combination of the steadily rotational motions.

Order estimation of the contribution of fluctuating force terms can be made based on the electrostatic description of intermolecular interactions [32] for the system constructed by small molecules. On the basis of the electrostatic description, the mean force terms between COMs of different CG particles should be expressed by the multipole interactions. The contribution of internal VIBs as fluctuating forces to the COM motion should be described by the interaction between the multipoles differentiated by normal coordinates. The relative order of the fluctuating force to the mean force for polar molecule systems can be understood as the ratio of the first and the second terms of the dipole moment function after brief considerations [31]. The common values of the permanent dipole moment and the first derivative of dipole moment function can be found in several literatures. Although the usual values of permanent dipole moment of common small polar molecules are several debye (D ≈ 3.33564 × 10^− 30 C m) [32], the first derivatives of dipole moment function of them are several D Å^− 1 [33]. The amplitude of internal VIB is thought to be of the order of 0.1 Å for fundamental vibrational mode. Therefore, the ratio of the first and the second terms of the dipole moment function is about the order of 0.1. This order estimation implies that considering the fluctuating force terms must be indispensable for usual polar molecules. For non-polar molecules, the intermolecular interaction is described by higher order terms of the multipole expansion of electrostatic interaction or dispersion force interaction. In these cases, the mean force terms must be smaller than that of polar molecules, whereas the fluctuating force terms can be estimated as similar values following the above consideration.

On the other hand, it is well known that the various phases and the phase transition in liquid crystals can be described in terms of reorientational order parameters. The order parameter is ordinarily defined by the averaged direction cosine of the principal axes of liquid crystal molecules to the direction of applied external field. The region of the average should contain sufficiently large number of molecules and the spatial distribution of the order parameter must be continuous to express entire thermodynamical balances in the system. To express the various phases, the Ginzburg–Landau (GL)-type free energy functionals are frequently adopted to the non-conservative density-functional equation of motion, because the total amount of the reorientational order parameters do not keep constant. Extension of the GL model of liquid crystal has been also discussed by introducing random properties to this fundamental equation of motion [34]. Extraction of the orientational DOF of CG particles via Equaton (17) could make another approach to describe liquid crystal phases, based on an explicit CG procedure. The previous phenomenological theory can be confirmed or analysed by introducing the present particle equation of motion to reorientational ordered systems.

7. On the CG equation of motion based on stochastic density function

In the previous discussions, the equation of motion for coarse-graining particle dynamics was considered. There are, on the other hand, possibly other approaches to investigate dynamics in complicated systems, which are based on the time evolution of distribution functions.

One possible approach is the introduction of the Fokker–Planck equation, although the Markovian process and the Gaussian random process as fluctuating force must be assumed here. According to the standard procedure to construct the Fokker–Planck equation [35], Equation (11) can be transformed to

where is the probability density to find particles having velocities v ₀ and v at time 0 and t, respectively, and D _v is defined as

Deriving the Fokker–Planck equation for Equation (8) is impossible without any further approximations, because the Fokker–Planck equation is based on the assumption of a Markovian process. When we consider a stochastic density function defined at each spatial point, we must simultaneously assume that the point contains sufficiently large number of DOFs. Therefore, the assumption of a Markovian process is acceptable in such treatments. In fact, the time-dependent density functional method [36] has been reformulated from the microscopic point of view based on the assumption [37].

In order to avoid arising the wide gap between coarser and finer level in a multi-scale modelling, one important condition is the non-Markovian treatment because the memories on previous events cannot be sufficiently damped in narrow-gap multi-scale representations. Equation (7) actually describes the time evolution of the phase space density, Equation (1), without the assumption of the Markovian process. Equation (7) can be operated not only by the momentum of CG particle, but also by continuum functions related to the COM of CG particles, because it is constructed by phase points in phase space and ‘relevant field variables’ as its variables. Despite such optimistic considerations, it is still difficult to make an explicit relation between the particle and the distribution-function expressions. While the force between particles should be expressed by the interparticle distance, changes in the distribution functions are calculated by the gradient of chemical potential, which is defined by the differentiation of the free energy by the density of a tagged property. The latter depends on the number and the configuration of particles in an element of space, which is not directly related to the interparticle distances in each elementary area. These two different types of expressions can be formally replaced by each other, but the contents of them are not identical. More detailed analyses on the coarse-graining procedure are still required to understand consistent descriptions of equations of motion in different spatio-temporal level of a multi-scale modelling.

8. Concluding remarks

Recently, a generalised CG equation of motion constructed from bare expressions at a finer level in the system has been derived via the projection operator method [5]. In this article, characteristics of this generalised CG equation of motion are discussed in detail, especially in the framework of a generalised Langevin equation. Most of the conventional coarse-graining particle dynamics simulations were found to be categorised in the standard Langevin equation with mean force terms. Therefore, it is meaningful to discuss in detail the characteristics of the general CG equation of motion as a common basis for coarse-graining dynamics simulations. The main attention is focused on natural establishment of the fluctuation–dissipation theorem in the general CG equation of motion. In relation to it, the determination procedures of the mean force terms in the present and the conventional coarse-graining dynamics simulations can be analysed. Direct estimation of the mean forces based on the bare expressions at a finer level of the system is expected to give a better procedure for coarse-graining simulations. Because it is easy to understand that the friction and fluctuating force terms are indispensable in straightforward expressions of CG equation of motion, introducing these terms into a kind of coarse-graining simulation having only the mean force terms like the rigid molecule model or the united atom model, should be important and effective. Assuming that a CG particle is constructed by tightly bounded finer particles, we derived similar formulae of the CG equation of motion to arbitrary DOFs such as reorientational motion and/or internal VIB of molecules. We can also consider the other type of CG equation of motion described by distribution functions as a continuum expression on the identical basis to the present CG equation of motion. The ability to describe both the particle and continuum expressions on the identical basis is a very important characteristic for more general and realistic multi-scale modelling.

The present CG equation of motion can be understood as a more definite case of the Mori's theory of generalised Langevin equation to performing explicit simulations for dynamics of COMs of CG particles without a priori assumptions. Existence of a more general expression promises progressing useful extensions to several kinds of coarse-graining dynamics methods. For such extensions, reconstruction of the extended CG equation of motion to each specific problem is required in addition to detailed analyses of the characteristics of the generalised CG equation of motion.

In order to bridge the wide gap between coarser and finer level in a multi-scale modelling, it is unavoidable to establish a concrete procedure of coarse-graining having explicit relation to bare expressions at a finer level in the system. When the coarser level in multi-scale expression is constructed by spatial points or areas having complete homogeneous properties, it is still unsatisfactory to have such restrictions for advanced multi-scale modelling. Recently derived generalised CG equation of motion would constitute a possible basis for such progress.

Acknowledgements

This work was partly supported by the Next Generation Super Computing Project, Nanoscience Program, MEXT, Japan.