On the inner workings of Monte Carlo codes

Abstract

We review state-of-the-art Monte Carlo (MC) techniques for computing fluid coexistence properties (Gibbs simulations) and adsorption simulations in nanoporous materials such as zeolites and metal–organic frameworks. Conventional MC is discussed and compared to advanced techniques such as reactive MC, configurational-bias Monte Carlo and continuous fractional MC. The latter technique overcomes the problem of low insertion probabilities in open systems. Other modern methods are (hyper-)parallel tempering, Wang–Landau sampling and nested sampling. Details on the techniques and acceptance rules as well as to what systems these techniques can be applied are provided. We highlight consistency tests to help validate and debug MC codes.

Keywords::

• Monte Carlo
• implementation
• configurational bias
• continuous fractional
• nested sampling

Introduction

To study thermodynamic properties at the molecular level, one needs to collect information of the positions of the atoms averaged over a long time. In molecular dynamics (MD) simulations,1234 successive configurations of the system are generated by integrating Newton's laws of motion, which then yields a trajectory that describes the positions, velocities and accelerations of the particles as they vary with time. MD is conceptually easy to understand. The complexity of MD codes is in speed optimisation such as parallelisation and in implementing derivatives of the energy to get the forces. The derivatives can be tedious to derive and implement, especially for bend–torsion cross potentials and anisotropic sites.

Monte Carlo (MC) takes a similar approach, but focuses on static properties. Therefore, there is no requirement that the systems should evolve in time. In MD, each state of the system depends on the previous state, related in time as a trajectory. But in MC, there is no such connection between ‘snapshots’ (states) of the system. Similar to MD, average properties are computed as averages over all the states of the system.[5] The method is much more amenable to other ensembles than just the canonical ensemble, as long as each state can be generated with the proper weight. In principle, each molecular state can be created from scratch. However, for efficiency, most MC algorithms base a new snapshot on the modification of the current snapshot by performing changes called ‘moves’. Common moves are to translate and/or rotate a molecule. Such an attempt can be ‘accepted’ or ‘rejected’ by an ‘acceptance rule’, which means that the state has changed or that the new state is simply equal to the old state. All these snapshots form a chain, called a Markov chain, and averages are computed as averages of this Markov chain. Only static properties can be computed in MC, because there is no time involved in an MC move. This might seem non-physical or unnatural, but it is in fact where the real power of MC lies. There are no constraints on MC moves other than that they generate the appropriate ensemble. This is guaranteed by the form of the acceptance rules. Of course, the MC moves should ‘sample’ all the relevant states of the system (‘ergodicity’). But, in addition to the required moves, there is an enormous opportunity to devise clever and efficient MC algorithms, sampling techniques and MC moves. For example, MC moves that change the composition or connectivity of the atoms can be devised. The biggest limitation of MC methods is that they are considerably harder to apply to chemically complex molecules than MD. Therefore, MC used to be limited to reasonably small molecules, but the range of systems sizes, molecules, and algorithms is rapidly advancing. For more details, Vitalis et al. published an overview of the state-of-the-art MC methods designed for efficient sampling of biomacromolecules.[6]

MC is all about generating and measuring probability distributions, which provide great opportunities but make MC codes notoriously difficult to debug and test. Errors in algorithms, coding errors and/or sampling errors are difficult to find and analyse. This is largely due to symmetry and cancellation where errors are in many systems hidden in the noise, only to show up in certain systems or conditions. Naively, one might think that two different (and both correct) algorithms should give the same result and in a perfect world they would. But, in practice, each method has its own range of applicability and efficiency. In this review, we therefore provide details on many MC algorithms that have been developed to study fluid properties and adsorption, and show many validation tests aimed at checking the correctness of the MC program implementation.

Molecular simulations

Force fields

The basic ideas behind molecular mechanics (MM) date back to the 1930s and 1940s.789 MM assumes that matter consists of atoms and for every set of positions of the atoms the potential energy surface (PES) can be defined.[10] In 1950–1970, the advent of computers caused MM methods to grow in popularity at a rapid rate, and currently, MM is one of the standard methods of structural chemistry. The classical molecular energy can be described as a Taylor expansion in bonds, bends, torsions, etc.[11,12]

This expansion captures all familiar entities such as atoms, bonds, angles and physical properties such as equilibrium structures, vibrational spectra and so on. The cross terms arise naturally from this expansion and are not ad hoc functions. For example, bonds and bends interact, as the bend angle becomes smaller the bond lengths tend to increase. Their inclusion leads to two advantages: (1) they increase the accuracy of the force field (especially the vibrational frequencies) and (2) they increase the transferability of the diagonal terms . On top of the terms in Equation (1), one can add ad hoc terms, such as hydrogen bonding, that are not adequately accounted for otherwise.

Just because a model lacks certain key elements does not mean that all results are wrong; similarly, a more sophisticated force field does not necessarily give better results. A well-calibrated simplistic model can often produce better results than a generic, elaborate model. The more parameters a model has to optimise, the harder it becomes. Parameterisation is an art.[13] There have been a number of approaches to parameterise a force field directly from the quantum chemical calculations (see Ref. [14] and references therein). As the true PES can be approximated using quantum mechanical (QM) methods, a force field can be directly fit to a calculated quantum mechanical PES (QM PES) by numerically matching the gradients or energy. Although it is theoretically possible to include non-bonded interactions in the fitting, it is more common to obtain charges and van der Waals parameters separately and use these as input. A common approach is to use genetic algorithms (GA).[15] Tafipolsky et al. parameterised a force field from first principles reference data by optimising a novel objective function with a GA.[15] The GA are able to efficiently parameterise the bonded terms, which reproduce the density functional theory (DFT) results (structure and vibrational modes) as close as possible.

It can be convenient to think of the optimisation process as bottom-up (left-to-right in Equation (1))

• Bonds/angles/torsion: Parameters can be obtained from gas-phase QM and spectroscopy.

• Point charges: Parameters can be obtained by minimising the difference of the classical electrostatic potential and a QM electrostatic potential over many grid points (ChelPG methods) 161718; REPEAT method [19,20]; partial equalisation of orbital electronegativity (PEOE) or the Gasteiger method [21] and charge equilibration methods.222324

• Polarisabilities: Parameters can be obtained from gas-phase quantum or from experiment.

• van der Waals: Vapour–Liquid Equilibrium (VLE) curves; inflections in isotherms [25,26]; small noble gases such as argon from second virial coefficients; in general, from comparison with experiments (e.g. density, heat capacity and compressibility).

Equation (1) is historically referred to as a force field. The name arose from the lowest order approximation using only springs with force constants. Force fields have matured, and many parameters exist for a wide range of structures. These parameters are crucial and determine the quality of the force field. A few examples of popular generic force fields are AMBER,2728293031 OPLS,32333435 AMBER/OPLS,36373839 CHARMM,404142 GROMOS,434445 CVFF,[46] CFF,474849 MM2,505152 MM3,[53,54] MM4,555657585960 MMFF94,616263646566 DREIDING,[67] COMPASS,[68] PCFF [68] and UFF.[69]

A computationally very efficient model is the transferable potentials for phase equilibria (TraPPE) force field by Martin and Siepmann.[70,71] The force field describes, e.g. linear alkanes, mono-branched and di-branched alkanes. Despite the fact that the model lumps CH₃, CH₂ and CH into single interaction centres, it reproduces the experimental phase diagram and critical points very accurately. This united-atom approach allows for much longer simulation times and larger systems because each of the CH_x groups is charge neutral and charge–charge interaction can be omitted. The TraPPE model has been extended over the years to include explicit hydrogen description of benzene and five-membered and six-membered heterocyclic aromatic compounds,[72] thiols, sulphides, disulphides and thiophene,[73] ethers, glycols, ketones and aldehydes,[74] primary, secondary and tertiary amines, nitroalkanes and nitrobenzene, nitriles, amides, pyridine and pyrimidine.[75]

The TraPPE models are calibrated hierarchically using VLE data, e.g. CH₄ using methane data, CH₃ using ethane data, CH₂ using propane data, CH using isobutane and C using neopentane. This then constitutes the ‘calibration set’. With the final parameters in hand, the remaining experimental data, e.g. for heptane or isopentane, can then be used to validate the predictions of the model. If for this ‘validation set’ unsatisfactory results are obtained and the experimental calibration data are not in doubt, then the model needs to be refined. A more sophisticated model could include explicit hydrogens [76] or anisotropic sites.[77,78] However, the united-atom TraPPE model for alkanes is able to accurately describe the properties of alkanes over a wide range of chain lengths, densities, pressures and temperatures.

Adjusting these force field parameters to VLE data is currently a cumbersome and computationally expensive task. For alkanes, a hierarchical optimisation (e.g. first CH₃ from ethane, then CH₂ from propane and so on) is possible due to the simplistic nature of alkanes, but this is an exception rather than the rule. A force field optimisation via the VLE of CO₂ involves optimising the van der Waals interactions of the carbon and oxygen atom type simultaneously, therefore requiring many time-consuming iterations. An objective function can be defined as the squared deviation between the computed and the experimental data. Current fitting strategies involve lowering this function below a defined threshold using Simplex- or gradient-based methods. Each iteration point requires a full molecular simulation run. Van Westen et al. developed a method to overcome this limitation.[79] The actual optimisation is performed in a faster, different framework than molecular simulation, i.e. using the perturbed-chain statistical associating fluid theory (PC-SAFT) equation of state.[80] The PC-SAFT is able to sufficiently capture the size and shape of molecules and the dispersion interactions of fluids to reduce the amount of iterations to only 2 or 3.

Molecular simulation codes

A list of molecular codes that employ force fields for classical molecular simulations is (by no means complete) given in the following:

• DLPOLY: DLPOLY is an MD software for macromolecules, polymers, ionic systems, solutions and other molecular systems. It can also perform MC simulations (DL MONTE) but only metropolis sampling.[81]

• TINKER: The TINKER molecular modelling software is a complete and general package for MM and dynamics, with some special features for biopolymers. The software by Jay Ponder performs energy minimisations, molecular, stochastic and rigid body dynamics with different periodic boundaries, normal mode vibrational analysis, simulated annealing, free energy calculations and global optimisation among other things. It can use a large array of common force fields (e.g. Amber, CHARMM, Allinger MM and OPLS).[82]

• DYNAMO: Library of modules developed for the simulation of molecular systems using hybrid QM and MM potentials. The library supports a range of different types of molecular calculation including geometry optimisations, reaction-path determinations, MD and MC simulations.[83,84]

• GULP (the General Utility Lattice Program): It is a powerful classical simulation code written by Julian Gale for performing a wide range of calculations on 3D periodic solids, 2D surfaces, gas-phase clusters and isolated defects in a bulk material.[85] In particular, the code has a large number of material-specific force fields, such as the shell model for simulating ionic materials. It can also be used to fit and develop new force fields with the wide range of potentials. GULP is integrated in the Materials Studio package from Accelrys.

• Materials Studio (forcite): It is an advanced classical MM tool that allows fast energy calculations and reliable geometry optimisation of molecules and periodic systems. For crystal structures, geometry optimisation with Forcite retains the crystal symmetry. Forcite provides the user with great flexibility, offering a range of force fields and charging methods.[86,87]

• LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator): It is a classical MD code with very good performance and scalability.[88] LAMMPS has potentials for soft materials (biomolecules and polymers) and solid-state materials (metals and semi-conductors) and coarse-grained or mesoscopic systems.

• GROMACS (GROningen MAchine for Chemical Simulations): It is a MD package primarily designed for simulations of proteins, lipids and nucleic acids.[89,90]

• BOSS (Biochemical and Organic Simulation System): Bill Jorgensen's general purpose molecular modelling system that performs MM calculations, MC statistical mechanics simulations and semi-empirical AM1, PM3 and PDDG/PM3 QM calculations.[91] The MM calculations cover energy minimisations, normal mode analysis and conformational searching with the OPLS force field. The MC simulations can be carried out for pure liquids, solutions, clusters or gas-phase systems.

• MCPRO: Performs MC statistical mechanics simulations of peptides, proteins and nucleic acids in solution; it was derived from BOSS, but makes extensive use of the concept of residues. The MC simulations can be performed in a periodic solvent box, in a solvent cluster or in a dielectric continuum including the gas phase.[92]

• Etomica: Java-based MC package by David Kofke and Andrew Schultz originally designed for use as a teaching tool, but potentially powerful enough for research grade application. The code is object oriented and can be used independent of development environment.[93]

• Towhee: An MC molecular simulation code originally developed in the group of J. Ilja Siepmann and designed for the prediction of fluid-phase equilibria using atom-based force fields and the Gibbs ensemble with particular attention paid to algorithms addressing molecule conformation sampling.[94] The code is now mainly developed and maintained by Marcus G. Martin and has subsequently been extended to several ensembles, many different force fields and solid (or at least porous) phases.

• MedeA^® Gibbs: Gibbs ensemble MC package from the group of Alain Fuchs to compute the thermophysical properties of single and multi-phase fluids as well as adsorption isotherms of fluids on solids.[95]

• BIGMAC: General purpose configurational-bias Monte Carlo (CBMC) code developed in the group of Berend Smit for grand canonical and Gibbs ensemble simulations of linear alkanes.[96,97]

• OPENMD: An open source MD engine, created mostly by graduate students in the Gezelter group at the University of Notre Dame, which is capable of efficiently simulating liquids, proteins, nanoparticles, interfaces and other complex systems. Proteins, zeolites, lipids and transition metals (bulk, flat interfaces and nanoparticles) have all been simulated using force fields included with the code.

• Cassandra: an open source MC package being developed in the Edward Maginn group at the University of Notre Dame.[98] Cassandra is capable of simulating any number of molecules composed of rings, chains or both, such as small organic molecules, oligomers and ionic liquids. Cassandra can simulate the following ensembles: canonical (NVT), isothermal–isobaric (NpT), grand (μVT), osmotic (μpT), Gibbs (NVT and NpT versions) and reactive (RxMC). Cassandra is parallelised with openMP.

• MUSIC (Multipurpose Simulation Code): Object-oriented code developed in the group of Randall Snurr the major application of which is in the computation of diffusion and adsorption in zeolites. It can also perform liquid and gas simulations, as well as GCMC, NVT-MC, NpT-MC, Hybrid MC, MD and NEMD simulations.[99,100]

• RASPA: Simulation package (MC, MD and optimisation) developed in the group of Randall Snurr at Northwestern University in collaboration with Universidad Pablo de Olavide with emphasis on adsorption and diffusion simulations in flexible nanoporous materials. It includes CBMC, CFMC, Gibbs, for single and multicomponents that can be flexible and/or rigid and can handle many ensembles.[101] All simulations in this work are performed with this code.

Three main types of parallel molecular dynamics simulations have been developed: the replicated data decomposition, the spatial decomposition, and the force decomposition.[102] Similar techniques can also be used to parallelise MC simulations.[103] MC is more amenable to parallelisation than MD, because most MC algorithms have at least some degree of inherent parallelism. Parallel tempering runs multiple synchronised Markov chains simultaneously. Only when random pairs of systems exchange information is communication necessary. Conventional MC moves in the canonical ensemble do not lend themselves to efficient parallelisation, but more advanced moves are straightforward to parallelise (e.g. in biasing moves ‘trial positions’ can be computed independently). Such parallel algorithms are described in Refs 104105106. The multiple first-bead method of Esselink et al. places many first beads and chooses the most favourable.[104,105] The method increases the probability of successful insertions especially at higher densities.

The effort of parallel implementation is significant, and there are two good reasons to do it: (1) memory problems (i.e. the memory would not fit onto a single processor) and (2) to get the final results faster. Both cases can occur for very large systems. If these situations do not apply, then MC is more amenable to a ‘task-farming approach’. Each node and, therefore, each simulation runs totally independently of all other nodes. Instead of running a single serial code 10 times longer (e.g. to get more accurate results), one can just run 10 independent serial runs on different nodes and combine the results for these 10 runs. It is for this reason that parallel MC codes are relatively scarce.

Ensembles

To describe the microscopic state of a system, classically, at some instant of time, we need 6 N variables; for each of the N atoms we have three positions and three velocities. This state is a point in a 6 N space, called phase space. The state evolves through phase space according to the laws of mechanics. The measurements of macroscopic variables such as temperature T, volume V and pressure p involve taking time averages over the phase-space curve of the system. This is in fact the basis of the MD technique. Around 1900, Gibbs introduced the concept of ‘ensembles’, in which the time averaging is replaced by averaging over a group of microstates with the same macroscopic state (e.g. N, V and T). The ergodic principle states that this ensemble averaging and time averaging are equivalent (when simulated infinitely long). The phase-space points Γ are distributed according to a probability density . The functional form depends on the chosen ensemble.

For single components, there is one fundamental thermodynamic function

from which three others can be derived by a Legendre transformation [107]

where the entropy is denoted by S, the chemical potential by μ, n is the number of moles, U is the internal energy, H is the enthalpy, A is the Helmholtz function and G is the Gibbs function, respectively. A system where the number of moles n varies is called an open system. Each of the four characteristic functions can be changed by a Legendre transformation of the chemical work term to obtain new ensembles.

• Transformation of the internal energy U

  where the function is known as the Hill energy.

• Transformation of the enthalpy H

  where the function is known as the Ray energy.

• Transformation of the Helmholtz function A

  where the function is known as the grand function.

• Transformation of the Gibbs function G

  where the function is known as the Guggenheim function.

All seven functions , , , , , and are derivable from a Legendre transformation of the fundamental law of the energy conservation expressed in the internal energy function (Equation (2)). Figure 1, taken from Ref. [108], shows the ensemble and their connection to the reservoirs. The reservoirs impose constant temperature, tension and pressure and chemical potential. The ensembles in the left-hand column in Figure 1 are constant energy ensembles, whereas the ensembles in the right-hand column have constant temperature.

Figure 1 (Colour online) Ensembles: Shown are the eight ensembles for a single component system. The systems interact through a combined temperature, pressure and chemical potential reservoir. The ensembles on the left are adiabatically insulated from the reservoir, whereas those on the right are in thermal contact with the reservoir. Pistons and porous walls allow for volume and particle exchange. Adiabatic walls are shown cross-hatched, whereas dithermal walls are shown as solid lines. Ensembles on the same height are related by Laplace and inverse Laplace transformations. The pressure stands for the pressure and the tension. Picture taken from Ref. [108].

All eight ensembles (for a single component system) may be simulated using either MD or MC simulations. The probability distributions are exponentials for the isothermal ensembles and power laws for the adiabatic ensembles.[109] For example, for the NVT ensemble the probability density has the Boltzmann form with U(r) the potential energy and C a constant. For the (Ht and pN) ensemble, the trial MC moves involve particle moves and simulation cell shape/size moves.[110] For the (Rt and pμ) ensemble, MC moves involve particle moves, shape/size moves and insertion and deletion of particles.[111] For MC simulations of these ensembles, one uses the probability density directly in the simulation, whereas for MD simulations, ordinary differential equations of motion are solved for equations arising from Hamilton's equations.

System set-up

The simulation cell and boundary conditions

Computer simulations are limited to a number of molecules that can be efficiently stored in memory. Although simulations of hundreds of thousands of atoms have been reported and will likely increase by orders of magnitude in the future, this number is still far removed from the thermodynamic limit. To be able to extrapolate the results for a finite system to macroscopic bulk values one usually employs periodic boundary conditions.[1] Periodic boundary conditions are commonly applied to overcome the problems of surface effects. The original simulation box, including all the atoms within it, is replicated throughout the space.[112] When a molecule in the original box moves, its periodic images in each of the surrounding boxes moves in exactly the same way. If a molecule leaves the central box, one of its images will enter the box through the opposite face. It is not necessary to store the coordinates and momenta of all the images, only those in the central box are needed, because the images can be obtained from translation operators. Usually, one imposes the minimum image convention: the distance between two particles is taken to be the shortest distance between their periodic images. The boundary of the periodic box does not have any physical significance, only the shape and orientation.[3] The use of periodic boundary conditions inhibits the occurrence of long-wavelength fluctuations. It is, for example, not possible to simulate a liquid close to the glass-liquid critical point where the range of critical fluctuations is macroscopic.[3]

In general, the unit cell is defined by the cell lengths a, b, c and angles α, β, γ and by the fractional coordinates s of the atoms within the unit cell. These coordinates form an orthonormal dimensionless space. The transformation from fractional space to Cartesian space can be carried out by the matrix h:

with

This aligns the a cell vector along the x-axis, b in the xy-plane. Conversely, h^− 1 transforms Cartesian coordinates r to fractional coordinates s. With the chosen h the scaled box has a length of 1. Potential force fields are defined in Cartesian space; therefore, it is convenient to store position in Cartesian space, transform them to fractional space, apply periodic boundary conditions in s space and transform back to Cartesian space to compute distances within the simulation box

where the ‘rint’ function returns the rounded integer value of its argument. The smallest perpendicular width of the unit cell has to be larger than twice the spherical cut-off in Cartesian space to be consistent with the minimum image convention.

In general, it is prudent to use a sufficiently large simulation cell (and a large amount of particles) to avoid ‘finite size’ effects. The error of thermodynamic properties in periodic systems with only a few hundred particles can be quite large,[113] especially in the vicinity of critical points. It is advisable to study the system properties as a function of system size to estimate the finite size effects. Also, sometimes theoretical corrections can be applied to the simulation results.114115116

Initialisation, equilibration and production runs

To prepare the system at the desired temperature in an equilibrium configuration for MD, we initialise the system by the following procedure:

• N molecules are inserted into the simulation box at random positions as long as no overlaps occur with a framework and/or other particles, and as long as the positions are accessible from the main cages and channels (when a framework solid is present). Inaccessible pockets need to be blocked.[117] One can use a list of volume shape/sizes that are automatically considered an overlap, either computed in advance or on-the-fly.[118]

• During the initialisation period, we perform an NVT MC simulation to rapidly achieve an equilibrium molecular arrangement.

• After the initialisation step, we assign all the velocities of atoms from the Maxwell–Boltzmann distribution at the desired average temperature. The total momentum of the system is set to zero (to avoid centre-of-mass drift of the system). Next, we equilibrate the system further by performing an NVT MD simulation using a thermostat.

• The equilibration is completed and during the production run we collect statistics using either the NVE or NVT ensemble. Following this equilibration procedure, the average temperature using NVE over the entire production period is usually within a few Kelvin of the desired average temperature, while NVT would give the exact desired average temperature if simulated sufficiently long.

The ability to insert molecule efficiently is important for an (almost) effortless initialisation process. An alternative method is to place molecules at regular intervals (‘on a grid’) but is only applicable at lower densities and is in general more cumbersome. Therefore, even with only MD in mind, the use of MC might make the initialisation more robust and efficient. This also applies to the equilibration of the positions. In MC, particles can be randomly moved around in the system (this does not have to follow a trajectory based on Newton's equation of motions like in MD). This is an advantage for systems with diffusional bottlenecks such as cage-type zeolites. With MC the particles can be distributed appropriately without physically having to go through the bottlenecks.

After these steps, the procedure for MC and MD differs. For MD, the next step is to equilibrate the velocities. Atoms are assigned velocities from a Maxwell–Boltzmann distribution, and the integration of the equations of motion is started. Due to previous equilibration of positions, the actual time to properly equilibrate the velocities (and also again the positions) is significantly reduced. The final step for MD is to start the actual ‘production run’ where properties of interest are measured. For MC, the production run can immediately be started after the equilibration of the positions.

MD is counted in MD steps, i.e. single integration steps, from which the total simulations time in ps or ns can be deduced. For MC, the duration of the simulation is measured in ‘MC steps’ or ‘MC cycles’. An MC step is one performed MC move, either accepted or rejected. The MC moves are chosen in random order with a preset probability. An MC cycle takes the number of particles into account, and in each cycle on average one MC move has been attempted per particle. The reason behind this is that one needs to sample longer if there are more molecules in the system. Therefore, the number of cycles is less dependent on the system size. To avoid poor sampling at low densities, the number of steps per cycle can have a set of lower limit of 20. A cycle is then, for example, defined as [96]

Long-range interactions

van der Waals

The most common repulsion/dispersion functional form for the van der Waals interaction is the Lennard-Jones potential (see Figure 2)

and the Hill or Buckingham potential function

The Hill potential, having three adjustable parameters versus two adjustable parameters for Lennard-Jones (the ‘strength’ parameter ε and the ‘size’ parameter σ), might be slightly more accurate. However, the Lennard-Jones potential is most commonly used for convenience. The parameters for generic force fields are usually self-parameters, and a ‘mixing rule’ is needed to compute the interaction between different types of atoms. Common mixing rules are as follows:

See Ref. [119] for many more mixing rules. A downside of the Hill potential is divergence to large negative energies at . In MD, assuming that all atoms initially do not overlap, the repulsive part of the potential avoids this issue. However, in MC, a move may choose a new random position on top of another particle's position. Therefore, the potential needs to be ‘blocked’ (such a move would be explicitly considered an overlap and rejected) or changed to a polynomial repulsion (e.g. MM2) at short distances.

Figure 2 (Colour online) The Lennard-Jones potential has two parameters: the ‘strength’ parameter ϵ and the ‘size’ parameter σ. Energy and force evaluations only take place within the cut-off distance. It is possible to estimate the neglected energy (called the ‘tail’ correction, green area in the picture). For MD, it is customary to use ‘smoothing’ which makes the potential smoothly go to zero at the cut-off (red line). Alternatively, the whole potential can be ‘shifted’ to be zero at the cut-off. The latter leads to continuous forces but remains divergent for higher derivatives. The tail correction calculation assumes that the RDF is approximately unity after the cut-off. The right figure shows that for methane–methane interactions, an arbitrary methane sees an ideal gas of other methane molecule at distances greater than about 12–14 Å for this system. The RDF/tail correction formulation breaks down inside nanoporous materials (here methane in ERI-type zeolites) where the particles are located at adsorption sites in a heterogeneous environment. The RDFs of methane in the fluid and in the pores of ERI are computed at the same density (102 kg/m³).

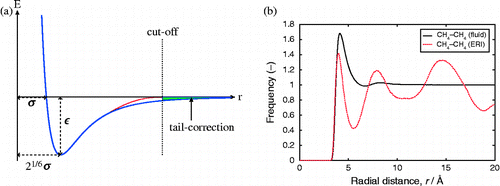
To make the simulations tractable, the van der Waals potentials are truncated at a certain distance where the interactions are considered sufficiently small. In MC, the truncated potential can be used, and the energy correction due to this truncation, called the ‘tail correction’, can be approximated (see Figure 2). The truncation distance and whether to use tail correction or not should be considered as part of the force field. For MD, the truncation in the energy leads to a divergence in the forces. Common approaches include to shift the van der Waals potential to zero at the cut-off and the use of a switching function where the energy is forced to smoothly go to zero 120121122

.

The cut-off is usually chosen as the distance where the radial distribution function (RDF) approaches unity. The requirement that the smallest perpendicular distance of the simulation cell has to be larger than twice the cut-off distance r_c determines the minimum amount of crystallographic unit cells to be used in adsorption simulations. If we assume the RDF for we can write

where N is the number of particles and is the average number density. The last term in Equation (24) is a tail correction, i.e. the systematic contribution to the energy due to truncation of the potential. Similar expressions have been derived for the pressure and chemical potential.[1] Note that this is only possible for potentials decaying faster than , like the van der Waals potentials. Another point worth mentioning is that for molecules adsorbed in a porous material the RDF does not approach unity, not even at long distances, because it is no longer a homogeneous system (see Figure 2). Analytical tail corrections therefore do not apply in nanoporous materials,[123] and they are usually just omitted.

Coulombic interactions

The Coulombic potential decays as r^− 1 and the tail correction diverges. The total electrostatic potential energy of interaction between point charges q_i at the positions r_i is given by

where ε₀ is the electric permittivity of free space (8.8541878176 × 10^− 12 F/m). In this expression, the first form explicitly counts all pairs, whereas the second form counts all interactions and divides by 2 to compensate for double counting. For a finite system of charges, this expression can be evaluated directly. However, for a large or infinite system, the expression does not converge and numerical tricks must be used to evaluate the energy. In fact, for the infinite system, one has an infinite amount of charge and the energy of interaction is undefined. If the system is neutral, it is possible to define a meaningful interaction energy by use of an Ewald transformation.124125126

The basic idea of the Ewald approach is as follows. The error function erf(x) and its complement are defined as:

Ewald noted that

In this expression, the first term goes to a constant as , but has a long tail as . The second term has a singular behaviour as , but vanishes exponentially as . Ewald's idea as to replace a single divergent summation with two convergent summations. The first summation has a convergent summation in the form of its Fourier transform, and the second summation has a convergent direct summation. A sum over lattice translation n may be transformed into an equivalent sum over reciprocal lattice translations k according to the identity:

where V denotes the unit cell volume.

The vectors , which need not be orthogonal, form the edges of the unit cell. The conjugate reciprocal vectors are defined by the relations

Let h be the 3 × 3 matrix having the lattice vectors as columns. Note that the volume V of the unit cell is given by the determinant of h. Furthermore, is the 3 × 3 matrix having the reciprocal lattice vectors as rows. We define the reciprocal lattice vectors k by with integers not all zero. We define the structure factor by

The structure factor can be viewed as a discrete Fourier transform of a set of charges placed irregularly within the unit cell.

The Ewald expression for the Coulombic energy in a truly periodic system reads

where the ′ in the summation over the lattice translations n indicates that all self-interaction terms should be omitted. Ewald expressions for energy, forces, stresses, electric fields and electric field gradients have been derived for the interaction between charges, dipoles and quadrupoles.[127,128]

For a net-charged system, the fully periodic Coulombic energy diverges. This does not happen with the Ewald method, as the divergence catastrophe is avoided by a ‘neutralising plasma’ – a uniform distribution of charge equal and opposite to the net charge of the system – which is usually said to be added to the system. The neutralising plasma is effectively represented in Ewald summations by the omission of the k = 0 term in the reciprocal space sum. Systems with a net charge possess a finite non-zero energy and pressure that may lead to artefacts in such systems. Bogusz et al. have derived corrections to the Ewald expressions to remove pressure and free energy artefacts in charged periodic systems.[129] The net-charge correction term can be logically broken into five terms: a reciprocal space term, a real space term, a self term, a surface dipole term and a system-dependent correction, such as a Born or Poisson–Boltzmann term (which corrects for missing long-range polarisation):

where SP refers to a single particle calculation. For example, the reciprocal space term is simply the reciprocal space energy of the Ewald sum for a single particle located at the origin:

which has to be computed only once for a given cell shape and size. The pressure artefacts can be removed by placing the net charge at the centre of charge of the system (and therefore has to be recomputed at every step).

The Ewald method can be implemented very efficiently for MC methods as only the change for moving atoms needs to be computed.[130] The real part and the imaginary part of the structure factor can be expressed as a summation over all particles in the system. It is convenient to store and in the memory of the computer (one complex number for each k). For particle displacements, rotations, regrows, (test) insertions, deletions and identity changes, one can easily calculate the new values for and by subtracting the contributions of the old configuration and by adding the contributions of the new configuration. This has to be done only for atoms that have a different position in the old and new configuration.

The Ewald summation is superior to the recently proposed Wolf method [131] and other direct summation methods, both in accuracy and in speed.[130] It is well known that a direct r^− 1 summation only converges for very large values of the cut-off radius,[3] for example more than 40 Å for neutral molecules. Damping the Coulombic potential reduces this range, although still a cut-off of at least 25 Å seems to be the minimum requirement,[130] but at the cost of uncertainty in the damping constant α. Different values for α are recommended in the literature implying that this damping is system specific and possibly dependent on the molecule type, framework topology, temperature, etc. The Ewald summation is able to compute the electrostatic energy exactly (to within any specified numerical precision) for a system of charges in an infinitely periodic structure at a cost less than quadratic with the number of particles (N^3/2 for Ewald). The energy and forces computed with the Ewald summation are well defined and unique. They do not depend on a judicious choice of damping parameters and cut-off values, and Ewald type methods are at the same level of accuracy significantly cheaper.

The MM2 and MM3 force fields calculate the electrostatic interaction in non-charged polar molecules by using bond dipoles. The electrostatic interaction potential is then given by

where χ is the angle between the two dipoles and α_i and α_j are the angles between the dipoles and the vector connecting them. There is little difference if properly parameterised. However, almost all force fields prefer the charge model because it is easier to parameterise.

Units

An excellent discussion of the handling of units is given in the manual of DLPOLY.[81] A small set of internal units needs to be chosen. A convenient set that is chosen in DLPOLY, RASPA and many other codes is given in the following:

• The unit of length l₀ is chosen as Å, i.e. l₀ = 10^− 10 m.

• The unit of time t₀ is chosen as picoseconds, i.e. t₀ = 10^− 12 s.

• The unit of mass m₀ is chosen as atomic mass units, i.e.  kg.

• The unit of charge q₀ is chosen as units of proton charge, i.e. C/particle.

All other units follow from this decision, for example:

• The unit of energy is 10 J mol^− 1. The Boltzmann factor k_B is 0.831451115 . This means that the Coulombic conversion factor

• The unit of pressure is 1.6605402 × 10⁷ Pa.

• The unit of diffusion is 10^− 8 m² s^− 1. The slope of the mean square displacement versus time will be in units of 10^− 8 m² s^− 1.

At the start of the simulation, the input is read and converted to internal units. At output, the internal values are converted back to physical units. That is, one is still free to input, e.g. pressure in either bar, atmosphere or psi, as long as the values are converted properly to internal units. The documentation of the code should clearly list what units are expected for the input (as well as describe the units of the output). There is hardly any need to have unit conversion elsewhere in the code with a few exceptions. For example, because the electric permittivity of free space ε₀ enters into the Coulombic potential, every time the charge–charge interaction is computed the value needs to be multiplied by γ₀ to be consistent with internal units.

Methodology

Monte Carlo

Statistical mechanics formulate the following postulates [4,132]:

• Postulate of ensemble averaging.

  The average behaviour of a macroscopic system in equilibrium is given by the average taken over a suitable ensemble consisting of an infinite number of randomised mental copies of the system of interest.

• Postulate of equal a priori probabilities.

  In a state of macroscopic equilibrium, all stationary quantum states of equal energy have equal a priori probability (in the micro-canonical ensemble).

• Postulate of equilibrium state.

  Equilibrium state is the one that occupies the maximum volume in the phase space.

The implications are as follows:

• The method of calculation is statistical in nature.

• The predictions are regarded as true on average rather than precisely expected for any particular system.

• The probability of finding a system in a given state being proportional to the phase-space volume associated with it, the most probable state would be one that occupies the maximum volume in the phase space. It follows that the equilibrium state is the state of maximum probability.

In its simplest form, the MC method is nothing more than a computer-based exploitation of the law of large numbers to estimate a certain probability or expectation. At the heart of the algorithm lies the ‘random numbers generator’, and therefore, it is advisable to use a high-quality generator such as the ‘Mersenne Twister’.[133,134] The Markov Chain Monte Carlo (MCMC) method is an important tool to estimate the average properties of systems with a very large number of accessible states.[135,136] The system evolves from state to state (possibly the same state), and averages of a property are computed as the average over the elements of the Markov chain. For an infinite Markov chain the expression is exact. The scheme makes use of the fact that only the relative probability of visiting points in configuration space is needed, not the absolute probability. To visit points with the correct frequency, the MCMC algorithm generates random trial moves from the current (‘old’) state (o) to a new state (n). To show that an arbitrary initial distribution eventually relaxes to the equilibrium distribution, it is often convenient to apply the condition of detailed balance (as is used in the original Metropolis scheme). If and denote the probability of finding the system in states (o) and (n), respectively, and and denote the conditional probability to perform a trial move from and , respectively, then the condition called ‘detailed balance’ can be written as

In equilibrium, the flow from the old state o to any other state n is exactly equal to the reverse flow. In the Metropolis, algorithm α is chosen as a symmetric matrix

For a symmetric transition matrix

which leads to

Metropolis et al. choose the following acceptance rule [135]

Let us recall for example the canonical partition function [137]

where the Hamiltonian , p the linear momentum and m the mass of the particle. The factor h³ is the phase-space volume, and arises because classically particles within a single species are indistinguishable.

In MC, only the positions are used. The momenta can be integrated analytically by making use of

The de Broglie wavelength Λ is the wavelength of a gas particle with momentum determined by the average thermal kinetic energy per degree of freedom . If we use the de Broglie relation , then from we have . The condition for the applicability of classical or Boltzmann statistics is equivalent to the condition , where Λ represents the critical length scale at which interactions are neglected. Closely related to h divided by the momentum, the de Broglie wavelength is defined as

we see that the differences between the partition functions with and without explicit momentum integration are and

For ensembles where the simulation cell is allowed to change, it is more convenient to redefine the positions in fractional coordinates using .[138] In fractional coordinates, it is easier to describe a volume change while leaving the particle positions the same. The partition function in fractional coordinates is related to the Cartesian version by a factor

where means that the Hamiltonian depends on the Cartesian positions,[138] i.e. potentials are usually defined in Cartesian space as opposed to fractional space.

Some of the most commonly used ensembles are the canonical ensemble, the isothermal–isobaric ensemble, the grand canonical ensemble, the Gibbs ensemble and the ensemble.

Canonical MC

In the canonical ensemble, the number of particles N, the temperature T and the volume V are constant. The partition function Q is 137139140141

where is the total energy of the system with N particles at positions r^N. The probability of finding configuration r^N is given by

The average of the variable in the NVT ensemble is given by

In MC, the quantity of interest is not the configurational part of the partition function itself, but averages of the type of Equation (50).

The particle moves such as translation and rigid rotation have the following acceptance rule:

NpT ensemble

The MC extension to the NpT ensemble is by Woods [142,143] and samples the phase space of a constant N, constant p, constant T ensemble with the appropriate phase-space probability. In addition to the particle moves performed at constant T, changes in the volume are attempted and accepted/rejected according to an evaluation of the enthalpy change. The NpT ensemble has volume trial moves which implies implicit particle scaling using a factor . The ΔV is a random number uniformly distributed over the interval . The isothermal–isobaric ensemble partition function, introduced by Guggenheimer,[144] is given in fractional positions by [138,145]

The factor is included to make the partition function dimensionless.146147148 The volume scale cannot be defined in general.[149] Common choices, corresponding to particular cases, include and . The differences become important when the volume of the system is small, but vanish in the thermodynamic limit. However, the choice is not of importance in simulations because of cancellation of the prefactors. A property A is averaged as

The change in enthalpy for a volume change

The acceptance rule can be derived as

and the new volume is accepted/rejected according to

However, often an alternative move is used, where the volume is changed not in V but in . The partition function is

and the probability of finding the volume is

The change in enthalpy for a volume change

leading to a slightly different acceptance rule (note the N+1 in Equation (40) compared with N in Equation (54)).

The particle moves have the same acceptance rules in the NpT ensemble as in the NVT ensemble

Gibbs ensemble

The Gibbs ensemble MC simulation technique allows direct simulation of VLE curves of fluids.[150,151] In some sense, it combines the NVT, the and the NpT ensembles and therefore provides a generic theoretical framework. Gibbs ensemble simulations are performed in two separate microscopic regions, each within periodic boundary conditions (Figure 3(a)). An n-component system at constant temperature T, total volume V and total number of particles N is divided into two regions, with volumes and and number of particles and . The partition function is given by

The probability of finding a configuration with particles in box I with volume and positions and is given by

In the Gibbs scheme, we consider the following trial moves:

• displacement of a randomly selected particle.

  Figure 3 (Colour online) Gibbs, adsorption using Gibbs, the osmotic and the grand canonical ensemble, (a) in the Gibbs ensemble the total volume and the total number of molecules are fixed. The volume move makes one box bigger and the other box smaller which leads to pressure equilibration. The exchange of particles between the boxes leads to equal chemical potential and in both boxes the same temperature is imposed. (b) Adsorption isotherms can be computed in the Gibbs ensemble where the fluid phase is explicitly simulated. (c) The osmotic ensemble replaces the explicit fluid phase by an imaginary reservoir. (d) The grand canonical ensemble also uses the imaginary reservoir but in addition keeps the volume fixed.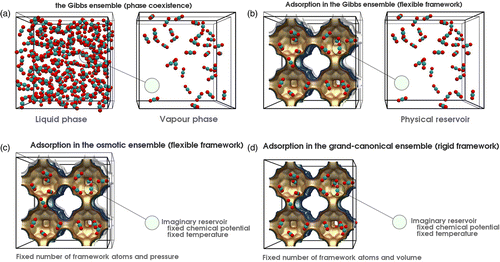

  

  The acceptance rule is identical to that used in a conventional NVT ensemble simulation

• change in box volumes while keeping the total volume constant.

  The acceptance rule for a random walk in is

• transfer of a randomly selected particle from one box to the other.

We can generate a new configuration n from configuration o ( particles in box I) by removing a particle from box I and by inserting this in box II. At random, it is selected to transfer a particle from box I to box II or vice versa. Out of the n components, one of the components j is selected at random. A particle that obeys the first two choices is selected at random and transferred to a random position in the other box. The acceptance rule is given by

Alternatively, one can first select a particle at random from all N particles and then try to move this particle to the other simulation box. The acceptance rule is

For pure component systems, the phase rule requires that only one intensive variable (the temperature) can be independently specified when two phases coexist. The vapour pressure is obtained from the simulation. By contrast, for multicomponent systems pressure can be specified in advance, with the total system being considered at constant NpT. The only change necessary is that the volume changes in the two regions are now independent. The acceptance rule for a random walk in of region I, while the volume remains unchanged which is given by

Adsorption simulation

In adsorption studies, one would like to know the amount of materials adsorbed as a function of pressure and temperature of the reservoir with which the adsorbent is in contact. Adsorption simulations can be performed in the Gibbs ensemble (adsorption equilibrium between a bulk fluid phase and the interior of an adsorbing material).[152] The reservoir is explicitly simulated from which the pressure can be obtained (see Figure 3(b)). Conversion using an equation of state is not necessary between pressure and fugacity, albeit that the fugacity coefficient is one of the models (but hopefully close to the experimental fugacity coefficient if the fluid model is sufficiently accurate). Two other ensembles for computing adsorption are the (Figure 3(c)) and grand canonical ensemble (Figure 3(d)). Gibbs ensemble simulations of adsorption are almost identical to grand canonical simulations. The only difference is that the total composition of the system is imposed, rather than the chemical potentials in the exterior of the pore.

Grand canonical ensemble

The most common ensemble for adsorption is the grand canonical ensemble or ensemble.[153] In this ensemble, the chemical potential μ, the volume V and the temperature T are fixed. MC simulations can be performed in the grand canonical ensemble by a direct generalisation of the NVT ensemble.[154,155] The partition function is given by

The probability of a particular configuration is

The acceptance rule can be derived

The particle moves again have the same acceptance rules as in the NVT ensemble.

The pressure p in the reservoir is related to the chemical potential

where is the fugacity and is the chemical potential of the reference state (ideal gas)

The fugacity is not the same as the pressure but it is closely related to it. Fugacity is the activity of a gas and has the same units as pressure. The fugacity coefficient is the exponential of the difference of the Gibbs free energy and the ideal gas Gibbs free energy at the system divided by RT [156]

where z is the compressibility. In simulations, the chemical potential μ is imposed which is closely related to the fugacity (see Equation (73)). For an ideal gas f = p and for every gas becomes an ideal gas. The conversion between pressure and fugacity can be performed using an appropriate equation of state. Fugacities and fugacity coefficients for components of mixtures can be estimated by the Lewis–Randall rule that states that the fugacity coefficient of a component i in a mixture of real gases is roughly equal to the fugacity coefficient of pure gas i at the temperature T and (total) pressure p of the mixture.[156] There are some limitations to this rule. Alternatively, one can use an EOS with appropriate mixing rules.[157]

The acceptance rules for insertion and deletion in the grand canonical ensemble are as follows:

For mixtures, a convenient method is to first randomly choose a component. The acceptance rules, Equations (53) and (53), remain the same except that N refers to the number of particles of the chosen component and p to the partial pressure.

μ₁N₂pT ensemble

The N₂pT ensemble [158] is the natural ensemble to compute adsorption for flexible frameworks. The system is considered as two components, where the chemical potential of component 1 is kept constant (and has variable particle number), while the component 2 has a constant particle number. In a constant pressure ensemble, the volume will automatically adjust to hold the pressure constant as the composition or temperature change. For a single component system, it is not possible to vary three intensive variables independently because of the Gibbs–Duhem relation which relates them. However, for two (or more) species systems, it is possible to derive, rigorously, a statistical ensemble in which T, P, and are held fixed. For this ensemble, is the chemical potential of the adsorbate and is the fixed number of atoms of the framework (host). This is a hybrid statistical ensemble which has some properties similar to the single species (NpT) and () ensembles.

The form of the probability distribution for the ensemble can be derived by performing three Laplace–Legendre transforms from the microcanonical (EVN_adsN_host) ensemble. The probability that the system with temperature T, pressure P, chemical potential of the adsorbate and host atoms has volume V and N_ads atoms, , where s stands for the positions of all the atoms in the system, is given by [158]

with and .

In (N₂pT) MC simulation, one carries out (at least) four distinct types of trial moves.[158]

which are the conventional acceptance rules. The N₂pT ensemble can be seen as a special case of the osmotic Gibbs ensemble.159160161

Configurational-bias Monte Carlo

Conventional MC is time consuming for long-chain molecules. Moreover, the configurations of long molecules in the framework become increasingly different from the gas phase. The fraction of successful insertions into the sieve becomes too low. To increase the number of successfully inserted molecules, the CBMC technique was developed. Figure 4 shows the definition of S2-butanol which will be used here to illustrate the method, and in a later section to validate the generated bond/bend/torsion distributions. Instead of generating ideal gas configurations and trying to insert the molecule as a whole, the CBMC method inserts chains part by part biasing the growth process towards energetically favourable configurations, and therefore significantly reduces overlap with the framework and other particles. The CBMC framework is based on the work by Rosenbluth and Rosenbluth [162] and developed by a variety of researchers.163164165166167168169 Later, CBMC was extended to include growpaths for branched molecules,[3,71,76,123,170,171] cyclic molecules 172173174175176 and reactive CBMC.[177]

Figure 4 (Colour online) S2butanol: the OPLS definition has 14 bond, 25 bend and 30 torsion potentials. The chiral centre is atom 7.

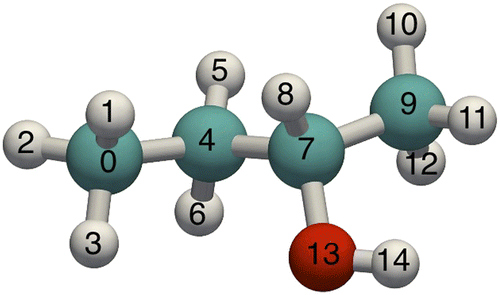
Growing a chain molecule

Let us first tackle the problem of how to generate a molecule with an appropriate intra-molecular energy (bond, bend and torsion). We can choose any of the atoms as a start point. Let us assume to start our growth process from atom 4 (the labelling is shown in Figure 4). The starting atom is connected to atoms 0, 5, 6 and 7. One of these can be chosen randomly, for example atom 7. The position of atom 7 lies on a sphere with a radius depending on the bond-length distribution (Figure 5(a)), and is determined by computing a random vector on a unit sphere adjusted in length for the bond potential. The chosen bond length can be generated either using an ‘acceptance–rejection’ scheme or using a small MC routine. Having grown atoms 4 and 7 one can continue to grow on either side but let us assume to continue along the atom 7 path. Atom 7 is connected to atom 4 (already grown) and atoms 8, 9 and 13. Vlugt et al. noted that atoms 8, 9 and 13 must be grown simultaneously.[97,170] That is, it would be wrong to first place atom 13, next atom 8 and then atom 9. Because of the bond-bending potentials, the branches connected to the same central atom cannot be added independently. Vlugt et al. developed an MC procedure that can be used to generate the positions of the branch atoms using the following moves:

• Changing the bond length

  Figure 5 (Colour online) Growing (branched) molecules, (a) bonds are grown by choosing random positions on a sphere; bond lengths (b) and bend angles (c and d) between atoms of a branch are changed by an MC algorithm. The MC moves displace atoms along the bond vectors, or change the bend angle, or rotate the branch atoms around the axis of the bond that was already grown.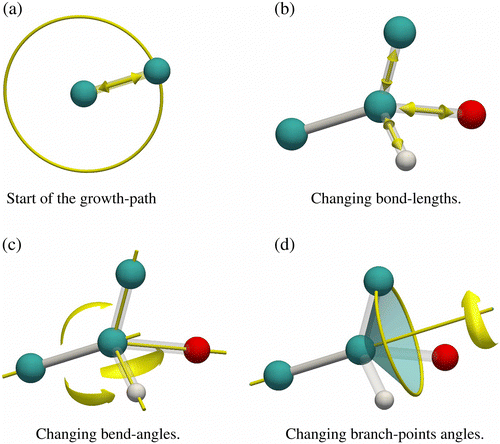

  

  One of the branch atoms is randomly chosen and an attempt is made to change the bond length (see Figure 5(b)). The probability of generating a branch position b with bond length l is given by

  and the acceptance rule for a change in bond length from to is

• Changing the bend angle

  One of the branch atoms is randomly chosen and an attempt is made to change the bend angle (see Figure 5(c)). The probability of generating a branch position b with bend angle θ is given by

  and the acceptance rule for a change in bend angle from to is

• Rotation on a cone

  One of the branch atoms is randomly chosen and rotated randomly on a cone (see Figure 5(d)). This move changes the bend angle between the branch atoms. The acceptance rule for a rotation on a cone is

A few hundred of these moves should be sufficient to equilibrate the positions of the branch atoms. The growing scheme of Vlugt et al. is able to handle stiff bond and bend potentials. Another advantage is that it is easy to include chirality. If a wrong chirality is detected during the small MC scheme then two branch atoms are switched, followed by further equilibration.

The scheme of Vlugt et al. handled torsion potentials by including the torsion energy in Equation (92). Unfortunately, this method still fails to generate the proper distribution when there are multiple torsional angles that share the same two central atoms because the bond bending and torsional angle distributions are no longer independent. Vlugt et al. modified the force field for branched alkanes such that only one torsion potential was defined over a central bond. For multiple torsions over a central bond all of the atoms connected to those central atoms must be generated simultaneously in order to get the correct distribution. This implies that the conformation of the entire 2,3-dimethylbutane molecule must be generated in a single step in order to obtain the correct distribution. One of the methods developed to solve this problem is the coupled–decoupled CBMC algorithm of Martin and Siepmann.[71,171]

The bond angles are selected based solely on the bond angle energies and the phase-space terms, and then those angles are used in all subsequent selections (torsion and non-bonded). Thus, the bond angle selection is decoupled from the other selections. In contrast, for each non-bonded trial a full selection is done to generate torsional angles, so these two selections are coupled. Before explaining this further, let us see how to actually increase acceptance of insertion using more than one set of ‘trail positions’.

Trial positions

So far we have shown how to generate a molecule. In order to be able to steer (to ‘bias’) the growth, at each step, k sets of branch atoms called ‘trial positions’ are generated of which one is chosen with the appropriate probability. The growth control is largely based on the ‘external’ environment of the molecule, for example the framework and/or other molecules that are present in the system. In the CBMC scheme, it is therefore convenient to split the total potential energy U of a trial site into two parts.

The first part is the internal, bonded potential which is used for the generation of trial orientations. The second part of the potential, the external potential , is used to bias the selection of a set from the other set of trial sites. This bias is exactly removed by adjusting the acceptance rules. In the CBMC technique, a molecule is grown segment-by-segment. For each segment, a set of k trial orientations is generated according to the internal energy and the external energy of each set of trial positions j of segment i is computed. The number of trial positions k is usually between 10 and 20. One of these trial positions is selected with a probability

The selected trial position is added to the chain, and the procedure is repeated until the entire molecule has been grown. For this newly grown molecule, the so-called new Rosenbluth factor is computed as

To compute the old Rosenbluth factor of an already existing chain, trial positions are generated for each segment. These positions, together with the already existing position, form the set of k trial positions.

Coupled–decoupled CBMC

The Vlugt CBMC scheme and other schemes for branched alkanes generate conformations according to the probability

where n is the growth step, is the total number of growth steps, i is a particular trial set and is the number of trials for which the Lennard-Jones interactions are computed. A move is accepted with probability

Martin and Siepmann developed a generic framework of very flexible CBMC schemes based on decoupled and coupled selections:

• Decoupled selections

  In the decoupled selection, the probability to generate a given configuration and the corresponding Rosenbluth weights are given by

  where , and are the number of trial sites for the Lennard-Jones, torsional and bend interactions, respectively. The move is accepted with probability
  Bend angles are chosen in a biased fashion and used as input for the subsequent biased selection of the torsional angles. These are then used as input for the Lennard-Jones selection, but the main drawback of this method is that once the torsional angles have been chosen in a biased fashion, there is only one possible trial site available for the Lennard-Jones selection ().

• Coupled selections

  In a coupled biased selection, the selections are coupled such that each biased selection sends multiple possible conformations to the next selection step. In this case

The coupled-biased selection growth now performs a separate torsional bias selection for each of the trial steps of the Lennard-Jones selection. The disadvantage of coupling all of the energy types is that trial vectors must be generated for the bond angle-biased selection.

Handling multiple torsions and intra-molecular VDW interactions

A combination of the coupled- and decoupled-biased selections allows a great deal of flexibility when designing CBMC schemes. To handle multiple torsions over a single bond and to handle Lennard-Jones interactions, we can use decoupled CBMC and generate trial vectors for the torsional selection, of which are selected for the Lennard-Jones step. The intra-molecular Lennard-Jones interactions are treated here as ‘external’ Lennard-Jones interactions. The CBMC scheme can also be used when the atoms of the molecule have charges, for molecules that have anisotropic sites and for molecules with cross terms such as bond–bond, bond–bend and bend–torsion potential. The molecule is grown without these terms but afterwards the weight is corrected (see section ‘Advanced bias corrections’).

Chemical potential reference state

The excess chemical potential is defined as the difference in chemical potential of the interacting chain and a chain in the ideal gas state. The Rosenbluth weight of the reference state of the ideal gas is needed when comparing with real experimental data. When CBMC is used, it is straightforward to show that has to be replaced by for inserting a particle and by for the deletion of a particle. Detailed balance is followed when is replaced by , i.e. the average Rosenbluth weight of a chain in the reservoir. This implies that has to be computed only once for a given molecule and temperature.[97]

The reference state is important and enters in the acceptance rules for CBMC insertion and deletion moves

It is best practice to compute in advance, but for single components the results can also be corrected afterwards for the ideal Rosenbluth weight by ‘correcting’ the fugacity. This is much more cumbersome for mixtures because both partial fugacities are changed and the initial imposed mole fraction is now different, i.e. an equimolar mixture would no longer be equimolar after correcting. For these reasons, it is important to compute first.

Advanced bias corrections

Dual-cut-off CBMC uses an additional bias in the selection of trial segments.[178] The motivation is that hard-core (repulsive) interactions are more important than long-range interactions in the selection of trial segments. Therefore, a second smaller cut-off radius can be used for the selection of trial positions (for LJ fluids one can use cut-off of around σ Å). The potential is split in two parts

where is less expensive to calculate and is the difference between the two potentials. The additional bias can be exactly removed in the acceptance/rejection rule

where and are the Rosenbluth weights calculated using .

Similarly, for anisotropic alkane models the chain can be grown as an ordinary united-atom model, but by correcting with the difference between the anisotropic and the approximate potential in the acceptance rule the correct distribution is recovered.[179]

For computational efficiency, for molecules with partial charges it is advantageous to grow beads only with the LJ part plus the real part of the Ewald energy, and correct the final configuration for the Ewald Fourier energy using Equation (111). The more expensive Fourier part of the Ewald summation then only has to be computed once (and not for all the trial positions of all the beads).[97] This also avoids the problem that during the growth the already grown part is not charge neutral.

Continuous fraction Monte Carlo

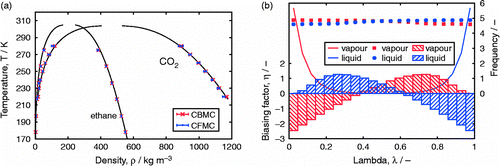
All open ensemble methods suffer from a major drawback: the insertion probability becomes vanishingly low at high densities. One of the schemes to remedy this problem is the CFMC method of Shi and Maginn.[180,181,182] The system is expanded with an additional particle scaled in interactions using a parameter λ. Various choices for the scaling are possible, but for example the Lennard-Jones and charge–charge interactions are scaled as

The modified form forces the potential to remain finite when for . The scaled potential has the correct behaviour at the limits of and . Note that only the inter-molecular energy is scaled (not the intra-molecular energy). Many variations on the algorithm are possible. For example, λ can be changed per molecule or per atom. Both methods slowly ‘inflate’ and ‘deflate’ the molecule like a balloon but differently.

CFMC uses conventional MC for thermalisation (such as translation, rotation moves and/or MC–MD hybrid moves), but in addition attempts to change λ of the fractional molecule using . The is chosen uniformly between and and scaled to achieve around 50% acceptance. However, many systems show behaviour where λ changes are hard. An additional bias η on λ can be used, where each λ has an associated biasing factor η. This bias will be removed by the acceptance rules. A careful calibration of η can make the λ histograms flat and hence can avoid the system getting stuck in a certain λ-range. There are three possible outcomes of a change from to

• λ remains between 0 and 1.

  The change in energy of the particle with the new compared to the old energy is computed and the move is accepted using

  There is no change in the number of particle, nor in the positions, nor in the intra-molecular energies. Only λ and the inter-molecular energy have changed.

• λ becomes larger than 1.

  When λ exceeds unity, , the current fractional molecule is made fully present (), and additional particle is randomly inserted with . Shi and Maginn used a methodology where a rigid conformation is chosen from a ‘reservoir’ of ideal gas molecules generated ‘on the fly’ during the simulation.

• λ becomes smaller than 0.

  When λ falls below 0, , the current fractional molecule is removed from the system (), and a new fractional molecule is chosen with a new lambda .

The acceptance rules for insertion and deletion depend on the ensemble. For use in the grand canonical ensemble, the rules are given by

where N is the number of integer molecules. Hence, appropriate measured densities and loadings should exclude the fractional molecule.

The fractional molecule has interactions with the systems but its influence vanishes in the thermodynamic limit. A scheme that completely avoids the influence of the fractional particle is to make discrete changes in λ and only take thermodynamic averages when or . However, this significantly reduces the amount of sampling points. A continuous distribution of couplings is therefore more convenient, and as we will show later, the influence of the fractional particle is in general small due to symmetry/cancellation.

The method is readily extended to other ensembles like the Gibbs ensemble. Here, an additional constraint is applied: the total lambda is unity, but the lambdas of the individual system are allowed to change, i.e. for box I and box II we require . The acceptance rule for a λ change which remains between 0 and 1 is

The insertion in box I is now accompanied by a deletion in box II and vice versa with acceptance rule

The case follows from symmetry, i.e. switching box labels I and II. Note that each box has a different set of biasing factors, for box I and for box II which are related by symmetry. The number of molecules N entering in the acceptance rules are the integer molecules (not including the fractional molecule). This is also the case for the volume move which has the conventional Gibbs acceptance rule. Also all other moves such as translation, rotation and MC-MD hybrid moves have conventional acceptance rules as these are done at constant λ.

Insertions become particularly difficult in strongly interacting fluids such as ionic liquids and water. At the low temperatures, the efficiency of Gibbs exchange moves was found to be two orders of magnitude higher than that obtained by state-of-the-art rotational and configurational bias moves. It is therefore a very powerful method to handle open systems at high densities. A downside of CFMC compared to CBMC is that it takes longer time to equilibrate at lower densities. Only at or , an attempt is made to delete or insert a molecule, respectively. Even when the λ moves are made equally likely using biasing, the diffusive nature of λ in the range makes the insertion/deletion rate lower. For this reason, Shi and Maginn used a relatively high percentage of λ moves in comparison to the other MC moves. To overcome this (small) issue in a practical way, one can first use CBMC or restart from a CBMC simulation.

The nature of the algorithm can lead to blocking issues. For example, in CFMC the potentials are scaled such that particle can overlap. Shi and Maginn noted that for water models the lack of Van der Waals interaction for the hydrogens leads to overlap of the negatively charged oxygen with the positively charged hydrogen. The repulsive force that normally prevents this has been reduced by the potential scaling. A simple solution is to reject all MC moves where atoms get closer, for example 1 Å.[180]

Reactive Monte Carlo

Many methods have been proposed to compute the equilibrium properties of chemically reacting or associating fluids.[183,184] The earlier methods required specification of chemical potentials or chemical potential differences. One of the most popular recent methods is the reactive Monte Carlo (RCMC) algorithm which samples reactions directly [185,186] (without going through the transition states). Therefore, only equilibrium properties can be computed. The method is conceptually simple, convenient and versatile. No chemical potentials or chemical potential differences need to be specified for the reaction steps, just the stoichiometry of the reactions. Essentially, the method enhances the GCMC with a ‘forward’ and ‘backward’ reaction step, which ensures that the chemical reaction equilibria between the reactants and the products are maintained. For a chemical reaction at equilibrium in a single- or a two-component system, the stoichiometric coefficient of each component i times the chemical potential of each component must be zero

The forward and reverse reaction steps are simply combinations of particle creation and destruction moves in the simulation box, and must be chosen with equal probability in order to maintain microscopic reversability in the system. For example, consider N₂+3H₂ → 2NH₃. In the forward move, one removes 3H₂ molecules and 1N₂ molecule and inserts 2NH₃ molecules, and accepts this move with the appropriate transition probability. In the backward move, 2NH₃ molecules are removed and 3H₂ molecules and 1N₂ molecule are inserted, and accepted/rejected with the appropriate transition probability. See Ref. [184] for details on the acceptance rules. Note that for open ensembles the chemical potential of only one of the components needs to be specified. One is free to choose which component to insert, but choosing the smallest molecule leads to faster convergence.[183]

RCMC simulations can be performed in the canonical,[185,186] grand canonical,[187,188] isothermal–isobaric,189190191 Gibbs [192] and other ensembles. When RCMC is used in conjunction with an ensemble that conserves the number of particles, the number of atoms rather than the number of molecules is held fixed.[183] The RCMC method has also been combined with the replica exchange scheme,[193] MD,[194] the CBMC scheme [177] and the CFMC scheme.[182]

MC moves

The two most common MC moves are rigid translation and rotation. The molecule is displaced or rotated by a small modification. The modification is usually scaled to achieve around 50% acceptance. In a strongly interacting fluid (e.g. water), the acceptance ratio of the rigid rotation becomes low and it might be better to do a full random rotation. The ‘reinsertion’ move removes a randomly selected molecule and reinserts it at a random position. For rigid molecules it uses orientational biasing, and for chains the molecule is fully regrown (the internal configuration is modified). The reinsertion move bypasses (free) energy barriers and is particularly useful to redistribute molecules over cages in nanoporous materials. At high densities, the acceptance ratio of the reinsertion move becomes vanishingly low. To properly sample the internal structure (i.e. bond/bend/torsions) the ‘partial reinsertion’ move is useful. Several atoms of the molecules are kept fixed, while others are regrown. Because there is already space for the atoms the acceptance ratios are high. For mixtures, especially at higher density, the ‘identity switch’ move becomes crucial. The identity-change trial move 152195196197 is called semi-grand ensemble,[198] but it can also be seen as a special case of the Gibbs ensemble. One of the components is selected at random, and an attempt is made to change its identity. The acceptance rule is given by [195]

where and are the fugacities of components A and B and and are the number of particles. CBMC operates on the ends of chains. To rearrange the conformation of interior segments, a concerted rotation MC method was introduced by Dodd et al. [199]. In the End-Bridging Monte Carlo method,[200,201] the end of a chain attacks the interior of another chain, separating it into two pieces by excision of a trimer segment. Subsequently, the attacking end is connected to one of the two pieces of the victim chain by construction of a new trimer. The move generally changes the lengths of the chains involved. Equilibration of long-chain polymer systems has been overcome through the development of connectivity-altering MC moves.[202]

To sample concerted motions of atoms the hybrid MC/MD can be used. To obtain a new configuration, a short NVE MD of M time steps is run and accepted or rejected.[203,204] The starting velocities are chosen from a Maxwell–Boltzmann distribution at the desired temperature. The acceptance rule is

Note that is the integration error and U is the total energy (potential energy and kinetic energy). The integrator must be time reversible and symplectic for the algorithm to obey detailed balance. The NVE hybrid algorithm has been extended to constant temperature, constant pressure and constant stress trajectories.205206207

The chiral inversion move is especially aimed to improve the sampling of chiral molecules.[208,209] In this operation, all atoms are transposed by a mirror operation that leaves the fixed framework invariant. This operation applies, in principle, to all atoms in the system. However, it only affects the orientation and position of guest molecules as zeolite atoms are just moved to a position that was previously occupied by an atom of exactly the same type. If chiral molecules are involved, the MC move changes every enantiomer to its opposite form in one single step, which can dramatically improve the ergodicity of the sampling. For MFI, for example, equals , with as the dimensions of the periodic simulation box. Let ξ denote the fractional content of the species in the bulk fluid phase such that . The acceptance rule is given by

where α now runs over all enantiomers and is the transposition of R

To overcome the low insertion rates at low temperature and/or high densities several advanced MC moves were developed. Uhlherr and Theodorou [210] developed a generic framework dubbed ‘MinMap Monte Carlo’. Insertions were performed over a series of m stages, with a separate minimisation after each stage. Initially, the atom was inserted as a repulsive soft sphere. Later stages slowly inflate the atom to a full Lennard-Jones interaction of the same size, complete with attractive tail. The main purpose of the quench is to relax the configuration by removing unrealistic interactions such as atom overlaps. Atom deletion moves followed the reverse procedure to deflate the selected atom prior to removal.

Many other moves and methods are published, e.g. energy–cavity biasing,[211] Reptation move,[212] aggregation–volume—bias,[213] as well as MC methods like recoil growth,[214,215] reverse MC,[216] phase switch MC,217218219 kinetic MC,220221222 rotational isomeric state MC,[223] basin-hopping MC,[224] tethered MC,[225] smart walking,[226] self-referential method,227228229 expanded ensembles,[230,231] Fragment regrowth MC [232] and Waste recycling MC.[233,234]

Parallel and hyper-parallel tempering

Parallel tempering, also known as replica exchange, is one of the methods that have been proposed to overcome the barriers facing traditional molecular simulation methods and to improve sampling of configuration space for complex systems.235236237238239 Open ensembles provide an effective means for overcoming some of the problems associated with slow relaxation phenomena. Yan and de Pablo proposed a combination of expanded ensembles (also known as simple tempering) and multidimensional parallel tempering, referred to as ‘hyper-parallel tempering’ Monte Carlo (HPTMC).[240] The hyper-parallel algorithm uses the three following moves:

• Conventional canonical MC moves to thermalise the system

• Trial shrink/growth moves are used to change the length of the tagged chain in each replica, thereby implementing the underlying expanded grand canonical formalism.

• Configuration swaps are proposed between pairs of replicas i and j. To enforce a detailed balance condition, the pair of replicas to be swapped are selected at random, and the trial swap move is accepted with probability

In addition to replica exchange in temperature the systems also differ in chemical potential. The algorithms have several parameters that need to be tuned such that there is sufficient overlap between the energy distributions of exchanging replicas: the amount and temperatures of the replicas and the frequency of swap attempts.

The general idea of parallel tempering is not limited to exchanges or swaps between systems at different temperatures. For example, Van Erp et al. performed parallel tempering in the mole fraction for adsorption of chiral mixtures.[209] The general distribution of an adsorbent that is in contact with a multicomponent gas is given by

where n is the number vector which denotes the number of molecules for each species α such that is the total number of adsorbed molecules, ξ denotes the fractional content of these species in the gas phase such that , μ gives the corresponding chemical potentials and is the thermal wavelength of species α. Van Erp et al. performed several simulations in parallel using the same fugacity and temperature but with different compositions of the external gas. The composition replica move has the following acceptance rule:

Using the ξ vector as an RE parameter is attractive, as the molecular content is also the parameter which is usually interested in when studying multicomponent adsorption.

Density-of-state (DOS) methods

The canonical partition function can be expressed as [241]

where is the lowest possible energy. Equation (126) suggests that if the unknown function can be generated for a wide range of energies then the partition function is known, and therefore any desired thermodynamic property. For example, the canonical partition function is related to the free energy by [241]

The computation of the partition function by numerical approximation is the basis for many DOS methods,[241] such as the reference system equilibration (RSE) method,[242] histogramming,[243,244] multihistogramming,[245,246] the histogram reweighting method,[247,248] the Wang–Landau sampling,[249,250] multicanonical methods,251252253 transition matrix methods [254,255] and the nested sampling (NS) algorithm.256257258259 DOS methods use a finite range of energies in practice, which means that the partition function can only be computed to within a multiplicative constant. It is easier to compute the partition function at a chosen temperature than to obtain the complete DOS. This is because the integrand is a sharply peaked function in E. Therefore, conventional MC is always more efficient for a predefined temperature, but when the objective is a range of temperatures then the DOS approach is more powerful.[241] The DOS technique, along with ‘work-based methods’, is able to compute free energy differences.[260]

Histogram reweighting method

The original histogram reweighting technique for MC simulations was developed by Ferrenberg and Swendsen for the canonical ensemble.[247,248] It has been extended to the grand canonical ensemble 261262263 and isothermal–isobaric ensemble.[264]

With only a few simulations, the entire vapour–liquid coexistence region of a pure fluid can be investigated.264265266267 The histogram methods can produce highly accurate data, especially in the vicinity of critical points.[266]

Histogram reweighting collects data for the probability of occurrence of N particles in the simulation cell with total configurational energy in the vicinity of E. The probability distribution has the following form

where is the microcanonical partition function and is the grand partition function. Neither nor are known at this stage but is a constant for a run at given conditions. The entropy can now be obtained as

with C a run-time constant.

In general, it is not possible to cover all thermodynamic states of interest from a single simulation. Instead, multiple simulations are required at various chemical potentials and temperatures. The histograms that result from the simulations can be combined by minimising the differences between predicted and observed histograms.[247,248] Let us assume that there are multiple overlapping runs, . The composite probability of observing N particles and energy E, assuming equal statistical efficiency, is

where is the total number of observations for run i. The weights , starting from an initial guess, can be obtained by iteration

Once convergence is achieved thermodynamic properties can be obtained (for the range of densities and energy covered). The mean configurational energy , and the mean density can be obtained from [266]

The pressure of a system can be obtained from the following expression. If the conditions for run 1 are and for run 2 , then

where P is the pressure, since . Only the pressure difference is obtained, but by performing a low-density simulation (for which the system follows the ideal gas equation of state ) the absolute pressure can be estimated. A plot of versus N gives a straight line of unit slope, which shows that the system behaves as an ideal gas at these conditions. It is possible to extrapolate to the limit, with the y intercept representing the additive constant.[268]

To combine multiple histograms, a reasonable amount of overlap must be present between neighbouring histograms. This means that when determining phase coexistence properties, there must be a connection between the liquid and vapour at the conditions of interest. In most cases, it is convenient to bridge the liquid and vapour regions with a run near the critical point. Additional histograms are added on the liquid and vapour sides as one progresses along the coexistence curve.

The methods have been generalised to mixtures.[266,268,269] In practice, it is impractical to work with 3D histograms as the range of phase space covered in a simulation can be quite large. Instead, it is more efficient to record periodically the set of , , E values. The required probability distribution is extracted from this list at the end of the simulation.[268]

Wang–Landau sampling

The Wang–Landau sampling method 4249250270271272273 has the objective to make all energies equally probable. During a random walk, the weights are iteratively adjusted using importance sampling. The weights that achieve a flat histogram are reciprocal to the DOS. The precision by which the weights are adjusted is iteratively increased until desired precision is reached. The algorithm proceeds as follows:

• Choose a set of energy ranges and set the density of states to unity in each

• Start random walk in energy space. The acceptance acceptance probability is

  The move is initially accepted with unity probability. Each time an energy level is visited, update the corresponding density of states by multiplying the existing value by a modification factor f>1

• Do the random walk until the accumulated histogram of energy is flat

• Reset the histogram and reduce the modification factor to continue and converge the

The main drawback of the method is that the statistics to estimate the convergence of the weight update factors are iteratively obtained. If the Wang–Landau technique is employed for systems with an infinite energy range, such as fluids, one often has to choose a finite range of energy (cutting off the high-energy range) either via trial and error or via calculation.

Shi and Maginn found that Wang–Landau sampling is very efficient in obtaining the biasing factors for CFMC.180181182 The λ range is for example divided into 10 bins. Initially, all biasing factors are zero. During equilibration, the bin corresponding to the current λ is modified according to after an MC move attempt, where ν is a scaling parameter initially set to 0.01. Histograms are measured, and in every 10,000 attempts the histograms are checked for flatness. The histogram is considered sufficiently flat when all bins are at least 30% as often visited as the most visited bin. If so, then histograms are set to zero and the scaling factor is modified to . Equilibration of η can be stopped once the value of ν is lower than .

Nested sampling

A recent method to explore the configurational phase space of systems is NS.[256,258,259,274] It is based on the original nested sampling algorithm proposed in the Bayesian statistics community by Skilling [275,276] and is able to explore the entire PES efficiently in an unbiased way. A unique strength of the method is that the sampling efficiency is not impeded by phase transitions, unlike the parallel tempering and Wang–Landau methods. To illustrate the differences, a hypothetical first-order phase transition is shown in Figure 6 (left), taken from Ref. [256]. Up-down denotes energy E and left–right the logarithm of available phase space . The thick lines in the parallel tempering and Wang–Landau sampling denote the region where a phase transition occurs. In this region, the energy rapidly changes over a small temperature range. This entropy jump makes equilibration and sampling difficult using these methods. NS avoids this by constructing a series of energy levels that are equispaced in . Hence, the energy level spacings near the phase transition will be narrow. The NS method constructs such a sequence of energy levels in a single top-down pass.

Figure 6 (Colour online) NS, (left) first-order transitions are dealt with differently by parallel tempering, Wang–Landau sampling, and NS (right). NS is a top-down approach where a set of random walkers converge downwards in energy at a rate equal to the logarithm of the phase space. Left figure taken from Ref. [256].

NS is a top-down approach (in energy) where the whole phase space is sampled using N sample points (‘random walkers’) that control the resolution. The error in scales as . The sampling procedure is as follows.

• Generate N random configurations, uniformly distributed over the space of all configurations.

• Find the highest energy among all with and remove the corresponding configuration.

• Replace the removed configuration with a new one subjected to the following two criteria:

  • the energy should be lower than the energy of the discarded configuration,

  • the energy should be uniformly distributed in the regions of the PES that has lower energy than .

  The new configuration should be drawn randomly from a uniform distribution over the space of configurations {x} with . A simple way to generate such configurations is to randomly choose one of the remaining sample points (which is guaranteed to be below the energy threshold ) and use MC to modify it.[257,276] Configurations that are lower in energy than are accepted and that are higher in energy than are rejected.

• Check for convergence, if not, go to 2.

Figure 6 (right) shows the procedure schematically. The top graph (‘Top’) shows the initialisation. One can use for example very high temperatures to obtain high energy random walkers uniformly distributed in phase space. In general, they will differ slightly in energy (they are enumerated in order of decreasing energy in the graph), and are able to explore a region of phase space around the walker (denoted with the thick blue dashed horizontal lines). A higher number N of walkers leads to a better estimation of the phase space. The process of going down in energy involves removing the highest energy walker (labelled 1) with energy and replacing it by a new configuration randomly sampled in phase space, but lower in energy than the walker 1. A convenient procedure is to randomly choose one of the other random walkers (here walker 3), and to do a random walk leading to a new energy and configuration of the random walker denoted with the red point. This new energy is required to be lower than . During the top-down scanning, the sequence of energies and the corresponding configurations {x} are recorded (e.g. stored to disc). This set is the input to compute expectation values of thermodynamic properties. The graph ‘Middle’ shows how, when the energies are lowered, some walkers will fall into local energy minima. These eventually will become the highest energy, and hence, they will be removed from the walkers. Therefore, the sampling is ergodic and the algorithm will not ‘get stuck’. Close to the global minimum (‘Down’) sampling becomes harder and harder. A random walk in phase space will rarely be accepted because there is exponentially more phase space for going up in energy rather than for going down. When no random walk is accepted anymore the algorithm can be considered converged.

After n iterations of the nested sampling procedure beginning with n = 0, the removed energy is assigned a phase-space weight of where is the phase-space volume ratio between neighbouring values, and the nested sampling approximation of the configurational partition function and of an observable is [256]

Since the sampled phase-space volume decreases exponentially with the iteration number n, the NS algorithm is able to sample exponentially small regions of configurational space. Because of the fixed α value, even energy regions where a phase transition occurs are properly sampled. Instead of using a fixed energy spacing, like in Wang–Landau, the NS algorithm automatically has more energy sampling in the region of a phase transition.

More generally, a smaller value of α could be used, but this would entail discarding more than one configuration per NS iteration and the expression to estimate the partition function would need to be modified. The NS is also able to compute free energy differences and rates. For free energy differences, the discarded configurations {x} need to be separated into ‘states’ using an appropriate metric.[256]

There is no temperature β in the sampling algorithm. The sampled weights are independent of β because is a monotonic function of E. Like all DOS methods, any observable can be evaluated at an arbitrary temperature just by re-summing over the same sample set. Of course for lower temperatures one needs more sampling of the energy basins, and for higher temperature the low-energy states contribute less to the partition function. In contrast to other DOS methods, the NS algorithm always converges with a resolution at the basins of the PES determined by the sample size N. High energies are sampled uniformly, with the low-energy samples directly obtained from the high-energy samples.

Pártay et al. demonstrate the new framework in the context of Lennard-Jones (LJ) clusters. For cluster size 2-5, N = 300, while for size 30–40, to achieve an essentially exact heat capacity versus temperature curve.[256] The latter corresponds to about energy evaluations. For LJ17, the efficiency gain of NS is a factor of 10 over parallel tempering, while for the larger LJ25 cluster, as the entropy jump is larger, the efficiency gain is a factor of 100.

Testing, debugging and verification

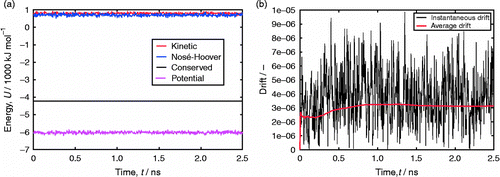
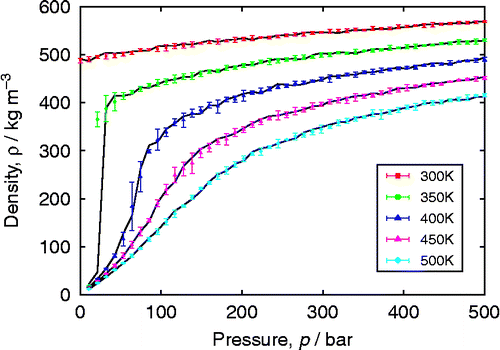
MC codes are notoriously difficult to debug. One deals with probabilities and energy distributions instead of generating deterministic trajectories like in MD. In MC, one can have sampling issues without knowing it. Error bars are in that respect not helping, because small error bars for short and intermediate runs usually are suspicious and indicatory of sampling problems. In this section, we describe tests that combine various methods (MC, MD and energy minimisation) and explore limiting cases (e.g. infinite dilution). It is therefore a good approach to not just have a code aimed at MC or only at MD, but have a code that combines all these methods. The advantage is that all energy evaluations and method details are consistent and can be controlled exactly. This combination of methods allows for a wide and various array of stress tests. In this section, we discuss a few examples.

Checking energies, gradients and higher derivatives

It is essential to implement the potential energy evaluation correctly. However, there is no real ‘test’ other than (1) checking the source routines carefully and (2) comparing to other codes. The first should be done regardless, but for the second option one has to make sure that all details are handled identically: e.g. cut-off radius, shifted at the cut-off or truncated or smoothed near the cut-off, tail corrections or not, charge method and Ewald precision. The different charge methods include shifted or smoothed Coulomb, Wolf's method, Ewald or Smoothed-Particle Mesh Ewald (SPME). VDW LJ size parameters are usually given in terms of σ, but sometimes the size value should be given as the potential minimum (e.g. default in TINKER). There are also force field conventions that must be handled identically which are as follows: Are 1-2 and 1-3 interactions removed from VDW and electrostatics? Is 1–4 removed or scaled or fully included or only handled when a torsion is also defined? Is the bendangle a conventional angle or handled as an in-plane/out-of-plane pair? and so on. Even codes that handle generic force fields (e.g. CHARMM, AMBER, OPLS, UFF and DREIDING) do not implement these details in exactly the same way or have different default settings. For testing (and other) purposes, it is convenient to have input/output converters for formats to and from other codes such as DLPOLY and TINKER. Table 1 shows a typical energy analysis of a snapshot done with these codes. The energies should be very close, but slight differences can appear due to different handlings of VDW cut-off and charge–charge interactions. For this comparison, these details were handled identically, except that RASPA uses conventional Ewald and TINKER/DLPOLY uses SPME for charge–charge interactions. One can generate snapshots of molecules and compare the energies between codes. One important source of error is the precision of writing/reading floating point numbers. Especially the use of file formats with limited precision such as pdb format is discouraged for this purpose.

Table 1 Energies of a snapshot of 20 CO₂ and 10 pentane molecules (TraPPE model) in a  Å box computed with RASPA, TINKER and DLPOLY 4.

	RASPA (K)	TINKER (K)	DLPOLY-4 (K)
Bond	7928.6266	7928.6266	7928.6
Bend	3729.0582	3729.0582	3729.1
Torsion	8410.5480	8410.5480	8410.5
VDW	− 11947.2181	− 11947.2184	− 12390.0 (includes tail)
Charge–charge	942.6349	942.429	942.70
Tail	− 442.9700		− 442.97
Total (with tail)	8620.6796	–	8620.7
Total (no tail)	9063.6496	9063.44368	–

Notes: All energies are given in Kelvin. Cut-off 12 Å, charge interaction computed with Ewald summation for RASPA and SPME for TINKER and DLPOLY.

Once energies are checked, the analytical forces can be compared with numerical estimates using finite difference methods. For example, using a central difference method with four energy evaluations one can obtain the gradient with fourth-order accuracy

The central difference divided by h approximates the derivative when h is small. Once the gradients have been tested and confirmed to be correct, the analytical gradients can be used to numerically evaluate the analytical second derivatives, again using finite differences. One thing to be aware of is that a truncated potential has a force divergence at the cut-off. A shifted potential is continuous in the force but discontinuous in the second derivative. For that smoothing functions are needed. Usually there are many particles in the system and it is in fact likely, despite the fact that h is small, that one of energy evaluations will place the particle outside of the cut-off while the other particles are inside. This can lead to errors in the numerical approximation of the forces. Keeping the positions the same and changing the cut-off slightly will show that the gradient was in fact correct. The comparison of smoothed potentials with continuous first and second derivatives should not have this problem.

In a similar way, it is possible to test the configurational part of the stress tensor and elasticity tensor. The stress tensor in the canonical ensemble is defined as

and the elasticity tensor

where the configurational parts are defined as energy derivatives with respect to strain ε

and where δ denotes the Kronecker delta. Often, the pressure tensor is defined as the negative of the stress tensor

The hydrostatic pressure is the trace of this tensor. The configurational part of the stress, pressure and the elasticity tensor can be approximated by deforming the simulation cell using a finite difference method. The atoms in the cell are kept fixed at their fractional coordinates and are not relaxed.

The instantaneous stress tensor is not necessarily symmetric. For example, for rigid molecules the tensor is asymmetric. The presence of intra-molecular constraints results in a force term to be added to the strain derivative of an atomic system.

and the conversion from atomic to molecular stress is

It is customary, however, to explicitly symmetrise the stress tensor.

Checking boundary conditions

The implementation of boundary conditions can be tested, e.g. by constructing different unit cells of a nanoporous material. The unit cell of the Chabazite zeolite (CHA) is usually defined as a triclinic structure with  Å, and . However, it is possible to transform the unit cell into different (but also periodic) cells. For example, to transform an , monoclinic cell to an , orthorhombic cell the following transformation matrix can be used

The unit cell volume is doubled. Figure 7 shows three possible CHA-type zeolite simulation cells. The primitive cell is the experimentally reported cell. However, one can convert this cell to body-centred, mono-clinic, orthorhombic, face-centre A, face-centre B, face-centre C and primitive 110 cells. In the Supporting Information Table S1 available via the article webpage, we list the data that show that statistically identical adsorption isotherms are obtained for all these structures.

Figure 7 (Colour online) Three possible CHA unit cells, (left) primitive cell, (middle) body-centred cell, (right) orthorhombic cell.

Orthorhombic cells allow for a faster implementation of the periodic boundary condition (Equation (16)), because the off-diagonal elements of the box matrix h are zero. When periodic unit cells are very large, for example MIL-101 with  Å and , the computation can be made tractable by converting the cell to a primitive cell  Å, .[277] The full cell has 14416 atoms, the primitive cell 3604 (4 times less).

Checking MD

Besides the force routines, MD needs an integration algorithm. In principle, MD is only well defined in the micro-canonical ensemble, but over the years integration algorithms have been developed for other ensembles such as the canonical, constant pressure and constant tension ensembles. These algorithms inevitable modify the trajectories, but only slightly and usually have negligible effects on dynamics properties. A good test is to first use the NVE ensemble as a reference simulation and measure the average temperature. Then an NVT simulation done exactly at that measured temperature can reveal any artefacts due to the thermostat. During an NVE trajectory, the sum of the potential and kinetic energy should be conserved, and this can be checked. But also the extended MD ensembles have a conserved quantity (when one adds the energy of the thermo- and barostats). Newton's equations of motion are time reversible and so should the integration algorithm. More generally, it is highly desirable to have a symplectic or measure-preserving integration algorithm.278279280281282283284 Figure 8 shows the excellent long-term energy conservation that is obtained when such integrators are used. The drift of the energy needs to be sufficiently small (usually smaller than ) for the trajectories to be considered accurate enough. To test the energy drift of the numerical integration algorithm for a given time step after N integration steps, one usually computes [278]

Figure 8 (Colour online) Energy conservation of rigid benzene molecules in MOF-74 at eight molecules per unit cells and 300 K.

Comparing average energies

For a single molecule, MC is able to compute the average interaction energy of a molecule inside a nanoporous material with high accuracy. MD, however, is not well suited to compute single-particle properties. For example, most thermostats require many particles and the intrinsic error decays inversely with the number of used particles. The low-density limit of MD remains difficult. The best (correct) solution is to view the limit as N very large and . However, this makes the simulations expensive, and the second best solution is to use, for example, 256 particles but remove all inter-particle interactions in the simulations (the particle only interacts with the framework; all particles feel the same thermostat). Figure 9 shows the comparison of MC and MD computing the average energy of a particle inside a nanoporous material as a function of temperature. The MC simulations use translation/rotation, and the CBMC simulation also includes the reinsertion move. Also included in the graph are the lowest binding energies obtained from energy minimisation. A combined view of all these methods shows that CBMC converges at low temperatures to the minimum energy at 0 K (as it should). Error bars on these simulations are small and the curve over temperature is smooth (as is physically expected). Conventional MC and MD shared the same flow at low temperature, namely these methods tend to get ‘stuck’ in local energy minima. The reinsertion move bypasses these free energy bottlenecks by simply deleting the molecule and randomly placing it elsewhere. To increase the acceptance of the reinsertion move, one can use multiple-first bead and orientational biasing (as is done here using k = 10 positions for the first bead, and k = 10 random orientations, out of which one is selected with the appropriate probability, usually the most energetically favourable one).

Figure 9 (Colour online) Comparison of average energies (left) using MC, CBMC and MD of methane in MgMOF 74 and CO₂ in DMOF at infinite dilution, (right) methane in FAU-type zeolite at N = 96 molecules per unit cell (lines CBMC, points MD). More than cycles were used for the production runs.

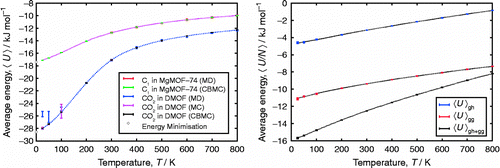
The data with error bars are listed in the Supporting Information (Tables S2 and S3) available via the article webpage. The results at higher temperatures where all used methods should be applicable for these systems show that MC with rotation and translation and MC with translation, rotation and reinsertion move and CBMC with just reinsertion give statistically identical results. There is also no influence (when simulated long enough) of the number k (number of first bead trials and trial orientations). This provides strong evidence that the reinsertion move is correctly implemented.

CBMC is very well suited to obtain the average energy of a single molecule, and this property is directly related to the enthalpy of adsorption at infinite dilution

where is the average energy of the particle inside the framework, the average energy of the framework and the average energy of the isolated (guest) molecule. The latter two energies are zero here, because the framework and the molecule are considered rigid. Figure 9 (left) shows a graph of the enthalpy of adsorption at infinite dilution. The low-temperature limit converges to the binding energy. At non-zero temperature, the (large) contribution of the entropy can be observed.

Figure 9 (right) shows a comparison of the average energy (per molecule) at finite loading. An excellent agreement between CBMC and MD is found (also see Table S4 of the Supporting Information available via the article webpage). Note that the average energy is not directly related to the enthalpy of adsorption, but rather has to be computed for example using the Clausius–Clapeyron equation, which requires the partial derivative of the pressure with respect to temperature at constant loading, or using a fluctuation formula

where the brackets denote an average in the grand canonical ensemble, N is the number of guest molecules and μ is the chemical potential of the guest molecules. Q in Equation (149) is usually defined as the isosteric heat of adsorption, and it is often applied at non-zero loading.[285] It is assumed here that the gas phase is ideal. The low loading limit should converge to Equation (148).

Validating NpT simulations

It is straightforward to verify NpT MC with NpT MD simulations. For consistency, in both simulation types a shifted potential is used (a cut-off of 12 Å). A starting box size of with 256 propane molecules was used. MC used 30000 initialisation cycles and 50000 cycles for production. The MD started with 10000 MC cycles, then 50 ps of velocity equilibration and 500 ps of time for the production run. The equations of motions were integrated using a measure-preserving integrator for MD in the isothermal–isobaric ensemble.[283,284] Figure 10 shows that both methods give statistically identical results (see Table S5 of the Supporting Information available via the article webpage).

Figure 10 (Colour online) NpT MC (points) versus MD (lines) for fluid properties of propane. MD simulations were run for 500 ps production run; MC used 30,000 initialisation cycles and 50,000 production cycles.

Validating CBMC growth

To validate the growth of CBMC, we examine the bond, bend and torsion distributions of S2butanol. The definition of the molecule was shown previously in Figure 4. The molecule has VDW and electrostatic interactions for atoms further than 1-4 apart (OPLS force field). Figure 11 shows the comparison of CBMC and MD. Note that for this molecule the energy landscape is already quite complex. The MD result for 16 and 1024 molecules is different. This is common and due to internal energy barriers between different conformations of molecules. For example, for n-alkanes, the experimental gauche–trans energy differences range from 0.5 to 1.0 kcal/mol.[286] Alkenes and cycloalkanes have rigid double bonds that prevent rotation, giving rise to cis and trans isomers. These geometric isomers cannot interconvert without breaking and re-forming bonds. Using more molecules in MD helps because it is closer to the proper distribution. (CB-)MC inherently generates the proper distribution and is therefore the most appropriate tool to investigate conformation energy barriers.[286] Another point to note is how different the dihedral distribution is without VDW and electrostatics. There are multiple torsions defined over the 4–7 bond, and the coupled–decoupled algorithm used here generates the correct internal energy distributions for the internal configurations. In the Supporting Information (Figures S1–S3) available via the article webpage, we have plotted all internal bond, bend and torsional distributions for CBMC and MD.

Figure 11 (Colour online) Growing S2butanol, comparison of CBMC and MD at 298 K of the torsional angle of atoms 0-4-7-9 (the four carbons of S2butanol): MD with 1024 and 16 molecules with internal VDW and electrostatics, MD with 16 molecules with no VDW and electrostatic interactions and CBMC.

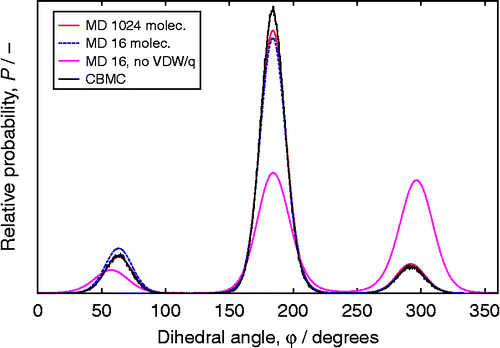
Martin and Siepmann validated their CBMC algorithms by performing some single-molecule calculations with a hit-and-miss integration program that creates individual molecule conformations from scratch by connecting n random vectors (where n is the number of bonds in that molecule).[71] Properties are then calculated by simple Boltzmann averaging using the total energy (the sum of bond bending, torsional and intra-molecular Lennard-Jones interactions). Although extremely inefficient, this allows one to compare the angle and torsional distributions generated via CBMC simulations with an independent, non-biased generation of the same quantities.

Validating adsorption isotherms

It is possible to validate the adsorption results by comparing to other codes, but there are less than a handful of codes that can do CBMC. However, a very good check is to validate CBMC against CFMC. In CFMC, no configurational biasing is used, only energy evaluations. The approach differs so much that an agreement between these methods is a high indication of the correct implementation of both algorithms. Of course, one must keep in mind that CBMC is limited up to a certain density while CFMC can handle dense systems.

Table 2 lists data for CO₂ and CH₄ in MFI-type zeolite. When run long enough both methods are statistical equivalent. Because of the diffusive nature of λ it can take quite some λ moves before an insertion or a deletion move is attempted. Equilibration therefore takes significantly longer at low loadings when compared to CBMC. However, for low temperatures and/or very high densities CFMC equilibrates much faster than CBMC. Figure 12 shows several isotherms run up to high densities. At low temperatures the CFMC leads to higher values, while the CBMC results are hampered by very low insertion rates (e.g. propane in UiO-66 at 200K). Note, however, that acceptance probabilities are only an indication of performance and not a proof. If a molecule is inserted, but subsequently removed before the environment could adjust to the insertion, then the insertion effort was basically in vain. Nonetheless, it is clear that acceptance probabilities should be at least a few per mill, and insertion and deletion probabilities should be equal in equilibrium.

Table 2 Comparison of CBMC and CFMC for adsorption of CO₂ and CH₄ in MFI, as a function of fugacity f.

	CO2 in MFI at 353 K				CH4 in MFI at 277 K
f (bar)	CBMC	acc. (%)	CFMC	acc. (%)	CBMC	acc. (%)	CFMC	acc. (%)
0.01	0.0295(5)	15.5	0.0287(8)	17.7	0.1052(8)	26.7	0.106(2)	52.3
0.1	0.292(2)	34.1	0.290(8)	37.4	1.005(4)	31.6	1.002(72)	73.0
1	2.55(1)	34.9	2.49(2)	41.1	6.492(18)	20.3	6.508(58)	65.4
10	11.21(9)	19.2	11.2(6)	46.1	14.091(9)	4.25	14.02(10)	68.8
100	17.81(12)	4.3	17.7(3)	43.7	17.266(25)	0.78	17.18(6)	75.0
1000	21.97(22)	0.9	21.9(6)	46.6	19.149(35)	0.08	19.06(11)	73.3
10000	26.3(1)	0.3	26.2(2)	46.4	20.740(49)	0.05	20.63(8)	75.8
100000	31.4(2)	0.06	31.0(7)	39.6	21.86(7)	0.01	21.76(8)	76.3

Notes: Adsorption in molec. uc^− 1. The acceptance percentages are, for both CBMC and CFMC, the insertion acceptances. The CFMC simulations used biasing. CBMC: 50,000 initialisation cycles, 500,000 production cycles, CFMC: 100,000 equilibration cycles (initialisation and Wang–Landau sampling), 500,000 production cycles.

Figure 12 (Colour online) CBMC (lines) versus CFMC (points) for (a) methane in MFI, (b) CO₂ in FAU, (c) propane in FAU, (d) propane in UiO-66.CBMC used 150,000 initialisation and 1,500,000 cycles for production; CFMC used 150,000 for initialisation and equilibration and 2,000,000 cycles for production.

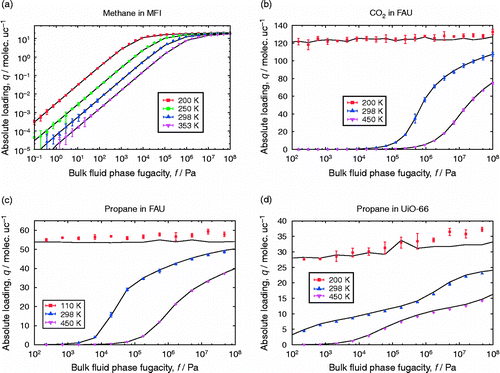
Validating Gibbs simulations

Similar to adsorption isotherms, also Gibbs CBCM simulations can be compared to CFMC. Numerical values for ethane and CO₂ VLE are listed in Tables 3 and 4, respectively. Again, excellent agreement is obtained. For strongly interacting fluids e.g. ionic liquids, methanol and water, the CFMC Gibbs is superior. Figure 13 shows the VLE data for CBMC and CFMC, also compared to published simulation data of Martin and Siepmann (who developed the TraPPE model for alkanes based on reproducing experimental VLE data). The right figure shows typical behaviour of λ. Without λ biasing the histogram of λ is peaked near unity. For more strongly interacting fluids λ will ‘get stuck’. Using WL sampling, biasing factors can be obtained which lead to essentially flat λ histograms. By construction, the vapour and liquid distributions are mirror images of each other. In the limit of the λ distribution being completely flat, the difference between adjacent values of is the free energy difference between these adjacent states.[181]

Table 3 Gibbs simulations of TraPPE ethane.

	TraPPE [70]		CBMC		CFMC		NIST (exp.)
T	Vapour	Liquid	Vapour	Liquid	Vapour	Liquid	Vapour	Liquid
178	2.2(1)	551(1)	2.3(2)	551.6(2.0)	2.3(3)	549.9(1.3)	1.5	552.1
197	5.6(5)	527(2)	5.2(2)	526.4(8)	5.2(5)	525.4(2.0)	3.7	527.9
217	10.0(3)	499(1)	10.7(7)	498.6(2.4)	11.0(1.1)	497.2(1.9)	8.1	500.0
236	20(2)	469(2)	19.2(1.1)	468.7(2.3)	20.2(3.4)	467.8(1.3)	15.4	471.6
256	31(4)	432(5)	33.8(1.7)	434.0(3.2)	33.3(2.9)	431.6(1.5)	28.2	436.8
275	56(8)	396(5)	53.8(1.2)	385.7(1.5)	53.2(4.6)	381.4(4.0)	48.8	396.1

Notes: Density is in kg m^− 3. CBMC: 50,000 initialisation cycles, 100,000 production cycles, CFMC: 50,000 equilibration cycles (initialisation and Wang–Landau sampling), 100,000 production cycles; in total, 500 molecules were used.

Table 4 Gibbs simulations of TraPPE CO₂.

	CBMC		CFMC		NIST (exp.)
T	Vapour	Liquid	Vapour	Liquid	Vapour	Liquid
220	17.9(0)	1169.8(0.8)	14.6(2.7)	1151.8(7.5)	15.817	1166.1
230	22.3(1.3)	1124.3(4.1)	22.8(2.6)	1119.1(7.7)	23.271	1128.7
240	30.4(1.7)	1086.0(2.6)	30.7(4.5)	1080(5.6)	33.295	1088.9
250	43.6(1.3)	1042.0(3.3)	46.4(2.9)	1037.5(8.9)	46.644	1046.0
260	60.3(0.7)	996.4(1.5)	61.0(2.1)	997.7(9.2)	64.417	998.89
270	82.2(4.1)	947.6(6.5)	84.3(8.5)	945.5(7.6)	88.374	945.83
280	117.1(5.5)	891.3(10.2)	107.9(9.7)	888.2(15.5)	121.74	883.58

Notes: Density is in kg m^− 3. CBMC: 50,000 initialisation cycles, 100,000 production cycles, CFMC: 50,000 equilibration cycles (initialisation and Wang–Landau sampling), 100,000 production cycles; in total, 500 molecules were used.

Figure 13 (Colour online) CBMC versus CFMC Gibbs comparison of computed coexistence properties, (a) VLE of ethane and CO₂ (lines are experimental data taken from NIST), (b) histograms of λ for ethane at 178 K (lines are without biasing; points are with biasing; boxes are the biasing factors).

Mixture isotherms, IAST and identity change

Mixtures can also be validated by comparing CBMC to CFMC. At low and medium densities, the results with and without the identity switch move should be identical. Furthermore, it is known that Ideal Adsorption Solution Theory (IAST) works very well for homogeneous systems (i.e. no segregation). IAST predicts the mixture based on pure components,[287] and can be used as a first guess where to expect the mixture results to be. MC simulation can be used to validate IAST, which then can be confidently applied to experimental isotherms (in experiments it is very difficult to measure mixture isotherms directly). Figure S4 in the Supporting Information available via the article webpage shows that IAST works qualitatively well for this system. In Table 5, we show that for a CO₂/N₂ mixture all the mixture simulations are in agreement with each other within the statistical error. The results with and without identity switch move are identical. Note that acceptance probabilities of the identity switch moves are high over the full loading range for molecules that are similar in size and shape.

Table 5 CBMC versus CFMC for an equimolar mixture of CO₂/N₂ in DMOF at 300 K, with and without the identity switch move.

	CBMC (identity)				CBMC (without identity)
p (bar)	CO2	acc. (%)	N2	acc. (%)	CO2	N2
0.2	0.409(5)	20.0	0.301(3)	75.1	0.404(5)	0.0331(5)
0.6	1.314(9)	32.2	0.099(7)	55.2	1.30(3)	0.0986(7)
1	2.27(3)	36.7	0.160(1)	47.4	2.27(2)	0.1600(8)
2	5.04(4)	37.1	0.284(2)	40.0	5.04(6)	0.284(4)
5	10.27(5)	31.6	0.388(3)	32.5	10.23(4)	0.388(3)
10	12.81(6)	27.1	0.397(5)	27.9	12.79(3)	0.393(6)
20	14.47(4)	23.2	0.397(4)	23.9	14.46(5)	0.394(7)
	CFMC (identity)		CFMC (without identity)		IAST
p (Pa)	CO2	N2	CO2	N2	CO2	N2
0.2	0.413(8)	0.0327(8)	0.40(2)	0.033(1)	0.590	0.034
0.6	1.30(5)	0.098(4)	1.28(5)	0.097(3)	1.694	0.095
1	2.28(4)	0.157(3)	2.22(8)	0.157(3)	2.75	0.15
2	4.92(13)	0.277(4)	4.95(24)	0.28(1)	5.10	0.26
5	10.05(14)	0.385(5)	10.16(21)	0.372(18)	9.68	0.43
10	12.64(8)	0.397(4)	12.58(9)	0.40(2)	12.82	0.54
20	14.32(3)	0.394(5)	14.3(2)	0.40(5)	14.57	0.55

Notes: The IAST is computed from the CBMC pure component isotherms. Units of adsorption in mol kg^− 1. The reported acceptance percentages are for the identity switch for an attempt to change it to the other component. CBMC: 50,000 initialisation cycles, 20,0000 production cycles, CFMC: 10,0000 equilibration cycles (initialisation and Wang–Landau sampling), 25,0000 production cycles.

Conclusions

We have reviewed modern MC algorithms and discussed some validation methodology. The basis of an MC code, the energy evaluations, can be compared to other codes or checked by hand for snapshots of molecules. Derivatives of energies can be easily checked numerically. To properly check more advanced MC algorithms, it is useful to implement two (or more) quite different techniques (e.g. CBMC and CFMC) that overlap in applicability for a large range of conditions. Comparison of MC and MD is feasible, but care must be taken so that the same property is measured.

Acknowledgements

The authors thank T.J.H. Vlugt for comments on the manuscript and detailed discussions on CBMC, coupled–decoupled CBMC and CFMC and Steven Nielsen for very helpful discussions regarding nested sampling. This material is supported by the Netherlands Research Council for Chemical Sciences (NWO/CW) through a VIDI grant (David Dubbeldam) and the National Science Foundation CAREER Award 0969261 and PECASE Award ARO W911-10-0079 (Krista S. Walton).