Finite-size effects of diffusion coefficients computed from molecular dynamics: a review of what we have learned so far

ABSTRACT

The number of molecules used in a typical Molecular Dynamics (MD) simulations is orders of magnitude lower than in the thermodynamic limit. It is therefore essential to correct diffusivities computed from Molecular Dynamics simulations for finite-size effects. We present a comprehensive review on finite-size effects of diffusion coefficients by considering self-, Maxwell–Stefan, and Fick diffusion coefficients in pure liquids, as well as binary, ternary, and quaternary mixtures. All finite-size corrections, both analytical and empirical, are discussed in detail. The finite-size effects of rotational and confined diffusion are also briefly discussed.

KEYWORDS:

• Finite-size effects
• self-diffusivities
• Maxwell–Stefan diffusivities
• Fick diffusivities
• molecular dynamics

1. Introduction

Mass transport by diffusion plays a crucial role in a wide variety of processes in nature and engineering. Such processes are separation, drug and protein delivery in living organisms, fog formation, powder metallurgy, and many others [1–5]. Diffusion is commonly described as the mass flux (i.e. transport) due to a gradient of concentration or chemical potential of a component [6–8]. In liquids, diffusion is a relatively slow process and is often a limiting factor in engineering applications [9–11]. Usually, the diffusion in engineering applications involves multicomponent liquid mixtures [11,12]. The accurate prediction of diffusivities of these mixtures is therefore very important [13]. Self-diffusivity is the motion of individual molecules in a pure liquid or in a mixture due to random Brownian motion, i.e. in the absence of an external driving force [14–16]. Technically, collective diffusivities are of greater interest in engineering applications. Collective diffusion describes the net transport of a component in a multicomponent mixture relative to a reference motion of another component. The mass flux in collective diffusion is described by a gradient in chemical potential due to differences in temperature, concentration, pressure and/or electric field [11,16,17].

The framework for the systematic study of diffusion was established by the pioneering studies of Graham [18] and Fick [19] in the mid-19th century. Since then, experimental methods for measuring the diffusivity in liquids have significantly improved. Such methods include Nuclear Magnetic Resonance (NMR) [20], Raman Micro-spectroscopy [21], Dynamic Light Scattering (DLS) [22,23] and holographic interferometry [24]. Despite this progress, experimental measurements are often challenging to perform. In many cases, experiments require special and costly equipment and can be very time consuming for mixtures with sluggish dynamics [25–27]. Moreover, experimental measurements can be dangerous when poisonous or explosive compounds are studied, and when high temperatures and/or pressures are required [28,29]. The resolution of experiments is generally too low for obtaining insight at the molecular level [30]. To this end, theoretical approaches based on the kinetic theory and hydrodynamics have been developed to predict diffusivities. Such approaches are the well-known Stokes–Einstein [31] and Wilke–Chang [32] models. Recently, Gross and co-workers [33] proposed a model according to which the self-diffusion coefficients of pure liquids can be calculated from the scaling of the excess entropy, using the Perturbed-Chain Polar Statistical Associating Fluid Theory (PCP-SAFT) equation of state. Nevertheless, such semi-empirical correlations cannot be generalised for all fluids. A detailed discussion on theoretical approaches for obtaining diffusion can be found elsewhere [3,11,12,34,35].

After more than half a century of practice, molecular simulation has been matured into a powerful tool for computing diffusion coefficients of pure fluids and mixtures, complementing experiments and models [6,10,30,36–55]. Diffusion coefficients can be computed by performing Molecular Dynamics (MD) or Kinetic Monte Carlo (KMC) simulations [37,38,56]. The MD approach is by far the most widely used, and thus the focus of this review. In MD, diffusion coefficients can be computed either by using equilibrium (EMD) or non-equilibrium (NEMD) simulations [57,58]. In NEMD simulations, an external driving force is used to exert a net flux in the system from which the transport properties can be calculated [36,37,59–62]. In EMD, diffusivities are computed in mixtures at equilibrium, i.e. in the absence of external forces. The Green-Kubo (GK) method and Einstein relations are two common approaches in EMD simulation. The GK method [52,53,63–66] is based on the computation of integrals of velocity-time correlation functions, while the Einstein relations are based on the linear fit to mean-squared displacements as a function of time [14,67–69].

EMD simulations have been extensively used for computing self-diffusivities of fluid models, e.g. hard spheres and Lennard-Jones (LJ) particles [70–74], as well of a wide variety of molecular fluids, e.g. water, carbon dioxide, hydrocarbons, ionic liquids, deep eutectic solvents, and biomolecules [48,75–85]. Many studies have focused on the computation of self-diffusivities in mixtures [86–89]. EMD has also been widely used to predict collective diffusivity in binary, ternary, and multicomponent mixtures [30,49–52,61,90–98]. To describe collective diffusion in mixtures, the Maxwell–Stefan (MS) theory and Fick's law are the most commonly used approaches [1,11,13,17,94]. According to the MS theory, a gradient in chemical potential is the driving force for mass transport [94]. Since chemical potentials cannot be directly measured in experiments, the determination of MS diffusion coefficients is challenging [13,50,94]. MS diffusivities can be computed in EMD simulations using so-called Onsager coefficients. Onsager coefficients allow for a phenomenological description of diffusion based on the Onsager theory of irreversible thermodynamics, which relates the velocity difference of the individual components to chemical potential gradients [17,94,99,100]. Contrary to MS diffusivities, Fick's diffusion [17,19] can be directly measured experimentally. Since MS and Fick describe the same physical phenomenon, these diffusivities are related. The conversion between Fick and MS diffusivities is enabled by the so-called matrix of thermodynamic factors, which is a measure of the non-ideality of the mixtures [101,102]. A way to obtain thermodynamic factors is via Kirkwood–Buff integrals (KBIs) [103–107]. KBIs are expressed as either integrals over the radial distribution functions (RDFs) of a closed subvolume in canonical MD simulations, or as density fluctuations of an open and infinite system in grand-canonical simulations [106,108,109]. For an in-depth discussion on KBIs as well as on self-, MS and Fick diffusivities, the reader is referred to the relevant literature [6,50,94,106,107,109–111].

A remaining challenge of MD simulations is the limited system size. The system sizes used in a typical MD simulation vary from a few hundred to several thousands of molecules. Periodic boundary conditions are traditionally imposed in all directions to mimic the bulk fluid phase and eliminate surface effects [36–39]. Due to the long-range nature of hydrodynamic and electrostatic interactions between molecules in the simulation box and with the periodic images (because of periodic boundary conditions), dynamical properties may suffer from the finite-size effects [37,112,113]. In particular, the computation of diffusivities [74,114–118], activity coefficients [119], thermal conductivities [120], ionic conductivities [121], and KBIs [122,123] have been shown to depend on the system size. Other properties, such as the shear viscosity are not affected by the system size [78,124–126]. As Dünweg and Kremer [114] explicitly state in their pioneering work on the dynamics of polymer chains, to avoid such finite-size effects one may consider performing simulations without periodic boundary conditions, e.g. using hard walls. Nevertheless, such a choice would simply introduce different effects which are possibly more difficult to control, e.g. unwanted fluid-wall interactions. It is important to note that finite-size effects are present in the computation of both self- [78,127] and collective diffusivities [91,117,128], both in pure liquids and multicomponent mixtures. To mitigate finite-size effects, researchers have used relatively large system sizes, large cut-off radii in the interaction potentials, or analytic corrections [51,77,115,129,130].

In this review paper, we present a comprehensive discussion of the finite-size dependence of self- and collective diffusion coefficients computed with EMD simulations for various molecular and LJ systems. Our study covers pure fluids, binary, ternary and quaternary mixtures. Finite-size effects for diffusivity computations in confined systems, and for rotational diffusion are also briefly discussed. The rest of the manuscript is organised as follows: In Section 2, the available MD codes for computing diffusion coefficients are presented. The finite-size dependence and available correction terms for self, rotational and collective diffusivities are discussed in Sections 3, 4 and 5, respectively. Finite-size effects of diffusion of confined liquids is also discussed in Section 3. Our main findings are summarised in Section 6.

2. Computational details and available software

The open-source MD packages LAMMPS [131] and GROMACS [132] are widely used for computing transport properties of liquids. One of the reasons for the popularity of these packages is the default built-in features and tools which can be used to calculate diffusion coefficients based on the Green-Kubo and Einstein methods [36,133]. The source codes of both LAMMPS and GROMACS are designed in a modular way which promotes the development of new features by the simulation community. Recently, a new open-source plugin for LAMMPS, called OCTP (On-the-fly Calculation of Transport Properties), has been developed by Jamali et al. [134,135]. OCTP uses Einstein relations combined with the order-n algorithm [36,136] to accurately compute the following properties: shear and bulk viscosities, radial distribution functions (RDFs), thermal conductivities, and self- and MS diffusivities. In addition, Humbert et al. [137] has recently developed the open-source post-processing tool PyLAT (Python Analysis Tools) for LAMMPS which enables the computation of several transport properties such as viscosities, self-diffusivities, ionic conductivities, dielectric constants, and RDFs. Deublein et al. [138] developed a molecular simulation program named ms2, to compute thermodynamic and transport properties of pure liquids and multicomponent mixtures based on classical MD and MC simulations. In ms2, static properties such as thermal and caloric properties, chemical potentials, vapour-liquid equilibria, Henry's law constant, and second virial coefficients, and dynamic properties such as self-diffusion coefficients, MS diffusivities, shear and bulk viscosities can be computed in different ensembles.

All diffusivities presented in this study are computed using the OCTP plugin in LAMMPS. A schematic representation of the workflow for computing self- and collective diffusivities is shown in Figure 1. The exact simulation scheme and force field details can be found in our previous studies [117,128].

Figure 1. (Colour online) The workflow on how to compute diffusion coefficients in liquid mixtures.

3. Finite-size dependence of self-diffusivities

The study by Dünweg and Kremer [114] was one of the first focusing on finite-size effects of dynamic properties computed in MD. The authors carried out MD simulations of a polymer chain diluted in a good solvent for different system sizes. It was shown that the computed diffusion coefficient of the chain scales linearly with the inverse of the simulation box length, L, which is proportional to $N^{1/3}$ (where N is the number of molecules). This means that the self-diffusivities of a molecule in the thermodynamic limit, $D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{\infty }}$, can be obtained by linear extrapolating to $1/L\to 0$. Almost a decade later, Yeh and Hummer [115] validated the findings of Dünweg and Kremer by performing MD simulations of LJ particles and TIP3P [139] water. To obtain $D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{\infty }}$, Yeh and Hummer [115] derived an analytic finite-size correction term based on hydrodynamics [115]. Although the same term has been already derived by Dünweg and Kremer [114], it is commonly referred to as the Yeh–Hummer (YH) correction: (1) $D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{\infty }}=D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{M}\mathrm{D}}+\frac{k_{\mathrm{B}}T\xi }{6\pi \eta L}$(1) where $D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{M}\mathrm{D}}$ is the finite self-diffusion coefficient computed in MD simulations, ($k_{\mathrm{B}}$) is the Boltzmann constant, T is the absolute temperature, $\eta$ is the shear viscosity computed in MD simulations, and $\xi$ is a dimensionless constant equal to 2.837298 for periodic (cubic) lattices [140,141]. $D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{M}\mathrm{D}}$ and $\eta$ can be directly computed in EMD simulations using the Einstein relations [36,37,134]: (2) $D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{M}\mathrm{D}}=\underset{t\to \mathrm{\infty }}{lim}\frac{1}{6N_{i}t}⟨\sum _{j=1}^{N_i}{\left({\mathit{r}}_{j,i}\right(t)-{\mathit{r}}_{j,i}(0\left)\right)}^2⟩$(2) and (3) $\eta =\underset{t\to \mathrm{\infty }}{lim}\frac{1}{2t}\frac{V}{k_{\mathrm{B}}T}⟨{\left({\int }_0^t{P}_{\alpha \text{β}}\left(t^{\prime }\right)\mathrm{d}{t}^{\prime }\right)}^2⟩$(3) where ${\mathit{r}}_{j,i}\left(t\right)$ is the position of the j-th molecule of species i at time t, and $N_i$ is the number of molecules of species i in the system. $P_{\alpha \text{β}}$ are the off-diagonal components of the stress tensor (i.e. $P_{xy}$, $P_{xz}$, and $P_{yz}$), and V is the volume of the system. The angular brackets denote an ensemble average. It is important to note that $\eta$ computed from EMD does not exhibit finite-size effects. [78,115,124–126]

In addition to LJ fluids and water, the validity and applicability of the YH correction has been shown for various components, e.g. carbon dioxide, n-alkanes, and deep eutectic solvents [30,78,130,142]. The magnitude of the finite-size effects may significantly vary, depending on the system type and the thermodynamic conditions [127,128]. For example, as shown by Moultos et al. [78], the YH correction needed to compensate for the finite-size effects of the computed diffusivity of CO${}_2$ at 323.15 K and 200 bar using 250 molecules is ca. 8%, a value which is comparable with the error in the calculation of the diffusivity of a finite-size system. In sharp contrast, for systems in which the solute size is significantly larger than the size of the solvent molecules, the YH correction can be even larger than the computed diffusivity. In particular, recently Erdös et al. [143] computed the diffusivity of cyclodextrins in water and showed that the YH correction is ca. 30% to 75% of the final (corrected) self-diffusion coefficients (depending on T and P). Thus, in such systems, the use of finite-size corrections is imperative, even if relatively large system-sizes are used in MD simulations (i.e. 6000 molecules [143]). Based on the YH correction (Equation (1(1) $D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{\infty }}=D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{M}\mathrm{D}}+\frac{k_{\mathrm{B}}T\xi }{6\pi \eta L}$(1) )), and by assuming that the self-diffusivity of a molecule, with effective hydrodynamic radius R, can be described using the Stokes–Einstein equation [14,31,144] (4) $D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{\infty }}=\frac{k_{\mathrm{B}}T}{6\pi \eta R}$(4) one can derive the following: (5) $\frac{D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{M}\mathrm{D}}}{D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{\infty }}}=1-\xi \frac{R}{L}$(5) Equation (4(4) $D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{\infty }}=\frac{k_{\mathrm{B}}T}{6\pi \eta R}$(4) ) shows that the finite-size effects of self-diffusivity depend on the size of the diffusing molecule with respect to the size of the simulation box. Hence, it is not surprising that finite-size effects in diffusivity computations were initially observed for polymers [115].

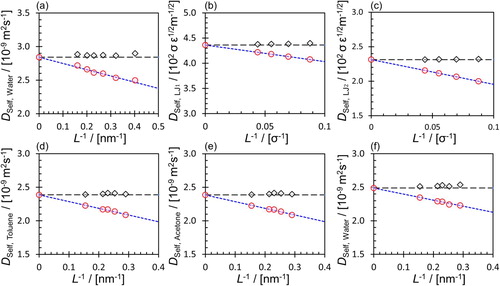
In Figure 2, finite-size effects are shown for the self-diffusivity of several pure fluids and mixtures. Figure 2(a) shows the self-diffusion coefficient of SPC/E water as a function of the system size. The simulations were carried out at 298.15 K and 1.0 atm, considering six system sizes in the range of 512–8000 molecules. The self-diffusivity of SPC/E water in the thermodynamic limit deviates by 1.3% from the corrected diffusivity using the YH expression (Equation (1(1) $D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{\infty }}=D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{M}\mathrm{D}}+\frac{k_{\mathrm{B}}T\xi }{6\pi \eta L}$(1) )). These results are in agreement with the self-diffusivity of SPC/E water reported in literature [127,142,145]. The finite-size effects of the self-diffusivity in a binary LJ system are shown in Figure 2(b) and (c). For this system, dimensionless reduced units were considered where $ϵ$, $\sigma$ and m are the LJ parameters, and the mass, respectively. The first component (LJ${}_1$) is used as the basis with ${ϵ}_1=ϵ=1$, ${\sigma }_1=\sigma =1$ and $m_1=m=1$. The parameters of the second component (i.e. LJ${}_2$) are ${ϵ}_2=1$, ${\sigma }_2=1.6\sigma$ and $m_2={\sigma }^3$. Equimolar binary mixtures for four system sizes (500, 1000, 2000 and 4000 particles) were considered. Simulations were performed at a reduced temperature of 0.65 and a reduced pressure of 0.05, corresponding to an average reduced density of 0.34. As in pure liquids, self-diffusion coefficients in binary mixtures vary proportionally with the inverse of the simulation box length. The difference between the corrected self-diffusion coefficients using the YH expression and extrapolated values to the thermodynamic limit is less than 1%. To test the validity of the YH correction for the self-diffusion coefficients in ternary molecular mixtures, MD simulations of the toluene/acetone/water mixture were carried out at 298.15 K and 1 atm. Results are shown in Figure 2(d–f). Four different system sizes consisting of 400–1500 molecules (in total) were simulated. The mole fractions of toluene, acetone and water are 0.10 0.65 and 0.25, respectively. The density of the system is 835 kg/m${}^3$, which agrees with the experimental density [146]. The OPLS-AA force field was used for Toluene [147] and Acetone [148], and the SPC/E force field [149] was used for water. As shown clearly in Figure 2, for both LJ fluids and molecular systems, the YH correction (Equation (1(1) $D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{\infty }}=D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{M}\mathrm{D}}+\frac{k_{\mathrm{B}}T\xi }{6\pi \eta L}$(1) )) can accurately predict the finite-size effects of self-diffusivity.

Figure 2. (Colour online) (a) Self-diffusion coefficients of pure water at 298.15 K and 1 atm for six system sizes consisting of 512–8000 molecules. (b) Self-diffusion coefficients of binary LJ mixtures at a reduced temperature of 0.65 and a reduced pressure of 0.05 for LJ${}_1$, and (c) LJ${}_2$ for four system sizes consisting of 500, 1000, 2000, and 4000 particles. (d) Self-diffusion coefficients of toluene, (e) acetone and (f) water in a ternary mixture of toluene-acetone-water at 298.15 K and 1 atm ($x^{\mathrm{t}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{e}\mathrm{n}\mathrm{e}}=0.1$, $x^{\mathrm{a}\mathrm{c}\mathrm{e}\mathrm{t}\mathrm{o}\mathrm{n}\mathrm{e}}=0.65$, and $x^{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}=0.25$) for 5 system sizes consisting of 400–1500 molecules. The uncorrected MD results are shown with red circles. Grey diamonds show the corrected self-diffusion coefficients using Equation (1(1) $D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{\infty }}=D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{M}\mathrm{D}}+\frac{k_{\mathrm{B}}T\xi }{6\pi \eta L}$(1) ). Blue dashed lines are the linear extrapolation of MD results to the thermodynamic limit and black dashed lines are the extrapolated values. The axes of subfigures scales differently.

Recently, Jamali et al. [126] proposed a method (called D-based) for computing shear viscosities of pure and multi-component fluids by exploiting the finite-size effects of self-diffusivities. In this method, a linear regression is performed to self-diffusivities computed for at least two different system sizes. The slope of the linear fit is proportional to the inverse of the shear viscosity because of the YH correction term (Equation (1(1) $D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{\infty }}=D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{M}\mathrm{D}}+\frac{k_{\mathrm{B}}T\xi }{6\pi \eta L}$(1) )). Jamali et al. [126] tested this method using 250 binary and 26 ternary LJ systems, pure water, and ionic liquid Bmim [Tf${}_2$N] ionic liquid. The obtained viscosities were shown to be in good agreement with the ones computed directly in EMD using the conventional methods (e.g. Einstein relations). For the exact details on the D-based method and guidelines for using it in the most efficient way, the reader is referred to the original paper [126].

3.1. Finite-size dependence of self-diffusivities of fluids in confinement

The self-diffusivity of a liquid in a nanochannel may significantly deviate from the self-diffusivity in the bulk phase due to both the actual confinement effect (fluid-wall interactions) and the use of periodic boundary conditions [116,150]. It has been shown that the physical properties of liquids in confinement such as the pressure, density, viscosity and diffusivity can spatially vary (i.e. evidence of localised phenomena) [151–161]. These local effects typically subside within a couple of molecular diameters away from the walls [162–165]. This means that, as channel diameter increases, dynamic properties (i.e. viscosity, diffusivity) eventually become equal to the respective quantity in the bulk phase [165–167]. Recently, Simonnin et al. [116] investigated how the self-diffusion coefficient of a nanoconfined fluid is affected by the confining distance (H) and the simulation box length parallel to the wall (L). Simonnin et al. [116] showed that the self-diffusion coefficient decreases as the simulation box length parallel to the wall (L) increases. This effect is evident due to the use of periodic boundary conditions. Furthermore, the diffusion coefficient increase with increasing confining distance. This is mainly due to the receding effect of wall-liquid interactions, as also discussed earlier in other studies [168–171]. An analytic correction term for finite-size dependence in nanoconfined fluids was derived by Simonnin et al. [116] using continuum hydrodynamics. This term accounts for the contribution of both L and H. The model was developed for an LJ fluid in a slit-like pore with no-slip condition, and the finite-size correction of such system was validated using MD simulations: (6) $D_{\mathrm{I}\mathrm{I}}^{\mathrm{\infty }}=D_{\mathrm{I}\mathrm{I}}^{\mathrm{M}\mathrm{D}}+\frac{k_{\mathrm{B}}T}{\eta }\left[\frac{3}{40}\frac{H}{L^2}-\frac{3\ln (1+\sqrt{2})}{4\pi L}\right]\mathrm{f}\mathrm{o}\mathrm{r}H>L$(6) (7) $D_{\mathrm{I}\mathrm{I}}^{\mathrm{\infty }}=D_{\mathrm{I}\mathrm{I}}^{\mathrm{M}\mathrm{D}}-\frac{1}{24}\frac{k_{\mathrm{B}}T}{\eta }\frac{H}{L^2}\mathrm{f}\mathrm{o}\mathrm{r}H\le L$(7) where $D_{\mathrm{I}\mathrm{I}}^{\mathrm{\infty }}$ and $D_{\mathrm{I}\mathrm{I}}^{\mathrm{M}\mathrm{D}}$ are the self-diffusion coefficients for nanoconfined liquid in thermodynamic limit and at finite-size, respectively. These finite-size correction terms (Equations (6(6) $D_{\mathrm{I}\mathrm{I}}^{\mathrm{\infty }}=D_{\mathrm{I}\mathrm{I}}^{\mathrm{M}\mathrm{D}}+\frac{k_{\mathrm{B}}T}{\eta }\left[\frac{3}{40}\frac{H}{L^2}-\frac{3\ln (1+\sqrt{2})}{4\pi L}\right]\mathrm{f}\mathrm{o}\mathrm{r}H>L$(6) ) and (7(7) $D_{\mathrm{I}\mathrm{I}}^{\mathrm{\infty }}=D_{\mathrm{I}\mathrm{I}}^{\mathrm{M}\mathrm{D}}-\frac{1}{24}\frac{k_{\mathrm{B}}T}{\eta }\frac{H}{L^2}\mathrm{f}\mathrm{o}\mathrm{r}H\le L$(7) )) are in good agreement with MD simulation results, except for very narrow channels [116]. In narrow channels, the assumptions based on classical constitutive equations break down, e.g. Newton's law of viscosity. Consequently, continuum variables such as viscosity, diffusivity, thermal conductivity obtained from constitutive equations become inaccurate [152,161,172].

4. Finite-size dependence of rotational diffusivities

Finite-size effects are also present in the computation of rotational diffusion [173] in EMD. The accurate prediction of rotational diffusivity is mainly important for the design of bio-engineering applications, which involves relatively large and rather asymmetric molecules (e.g. DNA, RNA, carbohydrates). To this purpose, studies have investigated the scaling of the rotational diffusivity with the system size [174–176]. Linke et al. [177] performed MD simulations of B-DNA dodecamer and horse-heart myoglobin using various system sizes. Linke et al. [177] developed an analytic correction term to account for the finite-size dependence of the computed rotational diffusion coefficients in three-dimensions (3-D): (8) $D_{\mathrm{R}\mathrm{o}\mathrm{t}}^{\mathrm{\infty }}=D_{\mathrm{R}\mathrm{o}\mathrm{t}}^{\mathrm{M}\mathrm{D}}+\frac{k_{\mathrm{B}}T}{6\eta V}$(8) where $D_{\mathrm{R}\mathrm{o}\mathrm{t}}^{\mathrm{\infty }}$ and $D_{\mathrm{R}\mathrm{o}\mathrm{t}}^{\mathrm{M}\mathrm{D}}$ is the rotational diffusion coefficient in the thermodynamic limit and the one computed in MD simulations, respectively. $\eta$ is the shear viscosity and V is the volume of the simulation box. A similar correction term for the finite-size effects of the rotational diffusivity of biological membrane proteins and carbon nanotubes was derived by Vögele et al. [178] based on a two-dimensional (2-D) periodic Stokes flow: (9) $D_{\mathrm{R}\mathrm{o}\mathrm{t}}^{\mathrm{\infty }}=D_{\mathrm{R}\mathrm{o}\mathrm{t}}^{\mathrm{M}\mathrm{D}}+\frac{k_{\mathrm{B}}T}{4\eta V}$(9) The difference between Equations (8(8) $D_{\mathrm{R}\mathrm{o}\mathrm{t}}^{\mathrm{\infty }}=D_{\mathrm{R}\mathrm{o}\mathrm{t}}^{\mathrm{M}\mathrm{D}}+\frac{k_{\mathrm{B}}T}{6\eta V}$(8) ) and (9(9) $D_{\mathrm{R}\mathrm{o}\mathrm{t}}^{\mathrm{\infty }}=D_{\mathrm{R}\mathrm{o}\mathrm{t}}^{\mathrm{M}\mathrm{D}}+\frac{k_{\mathrm{B}}T}{4\eta V}$(9) ) is the use of 2-D and 3-D flows for the correction of rotational diffusivities. Vögele et al. [178] suggested that mean square displacement expressions for rotational diffusion in 2-D are much simpler compared to the same expressions in 3-D (i.e. use of quaternions). As can be seen from Equations (1(1) $D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{\infty }}=D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{M}\mathrm{D}}+\frac{k_{\mathrm{B}}T\xi }{6\pi \eta L}$(1) ), (8(8) $D_{\mathrm{R}\mathrm{o}\mathrm{t}}^{\mathrm{\infty }}=D_{\mathrm{R}\mathrm{o}\mathrm{t}}^{\mathrm{M}\mathrm{D}}+\frac{k_{\mathrm{B}}T}{6\eta V}$(8) ) and (9(9) $D_{\mathrm{R}\mathrm{o}\mathrm{t}}^{\mathrm{\infty }}=D_{\mathrm{R}\mathrm{o}\mathrm{t}}^{\mathrm{M}\mathrm{D}}+\frac{k_{\mathrm{B}}T}{4\eta V}$(9) ), the correction term for the translational diffusion contains the inverse of the simulation box length, while the finite-size correction term for rotational diffusion contains the inverse box volume. This indicates that the required correction of rotational diffusion is much smaller than the one for translational diffusion.

5. Collective diffusivities

Fick diffusion coefficients relate liquid fluxes to concentration gradients. The generalised Fick's law in an n-component system with respect to a molar reference frame equals [11,19]: (10) $J_i=-c_{\mathrm{t}}\sum _{j=1}^{n-1}{D}_{ij}\mathrm{\nabla }{x}_j$(10) where $J_i$ is the diffusion flux, $c_{\mathrm{t}}$ is the total molar concentration, $x_j$ is the mole fraction of component j, and $D_{ij}$ are the Fick diffusion coefficients. For an n-component system, the Fick diffusion matrix consists of $(n-1)\times (n-1)$ components.

The MS theory relates the gradient in chemical potentials to the liquid friction at a constant driving force [17,94]: (11) $-\frac{1}{RT}{\mathrm{\nabla }}_{T,p}{\mu }_i=\sum _{i=1,j\ne i}\frac{x_j(u_i-u_j)}{{\mathrm{ð}}_{ij}}$(11) where R is the universal gas constant, $\mathrm{\nabla }{\mu }_i$ is the chemical potential gradient of component i at constant pressure and temperature. ($u_i-u_j$) is the difference in average velocities between components i and j, which is proportional to the friction force at a constant driving force. Đ _ij are the MS diffusion coefficients, which are (unlike Fick diffusivities of $D_{ij}$) symmetric, i.e. Đ _ij = Đ _ji. For an n-component system, there exist $n(n-1)/2$ MS diffusion coefficients. In a molar reference frame, the relation between Fick and MS diffusivities can be expressed by using the matrix of thermodynamic factors [${\mathrm{\Gamma }}_{ij}$] and the phenomenological diffusivity matrix [${\mathrm{\Delta }}_{ij}$] [17,94]: (12) $\left[D_{ij}\right]=\left[{\mathrm{\Delta }}_{ij}\right]\left[{\mathrm{\Gamma }}_{ij}\right]$(12) where [179] (13) ${\mathrm{\Gamma }}_{ij}={\delta }_{ij}+x_i{\left(\frac{\mathrm{\partial }\ln {\gamma }_i}{\mathrm{\partial }{x}_j}\right)}_{T,p,\mathrm{\Sigma }}$(13) where ${\delta }_{ij}$ is the kronicker delta, ${\gamma }_i$ is the activity coefficient of component i. The $\mathrm{\Sigma }$ symbol is used to point out that partial differentiation of $\ln {\gamma }_i$ with respect to $x_j$ is performed at constant mole fractions of all other components except for the $n$-th component [10].

The elements of $\left[{\mathrm{\Delta }}_{ij}\right]$ can be obtained as follows: (14) ${\mathrm{\Delta }}_{ij}=(1-x_i)\left(\frac{{\mathrm{\Lambda }}_{ij}}{x_j}-\frac{{\mathrm{\Lambda }}_{in}}{x_n}\right)-x_i\sum _{k=1,k\ne i}^{k=n}\left(\frac{{\mathrm{\Lambda }}_{kj}}{x_j}-\frac{{\mathrm{\Lambda }}_{kn}}{x_n}\right)\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}i,j=1,\dots ,(n-1)$(14) where ${\mathrm{\Lambda }}_{ij}$ are the Onsager coefficients computed using EMD simulations (here shown using the Einstein formulation) [90,94,99,100]: (15) ${\mathrm{\Lambda }}_{ij}=\frac{1}{N_t}\underset{t\to \mathrm{\infty }}{lim}⟨\left(\sum _{k=1}^{N_i}\left(r_{k,i}\right(t)-r_{k,i}(0\left)\right)\right)\times \left(\sum _{k=1}^{N_j}\left(r_{l,j}\right(t)-r_{l,j}(0\left)\right)\right)⟩$(15) where $N_i$ and $N_j$ are the number of molecules of species i and j, respectively. $N_t$ is the total number of molecules in the system, and $r_{i,j}$ is the position of i-th molecule of species j at time t. Onsager coefficients can be transformed into MS diffusivities using the [$B_{ij}$] matrix. The [$B_{ij}$] matrix is the inverse of [${\mathrm{\Delta }}_{ij}$]: (16) $\left[B_{ij}\right]=[{\mathrm{\Delta }}_{ij}{]}^{-1}$(16) MS diffusion coefficients is related to the elements of [$B_{ij}$] matrix by (17) $B_{ii}=\frac{x_i}{{\mathrm{ð}}_{in}}+\sum _{i=1,j\ne i}^n\frac{x_j}{{\mathrm{ð}}_{ij}}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}i=1,2,\dots \left(n-1\right)$(17) (18) $B_{ij}=-x_i\left(\frac{1}{{\mathrm{ð}}_{ij}}-\frac{1}{{\mathrm{ð}}_{in}}\right)\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}i,j=1,2,\dots (n-1)\mathrm{a}\mathrm{n}\mathrm{d}j\ne i$(18) The resulting expressions for binary, ternary, quaternary systems can be found in [6,49,90]. For ideal diffusing systems, MS diffusivities can be related to self-diffusivities [84], but in general this is not the case due to velocity cross-correlations.

5.1. Finite-size dependence of collective diffusivities

5.1.1. Binary mixtures

Jamali et al. [128] performed an in-depth investigation of finite-size effects of MS diffusivities in binary mixtures. These authors performed EMD simulations of 200 LJ and 9 molecular mixtures and showed that, similarly to self-diffusivities, MS-diffusivities scale linearly with the system size. On the basis of the YH-correction (Equation (1(1) $D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{\infty }}=D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{M}\mathrm{D}}+\frac{k_{\mathrm{B}}T\xi }{6\pi \eta L}$(1) )), and by taking into account the non-ideality of the mixtures, Jamali et al. [128] developed a phenomenological correction term which should be added to the computed MS diffusivity, ${\mathrm{ð}}^{\mathrm{M}\mathrm{D}}$, to obtain the property in the thermodynamic limit, Đ${}^{\mathrm{\infty }}$: (19) ${\mathrm{ð}}^{\mathrm{\infty }}={\mathrm{ð}}^{\mathrm{M}\mathrm{D}}+\left(\frac{1}{\mathrm{\Gamma }}\right)\frac{k_{\mathrm{B}}T\xi }{6\pi \eta L}={\mathrm{ð}}^{\mathrm{M}\mathrm{D}}+\left(\frac{1}{\mathrm{\Gamma }}\right)D^{\mathrm{Y}\mathrm{H}}$(19) where $\mathrm{\Gamma }$ is the thermodynamic factor (which can be obtained from MD simulations using KBIs [103,106]). As can be seen from Equation (19(19) ${\mathrm{ð}}^{\mathrm{\infty }}={\mathrm{ð}}^{\mathrm{M}\mathrm{D}}+\left(\frac{1}{\mathrm{\Gamma }}\right)\frac{k_{\mathrm{B}}T\xi }{6\pi \eta L}={\mathrm{ð}}^{\mathrm{M}\mathrm{D}}+\left(\frac{1}{\mathrm{\Gamma }}\right)D^{\mathrm{Y}\mathrm{H}}$(19) ), the magnitude of the required finite-size correction for MS diffusivities depends on the thermodynamic factor. This means that for non-ideal mixtures close to demixing ($\mathrm{\Gamma }\to 0$) the correction term becomes very large.

For binary mixtures, there is single MS and Fick diffusion coefficient defined. They are related to each other by (20) $D=\mathrm{\Gamma }\mathrm{ð}$(20) As shown in the work by Jamali et al. [128], the finite-size correction for Fick diffusivities in binary mixtures can be derived by combining Equations (19(19) ${\mathrm{ð}}^{\mathrm{\infty }}={\mathrm{ð}}^{\mathrm{M}\mathrm{D}}+\left(\frac{1}{\mathrm{\Gamma }}\right)\frac{k_{\mathrm{B}}T\xi }{6\pi \eta L}={\mathrm{ð}}^{\mathrm{M}\mathrm{D}}+\left(\frac{1}{\mathrm{\Gamma }}\right)D^{\mathrm{Y}\mathrm{H}}$(19) ) and (20(20) $D=\mathrm{\Gamma }\mathrm{ð}$(20) ) [128]: (21) $D^{\mathrm{\infty }}=D^{\mathrm{M}\mathrm{D}}+D^{\mathrm{Y}\mathrm{H}}$(21) Thus, the YH correction applies to the Fick diffusivities. This finding seems reasonable since the YH correction is a hydrodynamic effect and the Fick diffusivities appear in the hydrodynamic equations.

In Figure 3, the finite-size effects of the MS and Fick diffusivities are shown for the binary mixture methanol/methylamine and a binary LJ system. MD simulations were performed for equimolar methanol/methylamine mixtures consisting of four different system sizes (i.e. 250–2000 molecules) at 298 K and 1 atm. Force field parameters for methanol [180] and methylamine [181,182] were obtained from the Transferable Potential for Phase Equilibria (TraPPE) force field. For the LJ system, simulations were performed at a reduced temperature of 0.65 and a reduced pressure of 0.05. The mole fractions of species 1 and 2 were chosen as 0.3 and 0.7, respectively. This LJ system corresponds to an average reduced density of 0.22. The LJ system involves prominent dissimilarities in size (${\sigma }_2/{\sigma }_1$ equal to 1.6), interaction energy (${ϵ}_2/{ϵ}_1$ equal to 0.6), and mass ($m_2/m_1$ equal to 4.096). For all other simulation and force field details, the reader is referred to Ref. [128]. Analytic finite-size corrections for MS and Fick diffusion coefficients are computed using Equations (19(19) ${\mathrm{ð}}^{\mathrm{\infty }}={\mathrm{ð}}^{\mathrm{M}\mathrm{D}}+\left(\frac{1}{\mathrm{\Gamma }}\right)\frac{k_{\mathrm{B}}T\xi }{6\pi \eta L}={\mathrm{ð}}^{\mathrm{M}\mathrm{D}}+\left(\frac{1}{\mathrm{\Gamma }}\right)D^{\mathrm{Y}\mathrm{H}}$(19) ) and (21(21) $D^{\mathrm{\infty }}=D^{\mathrm{M}\mathrm{D}}+D^{\mathrm{Y}\mathrm{H}}$(21) ), respectively. The analytic corrections are compared with the linear regression of the MD results to the thermodynamic limit. As can be seen in Figure 3, the proposed correction accurately accounts for the finite-size effects of MS and Fick diffusion coefficients in binary molecular and LJ systems. Maximum deviations of 2.1% and 3.3% were observed from the extrapolated values in binary molecular and LJ systems, respectively.

Figure 3. (Colour online) (a) MS and (b) Fick diffusion coefficients of a binary equimolar methanol–methylamine mixture at 298 K and 1 atm as a function of the simulation box length (L). (c) MS and (d) Fick diffusion coefficients of binary LJ mixtures ($x_1=0.3$ and $x_2=0.7$) at a reduced temperature of 0.65 and a reduced pressure of 0.05 as a function of the simulation box length (L). The uncorrected MD results are shown with red circles. Blue dashed lines are the linear extrapolation of the MD results to the thermodynamic limit. Grey diamonds show the corrected MS and Fick diffusion coefficients using Equations (19(19) ${\mathrm{ð}}^{\mathrm{\infty }}={\mathrm{ð}}^{\mathrm{M}\mathrm{D}}+\left(\frac{1}{\mathrm{\Gamma }}\right)\frac{k_{\mathrm{B}}T\xi }{6\pi \eta L}={\mathrm{ð}}^{\mathrm{M}\mathrm{D}}+\left(\frac{1}{\mathrm{\Gamma }}\right)D^{\mathrm{Y}\mathrm{H}}$(19) ) and (21(21) $D^{\mathrm{\infty }}=D^{\mathrm{M}\mathrm{D}}+D^{\mathrm{Y}\mathrm{H}}$(21) ), respectively. Black dashed lines are the corrected diffusion coefficients computed from the linear extrapolation of the Onsager coefficients of the smallest sizes ($N_{\mathrm{M}\mathrm{o}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{r}}=250$ and $N_{\mathrm{L}\mathrm{J}}=500$) to the thermodynamic limit. For LJ systems, simulations were performed for four system sizes consisting of 250, 500, 1000, and 2000 particles. For the molecular mixture, four system sizes consisting of 500, 1000, 2000, and 4000 particles were considered. The results are based on the study in [128]. The axes of subfigures scales differently.

5.1.2. Ternary mixtures

Very recently, Jamali et al. [117] derived the generalised form for finite-size corrections of collective diffusion of multicomponent mixtures. By analysing the eigenvalues and eigenvectors of the Fick diffusion matrix, it was shown that only eigenvalues, which describe the speed of diffusion, are system-size dependent. The eigenvectors, which describe the direction of the diffusion process, do not depend on the size of the simulation box. Thus, the off-diagonal components of the Fick diffusion matrix exhibit no finite-size effects, while the diagonal components are system size dependent and can be corrected using the YH correction term. The generalised expression for finite-size corrections of the Fick diffusivity matrix is [117]: (22) $\left[D^{\mathrm{\infty }}\right]=\left[D^{\mathrm{M}\mathrm{D}}\right]+D^{\mathrm{Y}\mathrm{H}}\left[I\right]$(22) where [I] is the identity matrix. By combining Equations (12(12) $\left[D_{ij}\right]=\left[{\mathrm{\Delta }}_{ij}\right]\left[{\mathrm{\Gamma }}_{ij}\right]$(12) ) and (22(22) $\left[D^{\mathrm{\infty }}\right]=\left[D^{\mathrm{M}\mathrm{D}}\right]+D^{\mathrm{Y}\mathrm{H}}\left[I\right]$(22) ), one can obtain the generalised expression for finite-size corrections of the $\mathrm{\Delta }$ matrix: (23) $\left[{\mathrm{\Delta }}^{\mathrm{\infty }}\right]=\left[{\mathrm{\Delta }}^{\mathrm{M}\mathrm{D}}\right]+D^{\mathrm{Y}\mathrm{H}}[\mathrm{\Gamma }{]}^{-1}$(23) in which MS diffusivities are computed using Equations (16(16) $\left[B_{ij}\right]=[{\mathrm{\Delta }}_{ij}{]}^{-1}$(16) )–(18(18) $B_{ij}=-x_i\left(\frac{1}{{\mathrm{ð}}_{ij}}-\frac{1}{{\mathrm{ð}}_{in}}\right)\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}i,j=1,2,\dots (n-1)\mathrm{a}\mathrm{n}\mathrm{d}j\ne i$(18) ).

The validity of the generalised correction terms shown in Equations (22(22) $\left[D^{\mathrm{\infty }}\right]=\left[D^{\mathrm{M}\mathrm{D}}\right]+D^{\mathrm{Y}\mathrm{H}}\left[I\right]$(22) ) and (23(23) $\left[{\mathrm{\Delta }}^{\mathrm{\infty }}\right]=\left[{\mathrm{\Delta }}^{\mathrm{M}\mathrm{D}}\right]+D^{\mathrm{Y}\mathrm{H}}[\mathrm{\Gamma }{]}^{-1}$(23) ) was tested in the study by Jamali et al. [117] using a ternary mixture of chloroform/acetone/methanol, and 28 different ternary LJ liquids. In Figures 4 and 5, we show the computed Fick and MS diffusion coefficients of the ternary molecular mixture of chloroform ($x_1=0.3$), acetone ($x_2=0.3$) and methanol ($x_3=0.4$). MD simulations were carried out at 298 K and 1 atm, which correspond to a system with an average density of 1025 kg/m${}^3$. Diffusion coefficients were computed for four system sizes containing 500, 1000, 2000 and 4000 molecules. The OPLS force field was used to model chloroform, acetone and methanol [183]. All simulation details and the force field parameters can be found in [117]. As postulated in Equation (22(22) $\left[D^{\mathrm{\infty }}\right]=\left[D^{\mathrm{M}\mathrm{D}}\right]+D^{\mathrm{Y}\mathrm{H}}\left[I\right]$(22) ), the off-diagonal components of the Fick diffusivity matrix do not depend on the system size (see Figure 4). In sharp contrast, the diagonal components have a pronounced finite-size dependence, which can be accurately corrected using the YH correction (Equation (1(1) $D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{\infty }}=D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{M}\mathrm{D}}+\frac{k_{\mathrm{B}}T\xi }{6\pi \eta L}$(1) )). As shown in Figure 5, unlike Fick diffusivities, all MS diffusion coefficients depend on the system size and can be corrected using Equation (23(23) $\left[{\mathrm{\Delta }}^{\mathrm{\infty }}\right]=\left[{\mathrm{\Delta }}^{\mathrm{M}\mathrm{D}}\right]+D^{\mathrm{Y}\mathrm{H}}[\mathrm{\Gamma }{]}^{-1}$(23) ). The maximum difference observed between the diffusion coefficients obtained via the analytic correction and the linear extrapolation to the infinite system size was 1.5%. This difference is rather small considering that the error in the computed diffusivities is not higher than 5%.

Figure 4. (Colour online) Fick diffusion coefficients of a ternary molecular mixture (molar reference frame) of (1) chloroform (2) acetone, and (3) methanol ($x_{\mathrm{c}\mathrm{h}\mathrm{l}\mathrm{o}\mathrm{r}\mathrm{o}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}}=x_{\mathrm{a}\mathrm{c}\mathrm{e}\mathrm{t}\mathrm{o}\mathrm{n}\mathrm{e}}=0.3$ and $x_{\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{h}\mathrm{a}\mathrm{n}\mathrm{o}\mathrm{l}}=0.4$) at 298 K and 1 atm as a function of the simulation box length (L). (a) Diagonal component $D_{1,1}$, (b) Off-diagonal component $D_{1,2}$, (c) Off-diagonal component $D_{2,1}$, and (d) Diagonal component $D_{2,2}$. The uncorrected MD results are shown with red circles. Blue dashed lines are the linear extrapolation of the MD results to the thermodynamic limit. Grey diamonds show the corrected Fick diffusion coefficients using Equation (22(22) $\left[D^{\mathrm{\infty }}\right]=\left[D^{\mathrm{M}\mathrm{D}}\right]+D^{\mathrm{Y}\mathrm{H}}\left[I\right]$(22) ). Black dashed lines are the corrected Fick diffusion coefficients computed from the linear extrapolation of the Onsager coefficients of the smallest size (N=500) to the thermodynamic limit. Simulations were performed for four system sizes consisting of 500, 1000, 2000, and 4000 particles. The results are based on the study in [128]. The axes of subfigures scales differently.

Figure 5. (Colour online) MS diffusion coefficients of a ternary molecular mixture of (1) chloroform (2) acetone, and (3) methanol ($x_{\mathrm{c}\mathrm{h}\mathrm{l}\mathrm{o}\mathrm{r}\mathrm{o}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}}=x_{\mathrm{a}\mathrm{c}\mathrm{e}\mathrm{t}\mathrm{o}\mathrm{n}\mathrm{e}}=0.3$, and $x_{\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{h}\mathrm{a}\mathrm{n}\mathrm{o}\mathrm{l}}=0.4$) at 298 K and 1 atm as a function of the simulation box length (L). (a) ${\mathrm{ð}}_{1,2}$, (b) ${\mathrm{ð}}_{1,3}$, and (c) ${\mathrm{ð}}_{2,3}$. The uncorrected MD results are shown with red circles. Blue dashed lines are the linear extrapolation of the MD results to the thermodynamic limit. Grey diamonds show the corrected MS diffusion coefficients based on Equation (23(23) $\left[{\mathrm{\Delta }}^{\mathrm{\infty }}\right]=\left[{\mathrm{\Delta }}^{\mathrm{M}\mathrm{D}}\right]+D^{\mathrm{Y}\mathrm{H}}[\mathrm{\Gamma }{]}^{-1}$(23) ). Black dashed lines are the corrected MS diffusion coefficients computed from the linear extrapolation of the Onsager coefficients of the smallest size (N=500) to the thermodynamic limit. Simulations were performed for four system sizes consisting of 500, 1000, 2000, and 4000 particles. The results are based on the study in [117]. The axes of subfigures scales differently.

To further investigate the finite-size effects of collective diffusivities in ternary mixtures, an LJ system at a reduced temperature of 0.65 and reduced pressure of 0.05 was simulated. The σ and m parameters for all species are chosen to be equal. To induce dissimilarities in the system, the ε parameters were varied (i.e. ${ϵ}_1=1.0$, ${ϵ}_2=0.8$, and ${ϵ}_3=0.6$), and adjustable parameters ($k_{ij}$) were applied to the Lorentz–Berthelot mixing rules (i.e. $k_{12}=0.05$, $k_{13}=0.05$, and $k_{23}=-0.3$) [37]. The mole fractions are 0.4, 0.3 and 0.3 for LJ species 1, 2 and 3, respectively. Four system sizes, ranging from 500 to 4000 molecules, were considered. All other simulation details and force field parameters can be found in [117]. Figures 6 and 7 illustrate Fick and MS diffusivities, respectively, for this LJ system. In-line with the results of the molecular mixture, corrected diffusion coefficients are in a good agreement with the diffusivities obtained from the linear extrapolation to the infinite system size. The deviation in finite-size corrected diffusivities between two approaches is up to 2.5%.

Figure 6. (Colour online) Fick diffusion coefficients of a ternary LJ mixture (molar reference frame) ($x_1=0.4$ and $x_2=x_3=0.3$) at a reduced temperature of 0.65 and a reduced pressure of 0.05 as a function of the simulation box length (L). (a) Diagonal component $D_{1,1}$, (b) Off-diagonal component $D_{1,2}$, (c) Off-diagonal component $D_{2,1}$, and (d) Diagonal component $D_{2,2}$. The uncorrected MD results are shown with red circles. Blue dashed lines are the linear extrapolation of the MD results to the thermodynamic limit. Grey diamonds show the corrected Fick diffusion coefficients using Equation (22(22) $\left[D^{\mathrm{\infty }}\right]=\left[D^{\mathrm{M}\mathrm{D}}\right]+D^{\mathrm{Y}\mathrm{H}}\left[I\right]$(22) ). Black dashed lines are the corrected Fick diffusion coefficients computed from the linear extrapolation of the Onsager coefficients of the smallest size (N=500) to the thermodynamic limit. Simulations were performed for four system sizes consisting of 500, 1000, 2000, and 4000 particles. The results are based on the study in [117]. The axes of subfigures scale differently.

Figure 7. (Colour online) MS diffusion coefficients of a ternary LJ mixture ($x_1=0.4$ and $x_2=x_3=0.3$) at a reduced temperature of 0.65 and a reduced pressure of 0.05 as a function of the simulation box length (L). (a) ${\mathrm{ð}}_{1,2}$, (b) ${\mathrm{ð}}_{1,3}$, and (c) ${\mathrm{ð}}_{2,3}$. The uncorrected MD results are shown with red circles. Blue dashed lines are the linear extrapolation of the MD results to the thermodynamic limit. Grey diamonds show the corrected MS diffusion coefficients based on Equation (23(23) $\left[{\mathrm{\Delta }}^{\mathrm{\infty }}\right]=\left[{\mathrm{\Delta }}^{\mathrm{M}\mathrm{D}}\right]+D^{\mathrm{Y}\mathrm{H}}[\mathrm{\Gamma }{]}^{-1}$(23) ). Black dashed lines are the corrected MS diffusion coefficients computed from the linear extrapolation of the Onsager coefficients of the smallest size (N=500) to the thermodynamic limit. Simulations were performed for four system sizes consisting of 500, 1000, 2000, and 4000 particles. The results are based on the study in [117]. The axes of subfigures scales differently.

As proposed by Vrabec and co-workers [91], the finite-size corrected MS and Fick diffusivities can also be obtained by extrapolating the Onsager coefficients to the thermodynamic limit, i.e. by linear regression in a plot with 1/L. Figure 8 shows the Onsager coefficients for the ternary LJ system computed in this study ($x_1=0.4$ and $x_2=x_3=0.3$). It is important to note that this approach requires multiple simulations at various system sizes and that a linear extrapolation typically introduces uncertainties. Recently, Vrabec and co-workers [91] investigated the finite-size effects of collective diffusion coefficients of water/methanol/ethanol/2-propanol mixture. The required phenomenological coefficient (${\mathrm{\Delta }}_{ij}$) and thermodynamic factor (${\mathrm{\Gamma }}_{ij}$) matrices for Fick diffusivities were obtained from EMD simulations. A finite-size correction for Fick diffusion coefficients was proposed based on the linear extrapolation of the diagonal elements of the Onsager coefficient matrix to the thermodynamic limit. Vrabec and co-workers [91] suggested that off-diagonal Onsager coefficients do not depend on the system size for their relatively large systems (6000 molecules). In the binary, ternary, and quaternary systems studied here, both diagonal and non-diagonal elements of the computed Onsager coefficients show finite-size effects. In Figure 8, an example of the finite-size dependency of the Onsager coefficients for the ternary LJ system ($x_1=0.4$ and $x_2=x_3=0.3$) is shown. MS and Fick diffusion coefficients computed from the extrapolation of Onsager coefficients in thermodynamic limit show a good agreement with the analytic corrections, and also with the linear extrapolation of the Fick and MS diffusion coefficients (dashed lines in Figures 3–7). Using both the diagonal and off-diagonal elements of Onsager coefficients is therefore crucial, particularly when relatively small systems are considered. For large systems, the influence of the off-diagonal elements can be relatively small if the required finite-size correction is small.

Figure 8. (Colour online) Onsager coefficients of a ternary LJ mixture ($x_1=0.4$ and $x_2=x_3=0.3$) at a reduced temperature of 0.65 and a reduced pressure of 0.05 as a function of the simulation box length (L). (a) ${\mathrm{\Lambda }}_{11}$, (b) ${\mathrm{\Lambda }}_{22}$, (c) ${\mathrm{\Lambda }}_{33}$, (d) ${\mathrm{\Lambda }}_{12}$, (e) ${\mathrm{\Lambda }}_{13}$, and (f) ${\mathrm{\Lambda }}_{23}$. The finite-size MD results are shown with red circles. Blue dashed lines are the linear fits to the MD results. Simulations were performed for four system sizes consisting of 500, 1000, 2000, and 4000 particles. The results are based on the study in [117]. The axes of subfigures scale differently.

5.1.3. Quaternary mixtures

The generalised finite-size correction for collective diffusion (Equations (22(22) $\left[D^{\mathrm{\infty }}\right]=\left[D^{\mathrm{M}\mathrm{D}}\right]+D^{\mathrm{Y}\mathrm{H}}\left[I\right]$(22) ) and (23(23) $\left[{\mathrm{\Delta }}^{\mathrm{\infty }}\right]=\left[{\mathrm{\Delta }}^{\mathrm{M}\mathrm{D}}\right]+D^{\mathrm{Y}\mathrm{H}}[\mathrm{\Gamma }{]}^{-1}$(23) )) derived by Jamali et al. [117] has not yet been explicitly verified for systems containing more than three components, e.g. quaternary mixtures. Here, we performed MD simulations for an equimolar 4-component LJ colour mixture at a reduced temperature of 2.0 and a reduced pressure of 3.4, which corresponds to a reduced density of 0.72. Six different system sizes were simulated, i.e. 400, 800, 1200, 1600, 3200 and 4800 particles. The σ and ε LJ parameters for all species are chosen to be equal, so the mixture is ideal, i.e. [${\mathrm{\Gamma }}_{ii}]=1$ and $\left[{\mathrm{\Gamma }}_{ij,i\ne j}\right]=0$. This means that the matrix of thermodynamic factor reduces to the identity matrix. To induce a physical dissimilarity, the masses of the particles are varied as follows: $m_1=m$, $m_2=4m$, $m_3=16m$, and $m_4=64m$. In Figures 9 and 10, the Fick and MS diffusivities of the quaternary system are shown as a function of the system size, respectively. Figure 9 shows that the off-diagonal elements of the Fick diffusion matrix are size-independent, while the diagonal elements vary proportionally with the inverse of the simulation box length. In-line with our findings for the ternary mixtures, finite-size effects of the diagonal elements of the Fick diffusion matrix can be accurately corrected using the YH expression (Equation (1(1) $D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{\infty }}=D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{M}\mathrm{D}}+\frac{k_{\mathrm{B}}T\xi }{6\pi \eta L}$(1) )). Figure 10 shows that all MS diffusion coefficients are size-dependent. The finite-size correction for MS diffusivities is only a function of the YH term because the matrix of thermodynamic factors is equal to the identity matrix (see Equation (23(23) $\left[{\mathrm{\Delta }}^{\mathrm{\infty }}\right]=\left[{\mathrm{\Delta }}^{\mathrm{M}\mathrm{D}}\right]+D^{\mathrm{Y}\mathrm{H}}[\mathrm{\Gamma }{]}^{-1}$(23) )). Deviations between MS diffusivities corrected using the analytic correction and the ones obtained by linear extrapolation to the thermodynamic limit are in the range of 0 to 4.5%.

Figure 9. (Colour online) Fick diffusion coefficients of an equimolar quaternary LJ mixture (molar reference frame) at a reduced temperature of 2 and a reduced pressure of 3.4 as a function of the simulation box length (L). (a) Diagonal component $D_{1,1}$, (b) Off-diagonal component $D_{1,2}$, (c) Off-diagonal component $D_{1,3}$, (d) Off-diagonal component $D_{2,1}$, (e) Diagonal component $D_{2,2}$, (f) Off-diagonal component $D_{2,3}$, (g) Off-diagonal component $D_{3,1}$, (h) Off-diagonal component $D_{3,2}$, and (i) Diagonal component $D_{3,3}$. The uncorrected MD results are shown with red circles. Grey diamonds show the corrected Fick diffusion coefficients using Equation (22(22) $\left[D^{\mathrm{\infty }}\right]=\left[D^{\mathrm{M}\mathrm{D}}\right]+D^{\mathrm{Y}\mathrm{H}}\left[I\right]$(22) ). Blue dashed lines are the linear extrapolation of the MD results to the thermodynamic limit and Black dashed lines are the extrapolated values. Simulations were performed for six system sizes consisting of 400, 800, 1200, 1600, 3200, and 4800 particles. The axes of subfigures scales differently.

Figure 10. (Colour online) MS diffusion coefficients of an equimolar quaternary LJ mixture at a reduced temperature of 2 and a reduced pressure of 3.4 as a function of the simulation box length (L).(a) Ð_1,2, (b) Ð_1,3, (c) Ð_1,4, (d) Ð_2,3, (e) Ð_2,4, and (f) Ð_3,4. The uncorrected MD results are shown with red circles. Grey diamonds show the corrected MS diffusion coefficients using Equation (22(22) $\left[D^{\mathrm{\infty }}\right]=\left[D^{\mathrm{M}\mathrm{D}}\right]+D^{\mathrm{Y}\mathrm{H}}\left[I\right]$(22) ). Blue dashed lines are the linear extrapolation of the MD results to the thermodynamic limit and black dashed lines are the extrapolated values. Simulations were performed for six system sizes consisting of 400, 800, 1200, 1600, 3200, and 4800 particles. The axes of subfigures scales differently.

6. Conclusions

This review presents an in-depth discussion of the finite-size effects of diffusion coefficients computed with molecular dynamics simulations. The finite-size dependencies of self- and collective diffusivities in pure liquids, binary, ternary and quaternary mixtures are illustrated by considering various molecular and LJ systems. The effects of system size on the computation of diffusivities of confined liquids and rotational diffusivities are also briefly discussed. For all cases, we discuss the possible ways for obtaining the diffusivity values in the thermodynamics limit. It is shown that the self-diffusion coefficients of pure liquids and multicomponent mixtures scale linearly with the inverse of the simulation box length. A way to obtain self-diffusion coefficients in the thermodynamic limit is by linear extrapolation of the MD (finite-size) results to $1/L\to 0$. The disadvantages of this approach are that it requires multiple long MD simulations of various system sizes, and that linear regression introduces uncertainties. Instead, an analytic correction term proposed by Yeh and Hummer (Equation (1(1) $D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{\infty }}=D_{\mathrm{S}\mathrm{e}\mathrm{l}\mathrm{f}}^{\mathrm{M}\mathrm{D}}+\frac{k_{\mathrm{B}}T\xi }{6\pi \eta L}$(1) )) presents an alternative approach. The YH correction requires the shear viscosity of the fluid obtained from the conventional MD simulations (i.e. GK method, Einstein relations). Here, the YH correction for self-diffusion coefficient is illustrated for various molecular and LJ systems, i.e. SPC/E water, binary equimolar LJ, and toluene-acetone-water mixtures. The generalised form for finite-size corrections of MS and Fick diffusivities by Jamali et al. [117] is also discussed. For collective diffusion, our main conclusions are as follows: For multicomponent mixtures (n > 2), the off-diagonal elements of the Fick diffusivity matrix do not depend on the system-size, while the diagonal elements show a system-size dependency which can be corrected using the YH term. In sharp contrast to Fick diffusivities, all MS diffusion coefficients are system-size dependent. The required correction for MS diffusivities can be considered as a modification of the YH expression, which includes the matrix of thermodynamic factors. The validity of the generalised correction model for collective diffusivities is illustrated for binary (i.e. a molecular methanol-methylamine and a LJ mixture), ternary (i.e. a molecular chloroform-acetone-methanol and a LJ mixture) and quaternary (i.e. a LJ colour mixture) systems.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This study was sponsored by NWO Exacte Wetenschappen (Physical Sciences) for the high computing facilities, with financial support from the Nederlandse Organisatie voor Wetenschappelijk Onderzoek [NWO-CW,NWO-EW]. TJHV acknowledges NWO-CW (Chemical Sciences) for a VICI grant. O.A.M. gratefully acknowledges the support of NVIDIA Corporation with the donation of the Titan V GPU used for this research.