A Review of Capture-recapture Methods and Its Possibilities in Ophthalmology and Vision Sciences

ABSTRACT

Epidemiological information is expected to be used to develop key aspects of eye care such as to control and minimise the impact of diseases, to allocate resources, to monitor public health actions, to determine the best treatment options and to forecast the consequence of diseases in populations. Epidemiological studies are expected to provide information about the prevalence and/or incidence of eye diseases or conditions. To determine prevalence is necessary to perform a cross-sectional screening of the population at risk to ascertain the number of cases.

The aim of this review is to describe and evaluate capture-recapture methods (or models) to ascertaining the number of individuals with a disease (e.g. diabetic retinopathy) or condition (e.g. vision impairment) in the population.

The review covers the fundamental aspects of capture-recapture methods that would enable non-experts in epidemiology to use it in ophthalmic studies. The review provides information about theoretical aspects of the method with examples of studies in ophthalmology in which it has been used. We also provide a problem/solution approach for limitations arising from the lists obtained from registers or other reliable sources.

We concluded that capture-recapture models can be considered reliable to estimate the total number of cases with eye conditions using incomplete information from registers. Accordingly, the method may be used to maintain updated epidemiological information about eye conditions helping to tackle the lack of surveillance information in many regions of the globe.

KEYWORDS:

• Capture-recapture
• Prevalence
• Vision impairment
• Ophthalmology
• Optometry

Fundamental epidemiology

Epidemiology is an area of medicine concerned with the number of persons affected by a condition or disease in a defined population. In other words, epidemiology can be defined as “The quantitative study of the distribution, determinants and control of diseases in populations”.^1,2 Epidemiologic studies provide, amongst other relevant numbers, information about the prevalence and/or incidence of diseases or conditions.

Prevalence can be defined as “the proportion of a population, or sub-population, that has a particular disease at a particular point in time”.³ For example, the Coimbra study reported the prevalence of AMD in the Portuguese population. In addition, the Coimbra AMD study also characterized risk factors for disease development.^4,5 Prevalence can be reported as crude prevalence (crude rates), category-specific prevalence and standardized prevalence.³ Prevalence is commonly reported as a percentage, such as 1.5%, that is the number of cases per 100 people in the population.

Incidence can be defined as “the number of new cases arising in a given period of time in a specified group of people (population)”.⁶ The incidence of a disease will depend on its aetiology, i.e., why it occurs. The incidence of diabetic retinopathy in Portugal,⁷ incidence of tuberculosis⁸ or incidence of prostate cancer⁹ are examples of studies conducted in Portugal to monitor eye diseases or other relevant conditions. The prevalence of a disease depends not only on the incidence but also on the course of the disease, how long it lasts, whether it can be treated, and whether people die as a result of it.⁶

This review covers a method of ascertaining for the number of individuals with a disease (e.g. diabetic retinopathy) or condition (e.g. vision impairment) using capture-recapture methods. This method can be used to determine the prevalence and/or incidence, but in this review, we cover almost exclusively examples of prevalence with emphasis on the prevalence of vision impairment. Once affected by eye diseases that cause irreversible vision loss, individuals often have to live with the condition for the rest of their lives. Whilst the incidence of vision impairment may be low in developed countries, the prevalence is likely to rise due to the growing and aging population.¹⁰

Methods to determine the prevalence of eye conditions

There are several strategies to quantify the number of cases of a particular condition or disease in a population. However, the most reliable results are those obtained from a screening of the general population or cross-sectional studies.² In this case, a random and representative sample of the entire population or the target group, when the population of interest is a subgroup of the general population, must be screened for the condition by qualified researchers or clinicians. This method is reliable but has the disadvantage of being very expensive, time consuming and labour intensive. There are reports in the literature of studies that stopped due to budget and time constraints.¹¹ In many instances, this method represents a cost that is disproportional to the benefits of gathering the information in particular when studying rare conditions or events in the general population. A good example is the epidemiology of pterygium in Victoria (Australia) that surveyed 5147 persons and found only 6 cases of pterygium surgery.¹² Therefore, alternative methods can be and have been used.

An alternative to screening the population is to use population surveys. In this case information about the clinical condition of interest is self-reported. The most basic example of a survey with self-reported data is the national CENSUS that most countries conduct every 5 or 10 years. According to some authors, such a survey is not expected to provide data on the number of people with a disease of interest but is expected to tell how many are at risk of a disease in the general population.² However, self-reported information about disease suffers from several types of bias and leads to inaccurate estimates.¹³ Common causes for this include the lack of knowledge about the condition and social desirability^14,15 but they are still being used in some instances.¹⁶ An example of inaccurate self-reported information is the number of cases of vision-impaired individuals reached by CENSUS in Portugal.¹⁷ In 2011, 892860 persons reported “difficulties to see even when wearing optical correction” and 27659 reported to be “impossible to see”. When taken together, that is, summing these two numbers and dividing the result by the number of individuals living in the country, this would lead to a crude prevalence of vision impairment in Portugal of approximately 9%. This crude prevalence would be extremely alarming but, fortunately, is unlikely to be true. Another alternative to population studies is to use registers.

Registers are databases where patients or physicians can enrol cases with a particular condition that needs to be registered and they are frequently used to determine prevalence through what is sometimes defined as “case counting”. Registers are extensively used to monitor conditions such as cancer, diabetes or tuberculosis.^8,9,18 Registers are typically inexpensive and readily accessible when needed. The disadvantages include, for example, voluntary registration (in most cases), information dispersed through several registers and misdiagnosis. Case counting has been found to be an ineffective strategy to estimate the prevalence of conditions in the general population because many persons fail to register.^19,20 Although there are more elaborated ways to use registers, a methodology that has been shown to be useful in ascertaining the total number of cases using incomplete information from registers is capture-recapture (CR).

The aim of this review is to cover the fundamental aspects of this methodology that would enable non-experts in epidemiology to use it in ophthalmic studies. The structure that we adopted is expected to cover the fundamental theoretical aspects of the method and to provide examples of studies in ophthalmology in which the methodology has been used. We also provide a problem/solution approach for limitations arising, in particular, from the lists obtained from registers or other reliable sources.

The review is organized in small sections summarized here: section 3) section capture-recapture methods provides a brief historical perspective and a definition of CR methods; section 4) section assumptions and requirements describes what a researcher needs to know about the method before deciding on the use of this methodology to investigate prevalence (before collecting data); section 5) section data analysis describe what problems can arise during the process of combining information and analyse it (after collecting data); in section 6) section computation of prevalence we provide an example of the calculations of prevalence of vision impairment with three lists, in section discussion and recommendations we discuss the key messages of this review and section 8 section literature review gives a summary of the literature search.

Capture-recapture methods

CR methods were originally developed and used in ecology, but have been applied to characterize prevalence in human populations since 1949.²¹ In ophthalmology, it has been used to determine the prevalence of a range of conditions including congenital cataracts and vision impairment.^22–31

CR methods use lists from registers (or other reliable sources) of which the completeness is unknown. In health applications lists can be obtained from hospitals, laboratories, insurers, social service agencies, religious institutions, schools and others. Cases are identified from multiple sources, with a source defined as any location or origin where a case is reported. All cases from each source make up a list. Lists of cases obtained from two or more registers (or sources) can be combined and used to estimate the number of unregistered cases. A real-world example of this calculation is given in section computation of prevalence.

Estimating the total number of cases allows, in most circumstances, the estimate of prevalence or incidence of diseases in a population. The situations in which CR methods can be most useful are, for example, when it is too expensive to perform a screening of the entire population or when a condition is very rare (or both). There are basic requirements that need to be attained if the CR methods are to be utilized, requirements are described below.

Assumptions and requirements

To be used in CR, lists – defined as databases containing the profile of people with a condition of interest, need to be obtained at approximately the same time, or based on different sources that represent approximately the same population.²³ In addition, to obtain reliable results with CR methods certain assumptions need to be met: 1) the sources of lists are independent – this implies that the probability of a subject being in both list A and list B equals the product between the probability of being in A alone and the probability of being in B alone,³² 2) the probability of association within each source (catchability) is equal for all individuals – the probability may vary from one list to another, or be constant overall,^32,33 3) the population is closed (no births, deaths or migrants). These assumptions are restrictive and, when applied to medical conditions, are unlikely to be met.³² Below we clarify some of the most important and, eventually, less intuitive concepts: list (in)dependence and closed populations and we also explain how to proceed when assumptions are not met.

List requirements

A list is a collection of units from a population and the act of generating a list is said to be a capture. A list in the context of human populations needs to include a minimum of demographic information about the people with the condition of interest. To be useful, the list most contained information entered in an organized and reliable way. Examples of lists are the databases of cases associated with tuberculosis or human immunodeficiency virus. In most European countries these are communicable diseases, meaning that health professionals are required to communicate them to central health authorities.^34,35 One essential aspect is that each list needs to include accurate identifiers such as first and last name, date-of-birth and sex. In the case of diseases, the diagnosis should ideally be confirmed by medically qualified professionals. All lists must have the same minimum amount of case-information that can be used to compare records during prevalence estimation using CR. Case-information is used to create a unique tag or a combination of tags that corresponds to a unique identifier for each subject. Tags are then used to determine the intersection of records in different lists (see sub-section issues with tag-loss).

Here we need to distinguish two types of list independence: a) the local independence and b) homogeneity across individuals. A detailed explanation of these concepts is provided below.

Local independence considers individuals as fixed and their presence in a list does not affect their probability of being included in other lists that are used. Mathematically speaking the local independence between lists implies that the event that unit $i$ is in a certain list is independent of the event that unit $i$ is in any combination of the other lists.³⁶ Local list independence is a theoretical concept that needs to be discussed by the investigators that know the origin of their lists. Although there are “diagnostic tools” for list independence that are discussed in sections data analysis and computation of prevalence with numerical examples. An intuitive example how to use this definition consists of separated lists from primary eye care providers (e.g. optometrists, consider this list A) and specialized eye care (e.g. eye care clinics at hospital, consider this list B). This procedure can lead to local dependence between lists because the sources of the lists refer to each other. That is, the fact that a patient is seen by an optometrist changes the probability of this patient to be in the eye clinic at the hospital. Patients seen by optometrists are more likely to be referred to the eye clinic at the hospital than if they did not look for eye care with the optometrist.

Local dependence between lists can be positive or negative.^2,37 Positive dependence means that individuals captured in the first capture, for example list A, are more likely to be captured in the second list, e.g. list B, than those that were not captured in list A. That is the type of dependence that should be expected in the example above (local optometrist and hospital eye clinic). This type of dependence can lead to an underestimation of the true size of the population.³⁴ In contrast, negative dependence exists when individuals captured in a list are less likely to be captured in other subsequent lists. In other words, if the presence of an individual in list A excludes or reduces the probability of him/her from being in list B, then this can be considered negative dependence. This type of dependence leads to an overestimation of the true size of the population.^33,36 From the previous example, if we consider list A taken from an eye clinic at hospital A and list B taken from an eye clinic at hospital B (assuming equal levels of specialization in both clinics), the presence of an individual in list A is likely to reduce the probability of that individual being in list B. That is, because the patient is already in treatment in one hospital it is unlikely that he or she is treated, for the same condition, in a second hospital. The examples given show that researches need to think carefully about the sources for their lists before they start to collect data. There are some solutions when assumptions of independence are not met and that is discussed in section data analysis.

The homogeneity across individuals means that the probability of capture in a list is independent of the individual characteristics of the subjects and is the same to all subjects.³⁸ In contrast, if there is heterogeneity, then the probability of capture in any sample is an attribute of the individual and may vary across the population. Subjects may vary in their capture probability according to age, sex, disease severity, social status and other factors.³⁹ Using the previous example, heterogeneity between individuals may exist if the probability of being registered at the eye clinic is a function of the individual’s income and/or the distance between his home and the clinic.

In short, local dependence between lists means that probability of capture of a subject i in a list j depends on his past capture history. Heterogeneity means that the capture probability of a subject i in a list j depends on some specific attributes of the subject such as age, sex or income. These two concepts are linked to the concept of (equal) catchability. Equal catchability means that all individuals are equally likely to be chosen in each capture.⁴⁰ If local list independence fails, then the probability of capture in any list depends on the individual’s prior history of capture and, therefore, the equal catchability assumption is violated. When homogeneity fails the probability of capture in any list is related with attributes of individuals and varies across the population, which makes the equal catchability assumption to be violated. If the assumption of equal catchability holds, then the two types of independence are verified.

Population requirements

One requirement of the traditional CR methods is that the population needs to be closed. That is, during the sampling period there will be no subjects coming in or out of the population (no migrations, births and no deaths).⁴¹ Strictly speaking, this may be impossible to accomplish in human populations. Still, it is sometimes reasonable to admit that during the capture period the population is closed.^41,42 When the assumption of the closed population can be considered, methods described in sub-sections analysing list dependence with the Petersen estimator and using log-linear models with dependent lists can be used to determine the number of individuals with the condition of the interest in the population. If the population is open more elaborate and complicated methods are needed, those are briefly described in subsection using log-linear models with dependent lists. In this review, we provide only a superficial overview of complicated theoretical methods.

Data analysis

This section provides a list of procedures that need to be executed to assess if the lists and population meet the assumptions discussed in section assumptions and requirements. When assumptions are violated, we explain that and suggest some solutions. This section starts with the introduction of the Petersen estimator. This estimator can be used when there are only two lists, but it is also important to analyse dependence amongst pairs of lists when three or more are available. Then, we describe the use of log-linear models as an alternative when is desirable to use more than 2 lists or when the two available lists are dependent. Most studies use three lists and when more than 3 lists are available, the recommendations are to merge them.^43,44 The other three topics covered in this section are: 1) how to deal with open populations, 2) how to deal with poor information to identify subjects in lists (tag-loss) and 3) how to deal with false negatives or false positives.

Analysing list dependence with the Petersen estimator

The Petersen estimator is a formula that provides an estimate of size N of the population or, in other words, the unknown number of individuals affected by a disease (within a population) when two lists are available. To use the Petersen estimator (a) the population need to be considered closed, (b) the assumption of equal catchability holds (the capture probability may change throughout time, but within each capture, it is the same to all individuals) and (c) there are no problems with the individual’s identifiers. If lists are dependent, the Petersen estimator should not be used. The bias in $N$ induced by dependent lists can be significant.²²

Now we explain the basis of the Petersen formula with an example from ecology using two samples (equivalent to 2 captures). Assume that we want to estimate the total number of fish ($N$) in a lake. A sample A with $n_1$ fish is captured, fish are marked and then released back to the lake – the marked rate in the population is given by the $\frac{n_1}{N}$. Next, a sample B with $n_2$ fish is captured and from those $n_2$, there are m fish that are marked from the first capture. Thus, the recapture rate is given by the fraction $\frac{m}{n_2}$. If samples A and B are independent, then the marked rate in the population should be approximately equal to the recapture rate, that is, the equality:

$\frac{n_1}{N}=\frac{m}{n_2}$

is likely to occur.³⁶

This equation yields the Petersen estimator of the population size ($\hat{N}$):

$\hat{N}=\frac{n_1{n}_2}{m}$

The Petersen estimator can also be used in human populations. The captured samples are lists and the probability of an individual being captured in a certain list is often defined as ascertainment probability. The Petersen formula is used in computation of prevalence with a numerical example.

In sub-section list requirements we explained that two lists may have local dependence and dependence may be positive or negative. Positive local dependence occurs when individuals captured in a list A are more likely to be also in list B than those not in list A. When this occurs then the two fractions given above are unequal, $\frac{n_1}{N}<\frac{m}{n_2}$, which is equivalent to $N>\frac{n_1{n}_2}{m}$. Therefore, in this case, the Petersen formula underestimates the true size of the population. In contrast, if the two lists have local negative dependence, then $\frac{n_1}{N}>\frac{m}{n_2}$, which yields $N<\frac{n_1{n}_2}{m}$. In this case, there will be an overestimation of the true size of the population.

At this point, it is important to refresh the concept of capture history using mathematics. Given two generic lists, the capture history y for a particular individual may be (i) y = (1,0) – individual is in list A but is not in list B, (ii) y = (0,1) – individual is not in list A but is in list B, (iii) y = (1,1) – individual is in list A and B, and (iv) y = (0,0) – individual is neither in list A nor in list B. What CR methods try to estimate is the number of individuals with a capture history (0,0), that is, the population not captured in either list.

In this scenario, $n_1=n_{10}+n_{11}$, $n_2=n_{11}+n_{01}$ and $m=n_{11}$. By replacing these values in the initial Petersen equation, $\hat{N}=\frac{n_1{n}_2}{m}$, we obtain $\hat{N}=n_{10}+n_{11}+n_{01}+\frac{n_{10}{n}_{01}}{n_{11}}$. This is another expression to the Petersen estimator, in which $n_{10}$ is the number of individuals with capture history $\left(1,0\right)$, $n_{01}$ is the number of individuals with capture history $\left(0,1\right)$ and $n_{11}$ the number of individuals with capture history $\left(1,1\right)$.

The Petersen estimator is subject to bias if $n_{11}$ is small or zero.⁴⁵ Therefore, in 1951 Chapman modified the Petersen estimator, which resulted in the Chapman estimator:

$\hat{N}=\frac{\left(n_{10}+n_{11}+1\right)\left(n_{01}+n_{11}+1\right)}{n_{11}+1}-1$

Chapman showed that if $n_{10}+n_{01}+2n_{11}\ge N$ the previous estimator is an exactly unbiased estimator of $N$.⁴⁶ If $n_{10}+n_{01}+2n_{11}<N$, then the bias of the Chapman estimator is less than 2% if $\frac{\left(n_{10}+n_{11}\right)\left(n_{01}+n_{11}\right)}{N}>4$.⁴⁷ However, $N$ is unknown but if $n_{11}>7$ then there is a 95% chance that $\frac{\left(n_{10}+n_{11}\right)\left(n_{01}+n_{11}\right)}{N}>4$ and the bias of Chapman estimator is negligible.^48,49 In computation of prevalence we will use both the Petersen and the Chapman estimators.

In human populations, it is difficult to obtain two lists that are categorically independent⁵⁰; however, they can be considered independent if the dependence is low.³⁴ There are several methods to assess which, if any, lists are dependent. For example, some authors defined the “coefficient of covariation between samples” that measures the degree of dependence among them.³⁶ There is also the odds ratio implemented with capture-recapture methods developed by Wittes et al.,^22,51 that estimates the increased probability of a case being reported in a first source when it is also reported in a second source. Often more than 2 lists are available which is good to CR methods, but when this happens the formulas given for Petersen and Chapman estimators cannot be used to estimate the size of the population (N). Although when using three or more lists, the Petersen estimator or the Chapman estimator can be used to detect dependency amongst pairs of lists. Discrepancies between estimates of N produced by different pairs of lists are indicative of positive or negative local dependences, numerical examples are given in sub-section scenario D. This method is considered intuitive and can be complemented by investigating the lists, the context surrounding them and how they were built, which can suggest the dependences amongst them. These last two intuitive approaches combined are used in section computation of prevalence.

Using log-linear models with dependent lists

When dependence between two lists is unavoidable and/or more than two are available, log-linear models can be used to estimate the size of the population (N). However, log-linear models are not the only closed models that allow unequal catchability.³⁶ An important aspect to consider in CR is the number of lists. When more than 3 lists are available, researchers should consider merging them because more than 3 lists lead to complicate models without increasing significantly the accuracy of its predictions.^43,52

Log-linear models determine the expected value of $n_{ijk}$, that is, the expected value to the number of individuals with capture history $\left(ijk\right)$. It uses the Poisson distribution to model the count of a contingency table computed from the lists (each list has two categories, captured and not captured).⁵³ It models the logarithm of the expected value of each observable cell of such contingency table. If there are three lists and there is local dependence amongst the three and local dependence between any possible pair of lists, then the log-linear model is given by equation 1(1) $logE\left(n_{ijk}\right)=u_0+u_{1}I\left(i=1\right)+u_{2}I\left(j=1\right)+u_{3}I\left(k=1\right)+u_{12}I\left(i=j=1\right)+u_{13}I\left(i=k=1\right)+u_{23}I\left(j=k=1\right)+u_{123}I\left(i=j=k=1\right)$(1) :

(1) $logE\left(n_{ijk}\right)=u_0+u_{1}I\left(i=1\right)+u_{2}I\left(j=1\right)+u_{3}I\left(k=1\right)+u_{12}I\left(i=j=1\right)+u_{13}I\left(i=k=1\right)+u_{23}I\left(j=k=1\right)+u_{123}I\left(i=j=k=1\right)$(1)

As a matter of example, in the equation above $I\left(i=1\right)$ stands for the function that assigns $1$ to capture history $\left(1jk\right)$ and $0$ to all the others. Log-linear models estimate the logarithm of the expected value for the number of individuals with capture history $\left(ijk\right)$, that is, $logE\left(n_{ijk}\right)$. For example, the parameter $u_{12}$ models the dependence between lists 1 and 2, and $u_{13}$ the dependence among lists 1 and 3 and so on.³³

Consider now that only lists 1 and 3 are dependent. If we want to compute the expected number of individuals with capture history $\left(101\right)$, that is, $E\left(n_{101}\right)$, then we use the formula:

$logE\left(n_{101}\right)=u_0+u_1+u_3+u_{13}\iff E\left(n_{101}\right)=e^{u_0+u_1+u_3+u_{13}}$

The values of all parameters (in this case, $u_0$, $u_1$, $u_3$, $u_{13}$) can be obtained, for example, by using the R package Rcapture.^54,55 This package can be used to estimate the abundance and other demographic parameters for closed and open populations using log-linear models. By comparing the difference between the estimated value of individuals with a capture history $\left(101\right)$ and the actual number of subjects with that capture-history, the bias of the model can be computed. By doing the same to all observed capture-histories, the deviance of the model can be computed. The deviance of the model measures its quality in terms of how well its predictions fit the experimental data. Data is the set of vectors with all observed capture-histories, low deviance values correspond to better model fittings.

The main objective though is to compute an estimation of the size of the population $N$ (e.g. the number of people with vision impairment) and to do that we need to determine the expected number of subjects that are missing from our available lists. That is, we need to estimate the number of individuals with a capture history $\left(000\right)$ and that is given by the expression:

$logE\left(n_{000}\right)=u_0\iff E\left(n_{000}\right)=e^{u_0}$

The number of individuals with capture history (0 0 0) is then added to the number of individuals that have been captured on the lists:

$\hat{N}=n_{100}+n_{010}+n_{001}+n_{111}+e^{u_0}$

When there is an interaction between lists 1 and 2 and between lists 1 and 3, then equation 1(1) $logE\left(n_{ijk}\right)=u_0+u_{1}I\left(i=1\right)+u_{2}I\left(j=1\right)+u_{3}I\left(k=1\right)+u_{12}I\left(i=j=1\right)+u_{13}I\left(i=k=1\right)+u_{23}I\left(j=k=1\right)+u_{123}I\left(i=j=k=1\right)$(1) would yield the $\left(12,13\right)$ log-linear model:

$logE\left(n_{ijk}\right)=u_0+u_{1}I\left(i=1\right)+u_{2}I\left(j=1\right)+u_{3}I\left(k=1\right)+u_{12}I\left(i=j=1\right)+u_{13}I\left(i=k=1\right).$

There are more models, but they are not covered in this review. Usually, models are denoted as $M_{subscripts}$ and the subscripts are $t,b,h.$³³ Models allowing capture probabilities for a fixed population unit to vary between lists are indexed by $t$, with $t$ standing for time. Models with local list dependence, the behavioural effect, are indexed by $b$. Models that deal with heterogeneity are indexed by $h$. Therefore, in the more general structure, we have $M_{tbh}$ models; $M_{bh}$ or $M_b$ models and other combinations are also possible.^33,36 There is also the $M_0$ model, in which there is no local list dependence, no heterogeneity and the capture probability is the same to all individuals throughout the entire capture time.^38,40

Some models include covariates to explain the different capture probabilities among individuals due to heterogeneity.^37,56,57 For example, the probability of capture in a certain list for an individual may depend on covariates such as sex age or the severity of a disease. One possible solution consists of stratifying the data according to the values of the covariates, estimating the total number of population units within each stratum and finally combining these estimates.⁵⁶ There are also finite mixture models and random-effect models for heterogeneous closed populations.⁵⁸

The Bayesian approach to capture-recapture has also been proposed by some authors and we provide here a brief explanation and an example.^40,59,60 The Bayesian approach works by taking into account previous estimates of the population size $N$, in which $N$ is considered a random variable with a certain distribution. For example, it can be considered that $N=N_1$ with probability $p=p_1$, $N=N_2$ with probability $p=p_2$, $N=N_3$ with probability $p=p_3$ and so forth. This will be the prior probability distribution for $N$. Then, observations are collected, that is, a capture is produced. Such empirical information is used to update the prior probability distribution of $N$ into a posterior probability distribution of $N$. This posterior information will be used as prior information to the subsequent capture and it will be again updated, originating a new posterior distribution to $N$. These iterations go on for the desired number of times. The actual observed data changes our expectations concerning the values of certain population parameters.⁶¹

In some cases the population is open and, in those cases, capture-recapture models for open population need to be used. For instance, there is a method that has been proposed by Roberts and Brewer that allows for the control of admissions and departures of subjects.⁶² In this method, and based upon CENSUS information, there are variables modulating for probabilities of elements departing or being admitted to the population. Another solution are the Cormack-Jolly-Seber models that apply Hidden Markov Models.⁶³ Here, in addition to the capture probabilities (or ascertainment probabilities as it is referred to in human populations), there are also the survival probabilities, that is, the probability of an individual to remain part of the population in some time period between captures. The CR models are expressed as state-space models in which the survival process is distinguished from the detection process. It requires a significant dedication and is mathematically demanding; readers interested to know more about those are referred to the cited literature.

Issues with “tag-loss”

It is always advisable to use data with good personal identifiers allowing the linkage of individuals from different registers (lists). Sometimes this is not possible and we have what can be defined as “tag-loss”. Tag-loss is the name given to the event that some individuals are poorly identified and has its origin in ecology when captured animals lose their tags.

The event of losing a tag, in human CR studies, means that the subject’s identification has errors due to poor records caused by, for example, mistyping. Let us suppose that we have the following record in list 1: initials “JA”, birth date “13/06/1957”, sex “male”. If male is represented by the number 1 and female by the number 2, then we can create an identifier string for this record as “JA130619571”. Now in list 2: initials “HA”, birth date “13/06/1957”, sex “male”. This originates the identifier string “HA130619571”. Let us assume that the first initial in list 2 was mistyped (“H” instead of “J”) and initials should be “JA” in both cases. In this scenario, these two separated records refer to the same subject and this subject should be accounted as a double capture – in list 1 and in list 2. However, because of the typo, it will be counted twice, that is, as a separated record in each list. This is an example of tag-loss with false-negative matching. When this happens, it frequently leads to the significant bias of estimation.^60,64 False-positive matching, that is, distinct individuals being considered as the same is less likely.

Most CR methods as the Petersen estimator and log-linear models assume that no tags are lost and that all tags are correctly identified. When researchers suspect of tag-loss they can use some strategies to reduce bias in their estimation. One way to circumvent this problem is to use several combinations of the information provided. For example, to perform an initial match by last name, post code and sex and a second match by first and last initial, date of birth and sex, or other combinations. Still, tag-loss can always occur leading to errors in the estimate of the population size and its variance.^65,66

When tag-loss cannot be avoided, there are models that can incorporate this effect. For example, Wang and colleagues proposed a Bayesian model that can deal with tag-loss by using prior information about the population.^60,67,68 In this model, true and observed values are considered. For instance, the number of re-sightings in one list will be replaced with two values: the observed number of re-sightings on the list and the true number of re-sightings on the list. Concerning only the true number of re-sightings, there is no tag-loss effect. The discrepancy between observed data and real data is considered to be due to tag-loss and the true or latent data can be estimated with Bayesian models.

False positives and false negatives

Lists obtained from registers or clinical files can have false positives and false negatives or misdiagnosis. A false positive (Fp) for CR exists when someone is included on the list without having the expected diagnosis.³⁴ For example, when studying the prevalence of vision impairment, someone with good vision that is listed is a false positive. A false negative (Fn) is someone with vision impairment that is listed as having good vision (or not listed in the vision-impaired records).

Let us consider a scenario in which list A is prone to have Fp and list B in which Fp or Fn are inexistent. An individual x that is a Fp in list A can cause that either $n_{10}$ (number of cases in list A only) or $n_{11}$ (number of cases in both lists) are inflated one unit. However, despite individual x could be captured in list B, he or she is not listed – which classifies x as a Fp in list A only. In this scenario $n_{01}$ (number of cases in list B only) and $n_{11}$ are correct. However, $n_{10}$ is inflated because includes one Fp. When we put these numbers in the Petersen estimator $=n_{10}+n_{11}+n_{01}+\frac{n_{10}{n}_{01}}{n_{11}}$, the first and last addends have higher values than they should have and the total number of cases, given by N, will be overestimated.

When we have a Fn in list A, the effect in the population estimation will depend on whether the subject was diagnosed in the source of list B. If individual x is an Fn in list A, then $n_{10}$ (number of cases in list A only) or $n_{11}$ (number of cases in both lists) are reduced by one unit. If x is included in list B, then he was correctly diagnosed and therefore $n_{11}$ is reduced by one unit and $n_{01}$ is inflated by one unit. In this case, the sum $n_{10}+n_{11}+n_{01}$ will be correct, but the quantity $\frac{n_{10}{n}_{01}}{n_{11}}$ will be overestimated. Therefore, $N=n_{10}+n_{11}+n_{01}+\frac{n_{10}{n}_{01}}{n_{11}}$ is overestimated. Finally, if x is not diagnosed at the source of B, then only $n_{10}$ will be reduced by one unit, and consequently, N is underestimated. In summary, Fp lead to the overestimation of the population and Fn can lead to overestimation or underestimation of the population.

Computation of prevalence

In this section we provide an example of how to estimate the number of persons with vision impairment (VI) in the general population of a Portuguese municipality using CR methods. The study was conducted in the Municipality of Braga, Portugal, that has 181494 habitants.⁶⁹ After excluding non-residents, we obtained three lists formed of people with VI: 133 subjects issued with medical certificates of VI from a Primary Care Centre or PCC (L1); 556 subjects from Hospital of Braga or HoB (L2) and a 232 subjects from the blind association, ACAPO (L3).

The hospital information was collected during 12 months in the year 2014. Patients attending ophthalmology appointments with VI (acuity in the better eye equal or less than 0.3logMAR) were registered in a database. For this analysis, we use only people with an acuity 0.5logMAR or worse because people with acuity better than 0.5logMAR were unlikely to be registered with ACAPO. Details of the study can be obtained from our previous publications.^70–73 At the beginning of 2015, we collected a list of people applying for VI certificates seen at the PCC and at the same time, a list of members of ACAPO for the municipality was provided by the blind association. Despite referral between these three institutions not being a standard part of eye care practice, it is likely that when people ask, for example, for social support at the hospital they are directed to ACAPO and/or to the PCC. Therefore, the dependence between lists is likely to occur.

A unique identity string was constructed for each individual in the three lists consisting of the initials of the name, date of birth and sex. Such a string identifies each individual. We matched strings from all three lists. In the next sections, we show how to estimate the number of individuals with VI in the municipality of Braga that were not present in any of the three lists using a scenario-based approach.

Scenario A: using two independent lists

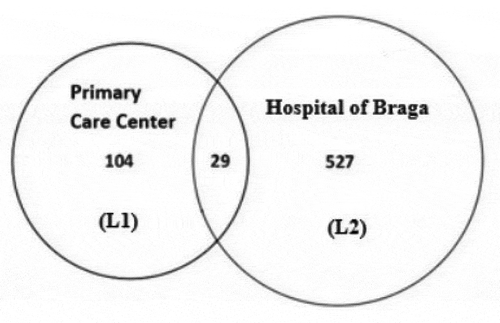
In this section, we apply the Petersen estimator and the Chapman estimator. It will, for now, be assumed that all possible pairs of lists are independent and that the population is closed. After matching lists L1 and L2 we found 29 individuals that were captured in both that interception is shown in Figure 1.

Figure 1. Venn diagram representing the matching of lists from PCC and HoB.

Individuals that are in L1 and not in L2 have the capture history $\left(1,0\right)$. The number of subjects with this capture history is $n_{10}=104$. Individuals appearing in both lists have the capture history $\left(1,1\right)$ corresponding to $n_{11}=29$. Subjects in L2 that are absent from L1 have the capture history $\left(0,1\right)$ and $n_{01}=527$. Applying the Petersen estimator, we have:

$\hat{N}=n_{10}+n_{11}+n_{01}+\frac{n_{10}{n}_{01}}{n_{11}}=104+29+527+\frac{104\times 527}{29}\approx 2550$

The Petersen estimator can be biased for small sample sizes⁷⁴; therefore, we are also using a slightly less biased estimator of the population size, that is, the Chapman estimator.⁷⁴

$\hat{N}=\frac{\left(n_{10}+n_{11}+1\right)\left(n_{01}+n_{11}+1\right)}{n_{11}+1}-1=\frac{\left(104+29+1\right)\left(527+29+1\right)}{29+1}-1\approx 2487$

The variance of Chapman estimator is given by:

$var\left(\hat{N}\right)=\frac{\left(n_{10}+n_{11}+1\right)\left(n_{01}+n_{11}+1\right)n_{10}{n}_{01}}{\left(n_{11}+1\right)\left(n_{11}+1\right)\left(n_{11}+2\right)}=\frac{\left(104+29+1\right)\left(527+29+1\right)104\times 527}{\left(29+1\right)\left(29+1\right)\left(29+2\right)}\approx 146622$

Chapman estimates are typically skewed, a log transformation has been used to obtain a confidence interval for the population size.⁷⁵ It is assumed that $log\left(\hat{N}-M\right)$ follows a normal distribution, with $M$ the total number of captured individuals, that is, $M=n_{10}+n_{11}+n_{01}$. The $95\mathrm{\%}$ confidence interval for Chapman estimator is given by:

$\left[M+\frac{\left(\hat{N}-M\right)}{C},M+\left(\hat{N}-M\right)\times C\right]$, with $C=exp\left\{1.96\sqrt{log\left[1+\frac{var\hat{N}}{{\left(\hat{N}-M\right)}^2}\right]}\right\}$

Therefore, a 95% confidence interval for the population size can be computed as follows:

$C=exp\left\{1.96\sqrt{log\left[1+\frac{var\hat{N}}{{\left(\hat{N}-M\right)}^2}\right]}\right\}=exp\left\{1.96\sqrt{log\left[1+\frac{146622}{{\left(2487-660\right)}^2}\right]}\right\}\approx 1.5\left[M+\frac{\left(\hat{N}-M\right)}{C},M+\left(\hat{N}-M\right)\times C\right]=\left[660+\frac{\left(2487-660\right)}{1.5},660+\left(2487-660\right)\times 1.5\right]=\left[1877,3403\right]$

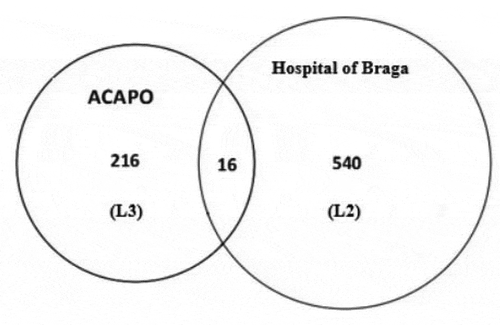
Doing the same with the list of ACAPO (L3) and the L2 the Venn diagram is shown in Figure 2.

Figure 2. Venn diagram representing the matching lists from ACAPO and HoB.

Thus, $n_{10}=216$, $n_{11}=16$ and $n_{01}=540$. Applying the Petersen estimator

$\hat{N}=n_{10}+n_{11}+n_{01}+\frac{n_{10}{n}_{01}}{n_{11}}=216+16+540+\frac{216\times 540}{16}\approx 8062$

Applying the Chapman estimator:

$\hat{N}=\frac{\left(n_{10}+n_{11}+1\right)\left(n_{01}+n_{11}+1\right)}{n_{11}+1}-1=\frac{\left(216+16+1\right)\left(540+16+1\right)}{16+1}-1\approx 7633$

The variance of this last estimator is

$var\left(\hat{N}\right)=\frac{\left(n_{10}+n_{11}+1\right)\left(n_{01}+n_{11}+1\right)n_{10}{n}_{01}}{\left(n_{11}+1\right)\left(n_{11}+1\right)\left(n_{11}+2\right)}=\frac{\left(216+16+1\right)\left(540+16+1\right)216\times 540}{\left(16+1\right)\left(16+1\right)\left(16+2\right)}=2909968$

Therefore, a 95% confidence interval to the population size is obtained as follows:

$C=exp\left\{1.96\sqrt{log\left[1+\frac{var\hat{N}}{{\left(\hat{N}-M\right)}^2}\right]}\right\}=exp\left\{1.96\sqrt{log\left[1+\frac{2909968}{{\left(7633-772\right)}^2}\right]}\right\}\approx 1.62$

$\left[M+\frac{\left(\hat{N}-M\right)}{C},M+\left(\hat{N}-M\right)\times C\right]=\left[772+\frac{\left(7633-772\right)}{1.62},772+\left(7633-722\right)\times 1.62\right]=\left[5048,11941\right]$

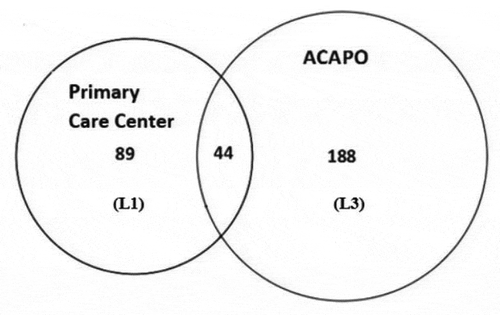
The matching of L1 (PCC) and L3 (ACAPO) originates Figure 3.

Figure 3. Venn diagram representing the matching lists from PCC and ACAPO.

The diagram shows that $n_{10}=89$, $n_{11}=44$ and $n_{01}=188$. Applying the Petersen estimator:

$\hat{N}=n_{10}+n_{11}+n_{01}+\frac{n_{10}{n}_{01}}{n_{11}}=89+44+188+\frac{89\times 188}{44}\approx 701$

Applying the Chapman estimator:

$\hat{N}=\frac{\left(n_{10}+n_{11}+1\right)\left(n_{01}+n_{11}+1\right)}{n_{11}+1}-1=\frac{\left(89+44+1\right)\left(188+44+1\right)}{44+1}-1\approx 693$

The variance of the estimator is

$var\left(\hat{N}\right)=\frac{\left(n_{10}+n_{11}+1\right)\left(n_{01}+n_{11}+1\right)n_{10}{n}_{01}}{\left(n_{11}+1\right)\left(n_{11}+1\right)\left(n_{11}+2\right)}=\frac{\left(89+44+1\right)\left(188+44+1\right)89\times 188}{\left(44+1\right)\left(44+1\right)\left(44+2\right)}\approx 5370$

Therefore, a 95% confidence interval to the population size is obtained as follows:

$C=exp\left\{1.96\sqrt{log\left[1+\frac{var\hat{N}}{{\left(\hat{N}-M\right)}^2}\right]}\right\}=exp\left\{1.96\sqrt{log\left[1+\frac{5370}{{\left(693-321\right)}^2}\right]}\right\}\approx 1.47\left[M+\frac{\left(\hat{N}-M\right)}{C},M+\left(\hat{N}-M\right)\times C\right]=\left[321+\frac{\left(693-321\right)}{1.47},321+\left(693-321\right)\times 1.47\right]=\left[575,866\right]$

Values of N obtained with each pair of lists vary significantly and this suggests that there may be dependence between lists. Because of that, we consider Scenario B.

Scenario B: using two dependent lists

We are now going to assume that the PPC (L1) and HoB (L2) have local dependence. The population size will be estimated by the $\left(12\right)$ log-linear model, that is expressed by:

$logE\left(n_{ij}\right)=u_0+u_{1}I\left(i=1\right)+u_{2}I\left(j=1\right)+u_{12}I\left(i=j=1\right).$

Because we want to ascertain the expected value for the number of subjects with capture-history $\left(0,0\right)$, that is, $E\left(n_{00}\right)$, then $logE\left(n_{00}\right)=u_0$, which yields $E\left(n_{00}\right)=e^{u_0}$. Then, the estimation can be done using the expression:

$\hat{N}=n_{10}+n_{11}+n_{01}+e^{u_0}$

To compute $u_0$ we can use the R package Rcapture.⁵⁴ Using Rcapture with lists L1 and L2 we get $\hat{N}=2550$, $95\mathrm{\%}$CI =$\left[1751,3349\right]$. Assuming also other possible pairs of dependencies, we obtain with the same package for L3 (ACAPO) and L2 (HoB) $\hat{N}=8062$, $95\mathrm{\%}$CI = $\left[4305,11819\right]$ and for L1 and L3 we get $\hat{N}=701$, $95\mathrm{\%}$CI =$\left[549,854\right]$. Estimations obtained with pairs of lists using log-linear models are similar to the estimations obtained in scenario A and this is indicative that dependences between lists may not be significant. However, Rcapture retrieves a warning message informing that the three models are unreliable because the algorithm does not converge. Therefore, the next step is to consider all the 3 lists in a single model, that is, Scenario C.

Scenario C: using three independent lists

Now, the three lists are going to be used simultaneously. If we consider that the three lists are independent (the three lists among themselves and every possible combination of two), then we can estimate the population size by applying the following log-linear model:

$logE\left(n_{ijk}\right)=u_0+u_{1}I\left(i=1\right)+u_{2}I\left(j=1\right)+u_{3}I\left(k=1\right).$

In this model, there are no parameters to model any dependence amongst lists. We will now obtain new parameters values using the Rcapture package to this new model $\hat{N}=n_{10}+n_{11}+n_{01}+e^{u_0}$. We provide the code in a supplementary methods file. The final result is $\hat{N}=2879$, $95\mathrm{\%}$CI =$\left[2409,3511\right]$. The model has a deviance of 120.5 and the AIC is 167.7. The goodness of fit test indicated that the model fit is not good because the $p-value=Pr\left({\chi }_{df}^2\ge deviance\right)=0$, $df$ represents the degrees of freedom of the saturated model minus the degrees of freedom of the proposed model. We have seen in scenarios A and B that different combinations of 2 lists were providing relatively inconsistent values and that would be caused by possible dependences between lists. In Scenario D we do a diagnostic analysis of the dependence and compute again estimates considering the dependences that we think are likely.

Scenario D: using three dependent lists

Values obtained in scenario A are summarized in Table 1. A brief analysis of the estimates leads us to suspect of two possible dependences. The first possible dependence is a local negative dependence between the ACAPO (L3) and HoB (L2). That is because the estimated population is too high when compared to the values reached when this same estimation is used with different pairs of lists. In addition, if this estimate of the number of people with impaired vision is used to compute prevalence, we would obtain values that are higher than expected for European countries, which is approximately 2.74%.⁷⁶ We can also suspect a positive dependence between L1 and L3 because the population size obtained by applying the Chapman estimator using these two lists is low and would lead to lower than expected prevalence.

Table 1. Prevalence values computed in Scenarios A, C and D.

Scenarios	Prevalence (%)	Estimate $\stackrel{⌢}{N}$	95% CI	Residual deviance	AIC	p-value
A: L1 and L2	1.37 (1.03–1.87)	2487	1877–3403	-	-	-
A: L1 and L3	0.38 (0.32–0.48)	693	575–866	-	-	-
A: L2 and L3	4.21 (2.78–6.58)	7633	5048–11941	-	-	-
C	1.59 (1.33–1.93)	2879	2409–3511	120.5	167.7	0
D	1.51 (1.10–2.26)	2741	1997–4110	16.13	67.34	<0.001

Therefore, considering the values obtained in Scenario A, we are going to use the $\left(13,23\right)$ log-linear model, that is:

$logE\left(n_{ijk}\right)=u_0+u_{1}I\left(i=1\right)+u_{2}I\left(j=1\right)+u_{3}I\left(k=1\right)+u_{13}I\left(i=k=1\right)+u_{23}I\left(j=k=1\right).$

To use the Rcapture package, we organize the information from Figure 4 in a matrix summarized in Table 2.

Table 2. Number of individuals presenting each possible capture history, except the unknown capture history (0 0 0).

[L1]	[L2]	[L3]	[Freq]
1	1	1	10
1	1	0	29
1	0	1	44
1	0	0	70
0	1	1	16
0	1	0	521
0	0	1	182

Figure 4. Venn diagram representing the matching lists from Primary Care Centre (PCC), ACAPO and Hospital of Braga (HoB).

In Table 2 the first three columns define the capture history and the fourth column is the number of cases with the correspondent capture history. Using the Rcapture package we obtained $\hat{N}=2741$, $95\mathrm{\%}$ CI $\left[1997,4110\right]$. This yields a crude prevalence of vision impairment of $1.51\mathrm{\%}$, $95\mathrm{\%}$CI =$\left[1.10,2.26\right]$. The model has a deviance of 16.13, the AIC is 67.34 and p-value<0.001. We choose this model over the one obtained in scenario C (deviance equals to 120.5, AIC = 167.7 and p-value<0.001) in which we assumed that all lists were independent of each other.

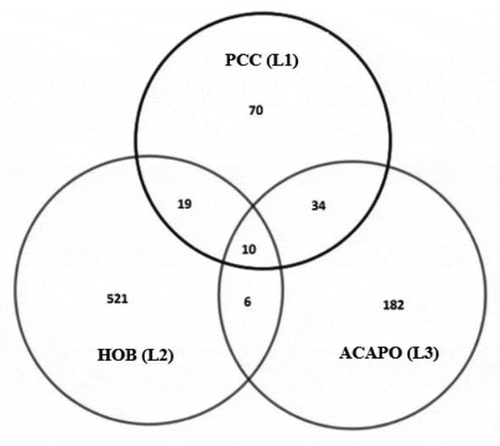
We can also perform the statistical test for the independence between lists conditioned to the universe of all individuals captured at least once. It is a chi-square test of independence between two categorical variables, for example, the variable first capture and the variable third capture (levels 1 and 0). Regarding L1 and L3, we obtained ${\chi }^2\left(1,N=842\right)=2.10$, $p=0.15$. Regarding L2 and L3, we obtained ${\chi }^2\left(1,N=842\right)=495.67$, $p<2.2\times {10}^{-16}$. These results do not reject independence between L1 and L3 and strongly reject independence between L2 and L3. However, this result should be evaluated with caution because the value in cell $\left(0,0\right)$ of the contingency table is not, for example, the true number of uncaptured individuals in L2 or L3. The value in cell (0,0) is the number of individuals not captured in either L2 or L3 within the universe of the subjects captured at least once, the subjects detected by our system. This test is not equivalent to test whether $u_{13}$ and $u_{23}$ are statistically different from 0. The test for the coefficients of the Poisson regression is a z-test.

We can now compute completeness which corresponds to the proportion of cases in our three lists (L1, L2 and L3) obtained from Primary Care Centre, Hospital of Braga and ACAPO. Completeness is given by the expression:

$\frac{n_{100}+n_{010}+n_{001}+n_{111}+n_{101}+n_{011}+n_{110}}{\hat{N}}\times 100=\frac{70+182+521+10+19+6+34}{2741}\times 100\approx 30.72\mathrm{\%}$

The results of completeness indicate that the observed data correspond to about 30% of the entire population.

In summary, in this section we have shown how to estimate the number of people with impaired vision in the municipality of Braga. Using all possible pairs of lists, assuming that lists were independent of each other, produced differing results, which suggests the existence of dependence between lists. When we used pairs of lists, assuming independence between the lists, the models were not reliable in the sense that the algorithm did not converge. When we used three lists, considering all independent of each other, we got a model with a deviance of 120.5, AIC = 167.7 and p-value<0.001. When we used the three lists with the dependences we suspect might exist, we obtained a model with a deviance of 16.13, AIC = 67.34 and p-value<0.001. We are led to believe that our dependence analysis is accurate and that the estimate of this last model is the most reliable. The best estimate was produced in, scenario D. However, the goodness of fit test of the model remains unsatisfactory and we will include more data in future estimations.

Discussion and recommendations

Capture-recapture methods are an alternative to traditional prevalence study methods such as case counting or cross-sectional studies of the population. The method allows the estimation of the number of individuals in a population that are missing from captures (registers). The method represents a fast and economical strategy to study the prevalence of diseases or conditions such as vision impairment. However, CR methods rely on assumptions that can easily be violated and researchers need to be careful when using the methodology otherwise unrealistic values will be produced.⁷⁷ Some recommendations for the presentation and evaluation of CR estimates should also be considered.⁷⁸

One important aspect that may lead to significant estimate bias is dependence between lists. It is important to explore the dependence scenarios thoroughly because the independence assumption is unlikely to hold in an epidemiological study. CR methods may be of limited use when there is a small overlap between the lists because that can lead to unstable log-linear models.⁷⁹ Another important factor that needs to be considered is tag-loss. Poor 'tags' or unique identifiers may impact significantly the estimates as well as false-positives and false-negatives.^65,66 Also, CR methods are more likely to produce a biased estimate of the population size if one source captures very few cases.⁸⁰

There are several CR models, applying different approaches, either classic or Bayesian. The models can vary, depending on whether the population is considered open or closed during the sampling period. Models can incorporate one or two types of dependences and they can even incorporate the tag-loss effect. Some studies advocate that the inclusion of capture-related covariates improves the accuracy of the estimate of the population size compared to estimates from simple models.⁵⁶ For example, some specific methodology can be used to identify patient characteristics related to the probability of capture by the different sources.⁵⁶ Thus, this technique can be used to identify both subsections of the population who are unlikely to be captured and population subsections who are more likely to be captured. Open population models try to produce estimates considering the population dynamics during the sampling period. The most common methodology regarding open populations use multistate CR models formulated as Hidden Markov Models.

Literature review

During the year of 2018, we searched PubMed and Web of Science to identify published articles using CR methods. Search terms focused mainly on “capture-recapture models”, “sample independence”, “heterogeneity”, “mixed capture-recapture models”, “log-linear models”, “tag-loss”, “completeness”, “Bayesian capture-recapture models”. In addition, we searched Pubmed for publications using combination of keywords as “prevalence visual impairment capture recapture”, “prevalence causes vision loss”, “prevalence visual impairment Portugal”. We obtained 6391 results from which we selected 22 possible inclusions listed in the Supplementary Table 1, 10 of these publications used CR method for estimating the prevalence of ocular diseases and are listed with comments in Supplementary Table 2.

Supplementary Material

Supplemental data for this article can be accessed here.

Additional information

Funding

This study was supported by FCT (COMPETE/QREN) grant reference [PTDC/DPT-EPI/0412/2012] in the context of the Prevalence and Costs of Visual Impairment in Portugal: a hospital-based study (PCVIP-study) and FCT Strategic Funding UID/FIS/04650/2013. PLR is funded by FCT (COMPETE/QREN) grant reference [SFRH/BD/119420/2016].