Raman solitons in nanoscale optical waveguides, with metamaterials, having polynomial law non-linearity

Abstract

This paper reports bright Raman soliton solutions in optical metamaterials. The polynomial law and triple law non-linearity are discussed. Travelling wave hypothesis is employed to conduct the mathematical analysis. Implicit solutions in terms of elliptic integral of the third kind are obtained. The analytical results are supplemented with numerical simulations.

Keywords:

• Solitons
• metamaterials
• integrability
• polynomial law
• triple-power law

1. Introduction

The dynamics of temporal optical solitons is a treasure-trove in the area of non-linear optics [1–42]. The starting point is Maxwell’s equation from electromagnetic theory. Electromagnetic properties of complex materials, with simultaneous negative dielectric permittivity ($\mathit{ϵ}$) and magnetic permeability ($\mathit{\mu }$), also known as double negative material (DNG), have attracted a lot of attention in research during recent times [1,14,21,25,31]. Novel and interesting features of these engineered materials, that are also known as metamaterials, and their possible applications to support short duration optical soliton pulses have been investigated in this paper. DNG materials in visible and infrared region by V. Shalaev and others have shown promise to manufacture optical waveguides with these materials [25,31]. Moreover, Boardman et. al have given a lot of insight with optical metamaterials [7–11]. For compact integration of photonic circuits, wavelength scale structures with high index contrast are a key requirement silicon on insulator (SOI) nanophotonic circuits appear to be the most appealing in photonic integration circuits [12,13]. Currently, ridge silicon wire [12,13,21] built in this (220 nm) waveguide are practically used in SOI structures. This structure provides higher confinement of light; so does higher non-linearity. Non-Kerr-type materials can also be used to guide lights.

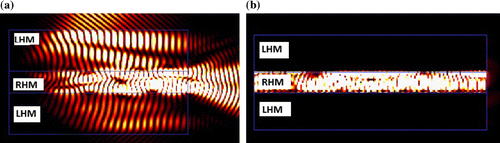
Frequency-dependent permittivity that follows the Drude model was considered in evaluating dispersion of the waveguide. A slab waveguide shown in Figure 1 is a dielectric type of waveguide that has core made up of right-handed materials (RHM) and two left-handed materials (LHM). DNG layers act as the cladding [21]. Earlier simulation, reported during 2016, shows that the waves are guided in the RHM due to total internal reflection and those are wavelength dependent. Figure 1(a) and (b) demonstrate that at short wavelength of 450 nm, light wave is scattered but at longer wavelength 1550 nm the wave is perfectly guided [21].

Figure 1. Optical wave propagation in slab waveguide with negative index materials: LHM as cladding and RHM as core; (a) unguided optical wave at 450 nm and (b) guided wave at 1550 nm.

Raman optical soliton pulses evolve due to a delicate balance between dispersion and non-linearity [21,31,42]. Solitons will dissipate in nature while propagating through DNG medium. Loss compensation is a challenge to engineer these type of materials. Dispersion profile of the wavelength structure is critically needed to determine the soliton pulse nature. In particular, Raman soliton self-frequency shift in metamaterials is induced by the stimulated Raman scattering (SRS) effect. Since the SRS effect enables the energy of the short pulse transferred from higher to lower frequency continuously by C. V. Raman and K. S. Krishnan [42]. It is possible that the whole spectrum moves toward the longer wavelength region. This paper conducted theoretical analysis to illustrate the controllability of the Raman soliton self-frequency shift in non-linear metamaterials by numerical results.

2. Governing model

The dimensionless form non-linear Schrödinger’s equation (NLSE) that governs the propagation of Raman solitons through optical metamaterials, with polynomial law non-linearity, is given by [2,6,15,22,31,34](1) $$\begin{array}{cc}& i{q}_t+a{q}_{xx}+\left(c_1{\left|q\right|}^2+c_2{\left|q\right|}^4+c_3{\left|q\right|}^6\right)q\hfill \\ \hfill & =i\mathit{\alpha }{q}_x+i\mathit{\lambda }{\left({\left|q\right|}^{2}q\right)}_x+i\mathit{\nu }{\left({\left|q\right|}^2\right)}_{x}q+{\mathit{\theta }}_1{\left({\left|q\right|}^{2}q\right)}_{xx}\hfill \\ \hfill & +{\mathit{\theta }}_2{\left|q\right|}^2{q}_{xx}+{\mathit{\theta }}_3{q}^2{q}_{xx}^{\ast }.\hfill \end{array}$$(1)

In this model, q(x, t) represents the complex-valued wave function with the independent variables being x and t that represent spatial and temporal variables, respectively. The first term represents the temporal evolution of non-linear wave, while the coefficient a is the group velocity dispersion (GVD). The coefficients of $c_j$ for $j=1,2,3$ corresponds to the non-linear terms. Together, they form polynomial law non-linearity. It must be noted here that when $c_2=c_3=0$ and $c_1\ne 0$, the model (1) collapses to Kerr law non-linearity. However, if $c_3=0$ and $c_1\ne 0$ and $c_2\ne 0$, one arrives at parabolic law non-linearity. Thus, polynomial law stands as an extension version to Kerr and parabolic laws.

On the right-hand side of (1), $\mathit{\alpha }$ represents the coefficient of inter-modal dispersion. This arises when the group velocity of light propagating through a metamaterial is dependent on propagation mode in addition to chromatic dispersion. The factors $\mathit{\lambda }$ and $\mathit{\nu }$ are accounted for self-steepening for preventing shock-waves, and non-linear dispersion. Finally, the terms with ${\mathit{\theta }}_j$ for $j=1,2,3$ arise in the context of optical metamaterials where functional variable method and first integral approach lead to bright and singular 1-soliton solution, as well as continuous waves [4]; the ansatz method of integration is employed to extract the 1-soliton solutions and numerical simulations are given to expose the dissipative effects [5]; the simplest equation approach also leads to topological soliton, rational solution and singular periodic solution [6]; the mapping method is applied to obtain soliton solutions with Kerr and Parabolic law [22]; by the aid of collective variables, the numerical simulations of soliton parameter variation are given for specific values of the super-Gaussian pulse parameters [28]; a theoretical investigation on the controllability of the Raman soliton self-frequency shift in the metamaterials [31]; bright 1-soliton solution is derived by the aid of travelling wave hypothesis in Kerr law, parabolic law and log law non-linearity [33].

This model equation has studied for five forms of non-linear media by the aid of ansatz method [5,29], travelling wave hypothesis [33] as well as mapping methods [22] and collective variables approach [28]. This paper will employ the travelling wave hypothesis to secure solutions to the model (1) that is with polynomial law non-linearity. The starting hypothesis is the travelling wave argument given by [2,3,33](2) $$\begin{array}{c}\hfill q(x,t)=g(s)e^{i\mathit{\varphi }}\end{array}$$(2)

where g(s) represents the shape of the wave profile, and(3) $$\begin{array}{c}\hfill s=x-vt,\end{array}$$(3)

with v being the speed of the wave. The phase component $\mathit{\varphi }(x,t)$ is defined as(4) $$\begin{array}{c}\hfill \mathit{\varphi }(x,t)=-\mathit{\kappa }x+\mathit{\omega }t+\mathit{\theta },\end{array}$$(4)

where $\mathit{\kappa }$ represents the soliton frequency, and $\mathit{\omega }$ the wave number while $\mathit{\theta }$ the phase constant. Therefore, by substituting the hypothesis (2(2) $$\begin{array}{c}\hfill q(x,t)=g(s)e^{i\mathit{\varphi }}\end{array}$$(2) ) into (1) and decomposing into real and imaginary parts one obtains the real part as:(5) $$\begin{array}{cc}& a{g}^{″}-\left(\mathit{\omega }+\mathit{\alpha }\mathit{\kappa }+a{\mathit{\kappa }}^2\right)g+\left(c_1-\mathit{\kappa }\mathit{\lambda }\right)g^3\hfill \\ \hfill & +c_2{g}^5+c_3{g}^7=0\hfill \end{array}$$(5)

and the imaginary part as:(6) $$\begin{array}{c}\hfill v+\mathit{\alpha }+2a\mathit{\kappa }+\left\{3\mathit{\lambda }+2\mathit{\nu }-2\mathit{\kappa }(3{\mathit{\theta }}_1+{\mathit{\theta }}_2-{\mathit{\theta }}_3)\right\}{g}^2=0\end{array}$$(6)

The notations $g^{\prime }=dg/ds$, $g^{″}=d^{2}g/d{s}^2$, and so on, are introduced in (5) for convenience.

Figure 2. Soliton profile with polynomial law non-linearity.

Figure 3. Soliton profile with general polynomial law non-linearity.

From the imaginary part Equation (6(6) $$\begin{array}{c}\hfill v+\mathit{\alpha }+2a\mathit{\kappa }+\left\{3\mathit{\lambda }+2\mathit{\nu }-2\mathit{\kappa }(3{\mathit{\theta }}_1+{\mathit{\theta }}_2-{\mathit{\theta }}_3)\right\}{g}^2=0\end{array}$$(6) ), upon setting the coefficients of linearly independent functions to zero gives(7) $$\begin{array}{c}\hfill v=-\mathit{\alpha }-2a\mathit{\kappa }\end{array}$$(7)

and the relation(8) $$\begin{array}{c}\hfill 3\mathit{\lambda }+2\mathit{\nu }=2\mathit{\kappa }(3{\mathit{\theta }}_1+{\mathit{\theta }}_2-{\mathit{\theta }}_3).\end{array}$$(8)

Equation (8(8) $$\begin{array}{c}\hfill 3\mathit{\lambda }+2\mathit{\nu }=2\mathit{\kappa }(3{\mathit{\theta }}_1+{\mathit{\theta }}_2-{\mathit{\theta }}_3).\end{array}$$(8) ) serves as the constraint condition between soliton parameters and its coefficients, while (7) reveals the soliton velocity in polynomial law medium.

From the real part Equation (5(5) $$\begin{array}{cc}& a{g}^{″}-\left(\mathit{\omega }+\mathit{\alpha }\mathit{\kappa }+a{\mathit{\kappa }}^2\right)g+\left(c_1-\mathit{\kappa }\mathit{\lambda }\right)g^3\hfill \\ \hfill & +c_2{g}^5+c_3{g}^7=0\hfill \end{array}$$(5) ), multiplying both sides by $g^{\prime }$ and integrating after separation of variables yields the implicit solution:(9) $$\begin{array}{cc}& \frac{x-vt}{2\sqrt{3a}}{g}_3\hfill \\ \hfill & \times \sqrt{6\left(\mathit{\lambda }\mathit{\kappa }-c_1\right)g^2-4c_2{g}^4-3c_3{g}^6+12\left(\mathit{\omega }+\mathit{\alpha }\mathit{\kappa }+a{\mathit{\kappa }}^2\right)}\hfill \\ \hfill & =-\mathrm{\Pi }\left(1-\frac{g_2}{g_3};{sin}^{-1}\left[\frac{g_3-g^2}{g_3-g_2}\right]|\frac{g_2-g_3}{g_1-g_3}\right)\hfill \\ \hfill & \times \sqrt{\frac{\left(g^2-g_1\right)\left(g^2-g_2\right)\left(g^2-g_3\right)}{g_1-g_3}},\hfill \end{array}$$(9)

where incomplete elliptic integral of third kind is defined as(10) $$\begin{array}{c}\hfill \mathrm{\Pi }\left(n;\mathit{\varphi }|\mathit{\alpha }\right)={\int }_0^{\mathit{\varphi }}\frac{\mathrm{d}\mathit{\theta }}{\left(\mathit{\alpha }-n{sin}^2\mathit{\theta }\right)\sqrt{1-{sin}^2\mathit{\alpha }{sin}^2\mathit{\theta }}}\end{array}$$(10)

and(11) $$\begin{array}{cc}\hfill g_1& =-\frac{1}{9c_3}\left\{4c_2-\frac{2\left(8c_2^2-27c_1{c}_3+27c_3\mathit{\lambda }\mathit{\kappa }\right)}{R^{\frac{1}{3}}}+R^{\frac{1}{3}}\right\}\hfill \end{array}$$(11) (12) $$\begin{array}{cc}\hfill g_2& =-\frac{1}{9c_3}\left\{4c_2-\frac{\left(1+i\sqrt{3}\right)\left(8c_2^2-27c_1{c}_3+27c_3\mathit{\lambda }\mathit{\kappa }\right)}{R^{\frac{1}{3}}}\right.\hfill \\ \hfill & \left.-\frac{\left(1-i\sqrt{3}\right)R^{\frac{1}{3}}}{2}\right\}\hfill \end{array}$$(12) (13) $$\begin{array}{cc}\hfill g_3& =-\frac{1}{9c_3}\left\{4c_2-\frac{\left(1-i\sqrt{3}\right)\left(8c_2^2-27c_1{c}_3+27c_3\mathit{\lambda }\mathit{\kappa }\right)}{R^{\frac{1}{3}}}\right.\hfill \\ \hfill & \left.-\frac{\left(1+i\sqrt{3}\right)R^{\frac{1}{3}}}{2}\right\}\hfill \end{array}$$(13)

with(14) $$\begin{array}{c}\hfill R=2r+\sqrt{r^2-8{\left(8c_2^2-27c_1{c}_3+27c_3\mathit{\lambda }\mathit{\kappa }\right)}^3}\end{array}$$(14)

and(15) $$\begin{array}{cc}\hfill r=& 2\left\{32c_2^3-162\left(\mathit{\lambda }\mathit{\kappa }-c_1\right)c_2{c}_3\right.\hfill \\ \hfill & \left.-729c_2^2\left(\mathit{\omega }+\mathit{\alpha }\mathit{\kappa }+a{\mathit{\kappa }}^2\right)\right\}.\hfill \end{array}$$(15)

Equation (14(14) $$\begin{array}{c}\hfill R=2r+\sqrt{r^2-8{\left(8c_2^2-27c_1{c}_3+27c_3\mathit{\lambda }\mathit{\kappa }\right)}^3}\end{array}$$(14) ) prompts the constraint condition(16) $$\begin{array}{c}\hfill r^2>8{\left(8c_2^2-27c_1{c}_3+27c_3\mathit{\lambda }\mathit{\kappa }\right)}^3\end{array}$$(16)

that must remain valid for the existence of the solution.

From a historic standpoint, it must be noted that such an algorithm has already been applied in the past for the study of soliton propagation through optical fibres [2,3]. During the second round, this analysis was carried out in presence of spatio-temporal dispersion (STD) in addition to GVD [2] (see Figures 2 and 3).

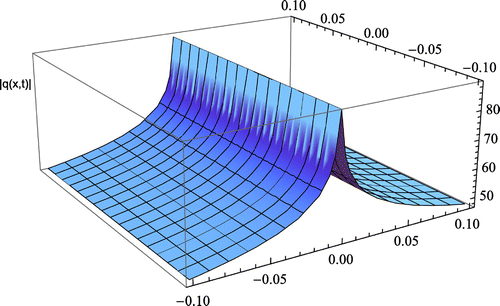
The following figure shows the profile of the soliton solution for selected parameter values. In this case, $a=1$, $c_1=10$, $c_2=-10,000$, $c_3=5$, $\mathit{\alpha }=100$, $\mathit{\lambda }=-2$, $\mathit{\nu }=-1$, $\mathit{\omega }=1$, $\mathit{\kappa }=1$.

3. Generalization

In this part, the triple-power law, i.e. the extension of parabolic law non-linearity that is given by(17) $$\begin{array}{cc}& i{q}_t+a{q}_{xx}+\left(c_4{\left|q\right|}^{2n}+c_5{\left|q\right|}^{4n}+c_6{\left|q\right|}^{6n}\right)q\hfill \\ \hfill & =i\mathit{\alpha }{q}_x+i\mathit{\lambda }{\left({\left|q\right|}^{2}q\right)}_x+i\mathit{\nu }{\left({\left|q\right|}^2\right)}_{x}q+{\mathit{\theta }}_4{\left({\left|q\right|}^{2}q\right)}_{xx}\hfill \\ \hfill & +{\mathit{\theta }}_5{\left|q\right|}^2{q}_{xx}+{\mathit{\theta }}_6{q}^2{q}_{xx}^{\ast }.\hfill \end{array}$$(17)

Therefore, the NLSE (17) transform to(18) $$\begin{array}{c}\hfill x-vt=\frac{\sqrt{2a\left(n+1\right)\left(2n+1\right)\left(3n+1\right)}}{n}\int \frac{\mathrm{d}g}{g\sqrt{Q\left(g\right)}},\end{array}$$(18)

Here(19) $$\begin{array}{cc}\hfill Q\left(g\right)& =\left(n+1\right)\left(2n+1\right)\left(3n+1\right)\hfill \\ \hfill & \times \left(2\left(\mathit{\omega }+a\mathit{\kappa }+\mathit{\alpha }{\mathit{\kappa }}^2\right)+\mathit{\kappa }\mathit{\lambda }{g}^2\right)\hfill \\ \hfill & -2\left(2n+1\right)\left(3n+1\right)c_{{}_4}{g}^{2n}\hfill \\ \hfill & -2\left(n+1\right)\left(3n+1\right)c_5{g}^{4n}\hfill \\ \hfill & -2\left(n+1\right)\left(2n+1\right)c_6{g}^{6n}.\hfill \end{array}$$(19)

Assume $\mathit{\lambda }=0$, integrating (18) leads to(20) $$\begin{array}{cc}& \frac{\left(x-vt\right)}{\sqrt{a\left(n+1\right)\left(2n+1\right)\left(3n+1\right)}}n\ast \hfill \\ \hfill & n\sqrt{\left(n+1\right)\left(2n+1\right)\left(3n+1\right)\left(\mathit{\omega }+a\mathit{\kappa }+\mathit{\alpha }{\mathit{\kappa }}^2\right)+\left(2n+1\right)\left(3n+1\right)c_4{g}^{2n}+\left(n+1\right)\left(3n+1\right)c_5{g}^{4n}+\left(n+1\right)\left(2n+1\right)c_6{g}^{6n}}{g}_6\hfill \\ \hfill & =-\mathrm{\Pi }\left(1-\frac{g_5}{g_6};{sin}^{-1}\left[\frac{g_6-g^{2n}}{g_6-g_5}\right]|\frac{g_5-g_6}{g_4-g_6}\right)\sqrt{\frac{\left(g^{2n}-g_4\right)\left(g^{2n}-g_5\right)\left(g^{2n}-g_6\right)}{g_4-g_6}}\hfill \end{array}$$(20)

where(21) $$\begin{array}{c}\hfill g_4=\frac{1}{3(1+3n+2n^2)}\left[2(1+4n+3n^2)-\frac{2^{\frac{1}{3}}{h}_1}{5R}+\frac{R}{5\ast 2^{\frac{1}{2}}}\right],\end{array}$$(21) (22) $$\begin{array}{c}\hfill g_5=\frac{1}{3(1+3n+2n^2)}\left[2(1+4n+3n^2)+\left(1+i\sqrt{3}\right)\frac{h_1}{5\ast 2^{\frac{2}{3}}R}-\left(1-i\sqrt{3}\right)\frac{R}{10\ast 2^{\frac{1}{2}}}\right],\end{array}$$(22) (23) $$\begin{array}{c}\hfill g_6=\frac{1}{3(1+3n+2n^2)}\left[2\left(1+4n+3n^2\right)+\left(1-i\sqrt{3}\right)\frac{h_1}{5\ast 2^{\frac{2}{3}}R}-\left(1+i\sqrt{3}\right)\frac{R}{10\ast 2\frac{1}{2}}\right],\end{array}$$(23)

with $R_1$ being given by(24) $$\begin{array}{cc}\hfill r_1& =4502000+675\mathit{\kappa }+67500{\mathit{\kappa }}^2+54024000n+8100\mathit{\kappa }n\hfill \\ \hfill & +810000{\mathit{\kappa }}^{2}n+261114000n^2+675\mathit{\omega }\hfill \\ \hfill & +40500(\mathit{\kappa }+100{\mathit{\kappa }}^2)n^2+648272000n^3\hfill \\ \hfill & +109350(\mathit{\kappa }+100{\mathit{\kappa }}^2)n^3+(868842000+172125\mathit{\kappa })n^4\hfill \\ \hfill & +17212500{\mathit{\kappa }}^2{n}^4+594216000n^5\hfill \\ \hfill & +157950(\mathit{\kappa }+100{\mathit{\kappa }}^2)n^5+162054000n^6\hfill \\ \hfill & +78300(\mathit{\kappa }+100{\mathit{\kappa }}^2+\mathit{\omega })n^6\hfill \\ \hfill & +16200(\mathit{\kappa }+100{\mathit{\kappa }}^2+\mathit{\omega })n^7+8100n\mathit{\omega }+40500n^2\mathit{\omega }\hfill \\ \hfill & +109350n^3\mathit{\omega }+172125n^4\mathit{\omega }+157950n^5\mathit{\omega },\hfill \end{array}$$(24) (25) $$\begin{array}{c}\hfill h_1=-(150100+1200800n+3452200n^2+4202400n^3+1800900n^4),\end{array}$$(25)

Equation() promotes the constraint condition(26) $$\begin{array}{c}\hfill 4h_1^3+r_1^2\ge 0.\end{array}$$(26)

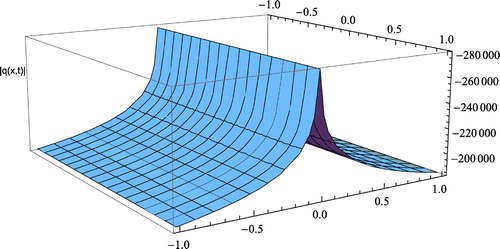
Figure (3) shows the profile of the soliton solution in formula (20) for selected parameter values. In this case, $a=100$, $c_4=-10000$, $c_5=-10$, $c_6=10$, $\mathit{\alpha }=100$, $\mathit{\nu }=-1$, $\mathit{\omega }=1$, $\mathit{\kappa }=1$.

4. Conclusions

This paper gives Raman soliton solutions in optical metamaterials that is studied with polynomial law and triple law non-linearity. The analytical results are supplemented with numerical simulation. This paper is an extension to the ones that were studied earlier in optical fibres [2,3]. The results of this paper are encouraging to conduct further research in this field.

In future, additional perturbation terms such as Raman scattering, saturable amplifiers, higher order dispersions and several others will be included. Additionally, solitons in optical metamaterials will be considered with STD in addition to GVD. There are several other forms of non-linear media that are yet to be explored. These are saturable law, exponential law, triple-power law and threshold law. In particular, the triple-power law non-linearity that is a direct generalization of polynomial law will be studied. Although this law is investigated in optical fibres, the results are unknown at this stage for optical metamaterials. Furthermore, optical metamaterials will be handled in the context of couplers. From a mathematical perspective, the governing NLSE will be analysed with fractional temporal evolution. This will lead to the attainment of slow-light solitons in optical metamaterials in order to address the Internet bottleneck that is a growing concern in this industry. The results of all of these researches will be gradually disseminated elsewhere.

Acknowledgements

The sixth (AB) and seventh (MB) authors thankfully acknowledge this support from QNRF. The third author (KRK) would like to acknowledge Dr. Khaleed Mnaymneh of National Research Council (NRC) in Ottawa, Canada for his help in fabricating photonic crystal waveguides

Additional information

Funding

This research is funded by Qatar National Research Fund (QNRF) [grant number NPRP 6-021-1-005].

Notes

These authors also declare that there is no conflict of interest.