Kelvin's foam structure: a commentary

Abstract

Kelvin's 1887 speculation on an ideal foam structure, which was intended to serve as a model for the ether, was a highly imaginative conception, brilliantly carried through into detailed calculations. It eventually launched the Kelvin Problem, which asks how space may be partitioned into cells of fixed equal volume with minimum surface area. Although it could be said to be misguided in motivation, faulty in logic and even mistaken in its conclusions, the paper nevertheless stands as an enduring classic and Kelvin's foam remains of great interest today.

1. A waste of time?

When Sir William Thomson (later Lord Kelvin) published his proposal 1 ‡ for an ideal foam, intended as a model for the ether of space, his colleagues were not impressed. “Utterly frothy” and “A pure waste of time” were two of the contemporary responses to his notion.

In 1887 Kelvin, if not in his prime, was still a major force in the world of physics, but his prejudices were beginning to look old-fashioned. So was the ether itself. For some it was “a real thing” as Kelvin himself insisted, but for many it was becoming an outmoded contrivance, at best an elegant figure of speech for something immaterial.

The material ether was supposed to carry light waves as vibrations, rather as air carries sound. The growing band of Maxwellians 2 needed no such substance for light propagation, but dealt directly with electromagnetic fields. The very year of 1887 in which Kelvin began his speculation on a foamy ether was that of the experiment of Hertz, the experimentum crucis of the Maxwell theory and a large nail in the ether's coffin.

Wilczek 3 has argued that the ether has been given a bad name unnecessarily, and that it can perfectly well stand for the modern vision of quantum fields and space-time (whose theorists even include foam in their conceptions of its nature on the Planck scale!).

Certainly Kelvin's foamy ether failed to ignite much positive interest at the time, and it has been largely overlooked by the great man's biographers. Even compendious histories of the ether 4 pay it little attention. In his long list of 650 or so papers, his proposal 1 of an ideal foam structure, intended for the ether, has been considered relatively insignificant. However, it must rank high in terms of the fashionable citation analysis of today: mathematicians, physicists, materials scientists and biologists all find it stimulating.

So let us return to it for a close reading, exactly one hundred years after Kelvin departed this life, still dreaming of the ether. It has not often been properly scrutinized. As Princen and Levinson 5 said of the authors that went before them, in the course of checking and extending Kelvin's calculations: Most of the authors involved may not, in fact, have consulted the original reference, it being rather inaccessible.

2. The search for the all-pervading ether

But first we step back a few decades. The search for a material ether went on throughout the nineteenth century, to the fascination of many and the irritation of some, such as Gibbs. It was, in particular, a recurrent subject of correspondence between Kelvin and George Gabriel Stokes 6.

Kelvin and Stokes were both Irishmen and both Cambridge-trained mathematicians, but their careers and characters were divergent. The energetic and impulsive Kelvin established himself at the industrial heart of the Empire, while the shy and methodical Stokes remained in the restful cloisters of Cambridge. But they continued to correspond affectionately to the end (“Stokes is gone and I shall never return to Cambridge again” said Kelvin).

Kelvin's lifelong pursuit of the ether was stimulated in part by the “jelly ether” model of Stokes. The merit of this concept was that it offered some rationalization of the paradoxical property of the ether, that it allowed bodies to pass through it with little resistance, but displayed an elastic stiffness at high frequencies in order to support light waves. Vortex models also came into play. This heady mix of fundamental physics, materials science and fluid dynamics never achieved its ostensible aim, but its fruits remain with us in many forms, not alone the subject of this article.

All that imaginative mind-play, spiralling off into the ether, started from solid ground, and was intended to return to it. It took off from the experimental facts of light propagation, invoked the observed properties of condensed matter and brought rigorous mathematics to bear on them.

3. Kelvin and Green

Further back in Kelvin's development, he was personally responsible for the recognition of the neglected mathematics of another Cambridge man, George Green, when the French mathematical school began to publish theorems similar to his.

One particular paper must have stuck in his mind. Green had addressed the problem of the nature of the material ether and reached a straightforward conclusion. Experimentally, light waves were entirely transverse, whereas elastic (sound) waves could also be longitudinal. This ruled out an elastic solid ether, unless it had a very peculiar property. Since the longitudinal waves have a squared frequency proportional to a particular elastic modulus, which represents the elastic response to the local distortion involved, this modulus must be either zero or infinite, in order to get rid of those superfluous waves. The modulus may be written as c ₁₁ in the modern notation. For an isotropic material, it will be independent of the choice of axes. It may be called the uniaxial compression modulus, as it refers to compression or extension in one direction.

It seems that Green's stipulation came back into Kelvin's mind in 1887. But what strange ethereal material could have such a paradoxical property?

4. Rigidity of foam?

Kelvin seems to have dreamed up the answer to the question implied by Green's analysis in his sleep 7. He convinced himself that the ether should be a foam.

Although his notebooks, in which he wrote the words of this section title while in bed, survive in Cambridge, it is difficult to discern his precise train of thought. It seems that he was at first thinking about two-dimensional (2D) models of foam. He made many sketches of the honeycomb structure (figure 1), which is the 2D analogue of a 3D foam, and perfectly ordered. It was here that he found a clue to the ether problem.

Figure 1. The honeycomb structure, the simplest (and lowest energy) 2D foam of bubbles of equal area.

And yet the ordinary 2D foam with the honeycomb structure does not satisfy the requirements of Green. There are two contributions to the modulus c ₁₁ (which is the same in all directions in this case). One contribution comes from the line tension associated with the cell edges (corresponding to the surface tension in 3D). It vanishes for the honeycomb structure, as Kelvin saw. This is because the foam can be compressed or extended in any direction with no quadratic change in the energy associated with surface tension. Its straight edges can be changed in length with only a linear change of energy. But the modulus c ₁₁ remains finite, on account of the second term, due to the finite bulk modulus of the enclosed gas, and so longitudinal waves would have finite frequency.

Suppose, thought Kelvin, one was simply to dispense with that gas: what about an empty 2D foam as a model? It should have precisely the required property, a zero modulus, since only line tension would contribute. Such a foam must somehow be maintained by an outward force at its boundary, to prevent it collapsing inwards. Hardly a serious consideration when talking imaginatively of the entire (infinite?) universe! He also noted that this ideal foam might be internally unstable, but he asserted that it was stable, and moved on.

He supposed a 3D foam to have the same property, with no explicit justification in notes or publication, and there were some indications of doubt in his later work. But what should be the structure of this empty 3D foam? The honeycomb structure is an almost inevitable choice in 2D (although only recently has it been proved to have the absolute minimum line length).What should be its natural counterpart in 3D?

Thus was launched the Kelvin Problem 7. This first paper on the subject dryly stated it in the title:

     On the Division of Space with Minimum Partitional Area.

As we shall see, it is not precisely clear what this was supposed to mean.

5. The paper

There is no mention whatsoever of the ether in the 1887 paper (see the facsimile reproduction following this commentary). The background that we have sketched above was distilled from the notebooks, later papers and the secondary literature. Kelvin covered his traces by simply posing a mathematical problem in the above title and proceeding to address it, rather as Einstein introduced relativity. However, the problem itself is not really well defined by the title or what follows, as we shall explain.

Kelvin immediately declared the problem to be “solved in foam”, and Plateau was credited with “some elements towards its solution”. This refers to the general principle of minimization of surface area as the essential equilibrium condition in theoretical models of foam, and the local conditions that are necessary to satisfy this principle.

Satisfaction of Plateau's conditions guarantees an equilibrium, but not that the configuration is of lowest energy in an absolute sense, or even that it is stable with respect to displacements other than those that Plateau considered.

We have often imputed to Kelvin the goal of finding the lowest energy structure for bubbles of equal size–that is, the absolute minimum–and in recent times we have called this the Kelvin Problem, by analogy with the Kepler Problem of sphere packing 8. However, his objective was apparently more modest: to find a simple structure that is in stable equilibrium, at least according to the rules of Plateau. There is no mention of it having the lowest possible area/energy, in the paper itself.

If I am guilty of misrepresenting the story as well as not thoroughly analyzing the paper (both faults common in the history of science), the great man must carry some of the blame, on account of the abrupt and ambiguous introduction to his publication, and the lack of any concluding section that might have clarified his aims and claims.

6. Plateau's rules

The more limited problem is still non-trivial. Otherwise a solution would be available in Plateau's book 9, which Kelvin had to hand.

Although Plateau repeatedly referred to foams as conforming to his principles, he remained focused on local configurations, represented in his celebrated wire frame experiments. With these he showed that films must meet symmetrically, three at a time, in lines (now called Plateau borders). The lines must meet symmetrically, four at a time, at vertices. A mathematical proof of these restrictions was provided by his colleague Lamarle, which was no mean feat. Plateau also adduced the Laplace–Young law, relating local film curvature to pressure difference between the two sides of a film. In the case of zero pressure difference, the film has zero curvature, but it is not necessarily flat: it can be saddle-shaped.

In a foam, the bubbles form polygonal cells, the curved faces of which are the films. Their edges (the lines, or Plateau borders) and the corners (vertices) are shared with neighbouring cells in a space-filling structure: hence the “Division of Space”.

7. Kelvin's approach

Given the pace at which he wrote up and published 7, what we see in the paper must be close to Kelvin's original train of thought, which takes a surprisingly indirect route to his solution.

As S.P. Thomson said of Kelvin's method, he was “daring in speculation, moving swiftly, almost erratically, to some intuitive result.” 10. There can be few better examples than what is before us.

One might have expected him to draw more on his pioneering expertise in practical crystallography, in terms of packing and space-filling: see for example his entertaining 1893 lecture to Oxford undergraduates 11. He used that knowledge at the outset, in immediately identifying a candidate cellular structure, but thereafter departed on a rambling excursion that eventually adapted that structure to his purpose.

Those of us who lack his talent for visualizing geometrical objects are quickly lost in this diversion. It includes several references to models that can be built by hand to help understanding, and he certainly made some himself (of clay and wire, not to mention a polygonal pin-cushion later made by his wife). He also repeated Plateau's experiments 7. This is in keeping with his view (shared with others of the British school) that physics, being concerned with real things, must be realizable in physical models. But it hardly helps the reader, and it is difficult to tell what is practical advice and what is merely gedanken.

Having invoked as his first choice what we would now call the fcc Wigner–Seitz cell and found it wanting, as described below, he had only to turn to bcc, the other common cubic crystal structure, to find a close approximation to his required solution. The bcc cell (the orthic tetrakaidecahedron in his terminology) was not yet uppermost in his mind. But if he had taken more time to review his conclusions he surely would have seen that they could be reached more expeditiously, and spared his readers several pages of determined sleuthing towards his obscure objective.

The cell that is appropriate to fcc is the rhombic dodecahedron, much discussed but never depicted in the paper: we supply a diagram in figure 2. The foam structure that results from tightly filling space with such polyhedra breaks only one rule of Plateau. Six fourfold vertices of the polyhedron are the confluence of eight lines in the extended structure: they are unstable vertices, according to Plateau.

Figure 2. The rhombic dodecahedron can fill space, with its centre placed on the points of an fcc lattice. Corners where four edges meet correspond to unstable vertices in the extended structure, when this is taken as a model for a foam.

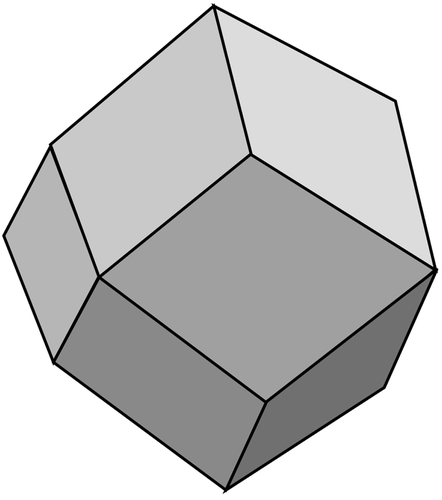
The instability in question is of the kind found by Plateau 9 in his cubic frame, as reproduced in Kelvin's figure 1. Whereas we might expect a symmetric configuration with a vertex at the centre, with eight lines converging to a point, this instability dissociates the vertex into four stable ones, breaking cubic symmetry.

This process introduces a new flat film with four curved edges. The adjoining films must acquire some curvature as well. The new film may be directed along any of the three cubic axes.

Kelvin's idea was to introduce the same quadrilateral faces into the structure of the foam made up of rhombohedral cells, to render it stable. To do so, he imagined attaching many copies of Plateau's wire cube together, edge to edge. If they contain the symmetric unstable configuration, they combine to form the rhombohedral cells. Now the new faces can be introduced, choosing the same cubic axis for all of them. The effect of this upon the rhombohedral cell of figure 2 is as follows. A square face is introduced at the top and bottom. Also new horizontal edges appear at the four fourbold vertices that lie on the equator. These are the edges of square faces belonging to adjacent cells.

If we now remove the frames, we have a new candidate structure that has no vertex instability. However, it is now tetragonal in symmetry. Kelvin recognized that it needed a shear stress to support it; he talked of “pulls” in various directions, and considered this undesirable. One might wonder why: after all, he had already invoked such “pulls” to prevent collapse. But he was looking for an isotropic ether, so he set out to relieve the shear stress by varying the axial ratio, bringing it to a value for which the shear stress vanished. Furthermore, the structure regained cubic symmetry at this point. His discourse is rather inadequate here, in stating the symmetry (which he calls “isotropic” at times, hardly a justifiable use of the term, because cubic structures are not elastically isotropic) without really showing how it is so. Recall that the bcc and fcc lattices may be regarded as tetragonal distortions of each other, which is the essence of what is going on here.

By this stage the nature of the cell that he had conceived so tortuously became clear to him. It was what he called a tetrakaidecahedron (fourteen-sided polyhedron), with cubic symmetry. There is no adequate picture of it in the paper: Figure 3 is a modern one.

Figure 3. The Kelvin cell, or tetrakaidecahedron. It fills space when its centre is placed on the points of a bcc lattice. It is closely approximated by the flat-sided Wigner–Seitz bcc cell.

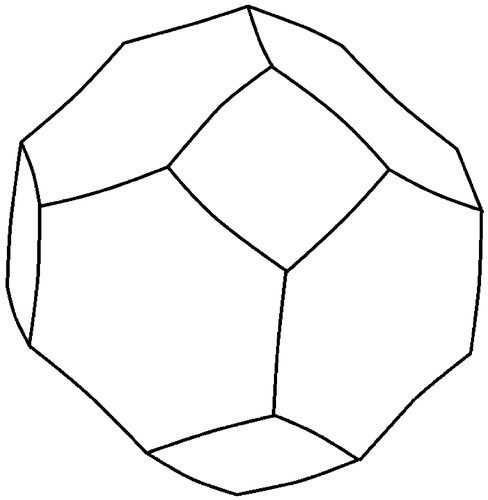
As we have noted, the flat-sided bcc Wigner–Seitz cell is such a polyhedron, and could have been his starting point, but Kelvin's tetrakaidecahedron is not quite the same, on account of the necessary equilibrium angle, and the consequent film curvature. Just as in Plateau's experiment, the quadrilateral faces are flat, by symmetry, but the others are curved (with zero total curvature).

At this point Kelvin could have concluded his paper with a summary. Instead, as we often feel compelled to do today, he embellished his qualitative proposal with some very impressive but perhaps unnecessary quantitative detail, determining the detailed shape of the cell with high precision.

In general this kind of problem is still impossibly difficult without the aid of computers. Only in the last decade or so has it become routinely possible to compute such surfaces accurately, thanks to the Surface Evolver of Ken Brakke 12. The constant-curvature condition that dictates the detailed shape of faces of a foam does not generally lend itself to tractable analytical mathematics or simple approximations.

But Kelvin recognized that this case was very special: the curved hexagonal faces are almost flat, with only a very slight double curvature. He therefore set out to describe them by an approximation that would enable him to work out the numbers by the methods of his day.

If a surface is slightly changed from a flat one by a perpendicular displacement z, a function of position x,y in the flat surface, then in lowest order the zero-curvature condition is simply

The surface in question here is any of the eight hexagonal faces of Kelvin's cell (see Kelvin's figure 7). Each such face has threefold symmetry and is crossed by six straight lines. An appropriate combination of circular harmonics represents the solution of equation (1). We keep only a few terms of the series, Kelvin-imposed boundary conditions (Plateau's angular conditions) at some arbitrarily chosen points, and hence numerically estimate the shape of the surface, testing the solution by examining other points. This neat and effective procedure is unfortunately of little applicability elsewhere in the physics of foams, owing to lesser symmetry and strong curvatures.

Disappointingly, the paper tails off at this point, without summary or conclusions. If you feel that you are on the trail of one of the Universe's great secrets you do not dally with publication.

8. The aftermath

Having failed to excite any interest as a model for the ether, Kelvin's structure remained intriguing as something to look out for in real foams and analogous cellular substances, since restoring the gas or a liquid to fill the cells does no damage to the arguments, as regards the structure itself. Moreover, the Kelvin Problem appealed to mathematicians: was this really the best structure? Hence, there has been a steady trickle of rather inconclusive contributions over the last century.

The Kelvin cell proved to be very rare in nature wherever it might be expected. Was this because of the trapping of real macroscopic structures in disordered configurations, or the variation in cell sizes, or was it because Kelvin's structure was not optimal after all?

Discrete geometers had little to say on the latter question, except to reiterate it: it was (and remains) simply too hard a problem. And for a while, no better structure turned up in computer searches.

9. Recent progress

In 1994, Weaire and Phelan 13 published the first counter-example to the conjecture that the Kelvin structure has lowest surface area, having computed its area with Brakke's software 13. The conjecture was somewhat dubiously attributed to Kelvin himself by these authors and many before them.

For the discrete geometer, the question has therefore shifted to that of the possible optimal nature of the new and more complex structure, which has two kinds of cells, with unequal gas pressure. The outlook for a rigorous treatment has worsened.

Enough time and computer time have now been expended in testing other structures for the conviction to grow that the Weaire–Phelan (WP) structure (see figure 4) really is the optimal, ultimate solution. Some of the new rivals succeed in defeating Kelvin, so that his solution drops steadily down the rankings. Nevertheless, the Kelvin structure lives on. Just when it seemed to be written off, it has re-emerged once more as a lively topic of research.

Figure 4. A group of cells in the Weaire–Phelan structure, the ideal foam structure that has the lowest known surface area, or energy.

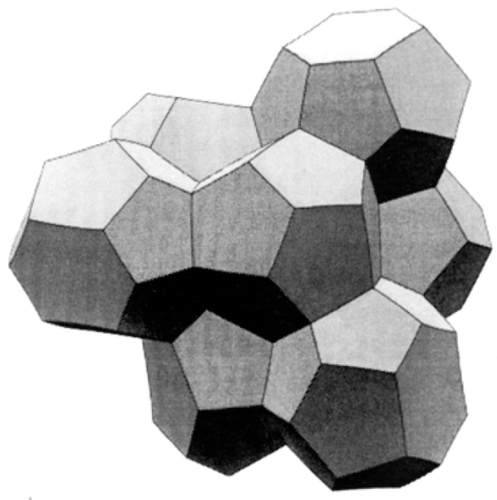
In recent years, it has been realized that by using small enough bubbles, which remain roughly spherical, ordered close-packed structures (mostly fcc) may form spontaneously 14. Why they readily do so is still a mystery, at least to the present author. When this happens, and most of the liquid is then extracted to leave the kind of “dry” foam that was the concern of Kelvin, his structure is often found 15, 16, in perfect order or nearly so.

So far the WP structure has not been found in this way. How can this be, if it (together with others that are broadly similar) has lower energy than Kelvin's?

Part of the answer may lie in the surface. The Kelvin or bcc structure has a special virtue that is lacking in most others. It is well adapted to lying against flat surfaces (for example, a glass wall or a free surface). A 110 layer of “half-Kelvin” or “Toth” cells forms a slightly distorted honeycomb surface structure 17. We have become accustomed for some time to recognizing this ordered surface in monodisperse foam samples the bulk of which is disordered. The availability of this low-energy-surface structure must favour the Kelvin structure in a finite sample with flat surfaces. To make the WP structure it may be necessary to grow it against a designed surface template.

It could be that bcc structure may also be reached more directly from the fcc structure of wet foam (see figure 5). This is the route taken in the latest experiments 15, 16. The precise mechanism for this transformation remains to be discovered–or recovered from the metallurgical literature, where coherent bcc/fcc interfaces are not unknown. With such samples to hand, calculations and proofs of the properties of the Kelvin structure now assume a significance not expected since 1994.

Figure 5. This sample (with a thickness corresponding to about ten layers of cells) shows perfectly ordered Kelvin (bcc) cells at the top and fcc at the bottom, in equilibrium under gravity. From 15.

For example, Huff 18 has provided some of the mathematical underpinnings (existence etc.) of the theory of the Kelvin cell. Reinelt and Kraynik 19 have performed accurate calculations of elastic properties. The surface tension contribution to the uniaxial compression modulus of Kelvin's foam is not, after all, zero, as he intuited. This has been evident for some time, since the simple argument that makes the modulus zero in 2D does not quite carry over to 3D. It is almost so, but not quite. We have noted Kelvin's wishful thinking on this point, as on the matter of isotropy, again misguided. Even if we were to sweep those low-frequency longitudinal modes under the carpet, we would still not have an isotropic model for the transverse waves of the ether.

Another modern conclusion would disappoint Kelvin if he still clung to his ether theory. Despite his hopeful assertion to the contrary, the Kelvin structure without gas is unstable 20. The instability is with respect to change of volumes of the cells and is related to the phenomenon of coarsening in foam physics. Since there is no gas to maintain the cell volumes, they should be allowed to vary, and such variation lowers the surface energy 20.

We have detected many misconceptions in the paper. An uncooperative and astute referee could have dismissed his letter as incomplete, ill-defined and erroneous. But then Kelvin himself was the Editor. The highly questionable contribution that he rushed into print became a classic, of modern relevance.

10. Postscript: Bubbles in Beijing

In 2008 this dry academic tale of the Kelvin Problem may cause a considerable splash, and receive more general public exposure than it would normally merit 21.

The Water Cube, the aquatic centre of the Olympic Games, consists of a gigantic steel framework, the beams of which represent the Plateau borders of the WP structure (figure 6). Its designers started with the Kelvin structure, in a search for something emblematic of water, but eventually turned to the more irregular (but nevertheless periodic) WP structure, as conforming better to today's aesthetic.

Figure 6. The Beijing Water Cube: the designer's conception of the part of the structure surrounding the restaurant. (Courtesy of Arup Corporation).

It will be admired by many hundreds of millions. For the mathematician or physicist, it may be a monument to Kelvin's restless curiosity, exercised even when happily drowsing in his seaside mansion in Ayshire. He had made a fortune and received many laurels, but was never content to rest upon either.

Acknowledgements

Research support is acknowledged: ESA/ESTEC, Science Foundation Ireland and a CNRS visiting appointment in 2007. I am grateful to Lord Kelvin's successor as Editor of this journal for the invitation to honour him.

Notes

‡The original paper from Philosophical Magazine 24 503 (1887) is reproduced as a facsimile following this commentary.