Assessment of Bayesian guidance strategy to develop bake-hardening ferritic steel

ABSTRACT

Developing alloys with optimal properties involves tuning several compositional and processing parameters. As the parametric space is often high-dimensional, doing so may require a prohibitively large number of experiments, which demand ample time and physical resources. In this study, we examine whether the method of Bayesian optimisation, which involves a sequential function evaluation scheme, applies to designing metallic alloys. We consider the example of bake-hardening ferritic steel and aim to maximise the extent of bake-hardening by tuning more than a dozen parameters while reducing the number of experimental fabrications and measurements. To this end, an existing dataset has been used to create a regression model, which acts as a surrogate for experimental measurements. The Bayesian optimiser has been implemented with three different covariance functions and two acquisition functions. Our results suggest that a design strategy guided by Bayesian optimisation has the potential to substantially reduce the time and cost of developing alloys through experimental routes.

KEYWORDS:

• Bayesian optimisation
• ferritic steel
• bake-hardening
• random forest

1. Introduction

Designing and synthesising new alloys with desired properties is a cumbersome task that can consume an overwhelming amount of resources and time. This is primarily because the properties often depend on numerous parameters describing the composition and processing of the alloy. As reliable quantitative models incorporating all such parameters are typically unavailable, the conventional approach is to perform a large number of experiments with some guidance provided by the experience and general understanding of the system under investigation. However, such a trial-and-error approach becomes unfeasible with an increase in the number of governing parameters on account of the ‘curse of dimensionality’, which is effectively a two-fold issue [1]. On the one hand, the number of samples that need to be examined diverges rapidly with the number of compositional and processing descriptors, while on the other, the fraction of the samples dwelling at the boundaries of the high-dimensional parametric hyperspace increases with the number of descriptors. As a result, a blind or empirically guided search for the optimal combination of parameters becomes an expensive approach with feeble odds of yielding the desired outcome.

In recent years, the approach of employing machine learning methods to discover new materials has attracted the attention of the materials science community. Several studies have explored the accelerated discovery of materials like perovskite crystal [2–5], novel thermoelectric materials [6–8], optoelectronic materials [9,10], etc. Similarly, a few studies have applied the ML-based prediction and design schemes for metallic solids. For instance, Akhil et al. [11] have identified the suitable descriptors for a classification model aimed at predicting the phase evolution in high-entropy alloys. Bajpai et al. [12] have proposed a modified Mendeleev number for prediction the composition of multicomponent metallic glasses. Similarly, Kumar et al. [13] have utilised a physics-informed neural network to explore the effect of composition on pseudo-binary diffusion couple. Recently, Hu et al. [14] have presented a comprehensive overview of machine learning application in alloy design. However, despite the exciting advances in this direction, extracting practical benefits from such approaches for designing metallic alloys is generally challenging. The major hindrance in this regard is that a sufficiently large database is required to create a reliable ML model. Unlike the materials, where the training and testing datasets are often obtained from high-throughput electronic structure calculations, most of the properties of interest of metallic materials are intrinsically macroscopic and extrapolation from the atomistic simulations are extremely challenging. High-throughput experimentations have been used for developing materials like porous inorganic catalysts [15], thin films [16], and nanoclusters [17]. Nevertheless, such methods usually involve the chemical routes of synthesis. Developing bulk metallic alloys for structural applications requires slow and cumbersome steps of fabrication and thermo-mechanical processing, which renders the high-throughput synthesis and characterisation extremely challenging.

The present study explores the feasibility of designing alloys using a sequence of experiments guided by Bayesian optimisation (BO) [18]. As a case study, we illustrate an approach to developing bake-hardening ferritic steel with the goal of maximising its hardening. This alloy is of particular importance to the automobile sector, where during the process of paint-baking, the carbon atoms segregate at the line defects and form the Cottrell atmosphere and precipitates [19]. As a result, the yield strength, typically measured with 2–5% pre-straining [20], exhibits remarkable improvement represented as the bake hardening response. A significant advantage of Bayesian optimisation is that in contrast with the global optimisation algorithms like those based on evolutionary computations [21,22] and swarm intelligence [23,24], it is fundamentally sequential and does not need an initial large database to begin with. Instead, it iteratively predicts the next set of descriptors, which has a large likelihood of being an optimal solution. An experiment can be done for this next predicted sample point, and the outcome is appended to the existing dataset. In this way, the dataset grows dynamically in a guided manner and gradually proceeds towards the desired result. As the Bayesian method does not require an initial pre-built dataset, but creates it sequentially, it can exhibit the desired convergence in much fewer iterations than the other optimisation methods. This advantage renders it a suitable choice for cases where the evaluation of an outcome for a given set of parameters is very slow and expensive, such as in experiments.

2. Regression model

We employ a dataset of bake-hardening steel compiled from several published and unpublished sources and used in an earlier study [25]. The dataset contains the bake-hardening measurements of 621 samples, and the feature space consists of 15 descriptors (refer to the supplementary material). The nine compositional descriptors are the amounts of alloying elements (in wt.%): C (0.002–0.03), Mn (0.09–0.53), S (0.003–0.023), Si (0–0.022), P (0.007–0.045), N (0.0016–0.0034), Nb (0–0.018), Ti (0–0.06), and Al (0–0.05). The six processing parameters involve the temperature (720–900°C) and time (1–250 s) of annealing, prestrain (0.001–0.1), prestrain-temperature (25–250°C), and the temperature (25–250°C) and time of baking (0.1–49803 min). One can refer to the work of Das et al. [25] for further details of the dataset.

It is pertinent to point out that the scheme of BO does not directly use the dataset. As a matter of fact, the primary intent behind employing the Bayesian scheme is to make sequential guided measurements while avoiding the need for a pre-built database or numerous parallel measurements. Here, the purpose of utilising the bake-hardening dataset is merely to mimic the results of a series of experimental measurements. To this end, we construct a random forest regression [1] model using the compiled dataset. The ensemble consists of 100 decision trees trained with bootstrap sampling. Each tree is allowed to grow to a maximum depth of 6 levels, and the training aims at minimising the L₂ loss. Once the model has been created, it is used to simulate the actual experimental measurements by the Bayesian optimiser. The scikit-learn [26] library has been employed to create the random forest model.

3. Bayesian optimisation

Bayesian optimisation is a probabilistic model-based approach for finding the minimum of a black-box function that is expensive to evaluate. Its iterative nature balances exploitation and the refinement of promising regions with exploration and the discovery of potentially superior areas. This interplay unfolds within a framework heavily influenced by kernel functions. The following steps briefly describe the process pipeline for implementing BO in the present study.

• The process begins with specifying a prior distribution over the objective function. The Gaussian process has been employed as the surrogate model in this investigation. This prior reflects initial beliefs about the function's behaviour before actual evaluations.

• Initial evaluations are conducted at 20 randomly sampled points within the 15-dimensional parameter space. These data points, representing the first glimpses of the objective function's landscape, inform the subsequent kernel-based model construction.

• Kernels, also known as covariance functions, are a crucial component in GPs. They determine the GP's smoothness and how points in the input space relate to each other. The choice of kernel greatly influences the GP's ability to capture the underlying structure of the function. As detailed in the subsequent section, we have compared the performances of squared-exponential, gamma, and Matérn kernels in maximising the bake-hardening response of ferritic steels.

• An acquisition function, also guided by the chosen kernel, directs the selection of subsequent evaluation points. This function balances exploitation, favouring regions predicted to hold the optimum based on the kernel-driven surrogate model, with exploration, prioritising areas with high uncertainty to potentially discover even better regions. The present study uses the method of expected-improvement as the acquisition function. The optimiser recommends the next set of descriptors with the largest expected-improvement.

• The recommended point within the parameter space is evaluated, revealing the true function value at that location. Here, the function is evaluated through the random forest regression described in the previous section. This model simulates the effect of experimentally measuring the value of bake-hardening. This new data point is then incorporated into the kernel-based surrogate model, refining its predictions and consequently influencing the acquisition function's landscape.

• The process of optimising the acquisition function and updating the model is iterated. With each iteration, the model becomes increasingly accurate in approximating the objective function, improving the chances of identifying the maximum of bake-hardening.

An important aspect of BO is the choice of the acquisition function. The acquisition function is essentially a statistical device that prescribes new search points in a sequential manner based on a heuristic criterion and may include hyperparameters controlling the exploration-exploitation trade-off. In this study, two of the most commonly employed acquisition functions, namely, the probability of improvement and expected improvement have been compared. The probability of improvement criterion considers the current best value of the objective function and looks for the next argument at which the likelihood of improvement is maximum. This likelihood is expressed in terms of the gap between the current best value and posterior mean at the current iteration. In contrast, the expected improvement acquisition function is somewhat more complex, for it involves not only the improvement in the objective function but the magnitude of improvement as well. Here, the next prescribed point for evaluating the objective function is the one with the maximum expectation of improvement over the current best value.

Bayesian optimisation has been used in multiple contexts, including materials science. Talapatra et al. [27] have demonstrated the applicability of combining BO with DFT calculations to discover MAX ternary carbides/nitrides. Mondal and Dutta [28] have used BO to construct virtual nanocrystalline samples with the desired average grain-boundary energies. Pulagam and Dutta [29] have employed the method to implement the semi-discrete Peierls-Nabarro model of dislocation core structure. Zhang et al. [30] have demonstrated a novel approach to applying BO to design solar cell materials with a combination of quantitative and qualitative descriptors. One can refer to Refs. [31,32] for detailed technical descriptions of the Bayesian optimisation scheme. In this study, the pyGPGO library developed by Jiménez and Ginebra [33] has been employed to implement the BO scheme, and an in-house Python-based interface was written to integrate the random forest model with the pyGPGO library.

4. Results and discussion

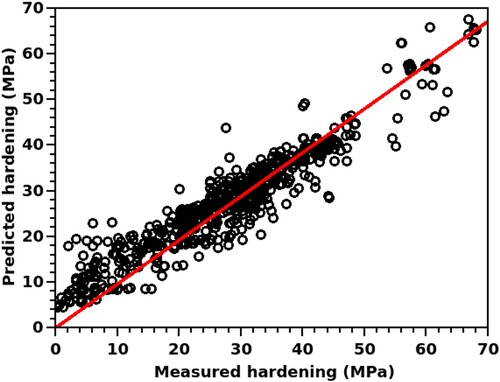
Figure 1 displays the performance of the random forest regressor in terms of the predicted bake-hardening values plotted against the measured ones. The plot shows an excellent agreement with R² ≈ 0.84, indicating that the regression model can function effectively by simulating the process of experimental measurement. Hence, evaluating the outcome of the random forest model for any given set of 15 compositional and process parameters described in Sec. 2 has henceforth been referred to as measurement’.

Figure 1. Predicted bake-hardening obtained from the random forest regression model plotted against the experimentally measured values.

Beginning with 30 initial measurements performed randomly, the Bayesian optimiser updates its posterior distribution and recommends the 31st data point corresponding to the maximum expected improvement. The bake-hardening is measured at this new data point, and the existing pool of data is updated by adding this new information. The posterior distribution is again updated based on the dataset containing 31 measurements, and the recommendation for the 32nd measurement is produced. This process continues iteratively, and at each iteration, the size of the dataset is extended by one. The optimiser keeps learning from the continuously growing dataset, and its recommendations become more effective at searching for the parameters with maximum bake-hardening.

The choice of a suitable covariance function can have a significant impact on the performance of the optimiser. The kernel function dictates the covariance matrix, which is an essential part of constructing the Gaussian prior [34]. As mentioned earlier, we have compared the performances of three different kernels in this study. Here, any given sample of ferritic steel is described as a vector in the 15-dimensional parameter space. The extent of similarity or dissimilarity between two samples, ${\mathit{S}}_i$ and ${\mathit{S}}_j$, is given by the Euclidean distance, $d_{\mathrm{ij}}$, between them. Accordingly, the squared-exponential kernel is given by, ${\mathrm{K}}_{\mathrm{se}}\left({\mathit{S}}_i,{\mathit{S}}_j;\mathrm{\Lambda }\right)={\sigma }^2{e}^{-d_{\mathrm{ij}}^2/\left(2{\mathrm{\Lambda }}^2\right)}$, where $\mathrm{\Lambda }$ is a characteristic length-scaling factor. Another covariance function examined here is the gamma-exponential kernel, ${\mathrm{K}}_{\gamma }\left({\mathit{S}}_i,{\mathit{S}}_j;\mathrm{\Lambda };\gamma \right)={\sigma }^2{e}^{-d_{\mathrm{ij}}^{\gamma }/\left(2{\mathrm{\Lambda }}^{\gamma }\right)}$, with $\gamma$ as a parameter. The third kernel tested for the bake-hardening problem is the so-called Matérn-3/2 function given by, ${\mathrm{K}}_{3/2}\left({\mathit{S}}_i,{\mathit{S}}_j;\mathrm{\Lambda };\gamma \right)={\sigma }^2\left(1+{\displaystyle \frac{\sqrt{3}{d}_{\mathrm{ij}}}{\mathrm{\Lambda }}}\right)e^{-\sqrt{3}{d}_{\mathrm{ij}}/\mathrm{\Lambda }}$. While the squared-exponential function efficiently captures the smoothness of the objective function, it behaves poorly in the presence of sharp discontinuities. Similarly, the gamma-exponential function has the advantage of less sensitivity to the characteristic length scale, $\mathrm{\Lambda }$, whereas the parameter, $\gamma$, dictates the decay-rate and skewness of similarity with distance. The Matérn-3/2 kernel, despite being computationally more expensive, is continuously differentiable, enabling it to capture smoother functions compared to the other two kernels.

Figure 2 exhibits the evolution of the optimal bake-hardening during the iterations with expected-improvement as the acquisition function [34]. As the goal here is to assess the comparative performances of the covariance kernels, the optimisations have been executed for the same number of iterations for all the three kernels. We find that the performances of the squared-exponential and Matérn-3/2 kernels are virtually similar, whereas the gamma-exponential function outperforms both. In these example runs the first measurements yield a bake-hardening value of ∼32 MPa, which quickly elevates to ∼51 MPa after 32 iterations of measurement and becomes ∼57 MPa in about 200 iterations. A similar trend is also observed for the probability-of-improvement acquisition function [34], as evident from Figure 3, where the gamma-exponential kernel outperforms the other two. Here, it must be pointed out that on account of the shape of the objective function rendered by the random forest regressor, both acquisition functions may explore the same data points on several steps of iterations. This is possible if a data point at which the expectation value of improvement over the current best result is also the one with the maximum probability of improvement. In the present case, this is found to happen very frequently for the gamma-exponential kernel, which results in hardly noticeable differences between Figures 2b and 3b. Further comparing Figures 2 and 3, we observe that the relative performance of the optimisation routine is less sensitive to the acquisition function and relies more on the choice of the covariance function. As both square-exponential and gamma-exponential kernels are known to be particularly suitable for the target functions with a higher degree of smoothness, the findings suggest that the bake-hardening model may create a hypersurface with steep variations. Such an outcome is not unexpected in experimental measurements, such as the bake-hardening, where the observable can have highly non-linear and non-monotonic dependencies on many compositional and processing parameters. This can be a possible reason for the relatively weaker performances of the squared-exponential and Matérn-3/2 kernels, irrespective of the choice of acquisition function.

Figure 2. Evolution of the bake-hardening with the number of iterations of the Bayesian optimiser implemented with the expected-improvement acquisition functions and using the (a) squared-exponential, (b) gamma-exponential, and (c) Matérn-3/2 kernels. The fluctuating gray plots show the instantaneous values at each iteration, while the dashed red plots indicate the best value at the iteration. The blue plots obtained from the moving-window averaging exhibit the smoothed trends of instantaneous measurements.

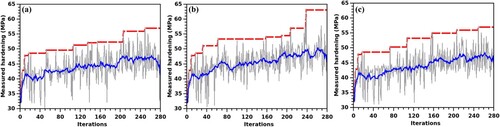
Figure 3. Bake hardening vs. iteration plots with the probability-of-improvement acquisition function. Results for the (a) squared-exponential, (b) gamma-exponential, and (c) Matérn-3/2 covariance functions are shown with the plotting scheme akin to that of Figure 2.

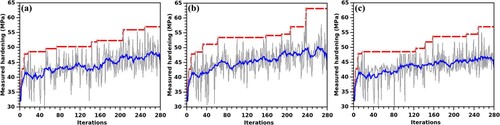
Figures 2 and 3 also show the smoothed versions of instantaneous measurements obtained through moving-window averaging, which aid in visualising the general trend of the optimised outcome over a sufficiently large number of iterations. As the smoothed plots show an overall increasing trend, they confirm that the solutions observed in Figure 2 do not emerge from blind and brute-force measurements. Instead, the Gaussian process is indeed successful in evolving dynamically by learning from the growing pool of measured data.

5. Conclusion

In a nutshell, the study examines the feasibility of employing Bayesian optimisation to design a sequence of experiments with the aim of developing an alloy with optimal properties. We demonstrate this idea by considering the example of bake-hardening ferritic steel. A random forest model is trained on a dataset of a few hundred samples, and its prediction is used as a simulation of actual experimental measurements. Finally, the compositional and processing parameters are tuned through Bayesian optimisation in a sequential manner using multiple combinations of acquisition functions and covariance kernels. We find that the optimiser is able to improve its predictive capability with iterations gradually and the gamma-exponential kernel is observed to yield the best results out of all the three tested kernels.

The present study is by no means exhaustive. While the Bayesian guidance can reduce the number of experiments searching for the optimal composition and processing parameters, alloy development is still a slow and resource-consuming endeavour. Therefore, the method must be fine-tuned to reduce the number of sequential iterations required to the maximum possible extent. This is a rapidly evolving domain and recent advances include several new acquisition functions, covariance kernels, and regression models. Moreover, recent developments have also enabled Bayesian optimisation to be used within a multi-objective framework. The present results highlight the potential of designing experiments and methods for developing technologically important alloys using Bayesian guidance and motivate further explorations in this direction.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Notes on contributors

Rajdeep Sarkar

Rajdeep Sarkar earned his integrated B.Tech.-M.Tech. degrees from the Indian Institute of Technology, Kharagpur, where he performed this study as a student at the Department of Metallurgical and Materials Engineering. He is presently working as a section engineer in the R&D Department of ArcelorMittal Nippon Steel India Limited. His research interests are in AI applications and alloy development.

Shiv Brat Singh

Shiv Brat Singh is a professor at the Indian Institute of Technology, Kharagpur, where he is the Head of the Department of Metallurgical and Materials Engineering and chairman of the Steel Technology Centre. He earned his Ph.D. from the University of Cambridge, UK, and worked for Tata Steel before joining IIT Kharagpur in 2000. Prof. Singh's primary research interests include the physical metallurgy of steels, phase transformations and thermomechanical simulation.

Amlan Dutta

Amlan Dutta is an assistant professor at the Department of Metallurgical and Materials Engineering of IIT Kharagpur. He carried out his doctoral research at the Variable Energy Cyclotron Centre, Kolkata, and earned his Ph.D. from Jadavpur University. Before joining IIT Kharagpur in 2018, Prof. Dutta worked as a scientist at the Department of Condensed Matter Physics and Materials Science of the S. N. Bose National Centre for Basic Sciences, Kolkata. His research is primarily in the domains of multiscale modelling and simulations of materials.