Decomposition analysis: when to use which method?

Abstract

Structural and index decomposition analyses allow identifying the main drivers of observed changes over time of energy and environmental impacts. These decomposition analyses have become very popular in recent decades and, many alternative methods to implement them have become available. Several of the most popular methods have been developed earlier in index number theory, a context in which each particular method is defined by adhering to a set of properties. The goal of the present paper is to review the main results of index number theory and discuss its connection to decomposition analyses. By doing so, we can present a decision tree that allows users to choose a decomposition method that meets desired properties. We report as hands-on example an empirical case study of the carbon footprint of the Netherlands in the period 2004–2005.

KEYWORDS:

• Index number theory
• index decomposition analysis
• structural decomposition analysis
• decision tree

1. Introduction

In recent decades, many studies have attempted to identify the drivers of observed changes over time of energy and environmental impacts (Hoekstra and van den Bergh, 2003; Su and Ang, 2012). Such decomposition analyses can fall under two distinct but related categories: index decomposition analysis (IDA), in which the link between impact (energy, environmental, employment or whatever) and production level is explored; and structural decomposition analysis (SDA), in which the link between impact and consumption activities is explored. Hence, SDA is more comprehensive than IDA (since it requires explicitly accounting for the link between production and consumption) but also requires more data. A practitioner who is new in the field of IDA and/or SDA can find much advice in literature, for example Ang (2004), Ang et al. (2009), Su and Ang (2012), Ang (2015) and Wang et al. (2017b). In fact, there are so many possible references that a general overview is tough to disentangle; in other words the new practitioner will have trouble to ‘see the forest for the trees’. Moreover, the mathematics employed and notation used is usually unduly complicated. In this paper, we follow a different route: we go back to the ‘forest’, that is to say to the collective stock of knowledge called index number theory in which the mathematics is usually easily accessed. Then, we turn to IDA and SDA, which – as one of the referees correctly points out- ‘in quite a number of cases proceeds by, knowingly or unknowingly, re-inventing or replicating well-known results from index number theory.’

This paper is structured as follows. In Section 2, we review the relevant properties and formulas of index number theory and, in Section 3, discuss its connection with IDA and SDA. Section 4 deals with the general case of ideal decompositions (index number theory), which leave no residual term (IDA and SDA), of an aggregate change into of n factors. Sections 5 and 6 are devoted to a hands-on example of a decomposition of carbon dioxide emissions of sectors of the Dutch economy into five factors. In the supplementary material, to enable replication we provide in the Appendices D–G our Matlab programs and Excel files used in the hands-on example. Based on theory and empirics we present in Section 7, a decision tree that we hope will help practitioners who seek to select the appropriate decomposition method for their problem at hand. Section 8 concludes.

2. Index number theory

2.1. Historical background

Traditionally index number theory is about the measurement of aggregate price and quantity change. Prominent applications are the consumer price index (CPI), producer price index (PPI), purchasing power parity (PPP) and human development index (HDI.) There is a vast literature on this subject. The oldest price index is attributed to the French economist Dutot (1738) who disposed of data on prices of several commodities in 1515 (base period), under the reign of King Louis XII, and in 1738 (comparison period), under the reign of King Louis XV. He took the arithmetic mean of the prices in the comparison period (1738) and of the prices in the base period (1515) and divided them by each other. According to the price index of Dutot the price level was multiplied by the factor 22. Dutot concluded that Louis XV was worse off, when compared to his ancestor, because his income was only multiplied by the factor 13. The price index of Dutot depends on the units of measurement (the price of, say, salt, can be measured per ounce or per pound) so that the outcome is arbitrary. The Italian economist Carli (1764) constructed the first index free from the units of measurement using price relatives, that is to say he divided the price of, say one ounce of salt, in the comparison period by the corresponding price in the base period, and took the arithmetic mean of the price relatives. The disadvantage of Carli’s approach is that it does not take into account the importance of a commodity in the budget of a consumer who will spend in (say) one year more money on bread than on salt. According to Balk (2008a) the first person who recognized the necessity of introducing weights into a price index was Young (1812). The two most important contributions in the nineteenth century are undoubtedly the ones by Laspeyres (1871) and Paasche (1874). Laspeyres considered a basket of commodities in the base period and computed the total expenditure. He also computed total expenditure of this basket in the comparison period. His price index is the ratio of the total expenditure in the comparison period and the total expenditure in the base period. Laspeyres’ choice of the base period’s basket is arbitrary. Paasche chose the basket of the comparison period. In his seminal book, Fisher (1922) introduced time reversal and the product test as two desirable properties of indices (to be described later in greater detail). Laspeyres and Paasche do not meet time reversal. Fisher proposed as new price (quantity) index the geometric mean of the price (quantity) indices of Laspeyres and Paasche which satisfies time reversal. He proved that from all at that time existing pairs of price and quantity indices only the product of his pair satisfied the product test. That is the reason why he called his pair of indices ‘ideal’. After the contribution of Fisher two other pairs of ideal index numbers were discovered. Montgomery (1929, 1937) and, independently, Vartia (1974; 1976), proposed a solution, the so-called Montgomery-Vartia index. Another solution was, independently, proposed by Sato (1976) and Vartia (1974; 1976), the so-called Sato-Vartia index.

Above, we give a short history of the classical index number problem in which one wants to decompose the ratio value change in expenditure into the product of two factors, called price and quantity ‘indices’ (singular ‘index’). The alternative problem, lesser known but equally old (and more relevant in the context of index and structural decomposition analysis), is the decomposition of the difference between the values of two expenditures as the sum of two parts, the price and quantity ‘indicators’, which measure respectively the changes due to price and quantity differences. The indicators of Bennet (1920) are the additive counterpart of the indices of Fisher. Another pair of ideal indicators was discovered by Montgomery (1929; 1937).

The remainder of this section is organized as follows. Section 2.2 is devoted to the notation, problem formulation and properties used to characterize indices and indicators. The following subsections then report specific indices and indicators. For computational purposes these turn out to cluster around two basic methods: Fisher and Bennet methods, which are combinatorial in nature (addressed in Section 2.3), while Montgomery-Vartia, Sato-Vartia and Montgomery involve logarithmic transformations (addressed in Section 2.4). In Section 2.5 we discuss another important contribution, viz. the concept of consistency-in-aggregation. Section 2.6, finally, summarizes the relevant properties and formulas of index number theory for IDA and SDA.

2.2. Notation, problem formulation and properties

2.2.1. Notation

$p_i^t>0:$$p_i^t>0:$	=	price of commodity $i$$i$ $\left(i=1,\dots ,N\right)$$\left(i=1,\dots ,N\right)$in base ($t=0$$t=0$) or in comparison period $\left(t=1\right)$$\left(t=1\right)$
$q_i^t>0$$q_i^t>0$:	=	quantity of commodity $i$$i$ $\left(i=1,\dots ,N\right)$$\left(i=1,\dots ,N\right)$in base ($t=0$$t=0$) or in comparison period $\left(t=1\right)$$\left(t=1\right)$
$v_i^t$$v_i^t$:	=	value of commodity $i$$i$ in base $\left(p_i^0{q}_i^0\right)$$\left(p_i^0{q}_i^0\right)$ or in comparison period $\left(p_i^1{q}_i^1\right)$$\left(p_i^1{q}_i^1\right)$(1)
$V^t$$V^t$:	=	total value in base $\left(\sum _{i=1}^N{v}_i^0\right)$$\left(\sum _{i=1}^N{v}_i^0\right)$ or in comparison period $\left(\sum _{i=1}^N{v}_i^1\right)$$\left(\sum _{i=1}^N{v}_i^1\right)$
$s_i^t$$s_i^t$:	=	share of value of commodity $i$$i$ in total value in base or in comparison period(2)
$RV:$$RV:$	=	ratio change in value : $V^1/V^0=\frac{{\sum }_{i=1}^N{p}_i^1{q}_i^1}{{\sum }_{i=1}^N{p}_i^0{q}_i^0}$$V^1/V^0=\frac{{\sum }_{i=1}^N{p}_i^1{q}_i^1}{{\sum }_{i=1}^N{p}_i^0{q}_i^0}$(3)
$RP$$RP$:	=	price index measuring the price change from the base to the comparison period
$RQ$$RQ$:	=	quantity index measuring the quantity change from the base to the comparison period
$DV$$DV$:	=	difference change in value: $V^1-V^0=\sum _{i=1}^N\left(v_i^1-v_i^0\right)=\sum _{i=1}^N{p}_i^1{q}_i^1-\sum _{i=1}^N{p}_i^0{q}_i^0$$V^1-V^0=\sum _{i=1}^N\left(v_i^1-v_i^0\right)=\sum _{i=1}^N{p}_i^1{q}_i^1-\sum _{i=1}^N{p}_i^0{q}_i^0$(4)
$DP$$DP$:	=	price indicator measuring the change in prices from the base to the comparison period
$DQ$$DQ$:	=	quantity indicator measuring the change in quantities from the base to the comparison period.

2.2.2. Problem formulation and properties

We quote from the abstract of Balk (2008b): ‘The index number problem is known as that of decomposing aggregate value change, in ratio or in difference form, into two, ideally symmetric, factors.’ In our notation: (5) $RV=RP\times RQ$$RV=RP\times RQ$(5) and (6) $DV=DP+DQ.$$DV=DP+DQ.$(6) The basic properties (Eichhorn and Voeller, 1976, and Eichhorn, 1978) on the price and quantity indices in Equation 5 comprise:

• global monotonicity: the price (quantity) index is non-decreasing in comparison prices and non-increasing in base prices (quantities);

• linear homogeneity in comparison prices (quantities): if all comparison prices are multiplied by a common factor, the price (quantity) index is multiplied by that common factor, as well;

• identity: if all comparison prices (quantities) in the comparison period are the same as those in the base period, the price (quantity) index is equal to one;

• homogeneity of degree zero in prices (quantities): if all prices (quantities) in comparison and base period are multiplied by a common factor, the price (quantity) index remains the same;

• invariance to changes to the units of measurement of the commodities.

A price (quantity) index that satisfies the requirements of ‘linear homogeneity in comparison prices (quantities)’ and of ‘identity’ satisfies a stronger requirement, namely that of

• proportionality with respect to prices (quantities). If all the individual price (quantity) relatives are the same, then the price (quantity) index number must be equal to these relatives.

Other desirable properties (Fisher, 1922) are:

• time reversal (symmetry): the price (quantity) index for the base period relative to the comparison period must be equal to the reciprocal of the price (quantity) index for the comparison period relative to the base period;

• product test: it requires that the ratio change in value can be decomposed as product of a price and a quantity index, like in Equation 5;

• idealness: a pair of price and quantity indices which, in addition to satisfying the product test, also have the same functional form, i.e. by interchanging prices and quantities the price index turns into the quantity index and vice versa, is called ‘ideal’.

Indicators return monetary values, which may be negative or zero. Therefore the basic properties must be modified a bit (Diewert, 2005, Balk, 2008a). They comprise: global monotonicity, modified identity (if all comparison prices and quantities in the comparison period are the same as those in the base period, the price (quantity) index is equal to zero); homogeneity of degree 1 in prices (quantities), invariance to changes to the units of measurement of the commodities. Please note that there is no analogue to the property of ‘linear homogeneity in comparison prices (quantities)’, so that there is no analogue of ‘proportionality’ for indicators, as well. Other desirable properties are:

• time reversal (symmetry): the price (quantity) indicator for the base period relative to the comparison period must be equal to the opposite of the price (quantity) indicator for the comparison period relative to the base period;

• sum test: the sum test requires that the difference change in value can be decomposed as the sum of a price and a quantity index, like in Equation 6;

• idealness: a pair of price and quantity indicators which, in addition to satisfying the sum test, also have the same functional form, i.e. by interchanging prices and quantities the price indicator turns into the quantity indicator and vice versa, is called ‘ideal’.

The property of idealness is an important contribution of index number theory to structural and index decomposition analysis since it implies that the decomposition is ‘complete’, that is to say that there is no residual term. We refer to the review of index number theory of Balk (2016) and to Balk’s monograph (Balk 2008a) for the mathematical presentation.

2.3. Combinatorial indices and indicators

2.3.1. Introduction

This class consists of the ‘traditional’ indices and indicators of Laspeyres (superscript $L$$L$), Paasche (superscript $P$$P$), Fisher (superscript $F$$F$) and its additive counterpart Bennet (superscript $B$$B$).

2.3.2. Indices

The indices are defined as: (7) $\begin{array}{rl}R{P}^L& =\frac{\sum _{i=1}^N{p}_i^1{q}_i^0}{\sum _{i=1}^N{p}_i^0{q}_i^0};R{Q}^L=\frac{\sum _{i=1}^N{p}_i^0{q}_i^1}{\sum _{i=1}^N{p}_i^0{q}_i^0},\end{array}$$\begin{array}{rl}R{P}^L& =\frac{\sum _{i=1}^N{p}_i^1{q}_i^0}{\sum _{i=1}^N{p}_i^0{q}_i^0};R{Q}^L=\frac{\sum _{i=1}^N{p}_i^0{q}_i^1}{\sum _{i=1}^N{p}_i^0{q}_i^0},\end{array}$(7) (8) $\begin{array}{rl}R{P}^P& =\frac{\sum _{i=1}^N{p}_i^1{q}_i^1}{\sum _{i=1}^N{p}_i^0{q}_i^1};R{Q}^P=\frac{\sum _{i=1}^N{p}_i^1{q}_i^1}{\sum _{i=1}^N{p}_i^1{q}_i^0},\end{array}$$\begin{array}{rl}R{P}^P& =\frac{\sum _{i=1}^N{p}_i^1{q}_i^1}{\sum _{i=1}^N{p}_i^0{q}_i^1};R{Q}^P=\frac{\sum _{i=1}^N{p}_i^1{q}_i^1}{\sum _{i=1}^N{p}_i^1{q}_i^0},\end{array}$(8) (9) $\begin{array}{rl}R{P}^F& =(R{P}^{L}R{P}^P{)}^{\frac{1}{2}}={\left(\frac{\sum _{i=1}^N{p}_i^1{q}_i^0}{\sum _{i=1}^N{p}_i^0{q}_i^0}\right)}^{\frac{1}{2}}{\left(\frac{\sum _{i=1}^N{p}_i^1{q}_i^1}{\sum _{i=1}^N{p}_i^0{q}_i^1}\right)}^{\frac{1}{2}}\\ R{Q}^F& =(R{Q}^{L}R{Q}^P{)}^{\frac{1}{2}}={\left(\frac{\sum _{i=1}^N{p}_i^0{q}_i^1}{\sum _{i=1}^N{p}_i^0{q}_i^0}\right)}^{\frac{1}{2}}{\left(\frac{\sum _{i=1}^N{p}_i^1{q}_i^1}{\sum _{i=1}^N{p}_i^1{q}_i^0}\right)}^{\frac{1}{2}}.\end{array}$$\begin{array}{rl}R{P}^F& =(R{P}^{L}R{P}^P{)}^{\frac{1}{2}}={\left(\frac{\sum _{i=1}^N{p}_i^1{q}_i^0}{\sum _{i=1}^N{p}_i^0{q}_i^0}\right)}^{\frac{1}{2}}{\left(\frac{\sum _{i=1}^N{p}_i^1{q}_i^1}{\sum _{i=1}^N{p}_i^0{q}_i^1}\right)}^{\frac{1}{2}}\\ R{Q}^F& =(R{Q}^{L}R{Q}^P{)}^{\frac{1}{2}}={\left(\frac{\sum _{i=1}^N{p}_i^0{q}_i^1}{\sum _{i=1}^N{p}_i^0{q}_i^0}\right)}^{\frac{1}{2}}{\left(\frac{\sum _{i=1}^N{p}_i^1{q}_i^1}{\sum _{i=1}^N{p}_i^1{q}_i^0}\right)}^{\frac{1}{2}}.\end{array}$(9)

Hence, Fisher’s price (quantity) index is the geometric mean of the price (quantity) indices of Laspeyres and Paasche. All above-mentioned indices satisfy the basic properties, so that they also satisfy the stronger property of ‘proportionality’ (Balk, 2008a; 2016). It is easily verified from (7) and (8) that the indices of Laspeyres and Paasche do not possess the property of time reversal. However, the indices of Fisher do possess it. It is also easily verified that: (10) $RV=R{P}^L\times R{Q}^P;RV=R{P}^P\times R{Q}^L\text{and}RV=R{P}^F\times R{Q}^F.$$RV=R{P}^L\times R{Q}^P;RV=R{P}^P\times R{Q}^L\text{and}RV=R{P}^F\times R{Q}^F.$(10)

It follows from (10) that the index pair of Fisher is ideal, but that the pairs of Laspeyres and Paasche are not ideal.

2.3.3. Indicators

The Laspeyres and Paasche price and quantity indicators are the additive counterparts of the Laspeyres and Paasche price and quantity indices and defined as: $\begin{array}{rl}D{P}^L& =\sum _{i=1}^N{q}_i^0\left(p_i^1-p_i^0\right);D{Q}^L=\sum _{i=1}^N{p}_i^0\left(q_i^1-q_i^0\right),\end{array}$$\begin{array}{rl}D{P}^L& =\sum _{i=1}^N{q}_i^0\left(p_i^1-p_i^0\right);D{Q}^L=\sum _{i=1}^N{p}_i^0\left(q_i^1-q_i^0\right),\end{array}$ $\begin{array}{rl}D{P}^P& =\sum _{i=1}^N{q}_i^1\left(p_i^1-p_i^0\right);D{Q}^P=\sum _{i=1}^N{p}_i^1\left(q_i^1-q_i^0\right).\end{array}$$\begin{array}{rl}D{P}^P& =\sum _{i=1}^N{q}_i^1\left(p_i^1-p_i^0\right);D{Q}^P=\sum _{i=1}^N{p}_i^1\left(q_i^1-q_i^0\right).\end{array}$ The additive counterpart of the Fisher indices are the indicators of Bennet (1920) defined as the arithmetic mean of the Laspeyres and Paasche price indicators: (11) $\begin{array}{rl}D{P}^B& =\frac{1}{2}\sum _{i=1}^N{q}_i^0\left(p_i^1-p_i^0\right)+\frac{1}{2}\sum _{i=1}^N{q}_i^1\left(p_i^1-p_i^0\right)=\sum _{i=1}^N\frac{\left(q_i^0+q_i^1\right)}{2}\left(p_i^1-p_i^0\right),\end{array}$$\begin{array}{rl}D{P}^B& =\frac{1}{2}\sum _{i=1}^N{q}_i^0\left(p_i^1-p_i^0\right)+\frac{1}{2}\sum _{i=1}^N{q}_i^1\left(p_i^1-p_i^0\right)=\sum _{i=1}^N\frac{\left(q_i^0+q_i^1\right)}{2}\left(p_i^1-p_i^0\right),\end{array}$(11) (12) $\begin{array}{rl}D{Q}^B& =\frac{1}{2}\sum _{i=1}^N{p}_i^0\left(q_i^1-q_i^0\right)+\frac{1}{2}\sum _{i=1}^N{p}_i^1\left(q_i^1-q_i^0\right)=\sum _{i=1}^N\frac{\left(p_i^0+p_i^1\right)}{2}\left(q_i^1-q_i^0\right).\end{array}$$\begin{array}{rl}D{Q}^B& =\frac{1}{2}\sum _{i=1}^N{p}_i^0\left(q_i^1-q_i^0\right)+\frac{1}{2}\sum _{i=1}^N{p}_i^1\left(q_i^1-q_i^0\right)=\sum _{i=1}^N\frac{\left(p_i^0+p_i^1\right)}{2}\left(q_i^1-q_i^0\right).\end{array}$(12) All above-mentioned indicators satisfy the basic properties (Balk, 2008a; 2016). It is easily verified that the indicators of Laspeyres and Paasche do not possess the property of time reversal. But Bennet’s indicators do possess it. It is also easily verified that (13) $DV=D{P}^L+D{Q}^P;DV=D{P}^P+D{Q}^L\text{and}DV=D{P}^B+D{Q}^B.$$DV=D{P}^L+D{Q}^P;DV=D{P}^P+D{Q}^L\text{and}DV=D{P}^B+D{Q}^B.$(13)

It follows from (13) that Bennet’s indicator pair is ideal, but Laspeyres’s and Paasche’s do not possess that property.

2.3.4. Fisher and Bennet: a combinatorial approach

De Boer (2009b) used the decomposition of the ratio change in value into the ratio changes in two factors (price and quantity) by means of the Fisher indices as a step towards the general case of $n$$n$ factors where he used the generalization of Siegel of the Fisher indices. Let $V$$V$ denote a certain aggregate to be decomposed and let $x_1$$x_1$ and $x_2$$x_2$ denote factors 1 and 2, respectively (in our example ‘price’ and ‘quantity’), then we have: (14) $V=\sum _{i=1}^N{x}_{1i}{x}_{2i}.$$V=\sum _{i=1}^N{x}_{1i}{x}_{2i}.$(14) The Fisher index for factor 1 reads: (15) $R{X_1}^F={\left(\frac{\sum _{i=1}^N{x}_{1i}^1{x}_{2i}^0}{\sum _{i=1}^N{x}_{1i}^0{x}_{2i}^0}\right)}^{\frac{1}{2}}{\left(\frac{\sum _{i=1}^N{x}_{1i}^1{x}_{2i}^1}{\sum _{i=1}^N{x}_{1i}^0{x}_{2i}^1}\right)}^{\frac{1}{2}}.$$R{X_1}^F={\left(\frac{\sum _{i=1}^N{x}_{1i}^1{x}_{2i}^0}{\sum _{i=1}^N{x}_{1i}^0{x}_{2i}^0}\right)}^{\frac{1}{2}}{\left(\frac{\sum _{i=1}^N{x}_{1i}^1{x}_{2i}^1}{\sum _{i=1}^N{x}_{1i}^0{x}_{2i}^1}\right)}^{\frac{1}{2}}.$(15) The first term gives the change in factor 1, weighted by the magnitudes of factor 2 in the base period, and the second term the change in factor 1, weighted by the values of factor 2 in the comparison period. The number of duplicates of each term is 1 and the weight of each term is ½. This is summarized by De Boer (2009b) in his Table 1.

TABLE 1. Summary for the case of two factors.

Number of ones	Combinations	Number of duplicates	Weight
0	{0}	1	$1/2$$1/2$
1	{1}	1	$1/2$$1/2$

The Bennet indicator for factor 1 reads: (16) $D{X}_1^B=\frac{1}{2}\sum _{i=1}^N\left(x_{1i}^1-x_{1i}^0\right)x_{2i}^0+\frac{1}{2}\sum _{i=1}^N\left(x_{1i}^1-x_{1i}^0\right)x_{2i}^1.$$D{X}_1^B=\frac{1}{2}\sum _{i=1}^N\left(x_{1i}^1-x_{1i}^0\right)x_{2i}^0+\frac{1}{2}\sum _{i=1}^N\left(x_{1i}^1-x_{1i}^0\right)x_{2i}^1.$(16) The first term gives the change in factor 1 (prices), weighted by the values of the factor 2 (quantities) in the base period, and the second term the change in factor 1 (prices), weighted by the values of the factor 2 (quantities) in the comparison period. The number of duplicates of each term is 1 and the weight of each term is ½. Consequently, Table 1 can also be used for the Bennet indicators. De Boer (2009b) also supplied the tables with 3–6 factors; the one for 5 factors is used in our empirical application.

2.4. Logarithmic indices and indicators

2.4.1. The logarithmic mean

The indices and indicators that belong to this class are based on the logarithmic mean, which for two positive numbers a and b is defined as: (17) $L\left(a,b\right)=\frac{a-b}{\text{ln}\left(\frac{a}{b}\right)}\text{and}L\left(a,a\right)=a.$$L\left(a,b\right)=\frac{a-b}{\text{ln}\left(\frac{a}{b}\right)}\text{and}L\left(a,a\right)=a.$(17) The logarithmic mean is very convenient when switching from a ratio to a difference and vice versa (Balk, 2003). It follows straightforwardly from (17) that: (18) $\begin{array}{rl}a/b& =\text{exp}\left\{\left(a-b\right)/L\left(a,b\right)\right\},\end{array}$$\begin{array}{rl}a/b& =\text{exp}\left\{\left(a-b\right)/L\left(a,b\right)\right\},\end{array}$(18) (19) $\begin{array}{rl}\left(a-b\right)& =L\left(a,b\right)\text{ln}\left(a/b\right).\end{array}$$\begin{array}{rl}\left(a-b\right)& =L\left(a,b\right)\text{ln}\left(a/b\right).\end{array}$(19) It is ‘zero value robust’: in practice we can replace zeros by epsilon small positive numbers. (Ang and Liu, 2007a). If a and b are both positive, it can still be used. However, if there is a change in sign, that is to say when a is positive (negative) and b is negative (positive), the logarithmic mean (17) is not defined so that it is not ‘change-in-sign robust’. According to Ang and Liu (2007b) the logarithmic mean might handle changes in sign using the so-called ‘Analytical Limit Strategy’. Their procedure has to be applied to each change in sign individually. In practice, this is so cumbersome that in case of the presence of changes in sign we do not advise to use methods based on the logarithmic mean.

2.4.2. The Montgomery indicator and Montgomery-Vartia index

Balk (2003) gave a simple derivation of the indicator of Montgomery (1929; 1937) that was used in the application of this indicator to SDA by de Boer (2008). Using, successively, definition (4) of the difference change in value, definition (17) of the logarithmic mean of the value in the comparison $\left(v_i^1\right)$$\left(v_i^1\right)$ and base period $\left(v_i^0\right)$$\left(v_i^0\right)$, and the definition (1) of $v_i^1$$v_i^1$ and $v_i^0$$v_i^0$ we obtain: (20) $\begin{array}{rl}D{V}^M& =\sum _{i=1}^N\left(v_i^1-v_i^0\right)=\sum _{i=1}^{N}L(v_i^1,v_i^0)\text{ln}\left(\frac{v_i^1}{v_i^0}\right),\\ & =\sum _{i=1}^{N}L\left(v_i^1,v_i^0\right)ln\left(\frac{p_i^1}{p_i^0}\right)+\sum _{i=1}^{N}L\left(v_i^1,v_i^0\right)\text{ln}\left(\frac{q_i^1}{q_i^0}\right),\end{array}$$\begin{array}{rl}D{V}^M& =\sum _{i=1}^N\left(v_i^1-v_i^0\right)=\sum _{i=1}^{N}L(v_i^1,v_i^0)\text{ln}\left(\frac{v_i^1}{v_i^0}\right),\\ & =\sum _{i=1}^{N}L\left(v_i^1,v_i^0\right)ln\left(\frac{p_i^1}{p_i^0}\right)+\sum _{i=1}^{N}L\left(v_i^1,v_i^0\right)\text{ln}\left(\frac{q_i^1}{q_i^0}\right),\end{array}$(20) in which the first term after the second equality is the definition of the price indicator and the second term of the quantity indicator according to Montgomery.

Using the following definition of the weight for the Montgomery decomposition: (21) $w_i^M=L\left(v_i^1,v_i^0\right),$$w_i^M=L\left(v_i^1,v_i^0\right),$(21) the price and quantity indicators read: (22) $D{P}^M=\sum _{i=1}^N{w}_i^M\text{ln}\left(\frac{p_i^1}{p_i^0}\right)\text{and}D{Q}^M=\sum _{i=1}^N{w}_i^M\text{ln}\left(\frac{q_i^1}{q_i^0}\right).$$D{P}^M=\sum _{i=1}^N{w}_i^M\text{ln}\left(\frac{p_i^1}{p_i^0}\right)\text{and}D{Q}^M=\sum _{i=1}^N{w}_i^M\text{ln}\left(\frac{q_i^1}{q_i^0}\right).$(22) These indicators exhibit the basic and desired properties of time reversal and being ideal, except the property of monotonicity. But, as argued by Balk (2003, Appendix A.2), this problem is unlikely to be of practical importance.

Using the definition of the logarithmic mean of the value in the comparison period $\left(V^1\right)$$\left(V^1\right)$ and the base period $\left(V^0\right)$$\left(V^0\right)$ and rewriting (19) we obtain: (23) $\text{ln}\left(\frac{V^1}{V^0}\right)=\frac{DV}{L\left(V^1,V^0\right)}.$$\text{ln}\left(\frac{V^1}{V^0}\right)=\frac{DV}{L\left(V^1,V^0\right)}.$(23) We define the weight according to Montgomery-Vartia decomposition as: (24) $w_i^{MV}=\frac{w_i^M}{L\left(V^1,V^0\right)}.$$w_i^{MV}=\frac{w_i^M}{L\left(V^1,V^0\right)}.$(24) Then, the application of (23) to the Montgomery decomposition (20) leads to the Montgomery-Vartia decomposition: (25) $\text{ln}\left(R{V}^{MV}\right)=\frac{D{P}^M}{L\left(V^1,V^0\right)}=\sum _{i=1}^N{w}_i^{MV}\text{ln}\left(\frac{p_i^1}{p_i^0}\right)+\sum _{i=1}^N{w}_i^{MV}\text{ln}\left(\frac{q_i^1}{q_i^0}\right).$$\text{ln}\left(R{V}^{MV}\right)=\frac{D{P}^M}{L\left(V^1,V^0\right)}=\sum _{i=1}^N{w}_i^{MV}\text{ln}\left(\frac{p_i^1}{p_i^0}\right)+\sum _{i=1}^N{w}_i^{MV}\text{ln}\left(\frac{q_i^1}{q_i^0}\right).$(25) The first term after the second equality of (25) is the logarithm of the price index and the second one the logarithm of the quantity index of Montgomery-Vartia. By exponentiation it follows from (25) that: (26) $R{P}^{MV}=\prod _{i=1}^N{\left(\frac{p_i^1}{p_i^0}\right)}^{w_i^{MV}}\text{and}R{Q}^{MV}=\prod _{i=1}^N{\left(\frac{q_i^1}{q_i^0}\right)}^{w_i^{MV}}.$$R{P}^{MV}=\prod _{i=1}^N{\left(\frac{p_i^1}{p_i^0}\right)}^{w_i^{MV}}\text{and}R{Q}^{MV}=\prod _{i=1}^N{\left(\frac{q_i^1}{q_i^0}\right)}^{w_i^{MV}}.$(26) Like the Montgomery indicators, the indices of Montgomery-Vartia do not exhibit the property of global monotonicity, but as argued by Balk (2003, Appendix A.1) this problem is unlikely to be of practical importance. More importantly, contrarily to the Fisher indices, the indices of Montgomery-Vartia fail to exhibit the property of ‘linear homogeneity in comparison prices (quantities)’ and, consequently the property of ‘proportionality’. Fulfilment requires the sum of the weights (24) being equal to one, but, using Jensen’s inequality, Balk (2003) proved that this sum is smaller than one.

2.4.3. The Sato-Vartia index and the Additive Sato-Vartia indicator

Balk (2003) supplied a simple derivation of the indices of Sato-Vartia that was used in the application of this index to SDA by de Boer (2009a). From the logarithmic mean of the value shares of commodity $i$$i$ in total expenditure in comparison and base period, i.c. $s_i^1$$s_i^1$ and $s_i^0$$s_i^0$, we derive $L\left(s_i^1,s_i^0\right)\text{ln}\left(s_i^1/s_i^0\right)=s_i^1-s_i^0$$L\left(s_i^1,s_i^0\right)\text{ln}\left(s_i^1/s_i^0\right)=s_i^1-s_i^0$. Summation over $i$$i$ results in: (27) $\sum _{i=1}^{N}L\left(s_i^1,s_i^0\right)\text{ln}\left(s_i^1/s_i^0\right)=\sum _{i=1}^N\left(s_i^1-s_i^0\right)=0,$$\sum _{i=1}^{N}L\left(s_i^1,s_i^0\right)\text{ln}\left(s_i^1/s_i^0\right)=\sum _{i=1}^N\left(s_i^1-s_i^0\right)=0,$(27) where the last equality follows from the adding-up of the shares to one.

From (1) and (2) it follows that $s_i^1=p_i^1{q}_i^1/V^1$$s_i^1=p_i^1{q}_i^1/V^1$ and $s_i^0=p_i^0{q}_i^0/V^0$$s_i^0=p_i^0{q}_i^0/V^0$. Consequently, (28) $\text{ln}\left(s_i^1/s_i^0\right)=\text{ln}\left(p_i^1/p_i^0\right)+\text{ln}\left(q_i^1/q_i^0\right)-\text{ln}\left(V^1/V^0\right).$$\text{ln}\left(s_i^1/s_i^0\right)=\text{ln}\left(p_i^1/p_i^0\right)+\text{ln}\left(q_i^1/q_i^0\right)-\text{ln}\left(V^1/V^0\right).$(28) Substitution of (28) into (27) leads to: $\text{ln}\left(V^1/V^0\right)\sum _{i=1}^{N}L\left(s_i^1,s_i^0\right)=\sum _{i=1}^{N}L\left(s_i^1,s_i^0\right)\text{ln}\left(p_i^1/p_i^0\right)+\sum _{i=1}^{N}L\left(s_i^1,s_i^0\right)\text{ln}\left(q_i^1/q_i^0\right),$$\text{ln}\left(V^1/V^0\right)\sum _{i=1}^{N}L\left(s_i^1,s_i^0\right)=\sum _{i=1}^{N}L\left(s_i^1,s_i^0\right)\text{ln}\left(p_i^1/p_i^0\right)+\sum _{i=1}^{N}L\left(s_i^1,s_i^0\right)\text{ln}\left(q_i^1/q_i^0\right),$ which after defining: (29) $w_i^{SV}=\frac{L\left(s_i^1,s_i^0\right)}{\sum _{i=1}^{N}L\left(s_i^1,s_i^0\right)},$$w_i^{SV}=\frac{L\left(s_i^1,s_i^0\right)}{\sum _{i=1}^{N}L\left(s_i^1,s_i^0\right)},$(29) can be rewritten to: (30) $\text{ln}\left(V^1/V^0\right)=\sum _{i=1}^N{w}_i^{SV}\text{ln}\left(p_i^1/p_i^0\right)+\sum _{i=1}^N{w}_i^{SV}\text{ln}\left(q_i^1/q_i^0\right).$$\text{ln}\left(V^1/V^0\right)=\sum _{i=1}^N{w}_i^{SV}\text{ln}\left(p_i^1/p_i^0\right)+\sum _{i=1}^N{w}_i^{SV}\text{ln}\left(q_i^1/q_i^0\right).$(30) The first term on the right-hand side of (30) is the logarithm of the price index and the second one the logarithm of the quantity index of Sato-Vartia. By exponentiation it follows from (30) that: (31) $R{P}^{SV}=\prod _{i=1}^N{\left(\frac{p_i^1}{p_i^0}\right)}^{w_i^{SV}};R{Q}^{SV}=\prod _{i=1}^N{\left(\frac{q_i^1}{q_i^0}\right)}^{w_i^{SV}}.$$R{P}^{SV}=\prod _{i=1}^N{\left(\frac{p_i^1}{p_i^0}\right)}^{w_i^{SV}};R{Q}^{SV}=\prod _{i=1}^N{\left(\frac{q_i^1}{q_i^0}\right)}^{w_i^{SV}}.$(31) Like the indices of Montgomery-Vartia, the indices according to Sato-Vartia do not exhibit the property of global monotonicity, but, as argued by Balk (2003, Appendix A.3), this problem is unlikely to be of practical importance either. More importantly, contrary to Montgomery-Vartia indices, due to the fact that the sum of the weights (29) is equal to one, the indices of Sato-Vartia exhibit the property of ‘proportionality’.

The additive counterparts of the Sato-Vartia indices do not exist in index number theory. Therefore we call them ‘Additive Sato-Vartia’. It was introduced in energy and environmental studies by Ang et al. (2003, Appendix B) under the name ‘Additive LMDI II’. We rewrite (23) to: (32) $DV=L\left(V^1,V^0\right)\text{ln}\left(\frac{V^1}{V^0}\right).$$DV=L\left(V^1,V^0\right)\text{ln}\left(\frac{V^1}{V^0}\right).$(32) Substitution of (30) into (32) and defining the weight of the Additive Sato-Vartia decomposition as: (33) $w_i^{ASV}=L\left(V^1,V^0\right)w_i^{SV},$$w_i^{ASV}=L\left(V^1,V^0\right)w_i^{SV},$(33) we arrive at: $DV=\sum _{i=1}^N{w}_i^{ASV}\text{ln}\left(\frac{p_i^1}{p_i^0}\right)+\sum _{i=1}^N{w}_i^{ASV}\text{ln}\left(\frac{q_i^1}{q_i^0}\right),$$DV=\sum _{i=1}^N{w}_i^{ASV}\text{ln}\left(\frac{p_i^1}{p_i^0}\right)+\sum _{i=1}^N{w}_i^{ASV}\text{ln}\left(\frac{q_i^1}{q_i^0}\right),$ so that the price indicators according to Additive Sato-Vartia are: $D{P}^{ASV}=\sum _{i=1}^N{w}_i^{ASV}\text{ln}\left(\frac{p_i^1}{p_i^0}\right)\text{and}D{Q}^{ASV}=\sum _{i=1}^N{w}_i^{ASV}\text{ln}\left(\frac{q_i^1}{q_i^0}\right).$$D{P}^{ASV}=\sum _{i=1}^N{w}_i^{ASV}\text{ln}\left(\frac{p_i^1}{p_i^0}\right)\text{and}D{Q}^{ASV}=\sum _{i=1}^N{w}_i^{ASV}\text{ln}\left(\frac{q_i^1}{q_i^0}\right).$ Like the other logarithmic indices and indicators, it will not exhibit the property of global monotonicity, either. But this problem is unlikely to be of much practical importance, as well.

2.5. A contribution of index number theory: consistency-in-aggregation

All indices (indicators) that we discussed above are one-stage indices (indicators). In practice, the computation of price and quantity indices might also be performed via a multistage process. As an example, Balk (2016) gives the computation of the price index of Laspeyres in two stages. The set of commodities $A$$A$ is partitioned into $K$$K$ disjoint subsets $A^k,\left(k=1,\dots ,K\right)$$A^k,\left(k=1,\dots ,K\right)$, that is to say: $A={\cup }_{k=1}^K{A}^k$$A={\cup }_{k=1}^K{A}^k$ with $A^k{\cap }^{A^l}=\mathrm{\varnothing }$$A^k{\cap }^{A^l}=\mathrm{\varnothing }$ for $k\ne l$$k\ne l$. In the first stage, the Laspeyres price index is computed for each subset $A^k$$A^k$. In the second stage the Laspeyres price index of all first stage indices is computed. Balk (2016) proves that the Laspeyres index according to (7) is equal to Laspeyres index computed in the two-stage process. If at each stage the same type of index is used the index called ‘consistent-in aggregation’ (CIA). Consequently, the indices of Laspeyres are CIA. As Balk (2016, p. 7) states: ‘However, this is the exception rather than the rule. For most indices, two-stage and one-stage variants do not coincide. Put otherwise, most indices are not consistent-in-aggregation.’

Balk (1996) formalized consistency-in-aggregation of a particular price index and proved that the ‘pseudo Montgomery’ price index (nowadays named ‘Montgomery-Vartia’) is CIA. Balk (2008a) reproduced this canonical form and the proof¹ in his section 3.7.2. The proofs that the indicators of Bennet and Montgomery² are CIA are given in his section 3.10.3. In Appendix A of the supplementary material, we give a numerical example from which it is immediately clear that the one-step indices according to Fisher and Sato-Vartia are not equal to the corresponding two-step indices. The same applies to the one- and two-step indicators according to the Additive Sato-Vartia indicator. As a consequence, ‘Fisher’, ‘Sato- Vartia’ and ‘Additive Sato-Vartia’ are not CIA.

2.6. Summary of relevant properties and formulas for IDA and SDA

2.6.1. Relevant properties

All pairs of indices and indicators share the properties of ‘identity’, ‘linear homogeneity of degree zero in prices (quantities)’, invariance to changes in the units of measurement’, ‘time reversal’ and being ‘ideal’. In Table 2 we summarize those theoretical properties, which are met with or not.

TABLE 2. Fulfilment of relevant properties of ideal indices and indicators.

	Fisher	Montgomery-Vartia	Sato-Vartia	Bennet	Montgomery	ASV
Monotonicity	Yes	No	No	Yes	No	No
Proportionality	Yes	No	Yes	N.A.	N.A.	N.A.
Consistency-in-aggregation	No	Yes	No	Yes	Yes	No

It follows from Table 2 that no ideal index meets all the three desired properties simultaneously. Fisher’s is the only one that meets the property of monotonicity; Montgomery-Vartia is the only one that meets consistency-in-aggregation; whereas Fisher and Sato-Vartia both meet the requirement of proportionality, but not Montgomery-Vartia. With respect to the ideal indicators Additive Sato-Vartia is the only one that does not meet the requirement of consistency-in-aggregation so that it not advisable to use it in practice.

2.6.2. Summary of formulas

The relevant formulas of index number theory are summarized in Table 3. From the empirical point of view they are as easily implemented. But remember that index number theory deals with only two factors. In Section 4, we present the generalization to $n$$n$ factors. We find that methods based on the logarithmic mean are easier to implement than the combinatorial ones (Fisher and Bennet). But knowing that these two factors only take on nonnegative numbers means that changes-in-sign cannot occur. In the practice of SDA, however, they might.³

TABLE 3. Decomposition of change in value into price and quantity effect of ideal methods.

Name	Weight	Price effect	Quantity effect
Fisher index	N.A.	${\left({\displaystyle \frac{\sum _{i=1}^N{p}_i^1{q}_i^0}{\sum _{i=1}^N{p}_i^0{q}_i^0}}\right)}^{{\displaystyle \frac{1}{2}}}{\left({\displaystyle \frac{\sum _{i=1}^N{p}_i^1{q}_i^1}{\sum _{i=1}^N{p}_i^0{q}_i^1}}\right)}^{{\displaystyle \frac{1}{2}}}$${\left({\displaystyle \frac{\sum _{i=1}^N{p}_i^1{q}_i^0}{\sum _{i=1}^N{p}_i^0{q}_i^0}}\right)}^{{\displaystyle \frac{1}{2}}}{\left({\displaystyle \frac{\sum _{i=1}^N{p}_i^1{q}_i^1}{\sum _{i=1}^N{p}_i^0{q}_i^1}}\right)}^{{\displaystyle \frac{1}{2}}}$	${\left({\displaystyle \frac{\sum _{i=1}^N{p}_i^0{q}_i^1}{\sum _{i=1}^N{p}_i^0{q}_i^0}}\right)}^{{\displaystyle \frac{1}{2}}}{\left({\displaystyle \frac{\sum _{i=1}^N{p}_i^1{q}_i^1}{\sum _{i=1}^N{p}_i^1{q}_i^0}}\right)}^{{\displaystyle \frac{1}{2}}}$${\left({\displaystyle \frac{\sum _{i=1}^N{p}_i^0{q}_i^1}{\sum _{i=1}^N{p}_i^0{q}_i^0}}\right)}^{{\displaystyle \frac{1}{2}}}{\left({\displaystyle \frac{\sum _{i=1}^N{p}_i^1{q}_i^1}{\sum _{i=1}^N{p}_i^1{q}_i^0}}\right)}^{{\displaystyle \frac{1}{2}}}$
Bennet indicator	N.A.	$\sum _{i=1}^N{\displaystyle \frac{\left(q_i^0+q_i^1\right)}{2}}\left(p_i^1-p_i^0\right)$$\sum _{i=1}^N{\displaystyle \frac{\left(q_i^0+q_i^1\right)}{2}}\left(p_i^1-p_i^0\right)$	$\sum _{i=1}^N{\displaystyle \frac{\left(p_i^0+p_i^1\right)}{2}}\left(q_i^1-q_i^0\right)$$\sum _{i=1}^N{\displaystyle \frac{\left(p_i^0+p_i^1\right)}{2}}\left(q_i^1-q_i^0\right)$
Montgomery indicator	$w_i^M=L\left(v_i^1,v_i^0\right)$$w_i^M=L\left(v_i^1,v_i^0\right)$	$\sum _{i=1}^N{w}_i^M\text{ln}\left({\displaystyle \frac{p_i^1}{p_i^0}}\right)$$\sum _{i=1}^N{w}_i^M\text{ln}\left({\displaystyle \frac{p_i^1}{p_i^0}}\right)$	$\sum _{i=1}^N{w}_i^M\text{ln}\left({\displaystyle \frac{q_i^1}{q_i^0}}\right)$$\sum _{i=1}^N{w}_i^M\text{ln}\left({\displaystyle \frac{q_i^1}{q_i^0}}\right)$
Montgomery-Vartia index	$w_i^{MV}={\displaystyle \frac{w_i^M}{L\left(V^1,V^0\right)}}$$w_i^{MV}={\displaystyle \frac{w_i^M}{L\left(V^1,V^0\right)}}$	${\displaystyle \prod _{i=1}^N{\left(\frac{p_i^1}{p_i^0}\right)}^{w_i^{MV}}}$${\displaystyle \prod _{i=1}^N{\left({\displaystyle \frac{p_i^1}{p_i^0}}\right)}^{w_i^{MV}}}$	${\displaystyle \prod _{i=1}^N{\left(\frac{q_i^1}{q_i^0}\right)}^{w_i^{MV}}}$${\displaystyle \prod _{i=1}^N{\left({\displaystyle \frac{q_i^1}{q_i^0}}\right)}^{w_i^{MV}}}$
Sato-Vartia index	$w_i^{SV}={\displaystyle \frac{L\left(s_i^1,s_i^0\right)}{\sum _{i=1}^{N}L\left(s_i^1,s_i^0\right)}}$$w_i^{SV}={\displaystyle \frac{L\left(s_i^1,s_i^0\right)}{\sum _{i=1}^{N}L\left(s_i^1,s_i^0\right)}}$	${\displaystyle \prod _{i=1}^N{\left(\frac{p_i^1}{p_i^0}\right)}^{w_i^{SV}}}$${\displaystyle \prod _{i=1}^N{\left({\displaystyle \frac{p_i^1}{p_i^0}}\right)}^{w_i^{SV}}}$	${\displaystyle \prod _{i=1}^N{\left(\frac{q_i^1}{q_i^0}\right)}^{w_i^{SV}}}$${\displaystyle \prod _{i=1}^N{\left({\displaystyle \frac{q_i^1}{q_i^0}}\right)}^{w_i^{SV}}}$
Additive Sato-Vartia indicator	$w_i^{ASV}=L\left(V^1,V^0\right)w_i^{SV}$$w_i^{ASV}=L\left(V^1,V^0\right)w_i^{SV}$	$\sum _{i=1}^N{w}_i^{ASV}\text{ln}\left({\displaystyle \frac{p_i^1}{p_i^0}}\right)$$\sum _{i=1}^N{w}_i^{ASV}\text{ln}\left({\displaystyle \frac{p_i^1}{p_i^0}}\right)$	$\sum _{i=1}^N{w}_i^{ASV}\text{ln}\left({\displaystyle \frac{q_i^1}{q_i^0}}\right)$$\sum _{i=1}^N{w}_i^{ASV}\text{ln}\left({\displaystyle \frac{q_i^1}{q_i^0}}\right)$

3. Correspondence between index number theory and IDA and SDA: overview of literature

3.1. Combinatorial indices

3.1.1. Index decomposition analysis

Sun (1998) derived a complete additive decomposition model for n factors by a refinement of the Laspeyres’s method. In it he assures that the residuals due to interactions are distributed equally among the main effects based on the principle of ‘jointly created and equally distributed principle’ (Sun, 1998, p. 88, citing Sun, 1996). Albrecht et al. (2002) used the Shapley value from noncooperative game theory to derive a complete additive decomposition model. Ang et al. (2003) proved that Sun’s approach is equivalent to using the Shapley value and, hence, named the method ‘Sun-Shapley’. But it was just the Bennet indicator applied to n factors. Ang et al. (2004) applied the multiplicative analogue of the Shapley value to the four-factor decomposition model of Chung and Rhee (2001). In their Appendix A they presented the decomposition formula using Shapley’s (1953) generic formula. They called it the ‘Generalized Fisher’ method. Siegel (1945) had already supplied the resulting decomposition formula in his generalization of the two-factor Fisher index.

3.1.2. Structural decomposition analysis

Dietzenbacher and Los (1998) decomposed additively the change in labor costs of 214 sectors in the Netherlands between 1986 and 1992 into four components: the effects of a change in the labor cost per unit of output; the effects of technical change; the effects of changes in the final demand mix; and the effects of the changes in the final demand levels. They computed the arithmetic mean of all $n!=24$$n!=24$ elementary decompositions and of the two polar decompositions, and concluded that both means were rather close to each other. In the framework of the same example Dietzenbacher et al. (2000) gave a multiplicative decomposition and computed the geometric mean of all 24 elementary decompositions and of the two polar decompositions and reached the same conclusion as before. De Haan (2001) collected the duplicates of the additive decomposition of Dietzenbacher and Los and gave, in his Table 1, the weights attached to each of the eight combinations. These weights are equal to those given in Siegel (1945) for the multiplicative analogue. The formula used by de Haan is nothing but the Bennet indicator. Seibel (2003) extended De Haan’s ‘Dutch approach’ and illustrated it for the five-factor case. But his approach is the same as Siegel’s, which we show via application in Appendix B. In Appendix C we apply Shapley’s approach and show the equivalence of the two approaches. De Boer (2009b) proved that the geometric mean of all elementary decompositions is equivalent to Siegel’s generalization of the index of Fisher to n factors. Since Bennet’s indicator is the additive counterpart of Fisher’s index (Balk, 2003), De Boer’s proof implies that the arithmetic mean of all elementary decompositions is equivalent to the Siegel’s (1945) generalization of Bennet’s indicator.

To summarize: all the approaches described above are either generalizations of the Fisher index or of the Bennet indicator applied to a decomposition into $n$$n$ factors. The generic formulae used are either Siegel’s or Shapley’s.

3.2. Logarithmic indices and indicators

3.2.1. Index decomposition analysis

Boyd et al (1987) introduced their so-called ‘Divisia index approach’, by assuming all variables are continuous and each is a function of time. The resulting equation is differentiated with respect to t, integrated over the time interval 0 to T, and the integral path is approximated using the arithmetic mean weight function. It resulted in the so-called AMDI method (‘Artihmetic Mean Divisia Index’.) In the theory of indices and indicators, this method is called the ‘Törnqvist index’ (Törnqvist and Törnqvist, 1937), which is defined as the geometric mean of the Geometric Laspeyres and Geometric Paasche indices (Balk, 2008a). Boyd and Roop (2004) explicitly introduced the Fisher ideal index for the decomposition of structural change in energy intensity into two factors (‘structure’ and ‘intensity’) and compared the results with those obtained by application of AMDI. Since the latter is not an ideal index we do not consider it in this paper. Ang and Choi (1997) introduced ‘a refined Divisia index method’ by replacing the arithmetic mean by the logarithmic mean weight scheme proposed by Sato (1976). Ang and Liu (2001) renamed it the LMDI-II method but is clearly equivalent to the Sato-Vartia index. Ang et al. (1998) proposed ‘a refined Divisia index method based on decomposition of a differential quantity’. This method is nothing but Montgomery’s indicator. Ang and Liu (2001) proposed a so-called LMDI-I method, which is equivalent to the Montgomery-Vartia index. They also rename the method proposed by (Ang et al. 1998) to (additive) LMDI-I. The mathematical derivations of the multiplicative LMDI-I and LMDI-II methods and of the additive LMDI-I method (which are, respectively, the Montgomery-Vartia and Sato-Vartia indices, and the Montgomery indicator) are mathematically complicated. As shown in Section 2, Balk (2003) supplied far simpler derivations. The additive LMDI-II method is introduced in Ang et al. (2003, Appendix B). As noted earlier, this method is unknown in the theory of indices and indicators.

3.2.2. Structural decomposition analysis

De Boer (2008) showed the correspondence between the theory of indices and indicators and SDA. He applied the Montgomery indicator to the additive decomposition of the example of Dietzenbacher and Los (1998), replicated their results and showed that the Montgomery decompositions were very close to the arithmetic mean of all elementary decompositions. De Boer (2009a) applied the index of Sato-Vartia to the multiplicative decomposition in the framework of the same example (Dietzenbacher et al., 2000). He replicated their results and showed that the Sato-Vartia decompositions were very close to the geometric means of all elementary decompositions. Table 4 reports the equivalence between names of methods in index number theory and in index/structural decomposition analysis.

3.3. Summary of names of methods

TABLE 4. Summary of names of methods.

Ratio change		Difference change
Index	Multiplicative decomposition	Indicator	Additive decomposition
Fisher	Dietzenbacher- Hoen-Los or Generalized Fisher	Bennet	Dietzenbacher- Los or Sun-Shapley
Montgomery-Vartia	LMDI- I	Montgomery	LMDI- I
Sato-Vartia	LMDI- II	Additive Sato-Vartia	LMDI- II

4. Ideal methods for decomposition: the case of n factors

4.1. Introduction

In Section 2, we decomposed the aggregate change in a variable $V$$V$, i.e. value, into two factors: price and quantity. The decomposition took on two different forms: a ratio change $RV=V^1/V^0$$RV=V^1/V^0$ (multiplicative decomposition), or a difference change $DV=V^1-V^0$$DV=V^1-V^0$ (additive decomposition.) We considered pairs of price and quantity indices (indicators) that are ideal, i.e, the decomposition is complete or, in other words, there is no residual term.

In this section, we deal with the decomposition of an aggregate change into $n$$n$ factors which can be written as⁴: (34) $V=\sum _{\left\{I\right\}}\prod _{f=1}^n{x}_f,$$V=\sum _{\left\{I\right\}}\prod _{f=1}^n{x}_f,$(34) where $V$$V$: aggregate to be decomposed; $\left\{I\right\}$$\left\{I\right\}$: set of summation indices; $x_f$$x_f$: factor $f=1,\dots ,n$$f=1,\dots ,n$.

The multiplicative decomposition reads:

$RV=\prod _{f=1}^n{R}_{x_f}$$RV=\prod _{f=1}^n{R}_{x_f}$ with $R_{x_f}$$R_{x_f}$: ratio change of factor $f$$f$

and the additive decomposition:

$DV=\sum _{f=1}^n{D}_{x_f}$$DV=\sum _{f=1}^n{D}_{x_f}$ with $D_{x_f}$$D_{x_f}$: difference change of factor $f$$f$

4.2. Fisher and Bennet

4.2.1. The generic formula of Siegel (1945)

For the multiplicative decomposition, Siegel (1945) reduced, by collecting duplicates, the calculation of $n!$$n!$ permutations (in SDA called ‘elementary decompositions’) to the calculation of $2^{n-1}$$2^{n-1}$ combinations. Then, he proposed to take the weighted geometric mean of all combinations, the fraction of the number of duplicates in the total number of elementary decompositions being the exponent. This is, of course, equal to the geometric mean of all elementary decompositions.

The generic formula for the geometric mean is given in Appendix B, in which it is applied to the case of five factors. It amounts to the calculation of $2^4=16$$2^4=16$ combinations, whereas the number of elementary decompositions is equal to $5!=120$$5!=120$, which constitutes a considerable decrease in the number of computations. The Bennet decomposition is the additive counterpart to the Fisher decomposition (Balk, 2003). It is the weighted arithmetic mean with the same combinations, the weights being the same as the exponents of the Fisher decomposition.

4.2.2. The generic formula of Shapley (1953)

Although independent of Siegel,⁵ Shapley (1953) followed an identical route for the additive decomposition. He reduced permutations to combinations and proposed taking the weighted arithmetic mean of all combinations, the divisor being again the fraction of the number of duplicates in the total number of permutations. In Appendix C we give the generic formula of Shapley and apply it to the case of five factors, as well. We present a table in which we prove that Siegel and Shapley yield exactly the result.

4.3. Logarithmic indices and indicators

Consider Equation 34 and define: (35) $v=\prod _{f=1}^n{x}_f,$$v=\prod _{f=1}^n{x}_f,$(35) and (36) $s=\frac{\prod _{f=1}^n{x}_f}{V}=\frac{v}{V}.$$s=\frac{\prod _{f=1}^n{x}_f}{V}=\frac{v}{V}.$(36) The four methods are summarized in Table 5 (compare Table 3).

It follows from Table 5 that all methods are a weighted mean of the logarithm of the relatives, i.e. the value of a factor in the comparison period relative to its value in the base period; the only difference being the weighting factor. It is easy to verify that the Montgomery-Vartia decomposition can be derived from Montgomery’s using the transformation (cf. (18)): (37) $R_{x_f}^{MV}=exp\left[D_{x_f}^M/L\left(V^1,V^0\right)\right]\left(f=1,\dots ,n\right),$$R_{x_f}^{MV}=exp\left[D_{x_f}^M/L\left(V^1,V^0\right)\right]\left(f=1,\dots ,n\right),$(37) and that the Additive Sato-Vartia decomposition can be derived from Sato-Vartia’s using the transformation (compare (19)): (38) $D_{x_f}^{ASV}=L\left(V^1,V^0\right)\text{ln}\left[R_{x_f}^{SV}\right]\left(f=1,\dots ,n\right).$$D_{x_f}^{ASV}=L\left(V^1,V^0\right)\text{ln}\left[R_{x_f}^{SV}\right]\left(f=1,\dots ,n\right).$(38) Equations 37 and 38 are used in the Matlab program given in Appendix E.

TABLE 5. Name of the method, the weight, the effect of a factor and the decomposition.

Name	Weight	Effect of factor	Decomposition
Montgomery (LMDI-I additive)	$w^M=L\left(v^1,v^0\right)$$w^M=L\left(v^1,v^0\right)$	$D_{x_f}^M=\sum _{\left\{I\right\}}{w}^M\text{ln}\left({\displaystyle \frac{x_f^1}{x_f^0}}\right)$$D_{x_f}^M=\sum _{\left\{I\right\}}{w}^M\text{ln}\left({\displaystyle \frac{x_f^1}{x_f^0}}\right)$	$\sum _{f=1}^n{D}_{x_f}^M$$\sum _{f=1}^n{D}_{x_f}^M$
Montgomery- Vartia (LMDI-I multiplicative)	$w^{MV}={\displaystyle \frac{w^M}{L\left(V^1,V^0\right)}}$$w^{MV}={\displaystyle \frac{w^M}{L\left(V^1,V^0\right)}}$	$\text{ln}\left(R_{x_f}^{MV}\right)=\sum _{\left\{I\right\}}{w}^{MV}\text{ln}\left({\displaystyle \frac{x_f^1}{x_f^0}}\right)$$\text{ln}\left(R_{x_f}^{MV}\right)=\sum _{\left\{I\right\}}{w}^{MV}\text{ln}\left({\displaystyle \frac{x_f^1}{x_f^0}}\right)$	$\prod _{f=1}^n{R}_{x_f}^{MV}$$\prod _{f=1}^n{R}_{x_f}^{MV}$
Sato-Vartia (LMDI-II multiplicative)	$w^{SV}={\displaystyle \frac{L\left(s^1,s^0\right)}{\sum _{\left\{I\right\}}L\left(s^1,s^0\right)}}$$w^{SV}={\displaystyle \frac{L\left(s^1,s^0\right)}{\sum _{\left\{I\right\}}L\left(s^1,s^0\right)}}$	$\text{ln}\left(R_{x_f}^{SV}\right)=\sum _{\left\{I\right\}}{w}^{SV}\text{ln}\left({\displaystyle \frac{x_f^1}{x_f^0}}\right)$$\text{ln}\left(R_{x_f}^{SV}\right)=\sum _{\left\{I\right\}}{w}^{SV}\text{ln}\left({\displaystyle \frac{x_f^1}{x_f^0}}\right)$	$\prod _{f=1}^n{R}_{x_f}^{SV}$$\prod _{f=1}^n{R}_{x_f}^{SV}$
Additive Sato-Vartia (LMDI-II additive)	$w^{ASV}=L\left(V^1,V^0\right)w^{SV}$$w^{ASV}=L\left(V^1,V^0\right)w^{SV}$	$D_{x_f}^{ASV}=\sum _{\left\{I\right\}}{w}^{ASV}\text{ln}\left({\displaystyle \frac{x_f^1}{x_f^0}}\right)$$D_{x_f}^{ASV}=\sum _{\left\{I\right\}}{w}^{ASV}\text{ln}\left({\displaystyle \frac{x_f^1}{x_f^0}}\right)$	$\sum _{f=1}^n{D}_{x_f}^{ASV}$$\sum _{f=1}^n{D}_{x_f}^{ASV}$

5. A hands-on toy model of decomposition of an aggregate change into five factors

5.1. The toy model and its decompositions

In our expository toy model we only deal with emissions of carbon dioxide of sectors of the Dutch economy and ignore the direct emissions of households. We dispose of two input–output tables and of the sectoral carbon dioxide emissions. The number of sectors is denoted by N and the number of final demand categories by m.

We define the following vectors and matrices:

$co2$$co2$: $N\times 1$$N\times 1$ vector of sectoral emissions of carbon dioxide;

$x$$x$: $N\times 1$$N\times 1$ vector of sectoral outputs;

$e$$e$: $N\times 1$$N\times 1$ vector of sectoral emissions per unit of output;

$\hat{e}$$\hat{e}$: $N\times N$$N\times N$ diagonal diagonal matrix with $e$$e$ on the main diagonal;

$A$$A$: $N\times N$$N\times N$ matrix of input–output coefficients $a_{ij}$$a_{ij}$ measuring the input from sector i in sector j, per unit of sector j’s output;

$B$$B$: $N\times m$$N\times m$ matrix of bridge coefficients $b_{jk}$$b_{jk}$ measuring the fraction of final demand in category k that is spent on products from sector j;

$u$$u$: $m\times 1$$m\times 1$ vector of shares $u_k$$u_k$ of final demand category k in total final demand; and

$y$$y$: total final demand.

We consider the model: $co2=\hat{e}x,$$co2=\hat{e}x,$ $x=Ax+Buy,$$x=Ax+Buy,$ of which the solution is: (39) $co2=\hat{e}DBuy,$$co2=\hat{e}DBuy,$(39) with: $D=(I-A{)}^{-1}$$D=(I-A{)}^{-1}$ the Leontief inverse.

In sum notation (39) reads: (40) $co{2}_i=\sum _{j=1}^N\sum _{k=1}^m{e}_i{d}_{ij}{b}_{jk}{u}_{k}y.$$co{2}_i=\sum _{j=1}^N\sum _{k=1}^m{e}_i{d}_{ij}{b}_{jk}{u}_{k}y.$(40) Consequently, the aggregate to be decomposed, $V$$V$ in (34), is ‘carbon dioxide emissions of sector $i$$i$’ ($co{2}_i$$co{2}_i$), the set of summation indices is $\left\{I\right\}=j,k$$\left\{I\right\}=j,k$; and the factors are: $x_1$$x_1$ (‘emission coefficients’, $e_i$$e_i$); $x_2$$x_2$ (‘production techniques’, $d_{ij}$$d_{ij}$); $x_3$$x_3$ (‘final demand mix’, $b_{jk}$$b_{jk}$);$x_4$$x_4$ (‘demand structure’, $u_k$$u_k$); and $x_5$$x_5$ (‘size of economy’, $y$$y$), respectively. We want to decompose the change in carbon dioxide emissions from the base period, denoted by the superscript 0, to the comparison period, denoted by the superscript 1, into the changes of these five factors.

5.1.1. Multiplicative (ratio) decomposition

The ratio change in carbon dioxide emissions of sector i is defined to be: $RCO{2}_i=\text{co}{2}_{\text{i}}^1/co{2}_i^0.$$RCO{2}_i=\text{co}{2}_{\text{i}}^1/co{2}_i^0.$ From (40) we obtain: (41) $RCO{2}_i=\frac{\sum _{j=1}^N\sum _{k=1}^m{e}_i^1{d}_{ij}^1{b}_{jk}^1{u}_k^1{y}^1}{\sum _{j=1}^N\sum _{k=1}^m{e}_i^0{d}_{ij}^0{b}_{jk}^0{u}_k^0{y}^0}.$$RCO{2}_i=\frac{\sum _{j=1}^N\sum _{k=1}^m{e}_i^1{d}_{ij}^1{b}_{jk}^1{u}_k^1{y}^1}{\sum _{j=1}^N\sum _{k=1}^m{e}_i^0{d}_{ij}^0{b}_{jk}^0{u}_k^0{y}^0}.$(41) We want to decompose (41) into the ratio changes in emission coefficients ($R{E}_i$$R{E}_i$), production techniques ($R{D}_i$$R{D}_i$), final demand mix $\left(R{B}_i\right)$$\left(R{B}_i\right)$, demand structure ($R{U}_i$$R{U}_i$) and size of the economy ($R{Y}_i$$R{Y}_i$), i.e.: $RCO{2}_i=R{E}_i\times R{D}_i\times R{B}_i\times R{U}_i\times R{Y}_i.$$RCO{2}_i=R{E}_i\times R{D}_i\times R{B}_i\times R{U}_i\times R{Y}_i.$

5.1.2. Additive (difference) decomposition

The difference change in carbon dioxide emissions of sector i is defined to be: $DCO{2}_i=co{2}_i^1-co{2}_i^0.$$DCO{2}_i=co{2}_i^1-co{2}_i^0.$ From (40) we obtain: (42) $DCO{2}_i=\sum _{j=1}^N\sum _{k=1}^m\left(e_i^1{d}_{ij}^1{b}_{jk}^1{u}_k^1{y}^1-e_i^0{d}_{ij}^0{b}_{jk}^0{u}_k^0{y}^0\right).$$DCO{2}_i=\sum _{j=1}^N\sum _{k=1}^m\left(e_i^1{d}_{ij}^1{b}_{jk}^1{u}_k^1{y}^1-e_i^0{d}_{ij}^0{b}_{jk}^0{u}_k^0{y}^0\right).$(42) We want to decompose (42) into the difference changes in emission coefficients ($D{E}_i$$D{E}_i$), production techniques ($D{D}_i$$D{D}_i$), final demand mix $\left(D{B}_i\right)$$\left(D{B}_i\right)$, demand structure ($D{U}_i$$D{U}_i$), and size of the economy ($D{Y}_i$$D{Y}_i$), i.e.: $DCO{2}_i=D{E}_i+D{D}_i+D{B}_i+D{U}_i+D{Y}_i$$DCO{2}_i=D{E}_i+D{D}_i+D{B}_i+D{U}_i+D{Y}_i$

5.1.3. One- and two-step decomposition

Due to the presence of two common factors, the multiplicative decomposition (41) can easily be rewritten to a two-step procedure (de Boer, 2009b): (43) $RCO{2}_i=\frac{e_i^1}{e_i^0}\frac{y^1}{y^0}\frac{\sum _{j=1}^N\sum _{k=1}^m{d}_{ij}^1{b}_{jk}^1{u}_k^1}{\sum _{j=1}^N\sum _{k=1}^m{d}_{ij}^0{b}_{jk}^0{u}_k^0}.$$RCO{2}_i=\frac{e_i^1}{e_i^0}\frac{y^1}{y^0}\frac{\sum _{j=1}^N\sum _{k=1}^m{d}_{ij}^1{b}_{jk}^1{u}_k^1}{\sum _{j=1}^N\sum _{k=1}^m{d}_{ij}^0{b}_{jk}^0{u}_k^0}.$(43) In the first step we compute the simple index numbers of the factors ‘emission coefficients’ and ‘size of the economy’ and in the second step the composite index numbers of the factors ‘production techniques’, ‘final demand mix’ and ‘demand structure’. The decompositions according to Fisher and Sato-Vartia possess the property of proportionality. Then, the one-step decomposition (41) and the two-step (43) yield the same results for the simple index numbers of the factors ‘emission coefficients’ and ‘size of the economy’. They are used as a assure that the Matlab programs performing the computation of multiplicative and additive decomposition at the same time are correct. The decomposition according to Montgomery-Vartia does not exhibit proportionality, so that the one- and two-step decompositions do not yield the same results. Unfortunately, such a simple device of two-step decomposition does not exist for additive decompositions. Evidently, Equation 42 cannot be rewritten to the sum of the two simple indicators for ‘emission coefficients’ and ‘size of the economy’ and the composite indicators of ‘production techniques’, ‘final demand mix’ and ‘demand structure’. Moreover, there is no analogue of ‘proportionality’ for indicators.

5.2. The Fisher and Bennet decompositions

In Appendix B we use Siegel’s generic formula, and in Appendix C Shapley’s generic formula to arrive at the following summarizing table. In a different format it is also given in De Boer (2009b).

In the first row of Table 6, we give the combination with the values that the other four other factors take on in the base period. In SDA literature this is called the Laspeyres perspective. There are 24 duplicates so that on the 120 elementary decompositions the first polar decomposition has a weight of 1 over 5. In the last row we give the combination with the values of the four other factors in the comparison period, the Paasche perspective. The weight of the second polar decomposition is also 1 over 5. If the mean of the two polar decompositions is taken the combinations given in the rows (A.2) up to and including (A.5) are neglected and the weights are increased to 1 over 2. For a small number of factors you may expect it to be close to the mean of all decompositions.

TABLE 6. Summary for the case of five factors.

Appendix A Equation	Number of ones	Combinations				Number of duplicates	Weight
(A.1)	0	{0,0,0,0}				24	1/5
(A.2)	1	{1,0,0,0}	{0,1,0,0}	{0,0,1,0}	{0,0,0,1}	6	1/20
(A.3)	2	{1,1,0,0}	{1,0,1,0}	{1,0,0,1}		4	1/30
(A.4)	2	{0,0,1,1}	{0,1,0,1}	{0,1,1,0}		4	1/30
(A.5)	3	{0,1,1,1}	{1,0,1,1}	{1,1,0,1}	{1,1,1,0}	6	1/20
(A.6)	4	{1,1,1,1}				24	1/5

From Table 6 we can derive the decomposition formulae for each of the five factors. For factor 1⁶, ‘ratio change in emission coefficients’, it results in: (44) $\begin{array}{rl}{R}_{x_1}^F& ={\left[\frac{\sum x_1^1{x}_2^0{x}_3^0{x}_4^0{x}_5^0}{\sum x_1^0{x}_2^0{x}_3^0{x}_4^0{x}_5^0}\right]}^{1/5}\times {\left[\frac{\sum x_1^1{x}_2^1{x}_3^0{x}_4^0{x}_5^0}{\sum x_1^0{x}_2^1{x}_3^0{x}_4^0{x}_5^0}\right]}^{1/20}\times \dots \times {\left[\frac{\sum x_1^1{x}_2^0{x}_3^0{x}_4^0{x}_5^1}{\sum x_1^0{x}_2^0{x}_3^0{x}_4^0{x}_5^1}\right]}^{1/20}\\ & \times {\left[\frac{\sum x_1^1{x}_2^1{x}_3^1{x}_4^0{x}_5^0}{\sum x_1^0{x}_2^1{x}_3^1{x}_4^0{x}_5^0}\right]}^{1/30}\times \dots \times {\left[\frac{\sum x_1^1{x}_2^0{x}_3^1{x}_4^1{x}_5^0}{\sum x_1^0{x}_2^0{x}_3^1{x}_4^1{x}_5^0}\right]}^{1/30}\times {\left[\frac{\sum x_1^1{x}_2^0{x}_3^1{x}_4^1{x}_5^1}{\sum x_1^0{x}_2^0{x}_3^1{x}_4^1{x}_5^1}\right]}^{1/20}\\ & \times \dots \times {\left[\frac{\sum x_1^1{x}_2^1{x}_3^1{x}_4^1{x}_5^0}{\sum x_1^0{x}_2^1{x}_3^1{x}_4^1{x}_5^0}\right]}^{1/20}\times {\left[\frac{\sum x_1^1{x}_2^1{x}_3^1{x}_4^1{x}_5^1}{\sum x_1^0{x}_2^1{x}_3^1{x}_4^1{x}_5^1}\right]}^{1/5}.\end{array}$$\begin{array}{rl}{R}_{x_1}^F& ={\left[\frac{\sum x_1^1{x}_2^0{x}_3^0{x}_4^0{x}_5^0}{\sum x_1^0{x}_2^0{x}_3^0{x}_4^0{x}_5^0}\right]}^{1/5}\times {\left[\frac{\sum x_1^1{x}_2^1{x}_3^0{x}_4^0{x}_5^0}{\sum x_1^0{x}_2^1{x}_3^0{x}_4^0{x}_5^0}\right]}^{1/20}\times \dots \times {\left[\frac{\sum x_1^1{x}_2^0{x}_3^0{x}_4^0{x}_5^1}{\sum x_1^0{x}_2^0{x}_3^0{x}_4^0{x}_5^1}\right]}^{1/20}\\ & \times {\left[\frac{\sum x_1^1{x}_2^1{x}_3^1{x}_4^0{x}_5^0}{\sum x_1^0{x}_2^1{x}_3^1{x}_4^0{x}_5^0}\right]}^{1/30}\times \dots \times {\left[\frac{\sum x_1^1{x}_2^0{x}_3^1{x}_4^1{x}_5^0}{\sum x_1^0{x}_2^0{x}_3^1{x}_4^1{x}_5^0}\right]}^{1/30}\times {\left[\frac{\sum x_1^1{x}_2^0{x}_3^1{x}_4^1{x}_5^1}{\sum x_1^0{x}_2^0{x}_3^1{x}_4^1{x}_5^1}\right]}^{1/20}\\ & \times \dots \times {\left[\frac{\sum x_1^1{x}_2^1{x}_3^1{x}_4^1{x}_5^0}{\sum x_1^0{x}_2^1{x}_3^1{x}_4^1{x}_5^0}\right]}^{1/20}\times {\left[\frac{\sum x_1^1{x}_2^1{x}_3^1{x}_4^1{x}_5^1}{\sum x_1^0{x}_2^1{x}_3^1{x}_4^1{x}_5^1}\right]}^{1/5}.\end{array}$(44) In the very same way, we use Table 6 for the Bennet decomposition. For factor 1, ‘difference change in emission coefficients’, we obtain: (45) $\begin{array}{rl}& \frac{1}{5}\left[\sum \left(\mathrm{\Delta }{x}_1\right)x_2^0{x}_3^0{x}_4^0{x}_5^0\right]+\frac{1}{20}\left[\sum \left(\mathrm{\Delta }{x}_1{x}_2^1{x}_3^0{x}_4^0{x}_5^0\right)\right]+\dots +\frac{1}{20}\left[\sum \left(\mathrm{\Delta }{x}_1\right)x_2^0{x}_3^0{x}_4^0{x}_5^1\right]\\ & +\frac{1}{30}\left[\sum \left(\mathrm{\Delta }{x}_1\right)x_2^1{x}_3^1{x}_4^0{x}_5^0\right]+\dots +\frac{1}{30}\left[\sum \left(\mathrm{\Delta }{x}_1\right)x_2^0{x}_3^1{x}_4^1{x}_5^0\right]\\ & +\frac{1}{20}\left[\sum \left(\mathrm{\Delta }{x}_1\right)x_2^0{x}_3^1{x}_4^1{x}_5^1\right]+\dots +\frac{1}{20}\left[\sum \left(\mathrm{\Delta }{x}_1\right)x_2^1{x}_3^1{x}_4^1{x}_5^0\right]\\ & +\frac{1}{5}\left[\sum \left(\mathrm{\Delta }{x}_1{x}_2^1{x}_3^1{x}_4^1{x}_5^1\right)\right].\end{array}$$\begin{array}{rl}& \frac{1}{5}\left[\sum \left(\mathrm{\Delta }{x}_1\right)x_2^0{x}_3^0{x}_4^0{x}_5^0\right]+\frac{1}{20}\left[\sum \left(\mathrm{\Delta }{x}_1{x}_2^1{x}_3^0{x}_4^0{x}_5^0\right)\right]+\dots +\frac{1}{20}\left[\sum \left(\mathrm{\Delta }{x}_1\right)x_2^0{x}_3^0{x}_4^0{x}_5^1\right]\\ & +\frac{1}{30}\left[\sum \left(\mathrm{\Delta }{x}_1\right)x_2^1{x}_3^1{x}_4^0{x}_5^0\right]+\dots +\frac{1}{30}\left[\sum \left(\mathrm{\Delta }{x}_1\right)x_2^0{x}_3^1{x}_4^1{x}_5^0\right]\\ & +\frac{1}{20}\left[\sum \left(\mathrm{\Delta }{x}_1\right)x_2^0{x}_3^1{x}_4^1{x}_5^1\right]+\dots +\frac{1}{20}\left[\sum \left(\mathrm{\Delta }{x}_1\right)x_2^1{x}_3^1{x}_4^1{x}_5^0\right]\\ & +\frac{1}{5}\left[\sum \left(\mathrm{\Delta }{x}_1{x}_2^1{x}_3^1{x}_4^1{x}_5^1\right)\right].\end{array}$(45) In Appendix D the Matlab program is given that performs the Siegel and Bennet decompositions at the same time. As noted earlier, the results of the simple index numbers for the factors ‘emission coefficients’ and ‘size of the economy’ were used to check that the program yields the correct result for Siegel, so that the result according to Bennet is correct, as well.

5.3. Decompositions based on the logarithmic mean

According to Equations 35 and 40, we have (46) $v_{ijk}^1=e_i^1{d}_{ij}^1{b}_{jk}^1{u}_k^1{y}^1\text{and}{v}_{ijk}^0=e_i^0{d}_{ij}^0{b}_{jk}^0{u}_k^0{y}^0,$$v_{ijk}^1=e_i^1{d}_{ij}^1{b}_{jk}^1{u}_k^1{y}^1\text{and}{v}_{ijk}^0=e_i^0{d}_{ij}^0{b}_{jk}^0{u}_k^0{y}^0,$(46) so that the weight of the Montgomery decomposition (cf. Table 5) is equal to: (47) $w_{ijk}^M=L\left(v_{ijk}^1,v_{ijk}^0\right).$$w_{ijk}^M=L\left(v_{ijk}^1,v_{ijk}^0\right).$(47) Using the transformation (37), and the fact that the variable to be decomposed $\left(V\right)$$\left(V\right)$ in Equation 34 is the emission of carbon dioxide of sector $i$$i$, $co{2}_i$$co{2}_i$, we arrive at the weight of the Montgomery-Vartia decomposition (cf. Table 5): (48) $w_{ijk}^{MV}=w_{ijk}^M/L\left(co{2}_i^1,co{2}_i^0\right).$$w_{ijk}^{MV}=w_{ijk}^M/L\left(co{2}_i^1,co{2}_i^0\right).$(48) According to Equation 36 we have: $s_{ijk}^1=v_{ijk}^1/co{2}_i^1\text{and}{s}_{ijk}^0=v_{ijk}^0/co{2}_i^0.$$s_{ijk}^1=v_{ijk}^1/co{2}_i^1\text{and}{s}_{ijk}^0=v_{ijk}^0/co{2}_i^0.$ Consequently, the weight of the Sato-Vartia decomposition (cf. Table 5) is: (49) $w_{ijk}^{SV}=\frac{L\left(s_{ijk}^1,s_{ijk}^0\right)}{\sum _{j^{\mathrm{\prime }}=1}^N\sum _{k^{\mathrm{\prime }}=1}^{m}L\left(s_{i{j}^{\mathrm{\prime }}{k}^{\mathrm{\prime }}}^1,s_{i{j}^{\mathrm{\prime }}{k}^{\mathrm{\prime }}}^0\right)}.$$w_{ijk}^{SV}=\frac{L\left(s_{ijk}^1,s_{ijk}^0\right)}{\sum _{j^{\mathrm{\prime }}=1}^N\sum _{k^{\mathrm{\prime }}=1}^{m}L\left(s_{i{j}^{\mathrm{\prime }}{k}^{\mathrm{\prime }}}^1,s_{i{j}^{\mathrm{\prime }}{k}^{\mathrm{\prime }}}^0\right)}.$(49) Using the transformation (38) we derive from (49) that the weighting factors of the additive Sato-Vartia decomposition (cf. Table 5) read: (50) $w_{ijk}^{ASV}=L\left(co{2}_i^1,co{2}_i^0\right)w_{ijk}^{SV}.$$w_{ijk}^{ASV}=L\left(co{2}_i^1,co{2}_i^0\right)w_{ijk}^{SV}.$(50) In Table 7, we summarize the formulas for the decompositions of the methods based on the logarithmic mean.

TABLE 7. Formulas for the methods based on the logarithmic mean.

Factor	Montgomery	Montgomery-Vartia	Sato-Vartia	Additive Sato-Vartia
$E_i$$E_i$	${\displaystyle \sum _{j=1}^N\sum _{k=1}^m{w}_{ijk}^M\text{ln}\left(\frac{e_i^1}{e_i^0}\right)}$${\displaystyle \sum _{j=1}^N{\displaystyle \sum _{k=1}^m{w}_{ijk}^M\text{ln}\left(\frac{e_i^1}{e_i^0}\right)}}$	${\displaystyle \prod _{j=1}^N\prod _{k=1}^m{\left[\frac{e_i^1}{e_i^0}\right]}^{w_{ijk}^{MV}}}$${\displaystyle \prod _{j=1}^N{\displaystyle \prod _{k=1}^m{\left[\frac{e_i^1}{e_i^0}\right]}^{w_{ijk}^{MV}}}}$	${\displaystyle \prod _{j=1}^N\prod _{k=1}^m{\left[\frac{e_i^1}{e_i^0}\right]}^{w_{ijk}^{SV}}}$${\displaystyle \prod _{j=1}^N{\displaystyle \prod _{k=1}^m{\left[\frac{e_i^1}{e_i^0}\right]}^{w_{ijk}^{SV}}}}$	${\displaystyle \sum _{j=1}^N\sum _{k=1}^m{w}_{ijk}^{ASV}\text{ln}\left(\frac{e_i^1}{e_i^0}\right)}$${\displaystyle \sum _{j=1}^N{\displaystyle \sum _{k=1}^m{w}_{ijk}^{ASV}\text{ln}\left(\frac{e_i^1}{e_i^0}\right)}}$
$D_i$$D_i$	${\displaystyle \sum _{j=1}^N\sum _{k=1}^m{w}_{ijk}^M\text{ln}\left(\frac{d_{ij}^1}{d_{ij}^0}\right)}$${\displaystyle \sum _{j=1}^N{\displaystyle \sum _{k=1}^m{w}_{ijk}^M\text{ln}\left({\displaystyle \frac{d_{ij}^1}{d_{ij}^0}}\right)}}$	${\displaystyle \prod _{j=1}^N\prod _{k=1}^m{\left[\frac{d_{ij}^1}{d_{ij}^0}\right]}^{w_{ijk}^{MV}}}$${\displaystyle \prod _{j=1}^N{\displaystyle \prod _{k=1}^m{\left[{\displaystyle \frac{d_{ij}^1}{d_{ij}^0}}\right]}^{w_{ijk}^{MV}}}}$	${\displaystyle \prod _{j=1}^N\prod _{k=1}^m{\left[\frac{d_{ij}^1}{d_{ij}^0}\right]}^{w_{ijk}^{SV}}}$${\displaystyle \prod _{j=1}^N{\displaystyle \prod _{k=1}^m{\left[{\displaystyle \frac{d_{ij}^1}{d_{ij}^0}}\right]}^{w_{ijk}^{SV}}}}$	${\displaystyle \sum _{j=1}^N\sum _{k=1}^m{w}_{ijk}^{ASV}\text{ln}\left(\frac{d_{ij}^1}{d_{ij}^0}\right)}$${\displaystyle \sum _{j=1}^N{\displaystyle \sum _{k=1}^m{w}_{ijk}^{ASV}\text{ln}\left({\displaystyle \frac{d_{ij}^1}{d_{ij}^0}}\right)}}$
$B_i$$B_i$	${\displaystyle \sum _{j=1}^N\sum _{k=1}^m{w}_{ijk}^M\text{ln}\left(\frac{b_{jk}^1}{b_{jk}^0}\right)}$${\displaystyle \sum _{j=1}^N{\displaystyle \sum _{k=1}^m{w}_{ijk}^M\text{ln}\left({\displaystyle \frac{b_{jk}^1}{b_{jk}^0}}\right)}}$	${\displaystyle \prod _{j=1}^N\prod _{k=1}^m{\left[\frac{b_{jk}^1}{b_{jk}^0}\right]}^{w_{ijk}^{MV}}}$${\displaystyle \prod _{j=1}^N{\displaystyle \prod _{k=1}^m{\left[{\displaystyle \frac{b_{jk}^1}{b_{jk}^0}}\right]}^{w_{ijk}^{MV}}}}$	${\displaystyle \prod _{j=1}^N\prod _{k=1}^m{\left[\frac{b_{jk}^1}{b_{jk}^0}\right]}^{w_{ijk}^{SV}}}$${\displaystyle \prod _{j=1}^N{\displaystyle \prod _{k=1}^m{\left[{\displaystyle \frac{b_{jk}^1}{b_{jk}^0}}\right]}^{w_{ijk}^{SV}}}}$	${\displaystyle \sum _{j=1}^N\sum _{k=1}^m{w}_{ijk}^{ASV}\text{ln}\left(\frac{b_{jk}^1}{b_{jk}^0}\right)}$${\displaystyle \sum _{j=1}^N{\displaystyle \sum _{k=1}^m{w}_{ijk}^{ASV}\text{ln}\left({\displaystyle \frac{b_{jk}^1}{b_{jk}^0}}\right)}}$
$U_i$$U_i$	${\displaystyle \sum _{j=1}^N\sum _{k=1}^m{w}_{ijk}^M\text{ln}\left(\frac{u_k^1}{u_k^0}\right)}$${\displaystyle \sum _{j=1}^N{\displaystyle \sum _{k=1}^m{w}_{ijk}^M\text{ln}\left({\displaystyle \frac{u_k^1}{u_k^0}}\right)}}$	${\displaystyle \prod _{j=1}^N\prod _{k=1}^m{\left[\frac{u_k^1}{u_k^0}\right]}^{w_{ijk}^{MV}}}$${\displaystyle \prod _{j=1}^N{\displaystyle \prod _{k=1}^m{\left[{\displaystyle \frac{u_k^1}{u_k^0}}\right]}^{w_{ijk}^{MV}}}}$	${\displaystyle \prod _{j=1}^N\prod _{k=1}^m{\left[\frac{u_k^1}{u_k^0}\right]}^{w_{ijk}^{SV}}}$${\displaystyle \prod _{j=1}^N{\displaystyle \prod _{k=1}^m{\left[{\displaystyle \frac{u_k^1}{u_k^0}}\right]}^{w_{ijk}^{SV}}}}$	${\displaystyle \sum _{j=1}^N\sum _{k=1}^m{w}_{ijk}^{ASV}\text{ln}\left(\frac{y^1}{y^0}\right)}$${\displaystyle \sum _{j=1}^N{\displaystyle \sum _{k=1}^m{w}_{ijk}^{ASV}\text{ln}\left({\displaystyle \frac{y^1}{y^0}}\right)}}$
$Y_i$$Y_i$	${\displaystyle \sum _{j=1}^N\sum _{k=1}^m{w}_{ijk}^M\text{ln}\left(\frac{y^1}{y^0}\right)}$${\displaystyle \sum _{j=1}^N{\displaystyle \sum _{k=1}^m{w}_{ijk}^M\text{ln}\left({\displaystyle \frac{y^1}{y^0}}\right)}}$	${\displaystyle \prod _{j=1}^N\prod _{k=1}^m{\left[\frac{y^1}{y^0}\right]}^{w_{ijk}^{MV}}}$${\displaystyle \prod _{j=1}^N{\displaystyle \prod _{k=1}^m{\left[{\displaystyle \frac{y^1}{y^0}}\right]}^{w_{ijk}^{MV}}}}$	${\displaystyle \prod _{j=1}^N\prod _{k=1}^m{\left[\frac{y^1}{y^0}\right]}^{w_{ijk}^{SV}}}$${\displaystyle \prod _{j=1}^N{\displaystyle \prod _{k=1}^m{\left[{\displaystyle \frac{y^1}{y^0}}\right]}^{w_{ijk}^{SV}}}}$	${\displaystyle \sum _{j=1}^N\sum _{k=1}^m{w}_{ijk}^{ASV}\text{ln}\left(\frac{y^1}{y^0}\right)}$${\displaystyle \sum _{j=1}^N{\displaystyle \sum _{k=1}^m{w}_{ijk}^{ASV}\text{ln}\left({\displaystyle \frac{y^1}{y^0}}\right)}}$

We use just one Matlab program to perform all four decompositions at the same time. It is given in Appendix E. As said earlier, we used the results of the simple index numbers for the factors ‘emission coefficients’ and ‘size of the economy’ to check that the program yields the correct result for Sato-Vartia, so that the results according to Montgomery-Vartia, Montgomery and Additive Sato-Vartia are correct, as well.

6. Empirical results

6.1. Dataset⁷

The dataset consists of two Excel files. In the ‘Base period’ the emissions of carbon dioxide (in million kg) are given for 60 sectors of the Dutch economy in 2004, together with the 60 × 60 matrix of intermediate deliveries (in million €) and the 60 × 5 matrix of final deliveries (consumption, government consumption, investments, change in stocks, and exports.) In ‘Comparison period’ the same data are given for 2005, the matrices of intermediate and final deliveries are recorded in prices 2004.

In the last row of Table 8, we give the percentages of the five largest emitters in the total economy. Together they count for 68 % of the emissions while their share in total final demand is 10.4 %. Between brackets we give the percentages in the total economy of the largest emitter. Not unsurprisingly for the Netherlands it is sector number 25 ‘Electricity and gas supply’. It accounts for about one third of total emissions whereas its share in total final demand is only 1.3%. From the column ‘DCO₂’ we gather that the largest emitter accounts for 51.8% of the reduction of carbon dioxide emissions from 2004 to 2005.

TABLE 8. Carbon dioxide emissions (million kg), ratio and difference change, and total final demand (million €) for the five largest emitters and for the total economy.

#	Sector	CO2 2004	CO2 2005	RCO2	DCO2	Final 2004	Final 2005
25	Electricity and gas supply	56,538	55,076	0.974	−1,462	7,689	7,657
13	Chemicals; man-made fibres	15,149	15,215	1.004	66	19,978	20,605
12	Petroleum products, cokes, etc.	12,941	12,826	0.991	−115	13,217	13,097
36	Air transport	12,425	12,940	1.041	515	5,910	6,332
34	Land transport	8,821	8,478	0.961	−343	8,121	8,195
	Five largest Emitters	105,874	104,534		−1,340	54,915	55,866
	Total economy	171,419	168,599	0.984	−2,820	580,936	592,633
	% five largest in total economy	67.9 (33.0)	68.2 (32.7)		52.2 (51.8)	10.4 (1.3)	10.4 (1.3)

6.2. Empirical implementation of the decompositions based on the logarithmic mean

As stated before, the logarithmic mean is ‘zero value robust’. That is to say, in practice we can replace zeros by epsilon small positive numbers (Ang and Liu, 2007a). In the Matlab program (Appendix D) ${10}^{-14}$${10}^{-14}$ is used. But it is not ‘change-in-sign robust’. We cannot apply the decompositions on our data set because of the presence of the final-demand category ‘change in stocks’. As argued by De Boer (2008), however, this is not a genuine final-demand category. A correct treatment is the following: the final-demand matrix should include a column with the (nonnegative) ‘addition to stocks’ and the input–output table should have a row with the (nonnegative) ‘depletion of stocks’. Due to problems of data collection, national account statisticians only include the balancing item ‘change in stocks’. De Boer (2008) solved the problem of changes in sign for stocks by splitting them over the other items of a row according to the pertinent shares in total output. The column sums are no longer equal to total output, so he added a row (that plays no role in decompositions) in which he recorded the adjustment for the stocks. We applied this procedure to our example. As a consequence, the number of final-demand categories is reduced from five to four.

6.3. Results for the multiplicative decompositions

As we conclude from Table 9 the decompositions are very close to each other. From an empirical point of view the split of ‘change in stocks’ over the other items of the pertinent row had no effect. If ‘change-in-sign robustness’ is required we need to apply the Fisher decomposition, but if it is not required, like in this example, we advise to use either the Montgomery- Vartia or the Sato-Vartia decomposition since the latter two are easier to program than Fisher’s.

TABLE 9. Results of the multiplicative decompositions.

Sector	Method	RE	RD	RB	RU	RY
25	Fisher	0.9093	1.0670	0.9839	1.0010	1.0201
	Sato-Vartia	0.9093	1.0655	0.9853	1.0003	1.0201
	Montgomery-Vartia	0.9102	1.0646	0.9854	1.0003	1.0119
13	Fisher	0.9850	0.9899	1.0002	1.0088	1.0201
	Sato-Vartia	0.9857	0.9899	1.0005	1.0084	1.0201
	Montgomery-Vartia	0.9857	0.9899	1.0005	1.0084	1.0201
12	Fisher	0.9960	0.9962	0.9732	1.0073	1.0201
	Sato-Vartia	0.9949	0.9962	0.9734	1.0071	1.0201
	Montgomery-Vartia	0.9949	0.9962	0.9734	1.0071	1.0201
36	Fisher	0.9734	1.0070	1.0354	1.0065	1.0201
	Sato-Vartia	0.9734	1.0064	1.0356	1.0063	1.0201
	Montgomery-Vartia	0.9734	1.0064	1.0356	1.0063	1.0201
34	Fisher	0.9449	0.9920	0.9980	1.0024	1.0201
	Sato-Vartia	0.9449	0.9920	0.9974	1.0024	1.0201
	Montgomery-Vartia	0.9499	0.9920	0.9974	1.0024	1.0201

The decompositions according to Fisher and Sato-Vartia (cf. Table 2) satisfy ‘proportionality’, which implies that for all sectors the effect of the factor ‘size of the economy’ $\left(y^1/y^0\right),$$\left(y^1/y^0\right),$ in six decimal places, is equal to 1.020135. Because Montgomery-Vartia does not satisfy this property $R{Y}^{MV}<1$$R{Y}^{MV}<1$ .020135. For the abovementioned sectors 25, 13, 12, 36 and 34, we find 1.011939, 1.020128, 1.020125, 1.020129, and 1.020130, respectively, which are all very close to the upper bound. For all 60 sectors the minimum effect is equal to 1.019438; the maximum to 1.020134; while the mean effect is equal to 1.020098 with a standard deviation of 0.000119. If in this example we desire to have consistency-in-aggregation, we can easily take the nonfulfilment of ‘proportionality’ for granted and apply Montgomery- Vartia either as one-step decomposition or as a two-step one. If not, we advise to use Sato-Vartia since it satisfies ‘proportionality’.

6.4. Results for the additive decompositions

Obviously, the results for the additive decompositions, presented in Table 10, show the same picture as those of the multiplicative decompositions with the same conclusion that the three methods yield the same results so that the split of ‘change in stocks’ over the other items of a row had no effect either. In subsection 2.6.1, we did not recommend the use of the Additive Sato-Vartia decomposition because it does not possess the theoretical property of consistency-in-aggregation. From the empirical point of view there is another serious drawback as pointed out by Ang et al. (2009). They provide a numerical example of an industry which is the aggregate of two sectors. At the aggregate level (industry) the decomposition is complete (‘no residual term’), but that at the disaggregated level (sectors) the decomposition is not complete since the residuals are unequal to zero. It can be shown that in the framework of this example the decompositions according to Bennet and Montgomery are not only complete at aggregate level, but also at disaggregate level so that the use of one of these methods is recommended. If ‘change-in-sign robustness’ is required we need to apply Bennet’s decomposition, but if it is not required, as in this example, we advise the use of Montgomery’s decomposition because it is easier to program than Bennet’s decomposition.

TABLE 10. Results of the three additive decompositions.

Sector	Method	DE	DD	DB	DU	DY
25	Bennet	−5,314	3,662	−912	17	1,115
	Montgomery	−5,253	3,492	−821	18	1,102
	Additive S-V	−5,304	3,540	−829	18	1,112
13	Bennet	−219	−154	3	132	303
	Montgomery	−218	−153	8	128	303
	Additive S-V	−219	−153	8	128	303
12	Bennet	−66	−49	−351	94	257
	Montgomery	−66	−49	−347	91	257
	Additive S-V	−66	−49	−348	91	257
36	Bennet	−342	81	441	82	253
	Montgomery	−341	81	443	80	253
	Additive S-V	−342	81	443	80	253
34	Bennet	−445	−69	−22	20	172
	Montgomery	−445	−70	−22	21	172
	Additive S-V	−445	−70	−22	21	172

7. Summary of methods, their properties and our recommendations

In Table 11 below we summarize the various methods and their properties. Since the nonfulfilment of monotonicity of the methods based on the logarithmic mean plays no role of importance in practice (Balk, 2003) we do not list its fulfilment in Table 11.

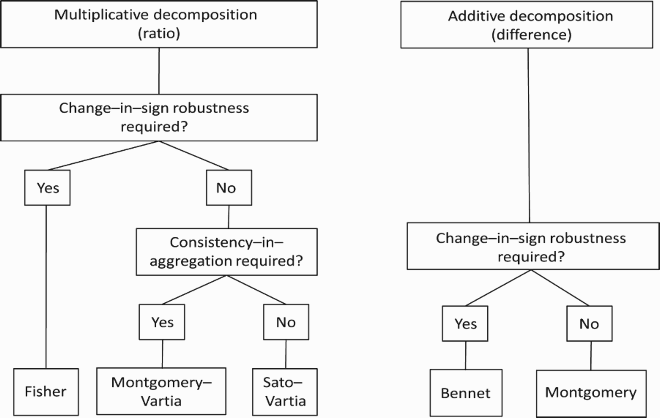
In the following picture we summarize our recommendations:

TABLE 11. Summary of methods and of their relevant properties.

Name	Change-in-sign robust	Proportionality*	Consistent- in- aggregation	Complete at disaggregate level	Simplicity of implementation
Fisher	Yes	Yes	No	Yes	Low
Montgomery- Vartia	No	No	Yes	Yes	High
Sato-Vartia	No	Yes	No	Yes	High
Bennet	Yes	N.A.	Yes	Yes	Low
Montgomery	No	N.A.	Yes	Yes	High
Additive Sato-Vartia	No	N.A.	No	No	High

*There is no analogue of the axiom of proportionality for indicators.

8. Concluding remarks

In this paper, we pay attention to six widely used decomposition methods, all of which share the properties of time reversal and of being ideal. On the basis of theoretical and empirical considerations we show when to use which method.

8.1. Multiplicative decomposition

We considered:

1. Fisher (SDA) is zero-value and change-in-sign robust, satisfies proportionality, but is not consistent-in-aggregation;

2. Montgomery-Vartia (multiplicative LMDI-I) is zero-value robust, but not change-in-sign robust, is consistent-in-aggregation, but does not satisfy proportionality; and

3. Sato-Vartia (multiplicative LMDI-II) is zero-value robust, but not change-in-sign robust, satisfies proportionality, but is not consistent-in-aggregation.

If there are changes in sign in the data set that cannot be resolved, so the only method that can be applied is Fisher. If the data set is ‘change-in-sign robust’ we can apply all three methods. If we wish to apply a method that is ‘consistent-in-aggregation’, we have to apply the Montgomery-Vartia decomposition and take the nonfulfilment of proportionality for granted. If we are not interested in consistency-in-aggregation, we can either apply Sato-Vartia or Fisher, both of which satisfy proportionality. Since the first method is simpler to implement than the latter, we recommend using Sato-Vartia.

8.2. Additive decomposition

We considered:

1. Bennet (SDA): consistent-in aggregation (CIA), zero-value and change-in-sign robust, and complete at aggregate and disaggregate level;

2. Montgomery (additive LMDI-I): CIA, zero-value robust, but not change-in-sign robust. It is complete at aggregate and disaggregate level;

3. Additive Sato-Vartia (additive LMDI-II): not CIA. It is zero-value robust, but not change-in-sign robust; and it is complete at aggregate level, but not at disaggregate level. These are the two reasons why we do not recommend this method.

If there are changes in sign in the data set which cannot be resolved, only Bennet can be applied. Otherwise, we can use either Montgomery or Bennet, but since the first method is simpler to implement we recommend the use of Montgomery.

8.3. Hands-on toy model

We applied all methods to an example in which the change from 2004 to 2005 in sectoral carbon dioxide emissions of the Netherlands are decomposed into five factors: emission coefficients, production techniques, final-demand mix, demand structure and size of the economy. The data set is not change-in-sign-robust because of the presence of ‘change in stocks’ which, as argued by de Boer (2008), is not a genuine final-demand category. It was resolved by spreading the change in stocks over the other items of the pertinent row in the input–output table. We applied the methods of Fisher and Bennet to the full data set, i.e. including the change in stocks, and the other methods which are based on the logarithmic mean to the data set where the number of final demand categories is reduced to four.

8.4. Multiplicative decomposition

From Table 9 it followed that all decompositions are very close to each other so that the split of ‘change in stocks’ over the other items of the pertinent row had no effect. We advise using either the Montgomery-Vartia or the Sato-Vartia decomposition since the latter two are easier to program than is Fisher’s. The effect of the factor ‘size of the economy’ for the Montgomery-Vartia decomposition turned out to be very close to the effect according to the decompositions of Fisher and Sato-Vartia, both of which satisfy ‘proportionality’. In the framework of this example, we can safely take its nonfulfillment for granted and apply, if desired, the two-step decomposition. In general, if one wishes to adopt a method that is consistent-in-aggregation Montgomery-Vartia should be applied, if not, Sato-Vartia is recommended since it satisfies ‘proportionality’.

8.5. Additive decomposition

From Table 10 it followed again that the split of ‘change in stocks’ over the other items of a row had no effect. We advise to use the Montgomery decomposition because it easier to program than Bennet’s.

Acknowledgements

This is a revised version of the paper presented at the 26th International Input Output Conference in Juiz de Fora (Brazil), June 2018, under the title ‘Energy and environmental studies: When to use which method of decomposition?’. We are indebted to Bert Balk for the numerous discussions on index number theory and decomposition analysis and to the chairperson, Mike Lahr, for his encouraging and stimulating comments. The revised version greatly benefitted from remarks of anonymous reviewers.

Disclosure statement

No potential conflict of interest was reported by the authors.

ORCID

João F. D. Rodrigues http://orcid.org/0000-0002-1437-0059

Notes

1 Without using the canonical form of Balk (1996, 2008a), Ang and Liu (2001) gave a direct proof that Montgomery-Vartia is CIA.

2 Without using the canonical form of Balk (1996, 2008a) Ang and Wang (2015) give a direct proof that Montgomery is CIA.

3 To give but one example: in the seven-sector decomposition model of Chung and Rhee (2001) the sector ‘petroleum, coal and town gas’ has a negative value for final demand in the base period, but a positive one in the comparison period. Methods based on the logarithmic mean cannot be used, but the combinatory ones are applicable.

4 In applied research there are often two-step decompositions, such as the decomposition of the Leontief matrix (Xu and Dietzenbacher, 2014; Zhang and Lahr, 2014) and multiplicative attribution analysis (Choi and Ang, 2012; Su and Ang, 2014; Su and Ang, 2015; Wang et al. 2017a; Yan et al., 2018). In all these cases (34) is the first step. Such two-step decompositions are beyond the scope of the present paper.

5 In IDA and SDA literature the generic formula of Siegel has not as yet been presented. De Boer (2009b) used Siegel’s formula but only gave a verbal description. Su and Ang (2014, Appendix B) use Shapley’s generic formula but erroneously attribute it to Siegel.

6 The same formulae are used for the other factors.

7 The authors are indebted to Sjoerd Schenau of Statistics Netherlands for putting these two tables at their disposal.