Sensorimotor coordination and metastability in a situated HKB model

Abstract

Oscillatory phenomena are ubiquitous in nature and have become particularly relevant for the study of brain and behaviour. One of the simplest, yet explanatorily powerful, models of oscillatory Coordination Dynamics is the Haken–Kelso–Bunz (HKB) model. The metastable regime described by the HKB equation has been hypothesised to be the signature of brain oscillatory dynamics underlying sensorimotor coordination. Despite evidence supporting such a hypothesis, to our knowledge, there are still very few models (if any) where the HKB equation generates spatially situated behaviour and, at the same time, has its dynamics modulated by the behaviour it generates (by means of the sensory feedback resulting from body movement). This work presents a computational model where the HKB equation controls an agent performing a simple gradient climbing task and shows (i) how different metastable dynamical patterns in the HKB equation are generated and sustained by the continuous interaction between the agent and its environment; and (ii) how the emergence of functional metastable patterns in the HKB equation – i.e. patterns that generate gradient climbing behaviour – depends not only on the structure of the agent's sensory input but also on the coordinated coupling of the agent's motor–sensory dynamics. This work contributes to Kelso's theoretical framework and also to the understanding of neural oscillations and sensorimotor coordination.

Keywords:

• sensorimotor coordination
• oscillatory dynamics
• metastability
• Coordination Dynamics

1. Introduction

Oscillatory phenomena are ubiquitous in nature, of particular importance to us is the study of oscillatory dynamics as the generating mechanism of sensorimotor behaviour, a phenomenon that expands from lower organisms (Dano, Sorensen, & Hynne, 1999; Gardner, Hubbard, Hotta, Dodd, & Webb, 2006) to large-scale neurodynamics of the mammalian brains (Buzsaki, 2006; Traub & Whittington, 2010). A prominent work in this area is the empirically grounded theoretical framework of Coordination Dynamics which seeks to identify general laws of coordination among rhythmic components operating at different spatial and temporal scales (Kelso, 1995). This framework has motivated many empirical studies of neural oscillatory dynamics underlying sensory and motor activities (Aramaki, 2005; Jantzen, 2004; Lagarde & Kelso, 2006; Meyer-Lindenberg, 2002; Swinnen, 2002) and has opened up discussion in different areas such as philosophy of cognitive science (Bechtel & Abrahamsen, 2010; Chemero, 2009; Kaplan & Bechtel, 2011; Stepp, Chemero, & Turvey, 2011) and theoretical neuroscience (Kelso & Tognoli, 2009).

The main illustrative model for the Coordination Dynamics framework is that described by the extended Haken–Kelso–Bunz (HKB) equation which captures the temporal relation between the activity of coupled oscillatory elements (Kelso, 1995; Kelso, DelColle, & Schoner, 1990). This equation has been carefully studied by manipulating a control parameter that modifies the oscillators’ natural frequencies or their coupling factor. One of its main dynamical properties is the metastable regime in which the phase relation variable engages when the control parameter crosses a certain threshold. Metastable dynamics have been hypothesised to be the dynamical signature of the nervous system underlying sensorimotor coordination (Bressler & Kelso, 2001; Kelso & Tognoli, 2009; Tognoli & Kelso, 2009). Empirical evidence favouring this hypothesis comes, for instance, from studies showing correlation between sensory stimulation and transiently synchronised networks in the brain of animals performing perceptual and motor coordination tasks (Buzsaki, 2006; Hipp, Engel, & Siegel, 2011; Pockett, Bold, & Freeman, 2009; Rodriguez et al., 1999; Singer, 2011; Varela, Lachaux, Rodriguez, & Martinerie, 2001). Despite such evidence supporting the existence of metastable regimes in the brain of behaving animals, to our knowledge, there are still very few models (if any) where the HKB equation generates the motor behaviour of an agent interacting in a spatial environment and, at the same time, has its control parameter modulated, through sensory feedback, by the motor behaviour it generates. Thus, in this work, we investigate the dynamics of the extended HKB equation within a closed sensorimotor loop by implementing it as the controller of an agent performing a functional behaviour (gradient climbing) in a simulated two-dimensional environment. The ‘output’ of the extended HKB equation (the phase relation variable) generates the agent's motor behaviour and, at the same time, its control parameter (in our particular case, the variable representing the oscillators’ frequency difference) is modulated by the agent's behaviour through its sensory activity. The extended HKB equation within the agent's sensorimotor loop will be referred to as the situated HKB model.

The HKB equation has been used to model cases of sensorimotor coupling such as in Kelso, Guzman, Reveley, and Tognoli (2009), where a human subject receives sensory feedback from a computer screen and the human's behaviour in turn affects the computer. The novelty of the situated HKB model is that the coupling is spatial and the HKB is not meant to capture the global feedback dynamics but is used directly as a robotic controller. The resulting dynamics will be shown to have special properties (e.g. multiple metastable regimes).

In the next section, we briefly present the Coordination Dynamics framework. Next, we describe the model and then analyse it; particularly, we start by identifying patterns in the agent's sensorimotor behaviour and studying their underlying metastable regimes; we analyse the mutual coordination between the situated HKB model and its control parameter; and carry out an experiment to compare the dynamical and informational properties of the situated HKB model under open and closed sensorimotor loops. Briefly, we will show (i) how different metastable dynamical patterns in the HKB equation are generated and sustained by the continuous interaction between the agent and its environment; and (ii) how the emergence of functional metastable patterns in the HKB equation – i.e. patterns that generate gradient climbing behaviour – depends not only on the structure of the agent's sensory input but also on the coordinated coupling of the agent's motor–sensory dynamics. The analysis of the extended HKB equation within a sensorimotor loop is a contribution to the Coordination Dynamics framework and, as such, it provides theoretical insights to understanding the interplay between neural oscillations and sensorimotor behaviour.

2. Coordination Dynamics

Coordination Dynamics is a consistent framework which can be used to investigate brain dynamics and behaviour, it was proposed and developed by Kelso (1995) based on Haken's work on synergetics (Haken, 1978). It extends von Holst's work (von Holst, 1937, 1939) by combining empirical experiments and theoretical models formulated mathematically to study how the components of a system interact and produce coherent coordination patterns.

The driving example of Coordination Dynamics is the HKB model which describes the relative phase dynamic between two non-linearly coupled oscillators (Haken, Kelso, & Bunz, 1985). This model was originally designed to replicate the type of phase relation dynamics observed in an empirical experiment involving rhythmic behaviour of human fingers. In this experiment, a subject rhythmically moves his right and left index fingers in a horizontal plane at the same frequency of a pacing metronome. The HKB model replicates how the angle between the left and right fingers changes over time (the phase relation dynamics) given different initial conditions – fingers in-phase or anti-phase – and at an increasing metronome frequency (Kelso, 1995, p. 46). This model was mainly used to explore the in-phase and anti-phase stable synchronisations, the transition between them, and their basins of attraction.

Later on Kelso et al. (1990) extended the HKB model by adding a symmetry-breaking parameter in order to replicate a type of phase relation dynamics between non-identical oscillatory components, i.e. components with different natural frequencies, which is a more realistic phenomenon in nature (Kelso & Engstrom, 2006). One of the main properties of the extended HKB model is the existence of metastable dynamics where the variable representing the temporal relation (i.e. the phase relation) constantly moves in a transient dynamic through regions of the phase space with low potential energy (representing moments of transient synchronisation) followed by regions with high potential energy (representing moments of desynchronisation) and without settling down in point attractors (representing moments of stable synchronisation). The graphic in Figure 1 depicts the attractor landscape of the extended HKB model considering different values for the parameter of symmetry breaking. A low value for the parameter of symmetry breaking generates multistable phase relation dynamics, as schematically represented by the lower curve with two stable (filled circles) and unstable (open circles) points depicted on the x-axis. As the symmetry-breaking parameter increases, the derivative of phase relation also increases (see middle curve) and consequently the attractor landscape becomes monostable – notice that the middle curve has only a single stable point. For higher values of the symmetry-breaking parameter, a saddle-node bifurcation takes place and both fixed points disappear.1 The dynamics of the phase relation near the region where the fixed points used to be are termed ‘metastable dynamics’, as Kelso and Tognoli (2009, p. 108) put it:

In coordination dynamics, metastability corresponds to a regime near a saddle-node or tangent bifurcation in which stable coordination states no longer exist (e.g. in-phase synchronisation where the relative phase between oscillating components lingers at zero), but attraction remains to where those fixed points used to be (remnants of attractor repellors).

Figure 1. Schematic representation of the extended HKB equation attractor landscape. Each curve depicts the derivative of phase relation (y-axis) throughout its state space (x-axis) given three different values for the symmetry-breaking parameter (lower, middle, and upper curves). Stable points are represented by filled circles and unstable ones by open circles. The phase relation dynamics changes from multistable (lower curve) to monostable (middle curve) and eventually metastable (upper curve).

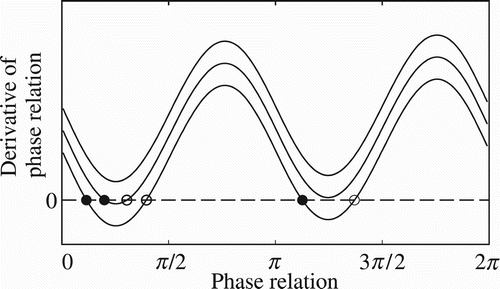
A numerical analysis of the extended HKB equation for a specific set of parameters will be presented in Section 4.

Bressler and Kelso (2001) describe the presence of metastable dynamical regimes of phase relations in oscillatory brain signals by recording the local field potential (LFP) from up to 15 sites in one cortical hemisphere of a macaque monkey performing a visual discrimination task. They analysed the density distribution function of phase relations between pairs of LFP signals and detected that two cortical sites transiently synchronised with phase relation near −54 degrees during the interval [105, 155] ms after the stimulus onset. Apart from that time window, during the whole task ([−70, 400] ms), the same cortical sites were found to be desynchronised (they did not present any other significant peaks on the distribution phase relations), which according to them indicates the functional involvement of these sites at a specific stage of the visual discrimination task. Other cortical sites presented different temporal patterns of coordination presumably reflecting different functional involvements during the task.

Despite the detailed mathematical and experimental understanding of oscillatory dynamics of the extended HKB equation, to our knowledge, there is no study of how this dynamics might be affected when it is situated within a sensorimotor loop. In parallel with this work, we have elsewhere studied what we have called ‘the situated HKB model’ (Aguilera, Bedia, Barandiaran, & Santos, in press), formalising the dynamics of spatial sensorimotor coupling and analytically solving and comparing the situated HKB model with its equivalent decoupled canonical HKB model for a monostable parametric configuration. In this paper, our goal is to study the situated HKB model operating in the metastable dynamics. We analyse the relationship between behavioural, sensorimotor and internal oscillatory dynamic patterns; we compare how metastable regimes of phase relations differ between the situated HKB model and the decoupled-HKB model and study the transitions between characteristic regimes in the situated HKB model; we carry out an experiment and show that the dynamical and informational properties of the situated HKB model change in the absence of a coordinated coupling between the agent's motor and its sensory dynamics, and also that the emergence of functional metastable regimes in the situated HKB model depends on the agent's motor–sensory coupling.

3. Model description

3.1. The agent and its controller

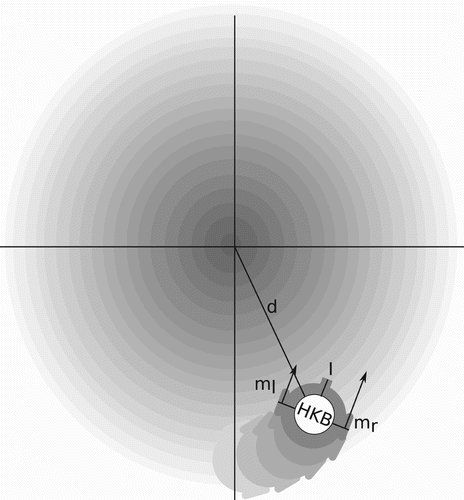
The model consists of a two-dimensional simulated environment and a circular agent whose task is to climb a linear gradient towards the centre of the environment where the peak is located. The agent has a body of five units diameter with two diametrically opposed motors and a sensor randomly positioned at 90°±5° relative to the motor axis.2 The agent's sensor is connected to a controller and the latter connected to both motors, as shown in Figure 2. The controller's dynamics are governed by the extended HKB equation where the difference in natural frequencies (ω) is modulated by the agent's sensory input (s), as defined in Equation (1).

where ϕ is the phase relation between two oscillators at an undetermined level of abstraction,3 s is the sensor activation given by s=c ₁ d˙, where c ₁ is a constant and d˙ is the derivative of the distance from the agent to the centre of the environment; ω is a constant representing the difference in natural frequencies between two oscillators; a and b are constants representing the coupling factor. By sensing the derivative of the distance d˙, the agent is able to perceive a linear radial gradient with its peak at the centre of the environment. We have chosen this type of derivative sensing because many organism's behaviour is based on interactions with different types of gradients.4 Also, for a minimal model, sensing the derivative has the advantage that the agent does not perceive a continuously increasing input, making the dynamics more regular throughout the behaviour of the agent.

Figure 2. Agent and its environment. The agent has a sensory input, two motors m _r and m _l and is controlled by the HKB equation, see Equation (1). The gradient in the environment is represented by the grey scale, where the darker the color the higher the gradient. The highest gradient is positioned at the coordinates x=0 and y=0 in the two-dimensional environment.

The equation is integrated with time step 0.001 s using the Euler method. The right and left motors of the agent are governed by Equations (2) and (3), where c ₂, c ₃ and c ₄ are constants.

3.2. Optimisation with a genetic algorithm

In order to obtain an agent performing gradient climbing, a total of seven parameters (c ₁, c ₂, c ₃, c ₄, ω, a, b) were optimised with the microbial genetic algorithm (GA) (Harvey, 2001). These parameters were encoded in a genotype as a vector of real numbers in the range [0,1] linearly scaled, at each trial, to their corresponding range (a=[0.1, 10], b=[0.1, 10], ω=17 22, c ₁=[0, 3], c ₂=[0, 0.4], c ₃=[0, 2π] and c ₄=[0, 2π]). The GA setup was: population size (50); mutation rate (0.05); recombination (0.60); reflexive mutation; normal distribution for mutation (μ=0, σ2=0.1); trial length (150 s); and trials for each agent (20). At the end of the 20th trial, the worst fitness (out of 20) was used as the selective fitness of the agent. The fitness function was defined by Equation (4):

where F is the fitness, d _i and d _f are the initial and final distances from the agent to the centre of the environment where the peak of the gradient is located. This fitness function selects the agents that perform gradient climbing in an environment with a peak at its centre. The optimised parameters found by the GA were the following: c ₁=2.72, c ₂=0.36, c ₃=3.44, c ₄=3.21, ω=19.67, a=0.99 and b=7.94. The GA ran for 150 tournaments (equivalent to six generations) and the best agent got a fitness of 0.98. Most solutions found by the GA were monostable controllers. In order to obtain metastable dynamics, we had to run different instances of GAs, each one with different ranges of ω.

There is no specific reason why the microbial GA was used, any other optimisation method would probably work as the problem is relatively simple. Neither is there a specific reason why c ₁ and ω are two different parameters, they could have been optimised as a single variable since their product is what is actually relevant. We have used two parameters to keep the model coherent in the sense that c ₁ represents the sensor strength and the ω the frequency difference.

Notice that the purpose of the model developed here is not to solve the problem of gradient climbing (which could be solved by a simple Braitenberg vehicle), but to raise and discuss theoretical issues about the interplay between oscillatory and sensorimotor dynamics based on the analysis of the HKB equation controlling an agent's behaviour under a metastable regime. In this sense, we are not looking for optimum nor general solutions for the gradient climbing behaviour, but for a solution where the controller is metastable while the agent is performing the desired behaviour.

The next sections present the analysis of the fittest agent found the by the GA.

4. Results

In Section 4.1, we briefly present two distinct sensorimotor behaviours that the agent engages in during its interaction with the environment and their underlying metastable regimes in the situated HKB model. In Section 4.2, we analyse how the metastable regimes are generated and how the transition between them takes place. In Section 4.3, we perform an experiment to compare the effects of motor–sensory coupling on the dynamical and informational properties of the situated HKB model.

4.1. Metastable regimes underlying sensorimotor behaviours

Figure 3(a) presents the behaviour of an agent during a single trial of gradient climbing. Figure 3(b) shows how the distance from the agent to the region of highest gradient (the centre of the environment) changes for 20 trials of the experiment; the agent's position, orientation and the controller's phase relation (ϕ) have a random value at the beginning of each trial. The agents take from 80 up to 105 s to move towards the centre of the environment and then they start moving around it. The patterns of sensorimotor behaviour that the agents engage in when they are approaching the centre and when they are moving around it are shown in Figure 4. These patterns are defined by different (repeatedly observed) closed orbits in the state space of sensory and motor activities and will be referred to as SM₁ and SM₂, respectively (SM _n standing for SensoriMotor pattern n).

Figure 3. (a) Single trial of an agent's behaviour in the environment. The agent starts at the position (x=−30, y=12) and moves up the gradient towards the centre (x=0, y=0). When the agent approaches the region of highest gradient, it starts moving around it, as shown in the inset that zooms into the agent's behaviour in the interval t=[80, 90] s. (b) Distance from the agent to the centre of the environment for 20 trials starting at random initial conditions. The inset zooms into the distance from 80 to 90 s for the trial shown in (a). The agents tested take at least 80 s to approach the region of highest gradient.

Figure 4. Patterns of sensorimotor behaviour in which the agents engage in when they are moving towards the region of highest gradient (a) and when they are moving around it (b). The agent's sensor is shown in the x-axis and the difference in speed between its right and left motors (m _r−m _l, defined in Equations (2) and (3)) is shown in the y-axis. Black lines highlight the sensorimotor dynamics within the time intervals [10, 50] s and [110, 150] s in (a) and (b), respectively. All agents converge to the same pattern of sensorimotor behaviour during those time intervals.

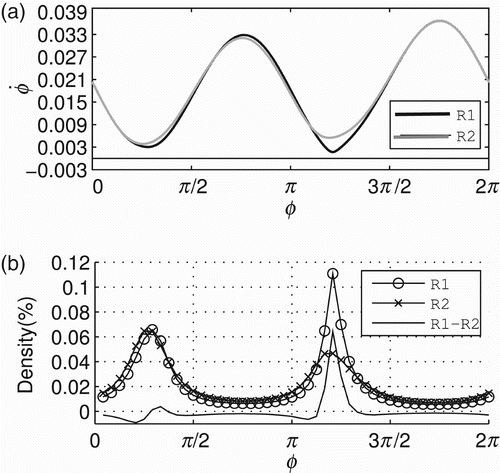
Underlying the sensorimotor behavioural patterns SM₁ and SM₂, there are two distinct metastable regimes of the phase relation (ϕ). The regimes are defined as the distinct regions of the agent's dynamics that correspond directly to the empirically observed behaviours SM₁ and SM₂. As the following analysis shows, the dynamics in these regions have clear differences. Figure 5(a) shows such regimes for 20 successful trials – those presented in Figure 3(b). Notice that these regimes are depicted by showing the state space of the agent's controller (ϕ∈[0, 2π) in the x-axis) and the derivative of ϕ throughout the state space (in the y-axis). The derivative ϕ˙ is calculated by Equation (1) at each time step of the simulation. For any initial conditions, all controllers converge to the metastable regimes R ₁ and R ₂ of ϕ for the sensorimotor patterns SM₁ and SM₂, respectively. In both regimes, the derivative of the phase relation is always greater than zero showing that the state of the controller never reaches a fixed point. Figure 5(b) shows the density distributions of ϕ for R ₁ and R ₂. These distributions were generated by dividing the state space [0, 2π) into 48 equally spaced bins and using the values of ϕ from the time windows [10, 50] s and [110, 150] s (a total of 40,000 data points for each time window) considering a single trial of gradient climbing. The regimes R ₁ and R ₂ have two regions where ϕ slows down, which can be seen by two peaks in the density distribution of each regime (ϕ spends more time in the regions with low derivative, that is why there are peaks in the density distributions). The difference between distributions (represented by the line without marks in the graphic) maintains a level slightly below zero and has a peak in between [π, 3π/2].

Figure 5. Metastable regimes of phase relation (ϕ) that the agent engages in while it is moving towards the centre of the environment and while it is moving around it. (a) shows the metastable regimes in terms of ϕ (x-axis) and ϕ˙ (y-axis) underlying SM₁ (black line) and SM₂ (grey line). These regimes will be referred to as R ₁ and R ₂, respectively (see legend). (b) shows the density distributions of R ₁ (line with circles), R ₂ (line with crosses) and the difference between the distributions (line without markers).

Basically, the purpose of the next section is to understand the coordination between the agent's metastable oscillatory regimes – R ₁ and R ₂ – and its sensorimotor behaviours – SM₁ and SM₂. We will study how these oscillatory regimes are generated and maintained during the agent's interactions with its environment and also how the transition between them takes place.

4.2. Generation and transition between metastable regimes

We shall start by analysing the extended HKB equation without the sensorimotor loop. This analysis does not present any new result that has not been previously presented by Kelso et al. (1990) and Kelso (1995). However, it is important in the context of this paper to set the ground to study the situated HKB model. The purpose here is to understand how the control parameter s affects the derivative of ϕ throughout its state space [0, 2π). The controller is studied within the parameter range s=[−3.92, 3.92], which is the interval of sensory activation when the agent is behaving in the environment.

Figure 6(a) shows ϕ˙ throughout the state space of ϕ given three constant values of s. When s=−3.92, the state space contains an attractor (black-filled circle) and a repeller (white circle). When s=0 and s=3.92, there are no fixed points and the dynamics of ϕ are metastable. By keeping s constant, the derivative ϕ˙ always presents a global minimum at ϕ=0.796 and a local minimum at ϕ=3.916 radians. From now on, these two points will be referred to as ϕ_G and ϕ_L, respectively. Figure 6(b) shows how s changes the derivative at minima ϕ_G and ϕ_L; note the linear relationship between these variables. For s<−3.09 (see vertical dashed line), the derivative is negative at global minimum ϕ_G and positive at the local minimum ϕ_L, showing that the state space has at least two fixed points. Above s>−3.09, the derivative is positive at ϕ_G, showing that the state space does not have fixed points. Figure 6(c) shows the bifurcation diagram of ϕ for the independent variable s. As s increases within the range [−3.92,−3.09), both fixed points (attractor and repeller) approach each other; when s≈−3.09, both points merge into a single half-stable point; and when s>−3.09, this single point disappears and ϕ’s dynamics become metastable. Summing up, s affects the dynamics of the agent's controller by linearly changing the derivative of ϕ throughout the entire state space [0, 2π); additionally, (a) within a certain range of s, the attractor landscape presents two fixed points (an attractor and a repeller) that approach each other as s increases; and (b) above this range, the fixed points disappear and the phase relation dynamics fall into a metastable regime.

Figure 6. (a) Phase relation ϕ (x-axis) and its derivative ϕ˙ (y-axis) for three different values of constant inputs s=−3.92 (lower curve), s=0 (middle curve) and s=3.92 (upper curve). When s=−3.92, the state space contains an attractor (black-filled circle) and a repeller (white circle). When s=0 and s=3.92, there are two points of minima at ϕ=0.796 and ϕ=3.916, respectively. (b) Relation between s and the derivative at the points of minima ϕ=0.796 (black line) and ϕ=3.916 (grey dashed line). For s<−3.09 (see vertical dashed line), the derivative at ϕ=0.796 is negative, and for s>−3.09 both points of minima are positive. (c) Bifurcation diagram of ϕ (see y-axis) for the independent variable s (x-axis). Vertical dashed line is at s=−3.09. The black-filled circles represent point attractors and the white circles represent the repellers. When s>−3.09, the phase relation dynamics are metastable.

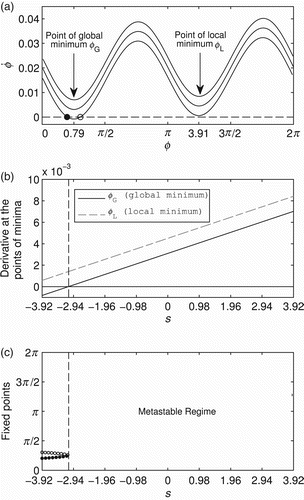
We now move to the analysis of the situated HKB model which has its control parameter s and phase relation ϕ co-modulating each other through the sensorimotor loop. We selected a small time window of 1.5 s during a single trial of gradient climbing in order to start presenting the dynamics of s and ϕ (see Figure 7). Figure 7(a) shows how the derivative ϕ˙ at the points of minima ϕ_G and ϕ_L are changing over time. The sensor dynamics s (in Figure 7(b)) and the derivative at ϕ_G and ϕ_L (in Figure 7(a)) move up and down together due to their linear relationship. Although the fixed points appear in the state space around the minimum ϕ_G during t ₁=[10.53, 10.60] and t ₂=[11.18, 11.25] s, the phase relation does not reach the attractor. The reason for that is that during t ₁ and t ₂, the phase relation ϕ is away from the minimum ϕ_G moving in the region near the local minima ϕ_L=3.916 (see horizontal line in Figure 7(c)) and when ϕ reaches the region near ϕ_G, the sensor value has increased and the fixed points have disappeared. The main point to understand from this analysis is that the control parameter s linearly changes the derivative throughout the entire state space of ϕ, as a result, although for some values of s, the state space shows one or two attractors, the continuous sensorimotor modulation of s in coordination with ϕ never allows the system to settle down on such attractors.

Figure 7. (a) shows how the derivative ϕ˙ at points of minima ϕ_G (black line) and ϕ_L (grey line) are changing over time. The horizontal line highlights ϕ˙=0. (b) shows how s (y-axis) is changing over time. The horizontal line highlights s=−3.09, the threshold at above which the fixed points disappear. Note the linear relation between the dynamic of s (in (b)) and the derivatives at the points of global ϕ_G=0.796 and local ϕ_L=3.916 minima (in (a)). (c) shows how ϕ is changing over time. The horizontal lines highlight the points ϕ_G and ϕ_L. Vertical dashed lines highlight the time intervals t ₁=[10.53, 10.60] and t ₂=[11.18, 11.25] s where the fixed points appear in the state space.

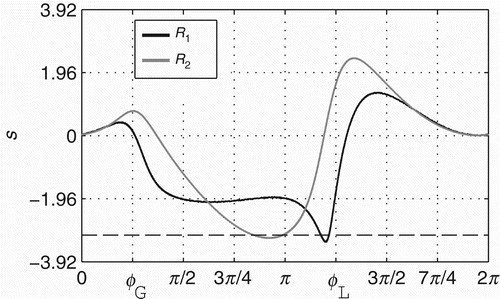
By looking at the values of s shown in Figure 8, we can see how the derivative throughout the state space of ϕ is changing during R ₁ and R ₂. The greatest difference in the derivative takes place when ϕ is around the local minima ϕ_L; exactly at ϕ_L, for instance, the values of s are ≈−1.94 and ≈1.55 during R ₁ and R ₂, respectively; showing that when ϕ is at the point of local minima, the derivative throughout the entire state space is lower during R ₁ than during R ₂. This difference explains why there is a peak in between π and 3π/2 in the graphic of density distribution shown in Figure 5(b). The state space has its lowest derivative and also fixed points around the global minimum ϕ_G in two situations: (a) when ϕ is within [3.69, 3.82] during R ₁, and (b) when ϕ is within [2.65, 3.12] during R ₂; both shown in the graphic by the values of s below the horizontal dashed line. Despite the presence of fixed points, ϕ dynamics never reaches a stable or unstable state as the state space changes when ϕ is around the global minimum ϕ_G (see that the values of s are above the horizontal dashed line when ϕ is around the global minimum ϕ_G=0.796). The main point to understand from this analysis is how s changes the derivative of the state space of ϕ in different ways during the regimes R ₁ and R ₂.

Figure 8. Relations between s and ϕ that generate the dynamical regimes R ₁ (black line) and R ₂ (grey line), respectively. Horizontal dashed line highlights the value of s below which the fixed points appear in the state space of ϕ.

We have been describing how s modulates ϕ by changing the derivative of the latter; however, ϕ also modulates the dynamics of s by moving the agent in the environment – i.e. the dynamics of s and ϕ are generated by a process of co-modulation between these variables. Thus, the regimes R ₁ and R ₂ are generated and sustained by continuously modifying the derivative throughout the state space of ϕ in a structured way through s and, at the same time, by continuously modulating s through m _r and m _l . Notice that as ϕ maps onto m _r and m _l according to Equations (2) and (3), respectively, it is possible to analyse the system by considering only s and ϕ; that is, the dynamics of the loop s→ϕ→(m _r, m _l)→s can be reduced to the co-modulation dynamics s↔ ϕ. Briefly, the main message of the analysis we have presented so far is that the regimes R ₁ and R ₂ are generated and sustained by different dynamics of co-modulation s↔ ϕ. Having seen how R ₁ and R ₂ are generated, in the rest of this section, we analyse the transition between these regimes in terms of the stability of the co-modulation s↔ ϕ.

The stability of s↔ ϕ during a single trial of gradient climbing is presented in Figure 9 by using the Poincare map. At t=0.2 and t=0.7 s, the co-modulation is unstable but moving towards the region of stability represented by the diagonal line; at t=1.2 s, it is near the stable region with s=−2.3; at t=7.7 s, it stabilises with s=−1.98, corresponding to R ₁ (some values are not shown in the graphic). The co-modulation dynamics maintains stability while the agent is moving towards the centre of the environment engaged in the sensorimotor behaviour SM₁. As soon as the agent approaches the centre, at t=80 s, the co-modulation starts losing its stability, as shown by the sequence of grey points near the region pointed at by the arrow R ₁. At t=101 s, the co-modulation is totally unstable and transiting to another stable region; after t=104 s, it is near the stable region, and at t=107 s, it stabilises with s=1.2. The stabilisation completes the transition from R ₁ to R ₂. In summary, the dynamics of s↔ ϕ starts unstable, converges to the stable pattern corresponding to R ₁, becomes unstable again, and then converges to another stable pattern corresponding to R ₂.

Figure 9. Poincare map showing the values of s at every time ϕ=π/2. The diagonal line highlights the region of the map where s remains constant at ϕ=π/2. The numbers near the black points show the approximated time in seconds of the value of s shown on the y-axis. The arrows indicate the regions to where the co-modulation dynamics s↔ ϕ converge during R ₁ and R ₂. These regions are highlighted by the black points.

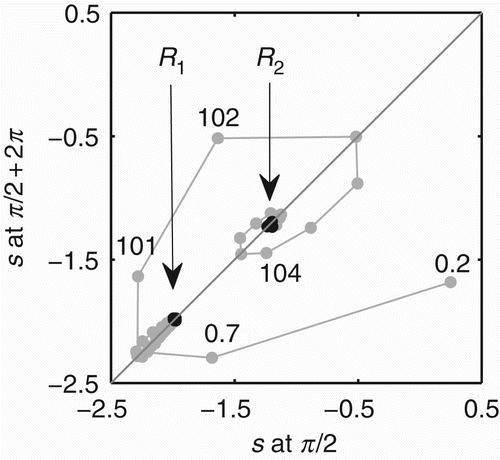
The Poincare map can also be interpreted in an alternative way. This map was generated for the phase relation ϕ=π/2 which corresponds to the motor activity m _r=1.16 and m ₁=0.96 – according to Equations (2) and (3), respectively. We can read the Poincare map as being the representation of the agent's sensory input when its motor states are m _r=1.16 and m _l=0.96. In this case, when the agent is moving towards the centre of the environment, these motor states map onto a sensory input s∼−1.98 (point of stabilisation in the Poincare map corresponding to the regime R ₁); and when it approaches the centre, the motor–sensory dynamics become unstable and eventually settle down in a different stable pattern with s∼1.2 (point of stabilisation in the Poincare map corresponding to the regime R ₂). For both values of s (s∼−1.98 and s∼1.2), there is a micro variation in the order of 10⁻² as the agent's movement and consequently the derivative of the distance to the centre of the environment, which is measured by the agent's sensor, do not vary smoothly (shown by the small oscillations in the distance depicted in Figure 3(b)).

Notice that the topology of the state space underlying R ₁ is different from the one underlying R ₂; more specifically, the transition from R ₁ to R ₂ is not characterised by a movement of the system to a different region of the state space (e.g. movement to a different basin of attraction), but by a modification on the topology of the state space [0, 2π) caused by a different dynamic structure of s.

Also notice that whereas the agent's internal dynamics operates in a metastable regime, the agent as a whole operates in a stable limit cycle dynamics – represented by the trajectories in state space defined by s and ϕ depicted in Figure 8. These regimes are compatible with each other as the fact that the variable ϕ is metastable – characterised by the passage near saddle-node bifurcation points (ϕ_G and ϕ_L) – does not exclude the existence of stable limit cycles in the whole system consisting of s, ϕ, m _r and m _l.

Basically, so far we have shown two patterns of sensorimotor behaviours SM₁ and SM₂ and their underlying metastable dynamical regimes R ₁ and R ₂, we have shown that these dynamical regimes are generated and sustained by the continuous co-modulation between s and ϕ; and have analysed how the transition between regimes takes place in relation to the stability of the co-modulation s↔ ϕ.

4.3. Effects of the motor–sensory coordinated coupling on the HKB model

In this section, we perform an experiment to analyse how the dynamical and informational properties of the agent's internal oscillatory dynamics change when the modulations s→ϕ and ϕ→s are not coupled with each other. A single trial of the experiment consists of an agent performing gradient climbing starting from a random position and orientation in the environment and with random initial phase relation. We record the sensory dynamics of this agent and then play it back to the same agent starting from the same position and random initial phase relation. By doing that the controller of both agents (normal and recorded) are modulated by the same control parameter dynamics – i.e. s→ϕ is the same for both agents – however only the first agent is able to modulate its own control parameter – i.e. only the first agent has ϕ→s coupled to s→ϕ. These agents will be referred to as ‘coupled’ and ‘decoupled’, respectively.

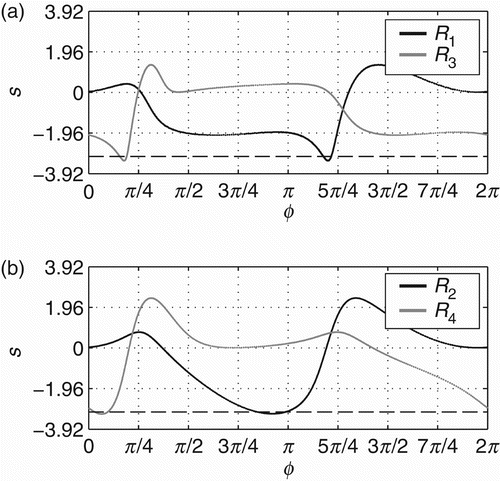
For all initial conditions tested (10,000 trials), the dynamics of the internal oscillatory dynamics of the coupled agent always converges to R ₁ and then it switches to R ₂ (such dynamical pattern transition will be written as R ₁↭ R ₂). This result is exactly what we have shown in the previous section. On the other hand, the internal dynamics of the decoupled agent might converge either to the same pattern R ₁ ↭ R ₂ or to a different one R ₃ ↭ R ₄, see the density distributions of phase relations for these patterns in Figure 10. Accordingly, the dynamics between s and ϕ in the coupled and decoupled agents may also differ from each other, as shown in Figure 11.

Figure 10. Density distributions of the oscillatory regimes that the decoupled agents (those that receive the recorded input of an agent with full sensorimotor coupling – see text for details) might converge to. The oscillatory dynamics converges either to R ₁ ↭ R ₂ or to R ₃ ↭ R ₄ (see legends). Lines without markers show the difference between R ₁ and R ₃ (a) and R ₂ and R ₄ (b).

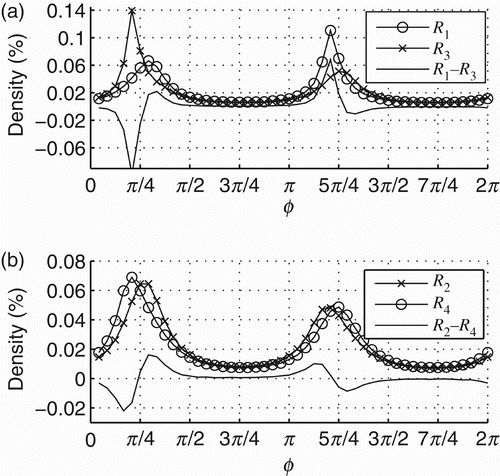
Figure 11. Trajectories in the state space of s and ϕ for the decoupled agent. Initially, s and ϕ converge to either a pattern that generates R ₁ or to another one that generates R ₃ (shown in (a)). Then, they switch either to a pattern that generates R ₂ or R ₄ (shown in (b)).

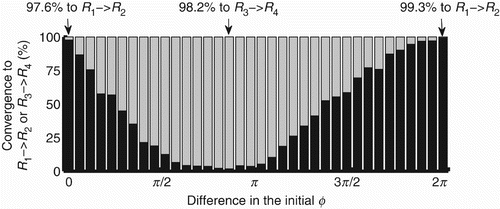
The probabilities of convergence to either R ₁ ↭ R ₂ or R ₃ ↭ R ₄ depend on the difference between the initial values of ϕ in the coupled and decoupled agents, as shown in Figure 12. The initial distance from the agent to the centre of the environment and the angle of the agent's body in relation to the centre do not affect the regimes to which the controller converges. The probability of the decoupled agents to converge to R ₁↭ R ₂ given an initial phase lag within (0,0.17] is 97.6% (see first bar on the left of the graphic); and for a lag within (6.11,6.28] the probability is 99.3% (see last bar on the right of the graphic). The probability of the decoupled agents to converge to R ₃↭ R ₄ given an initial phase lag within (2.62,2.79] is 98.2% (see the longest grey bar in the region before π radians). When the agent converges to R ₃↭ R ₄, the agent's behaviour is totally non-functional as it keeps moving in circles around its starting position.

Figure 12. Percentage of agents (y-axis) that converge to either R ₁ ↭ R ₂ (black bars) or R ₃ ↭ R ₄ (grey bars) according to the difference between the initial ϕ in coupled and decoupled agents. The state space [0, 2π) was divided into 36 equally spaced intervals represented by the bars.

Summing up, the dynamical properties of the agent's controller depends on whether ϕ modulates s; when there is modulation, the controller always converges to R ₁ ↭ R ₂. In the absence of modulation, the controller might converge either to the functional R ₁ ↭ R ₂ or to the non-functional R ₃ ↭ R ₄. This result suggests that the emergence of functional metastable patterns in the situated HKB model – i.e. patterns that generate gradient climbing behaviour – depend not only on the structure of the agent's sensory input, but also on a coordinated coupling of the agent's motor–sensory dynamics.

Finally, we study how the informational properties of the system change when the modulations s→ϕ and ϕ→s are not coupled to each other. The amount of information that the controller of the decoupled agent carries about sensory stimulation is equal to or smaller than the amount of information carried by the controller of the coupled agent. The amount of information is equal when the controller converges to R ₁ ↭ R ₂ and smaller when it converges to R ₃ ↭ R ₄. This difference is analysed with information-theoretic measures applied to s and ϕ dynamics considering 20 trials of the experiment in which the coupled agent converges to R ₁ ↭ R ₂ and the decoupled one to R ₃ ↭ R ₄ (methods are described in Appendix 1). Particularly, we measured (a) the Shannon entropy of the sensor – referred to as H(s) – which gives the amount of bits needed to ‘codify’ the sensory dynamics; (b) the mutual information between s and ϕ of the decoupled agent – referred to as I(s; ϕ _d ) – which gives the amount of information the controller has about the sensory dynamics; and (c) the conditional mutual information between s and ϕ of the coupled agent given ϕ dynamics of the decoupled agent – referred to as I(s; ϕ _c |ϕ _d ) – which gives the amount of information carried by the controller of the coupled agent that is not already present in the controller of the decoupled agent. In essence, these measures will inform us about how the information present in the controller about sensory activity changes with and without the modulation ϕ→s – see Figure 13.

Figure 13. Information-theoretic measures for the agent's controller with and without the modulation ϕ→s. All measures represent the mean over 20 trials and error bars their standard deviation. On average, the agent's sensor entropy H(s) remains around 5 bits. Under open-loop, the mutual information between the decoupled agent's controller and its sensor I(s; ϕ _d ) stays at ≈3.3 bits while the agent is approaching the centre of the environment (time in seconds is represented on the x-axis) and slightly increases to ≈3.6 when the agent is moving around the centre of the environment. The controller of the coupled agent carries 0.5 bits of additional information about the sensor that is not present in the controller of the decoupled agent, shown by I(s; ϕ _c |ϕ _d ).

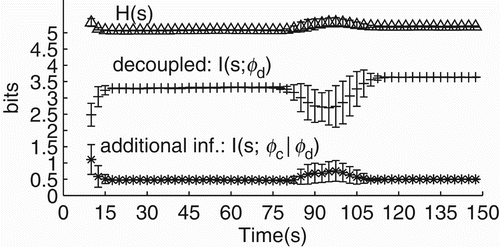
The agent's sensory dynamics needs ≈5 bits to represent all its possible states, as shown by H(s). The controller of the decoupled agent carries ≈3.5 bits of information about the sensory dynamics, as shown by I(s; ϕ _d ); and by adding the modulation ϕ→s, the amount of information increases by ≈0.5 bits (≈14% ), as shown by I(s; ϕ _c |ϕ _d ). This result suggests that the informational content that the agent's controller carries about its control parameter s is greater when ϕ and s modulates each other than when only s modulates ϕ or, in other words, the modulation of sensory activity by motor behaviour increases the amount of information present in the agent's oscillatory network.

5. Discussions and conclusions

The contribution of this paper is twofold, it presents a dynamical analysis of the extended HKB equation within a closed sensorimotor loop and also gives theoretical insights into the interplay of sensorimotor behaviour and neural oscillatory dynamics.

We have shown qualitatively different sensorimotor behaviours – SM₁ and SM₂ – and their underlying metastable regimes of phase relations – R ₁ and R ₂, respectively. This result is relevant mainly in the context of the Coordination Dynamics framework as it presents a simple case of the relation between metastability in the HKB model and sensorimotor behaviour. We have also shown that the regimes R ₁ and R ₂ are generated and sustained by continuously modifying the derivative throughout the state space of ϕ in a structured way through s and, at the same time, by continuously modulating s through ϕ via m _r and m _l . In the context of Coordination Dynamics, this result helps to understand how different metastable regimes can be generated and sustained by the HKB model when it is within a sensorimotor loop. More generally, this result suggests that an agent's internal oscillations depend on sensorimotor dynamics to engage in functional metastable regimes; that is, the on-going interaction involving an agent and its environment generates and sustains the agent's coherent metastable oscillatory regimes.

The density distributions of phase relations for the regimes R ₁ and R ₂ – presented in Figure 5(b) – suggest that, for this specific model, the synchronisation strength between the oscillators is enough to distinguish between the different sensorimotor patterns the agent can engage in. Particularly, during SM₁ and SM₂, the oscillators get synchronised in the same ranges of phase difference [0, π/2] and [π, 3π/2]; but the magnitude of synchronisation at [π, 3π/2] is higher during SM₁ than during SM₂. This result is in accordance with some empirical works in neuroscience that seek to identify synchronised clusters in the brain correlated to an animal perceptual-motor activity, as cited in Section 1. Hipp et al. (2011), for instance, have found that the magnitude of synchronisation in the beta and gamma frequencies across distributed brain areas could predict a subject perception – bars crossing one another or bouncing off each other. For a more detailed discussion on the functional roles of synchronous and desynchronous oscillations for the generation of coherent sensorimotor coordinations, see Santos, Barandiaran, and Husbands (2012). There, the authors analyse a theoretical model and suggest that (i) the information about an agent's sensorimotor dynamics is evenly distributed throughout the entire range of phase relations without a privileged status to either synchronous or desynchronous oscillations and (ii) both synchronous and desynchronous oscillations carry similar causal contribution for the generation of an agent's coherent sensorimotor coordination.

Another result we have shown is that the transition from R ₁ to R ₂ takes place when the co-modulation between s and ϕ becomes unstable. This result suggests that an agent's internal oscillations switches between functional metastable regimes when the dynamics of interaction involving the agent and its environment becomes unstable. While a pattern of motor activity is mapped onto another pattern on the agent's sensory activity – i.e. the interaction is stable – the agent's internal dynamics settles down into a metastable pattern (e.g. R ₁); but once the same motor activity starts generating a different sensory stimulation – i.e. the interaction becomes unstable – the agent's internal dynamics makes a transition to another metastable pattern (e.g. R ₂). This result shows how the transition between dynamical regimes in the situated HKB model depends on the stability of the agent's sensorimotor contingencies.

The experiment with recorded input further investigates the continuous mutual coordination and interdependence between the agent's sensorimotor behaviour and its internal oscillatory dynamics. It shows that the dynamical properties of the agent's controller depends on whether ϕ modulates s; when there is modulation, the controller always converges to R ₁ ↭ R ₂ and in the absence of modulation, the controller converge to either R ₁ ↭ R ₂ or R ₃ ↭ R ₄ . In other words, the modulation of the agent's sensory dynamics by its motor activity (ϕ→s) assures that the controller converges to the functional metastable regimes R ₁ and R ₂ that generate coherent sensorimotor behaviours for the agent to perform gradient climbing. In the absence of this modulation, the agent's internal oscillations and its motor–sensory dynamics might become uncoordinated and consequently generate a non-functional interaction between the agent and its environment. More generally, this experiment suggests that functional metastable oscillatory regimes are tightly dependent on the agent's sensorimotor contingencies, as when the agent's sensory activity is not coordinated to what the agent is doing then the internal oscillations might converge to a non-functional regime.

The modulation of the agent's sensor by its motor behaviour through the environment not only influences the dynamical properties of the agent's controller, but might as well increase the mutual information between the agent's controller and its sensory dynamics. Particularly, we have shown that the mutual information between ϕ and s is greater when there is co-modulation s↔ ϕ than when only s modulates ϕ. This result should be more carefully investigated with more variations of the experiment as it could be only by chance that the regimes R ₃ and R ₄ presented a mutual information lower than R ₁ and R ₂; however, it still remains interesting for opening the discussion on whether the uncertainty of neural oscillations about sensory stimuli decreases under modulation of motor activity.

These results and the type of mathematical analysis we have carried out throughout this paper can contribute to the on-going debate about the constitutive role of action for perception, bringing it down to the field of neurodynamics. In short, proponents of the constitutive role of action for perception (Myin & O'Regan, 2008; Noe, 2004; O'Regan & Noe, 2001a,b) claim that perceiving is a form of action:

In the sensorimotor contingency theory, the experienced quality of perceptual feelings is taken to arise from the precise ways in which one perceptually explores one's environment. Sensorimotor contingencies […] are the ways in which, during such an exploration, perceptual input varies as a function of perceptual exploratory actions. (Myin & O'Regan, 2008, p. 192)

Opponents of this view (Clark, 2006; Prinz, 2006) concede that action is causally relevant for perception, but not that it is necessary for perception to occur, i.e. action is not constitutive of perception. Without going into details, we want to point out that the abstract philosophical discussion about the role of action for perception can benefit from the mathematical and computational modelling we have presented here. In particular, it can illustrate in detail the notion of constitution. In the case of our agent, reaching R ₁ ↭ R ₂ was not just the result of receiving the appropriate input (caused by direct or indirect motor activity), but the result of a fine-grained coordination process that depends on fine-grained sensorimotor contingencies. In more complex and realistic sensorimotor conditions (both on the side of the controller, the environment and the sensory and motor functions), it is to be expected that the available number of metastable regimes (R _n ) be much higher than the four we found on our agent. As a result, if one was to interpret a particular metastable regime as a neural correlate of a perceptual ‘state’, it would be practically impossible to achieve it without the right sensorimotor contingencies being generated-by and, in turn, modulating the very metastable oscillatory regime. It is in this sense that the constitutive nature of action for perception can be explicitly identified and characterised. In the context of the Coordination Dynamics theoretical paradigm, the present model becomes an explicit illustration of the interaction between what Kelso and Engstrom (2006) call the organism–environment complementary pair and the perception–action complementary pair.

The metastable regimes that the HKB model can illustrate have been hypothesised to be the signature of brain functioning. Despite evidence of metastability in empirical experiment of animals performing perceptual motor coordination tasks (as described in the introduction), to our knowledge, there was no previous model of a situated HKB system that operates in a metastable region, coupling internal metastable oscillations to sensorimotor Coordination Dynamics through a control parameter. The model we have developed and analysed in this paper has contributed to fill this gap and has shown the tight dependency that can be established between an agent's neural oscillatory metastable regimes and the sensorimotor contingencies they make possible when coupled to the environment.

Acknowledgements

We thank three anonymous reviewers for providing us with very detailed and valuable comments.

Bruno A. Santos acknowledges financial support from Brazilian National Council of Research, CNPq. Miguel Aguilera holds a FPU predoctoral fellowship from the Spanish Ministerio de Educacion. During the development of this paper, Dr Xabier E. Barandiaran held a postdoctoral position funded by FP7 project eSMC IST-270212 (EU Seventh Framework through ‘ICT: Cognitive Systems and Robotics’) and also held a Postdoc with the FECYT foundation (funded by Programa Nacional de Movilidad de Recursos Humanos del MEC-MICINN, Plan I-D+I 2008-2011, Spain). XEB also acknowledges funding from Subvencion General a Grupos de Investigacion del sistema universitario vasco. Grupo Filosofia de la Biologia’ from Gobierno Vasco IT 505-10 and financial support from ‘Autonomia y niveles de organizacion’ project funded by the Spanish Ministerio de Ciencia e Innovacion FFI2011-25665 (currently Ministerio de Economia y Competitivad) and FEDER funds from the E.C.

The work presented here benefited from the economic support of the Retecog Network (Red Espanola de Ciencia Cognitiva, FFI2010-09796-E, Ministerio de Ciencia e Innovacion. Acciones Complementarias a Proyectos de Investigacion Fundamental no orientada, Government of Spain) that financed a one month visit of Dr Manuel Bedia, Miguel Aguilera and Bruno Santos at the IAS-Research Centre for Life, Mind and Society at the University of the Basque Country.

Notes

‘The saddle-node bifurcation is the basic mechanism by which fixed points are created and destroyed. As a parameter is varied, two fixed points move toward each other, collide, and mutually annihilate’ (Strogatz, 2000).

Although the variation of five degrees in the sensor's position increases the likelihood of the optimisation algorithm (explained below) to obtain a more robust solution for the gradient climbing behaviour, it is not necessary for evolving the parameters of the model.

In the experiment carried out by Kelso, the phase relation ϕ models the angle between the right and left fingers, as described in Section 2. This variable has also been interpreted as the phase relation between neural oscillatory components underlying the fingers’ coordination (Kelso & Tognoli, 2009). In the context of this work, ϕ describes the phase relation of oscillatory components at an undetermined level of abstraction (it can be interpreted, for instance, as the phase relation between individual neurons, or neuronal groups). Our goal here is not to develop a model with empirical accuracy, but to raise theoretical issues about oscillatory dynamics underlying sensorimotor coordination.

Most of small scale adaptive behaviour occurs along chemical gradients. The microscopic world is a world of gradients (like thermal gradients or light gradients but mostly chemical gradients). The adaptive behaviour of small animals (e.g. Caenorhabditis elegans) and individual motile cells (e.g. bacteria but also animal cells migrating during development) is mostly a gradient-related adaptive behaviour. Navigating smell or heat gradients is also a stereotypical adaptive task for higher animals.

Appendix 1. Information-theoretic measures

Shannon's entropy (Shannon, 1948) is shown in Equation (A1), where p(x _k ) is probability mass function of the outcome x _k .

The mutual information (Shannon, 1948; Cover & Thomas, 2005) is shown in Equation (A2), where H(X) and H(Y) are the entropies of the sets X and Y, respectively, and H(X, Y) is the joint entropy of both sets.

The standard measure of conditional mutual information (Cover & Thomas, 2005) is shown in Equation (A3).

where X, Y and Z are sets of discrete random variables; and p is the probability mass function for the given subscripts (x, y and z).

The temporal dynamics of the information-theoretic measures were captured by using a moving window of 10 s; i.e. the probability mass functions were calculated considering a moving window containing 10,000 data points. The continuous values of s ∈[−3.92, 3.92], ϕ _c and ϕ _d ∈[0, 2π) were discretised into 50 equally spaced bins.