An improved water wave optimisation algorithm enhanced by CMA-ES and opposition-based learning

ABSTRACT

Water Wave Optimisation algorithm (WWO) is a new swarm-based metaheuristic inspired by shallow wave models for global optimisation. In this paper, an enhanced WWO, which combines with multiple assistant strategies (EWWO), is proposed. First, the random opposition-based learning (ROBL) mechanism is introduced to generate the initial population with high quality. Second, a new modified operation is designed and embedded into propagation operation to balance the global exploration and the local exploitation. Third, the covariance matrix self-adaptation evolution strategy (CMA-ES) is employed by the refraction operation to further strengthen the local exploitation. Furthermore, the diversity of the population is maintained in the evolution process by using a crossover operator. The experiment results based on CEC 2017 benchmarks indicate that the EWWO outperforms the state-of-the-art variant algorithms of the WWO and the standard WWO.

KEYWORDS:

• Water wave optimisation
• covariance matrix self-adaptation evolution strategy
• differential evolution
• opposition-based learning mechanism
• enhanced water wave optimisation

1. Introduction

Research on the evolutionary algorithms (EAs) has been raised as an attractive methodology to solve the complex combinatorial problems for several decades. Numerous evolutionary algorithms have been proposed to solve complex optimisation problems. Single-objective optimisation plays an important role in various research domains and application fields. Traditional optimisation algorithms and traditional mathematical methods, which are generally determined by fixed structure and parameters, are applied to solve the single-objective optimisation problems. However, the two methods have certain limitations and their performances are unsatisfactory in solving complex optimisation problems such as premature convergence and poor search ability. Due to these shortcomings, meta-heuristics are proposed to overcome the disadvantages of the traditional mathematical methods and the traditional optimisation algorithms. Meta-heuristics, inspired by the natural evolutionary process, were proposed by various researchers. As the mechanisms of the algorithms have the advantages on simple procedure of implementation, Meta-heuristics are becoming increasingly popular in research and engineering practitioners. Most importantly, meta-heuristics are applied to a wide range of problems in different disciplines.

The classical algorithms to large-scale combinatorial optimisation problems have to address the complexity related to the dimensions, such as Genetic Algorithm (GA) (Das, Das, & Ghosh, 2017; Yu, Qiang, & Benfei, 2019), Simulated annealing (SA) (Grobelny & Michalski, 2017), Differential Evolution (DE) (Awad, Ali, Mallipeddi, & Suganthan, 2018; Price, 1999), Particle Swarm Optimisation (PSO) (Bijan & Pillay, 2019; Kennedy & Eberhart, 1995), Harmony search (HS) (Geem, Kim, & Loganathan, 2001; Tian & Zhang, 2018 ). A series of advanced evolutionary algorithms have been emerged, such as Biogeography-based Optimisation Algorithm (BBO) (Simon, 2008), Cuckoo Search algorithm (CS) (Yang, Deb, & Mishra, 2018), Bat Algorithm (BA) (Cheng, 2010), self-adaptive harmony PSO search algorithm (SHPSO) (Zhao, Liu, Zhang, & Wang, 2015), Gravitational Search Algorithm (GSA) (Rashedi, Nezamabadi-pour, & Saryazdi, 2009), hybrid algorithm based on self-adaptive gravitational search algorithm (SGSADE) (Zhao, Xue, et al., 2018), two-stage differential biogeography-based optimisation algorithm (TDBBO) (Zhao, Qin, et al., 2019). These algorithms have a unique search mechanism and the ability to better balance global and local search studies. In addition, among the above algorithms the following are utilised for solving the flow shop scheduling problem, such as flexible flow shop (Abdollahpour & Rezaian, 2016), the chaotic local search bacterial foraging optimisation (CLS-BFO) (Zhao et al., 2016), P-EDA for the blocking flow-shop scheduling problem (Shao, Pi, & Shao, 2018a). The key of evolutionary algorithms depends on the balance of exploration and exploitation at different evolutionary stages. However, most evolutionary algorithms are either biased towards exploitation or exploration and fell into local optimum to solve optimisation problems.

Water Wave Optimisation Algorithm based on the shallow water wave model is a novel nature-inspired metaheuristic method proposed by Zheng (2015). The framework of the WWO has three effective mechanisms: propagation, refraction and breaking, to balance the capabilities of local search and global search. A large number of experiments have been shown that the WWO shows efficient performance in numerical tests and practical applications. WWO has been testified to be an effective algorithm on various problems. For instance, WWO is utilised to deal with the travelling salesman problem (TSP) (Wu, Liao, & Wang, 2015). WWO is applied to the permutation flow shop scheduling problems (PFSP) (Yun, Feng, Lyu, Wang, & Liu, 2016). A discrete WWO (DWWO) (Zhao, Liu, et al., 2018) is used to solve the no-wait flow shop scheduling problem (NWFSP) (Allahverdi, Aydilek, & Aydilek, 2018). WWO with the single-wave mechanism (SWWO) (Zhao, Zhang, et al., 2019) is introduced for the NWFSP and a novel discrete WWO for blocking flow-shop scheduling problem (BFSP) (Shao, Pi, & Shao, 2018b). Although the exploitation level of WWO is excellent, the standard WWO has certain drawbacks such as convergence rate and calculation accuracy. To overcome the shortcoming of the WWO, various operations and improvements have been proposed to enhance the performance of search capacity by researchers. Four aspects are included in the improvement of WWO. (1) The theoretical research of WWO algorithm. (2) The performance of WWO algorithm is improved by modifying the main operations. (3) Hybrid WWO and other evolutionary algorithms are combined for the advantages of different algorithms. (4) WWO algorithm is applied to practical problems. The literatures are summarised as follows.

Various modified approaches have been introduced to strengthen the performance of WWO. A simplified version, named Sim-WWO, is proposed by Zheng and Bei (2015). In Sim-WWO, the refraction operator is removed in the case of ignoring the wave height. Meanwhile, population size reduction strategy is introduced to balance exploration and exploitation as well as partially compensate the weeding-out effect of the refraction operator. An improved version with variable population size (VC-WWO) is proposed by Zhang, Zhang, Zhang, and Zheng (2015). While the variable population size was introduced to VC-WWO, a comprehensive learning mechanism was used to increase the diversity of the solution in the refraction operator. A method of text feature selection based on WWO, named WWOTFS, is proposed by Chen, Hou, Luo, Hu, and Yan (2018). WWO is utilised to excavate the text feature selection rules. WWO-SM proposed by Zhao et al. (2017) is labelled as WWO to identify the unknown parameters for the IIR filter. An improved sine cosine WWO algorithm (SCWWO) that used elite opposition based is proposed by Zhang, Zhou, and Luo (2018) and to solve optimisation functions and structure engineering design problems. The performance of WWO is constantly improved after the WWO is proposed. However, there are still various problems in initialising the population, balancing the capabilities of exploration and exploitation, improving the convergence rate and calculation accuracy. Therefore, a new hybrid algorithm assisted by multiple strategies, named EWWO, is presented to address the premature convergence problem and calculation accuracy problem. In EWWO, the original population initialised has been modified by the opposition-based learning (OBL) (Mahdavi, Rahnamayan, & Deb, 2018) to maintain the diversity and stability of population. The modified propagation operation according to $DE/best/1$, named MPO, is presented to improve the capability of global search and crossover operator is used to increase. In the MPO, the wave length $\lambda$ is replaced by the mutation factor $F$ to control the different step size of the population. In the new breaking operator, the identical mutation strategy as MPO is applied to generate the current population and strengthen the diversity of population. CMA-ES (Hansen & Hansen, 2006 ) is a novel evolutionary optimisation strategy and the covariance matrix adaptation has a function of storing and learning from the historical optimal information. Therefore, the covariance matrix adaptation, as a local search strategy, is introduced into WWO and the refraction operation is replaced by updating the covariance matrix adaptation to learn from the information of historical water wave optimal and enhance local search while avoiding local optimisation. In addition, another purpose of the all operators is adopted to improve the convergence rate of the proposed algorithm. In general, EWWO has better performance than the state-of-the-art variants of WWO by testifying on the CEC 2017 benchmark functions with 10, 30, 50 and 100 dimensions. In this paper, the novel methodology and mechanisms are presented and the contributions are summarised as follows.

• The random opposition-based learning (ROBL) mechanism is introduced to initialise the population, maintain the diversity and stability of population and increase the high probability of finding the optimal solution.

• A modified propagation operation, which is referred to as $DE/best/1$, named MPO, is proposed to enhance the capability of the global search. The difference step is controlled by the wave length $\lambda$ rather than the mutation factor $F$.

• According to the disadvantages of WWO in convergence rate and calculation accuracy, the refraction operation is replaced by the covariance matrix adaptation to improve the local search.

• The convergence of the proposed algorithm is analysed by the iterative methods.

The remainder of the paper is organised as follows. A brief background material is given in Section 2. The proposed algorithm is described in Section 3. In Section 4, the DOE, the operation analysis, the experimental results and comparisons are analysed. A conclusion is given in Section 5.

2. Background materials

The notation used in this paper is summarised as follows.

$n$	=	population size
$L(d)$	=	the length of the $d\text{th}$ dimension of the search space ($1\le d\le n$)
$\lambda$	=	wavelength $\lambda \in {\mathbb{R}}^{+}$
$h$	=	a “wave” has a height (or amplitude)
$\alpha$	=	the wavelength reduction coefficient
$ϵ$	=	a very small positive number to avoid division-by-zero
$x^{\ast }$	=	the best solution found so far
$k$	=	a random number between 1 and a predefined number $k_{max}$
$\beta$	=	the breaking coefficient
$nfes$	=	the maximum fitness evaluations of the algorithm.
${\mu }_{cov}$	=	parameter for weighting between rank-one and rank-$\mu$ update
${\mu }_{eff}$	=	the variance effective selection mass
${\sigma }^g$	=	step-size, ${\sigma }^g\in {\mathbb{R}}_{+}$
$B\in {\mathbb{R}}^n$	=	an orthogonal matrix
$C^{(g)}\in {\mathbb{R}}^{n\times n}$	=	covariance matrix at generation $g$
$c_{ii}$	=	diagonal elements of $C$
$c_c\le 1$	=	learning rate for cumulation for the rank-one update of the covariance matrix
$c_1\le 1$	=	learning rate for the rank-one update of the covariance matrix update
$c_{\mu }\le 1$	=	learning rate for the rank-$\mu$ update of the covariance matrix update
$c_{\sigma }<1$	=	learning rate for the cumulation for the step-size control
$D\in {\mathbb{R}}^n$	=	a diagonal matrix
$d_{\sigma }\approx 1$	=	damping parameter for step-size update
$E$	=	expectation value
$g\in {\mathbb{N}}_0$	=	generation counter, iteration number
$I\in {\mathbb{R}}^{n\times n}$	=	identity matrix, unity matrix
$m^{(g)}\in {\mathbb{R}}^n$	=	mean value of the search distribution at generation $g$
$p\in {\mathbb{R}}^n$	=	evolution path
$w_i$	=	where $i=1,\dots ,\mu$, recombination weights

2.1. Water wave optimisation

The WWO has the characteristics of simple algorithm framework, fewer control parameters and smaller population size. In the WWO, the initialised population is simulated into water waves in a shallow water wave model, which is similar to the solution in the solution space. Each wave has a wavelength $\lambda$ and a wave height $h$ which is initialised to a constant $h_{max}$. Three operations – propagation, breaking and refraction – are executed by WWO at each generation to gradually approach the global optimum. In the propagation operator, a new wave $x^{\mathrm{\prime }}$ is produced by shifting each dimension of the original wave $x$, and then the wavelength $\lambda$ of water wave $x$ is updated as follows. (1) $\begin{array}{rl}{x}^{\mathrm{\prime }}(d)& =x(d)+rand(-1,1)\cdot \lambda L(d)\end{array}$(1) (2) $\begin{array}{rl}\lambda & =\lambda \cdot {\alpha }^{-\frac{f(x)-f_{min}+ϵ}{f_{max}-f_{min}+ϵ}}\end{array}$(2) where $rand(-1,1)$ is a uniformly distributed random number fixed in [−1,1], and $L(d)$ is the length of the $d\text{th}$ dimension of the search space, $f_{max}$ and $f_{min}$ are the maximum and minimum fitness values, respectively, among the current population, $\alpha$ is the wavelength reduction coefficient. $ϵ$ is a tiny positive integer to avoid division-by-zero. To increase the diversity of population, the breaking operator performs a local search around the best solution $x^{\ast }$ to further enhance its quality. To be specific, $k$ dimensions are selected randomly (where $k$ is a random number between 1 and constant $k_{max}$), and a solitary wave $x^{\mathrm{\prime }}$ is generated at each dimension as follows. (3) $x^{\mathrm{\prime }}(d)=x(d)+N(0,1)\cdot \beta L(d)$(3) where $\beta$ is the breaking coefficient. When the wave height decreases to zero, the refraction operator is only performed by Equation (4) and the wavelength is set as ${\lambda }^{\mathrm{\prime }}=\lambda f(x)/f(x^{\mathrm{\prime }})$. Afterwards, the propagation, breaking and refraction are repeated until a termination criterion is satisfied. (4) $x^{\mathrm{\prime }}(d)=N\left(\frac{x^{\ast }(d)+x(d)}{2},\frac{|x^{\ast }(d)-x(d)|}{2}\right)$(4) where $x^{\ast }(d)$ is the best solution found so far, and $N(\mu ,\sigma )$ is a Gaussian random with mean $\mu$ and standard deviation $\sigma$.

As shown above, a desirable trade-off between exploration and exploitation for WWO is established by the three operators. In Section 3, the new operators are designed to satisfy the characteristics and requirements of the considered problem based on the idea of the original WWO algorithm.

2.2. Covariance matrix adaptation evolutionary strategy

The adaptive covariance matrix evolution strategy (CMA-ES) algorithm is a novel evolutionary algorithm proposed by Hansen, Müller, and Koumoutsakos (2014). CMA-ES is a stochastic evolutionary method that updates and samples population by covariance matrices and evolutionary paths to obtain optimal solutions. During each iteration, individuals are sampled in the Gaussian distribution, and a solution with a desirable fitness is selected to update individuals in the Gaussian distribution. CMA-ES has the characteristics of rotation invariance for solving non-separable and ill-conditioned optimisation problems. In addition, CMA-ES is performed well on complex optimisation problems.

The basic process of CMA-ES is divided into three parts: sampling and recombination, updating the step size control and covariance matrix adaptation. The $\lambda$ offsprings of generation $g+1$ are calculated by $x_i^{g+1}\sim N({\mathit{m}}^g,{({\mathit{\sigma }}^{\mathit{g}})}^2{\mathit{C}}^g),i=1,\dots ,\lambda$, where ${\mathit{m}}^g$ means the centre of mass of the selected individuals of generation $g$. ${\mathit{C}}^g$ represents the covariance matrix. ${\mathit{\sigma }}^{\mathit{g}}$ is the global step size. Evaluating the solutions, sort them by quality and find the best solution. According to the weighted recombination of the $\mu$ best solutions, the new mean is calculated by ${\mathit{m}}^{g+1}=\sum _{i=1}^{\mu }{w}_i\cdot {\mathit{x}}_{i:\lambda }^{g+1}$. Afterwards, the evolution path $p_{\sigma }$ is updated and applied to update the step size ${\sigma }^{g+1}$ according to Equation (5). (5) $p_{\sigma }^{g+1}\leftarrow (1-c_{\sigma })p_{\sigma }^g+\sqrt{c_{\sigma }(2-c_{\sigma }){\mu }_{eff}}{{\mathit{C}}^g}^{-\frac{1}{2}}\frac{m^{g+1}-m^g}{{\sigma }^g}$(5) where ${\mu }_{eff}$ is the variance effective selection mass, ${\mu }_{eff}={\left({\sum }_{i=1}^{\mu }{w}_i^2\right)}^{-1}$, $c_{\sigma }$ is a learning rate for the cumulation for the step-size control, $c_{\sigma }=(({\mu }_{eff}+2)/(dimension+{\mu }_{eff}+5))$. $p_{\sigma }^g$ obeys the Gaussian distribution, so does $p_{\sigma }^{g+1}$. Additionally, $||p_{\sigma }^{g+1}||$ is compared with $E||N(0,I)||$ to calculate the step size $\sigma$ as follows. (6) ${\sigma }^{g+1}\leftarrow {\sigma }^g\times \exp \left(\frac{c_{\sigma }}{d_{\sigma }}\left(\frac{||p_{\sigma }^{g+1}||}{E||N(0,I)||}\right)-1\right).$(6) where the $d_{\sigma }$ is a damping parameter for step-size update, $d_{\sigma }=1+2max\left(0,\sqrt{(({\mu }_{eff}-1)/(dimension+1))}-1\right)+c_{\sigma }$, $E||N(0,I)||$ is an expectation of the Euclidean norm of a $N(0,I)$ distributed random vector, $E||N(0,I)||=\sqrt{n}(1-(1/4{}^{\ast }n)+(1/21{}^{\ast }{n}^2))$. Finally, the covariance matrix adaptation is updated according to Equation (7). (7) $\begin{array}{rl}{\mathit{C}}^{g+1}& \leftarrow (1-c_1-c_{\mu }){\mathit{C}}^g+c_1(p_c^{g+1}{(p_c^{g+1})}^T)+\delta (h_{\sigma })C)\\ & +c_{\mu }\left(\frac{1}{{({\mathit{\sigma }}^{\mathit{g}})}^2}\right)\sum _{i=1}^{\mu }{w}_i({\mathit{x}}_{i:\lambda }^{g+1}-{\mathit{m}}^g)({\mathit{x}}_{i:\lambda }^{g+1}-{\mathit{m}}^g{)}^T\end{array}$(7) where $c_1$ is the learning rate for the rank-one update of the covariance matrix, $c_1=\frac{2}{{(dimension+1.3)}^2+{\mu }_{eff}}$. $c_{\mu }$ is the learning rate for the rank-$\mu$ update of the covariance matrix, $c_{\mu }=min\left(1-c_1,{\alpha }_{\mu }\left(\left({\mu }_{eff}-2+\frac{1}{{\mu }_{eff}}\right)/\left({(n+2)}^2+\frac{{\alpha }_{\mu }{\mu }_{eff}}{2}\right)\right)\right)\text{ with }{\alpha }_{\mu }=2$. $\delta (h_{\sigma })$ is of minor relevance, $\delta (h_{\sigma })=(1-h_{\sigma })c_c(2-c_c)\le 1$, $p_c^g$ is another evolution path, which is updated according to Equation (8). It is worth noting that two methods named rank-$\mu$-update and rank-$\text{one}$-update are combined to enhance robust and rapid search in the updating of the covariance matrix adaptation. (8) $p_c^{g+1}=(1-c_c)p_c^g+\sqrt{c_c(2-c_c){\mu }_{eff}}\frac{m^{g+1}-m^g}{{\sigma }^g}$(8) where $c_c$ is a learning rate for cumulation for the rank-one update of the covariance matrix, $c_c=\left(\left(4+\frac{{\mu }_{eff}}{dimension}\right)/\left(dimension+4+\frac{2{\mu }_{eff}}{dimension}\right)\right)$. The property of the covariance matrix is determined by $p_c^{g+1}$.

2.3. Differential evolution

Differential Evolution (DE) is proposed by Storn and Price (1997) . DE, which is the same as other evolutionary algorithms, is a stochastic model to simulate biological evolution and individuals who adapt to the environment are preserved through repeated iterations. The DE is mainly used to solve the global optimisation problem of continuous variables and the main steps are basically mutation, crossover and selection. DE is to retain desirable individuals, eliminate inferior individuals and guide the search process to the global optimal solution through continuous iterative calculation. Researchers have proposed various different strategies to improve the mutation operation. Five different mutation schemes, including $DE/rand/1$ and $DE/best/1$, are suggested by Swagatam Das, Mullick, and Suganthan (2016). (9) $\begin{array}{rl}{}^{″}DE/rand/1^{″}:V_{i,G}& =X_{r_1^i,G}+F{}^{\ast }(X_{r_2^i,G}-X_{r_3^i,G})\end{array}$(9) (10) $\begin{array}{rl}{}^{″}DE/best/1^{″}:V_{i,G}& =X_{best,G}+F{}^{\ast }(X_{r_1^i,G}-X_{r_2^i,G})\end{array}$(10)

The indexes $r_1$, $r_2$, $r_3$ are mutually unequal integers which were randomly selected from the range $[1,n]$, the scaled factor $F$ is the mutation operator and the difference step size of the population individual is determined by $F$. $F$ with a small value will affect the difference among the individuals and make the algorithm fall into the local optimal. $F$ with a large value enhances the global search ability of the algorithm, which is beneficial to the search of the optimal solution; however, the convergence rate of the algorithm is affected by $F$ with a large value. $X_{i,G}$ is the current population and $X_{best,G}$ is the best individual with the best fitness in the population at generation $G$. In this paper, the propagation operator is assisted by the $DE/best/1$ to trade off the exploration and exploitation.

3. The proposed algorithm

3.1. Initialise population

In various evolutionary algorithms, the population is initialised using a stochastic strategy, and the population generated by the stochastic strategy is said to undesired in the quality of the final result and the convergence rate of the population. The populations are generated by the original WWO in the search space, which leads to the unpredictability of the convergence of the algorithm. The opposition-based learning (OBL) (Xu, Wang, Wang, Hei, & Zhao, 2014) has been proved an effective way to initialise population in optimisation problem. Given the solution $X$ for a set of problem evaluation, each individual in $x_i$ has a reverse individual ${x_i}^{\mathrm{\prime }}$, the probability that the individual and the reverse individual are closer to the optimal individual is 50%. The closer individual is selected as the initial individual of the solution $X$ and the individual in the population is close to the optimal solution. It is assumed that the opposite solution for $X$ obtained a desirable solution $X^{\mathrm{\prime }}$, the distance between $X$ and the best solution $X^{\mathrm{\prime }}$ is reduced. 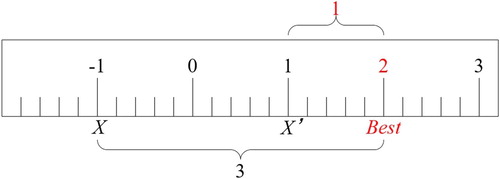Namely, the opposite solution $X^{\mathrm{\prime }}$ is closer to the best solution. An example is shown in Figure 1, 2 is the best solution, −1 is an individual and its reverse individual is 1, the distance between −1 and 2 is 3, while the distance from 1 to 2 is 1. Therefore, the reverse individual is closer to the optimal. The details of the OBL are shown in Algorithm 1.

Figure 1. The distance among $X$, $X^{\mathrm{\prime }}$ and the best solution.

Assuming $X(x_1,x_2\dots x_i)$ is the solution in the search range, the opposite solution $X^{\mathrm{\prime }}({x_1}^{\mathrm{\prime }},{x_2}^{\mathrm{\prime }}\dots {x_j}^{\mathrm{\prime }})$ is calculated as follows. (11) $\{\begin{array}{l}{x}_j=l{b}_j+rand\ast (u{b}_j-l{b}_j)\\ {x_j}^{\mathrm{\prime }}=(a_j+b_j)/2-x_j\end{array}$(11) where $a$ is the lower bound $b$ is the upper bound of the search range.

After initialising population, the LSHAED-SPACMA algorithm is introduced before the propagation operation to more effectively help the propagation operation find the global optimal solution in this range, and improve the exploration ability and performance of the proposed algorithm (The role of LSHAED-SPACMA algorithm (Mohamed, Hadi, Fattouh, & Jambi, 2017) is to improve the global search, please refer to the literature for details.).

Table

Algorithm 1 Initialisation
1	Input $n$, $D$, $UpperandLowerbounds$, $fun{c}_{-}num$
2	for $i=1to\mathit{n}\mathbf{d}\mathbf{o}$
3	for $j=1to\mathit{D}\mathbf{d}\mathbf{o}$
4	Generate population according to Equation (11);
5	End
6	Calculate fitness value;
7	if $f(x^{\mathrm{\prime }})<f(x)$
8	Update $x$ with $x^{\mathrm{\prime }}$;
9	end
10	End
11	Output $x$;

3.2. The modified propagation operator

The propagation operation is executed after the population is initialised and a global search within the specified search range. The position of the new water wave $x^{\mathrm{\prime }}$ is calculated according to Equation (1) to balance the global exploration and local exploitation. The disadvantage of WWO is that the undesirable search accuracy leads to the solution found is deviated from the global optimal solution. Therefore, the mutation strategy of DE is introduced to give the water wave a vector that propagates in a better direction to find the optimal solution. Several mutation strategies of DE are widely applied in evolutionary algorithms and each mutation strategy has its advantages and disadvantages. The $DE/best/1$ is frequently appeared in numerous literatures. The difference step size of the population is determined by the mutation operator $F$. However, the difference step size of the population is controlled by the wave length $\lambda$ in the proposed algorithm. The reason is that the greater the fitness value, the shorter the wavelength and the smaller the corresponding propagation range. Not only that the breaking is closely related to the wave length reduction. Thus, the wave length is applied to control the influence of the difference vector. Meanwhile, a random variable named $X_{better}^{(g)}$ (“better” represents “better solutions in terms of probability”) (He & Zhou, 2017) is generated for each individual $x$ by sampling the Gaussian distribution $N(m^g,C^g)$. Furthermore, $X_{better}^{(g)}$ is applied to guide the search direction of $x^{\mathrm{\prime }}(d)$ to enhance the exploration. Combined with Equations (13) and (14), the modified propagation operation is applied to assist the proposed algorithm. (12) $\begin{array}{rl}& X_{better}^{(g)}\sim N(m^g,C^g)\end{array}$(12) (13) $\begin{array}{rl}& V_i^{(g)}=X_{better}^{(g)}+{\lambda }^{\ast }(X_{r1}^{(g)}-X_{r2}^{(g)})\end{array}$(13) (14) $\begin{array}{rl}& x^{\mathrm{\prime }}(d)=x(d)+rand(-1,1{)}^{\ast }\lambda L(d{)}^{\ast }{V}_i^{(g)}\end{array}$(14) (15) $\begin{array}{rl}& \alpha ={\alpha }_{max}-({\alpha }_{max}-{\alpha }_{min}{)}^{\ast }nfe/nfes\end{array}$(15) where $V_i^{(g)}$ is a mutation population, $\lambda$ is wavelength, $X_{better}^{(g)}$ is the current better solution, ${\alpha }_{max}$ is the maximum and ${\alpha }_{min}$ is the minimum wavelength reduction coefficient, ${\alpha }_{max}=1.01$, ${\alpha }_{min}=1.001$.

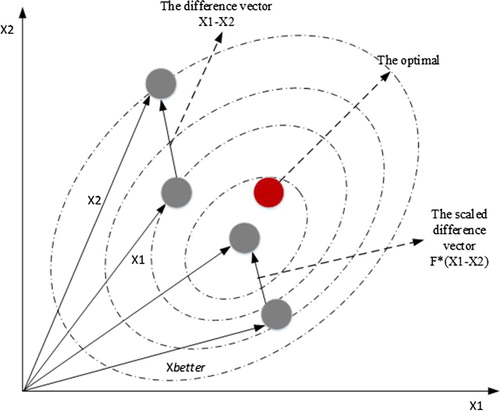
The process of the mutation strategy is illustrated in Figure 2.

Figure 2. The modified mutation scheme.

3.3. The modified breaking operator

In original WWO, the individual $x^{\mathrm{\prime }}$ which is generated by propagation operator is to find global optimal. However, the global optimal solution found in this way is relatively random. Although the optimal solution is found in the population via the change of the wavelength to a certain extent, the direction of finding the optimal solution is uncertain. Therefore, this problem is solved by proposing the mutation-propagating individuals., Let the population find the position which is closer to the optimal solution through the variable wavelength based on the original propagation according to Equation (1). In each iteration, a mutation propagation individual is approached toward the optimal solution according to Equation (13). After the modified propagation operator, the population for the breaking operation is determined by a crossover operator. The breaking operation is performed by WWO to find the optimal solution $x^{\ast }$. In this paper, the identical mutation strategy, as the propagation operator, is applied in a modified breaking operator. The specific method is each solitary wave $x^{\mathrm{\prime }}$ of $x$ is obtained by randomly selecting $k$ dimensions (where $k$ is a random number between 1 and a predefined number $k_{max}$) and adding variation (The variation is obtained by the mutation strategy mentioned in section 3.2) to the original position at each dimension $d$. A new solitary wave $x^{\mathrm{\prime }}$ is generated in the search space according to Equation (16). (16) $\begin{array}{rl}{x}^{\mathrm{\prime }}(d)& =x(d)+N(0,1{)}^{\ast }{\beta }^{\ast }L(d{)}^{\ast }{V}_i^{(g)}\end{array}$(16) (17) $\begin{array}{rl}\beta & ={\beta }_{max}-({\beta }_{max}-{\beta }_{min}{)}^{\ast }nfe/nfes\end{array}$(17) where $\beta$ is the breaking coefficient, and $N(0,1)$ is a Gaussian random number with mean 0 and standard deviation 1, $V_i^{(g)}$ is the mutation population.

3.4. Local search strategy

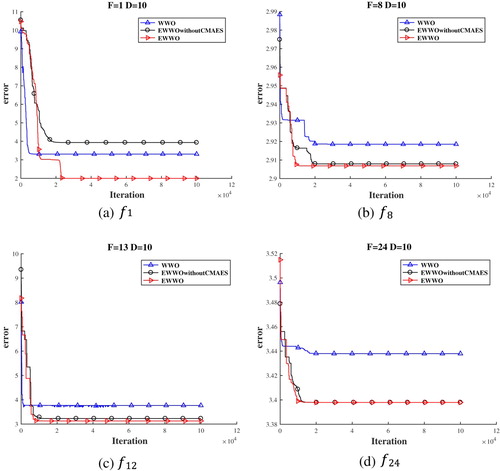
The refraction operator is to avoid search stagnation, escape the local optimum and enhance the diversity of the population. When the water wave height is reduced to 0, the WWO tends to fall into the local optimal solution. At this time, the algorithm has escaped the local optimum by the refraction operation. After the propagation operator and the breaking operator are performed, the fitness values of the population remain unchanged and the local search strategy is executed to help the algorithm escape the local optimum, the newly generated water wave continuously approaches the optimal water wave. However, the risk of premature convergence is increased by the refraction operator. Therefore, CMA-ES is employed to reduce the complexity of the algorithm and improve the search ability of the algorithm. The detailed process is as follows. Assume that the wave height is ignored. When the global optimal solution is updated after the breaking operator, the covariance matrix adaptation is applied as a local search strategy for adaptive adjustment and self-learning. As a well-performing evolutionary algorithm, the covariance matrix adaptation shows desirable results in medium-scale complex optimisation problems, such as non-separable, ill-conditioned or rugged and multi-modal. Meanwhile, CMA-ES has a desirable ability of convergence. In this paper, the covariance matrix adaptation, as a local search strategy, helps EWWO to escape the local optimum by storing the information of the historical optimal solution in the covariance matrix and continuously updating the covariance matrix adaptation to learn from the historical optimal solution. The optimal solution is found by the individuals in the population along the direction in which the covariance matrix is updated. In addition, in order to verify the impact of the covariance matrix adaptation on EWWO, in this section, the original WWO has been compared with the EWWO without a local search strategy CMA-ES and the proposed EWWO on 10D. The three algorithms are testified on the CEC2017 benchmark problem set (The detailed of the CEC2017 benchmark is described in Section 4). As seen in Figure 3, EWWO has better convergence speed and convergence accuracy than the original WWO and EWWO without CMA-ES. From Figure 3(a), EWWO falls into the local optimum after the new breaking operator is executed. Afterwards, EWWO is disturbed by the covariance matrix adaptation to escape the local optimum. Compared with EWWO without CMA-ES, the convergence speed and convergence accuracy of EWWO are improved in other three.

Figure 3. Convergence plots of EWWO, WWO and EWWO without CMA-ES on some typical benchmark functions (10D).

3.5. Pseudocode of EWWO

With the above-detailed description, the pseudocode of the EWWO is illustrated in Algorithm 2.

According to the pseudocode, it is clear that a new mutation strategy and the covariance matrix adaptation work together to balance the exploration and exploitation of the EWWO. However, it is not a mere mix of the two algorithms. After the initialisation of the population, the propagation operation is executed to control the global exploration, where the new individuals are generated by sampling a Gaussian distribution $N(m^g,C^g)$ and a mutation strategy combined with the wavelength $\lambda$, the global exploration is stressed. To ensure that the diversity of the population is not destroyed, the identical mutation strategy is applied into the breaking operation. At the moment, the algorithm is easy to fall into local exploitation and the covariance matrix adaptation is introduced to address the problem. Since the CMA-ES has the ability of self-learning and the covariance matrix is updated to control the current population and learn from the history optimal solution to enhance the local exploitation. Furthermore, by balancing the global exploration and the local exploitation, EWWO is testified on the CEC2017 benchmark test functions and expected to solve the practical problems.

Table

Algorithm 2 The proposed EWWO algorithm.
1	Initialize a population P of $\mathit{n}$. solutions(waves) according to Algorithm 1;
2	Initialize parameters;
3	Initialize CMAES parameters;
4	Initialize WWO parameters;
5	while stop criterion is not satisfied do
6	Global Search based on LSHADE-SPACMA
7	for each wave $X\in P\mathbf{d}\mathbf{o}$.
8	Generate a mutation population according to Equations (12) and (13);
9	Propagate $X$ to a new $X^{\mathrm{\prime }}$ according to Equation (14);
10	if $f(X^{\mathrm{\prime }})>f(X)\mathit{t}\mathit{h}\mathit{e}\mathit{n}$
11	Crossover Operation;
12	if $f(X^{\mathrm{\prime }})>f$($X_{best}$) $\mathit{t}\mathit{h}\mathit{e}\mathit{n}$
13	Break $X^{\mathrm{\prime }}$ into new waves according to Equation (16);
14	Update $X_{best}$ with $X^{\mathrm{\prime }}$;
15	Replace $X$ with $X^{\mathrm{\prime }}$;
16	end
17	end
18	calculate ${\mathit{m}}^{g+1},{\mathit{C}}^{g+1}$ according to Equation (7)
19	Update the wavelengths according to Equation (2);
20	Update $\alpha$ according to Equation (15);
21	Update $\beta$ according to Equation (17);
22	Return the best solution found so far.

3.6. Complexity analysis

A set of fitness evaluations and iterations are given to generally calculate the time complexity of an EA (Ren, Zhang, Wen, & Feng, 2013) by an analysing the extra time in each generation. However, the time of function evaluations is not considered. In this paper, the population size and the dimension of problem are denoted as $N$ and $D$, respectively. In terms of initialisation population evolution, the time complexity is $O(N^{\ast }D)$, which are obtained by lines 2–10 in Algorithm 3. From Algorithm 4, it takes $O(N\ast \text{log}(N))$ to execute the LSHADE-SPACMA at each generation in line 6. During the update of the propagation and breaking operations, $O(N^{\ast }D)$ (lines 7–17) is taken to generate the next generation. In addition, the time complexity of the CMA-ES, which is analysed by Hansen et al. (2014), is reduced from $O(N^2)$ to $O(N)$ (line 18). Furthermore, the update of all parameters takes $3^{\ast }O(N)$. Therefore, the overall time complexity of EWWO is $O(N^{\ast }D+N^{\ast }\text{ log}(N))$.

3.7. Convergence analysis of EWWO

In general, the analysis of the convergence of evolutionary algorithms helps to understand the algorithm and guide the improvement of the algorithm. The convergence of evolutionary algorithms mainly refers to whether the algorithm finally searches for and retains the global optimal solution of the problem under the condition that the iteration time or algebra tends to infinity, or whether the individual in the whole population become global optimal according to Zhang and Muhlenbein (2004) In this paper, the iterative method (Argyros, Behl, Machado, & Alshomrani, 2019) is introduced to analyse the convergence of EWWO. The itterative method adopted an initial hypothesis value to generate a sequence of approximate solutions for a set of problems, if the corresponding sequence converges for given initial approximations, the iterative method is a convergent process.

Theorem 3.1.

$\underset{k\to \mathrm{\infty }}{lim}{A}_k=A\iff \text{for }\mathrm{\forall }x\in R^n,\underset{k\to \mathrm{\infty }}{lim}{A}_{k}x=Ax$.

Theorem 3.2:

Suppose that $\text{B}=(b_{ij})\in R^{n^{\ast }n}$. Then, the necessary and sufficient condition for $\underset{k\to \mathrm{\infty }}{lim}{B}^k=0$ is the spectral radius of the matrix $B$, $\rho (B)<1$.

Theorem 3:

Suppose that $x=B^{\ast }x+f$ is a system of equation and its first-order linear stationary iteration method is $x^{(k+1)}=B^{\ast }{x}^{(k)}+f$. For the arbitrarily selected initial vectors $x^{(0)}$, the necessary and sufficient condition for convergence of the iteration method is the spectral radius of the matrix $B$, $\rho (B)<1$.

Proof:

(1) Sufficiency. Let the exact solution is $x^{\ast }=B^{\ast }{x}^{\ast }+f$, the error vector is ${\epsilon }^k$. (18) $\begin{array}{rl}{\epsilon }^{(k)}& =x^{(k)}-x^{\ast }=B^{\ast }{\epsilon }^{(0)}\\ {\epsilon }^{(0)}& =x^{(0)}-x^{\ast }\end{array}$(18) Let $\rho (B)<1$, according to Theorem 3.2, $\underset{k\to \mathrm{\infty }}{lim}{B}^k=0$, then,$\underset{k\to \mathrm{\infty }}{lim}{\epsilon }^k=0$ for $\mathrm{\exists }{x}^{(0)}$, namely, $\underset{k\to \mathrm{\infty }}{lim}{x}^{(k)}=x^{\ast }$. (2) Necessity. $\underset{k\to \mathrm{\infty }}{lim}{x}^{(k)}=x^{\ast }$ for $\mathrm{\exists }{x}^{(0)}$, $x^{k+1}=B^{\ast }{x}^k+f$. It is obvious that the limit $x^{\ast }$ is the solution of equation set and for $\mathrm{\exists }{x}^{(0)}$, ${\epsilon }^{(k)}=x^{(k)}-x^{\ast }=B^{\ast }{\epsilon }^{(0)}\to 0(k\to \mathrm{\infty }).$ According to Theorem 3.1 and Theorem 3.2, $\rho (B)<1$.

The convergence analysis of the EWWO is analysed by the iterative method. It has proved that any individual in WWO converges in two special cases by simplifying the target problem and parameter settings in the literature (Zheng & Zheng, 2016). (1) Propagation operator is only performed. (2) Refraction operator is only performed. However, refraction operator has been removed in this paper, only the MPO is performed and analysed. Based on the basic process of the WWO, the position of the water wave $X$ is affected by its wavelength $\alpha$, and the change of wavelength $\alpha$ is related to the fitness of the water wave $X$. Let $k$ denote the iteration number of EWWO, $L=L(d)$, $r$ is a random number. Equations (2) and (17) are expressed as follows. (19) $\begin{array}{rl}X(k+1)& =r^{\ast }\lambda (k{)}^{\ast }L(d{)}^{\ast }V(k)+X(k)\end{array}$(19) (20) $\begin{array}{rl}\lambda (k)& =\lambda (k-1{)}^{\ast }{\alpha }^{-\left(\frac{(f(X(k-1))-f_{min}(X(k-1))+ϵ)}{(f_{max}(X(k-1))-f_{min}(X(k-1))+ϵ)}\right)}\end{array}$(20) Equation (23) is described as follows. (21) $\begin{array}{rl}\lambda (k-1)& =\lambda (k-2{)}^{\ast }{\alpha }^{-\left(\frac{(f(X(k-2))-f_{min}(X(k-2))+ϵ)}{(f_{max}(X(k-2))-f_{min}(X(k-2))+ϵ)}\right)}\end{array}$(21) (22) $\begin{array}{rl}\lambda (k)& =\lambda (k-2{)}^{\ast }{\alpha }^{-\left(\frac{(f(X(k-2))-f_{min}(X(k-2))+ϵ)}{(f_{max}(X(k-2))-f_{min}(X(k-2))+ϵ)}\right)}{}^{\ast }{\alpha }^{-\left(\frac{(f(X(k-1))-f_{min}(X(k-1))+ϵ)}{(f_{max}(X(k-1))-f_{min}(X(k-1))+ϵ)}\right)}\end{array}$(22) And so forth, (23) $\lambda (1)=\lambda (0{)}^{\ast }{\alpha }^{-\sum _{i=0}^{k-1}-\left(\frac{(f(X(i))-f_{min}(X(i))+ϵ)}{(f_{max}(X(i))-f_{min}(X(i))+ϵ)}\right)}$(23) Let $f$ represent the exponential term $\sum _{i=0}^{k-1}-\left(\frac{(f(X(i))-f_{min}(X(i))+ϵ)}{(f_{max}(X(i))-f_{min}(X(i))+ϵ)}\right)$ and $\overline{f}$ representsthe mean value of $f.$

Equation (23) is described as follows. (24) $\lambda (k)=\lambda (0{)}^{\ast }{\alpha }^{-k\ast \overline{f}}$(24) At this time, the propagation formula is described as follows. (25) $X(k+1)=r^{\ast }\lambda (0{)}^{\ast }{{\alpha }^{-k\ast \overline{f}}}^{\ast }L(d{)}^{\ast }V(k)+X(k)$(25) where $\lambda (0)=0.5$.

Assuming in the $i$ iteration, if $f(X(i))=f_{min}(X(i))$, $(((f(X(i))-f_{min}(X(i))+ϵ))/((f_{max}(X(i))-f_{min}(X(i))+ϵ)))=0$. If $f(X(i))=f_{max}(X(i))$, $(((f(X(i))-f_{min}(X(i))+ϵ))/((f_{max}(X(i))-f_{min}(X(i))+ϵ)))=1.$ If $f_{min}(X(i))<f(X(i))<f_{max}(X(i))$, $0<(((f(X(i))-f_{min}(X(i))+ϵ))/((f_{max}(X(i))-f_{min}(X(i))+ϵ)))\frac{}{}<1$. Therefore, $0<\overline{f}<1$. When $k\to \mathrm{\infty }$, $\underset{k\to \mathrm{\infty }}{lim}X(k+1)=X(k)$, namely, the position of the water wave no longer changes with time and the EWWO iteratively converges.

4. The experiment and comparisons

In this section, EWWO is evaluated on the CEC 2017 benchmark problem set and compared with the standard WWO algorithm, three state-of-the-art variant algorithms of the WWO and CMA-ES. The compared algorithms are listed as follows. WWO (Zheng, 2015), MWWO (Soltanian, Derakhshan, & Soleimanpour, 2018), SCWWO (Zhang et al., 2018), Sim-WWO (Zheng & Bei, 2015), CMA-ES (Zheng & Bei, 2015). All the parameter settings are shown in Table 1. The benchmark problem set is divided into four classes: Unimodal Functions ($f_1-f_3$), Simple Multimodal Functions ($f_4-f_{10}$), Hybrid Functions ($f_{11}-f_{20}$) and Composition Functions ($f_{21}-f_{30}$). More details for a description of the benchmark functions are found in the literature (Awad, Ali, Liang, Qu, & Suganthan, 2016). The EWWO was coded using MATLAB. Section 4.1 describes the experimental condition when the simulation is run. Section 4.2 discusses the experimental results on 30 benchmark test functions in IEEE CEC2017. The experimental results of EWWO with some state-of-the-art proposed algorithms are described in Section 4.3. It is necessary to point out that according to the evaluation criteria of CEC2017, $f_2$ has been excluded because it shows unstable behaviour especially for higher dimensions, and significant performance variations for the same algorithm implemented in MATLAB. The simulation experiments were implemented on a personal computer (PC) with Intel (R) Core (TM) i7-6700 CPU 3.4GHz and 8.00GB memory with a windows Server 2012 OS. The maximum number of fitness evaluations ($nfes$) is set to $Dimensio{n}^{\ast }10000$ for each algorithm on the problems to ensure a fair comparison. A brief description of compared algorithms is as follows.

• MWWO is a modified variant of WWO, which is a new kind of exploration parameter to increase the exploration ability of algorithm and uses an exponential adaptive $\alpha$ strategy.

• SCWWO is the sine cosine algorithm combined with WWO. Additionally, the elite opposition-based learning strategy is introduced into the refraction operation to improve the diversity of the population and enhance the exploration capability of WWO.

• Sim-WWO is a simplified version of WWO by removing the refraction operation and introducing a population size reduction strategy to balance exploration and exploitation.

• CMA-ES is an evolutionary method that updates and samples population by covariance matrix and evolutionary paths to obtain optimal solutions. The detailed parameter setting is referred to the literature according to Section 2.2.

Table 1. Parameter settings of competitive algorithms.

Algorithm	Parameter Setting
WWO	$\begin{array}{c}n=Dimension,\alpha =1.0026,\beta =[0.001,0.25],h_{max}=12,\lambda =0.5\\ \epsilon =0.00000001,k_{max}=\text{min}(12,Dimension/2)\end{array}$
MWWO	$\begin{array}{c}n=Dimension,\alpha =1.0026,\beta =[0.001,0.25],h_{max}=12,\epsilon =0.00000001,\lambda =0.5\\ k_{max}=\text{min}(6,Dimension/2)\end{array}$
SCWWO	$\begin{array}{c}n=Dimension,\text{constant}=2,\alpha =1.0026,\beta =[0.01,0.25],h_{max}=12,\epsilon =0.00000001,\lambda =0.5\\ k_{max}=min\left(12,\frac{Dimension}{2}\right),\text{random number }{r}_2=[0,2\pi ],r_3=[-2,2],\\ r_4=[0,1]\end{array}$
Sim-WWO	$\begin{array}{c}n=[6,Dimension],\alpha =1.0026,\beta =[0.001,0.25],h_{max}=12,\lambda =0.5\\ \epsilon =0.00000001,k_{max}=\text{min}(6,Dimension/2)\end{array}$
CMA-ES	$n=Dimension,xmean=rand(n,1),\sigma =0.5,\lambda =4+floor(3\ast \log (n)),\mu =ceil\left(\frac{\lambda -1}{2}\right)$, $cc=\frac{4}{n+4},cs=\frac{m\mu +2}{m\mu +n+3},eigeneval=0$

4.1. Parameters analysis

The parameters have important influence on the performance of stochastic algorithms, whereas it is difficult to exactly determine their values. Therefore, the goal of the parameter control is to trace desirable parameter values during the optimisation procedure. In this paper, the design of experiments method (DOE) (Montgomery, 2006) is adopted to calibrate the parameters of EWWO. There are five critical parameters to analyse according to the description of EWWO in Section 3. $CrMean$ (the crossed factor), $\alpha$ (the wavelength reduction coefficient), $\beta$ (the breaking reduction coefficient), $pc$ (which solutions is utilised in updating the population distribution is determined by $pc$) and $k_{max}$ (search accuracy is determined by $k_{max}$). In this paper, parameter adaptation is applied to adjust the two parameters $\alpha$ and $\beta$. A linear adaptive $\alpha$ strategy is updated as follows. (26) $\alpha ={\alpha }_{max}-({\alpha }_{max}-{\alpha }_{min}{)}^{\ast }nfe/nfes$(26) where ${\alpha }_{max}$ is the maximum and ${\alpha }_{min}$ is the minimum wavelength reduction coefficient, ${\alpha }_{max}=1.01$, ${\alpha }_{min}=1.001$. $\alpha$ has a larger value to improve the performance of the global search in the exploration stage. $\beta$ linearly decreases from 0.01 to –0.001 according to the standard WWO as follows. (27) $\beta ={\beta }_{max}-({\beta }_{max}-{\beta }_{min}{)}^{\ast }nfe/nfes$(27) where ${\beta }_{max}$ is the maximum and ${\beta }_{min}$ is the minimum breaking reduction coefficient.

For the remaining three parameters, a full factorial design is considered where the different choices for the five parameters are considered. The choice of each parameter is as follows. $CrMean\in \{0.3,0.5,0.9\}$, $pc\in \{0.8,0.5,0.3,0.1\}$, $k_{max}\in \{24,12,6\}$. All the possible combinations of the three parameters is in total of $3^{\ast }{4}^{\ast }3=36$. The experimental results are analysed by means of a multifactor analysis of variance (ANOVA) according to the literatures (Shao, Pi, & Shao, 2018). The importance of the interaction between parameters is illustrated by the ANOVA. The $F-ratio$ in ANOVA is an indicator of significance when the $p-value<0.05$. 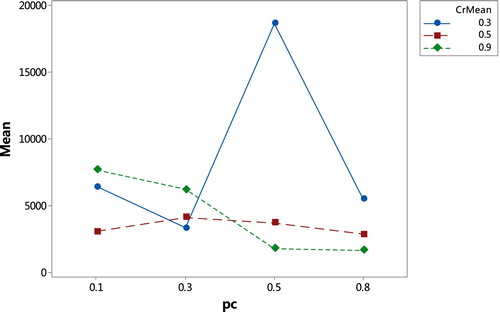The ANOVA results of parameter calibration are shown as Table 2.

Table 2. The experimental result of the ANOVA on parameter calibration of EWWO.

Source	Sum of squares	Degrees of freedom	Mean Square	$F-ratio$	$p-value$
$CrMean$	1.73292e + 08	2	8.66459e + 07	3.94	0.0483
$pc$	1.09539e + 08	3	3.65131e + 07	1.66	0.2279
$kmax$	6.3155e + 07	2	3.15775e + 07	1.44	0.2758
$CrMean\ast pc$	4.10261e + 08	6	6.83768e + 07	3.11	0.0447
$CrMean\ast kmax$	1.22748e + 08	4	3.06871e + 07	1.4	0.2935
$pc\ast kmax$	1.0481e + 08	6	1.74684e + 07	0.79	0.5916
Residual	2.63772e + 08	12	2.1981e + 07
Total	1.24758e + 09	35

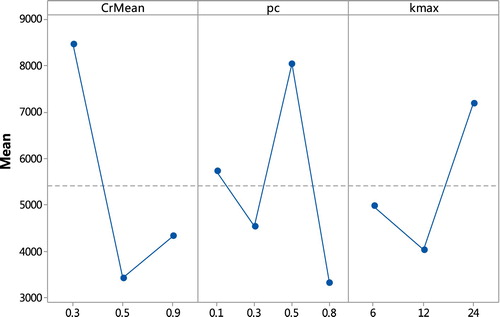
As shown in Table 2, the maximal $F-ratio$ corresponds to $CrMean$. It suggests that the $CrMean$ has the most important effect over the average performance of EWWO among the considered factors. According to the main effect plot of parameters in Figure 4, the choice of $CrMean=0.5$ is better than other candidates. The diversity of population evolution and the convergence rate of population are affected by the value of $CrMean$. From Figure 4, the diversity of population is enhanced, but the algorithm is easy to premature convergence when $CrMean=0.3$. When $CrMean=0.9$, the exploitation is improved, while the diversity of population is destroyed. However, the main effect plot is not comprehensive if there are significant interactions among the parameters. The interaction between $CrMean$ and $pc$ explains that $CrMean=0.5$ is the best choice on the basis of Figure 5.

Figure 4. Main effect plot of parameters.

Figure 5. Interaction plot for significant combination of parameters.

The second biggest $F-ratio$ corresponds to $CrMea{n}^{\ast }pc$. It has demonstrated that the interactions between the crossed factor $CrMean$ and the updating rate $pc$ are significant. In addition, $CrMea{n}^{\ast }pc$ interaction is significant as the $p-value$ is less than 0.05. $CrMean=0.9$ and $pc=0.8$ lead to the best performance of EWWO according to Figure 5. However, in order to maintain the diversity of population and balance the exploration and exploitation, the role of $CrMean=0.5$ is important according to Figure 4.

To sum up, the values of the parameters are determined to apply in the EWWO. $CrMean=0.5$, $pc=0.8$ and $k_{max}=12$.

4.2. Operator analysis

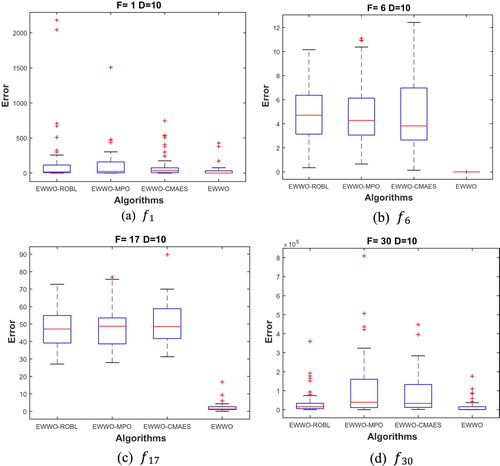
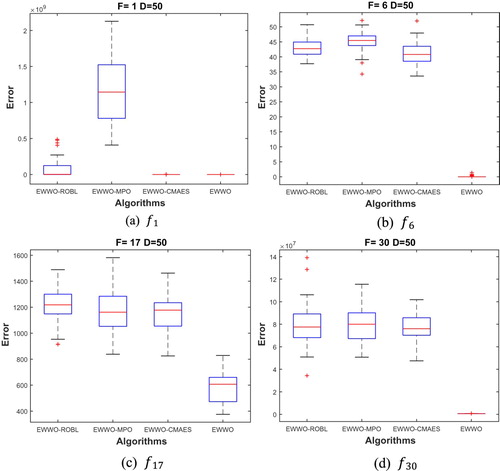
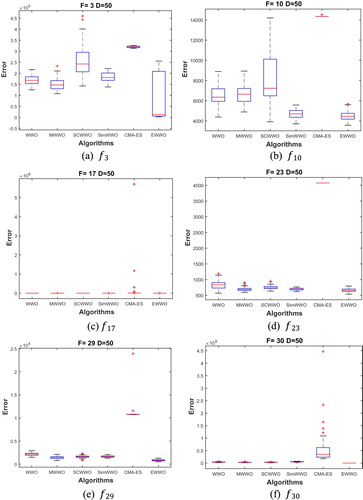
In this section, EWWO is compared with EWWO without random OBL (EWWO-ROBL), EWWO without the MPO (EWWO-MPO) and EWWO without the covariance matrix adaptation (EWWO-CMAES) to verify the impact of each strategy on the proposed algorithm. The average results of EWWO, EWWO-ROBL, EWWO-MPO and EWWO-CMAES on 10 and 50 dimensions are testified on the CEC2017 test suite (Awad et al., 2016) and the stability of each category is shown with boxplots. The effectiveness of each strategy is demonstrated by experimental results. The proposed algorithm is superior to EWWO-ROBL, EWWO-MPO and EWWO-CMAES in high- and low-dimensional functions. The performance of the multiple strategy algorithm is better than the single strategy algorithm owing to the difference of the landscape of each function and the diversity. The boxplots of certain typical benchmark functions for each strategy on 10 and 50 dimensions are shown in Figures 6 and 7, respectively, the stability of EWWO is stronger than EWWO-ROBL, EWWO-MPO and EWWO-CMAES, namely, the combination of the three operations contributes to enhance the stability of EWWO.

Figure 6. Boxplots of some typical benchmark functions for each strategy on each category. (10D).

Figure 7. Boxplots of some typical benchmark functions for each strategy on each category. (50D).

4.3. Experimental analysis and result

In order to evaluate the performance of the proposed EWWO, four groups of the simulations are executed on 10, 30, 50 and 100 dimensions over the CEC2017 test suite, and five statistical metrics are calculated, that is Best, Worse, Median, Mean and Std (Awad et al., 2016). These metrics are used to analyse the performance of EWWO. The results of EWWO, including the mean error and standard deviation, for 100-dimensions are shown in Table 7. The results of 10, 30 and 50-dimensions are moved into the supplementary materials. The best value in each run is set to zero if the value is less than 10e-8 in this research. All experimental algorithms are run independently 51 times on each test problem, and Mean and Std metrics are calculated. The experimental results are depicted. The best result for each function is shown in boldface. For the evolution algorithms to solve CEC2017 benchmark functions is an immense challenge. With the dimensions increasing of functions, the optimisation problems become increasingly complicated. All the benchmark functions with $D=100$ are also executed to detect the stable of EWWO and the results of the five algorithms for $D=100$ are shown in Table 7, which show that the performance of EWWO is better than that of other variants of WWO on the most functions. EWWO significantly outperforms other variants of WWO with $D=100$ and the performance of EWWO increases with the dimension increased. The detailed analysis is as follows. As shown in Table 7, the EWWO performs desired results in simple multimodal functions from $f_5$, $f_6$, $f_8$ and $f_{10}$ for 100 dimensions. While for hybrid functions and composition functions from $f_{11}$, $f_{12}$, $f_{17}$ and $f_{20}$, the proposed algorithm achieves the optimal solution. For the remaining composition functions, EWWO shows an advantage from $f_{29}$ and $f_{30}$. In sum, the EWWO has obtained good results on the most of functions from low dimensions to high dimensions and EWWO outperforms other compared algorithms on the CEC 2017 benchmark especially on high-dimensional functions.

The statistical tests show that EWWO has a significant improvement than the compared algorithms to testify the performance of the EWWO. The Wilcoxon’s test (García, Molina, Lozano, & Herrera, 2009), which compares the algorithms in pairs, is introduced to detect the significant difference between EWWO and other algorithms. Tables 3–6 show the statistical analysis result of the Wilcoxon’s test between EWWO and other variants of WWO on the functions with different dimensions, considering EWWO as a control algorithm. If EWWO is significantly better than the compared algorithm with a confidence level, the test results are marked in boldface. 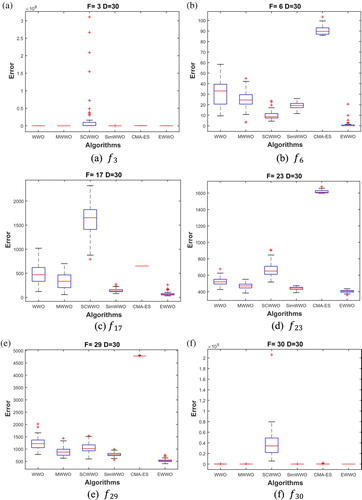In Tables 3–6, $R+$ is the sum of the rank that EWWO outperforms than another algorithm in the current row, and $R-$ is the sum of the levels that EWWO another algorithm in the current row outperforms than EWWO. A yes means that EWWO is significantly superior to other algorithms in the current row, no is the opposite mean. The stability of the result for the algorithms is shown in Figures 8 and 9 for 30 and 50 dimensions, respectively. Meanwhile, the convergence plots of the compared algorithms are described in Figures 10 and 11 on $f_3$, $f_{10}$, $f_{17}$, $f_{23}$, $f_{29}$, $f_{30}$ which includes four categories of CEC2017 benchmark function. It is observed that the convergence rate of EWWO is better than the compared algorithms in 50 dimensions. The modified propagation and breaking operations play a desirable role to balance the global exploration and local exploitation. In addition, the convergence rate and the convergence speed are improved by the covariance matrix adaptation. However, no algorithms are better than the linear enumeration of the search space or the pure random search algorithm according to the no-free lunch theorem (NFL) (Wolpert, 1997).

Figure 8. Boxplots of some typical benchmark functions (30D).

Figure 9. Boxplots of some typical benchmark functions (50D).

Figure 10. Convergence plots of EWWO, WWO, SCWWO, Sim-WWO, CMA-ES and MWWO on some typical benchmark functions (30D).

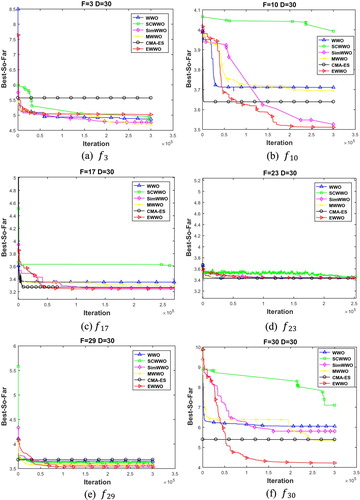
Figure 11. Convergence plots of EWWO, WWO, SCWWO, Sim-WWO, CMA-ES and MWWO on some typical benchmark functions (50D).

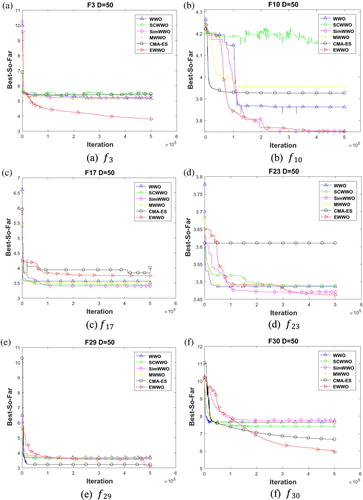
Table 3. p-Value of Wilcoxon’s rank-sum test for 10D.

EWWO VS	R+	R−	Z	$p\text{ - }Value$	$\alpha =0.05$	$\alpha =0.1$
CMA-ES	434	1	−4.681	3.00E-06	yes	yes
WWO	393	42	−3.794	1.48E-04	yes	yes
MWWO	315	91	−2.550	1.08E-02	yes	yes
Sim-WWO	246	171	−1.005	3.15E-01	no	no
SCWWO	404	31	−4.033	5.50E-05	yes	yes

Table 4. p-Value of Wilcoxon’s rank-sum test for 30D.

EWWO VS	R+	R−	Z	$p\text{ - }Value$	$\alpha =0.05$	$\alpha =0.1$
CMA-ES	434	1	−4.681	3.00E-06	yes	yes
WWO	414	21	−4.249	2.10E-05	yes	yes
MWWO	310	125	−2.000	4.55E-02	yes	yes
Sim-WWO	359	47	−3.552	3.82E-04	no	no
SCWWO	434	1	−4.682	3.00E-06	yes	yes

Table 5. p-Value of Wilcoxon’s rank-sum test for 50D.

EWWO VS	R+	R−	Z	$p\text{ - }Value$	$\alpha =0.05$	$\alpha =0.1$
CMA-ES	428	7	−4.552	5.00E-06	yes	yes
WWO	433	2	−4.660	3.00E-06	yes	yes
MWWO	377	58	−3.449	5.63E-04	yes	yes
Sim-WWO	348	87	−2.822	4.78E-03	no	no
SCWWO	433.5	1.5	−4.671	3.00E-06	yes	yes

Table 6. p-Value of Wilcoxon’s rank-sum test for 100D.

EWWO VS	R+	R−	Z	$p\text{ - }Value$	$\alpha =0.05$	$\alpha =0.1$
CMA-ES	399	36	−3.925	8.69E-05	yes	yes
WWO	388	47	−3.687	2.27E-04	yes	yes
MWWO	388	47	−3.687	2.27E-04	yes	yes
Sim-WWO	384	51	−3.600	3.18E-04	yes	yes
SCWWO	341	94	−2.670	7.57E-03	yes	yes

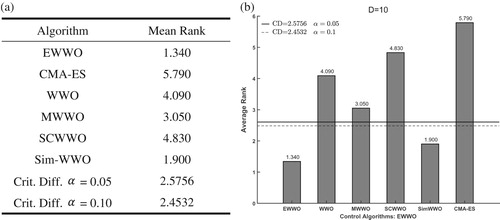
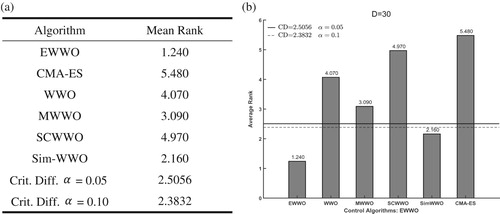
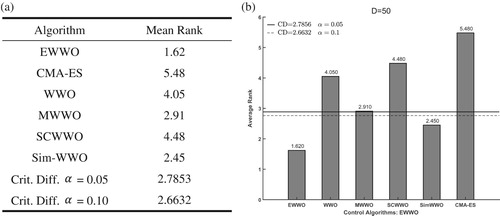
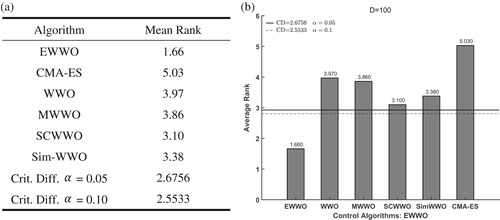
To further check the significant differences between EWWO and the five competitors, the Friedman’s test (García et al., 2009) is carried out to detect all compared algorithms. The rank of EWWO and compared algorithms on Friedman’s test is shown in Figures 12–15 for $D=10,30,50\text{ and }100$. All the figures about Friedman’s test illustrate that the proposed algorithm has the best ranking among all algorithms. To evaluate the significance level of all algorithms, an additional Bonferroni–Dunn’s procedure is applied as a post hoc procedure to calculate the critical difference (CD in Equation (28)) for comparing their differences with α=0.05 and $\alpha =0.1$. (28) $CD=q_{\alpha }\sqrt{\frac{k(k+1)}{6N}}$(28) In Equation (34) parameters $k$ and $N$ are the number of algorithms to be compared and the number of benchmarks, respectively. There are $k=6$ and $N=30$ in the experimental evaluations. When $\alpha =0.05$, $q_{\alpha }$ is 2.576 and $\alpha =0.1$, $q_{\alpha }$ is 2.327 from Table B.16 (two-tailed $\alpha (2)$) of (Ransom, 1974). Figures 12–15 sketch the results of Bonferroni–Dunn’s test which considers EWWO as a control algorithm. There is a significant difference between EWWO and the five compared algorithms with $\alpha =0.05$ and $\alpha =0.1$ for 30 and 50 dimensions, respectively. However, there is no significant difference between EWWO and Sim-WWO with $\alpha =0.05$ and $\alpha =0.1$ for 10 dimensions.

Figure 12. Rankings obtained through Friedman’s test for 10D.

Figure 13. Rankings obtained through Friedman’s test for 30D.

Figure 14. Rankings obtained through Friedman’s test for 50D.

Figure 15. Rankings obtained through Friedman’s test for 100D.

In sum, statistical analysis of the results obtained by comparing the algorithms in the study shows that the proposed EWWO is the best for the 30, 50 and 100 dimensions on the multimodal functions, hybrid functions and composition functions, respectively. Although EWWO is not able to achieve the best results on some test problems, it achieves suboptimal results compared to all experimental algorithms. Compared with other algorithms, EWWO achieves the best results on unimodal and multimodal functions of different dimensions. On the remaining test questions, the proposed algorithm still maintains the stable solution performance.

The experimental results of CMA-ES, WWO, SCWWO, Sim-WWO and EWWO are shown in Table 7 for 100-dimensions as follows.

Table 7. The results of all algorithms for 100-dimensional benchmark functions.

Function	Criterion	CMA-ES	WWO	SCWWO	SimWWO	MWWO	EWWO
1	Mean	0.00E + 00	8.88E + 03	4.08E + 08	3.95E + 06	5.76E + 03	1.67E + 03
	Std. Dev.	0.00E + 00	1.53E + 04	1.64E + 08	5.38E + 06	6.38E + 03	4.17E + 03
3	Mean	5.87E + 05	4.48E + 05	2.29E + 06	5.32E + 05	4.55E + 05	1.69E + 05
	Std. Dev.	6.71E + 04	4.59E + 04	3.74E + 06	3.38E + 04	4.54E + 04	2.00E + 05
4	Mean	2.01E + 03	4.22E + 02	5.57E + 02	5.55E + 02	9.75E + 02	2.53E + 02
	Std. Dev.	5.59E + 03	7.16E + 01	6.82E + 01	5.00E + 01	1.64E + 02	8.73E + 01
5	Mean	1.65E + 03	7.40E + 02	5.31E + 02	5.65E + 02	5.55E + 02	4.48E + 02
	Std. Dev.	1.50E + 01	1.05E + 02	8.54E + 01	4.23E + 01	8.28E + 01	6.41E + 01
6	Mean	8.32E + 01	5.80E + 01	4.82E + 01	5.13E + 01	4.75E + 01	4.78E + 00
	Std. Dev.	1.90E + 00	6.08E + 00	4.89E + 00	2.68E + 00	3.80E + 00	7.60E + 00
7	Mean	1.16E + 04	8.72E + 02	9.52E + 02	1.41E + 03	5.94E + 02	6.87E + 02
	Std. Dev.	2.83E + 01	3.34E + 02	3.49E + 02	2.34E + 02	2.05E + 02	1.03E + 02
8	Mean	2.36E + 03	8.15E + 02	5.81E + 02	7.98E + 02	5.80E + 02	4.42E + 02
	Std. Dev.	6.75E + 01	1.53E + 02	8.37E + 01	4.73E + 01	9.34E + 01	6.76E + 01
9	Mean	5.27E + 04	2.37E + 04	8.80E + 03	2.40E + 04	1.05E + 04	2.03E + 04
	Std. Dev.	9.25E + 03	4.16E + 03	6.53E + 03	1.94E + 03	5.63E + 03	3.46E + 03
10	Mean	1.59E + 04	1.44E + 04	2.08E + 04	1.36E + 04	1.48E + 04	1.15E + 04
	Std. Dev.	1.13E + 03	1.53E + 03	6.09E + 03	5.70E + 02	1.19E + 03	8.57E + 02
11	Mean	2.93E + 05	1.36E + 05	4.42E + 05	6.81E + 04	2.77E + 04	1.56E + 04
	Std. Dev.	2.04E + 05	4.75E + 04	1.05E + 05	1.29E + 04	1.23E + 04	2.19E + 04
12	Mean	3.39E + 08	2.26E + 08	5.32E + 08	1.90E + 08	3.10E + 08	2.06E + 07
	Std. Dev.	5.98E + 08	1.11E + 08	2.41E + 08	5.57E + 07	1.27E + 08	2.08E + 07
13	Mean	8.50E + 04	5.47E + 04	3.01E + 04	2.62E + 04	2.32E + 04	5.37E + 05
	Std. Dev.	3.66E + 04	2.04E + 04	8.84E + 03	4.95E + 03	8.15E + 03	7.27E + 05
14	Mean	2.22E + 05	3.94E + 05	2.61E + 05	1.03E + 06	8.63E + 05	4.94E + 04
	Std. Dev.	2.79E + 05	2.73E + 05	1.44E + 05	4.50E + 05	5.51E + 05	6.73E + 04
15	Mean	5.13E + 05	2.79E + 04	1.21E + 04	2.13E + 04	1.21E + 04	1.72E + 04
	Std. Dev.	1.65E + 06	1.19E + 04	4.87E + 03	4.86E + 03	5.40E + 03	1.32E + 04
16	Mean	2.10E + 04	4.91E + 03	4.45E + 03	3.80E + 03	3.96E + 03	3.37E + 03
	Std. Dev.	4.41E + 02	7.54E + 02	6.64E + 02	2.96E + 02	7.57E + 02	5.28E + 02
17	Mean	5.80E + 03	3.47E + 03	3.09E + 03	2.55E + 03	2.95E + 03	2.10E + 03
	Std. Dev.	1.96E + 02	5.99E + 02	5.52E + 02	2.33E + 02	4.49E + 02	3.19E + 02
18	Mean	1.20E + 07	4.40E + 05	4.48E + 05	1.39E + 06	1.40E + 06	1.45E + 05
	Std. Dev.	2.45E + 07	3.34E + 05	1.73E + 05	3.97E + 05	9.78E + 05	8.75E + 04
19	Mean	5.63E + 04	2.24E + 06	1.76E + 04	9.01E + 05	7.63E + 03	6.32E + 02
	Std. Dev.	6.17E + 04	1.55E + 06	1.32E + 04	4.95E + 05	5.92E + 03	4.06E + 02
20	Mean	5.85E + 03	3.49E + 03	6.78E + 03	2.25E + 03	3.49E + 03	1.58E + 03
	Std. Dev.	9.82E + 01	7.01E + 02	3.10E + 02	2.54E + 02	5.56E + 02	1.89E + 01
21	Mean	4.49E + 03	1.02E + 03	8.41E + 02	1.05E + 03	7.93E + 02	6.69E + 02
	Std. Dev.	5.47E + 01	1.74E + 02	9.79E + 01	9.06E + 01	1.40E + 02	4.78E + 01
22	Mean	3.02E + 04	1.62E + 04	2.00E + 04	1.53E + 04	1.59E + 04	1.18E + 04
	Std. Dev.	2.15E + 03	1.24E + 03	5.45E + 03	6.09E + 02	1.33E + 03	1.76E + 03
23	Mean	5.87E + 03	1.53E + 03	1.32E + 03	1.68E + 03	1.25E + 03	1.42E + 03
	Std. Dev.	3.20E + 01	1.95E + 02	1.46E + 02	7.53E + 01	1.62E + 02	2.23E + 02
24	Mean	1.39E + 04	2.17E + 03	1.70E + 03	2.20E + 03	1.62E + 03	2.83E + 03
	Std. Dev.	1.39E + 02	2.82E + 02	2.18E + 02	3.06E + 02	1.32E + 02	2.27E + 02
25	Mean	4.06E + 03	1.11E + 03	1.02E + 03	1.22E + 03	1.75E + 03	7.62E + 02
	Std. Dev.	1.49E + 04	9.35E + 01	8.41E + 01	6.84E + 01	2.27E + 02	8.14E + 01
26	Mean	2.87E + 04	1.39E + 04	1.04E + 04	1.96E + 04	1.03E + 04	9.67E + 03
	Std. Dev.	3.99E + 02	3.24E + 03	2.81E + 03	1.64E + 03	1.28E + 03	1.62E + 02
27	Mean	5.00E + 02	1.55E + 03	1.32E + 03	1.33E + 03	1.39E + 03	1.24E + 03
	Std. Dev.	1.62E-07	2.83E + 02	2.67E + 02	3.03E + 02	1.27E + 02	2.23E + 02
28	Mean	5.00E + 02	8.68E + 02	7.96E + 02	1.03E + 03	2.18E + 03	2.16E + 03
	Std. Dev.	4.17E-06	7.85E + 01	6.95E + 01	8.60E + 01	6.34E + 02	6.04E + 02
29	Mean	9.79E + 03	5.63E + 03	4.75E + 03	5.44E + 03	5.53E + 03	3.66E + 03
	Std. Dev.	1.25E + 02	7.10E + 02	5.70E + 02	4.56E + 02	7.45E + 02	1.24E + 02
30	Mean	1.10E + 08	4.84E + 07	1.09E + 07	5.60E + 07	1.88E + 07	2.50E + 06
	Std. Dev.	1.64E + 08	2.21E + 07	4.79E + 06	1.54E + 07	1.73E + 07	1.45E + 06

5. Conclusions

In this paper, an enhanced water wave optimisation assisted by the random OBL, mutation strategies and CMA-ES, named EWWO, are proposed to enhance the convergence rate and computational accuracy of WWO. In EWWO, a new modified operation for propagation operation and breaking operation is designed to improve the ability of global search and to balance the exploration and exploitation. Crossover operation between propagation and breaking operations are embedded to maintain the diversity of population. Furthermore, the refraction operation is removed to improve the convergence rate of EWWO and CMA-ES, as a local search strategy, is added to improve the calculation accuracy of EWWO and avoid EWWO falling into the local optimal solution and taking place the phenomenon of premature convergence. In addition, the wavelength reduction coefficient and the breaking coefficient are linearly decreased in order to find the optimal solution in a variable state. The other parameters are testified on DOE. CEC 2017 benchmark functions are applied to verify the performance of EWWO and the experiential results demonstrate that the EWWO is superior to WWO, SCWWO, MWWO, Sim-WWO and CMA-ES. To sum up, EWWO is an efficiency and effectiveness algorithm.

For the future work, several issues are worthy to further research. It is a worthwhile research direction for applying EWWO to solve the combinatorial optimisation problem in practical application domains. For instance, the standard WWO has been applied to solve the energy consumption problem, the distribution flow shop scheduling problem (DFSP) for discrete optimisation problems. Furthermore, the proposed algorithm will be utilised in the other fields of combination to solve real optimisation problems.

Disclosure statement

No potential conflict of interest was reported by the authors.

ORCID

Fuqing Zhao http://orcid.org/0000-0002-7336-9699

Additional information

Funding

This work was financially supported by the National Natural Science Foundation of China under grant number 61663023. It was also supported by the Key Research Programs of Science and Technology Commission Foundation of Gansu Province [grant number 2017GS10817], Lanzhou Science Bureau project [grant number 2018-rc-98], Public Welfare Project of Zhejiang Natural Science Foundation [grant number LGJ19E050001], Wenzhou Public Welfare Science and Technology project [grant number G20170016].