A novel particle swarm optimisation with mutation breeding

Abstract

The diversity of the population is a key factor for particle swarm optimisation (PSO) when dealing with most optimisation problems. The best previously visited positions of each particle are the exemplar in PSO to guide particle swarm to search, and the diversity of the population can be controlled by these best previously visited positions. Base on this idea of to control the diversity of population to improve the performance of PSO, this paper proposes a novel PSO with mutation breeding (MBPSO), which performs a mutation breeding operation periodically, to control the diversity of the population to improve the global optimisation ability. The mutation breeding operation can be divided into two steps: breeding and mutation. The breeding step is to replace all of best previously visited positions of each particle with the global best previously visited position, and the mutation step is to perform a mutation operation for those new generated best previously visited positions. In addition, we adopt a new updating mechanism of the global best previously position to avoid falling into local optimum. The experimental results on a suit of benchmark functions verifies that the proposed PSO is a competitive algorithm when compare with other PSO variants.

Keywords:

• Particle swarm optimisation
• mutation breeding
• global optimisation
• population diversity

1. Introduction

In recent years, particle swarm optimisation (PSO), which was first introduced by Kennedy and Eberhart (1995), has been widely used and researched by many scholars due to its simple algorithm description, easy to understand, and requires fewer parameters to be adjusted (Han & Liu, 2014; Pare, Kumar, Bajaj, & Singh, 2019; Tran, Xue, Zhang, & Nguyen, 2016). PSO has good extensibility to adapt various optimisation problems both in single-objective problems and multi-objective problems (Li, Wang, & Xu, 2017; Lv, Wang, Han, Zhao, & Wang, 2019), and it has been widely applied to many real optimisation problems (Wang et al., 2018), such as neural networks optimisation (Han & Zhu, 2011), flow-shop scheduling problem (Huang & Chen, 2009), mechanical engineering optimisation problem (Guedria, 2016), image segmentation problem (Pare et al., 2019; Tan, Chen, & Li, 2018), etc. (Cao, Jiang, & Wang, 2017; Guan, Yang, Gu, Jiang, & Lin, 2018; Jegan & Ravindran, 2017; Lin et al., 2017; Lu, Yan, Zhang, & Levy, 2014; Raja, 2014; Sivakoti, Basava, Balaga, & Sannidhi, 2017; Tan & Xia, 2018; Tran, 2018; Wang, Shi, Ding, & Gu, 2016).

However, PSO also has some disadvantages such as premature convergence and easiness getting trapped into local minima (Li, Zhan, Lin, Zhang, & Luo, 2015), especially in dealing with some high-dimensional problems (Han & Liu, 2015). Many scholars have done a lot of research on this issue, and many variants have been proposed to improve the performance of PSO algorithm. In general, these variants can be classified under four categories (Tanweer, Suresh, & Sundararajan, 2015):

The first category is based on algorithm parameter settings. In order to improve the convergence performance, a method of linearly varying inertial weight (PSO-LVIW) was proposed in Shi and Eberhart (1998), and this strategy was adopted by many PSO variants. In Nagra, Han, and Ling (2019), an improved hybrid self-inertia weight adaptive PSO with gradient-based local search was proposed. In Taherkhani and Safabakhsh (2016), this paper proposed a strategy of dynamically adjusting the inertial weight or acceleration coefficients according to the state of the algorithm, which can reduce the risk of premature convergence. In Eberhart and Shi (2000), a new constriction coefficient was employed to control the convergence of the particles, which can improve the convergence speed. Ecological particle swarm optimisation algorithm was proposed in Kang, Wang, and Wu (2008), which defines a ecological hierarchy and competition model based on population density, and assigns the different inertia weight factors for different ecological hierarchies. In Tanweer et al. (2015), a self regulating particle swarm optimisation algorithm was proposed, which uses a self-regulating inertia weight strategy and a self-perception of global search direction strategy for intelligent exploitation of the solution space. An adaptive PSO with supervised learning and control was introduced in Dong and Zhou (2017), through the method that treats PSO with optimisation problem as a system to be controlled, to choose parameters adaptively to improve its exploration competence.

The second category is based on neighbourhood topology. Different kinds of neighbourhood topology such as fully connected, wheel connected, Von-Neumann connected were researched and compared in Kennedy and Mendes (2002). A novel method of using a weighted sum of all the neighbouring particles to update the position of a given particle which named fully informed particle swarm was proposed in Mendes, Kennedy, and Neves (2004). Club-based PSO and adaptive default membership club based PSO was proposed in Emara (2009), which split the particle swam into some small groups, and dynamically change the group members. In Liang, Li, Zhang, and Zhou (2015), a variation called adaptive PSO based on clustering was introduced, which via a K-means clustering operation to divide the swarm dynamically and use a ring neighbourhood topology for information sharing among these clusters. In Liang, Qin, Suganthan, and Baskar (2006), a new variant PSO named Comprehensive Learning PSO (CLPSO)was proposed, in this paper a comprehensive learning strategy was adopted which uses all other particles' historical best information to update a particle's velocity. In Cheng and Jin (2015), a social learning particle swarm optimisation was introduced in this paper, which uses the strategy of the particles learning from any better particles in the current swarm.

The third category is to improve the search strategy of PSO. Attractive and Repulsive PSO (ARPSO)was proposed in Riget and Vesterstrom (2002), which uses a diversity measure to control particle's motion strategy, to overcome the problem of premature convergence. Spatial Extension PSO (SEPSO) (Krink, Vesterstrom, & Riget, 2002) endowing each particle with a radius, then causing particles to bounce off of one another, to prevent particles overcrowding in a small range. Bare-Bones PSO (BBPSO) (Kennedy, 2003) through Gaussian normal distribution to update the particles instead of using acceleration coefficient and velocity. A CLPSO embedded with local search was proposed in Cao et al. (2019), this paper proposes an adaptive local search starting strategy by utilising the quasi-entropy index to improve the optimisation performance both in global search capability and fast convergence ability. An adaptive two-layer particle swarm optimisation algorithm with elitist learning strategy was proposed in Lim and Isa (2014), this algorithm performs evolution on both the current swarm and the memory swarm, self-adaptively dividing the swarms into exploration and exploitation sections, and uses an elitist learning strategy to enhance the search efficiency and to mitigate premature convergence.

The last category is to combine PSO with other heuristic algorithms. In Gong et al. (2016), a genetic learning particle swarm optimisation algorithm was proposed in this paper, which composed of two cascading layers of GA and PSO respectively, and using genetic evolution to breed promising exemplars for PSO. In Nie and Yue (2008), a GA and PSO hybrid algorithm was introduced, which create individuals in a new generation both by crossover and mutation operations and the mechanisms of PSO. In Yang, Niu, and Cai (2018), the simulated annealing and chaos mechanism was introduced in the process of optimal information to increase the population diversity. A new ACO-PSO combined Ant Colony Algorithm and PSO was proposed in Pal, Verma, Gautam, and Indait (2016), which defines that the selection of parameter does not depend on artificial experience, but relies on the robust search on the particles in the PSO. In Bao and Han (2017), a hybrid multi-swarm PSO based on shuffled frog leaping algorithm was proposed, which group the particle swarms by fitness, and use shuffled frog leaping algorithm to update the particles.

In addition, many PSO variants with mutation operation have been presented beside the PSO and GA hybrid algorithms. A particle swarm optimiser with two differential mutation (PSOTD) was proposed in Chen et al. (2017). This paper design a novel structure with two swarms and two layers, the top layer and the bottom layer, which consists all the personal best particles and all the particles respectively, and uses two differential mutation operators with different characteristics to generate promising particles in the top layers. Through this method, the bottom particles can achieve a good trade-off between exploration and exploitation. Particle swarm algorithm with hybrid mutation strategy (HPSO) was proposed in Gao and Xu (2011), which uses a global Henon mutation operator to enhance the global searching ability of particles, and use a local Henon mutation operator to improve the convergence speed, where the global henon mutation operator mutate the velocity and the local henon mutation operator mutate the global best previously visited position. In Dong, Kang, and Zhang (2017), an opposition-based particle swarm optimisation with adaptive mutation strategy (AMOPSO) was proposed. This algorithm uses an adaptive mutation selection strategy and an adaptive nonlinear inertia weight strategy, where the adaptive mutation selection strategy is to disturb the position of the current global optimal particle, and gains a new mutation position adaptively, which base on the distance between the best previously visited positions of each particle and the global best previously visited position.

The diversity of the population is a key factor for particle swarm optimisation. A great diversity of the population usually means that the positions of the population contain too much useless information, which may distract the particle swarm and result in difficult to convergence. However if the population lack diversity, which usually leads to a premature convergence. In PSO, the sets of each particle's best previously visited positions, which is represented as p in this paper, and the global best previously visited position, which is represented as $p_g$ in this paper, are the exemplars to guide the particle swarm to search. Thus, the diversity of the population can be controlled by the p in PSO. In terms of this, inspired by the mutation breeding technique, we present a novel PSO with mutation breeding (MBPSO), to improve the ability of global optimisation. The main contributions of this work can be highlighted as follows:

1. The mutation breeding operation is proposed to generate a population with a limited diversity. The mutation breeding operation is consisted of two steps: breeding and mutation. In the breeding step, only select the $p_g$ and discard all of positions in p, then copy the selected position to replace those discarded positions in p. Through the breeding step, we can obtain a p which the diversity is 0. In the mutation step, the new generated positions sets p will be mutated randomly, i.e. randomly select some dimensions from some randomly selected positions base on the mutation probability, then initial the value of these dimensions, to generate a population with a limited diversity. The diversity can be controlled easily by the probability of mutation.

2. The mutation breeding operation is performed periodically in MBPSO to obtain a limited diversity of p, to control the diversity of the population. It's worth noting that these positions in p which were generated and mutated by the mutation breeding operation need not evaluate the fitness, and these positions in p will be updated with the current positions in the population at the next iteration.

3. A new updating mechanism of the global best previously position is adopted to enhance the ability of jump out from the local optimum. This new updating mechanism is that whenever the mutation breeding operation has been performed, the $p_g$ will be replaced with the best position in the current population at the next iteration.

The rest of this paper is organised as follows. Section 2 reviews the classical PSO and its weaknesses. The MBPSO was presented in Section 3 including its computational complexity and search behaviour. Section 4 experimentally compares MBPSO and other PSO variants through a series of benchmark functions. Section 5 discusses the parameter settings for MBPSO, and the conclusion is drawn in Section 6.

2. Classical PSO

PSO algorithm is a population intelligence-based random search algorithm and it was widely used to solve various optimisation problems. In the PSO algorithm, the particle swarm's position sets is denoted as x, and the positions of these particles can be denoted as $x_1$, $x_2$,…, $x_n$, where n is the number of particles, corresponding to a candidate solution of the objective function. Similarly, for the best previously visited positions sets p, each best previously visited position in it can be denoted as $p_1$, $p_2$,…, $p_n$, corresponding to the positions of each particle respectively. The process of searching for the best result of the objective function in PSO is the process of updating the particle swarm's positions, and the positions sets x of the particle swarm is updated by Equations (1(1) $\begin{array}{rl}{v}_i^{t+1}& =w{v}_i^t+c_1{r}_1(p_i-x_i^t)+c_2{r}_2(p_g-x_i^t)\end{array}$(1) ) and (2(2) $\begin{array}{rl}{x}_i^{t+1}& =x_i^t+v_i^{t+1}\end{array}$(2) ): (1) $\begin{array}{rl}{v}_i^{t+1}& =w{v}_i^t+c_1{r}_1(p_i-x_i^t)+c_2{r}_2(p_g-x_i^t)\end{array}$(1) (2) $\begin{array}{rl}{x}_i^{t+1}& =x_i^t+v_i^{t+1}\end{array}$(2) where v is the velocity of the particle, i is the ith particle of the swarm, t is time, w is inertia weight of the particle, $c_1$, $c_2$ are the acceleration constants with positive values, $r_1$, $r_2$ are two uniformly distributed random number within range from 0 to 1, $p_i$ is the best previously visited position of the ith particle, and $p_g$ is the global best previously visited position of the particle swarm. The best previously visited positions sets p and the global best previously visited position $p_g$ in PSO are updated by Equations (3(3) $\begin{array}{rl}{p}_i^{t+1}& =\{\begin{array}{ll}{p}_i^t,& \mathrm{if}f(p_i^t)\le f(x_i^{t+1})\\ x_i^{t+1},& \mathrm{if}f(p_i^t)>f(x_i^{t+1})\end{array}\end{array}$(3) ) and (4(4) $\begin{array}{rl}\mathrm{\exists }k& \in 1,2,\dots ,n,f(p_k^{t+1})=min(f(p_i^{t+1}))\\ p_g^{t+1}& =\{\begin{array}{ll}{p}_g^t,& \mathrm{if}f(p_g^t)\le f(p_k^{t+1})\\ p_k^{t+1},& \mathrm{if}f(p_g^t)>f(p_k^{t+1})\end{array}\end{array}$(4) ): (3) $\begin{array}{rl}{p}_i^{t+1}& =\{\begin{array}{ll}{p}_i^t,& \mathrm{if}f(p_i^t)\le f(x_i^{t+1})\\ x_i^{t+1},& \mathrm{if}f(p_i^t)>f(x_i^{t+1})\end{array}\end{array}$(3) (4) $\begin{array}{rl}\mathrm{\exists }k& \in 1,2,\dots ,n,f(p_k^{t+1})=min(f(p_i^{t+1}))\\ p_g^{t+1}& =\{\begin{array}{ll}{p}_g^t,& \mathrm{if}f(p_g^t)\le f(p_k^{t+1})\\ p_k^{t+1},& \mathrm{if}f(p_g^t)>f(p_k^{t+1})\end{array}\end{array}$(4)

where f is the evaluation function, $f(p_i^t)$ is the fitness of the ith position in p which evaluated by f at the time t, and $f(p_g^t)$ is the fitness of $p_g$ which evaluated by f at the time t. Due to the position updating formula of PSO, a scattered p may throw particles into chaos and result in a low convergence speed, however a low diversity of p may stagnate these particles near to the position of $p_g$ and unable continuing to search. If $p_g$ is a local minimum, which usually result in premature convergence (Monson & Seppi, 2006). In addition, because the $p_i$ and $p_g$ can only be replaced with a better position, a local optimum will usually prevent the particle swarm to jump out of it because in this situation the $p_i$ and $p_g$ are hard to change.

3. The proposed MBPSO algorithm

3.1. Mutation breeding operation

Mutation breeding is an agriculture technique which was widely used in breeding new varieties of plants, and more than 3088 mutagenic plant varieties were released by the end of 2009 (Bradshaw, 2016). Mutation breeding is the process of using radiation, chemicals, T-DNA or transposons to treat seeds to generate mutants, and to select mutants with desirable traits to be bred. Inspired by mutation breeding, we suggest this mutation breeding operation to control the diversity of the population to improve the global optimisation ability of the PSO algorithm. Just as the mutation breeding, the mutation breeding operation in MBPSO can be divided into two steps: breeding and mutation. In the first step, only select the global best position and breed it to replace the best previously visited positions of each particle; in the second step, mutate these new generated best previously visited positions. Set the best previously visited positions sets of each particle to p, the global best previously visited position to $p_g$, the number of particles to n, the number of dimensions to d, the mutation probability to pm, this operation can be described as Algorithm 1:

3.2. The MBPSO algorithm

The MBPSO algorithm is a variant PSO based on the classical PSO, and the difference is that in MBPSO, a mutation breeding operation is periodically performed to update the p, and the $p_g$ will be replaced with the best current position of the particle swarm at the next iteration. In order to explain this operation, set the current positions sets of particle swarm to x, the best previously visited positions sets of each particle to p, the global best previously visited position to $p_g$, the number of particles to n, the maximum optimisation iteration number to m, the number of dimensions to d, the cycle of mutation breeding operation to cm, the pseudocode of MBPSO algorithm is described in Algorithm 2.

The mutation breeding operation has some similarities to the Genetic Algorithm (GA), both of them use the mutation operation to try to find potential offsprings. However, there is much difference between mutation breeding operation and GA. In GA, the order to generate offsprings is crossover, mutation and selection. Unlike the GA, the the order in mutation breeding operation is breeding and mutation. Mutation breeding operation is much simpler than GA, on one hand, it does not have the crossover operation, which means the computation complexity is much lower than GA, on the other hand, the selection strategy in the breeding step is very simple, just ”winner-takes-all”, i.e. only the global best previously visited position can be preserved to breed offsprings. The reason of why we use mutation breeding operation and not GA to generate p in MBPSO is that the diversity of offsprings can be easily controlled through mutation breeding operation by the probability of mutation, however, because of the selection operation is the last step in GA, the diversity of these generated offsprings is hard to control.

3.3. Complexity analysis of MBPSO

The computational costs of the classical PSO algorithm include the particle swarm initialisation ($T_{ini}$), the evaluation of each particle's position ($T_{eva}$), and update the positions of each particle ($T_{upd}$). Assume the dimensions of the search space is D, the MaxFEs is the maximum number of fitness evaluation, the time complexity of PSO can be estimated as Equation (5(5) $\begin{array}{rl}T(D)& =T_{ini}+(T_{eva}+T_{upd})\cdot MaxFEs\\ & =D+(D+2\cdot D)\cdot MaxFEs=D\cdot (1+3\cdot MaxFEs)\end{array}$(5) ) (5) $\begin{array}{rl}T(D)& =T_{ini}+(T_{eva}+T_{upd})\cdot MaxFEs\\ & =D+(D+2\cdot D)\cdot MaxFEs=D\cdot (1+3\cdot MaxFEs)\end{array}$(5) Therefore, $O(D\cdot MaxFEs)$ is the time complexity of the classical PSO (Gong et al., 2016).

The major difference between classical PSO and MBPSO is that MBPSO performs a mutation breeding operation periodically during the optimisation process. Assume that the cycle of mutation breeding operation is cm, the computational costs of the breeding step ($T_{bre}$) is $O(1)$, and the mutation step ($T_{mut}$) is $O(D)$. The time complexity of MBPSO can be estimated as Equation (6(6) $\begin{array}{rl}T(D)& =T_{ini}+(T_{eva}+T_{upd})\cdot MaxFEs+(T_{bre}+T_{mut})\cdot (MaxFEs/cm)\\ & =D\cdot (1+3\cdot MaxFEs)+(1+D)\cdot (MaxFEs/cm)\end{array}$(6) ) (6) $\begin{array}{rl}T(D)& =T_{ini}+(T_{eva}+T_{upd})\cdot MaxFEs+(T_{bre}+T_{mut})\cdot (MaxFEs/cm)\\ & =D\cdot (1+3\cdot MaxFEs)+(1+D)\cdot (MaxFEs/cm)\end{array}$(6) Therefore, $O(D\cdot MaxFEs)$ is the time complexity of the MBPSO, just as same as the classical PSO.

3.4. Analysis of MBPSO's search behaviour

The mutation breeding operation is periodically performed in MBPSO, which will take some different search behaviour from the classical PSO. After a mutation breeding operation, the updated sets of each particle's best previously visited positions p will retain a limited diversity. The different changes of the p between the classical PSO and the MBPSO can be observed from Figures 1 and 2.

Figure 1. Changes of the p in classical PSO on 3-D Sphere function.

Figure 2. Changes of the p in MBPSO on 3-D Sphere function.

Through the mutation breeding operation to control the diversity of population is the main difference between MBPSO and the classical PSO. The diversity of positions can be calculated by Equation (7(7) $diversity(p)=\frac{1}{|p|\cdot |L|}\cdot \sum _{i=1}^{|p|}\sqrt{\sum _{j=1}^D(p_{ij}-\overline{p_j}{)}^2}$(7) ) according to Han and Zhu (2011) (7) $diversity(p)=\frac{1}{|p|\cdot |L|}\cdot \sum _{i=1}^{|p|}\sqrt{\sum _{j=1}^D(p_{ij}-\overline{p_j}{)}^2}$(7) where p is the positions sets of the particle swarm, $diversity(p)$ is the diversity of the positions sets p, $|p|$ is the population size, $|L|$ is the length of the longest radius of the search space, D is the dimensions of the problem, $p_{ij}$ is the value of the ith position in p in the jth dimension, and $\overline{p_j}$ is the average value of all the positions in p in the jth dimension.

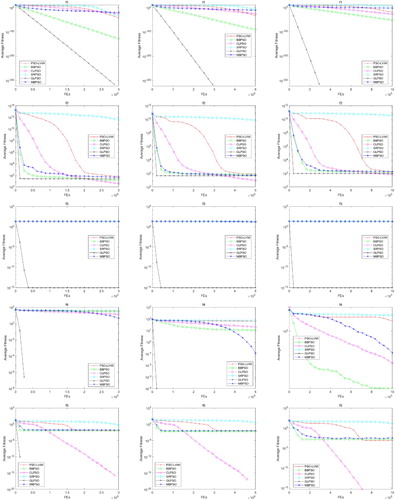
In order to illustrate the effect of mutation breeding operation, Four test functions, Sphere function, Schwefel's function, Griewank's function and Rosenbrock's function are chosen to investigate the difference of diversity change between classical PSO and MBPSO. Figure 3 shows the diversity curve of the particle's best previously visited positions p, the diversity curve of the population and the fitness curve from left to right, respectively, where the first line is on Sphere function, the second line is on Schwefel function, the third line is on Griewank function and the fourth line is on Rosenbrock function.

Figure 3. The diversity curve of p, the diversity curve of x and the fitness curve on Sphere, Schwefel, Griewank and Rosenbrock.

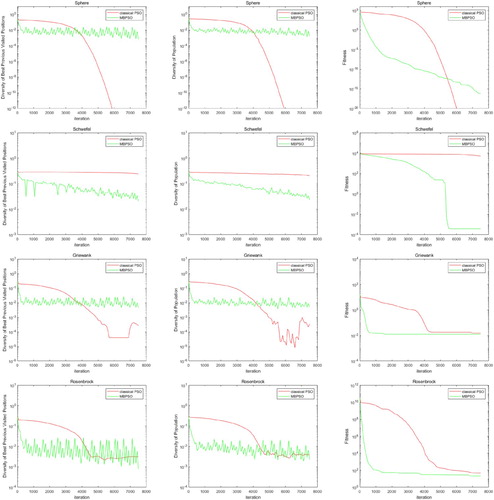
By observing Figure 3, we can find that the p and the population in MBPSO maintains a stable diversity along with the iteration, meanwhile in classical PSO the diversity has a big value at the early stage of iteration and has a small value at the latter iteration on Sphere, Griewank and Rosenbrock. Different from those three functions, the diversity on Schwefel's function of classical PSO is always too large, which causes the particle swarm hardly to convergence. Generally, for a multimodal problem, if the diversity of population is too large, which usually means the population lack of direction and fall into disorder, and will result hardly to convergence. However, if the diversity of population is too small, which usually means the particle swarm lack of motivation and hard to jump out from current positions. MBPSO keeps a reasonable diversity for the population to avoid this problem, and has a better global optimisation ability when compared with the classical PSO.

4. Numerical simulation and analysis

4.1. Experimental setup

In this section, the performance of the proposed MBPSO algorithm is compared with the PSO-LVIW (linearly varying inertial weight PSO), BBPSO (Bare-Bones PSO), CLPSO (Comprehensive Learning PSO), SRPSO (Self Regulating PSO) and GLPSO (Genetic Learning PSO). To thoroughly evaluate the performance of the proposed MBPSO, ten basic benchmark functions, $f_1-f_{10}$, and CEC'15 Learning-Based Benchmark Suite, $F_1-F_{15}$, which are more complex than the basic functions, are chosen to test the performance of each algorithm. The basic benchmark test functions contain two unimodal functions, $f_1-f_2$, six multimodal functions, $f_3-f_8$, and two expanded functions, $f_9-f_{10}$, which are shown in Table 1. The CEC'15 Learning-Based Benchmark Suite please refer to Liang, Qu, Suganthan, and Chen (2014), which contain two unimodal functions, $F_1-F_2$, three simple multimodal functions, $f_3-f_5$, three hybrid functions, $F_6-F_8$, and seven composition functions, $f_9-f_{15}$. The search ranges are set to $[-100,100{]}^D$ for all of test functions except the $f_7$. For $f_7$, the search range is set to $[-500,500{]}^D$.

Table 1. Basic Test function used in experiment.

Test function	Expression	Global minima
High Conditioned Elliptic Function $f_1$	${\displaystyle f_1(x)=\sum _{i=1}^D({10}^6{)}^{\frac{i-1}{D-1}}{x}_i^2}$	0
Rosenbrock's Function $f_2$	${\displaystyle f_2(x)=\sum _{i=1}^{D-1}[100(x_i^2-x_{i+1}{)}^2+(x_i-1{)}^2]}$	0
Ackley's Function $f_3$	$\begin{array}{rl}{f}_3(x)& =-20\exp (-0.2\sqrt{\frac{1}{D}\sum _{i=1}^D{x}_i^2})\\ & -\exp (\frac{1}{D}\sum _{i=1}^D\cos (2\pi x_i))+20+\exp (1)\end{array}$	0
Weierstrass Function $f_4$	$\begin{array}{rl}{f}_4(x)& =\sum _{i=1}^D(\sum _{k=0}^{kmax}[a^k\cos (2\pi b^k(x_i+0.5))])\\ & -D\sum _{k=0}^{kmax}[a_k\cos (2\pi b^k\cdot 0.5)]\\ a& =0.5,b=3,kmax=20\end{array}$	0
Griewank's Function $f_5$	${\displaystyle f_5(x)=\sum _{i=1}^D\frac{x_i^2}{4000}-\prod _{i=1}^D\cos \left(\frac{x_i}{\sqrt{i}}\right)+1}$	0
Rastrigin's Function $f_6$	${\displaystyle f_6(x)=\sum _{i=1}^D[x_i^2-10\cos (2\pi x_i)+10]}$	0
Schwefel's Function $f_7$	${\displaystyle f_7(x)=418.9829\times D-\sum _{i=1}^D{x}_i\sin (|x_i{|}^{\frac{1}{2}})}$	0
Katsuura Function $f_8$	${\displaystyle f_8(x)=\frac{10}{D^2}\prod _{i=1}^D{(1+i\sum _{j=1}^{32}\frac{|2^j{x}_i-round(2^j{x}_i)|}{2^j})}^{\frac{10}{D^{1.2}}}-\frac{10}{D^2}}$	0
Expanded Griewank's plus Rosenbrock's Function $f_9$	$\begin{array}{rl}{f}_9(x)& =f_5(f_2(x_1,x_2))+f_5(f_2(x_2,x_3))+\cdots \\ & +f_5(f_2(x_{D-1},x_D))+f_5(f_2(x_D,x_1))\end{array}$	0
Expanded Scaffer's F6 Function $f_{10}$	$\begin{array}{rl}{f}_{10}(x)& =g(x_1,x_2)+g(x_2,x_3)+\cdots +g(x_{D-1},x_D)+g(x_D,x_1)\end{array}$	0
	$\begin{array}{rl}g(x,y)& =0.5+\frac{({\sin }^2(\sqrt{x^2+y^2})-0.5)}{(1+0.001(x^2+y^2){)}^2}\end{array}$

4.2. Parameter settings for the involved algorithms

All the algorithms are carried out in Matlab R2018b environment on an Intel Core(TM) i7-8750H CPU. The population size for all of algorithms are set to 40 in all experiments. Each algorithm performs 30 times independently to run over the 10 basic benchmark functions and the fifteen CEC'15 benchmark functions in 30, 50 and 100 dimensional respectively (García, Molina, Lozano, & Herrera, 2008), and the MaxFEs is set to $1\times {10}^4\cdot D$. The parameter configurations of each algorithm are according to the corresponding reference (Gong et al., 2016; Liang et al., 2006; Shi & Eberhart, 1998; Tanweer et al., 2015), which are shown in Table 2.

Table 2. Parameter configurations.

Algorithm	Parameter configurations
PSO-LVIW	$w=0.9\sim 0.4,c_1=c_2=2.0$
BBPSO
CLPSO	$w=0.9\sim 0.2,c=1.49445,m=5,Pc=0\sim 0.5,V_{max}=0.2\cdot Range$
SRPSO	$w=1.05\sim 0.5,c_1=c_2=1.49445,V_{max}=0.06708\cdot Range$
GLPSO	$w=0.7298,c=1.49618,pm=0.01,sg=7$
MBPSO	$w=0.5\sim 0.2,c_1=c_2=2.0,cm=10,pm=0.01$

4.3. Experimental results and discussions

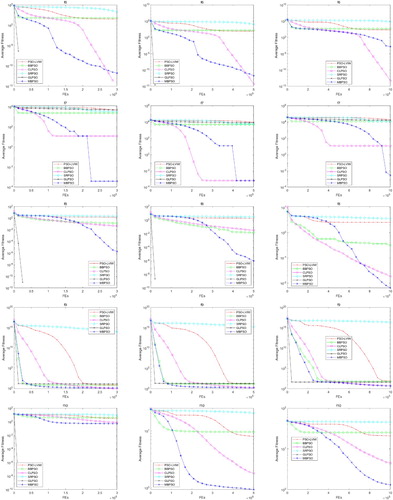
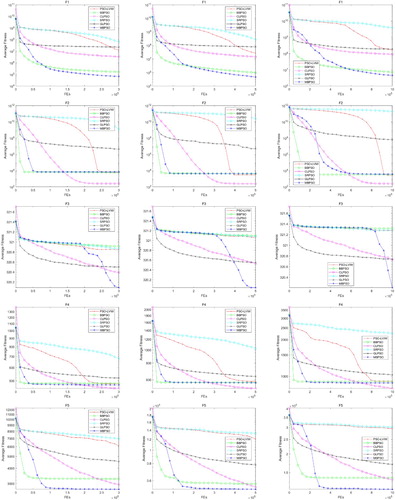
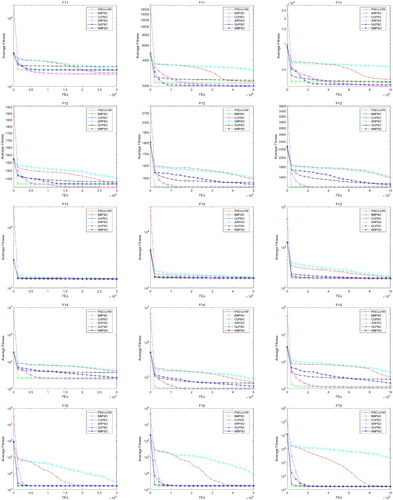
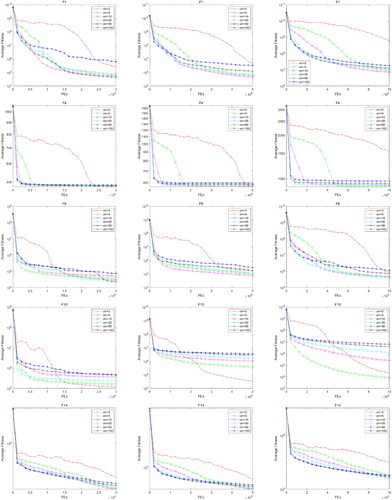
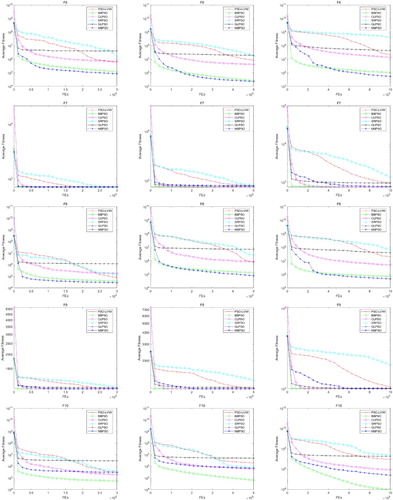
The test results are shown in follows. Table 3 shows the results on the 10 basic test functions and Tables 4 and 5 show the results on the CEC'15 Learning-Based Test Suite. The best results among the six PSO variants are shown in bold and the second best are shown in italic. Figures 4 and 5 present the convergence curve of the six PSO variants on $f_1-f_5$, $f_6-f_{10}$ from top to bottom, each test function with 30, 50 and 100 dimensional are shown in figures from left to right, respectively. Similar to the above, Figures 6–8 present the convergence curve of the six PSO variants on $F_1-F_5$, $F_6-F_{10}$, $F_{11}-F_{15}$, respectively.

Figure 4. The curve of the average fitness from 30 independent runs on $f_1-f_5$.

Figure 5. The curve of the average fitness from 30 independent runs on $f_6-f_{10}$.

Figure 6. The curve of the average fitness from 30 independent runs on $F_1-F_5$.

Figure 7. The curve of the average fitness from 30 independent runs on $F_6-F_{10}$

Figure 8. The curve of the average fitness from 30 independent runs on $F_{11}-F_{15}$.

Table 3. Results for basic test functions $f_1-f_{10}$.

Func.	Dim		PSO-LVIW	BBPSO	CLPSO	SRPSO	GLPSO	MBPSO
$f_1$	30	mean	8.752e−43	5.354e−129	2.277e−25	1.123e−34	0.000e+00	1.269e−20
		std	3.576e−42	2.779e−128	1.894e−25	5.912e−34	0.000e+00	5.871e−20
	50	mean	8.602e−34	3.069e−91	1.140e−25	8.985e−08	0.000e+00	1.470e−11
		std	1.933e−33	1.146e−90	7.718e−26	4.913e−07	0.000e+00	2.548e−11
	100	mean	1.081e−20	2.740e−53	2.969e−28	7.071e+04	0.000e+00	6.772e−04
		std	2.766e−20	5.874e−53	1.275e−28	1.270e+05	0.000e+00	5.504e−04
$f_2$	30	mean	2.876e+01	1.836e+01	2.702e+00	6.675e+08	2.473e+01	8.735e+00
		std	2.960e+01	2.587e+01	2.226e+00	3.951e+08	6.309e−01	1.062e+01
	50	mean	7.940e+01	6.400e+01	9.255e+00	6.762e+09	4.565e+01	5.308e+01
		std	4.706e+01	4.141e+01	1.002e+01	2.246e+09	5.450e−01	4.303e+01
	100	mean	1.557e+02	1.256e+02	7.218e+01	3.633e+10	9.685e+01	1.851e+02
		std	8.094e+01	3.761e+01	5.482e+01	6.557e+09	7.957e−01	4.923e+01
$f_3$	30	mean	2.011e+01	2.002e+01	2.002e+01	2.086e+01	8.882e−16	1.973e+00
		std	3.053e+00	9.324e−02	7.808e−02	6.599e−02	0.000e+00	5.732e+00
	50	mean	2.067e+01	2.000e+01	2.005e+01	2.105e+01	8.882e−16	1.394e+01
		std	3.448e−01	3.726e−03	7.747e−03	6.140e−02	0.000e+00	9.155e+00
	100	mean	2.067e+01	2.010e+01	2.005e+01	2.126e+01	8.882e−16	2.008e+01
		std	4.451e−01	8.180e−04	7.339e−03	3.339e−02	0.000e+00	6.140e−02
$f_4$	30	mean	3.467e+01	2.850e+01	1.368e+01	3.828e+01	0.000e+00	4.343e+00
		std	3.372e+00	1.423e+01	6.799e−01	1.440e+00	0.000e+00	4.899e+00
	50	mean	6.264e+01	1.062e+01	1.975e+01	7.004e+01	0.000e+00	1.107e−01
		std	8.215e+00	1.706e+01	1.072e+00	1.575e+00	0.000e+00	3.002e−01
	100	mean	1.334e+02	1.959e+01	4.047e+01	1.569e+02	0.000e+00	5.383e+01
		std	2.376e+01	8.851e+00	2.572e+00	2.887e+00	0.000e+00	7.248e+00
$f_5$	30	mean	1.017e−02	1.170e−02	0.000e+00	5.774e−01	0.000e+00	1.622e−02
		std	1.527e−02	1.798e−02	0.000e+00	5.691e−01	0.000e+00	1.778e−02
	50	mean	1.163e−02	6.481e−03	0.000e+00	3.475e+00	0.000e+00	1.040e−02
		std	1.729e−02	9.142e−03	0.000e+00	2.604e+00	0.000e+00	1.305e−02
	100	mean	7.396e−04	1.479e−03	0.000e+00	1.346e+01	0.000e+00	3.197e−03
		std	2.339e−03	3.118e−03	0.000e+00	7.894e+00	0.000e+00	7.862e−03
$f_6$	30	mean	3.506e+01	6.056e+01	0.000e+00	1.886e+03	0.000e+00	1.694e−12
		std	1.013e+01	1.840e+01	0.000e+00	2.275e+03	0.000e+00	6.180e−12
	50	mean	8.159e+01	1.535e+02	4.263e−15	1.056e+04	0.000e+00	1.699e−12
		std	1.936e+01	3.213e+01	8.883e−15	7.253e+03	0.000e+00	2.933e−12
	100	mean	2.122e+02	4.601e+02	5.311e−14	6.437e+04	0.000e+00	1.540e−03
		std	2.051e+01	7.478e+01	3.413e−14	4.179e+04	0.000e+00	1.836e−03
$f_7$	30	mean	4.344e+03	2.357e+03	1.184e+01	3.334e+03	4.996e+03	3.818e−04
		std	8.943e+02	5.415e+02	3.745e+01	8.850e+01	1.359e+03	9.393e−13
	50	mean	8.934e+03	4.862e+03	6.364e−04	5.596e+03	8.073e+03	6.364e−04
		std	1.373e+03	9.248e+02	0.000e+00	1.610e+02	2.125e+03	8.089e−12
	100	mean	1.894e+04	1.180e+04	1.185e+01	1.171e+04	1.638e+04	2.822e−03
		std	3.079e+03	1.040e+03	3.745e+01	2.128e+02	2.198e+03	8.678e−04
$f_8$	30	mean	1.430e+00	1.408e−01	4.509e−02	2.145e+00	0.000e+00	1.879e−06
		std	5.638e−01	5.390e−01	7.289e−03	1.937e−01	0.000e+00	1.787e−06
	50	mean	1.709e+00	1.417e−02	3.161e−02	2.957e+00	0.000e+00	9.667e−07
		std	6.616e−01	6.812e−02	5.109e−03	2.719e−01	0.000e+00	6.519e−07
	100	mean	2.560e+00	3.174e−01	1.821e−02	3.600e+00	0.000e+00	6.426e−03
		std	6.237e−01	1.001e+00	1.799e−03	2.309e−01	0.000e+00	2.584e−03
$f_9$	30	mean	5.692e+00	5.115e+00	6.859e−01	9.046e+13	1.123e+01	1.058e+00
		std	1.673e+00	1.837e+00	2.907e−01	4.648e+13	5.556e−01	2.220e−01
	50	mean	1.602e+01	1.499e+01	1.656e+00	1.912e+15	1.949e+01	1.865e+00
		std	4.367e+00	3.079e+00	3.314e−01	7.419e+14	2.690e+00	4.556e−01
	100	mean	8.997e+01	6.091e+01	5.025e+00	2.282e+16	4.235e+01	5.030e+00
		std	2.968e+01	1.560e+01	9.456e−01	6.605e+15	1.042e+00	2.814e−01
$f_{10}$	30	mean	3.104e+00	4.088e+00	7.810e−01	9.648e+00	0.000e+00	5.185e−01
		std	8.261e−01	1.005e+00	1.085e−01	1.556e+00	0.000e+00	3.007e−01
	50	mean	7.990e+00	9.584e+00	1.795e+00	2.052e+01	0.000e+00	9.355e−01
		std	1.866e+00	1.542e+00	2.501e−01	1.046e+00	0.000e+00	3.852e−01
	100	mean	2.098e+01	2.526e+01	4.487e+00	4.546e+01	0.000e+00	1.312e+00
		std	1.923e+00	3.198e+00	7.581e−01	4.981e−01	0.000e+00	2.822e−01

Table 4. Results for CEC'15 Learning-Based Benchmark Suite $F_1-F_{10}$.

Func.	Dim		PSO-LVIW	BBPSO	CLPSO	SRPSO	GLPSO	MBPSO
$F_1$	30	mean	1.254e+07	1.655e+05	3.399e+06	6.623e+07	2.273e+07	6.688e+04
		std	1.984e+07	8.426e+04	1.061e+06	6.659e+07	1.540e+07	4.458e+04
	50	mean	2.700e+07	9.800e+05	1.429e+07	2.731e+08	7.842e+07	4.665e+05
		std	5.609e+07	5.269e+05	4.658e+06	1.451e+08	4.475e+07	4.327e+05
	100	mean	1.636e+08	7.137e+06	8.933e+07	3.869e+09	1.868e+08	4.555e+06
		std	1.074e+08	3.096e+06	1.523e+07	1.943e+09	4.530e+07	2.847e+06
$F_2$	30	mean	6.254e+03	6.003e+03	2.524e+02	1.319e+09	4.372e+06	6.998e+03
		std	7.550e+03	8.240e+03	9.261e+01	2.136e+09	1.788e+07	7.890e+03
	50	mean	2.928e+03	4.141e+03	2.410e+02	2.465e+10	4.996e+06	4.273e+03
		std	3.359e+03	5.206e+03	1.226e+02	1.262e+10	2.093e+07	4.500e+03
	100	mean	2.540e+03	3.195e+03	2.458e+02	1.864e+11	6.475e+07	3.690e+03
		std	2.282e+03	3.249e+03	8.737e+01	5.877e+10	8.940e+07	2.696e+03
$F_3$	30	mean	3.208e+02	3.209e+02	3.204e+02	3.209e+02	3.205e+02	3.201e+02
		std	9.566e−02	1.272e−01	5.363e−02	8.210e−02	9.270e−02	2.707e−01
	50	mean	3.211e+02	3.211e+02	3.205e+02	3.211e+02	3.205e+02	3.200e+02
		std	7.006e−02	1.530e−01	3.988e−02	5.002e−02	7.020e−02	2.058e−01
	100	mean	3.213e+02	3.213e+02	3.207e+02	3.213e+02	3.207e+02	3.202e+02
		std	4.822e−02	2.115e−02	2.708e−02	3.392e−02	6.402e−02	4.413e−01
$F_4$	30	mean	4.793e+02	4.830e+02	4.498e+02	6.792e+02	5.202e+02	4.722e+02
		std	2.046e+01	2.322e+01	5.197e+00	5.699e+01	2.289e+01	1.730e+01
	50	mean	5.848e+02	5.737e+02	5.173e+02	1.022e+03	6.355e+02	5.710e+02
		std	3.828e+01	4.075e+01	1.328e+01	9.912e+01	3.794e+01	3.586e+01
	100	mean	9.143e+02	9.063e+02	7.954e+02	2.248e+03	1.028e+03	8.841e+02
		std	4.168e+01	9.196e+01	4.139e+01	1.273e+02	8.440e+01	5.372e+01
$F_5$	30	mean	6.106e+03	3.281e+03	2.942e+03	6.952e+03	4.543e+03	2.696e+03
		std	1.242e+03	6.451e+02	1.876e+02	5.424e+02	5.729e+02	4.189e+02
	50	mean	1.210e+04	5.680e+03	5.383e+03	1.327e+04	7.819e+03	5.185e+03
		std	1.686e+03	8.475e+02	4.151e+02	3.994e+02	9.045e+02	5.537e+02
	100	mean	2.959e+04	1.385e+04	1.345e+04	3.024e+04	1.706e+04	1.161e+04
		std	1.216e+03	1.172e+03	6.221e+02	4.994e+02	1.478e+03	1.189e+03
$F_6$	30	mean	6.067e+05	1.230e+05	6.749e+05	1.609e+06	4.092e+06	8.486e+04
		std	1.209e+06	8.402e+04	4.037e+05	1.295e+06	3.645e+06	1.170e+05
	50	mean	8.012e+06	2.614e+05	4.073e+06	1.714e+07	1.922e+07	2.307e+05
		std	5.051e+06	1.218e+05	1.535e+06	1.039e+07	1.015e+07	1.474e+05
	100	mean	2.047e+07	1.042e+06	1.374e+07	3.952e+08	4.403e+07	5.352e+05
		std	1.115e+07	5.142e+05	3.612e+06	9.129e+07	2.040e+07	3.247e+05
$F_7$	30	mean	7.101e+02	7.056e+02	7.064e+02	7.110e+02	7.152e+02	7.071e+02
		std	3.640e+00	1.067e+00	9.552e−01	4.311e+00	3.398e+00	1.334e+00
	50	mean	7.936e+02	7.419e+02	7.355e+02	8.190e+02	7.843e+02	7.728e+02
		std	7.763e+00	2.023e+01	1.983e+01	2.838e+01	1.089e+01	1.966e+01
	100	mean	9.561e+02	7.508e+02	7.452e+02	1.357e+03	9.524e+02	7.761e+02
		std	1.344e+02	3.043e+01	2.822e+00	3.869e+02	1.075e+02	1.876e+01
$F_8$	30	mean	7.787e+04	3.794e+04	1.775e+05	1.454e+05	1.232e+06	2.825e+04
		std	1.141e+05	2.722e+04	2.023e+05	1.114e+05	1.310e+06	2.615e+04
	50	mean	8.091e+05	1.327e+05	8.641e+05	2.735e+06	7.135e+06	8.081e+04
		std	1.194e+06	1.101e+05	3.224e+05	1.647e+06	5.313e+06	3.389e+04
	100	mean	2.013e+07	7.093e+05	4.949e+06	6.983e+07	3.961e+07	4.705e+05
		std	1.752e+07	3.205e+05	1.518e+06	3.171e+07	2.103e+07	2.455e+05
$F_9$	30	mean	1.005e+03	1.001e+03	1.001e+03	1.029e+03	1.025e+03	1.002e+03
		std	3.427e+00	8.460e−02	5.074e−02	2.420e+01	6.840e+01	2.512e−01
	50	mean	1.016e+03	1.002e+03	1.002e+03	1.234e+03	1.035e+03	1.003e+03
		std	1.479e+01	1.599e−01	1.101e−01	5.026e+01	9.757e+01	2.883e−01
	100	mean	1.059e+03	1.006e+03	1.005e+03	1.966e+03	1.012e+03	1.007e+03
		std	4.260e+01	7.105e−01	2.443e−01	2.285e+02	1.101e+00	5.486e−01
$F_{10}$	30	mean	3.279e+05	5.382e+04	1.925e+05	3.915e+05	2.976e+06	2.999e+05
		std	3.989e+05	5.408e+04	7.469e+04	1.845e+05	2.416e+06	3.079e+05
	50	mean	1.972e+06	6.445e+04	5.992e+05	7.240e+05	5.105e+06	6.832e+05
		std	1.589e+06	5.427e+04	3.545e+05	3.956e+05	3.435e+06	7.094e+05
	100	mean	8.749e+06	8.912e+03	7.821e+05	2.284e+07	1.744e+07	2.349e+05
		std	3.606e+06	2.135e+03	3.056e+05	1.102e+07	7.934e+06	3.214e+05

Table 5. Results for CEC'15 Learning-Based Benchmark Suite $F_{11}-F_{15}$.

Func.	Dim		PSO-LVIW	BBPSO	CLPSO	SRPSO	GLPSO	MBPSO
$F_{11}$	30	mean	1.586e+03	1.759e+03	1.524e+03	1.735e+03	1.959e+03	1.741e+03
		std	1.303e+02	5.378e+01	1.321e+01	2.636e+02	1.161e+02	6.017e+01
	50	mean	2.242e+03	2.154e+03	1.959e+03	3.018e+03	2.317e+03	2.000e+03
		std	1.121e+02	6.849e+01	2.863e+02	2.136e+02	1.267e+02	1.051e+02
	100	mean	3.836e+03	3.607e+03	3.163e+03	5.391e+03	3.571e+03	3.310e+03
		std	2.119e+02	3.069e+02	5.251e+02	1.969e+02	6.466e+02	1.600e+02
$F_{12}$	30	mean	1.424e+03	1.418e+03	1.400e+03	1.458e+03	1.432e+03	1.421e+03
		std	8.107e+00	1.289e+00	5.258e+01	9.337e+00	2.843e+01	1.253e+00
	50	mean	1.493e+03	1.433e+03	1.430e+03	1.506e+03	1.466e+03	1.453e+03
		std	1.375e+01	4.336e−01	3.170e−01	1.472e+01	7.372e+00	2.714e+00
	100	mean	1.586e+03	1.430e+03	1.426e+03	1.611e+03	1.485e+03	1.462e+03
		std	2.712e+01	1.106e+00	1.600e−01	2.529e+01	1.986e+01	8.188e+00
$F_{13}$	30	mean	1.434e+03	1.407e+03	1.401e+03	1.449e+03	1.423e+03	1.399e+03
		std	1.217e+01	6.431e+00	4.069e+00	3.943e+00	9.346e+00	1.114e+01
	50	mean	1.550e+03	1.497e+03	1.487e+03	1.564e+03	1.520e+03	1.490e+03
		std	1.125e+01	1.162e+01	4.427e+00	1.750e+01	1.107e+01	7.044e+00
	100	mean	1.861e+03	1.726e+03	1.711e+03	1.915e+03	1.762e+03	1.715e+03
		std	3.043e+01	1.614e+01	5.806e+00	4.923e+01	1.745e+01	1.427e+01
$F_{14}$	30	mean	4.363e+04	2.467e+04	2.394e+04	4.822e+04	3.968e+04	2.607e+04
		std	3.111e+03	9.355e+02	8.893e+02	4.185e+03	6.436e+03	1.287e+03
	50	mean	7.267e+04	4.786e+04	4.613e+04	8.884e+04	6.725e+04	5.457e+04
		std	4.405e+03	5.472e+03	4.822e−02	9.238e+03	3.513e+03	3.893e+03
	100	mean	2.781e+05	1.180e+05	1.124e+05	4.163e+05	2.251e+05	1.625e+05
		std	3.616e+04	2.660e+03	6.895e+02	5.328e+04	1.373e+04	1.272e+04
$F_{15}$	30	mean	1.710e+03	1.700e+03	1.700e+03	2.998e+03	1.705e+03	1.700e+03
		std	9.734e+00	2.144e−13	6.296e−13	1.378e+03	2.220e+00	2.061e−08
	50	mean	1.738e+03	1.700e+03	1.700e+03	8.599e+03	1.721e+03	1.700e+03
		std	9.112e+00	4.151e−13	6.386e−13	5.630e+03	1.185e+01	8.006e−09
	100	mean	1.767e+03	1.707e+03	1.700e+03	2.221e+05	1.747e+03	1.700e+03
		std	2.872e+01	4.873e+00	1.378e−11	8.763e+04	1.418e+01	2.824e−09

4.3.1. Experimental results on the basic test functions

For the ten basic test functions $f_1-f_{10}$, benefited from the GA operation, GLPSO shows its excellent accuracy and convergence speed on $f_1$, $f_3$, $f_4$, $f_5$, $f_6$, $f_8$ and $f_{10}$ whether in 30-dimensional, 50-dimensional or 100-dimensional, however it fails to converge on $f_7$. MBPSO shows a stable convergence ability on those basic test functions, and it is the only one that the result could close to the global optimum on $f_7$ in 30, 50 and 100 dimensional. Meanwhile, MBPSO is the second best algorithm on $f_2$, $f_3$, $f_4$, $f_8$, $f_9$ and $f_{10}$ in 30-dimensional, on $f_3$, $f_4$, $f_8$, $f_9$ and $f_{10}$ in 50-dimensional, on $f_3$, $f_8$, $f_9$ and $f_{10}$ in 100-dimensional. From the Figures 4 and 5, we can observe that although the convergence accuracy is not the strengths for MBPSO, it performs competitively on most functions when compared with PSO-LVIW, BBPSO, CLPSO and SRPSO.

4.3.2. Experimental results on the CEC'15 learning-based benchmark suite

It can be easily observed that MBPSO is a competitive PSO variant for the CEC'15 Learning-Based Benchmark Suite. When the dimensions are 30, MBPSO is ranked the first on $F_1$, $F_3$, $F_5$, $F_6$, $F_8$, $F_{13}$ and $F_{15}$ and ranked the second on $F_4$. When the dimensions are 50, MBPSO is ranked the first on $F_1$, $F_3$, $F_5$, $F_6$, $F_8$ and $F_{15}$ and ranked the second on $F_4$, $F_{11}$ and $F_{13}$. When the dimensions are 100, MBPSO is ranked the first on $F_1$, $F_3$, $F_5$, $F_6$, $F_8$ and $F_{15}$ and ranked the second on $F_4$, $F_{10}$, $F_{11}$ and $F_{13}$. GLPSO performs best on the basic test functions, however the performance is worse than MBPSO, CLPSO and BBPSO significantly when it be tested on the CEC'15 Learning-Based Benchmark Suite. The results on the CEC'15 Learning-Based Benchmark Suite verifies that MBPSO has a good adaptive capability, especially for some complex problems.

4.4. Statistical comparison

In order to further compare MBPSO with other PSO variants, the comparisons of PSO-LVIW, BBPSO, CLPSO, SRPSO, GLPSO and MBPSO for benchmark functions $f_1-f_{10}$ and $F_1-F_{15}$ on 30-dimensional, 50-dimensional and 100-dimensional are shown in Tables 6–8, respectively, where $(+)$ and $(-)$ denote that the t-test results of compared algorithm are significantly better and worse than MBPSO (p<0.05), and $(=)$ stands for the differences between the results are not significant.

Table 6. Comparisons between MBPSO and other PSO variants for the average fitness (30-dimensional).

Function	PSO-LIVE Rank(WTR)	BBPSO Rank(WTR)	CLPSO Rank(WTR)	SRPSO Rank(WTR)	GLPSO Rank(WTR)	MBPSO Rank
$f_1$	$3(=)$	$2(=)$	$5(=)$	$4(=)$	$1(=)$	6
$f_2$	$5(-)$	$3(=)$	$1(+)$	$6(-)$	$4(-)$	2
$f_3$	$5(-)$	$3(-)$	$4(-)$	$6(-)$	$1(+)$	2
$f_4$	$5(-)$	$4(-)$	$3(-)$	$6(-)$	$1(+)$	2
$f_5$	$3(=)$	$4(=)$	$1(+)$	$6(-)$	$1(+)$	5
$f_6$	$4(-)$	$5(-)$	$1(=)$	$6(-)$	$1(=)$	3
$f_7$	$5(-)$	$3(-)$	$2(-)$	$4(-)$	$6(-)$	1
$f_8$	$5(-)$	$4(-)$	$3(-)$	$6(-)$	$1(+)$	2
$f_9$	$4(-)$	$3(-)$	$1(+)$	$6(-)$	$5(-)$	2
$f_{10}$	$4(-)$	$5(-)$	$3(-)$	$6(-)$	$1(+)$	2
$F_1$	$4(-)$	$2(-)$	$3(-)$	$6(-)$	$5(-)$	1
$F_2$	$3(=)$	$2(=)$	$1(+)$	$6(-)$	$5(=)$	4
$F_3$	$4(-)$	$5(-)$	$2(-)$	$6(-)$	$3(-)$	1
$F_4$	$3(=)$	$4(-)$	$1(+)$	$6(-)$	$5(-)$	2
$F_5$	$5(-)$	$3(-)$	$2(-)$	$6(-)$	$4(-)$	1
$F_6$	$3(-)$	$2(=)$	$4(-)$	$5(-)$	$6(-)$	1
$F_7$	$4(-)$	$1(+)$	$2(+)$	$5(-)$	$6(-)$	3
$F_8$	$3(-)$	$2(=)$	$5(-)$	$4(-)$	$6(-)$	1
$F_9$	$4(-)$	$1(+)$	$2(+)$	$6(-)$	$5(=)$	3
$F_{10}$	$4(=)$	$1(+)$	$2(=)$	$5(=)$	$6(-)$	3
$F_{11}$	$2(+)$	$5(=)$	$1(+)$	$3(=)$	$6(-)$	4
$F_{12}$	$4(-)$	$2(+)$	$1(+)$	$6(-)$	$5(-)$	3
$F_{13}$	$5(-)$	$3(-)$	$2(=)$	$6(-)$	$4(-)$	1
$F_{14}$	$5(-)$	$2(+)$	$1(+)$	$6(-)$	$4(-)$	3
$F_{15}$	$5(-)$	$1(=)$	$1(=)$	$6(-)$	$4(-)$	1
Avg.Rank	4.04	2.88	2.16	5.52	3.88	2.36
Final.Rank	5	3	1	6	4	2
Sig.Better	1	5	10	0	5	∖
Sig.Worse	19	12	10	22	16	∖

Table 7. Comparisons between MBPSO and other PSO variants for the average fitness (50-dimensional).

Function	PSO-LIVE Rank(WTR)	BBPSO Rank(WTR)	CLPSO Rank(WTR)	SRPSO Rank(WTR)	GLPSO Rank(WTR)	MBPSO Rank
$f_1$	$3(+)$	$2(+)$	$4(+)$	$6(=)$	$1(+)$	5
$f_2$	$5(-)$	$4(=)$	$1(+)$	$6(-)$	$2(=)$	3
$f_3$	$5(-)$	$3(-)$	$4(-)$	$6(-)$	$1(+)$	2
$f_4$	$5(-)$	$3(-)$	$4(-)$	$6(-)$	$1(+)$	2
$f_5$	$5(=)$	$3(=)$	$1(+)$	$6(-)$	$1(+)$	4
$f_6$	$4(-)$	$5(-)$	$2(+)$	$6(-)$	$1(+)$	3
$f_7$	$6(-)$	$3(-)$	$1(=)$	$4(-)$	$5(-)$	1
$f_8$	$5(-)$	$3(-)$	$4(-)$	$6(-)$	$1(+)$	2
$f_9$	$4(-)$	$3(-)$	$1(+)$	$6(-)$	$5(-)$	2
$f_{10}$	$4(-)$	$5(-)$	$3(-)$	$6(-)$	$1(+)$	2
$F_1$	$4(-)$	$2(-)$	$3(-)$	$6(-)$	$5(-)$	1
$F_2$	$2(=)$	$3(=)$	$1(+)$	$6(-)$	$5(=)$	4
$F_3$	$4(-)$	$5(-)$	$2(-)$	$6(-)$	$3(-)$	1
$F_4$	$4(-)$	$3(-)$	$1(+)$	$6(-)$	$5(-)$	2
$F_5$	$5(-)$	$3(-)$	$2(=)$	$6(-)$	$4(-)$	1
$F_6$	$4(-)$	$2(=)$	$3(-)$	$5(-)$	$6(-)$	1
$F_7$	$5(-)$	$2(+)$	$1(+)$	$6(-)$	$4(-)$	3
$F_8$	$3(-)$	$2(-)$	$4(-)$	$5(-)$	$6(-)$	1
$F_9$	$4(-)$	$1(+)$	$2(+)$	$6(-)$	$5(=)$	3
$F_{10}$	$5(-)$	$1(+)$	$2(=)$	$4(=)$	$6(-)$	3
$F_{11}$	$4(-)$	$3(-)$	$1(=)$	$6(-)$	$5(-)$	2
$F_{12}$	$5(-)$	$2(+)$	$1(+)$	$6(-)$	$4(-)$	3
$F_{13}$	$5(-)$	$3(-)$	$1(=)$	$6(-)$	$4(-)$	2
$F_{14}$	$5(-)$	$2(+)$	$1(+)$	$6(-)$	$4(-)$	3
$F_{15}$	$5(-)$	$1(=)$	$1(=)$	$6(-)$	$4(-)$	1
Avg.Rank	4.40	2.76	2.04	5.76	3.60	2.28
Final.Rank	5	3	1	6	4	2
Sig.Better	1	6	11	0	7	∖
Sig.Worse	22	14	8	23	15	∖

Table 8. Comparisons between MBPSO and other PSO variants for the average fitness (100-dimensional).

Function	PSO-LIVE Rank(WTR)	BBPSO Rank(WTR)	CLPSO Rank(WTR)	SRPSO Rank(WTR)	GLPSO Rank(WTR)	MBPSO Rank
$f_1$	$4(+)$	$2(+)$	$3(+)$	$6(-)$	$1(+)$	5
$f_2$	$4(=)$	$3(=)$	$1(+)$	$6(-)$	$2(+)$	5
$f_3$	$5(=)$	$2(=)$	$3(=)$	$6(-)$	$1(+)$	4
$f_4$	$5(-)$	$2(+)$	$3(+)$	$6(-)$	$1(+)$	4
$f_5$	$3(=)$	$4(=)$	$1(+)$	$6(-)$	$1(+)$	5
$f_6$	$4(-)$	$5(-)$	$2(+)$	$6(-)$	$1(+)$	3
$f_7$	$6(-)$	$4(-)$	$2(-)$	$3(-)$	$5(-)$	1
$f_8$	$5(-)$	$4(-)$	$2(-)$	$6(-)$	$1(+)$	2
$f_9$	$5(-)$	$4(-)$	$1(=)$	$6(-)$	$3(-)$	2
$f_{10}$	$4(-)$	$5(-)$	$3(-)$	$6(-)$	$1(+)$	2
$F_1$	$4(-)$	$2(-)$	$3(-)$	$6(-)$	$5(-)$	1
$F_2$	$2(=)$	$3(=)$	$1(+)$	$6(-)$	$5(-)$	4
$F_3$	$4(-)$	$5(-)$	$2(-)$	$6(-)$	$3(-)$	1
$F_4$	$4(-)$	$3(=)$	$1(+)$	$6(-)$	$5(-)$	2
$F_5$	$5(-)$	$3(-)$	$2(-)$	$6(-)$	$4(-)$	1
$F_6$	$4(-)$	$2(-)$	$3(-)$	$6(-)$	$5(-)$	1
$F_7$	$5(-)$	$2(+)$	$1(+)$	$6(-)$	$4(-)$	3
$F_8$	$4(-)$	$2(-)$	$3(-)$	$6(-)$	$5(-)$	1
$F_9$	$5(-)$	$2(+)$	$1(+)$	$6(-)$	$4(-)$	3
$F_{10}$	$4(-)$	$1(+)$	$3(-)$	$6(-)$	$5(-)$	2
$F_{11}$	$5(-)$	$4(-)$	$1(=)$	$6(-)$	$3(-)$	2
$F_{12}$	$5(-)$	$2(+)$	$1(+)$	$6(-)$	$4(-)$	3
$F_{13}$	$5(-)$	$3(-)$	$1(=)$	$6(-)$	$4(-)$	2
$F_{14}$	$5(-)$	$2(+)$	$1(+)$	$6(-)$	$4(-)$	3
$F_{15}$	$5(-)$	$3(-)$	$1(=)$	$6(-)$	$4(-)$	1
Avg.Rank	4.44	2.96	1.88	5.88	3.28	2.52
Final.Rank	5	3	1	6	4	2
Sig.Better	1	7	11	0	8	∖
Sig.Worse	20	13	9	25	17	∖

From Tables 6–8 we can obverse that although MBPSO is not the best algorithm among the six algorithms, it is a competitive algorithm that significantly better than PSO-LVIW, BBPSO, SRPSO and GLPSO. Compare with CLPSO, the ratio of significantly better and significantly worse on 30-dimensional, 50-dimensional and 100 dimensional are 10:10, 11:8 and 11:9 respectively, which reports that there are little difference between the two algorithms for the optimisation, and each of them has its own strengths and weaknesses when dealing with different problems.

5. Discussion of parameter settings for MBPSO

In MBPSO, two new parameters were introduced. One is the mutation probability pm, and the other is the cycle of mutation breeding operation cm. In order to thoroughly investigate the sensitivity of MBPSO to the pm and cm, we choose ten representative functions among the 25 benchmark functions, to evaluate the effect of the two parameters in 30, 50 and 100 dimensional. Five basic test functions, $f_1$, $f_3$, $f_5$, $f_7$ and $f_9$, and five CEC'15 test functions, $F_1$, $F_4$, $F_8$, $F_{10}$ and $F_{14}$, are chosen for the experiment. The population size is set to 40, and the maximum optimisation iteration number is set to $1\times {10}^4\cdot D$.

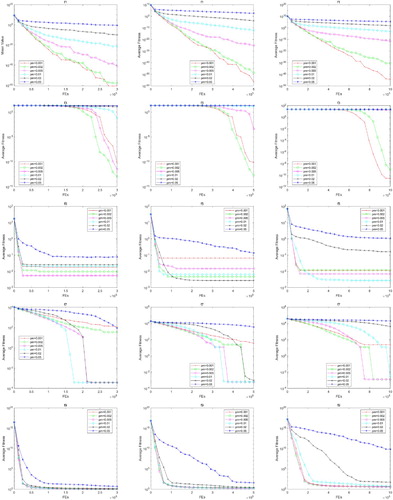
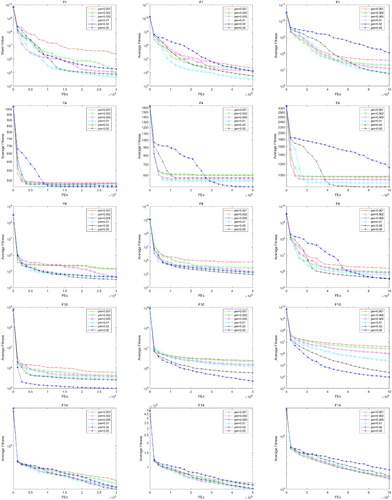
First, the mutation probability pm is investigated with $pm=$ 0.001, 0.002, 0.005, 0.01, 0.02 and 0.05, respectively. The parameters of the cycle of mutation breeding operation cm is fixed to 10. The test results on basic test functions $f_1$, $f_3$, $f_5$, $f_7$ and $f_9$ have been shown in Figure 9 from top to bottom. The test results on CEC'15 test functions $F_1$, $F_4$, $F_8$, $F_{10}$ and $F_{14}$ have been shown in Figure 10 from top to bottom.

Figure 9. The average fitness curve of different pm of MBPSO runs on $f_1$, $f_3$, $f_5$, $f_7$ and $f_9$.

Figure 10. The average fitness curve of different pm of MBPSO runs on $F_1$, $F_4$, $F_8$, $F_{10}$ and $F_{14}$.

By observing the Figure 9, we can find that for $f_1$, the pm is smaller the better. For $f_3$, pm = 0.001 or 0.002 is better than other options. For $f_5$, except pm = 0.05 is a bad choice in every conditions, there are no significant differences between other options. For $f_7$, $pm=0.002$, 0.005 and 0.01 can obtain a stable convergence. For $f_9$, the convergence result is not sensitive to the pm when pm<0.05.

Let us observe the Figure 10. For $F_1$, pm = 0.01 or 0.02 is better than others, whether a too small or too big value will reduce the performance. For $F_4$, a relatively large value of pm may help the algorithm to jump out from local minimum more easily. For $F_8$, pm = 0.02 or 0.05 is relatively better than other options. For $F_{10}$, pm is the larger the better, just contrary to the curves of $f_1$. For $F_{14}$, the convergence is not sensitive to the pm, pm = 0.01 is relatively better than others.

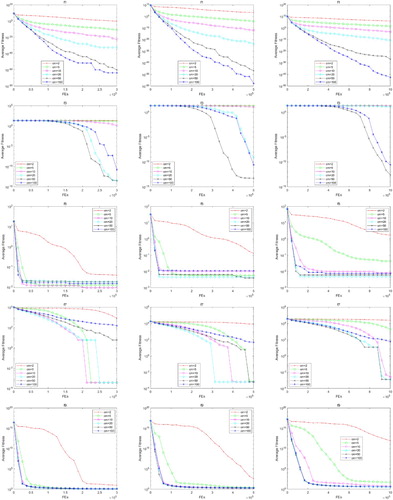
Second, the cycle of mutation breeding operation cm is investigated with cm = 2, 5, 10, 20, 50 and 100, respectively. The parameters of the probability of mutation breeding pm is fixed to 0.01. The test result have been shown in Figures 11 and 12.

Figure 11. The average fitness curve of different cm of MBPSO runs on $f_1$, $f_3$, $f_5$, $f_7$ and $f_9$.

Figure 12. The average fitness curve of different cm of MBPSO runs on $F_1$, $F_4$, $F_8$, $F_{10}$ and $F_{14}$.

Figure 11 shows that a large cm will help to improve the convergence accuracy for $f_1$. For $f_3$, cm = 50 is the best option. For $f_5$, a small cm may cause difficult to convergence. For $f_7$, in the condition of $cm=10$, 20, or 50 the algorithm can reach a low error to the global minimum, and whether the cm is too small or too large will generate a poor result. For $f_9$, the pm<5 will slow down the convergence speed obviously.

Figure 12 reports that for $F_1$, cm = 10 is the best option when the dimensions are 50 or 100. For $F_4$, the convergence speed will be reduced when the pm is small, while the results have no significant difference. For $F_8$, the results are not sensitive to the different cm. For $F_{10}$, $cm=2$ or 5 is better than other options, and the convergence accuracy will be reduced with the increasing cm. For $F_{14}$, the best value of pm is 10 or 20.

From the above, MBPSO is a parameter sensitive algorithm, for different problems, the most appropriate parameter settings are also different. In generally, for a simple problem, a small pm and a large cm can improve the convergence speed, on the contrary, a big pm and a small cm will provide a higher probability to jump out from the local optimum, which is more appropriate for some complex problem. In this paper, we set the pm to 0.01 and the cm to 10, which is a compromise for most problems to get a relatively good results.

6. Conclusions

This paper presents a novel PSO algorithm inspired by mutation breeding. The proposed algorithm through a method that to perform a mutation breeding operation periodically to control the diversity of population, which can overcome the shortcoming of classical PSO like premature convergence or difficult to convergence for some problems. The mutation breeding operation can be divided into two steps, first, breed the global best previously visited position to replace all of the best previously visited positions of each particle, second, mutate those new generated best previously visited positions randomly. After a mutation breeding operation, the global best previously visited position will be replaced with the best position in the current population at the following iteration. The experiments results illustrate that the MBPSO algorithm has a competitive performance when compared with other PSO variants. However, the discussion of parameter settings shows that MBPSO is a parameter sensitive algorithm, and to further improve the optimisation ability of MBPSO, the strategy of parameter adaption should be borrowed. In the future, we will study the MBPSO with parameter adaption to improve the optimisation ability of the proposed algorithm.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by the National Natural Science Foundation of China [Nos. 61572241 and 61976108], the National Key R&D Program of China [No. 2017YFC0806600], the Foundation of the Peak of Six Talents of Jiangsu Province [No. 2015-DZXX-024], the Fifth ”333 High Level Talented Person Cultivating Project” of Jiangsu Province [No. (2016) III-0845], and the Research Innovation Program for College Graduates of Jiangsu Province [No. KYLX-1056].