?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.Abstract
In this paper, adaptive-sliding mode control method is proposed for synchronisation of two 6D hyper-chaotic systems in the presence of external disturbance and parametric uncertainty and unknown parameters in the slave system. In the first section of this paper, two 6D integer order hyper-chaotic systems in the presence of external disturbance signal, parametric uncertainty and unknown parameters in the slave system are studied. In the second part of this paper, after identifying chaos in fractional order dynamic of the mentioned system, synchronisation of two 6D fractional derivative hyper-chaotic systems in the presence of external disturbance signal, parametric uncertainty and unknown parameters in the slave system is investigated, in which fractional order Riemann-Liouville derivative is used; a new fractional order sliding surface is defined for the hyper-chaotic system to determine the proper active control. Proper adaptive control laws are used to estimate the uncertainty bound, unknown disturbance signal and system parameters. Stability of the closed-loop control system is proved using Lyapunov theory in both modes. Simulation results in MATLAB show the desired application of the proposed controllers in the presence of disturbance and parametric uncertainty.
1. Introduction
Chaos theory has important features like nonlinear dynamic and sensitivity to initial condition. The main characteristic of the chaotic systems is sensitivity to initial conditions. Edward Lorenz published results of differential system calculations of atmospheric thermal displacement and observed that in a certain range of factors, without the involvement of random elements or external disturbance, irregular fluctuations emerge in the system response. He concluded that a small change in the initial condition of the equations predicting atmospheric condition, results in fluctuations in system response and considerable changes in the results. Chaos has attracted attention in many sciences including secure communication (Belkhouja, Du, Mohamed, Al-Ali, & Guizani, Citation2018), nonlinear circuits (Chithra & Raja Mohamed, Citation2017), power electronics (Kumar, Banerjee, Kumar, & Kumar, Citation2018; Zribi, Alrifai, & Smaoui, Citation2018), robotics (Zang, Iqbal, Zhu, Liu, & Zhao, Citation2016), etc.
Lyapunov exponent was used before the emergence of chaos theory for specifying stability of linear and nonlinear systems. Lyapunov exponent is calculated through measuring the extension or contraction of a system. In fact, in this method, the mean speed with which two-point transition paths which were close at the beginning and deviate from each other exponentially, is calculated. Various methods have been proposed for calculating Lyapunov exponent among which Jacobin matrix method can be mentioned in which a negative Lyapunov exponent indicates convergence rate and a positive Lyapunov exponent indicates divergence rate. Chaotic systems of higher dimensions are called hyper-chaotic systems. Hyper-chaotic systems which have at least one positive Lyapunov exponent have more irregular and complicated behaviour compared to the chaotic systems which are used in many applications including secure communication (Liu et al. Citation2018) and cryptography (Lagmiri, Amghar, & Sbiti, Citation2017).
Fractional calculus improves the efficiency of the control systems in two ways: (a) improving modelling quality. (b) Improving the efficiency of the controllers. Fractional calculus helps accurate modelling of the processes and control systems. It is obvious that using a more accurate model of the system, a more appropriate controller can be designed for controlling the intent system and process.
There are many fractional order systems with fractional order dynamic in which chaos and hyper-chaos phenomena are observed. Like Lu integer order hyper-chaotic system (Wang, Citation2015) and Lu fractional order hyper-chaotic system (Huang, Wang, Zhang, & Guo, Citation2018), Lorenz integer order hyper-chaotic system (Chen, Citation2018; Yang & Bai, Citation2017) and Lorenz fractional order hyper-chaotic system (Khamsuwan, Sangpet, & Kuntanapreeda, Citation2018), Liu integer order hyper-chaotic system (Wang, Citation2016) and Liu fractional order hyper-chaotic system (Qiang, Chong-Xin, Lei, & Da-Rui, Citation2013) which have attracted attention of researchers.
Various studies in recent decades have been conducted on synchronisation of integer order hyper-chaos like Daltzis, Volos, Nistazakis, Tsigopoulos, and Tombras (Citation2018), and Lu et al. (Citation2018) in which synchronisation of hyper-chaotic systems using adaptive control has been studied. In Ahmad, Saaban, Ibrahim, and Shahzad (Citation2018), synchronisation of hyper-chaotic system using active control has been investigated. In Rajagopal, Vaidyanathan, Karthikeyan, and Srinivasan (Citation2018), synchronisation of hyper-chaotic systems using adaptive sliding mode control has been studied. In the study by Vaidyanathan et al. (Citation2018), Vaidyanathan et al. (Citation2018), and Vaidyanathan (Citation2017), synchronisation of hyper-chaotic systems with adaptive backstepping control has been proposed. In Wu, Xiong, Hu, Feng, and Li (Citation2018), synchronisation of hyper-chaotic systems with sandwich control has been investigated. In the presented papers, dimension of chaotic systems is less than 6, but in recent years, researchers have focused considerably on fractional order chaotic systems. But, fewer studies have been conducted on fractional order hyper-chaotic systems among which Noghredani and Balochian (Citation2015) study can be mentioned which has investigated synchronisation of fractional order hyper-chaotic systems using sliding mode control. In Khan and Tyagi (Citation2017), and Khan and Tyagi (Citation2018), two fractional order chaotic systems with adaptive-sliding mode control have been synchronised. In Zhou, Liu, Cao, and Li (Citation2019), two fractional order neural network systems with fuzzy control have been synchronised in Caputo definition of fractional derivative. In Wang, Ni, and Yang (Citation2018), fractional order hyper-chaotic systems with fuzzy control have been synchronised. In Khan, Khattar, and Agrawal (Citation2018), and Liu, Chen, Li, Xiang, and Xu (Citation2017), feedback control has been used for synchronisation of fractional order systems. In Fu and Liu (Citation2018), fractional order hyper-chaotic systems with adaptive-fuzzy control have been synchronised and in Liu et al. (Citation2018), synchronisation of two identical fractional order neural networks with full/under-actuation and Caputo definition of fractional derivative is presented via fractional order sliding mode controller, and a sufficient condition is given to seek the control gain matrix by solving LMI.
In many of these studies, synchronisation of fractional order hyper-chaotic systems which their dimension is less than 6 has been investigated.
One important application of chaos in information exchange is security and protection. In this communication, chaotic systems can be used to increase the security of the exchanged information. Since the behaviour of chaotic systems is close to the behaviour of complicated and noisy systems, information can be hidden in such systems with high reliability. The main idea of information exchange using chaotic systems is based on embedding information in the transmitter which creates a chaotic signal. In secure communication, high order chaotic systems and fractional order chaotic systems can be used due to higher complexity. There are many studied on the application of chaos and hyper-chaos in secure communication (Djennoune, Bettayeb, & Al-Saggaf, Citation2019; Ouannas, Bendoukha, Volos, Boumaza, & Karouma, Citation2019).
In most studies of chaos and synchronisation, authors have used sliding mode controller design for synchronising integer order or fractional order chaotic and hyper chaotic systems in the presence of disturbance, uncertainty and unknown parameters which are not simultaneous. Also, fractional order chaotic systems which their order is 6 or higher than 6 have not been synchronised.
But in this paper, not only 6D like-Lorenz fractional order chaotic system is identified but also two similar 6D like-Lorenz chaotic systems in the presence of disturbance and bounded uncertainty with unknown bounds and unknown system parameters are synchronised using adaptive-sliding mode controller in which, stability and estimation of unknown parameters of the systems are proved using Lyapunov theorem. Efficiency of the proposed method is shown in a practical application which is considered to be secure communication.
Briefly, main contributions of this paper are as follows:
Identification of new fractional order dynamic of the 6D hyper-chaotic systems
Synchronisation of identified 6D fractional order hyper-chaotic systems
Proper adaptive control laws are used to estimate uncertainty and disturbance signal bounded with unknown bounds and unknown system parameters for 6D fractional order hyper chaotic system.
2. Introduction of the dynamic model of the 6D hyper chaotic system
In 2009, a linear feedback controller and a nonlinear feedback control were proposed for 5D Lorenz hyper-chaotic system (Hu, Citation2009).
(1)
(1) Considering system (1), a novel 6D chaotic system similar to Lorenz system is presented which is formed by adding linear feedback and nonlinear feedback to the above system which has four positive Lyapunov exponents. Therefore, one version of the 6D hyper-chaotic system is considered as follows:
(2)
(2) where
is the state vector of the system and
are constants of the system.
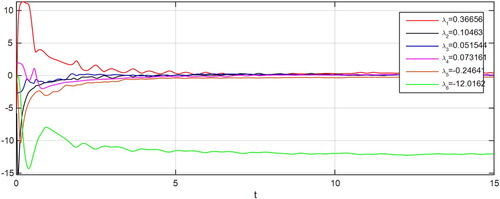
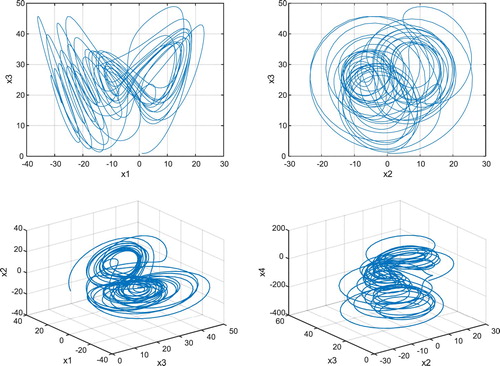
System (1) is a hyper-chaotic system. Because it has more than two Lyapunov exponents. To calculate Lyapunov exponent with according to (Vallejo & Sanjuan, Citation2017) we have:
Jacobian matrix of system (1) is as follows:
Lyapunov exponents and Lyapunov exponent graph of the 6D hyper chaotic system are as follows.
In addition, considering disturbance and uncertainty in parameters, the slave system is described as follows:
(3)
(3)
in which, is the control signal,
is state variable vector of the slave system,
is an uncertain bounded function of the states with unknown bound and
is the bounded disturbance input with unknown bound and
are unknown parameters of the slave system.
Figures and show the hyper chaotic system and Lyapunov exponent graph for the parameter set of , respectively.
In this part, synchronisation of two 6D hyper chaotic systems with unknown parameters, Input uncertainty and disturbance with unknown bound is presented. Input disturbance bound and parametric uncertainty are unknown. Therefore, synchronisation might be difficult. Consider the master and slave systems (2) and (3), respectively. Defining error as :
(4)
(4)
If error dynamic of Equation (4) is asymptotically stable through determining control signal , all states of the slave system converge to states of the master system. But the problem is the presence of uncertainty, disturbance and more important unknown parameters of the slave system and disturbance bound and uncertainty bound. In order to solve this problem, synchronisation of two hyper-chaotic systems in the presence of unknown parameters and disturbance and uncertainty with unknown bounds is solved using the proposed adaptive-sliding mode control.
Sliding mode control is a nonlinear control method that guarantees control strategy over uncertainties. In this way, stability is achieved by keeping the system modes on the sliding surface.
Disturbance and parametric uncertainty bounds of the slave system are estimated using adaptive control.
Now, considering the following sliding surface,
(5)
(5) Gives
(6)
(6)
and assuming , we have:
(7)
(7)
In which, are estimation error of the parameters of the slave system.
On the other hand, the control signal of the proposed controller is considered as follows.
(8)
(8)
In which, and
are positive real constants and:
(9)
(9)
And estimation rules are as follows:
(10)
(10)
Theorem 1
If the control rule (8), where parameters are unknown constants of the chaotic slave system and estimation rule Equations (10), then all states of system (3) will converge to those of system (2).
Proof: Suppose that the Lyapunov function is considered as (11) which is a positive definite function. Given the Lyapunov stability theorem, to prove the stability of the error dynamic (4), it should be shown that the derivative of the Lyapunov function is negative, so according to selective s, u proves the asymptotic stability using the Lyapunov stability.
The proposed Lyapunov function is as follows:
(11)
(11)
And its derivative is as follows.
(12)
(12)
Using Equation (5), we have
(13)
(13)
According to and
, the relations would be as follows:
(14)
(14)
Now, according to Equations (8), (9) and (10), the relations can be rewritten as follows:
(15)
(15)
By choosing, values of ρ and r greater than zero, becomes negative and Lypanov’s stability condition is met.
Remark 1
the control parameter gives us the privilege to synchronise the states in less time by regulating this parameter. And the larger the selection, the faster the synchronisation will be. The parameters
and
are also other control parameters, whose main condition in the Theorem 1, is that they must be selected greater than zero, otherwise the derivative of the Lyapunov function will not be negative and no stability will be achieved.
3. 6d fractional order hyper chaotic system
In this paper, Reimann–Liouville fractional order derivative is used. Definition of Riemann–Liouville from the fractional derivative is as follows:
where a and t are lower and upper bounds of the fractional integral in the definition of this operator and
is the gamma function.
is described as follows:
In the following, a 6D fractional order nonlinear system is introduced:
In which, is a vector function of the state variables
and
is the fractional order derivative and
are initial values and
is the Riemann–Liouville fractional order differentiation. Consider the 6D dynamic as follows:
(16)
(16) where
is the fractional order of differentiation and
is the state vector of the system and
are constants of the system.
Therefore, considering the disturbance and uncertainty of the parameters, the slave system is described as follows:
(17)
(17)
In which, is the control signal,
is the vector of state variables of the slave system,
are uncertain bounded functions of the states with unknown bound and
are bounded disturbance input with unknown bound and
are unknown parameters of the slave system. Also, the following relationships are given.
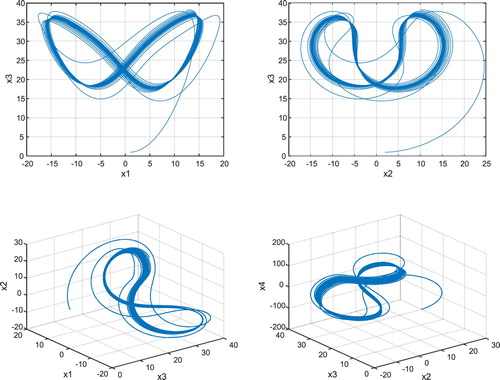
Figure shows the fractional derivative of the hyper chaotic system for the parameter set of
Consider master and slave systems (16) and (17), respectively. Defining error as , we have:
(18)
(18)
Now, synchronisation of two fractional order hyper-chaotic systems in the presence of disturbance and uncertainty with unknown bounds and unknown parameters is presented using adaptive-sliding mode control and bounds of disturbance and parametric uncertainty of the slave systems are estimated using the adaptive rules.
Now, considering the following sliding surface,
(19)
(19) Gives
(20)
(20)
We have the following through mathematical manipulation:
(21)
(21) In which
are estimation errors of parameters of the slave system. On the other hand, the control signal of the proposed controller is considered as follows.
(22)
(22)
In which, ρ and r are positive real constants and:
(23)
(23) And estimation rules are as follows:
(24)
(24)
Theorem 1
By applying the control laws in Equation (22) to the system of Equation (17) and adaptive laws of Equation (24), all system states (17) converge to system (16), asymptotically.
Proof: Suppose that the Lyapunov function is considered as (25) which is a positive definite function. Given the Lyapunov stability theorem, to prove the stability of the error dynamic (18), it should be shown that the derivative of the Lyapunov function is negative, so according to selective s, u proves the asymptotic stability using the Lyapunov stability.
The proposed Lyapunov function is as follows:
(25)
(25)
And its derivative is as follows.
Using Equations (20), we have
(26)
(26)
According to and
, the relations would become as follows:
(27)
(27)
Now, according to Equations (22), (23) and (24), the relations can be rewritten as follows:
(28)
(28)
(29)
(29)
By choosing values of ρ and r greater than zero, becomes negative and the Lypanov’s stability condition will be met.
4. Simulation
In this section, numerical simulation for three examples of synchronisation of two 6D integer order and fractional order hyper-chaotic systems with unknown parameters in the presence of disturbance and parametric uncertainty with unknown bounds is presented. Examples 1 and 2 show the performance of the proposed method and Example 3 shows the application of the proposed method in secure communication. Simulation results are obtained using MATLAB software with sampling time 0.00001 s.
Example 1
Consider systems (1) and (2). Simulation is performed with the following initial conditions: ,
, and
. The parameters used in the designed controller are
. Uncertainty and chaos bounded disturbance applied to the system are
and
.
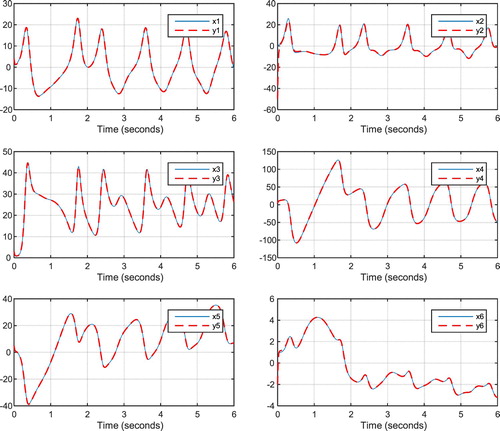
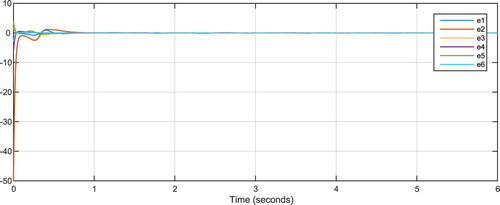
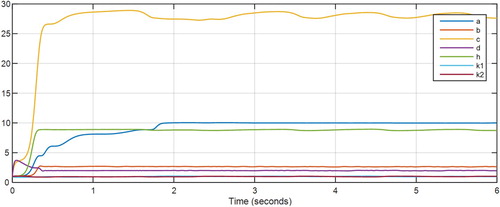
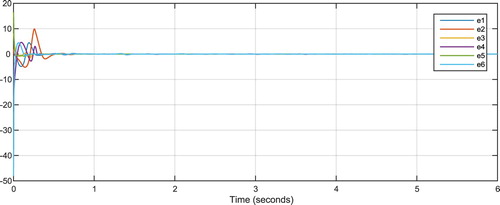
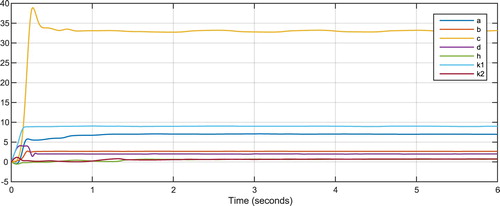
Figures and show the results of synchronisation of the two hyper chaotic 6D systems after applying the controller Equation (8), representing the performance of the proposed controller. Figure shows control signals of Equation (8) and Figure shows the estimates of using Equation (10).
Figure 4. Master and slave system states after applying the proposed controller in Equation (8) for the 6D hyper chaotic system.
Example 2
Consider the fractional derivative systems (16) and (17) with . Simulation is performed with the following initial conditions:
,
, and
. The parameters used in the designed controller are
. Uncertainty and chaos bounded disturbance applied to the system are
.
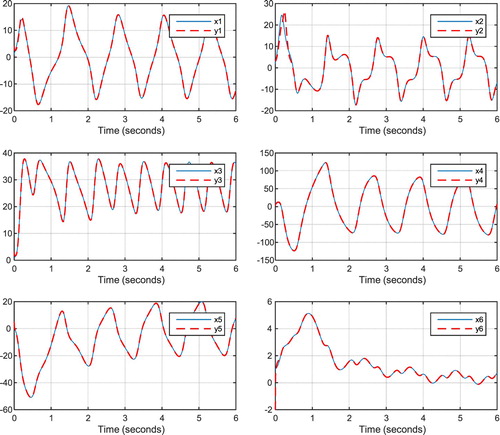
Figures and show the results of synchronisation of the two fractional order hyper chaotic 6D systems after applying the controller as per Equation (22), representing the performance of the proposed controller. Figure shows control signals of Equation (22) and Figure estimates of with using Equation (24).
Figure 8. Master and slave system states after applying the proposed controller in Equation (22) for the 6D fractional order hyper chaotic system.
Example 2
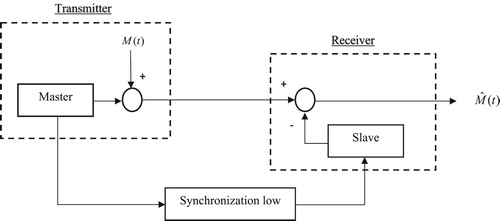
In this example, the mentioned chaotic system is used for secure communication. In the proposed scheme, the message signal is covered by variables of the chaotic system and then it is transmitted. Its simplified block diagram is shown in Figure . Encoding and decoding equations in the transmitter and receiver are as follows.
and
In which, and
are outputs the master and slave systems, respectively.
and
are secondary sides of equations of the 6D like Lorenz fractional order hyper chaotic systems of (16) as the master system and (17) as the slave system with α = 0.89. u is the control signal and
is the message signal combined with state variable
and considered as the output of the master system. After synchronisation and calculating error as follows, we have:
Simulation is performed with the following initial conditions:
and
The parameters used in the designed controller are
. Uncertainty and bounded disturbance applied to the system are
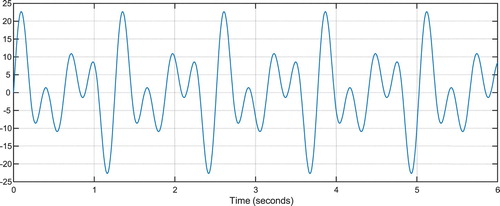
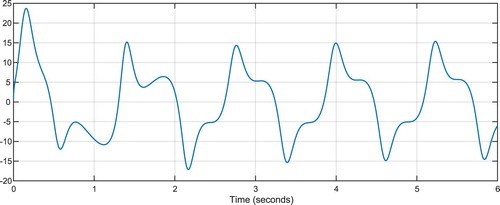
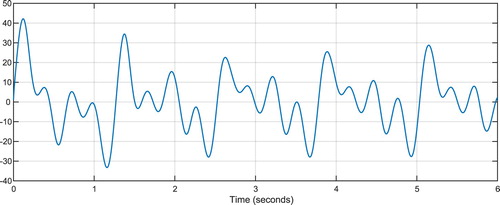
Figure shows the transmitted message signal
. Figure shows chaotic state variable
. Figure shows output of the master system. As can be seen, by adding the message signal, behaviour of
has remained chaotic. Output signal of the system is received at the receiver and by applying the control law in Equation (22) which is shown in Figure , the slave system is synchronised with the master system and output of the slave system is received and compared with the received signal to extract the message signal. Figure shows control signals for initial values of Example 3. Figure shows the difference of the transmitted message signal
and the extracted message signal
. As can be seen, after synchronisation, the difference of
and
becomes zero. In order to eliminate mismatch between the two signals at the beginning of the signal, the message signal is usually transmitted with delay.
In most studies on secure communication, high order chaotic systems are less used for synchronisation of two chaotic systems or chaotic systems in the presence of disturbance, uncertainty and unknown parameters are used. For example:
In Li and Wu (Citation2019), 3D fractional order chaotic system without disturbance, uncertainty and known parameters have been studied. In Djennoune et al. (Citation2019), 3D chaotic system without disturbance and uncertainty has been studied in the context of secure communication. In Ouannas et al. (Citation2019), 4D hyper-chaotic fractional order system without disturbance and uncertainty in the presence of known parameters has been studied.
5. Conclusion
The main purpose of this paper is to design an adaptive-sliding mode controller for 6D integer order and fractional order hyper-chaotic systems in the presence of parametric uncertainty and disturbance with unknown bounds and unknown system parameters. First, the proposed controller is designed for 6D integer order system, then the chaos is observed in the system with fractional order dynamic and an adaptive-sliding mode controller is designed. In order to achieve this goal and synchronise two fractional order and integer order hyper-chaotic systems, sliding control methods which are robust against uncertainty is used. In order to identify the disturbance bounds and unknown parametric uncertainty and system parameters, adaptive controller is used and stability of the chaotic system is proved using Lyapunov theorem. Simulation results in MATLAB show the efficiency of the designed controller. Some of the open problems in this context are: the investigation of chaotic fractional order systems with orders greater than 6 and solution of the problem in presence of measurement noise, synchronisation of two 6D hyper chaotic systems with less control signals with respect to system’s dimensions, and the presence of the uncertainty and disturbance in slave system.
Disclosure statement
No potential conflict of interest was reported by the author(s).
References
- Ahmad, I., Saaban, A., Ibrahim, A., & Shahzad, M. (2018). Modified active controller for the complete synchronization of hyperchaotic system. Mathematical Sciences Letters, 7(1), 1–6.
- Belkhouja, T., Du, X., Mohamed, A., Al-Ali, A. K., & Guizani, M. (2018). Symmetric encryption relying on chaotic Henon system for secure hardware-friendly wireless communication of implantable medical systems. Journal of Sensor and Actuator Networks, 7(2), 21–24.
- Chen, Y.-M. (2018). Dynamics of a Lorenz-type multistable hyperchaotic system. Mathematical Methods in the Applied Sciences, 41(16), 6480–6491.
- Chithra, A., & Raja Mohamed, I. (2017). Synchronization and chaotic communication in nonlinear circuits with nonlinear coupling. Journal of Computational Electronics, 16(3), 833–844.
- Daltzis, P. A., Volos, C. K., Nistazakis, H. E., Tsigopoulos, A. D., & Tombras, G. S. (2018). Analysis, synchronization and circuit design of a 4D hyperchaotic Hyperjerk system. Computation, 6(1), 14.
- Djennoune, S., Bettayeb, M., & Al-Saggaf, U. M. (2019). Synchronization of fractional–order discrete–time chaotic systems by an exact delayed state reconstructor: Application to secure communication. International Journal of Applied Mathematics and Computer Science, 29(1), 179–194.
- Fu, W., & Liu, H. (2018). Adaptive fuzzy synchronization of fractional-order chaotic neural networks with backlash-like hysteresis. Advances in Mathematical Physics, 2018, 1–13.
- Hu, G. (2009). Generating hyperchaotic attractors with three positive lyapunov exponents via state feedback control. International Journal of Bifurcation and Chaos, 19(2), 651–660.
- Huang, Y., Wang, D., Zhang, J., & Guo, F. (2018). Controlling and synchronizing a fractional order chaotic system using stability theory of a time-varying fractional-order system. PLoS One, 13(3), 1–11.
- Khamsuwan, P., Sangpet, T., & Kuntanapreeda, S. (2018). Chaos synchronization of fractional-order chaotic systems with input saturation. Journal of Computational and Nonlinear Dynamics, 13(9), 1–8.
- Khan, A., Khattar, D., & Agrawal, N. (2018). Synchronization between two non identical fractional order hyperchaotic system. Journal of Mathematical and Computational Science, 8(3), 318–330.
- Khan, A., & Tyagi, A. (2017). Fractional orderd is turbance observer based adaptives lidingmode synchronization of commensurate fractional order Genesio-Tesisystem. International Journal of Electronics and Communications, 82, 346–357.
- Khan, A., & Tyagi, A. (2018). Disturbance observer-based adaptive sliding mode hybrid projective synchronisation of identical fractional-order financial systems. Pramana, 90(5), 67.
- Kumar, S., Banerjee, G., Kumar, P., & Kumar, R. (2018). Study of nonlinear behavior and chaos phenomena in power Inverter. International Journal of Engineering and Applied Sciences, 5(2), 59–65.
- Lagmiri, S. N., Amghar, M., & Sbiti, N. (2017). Hyperchaos based cryptography: New seven dimensional systems to secure Communications. Circulation in Computer Science, 2(2), 20–30.
- Li, R.-G., & Wu, H.-N. (2019). Secure communication on fractional-order chaotic systemsvia adaptive sliding mode control withteaching–learning–feedback-based optimization. Nonlinear Dynamics, 95(2), 1221–1243.
- Liu, H., Chen, Y., Li, G., Xiang, W., & Xu, G. (2017). Adaptive fuzzy synchronization of fractional-order chaotic (hyperchaotic) systems with input saturation and unknown parameters. Complexity, 2017, 1–16.
- Liu, H., Pan, Y., Li, S., & Chen, Y. (2018). Synchronization for fractional–order neural networks with full/under–actuation using fractional–order sliding mode control. International Journal of Machine Learning and Cybernetics, 9(7), 1219–1232.
- Liu, P., Xi, R., Ren, P., Hou, J., & Li, X. (2018). Analysis and implementation of a new switching Memristor scroll hyperchaotic system and application in secure communication. Complexity, 2018, 1–15.
- Lu, Y., Xiong, L., Zhang, Y., Zhang, P., Liu, C., Li, S., & Kang, J. (2018). Synchronization, anti-synchronization and circuit realization of a novel hyper-chaotic system. Circuit World, 44(3), 132–149.
- Noghredani, N., & Balochian, S. (2015). Synchronization of fractional-order uncertain chaotic systems with input nonlinearity. International Journal of General Systemsi, 44(4), 485–498.
- Ouannas, A., Bendoukha, S., Volos, C., Boumaza, N., & Karouma, A. (2019). Synchronization of fractional hyperchaotic rabinovich systems via linear and nonlinear control with an application to secure communications. International Journal of Control, Automation and Systems, 17(9), 2211–2219.
- Qiang, H., Chong-Xin, L., Lei, S., & Da-Rui, Z. (2013). A fractional order hyperchaotic system derived from a Liu system and its circuit realization. Chinese Physics B, 22(2), 1–6.
- Rajagopal, K., Vaidyanathan, S., Karthikeyan, A., & Srinivasan, A. k. (2018). Complex novel 4D memristor hyperchaotic system and its synchronization using adaptive sliding mode control. Alexandria Engineering Journal, 57(2), 683–694.
- Vaidyanathan, S. (2017). A new 3-D jerk chaotic system with two cubic nonlinearities and its adaptive backstepping control. Archives of Control Sciences, 27(3), 409–439.
- Vaidyanathan, S., Akgul, A., Kacar, S., & çavuşoğlu, Ü. (2018). A new 4-D chaotic hyperjerk system, its synchronization, circuit design and applications in RNG, image encryption and chaos-based steganography. The European Physical Journal Plus, 133(2), 1–18.
- Vaidyanathan, S., Sambas, A., Mohamed, M. A., Mamat, M., & Sanjaya, W. M. (2018). A new hyperchaotic hyperjerk system with three nonlinear terms, its synchronization and circuit simulation. International Journal of Engineering & Technology, 7(3), 1585–1592.
- Vallejo, J. C., & Sanjuan, M. A. (2017). Predictability of chaotic dynamics. Madrid: Springer.
- Wang, L., Ni, J., & Yang, C. (2018). Synchronization of different uncertain fractional-order chaotic systems with external disturbances via T-S fuzzy model. Journal of Function Spaces, 2018, 1–11.
- Wang, M. (2015). Impulsive synchronization of hyperchaotic Lü systems with two method. International Journal of Modern Nonlinear Theory and Application, 4(1), 1–9.
- Wang, M. (2016). Controlling Liu chaotic system with feedback method and its circuit realization. International Journal of Modern Nonlinear Theory and Application, 5(1), 40–47.
- Wu, H., Xiong, J., Hu, X., Feng, Y., & Li, L. (2018). Sandwich synchronization of memristor-based hyperchaos systems with time delay. Advances in Difference Equations, 2018(1), 1–10.
- Yang, Q., & Bai, M. (2017). A new 5D hyperchaotic system based on modified generalized Lorenz system. Nonlinear Dynamics, 88(1), 189–221.
- Zang, X., Iqbal, S., Zhu, Y., Liu, X., & Zhao, J. (2016). Applications of chaotic dynamics in robotics. International Journal of Advanced Robotic Systems, 13(2), 60.
- Zhou, Y., Liu, H., Cao, J., & Li, S. (2019). Composite learning fuzzy synchronization forincommensurate fractional-order chaotic systems withtime-varying delays. International Journal of Adaptive Control and Signal Processing, 33, 1739–1758.
- Zribi, M., Alrifai, M., & Smaoui, N. (2018). Control of chaos in a single machine infinite Bus power system using the discrete sliding mode control technique. Discrete Dynamics in Nature and Society, 2018, 1–14.

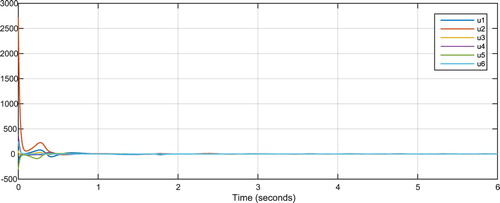
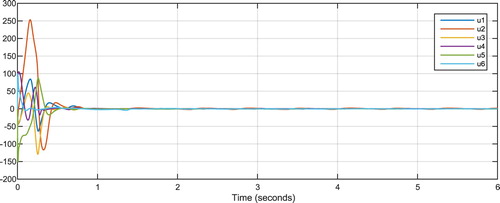
![Figure 16. Control signals using the controller in Equation (22) with α = 0.89 and [x1,x2,x3,x4,x5,x6]T=[3,1,2,8,−2,3]T, [y1,y2,y3,y4,y5,y6]T=[3,6,3,1,7,−1]T.](/cms/asset/4203a5d2-86ed-4c3a-b0a0-2c57c14953d5/ccos_a_1723491_f0016_oc.jpg)