A multi-objective bilevel optimisation evolutionary algorithm with dual populations lower-level search

Abstract

In multi-objective bilevel optimisation problems, the upper-level performance of different lower-level optimal solutions may be very different, even though they belong to the same lower-level problem. It may lead to poor optimisation results. Therefore, the lower-level search should search lower-level non-dominated solutions that are also non-dominated in the upper-level objective space. In this paper, we use two populations in the lower-level search. The first population maintains non-dominance and diversity in the lower-level objective space and provides the second population with convergence pressure from the lower level. The second population selects the upper-level non-dominated solutions that are not dominated by the first population in the lower-level objective space, which make the second population maintain the non-dominance at both upper and lower levels. Besides, to improve the search efficiency, we set up the upper-level mating pool to generate the upper-level vectors of offsprings near the upper-level vectors of the better individuals in the current population. To balance convergence and diversity, the selection operator of  a decomposition based multi-objective evolutionary algorithm is adopted. The proposed algorithm has been evaluated on a set of benchmark problems and a real-world optimisation problem. Experimental results demonstrate that the proposed algorithm is efficient and effective.

Keywords:

• Multi-objective
• bilevel
• dual populations
• multi-objective to multi-objective (M2M)
• differential evolution (DE)

1. Introduction

In multi-objective bilevel optimisation problems, the upper-level performance of different optimal solutions may be very different, even though they belong to the same lower-level problem. The existing multi-objective bilevel optimisation algorithms ignore this point and may only find the lower-level non-dominated solutions with poor upper-level performance in the lower-level search, resulting in a poor quality upper-level Pareto front (PF). To solve this problem, we proposed a dual populations lower-level search to get those lower-level non-dominated solutions with good upper-level performance in this paper. In addition, we generate the upper-level vectors of offsprings near the upper-level vectors of the better individuals in the current population, which can effectively reduce the computational overhead.

In engineering design and business decision-making, there are a lot of applications of multi-objective bilevel optimisation problems (Cai et al., 2018; Chen et al., 2022; Kamal et al., 2019; Kolak et al., 2018; Lin et al., 2010; Lv et al., 2016; Ni et al., 2020; Shaikh et al., 2020; Yanhong et al., 2011; Zhang, 2014). For example, in a manufacturing corporation, the chief executive officer (CEO) aims to maximise the profits and the quality of the products. The CEO sends the design parameters (such as material and appearance), quantity and delivery date of the product to several branch heads working under him. According to these requirements of the CEO, branch heads plan the number of production lines and the scheduling of workers to manufacture one or more components of the final product, maximising their branch profits and the worker satisfaction. Obviously, a CEO's possible decisions must consider the reactions of the heads, which makes the decision-making a multi-objective bilevel optimisation problem by nature and can be described by the following general model of multi-objective bilevel problem: (1) $\begin{array}{rl}\underset{\begin{array}{c}{\mathbf{x}}_{\mathbf{u}}\in {\mathbf{\Omega }}_u\\ {\mathbf{x}}_{\mathbf{l}}\in {\mathbf{\Omega }}_l\end{array}}{min}& \mathbf{F}({\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}})=\left[F_1\right({\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}}),\dots ,F_M({\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}}){]}^T\\ \mathbf{s}\mathbf{.}\mathbf{t}\mathbf{.}& {\mathbf{x}}_{\mathbf{l}}\in \underset{{\mathbf{x}}_{\mathbf{l}}\in {\mathbf{\Omega }}_l}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}\left\{\mathbf{f}\right({\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}})=[f_1({\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}}),\dots ,f_m({\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}}){]}^T\mid \\ & \mathbf{g}({\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}})\le \mathbf{0},\mathbf{h}({\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}})=\mathbf{0}\},\\ & \mathbf{G}({\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}})\le \mathbf{0},\\ & \mathbf{H}({\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}})=\mathbf{0},\end{array}$(1) where $\mathbf{F}({\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}})$ is the upper-level optimisation task (e.g. the profits and the quality of the products), and $\mathbf{f}({\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}})$ is the lower-level optimisation task (e.g. branch profits and the worker satisfaction). The functions $\mathbf{g}({\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}})$ and $\mathbf{h}({\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}})$ are lower-level constraints, which define the feasible space of the lower-level optimisation task. The decision vector $\mathbf{x}$ of the upper-level optimisation task consists of two smaller vectors, i.e. $\mathbf{x}=[{\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}}]$, where ${\mathbf{x}}_{\mathbf{u}}$ is the upper-level vector (e.g. the design parameters, quantity and delivery date of the product), which is defined in the upper-level variable space ${\mathbf{\Omega }}_{\mathbf{u}}$, while ${\mathbf{x}}_{\mathbf{l}}$ is the lower-level vector (e.g. number of production lines and the scheduling of workers), which is defined in the lower-level variable space ${\mathbf{\Omega }}_{\mathbf{l}}$. It is noteworthy that the lower-level optimisation task only optimises ${\mathbf{x}}_{\mathbf{l}}$, while ${\mathbf{x}}_{\mathbf{u}}$ is fixed as parameters. Hence, the optimal solutions of the lower-level optimisation task can be expressed as functions of ${\mathbf{x}}_{\mathbf{u}}$. Then, the feasible space of the upper-level optimisation task is defined by the upper-level unequal constraints $\mathbf{G}({\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}})$ and the upper-level equal constraint $\mathbf{H}({\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}})$ as well as the lower-level multi-objective optimisation. In other words, a feasible solution of the upper-level optimisation task must not only satisfy $\mathbf{G}({\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}})\le \mathbf{0}$ and $\mathbf{H}({\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}})=\mathbf{0}$ but also belong to the Pareto optimum solution set (PS) of the lower-level optimisation task. Both the nested structure of bilevel problems and the characteristics of multiple optimum solutions of multi-objective optimisation problems make the multi-objective bilevel optimisation problems computationally demanding and difficult to be solved. In addition, although some representative multi-objective methods of multi-objective evolutionary algorithms (MOEAs) have achieved remarkable results in large-scale multi-objective and multi-objective optimisation problems (Ma et al., 2021) as well as feature selection problem (Zhang et al., 2017), due to the lack of consideration of nested structure, these methods may not be effective for multi-objective bilevel problems.

Given the difficulty of solving multi-objective bilevel optimisation problems, there are few related researches. In addition to the design of test problems (Deb & Sinha, 2010) and special multi-objective bilevel problems (Sinha et al., 2016), most of the existing researches focus on methods to reduce the computational overhead (i.e. the number of real function evaluations (FEs), especially the lower-level FEs). These methods can be classified into:

1. Single-level reduction methods

   The idea of the single-level reduction to transform the multi-objective bilevel problem into a simple single-level problem has achieved some results, but these methods often need to meet some extremely harsh conditions, which are difficult to apply in practical problems. For example, based on the theoretical progress of establishing the relationship between bilevel optimisation and multi-objective optimisation in recent years, Ruuska and Miettinen (2012) transform the multi-objective bilevel optimisation problem into a multi-objective optimisation problem and then solve it, but this method is only applicable to optimistic multi-objective bilevel optimisation problems. Pieume et al. (2013) show how to construct two artificial multi-objective programming problems so that any point which is Pareto efficient solution to the two problems is an efficient solution to the multi-objective bilevel optimisation problem, and some necessary and sufficient conditions are given for the results to be applicable. He and Lv (2017) use Kuhn–Tucker optimality condition to replace the lower-level problem of a class of multi-objective bilevel optimisation problems, and the perturbed Fischer–Burmeister function is used to smooth the complementary condition. On this basis, a particle swarm optimisation algorithm is used to solve the smooth multi-objective programming problem.

2. Surrogate-model-based methods

   Surrogate-model-based methods usually adopt an approximated surrogate model to approximate the mapping from the upper-level vector to the optimal solution set of its corresponding lower-level problem. Sinha et al. (2017) introduce an approximated set-valued mapping to obtain approximate lower-level PS for any upper-level vector, greatly reducing the number of evaluations for lower-level tasks.

3. Population migration methods

   Learning from the idea of transfer learning (Cao et al., 2021; Li et al., 2022; Sundar & Sumathy, 2022), population migration methods are to migrate the PS of the adjacent lower-level problem to the population of the current lower-level problem, so as to speed up the search of the current lower-level problem. For example, Deb and Sinha (2010) established an archiving set to store the currently found upper-level non-dominated individuals. When searching for the lower-level optimal solutions corresponding to a new upper-level vector, the lower-level initialised population is selected from the archive set according to the distance in the upper-level decision space. Said et al. (2020) study the bilevel combinatorial optimisation problem. They reduced the computational cost through multi-population strategy and migration mechanism, and introduced an index in the lower level optimisation to measure the performance of the lower-level non-dominated solution in the upper-level problem. Although it improves the searching efficiency to some extent using the information of individuals that have been the searched, this method only simply transfers the existing data without summarising, extracting and utilising the knowledge contained in the data, so the effect may not be satisfactory.

4. Variable decomposition (grouping) methods

   Variable decomposition (grouping) methods adopt divide-and-conquer framework. Recently, Cai et al. (2022) use an interaction matrix to represent the variable interactions. Based on the interaction matrix, the variables are divided into different groups and are optimised in a collaborative way.

5. Others

   There are also some other methods. For example, Tao et al. (2012), Zhang et al. (2012) and Zhang et al. (2013) adopt the framework of alternately executing fixed upper-level vector for lower-level optimisation and fixed lower-level vector for upper-level optimisation. It simplifies the optimisation process of the bilevel problem and reduces the computational cost to a certain extent, and also changes the nested structure of the bilevel problem. Therefore, the solution obtained by the algorithm is only a rough approximation of the optimal solution of the bilevel problem, and the accuracy is not good

As shown in (Table 1), although the above algorithms can greatly reduce the computational overhead, they only use the lower-level objective value as the basis for environment selection in the lower-level search, and the result is to obtain a set of solutions evenly distributed on the lower-level PF. However, the upper-level performance of different optimal solutions may be very different, even they belong to the same lower-level problem. For example, Figure 1 shows the performance of the PS of a lower-level problem in the lower-level objective space and the upper-level objective space, respectively. We can see that only those diamonds remains non-dominant in both the upper-level and lower-level objectives. If the proportion of such points in the lower-level PS is further reduced, the lower-level search of the above algorithm is difficult to obtain these points, which may result in a poor quality upper-level PF. Therefore, the lower-level search should not only ensure the non-dominance of the final individuals in the lower-level objective space but also ensure their non-dominance in the upper-level objective space. In this paper, we propose a multi-objective bilevel optimisation evolutionary algorithm with dual populations lower-level search (MOBEA-DPL), which adopts a dual populations (population $S{P}_i$ and $R{P}_i$) lower-level search strategy in the lower-level search. In the early stage of lower-level search, the members of the two populations are consistent and evolve towards lower-level PF. However, in the later stage, the first population continue to select individuals according to the convergence and diversity in the lower-level objective space, providing the second population with convergence pressure from the lower level , while the second population is selected according to the upper-level objective on the premise that they are not dominated by the first population. In this way, the second population not only meet the lower-level optimality constraints but also have a good performance in the upper-level objective space.

Figure 1. In the upper-level objective space, the performance of different optimal solutions belonging to the same lower-level problem may be very different. (a) There are different optimal solutions belonging to the same lower-level problem and (b) only three lower-level non-dominated solutions can remain non-dominated in the upper-level objective space.

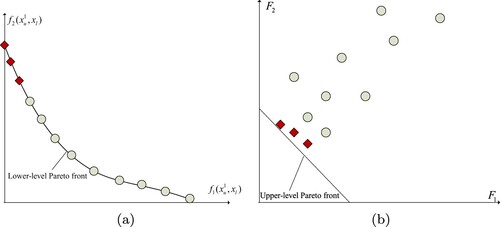
Table 1. The pros and cons of existing works.

Pros	Cons
By means of single-level reduction,	It is impossible to ensure that
surrogate-model-based, population	lower-level non-dominated solutions
migration and variable decomposition	obtained by the lower-level search
(grouping) methods, the cost of solving	remains non-dominated in the
multi-objective bilevel optimisation problems	upper-level objective space, which
is greatly reduced	may lead to poor quality upper-level PF

In addition, in order to improve the search efficiency, we set up the upper-level mating pool according to the performance of the current generation of individuals in the upper-level task. Compared with the previous practice of treating all upper-level vectors equally and ignoring the quality differences of sub-populations corresponding to different upper-level vectors, it is obviously more reasonable and efficient that the upper-level vector with higher quality sub-population should have more opportunities to produce offspring. However, due to the nested structure of bilevel problems, it is likely to lead to the loss of diversity of the mating pool if the upper-level vector is selected to join the mating pool according to the principle of convergence first, resulting in the population can only search the part of the upper-level PF or even premature convergence. Therefore, we adopt the principle of diversity first in MOEA/D-multi-objective to multi-objective (M2M) proposed by Liu et al. (2014) to improve the search efficiency and maintain diversity at the same time.

As shown in Table 2, the contributions of this paper are as follows:

1. We design a dual populations lower-level search strategy. Individuals obtained by means of this strategy not only meets the lower-level optimality constraints but also have good performance in the upper-level objective space.

2. We select the upper-level mating pool according to the performance of the current generation of individuals in the upper-level objective space using the principle of diversity first, so that the upper-level vector with good performance can obtain more mating opportunities. Then, the upper-level vectors of offsprings are generated near the upper-level vectors of the better individuals in the current population, which greatly improves the search efficiency and maintain diversity at the same time.

Table 2. The contributions of this paper.

Motivation	Method
To obtain lower-level non-dominated solutions with	Dual populations lower-level search strategy
good upper-level performance
To reduce computational overhead	Generate the upper-level vectors of the next generation
	of individuals near the upper-level vectors of the better
	individuals in the current population

The remainder of this paper is organised as follows. In Section 2, we describe the proposed MOBEA-DPL in detail. Experimental settings and the results on test problems with varying complexities and a real-world optimisation problem are presented in Section 3. Finally, conclusions are drawn in Section 4.

2. Proposed algorithm

The overall framework of the proposed MOBEA-DPL is presented in Algorithm 1. First, a set of upper-level vectors $A{r}_u$ of size $n_u$ are randomly initialised. Next, the dual populations lower-level search is executed to optimise the lower-level multi-objective task for all $x_{u,i}$ in $A{r}_u$. Then, the upper-level population Pop are selected from lower-level sub-population SP through upper-level environment selection. Finally, offspring reproduction, upper-level environment selection and refine search are repeated until the termination criteria is met.

2.1. Dual populations lower-level search

In the initialisation and offspring reproduction operations, for each upper-level vector, the corresponding optimal lower-level vectors would be obtained through lower-level search. It should be noted that not all lower-level non-dominated solutions can remain non-dominated in the upper-level objective space. In the upper-level objective space, the performance of different optimal solutions may be very different, even they belong to the same lower-level problem. Thus, the lower-level search should not only ensure the non-dominance of the final individuals in the lower-level objective space but also ensure their non-dominance in the upper-level objective space. Therefore, we propose a dual populations lower-level search in this paper, which is shown in Algorithm 2.

First, a set of lower-level vectors $S{P}_i$ of size $n_l$ are randomly initialised and $R{P}_i$ has the same members, which is shown as Figure 2(a). Second, the offspring (SQ) of $S{P}_i$ are reproduced through differential evolution (DE) operator (Song & Li, 2022; Zhao et al., 2021). Then, $S{P}_i$, SQ and $R{P}_i$ are merged into r and all members in r are sorted using non-dominated sorting approach according to their lower-level objectives. Next, $R{P}_i$ is updated by the best $n_l$ individuals from r using reference-point-based non-dominated sorting approach (Jain & Deb, 2014) according to their lower-level objective value, which is followed by the update of $S{P}_i$. If the number of lower-level non-dominated individuals in r is no more than $n_l$ (Figure 2(b)), $S{P}_i$ is updated by $R{P}_i$; otherwise, $S{P}_i$ is updated by the best $n_l$ individuals from lower-level non-dominated individuals in r using reference-point-based non-dominated sorting approach according to their upper-level objective value. Finally, offspring reproduction and the update of $R{P}_i$ and $S{P}_i$ are repeated until the termination criteria are met .

Figure 2. The proposed dual populations lower-level search. (a) In the early stage of lower-level search, the members of the two populations are consistent and evolve towards lower-level PF and (b) In the later stage, $R{P}_i$ uniformly converges to the whole lower-level PF, and $S{P}_i$ converges to the part of the lower-level PF that remains non-dominated in the upper-level objective space.

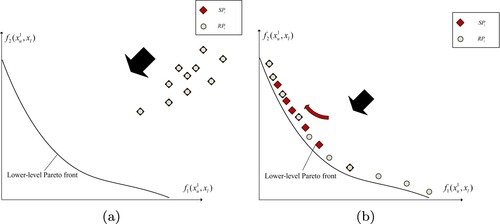
It is worth noting that the proposed dual populations lower-level search can adaptively select the upper-level objectives or the lower-level objectives for optimisation. In the early stage of lower-level search, the number of lower-level non-dominated individuals in r is no more than $n_l$, and the search focuses on optimising the lower-level objectives. The members of the two populations are consistent and evolve towards lower-level PF. As the search progresses, the number of lower-level non-dominated individuals increased gradually. Once the number of lower-level non-dominated individuals exceeds $n_l$, the evolutionary direction of the two populations will differ. $R{P}_i$ continue to select individuals according to the convergence and diversity in the lower-level objective space, providing $S{P}_i$ with convergence pressure from the lower level, while $S{P}_i$ is selected according to the upper-level objectives on the premise that it is not dominated by $R{P}_i$. In this way, $R{P}_i$ is a group of points evenly distributed on the lower-level PF, while $S{P}_i$ not only meet the lower-level optimality constraints but also have a good performance in the upper-level objectives space.

2.2. Upper-level environment selection

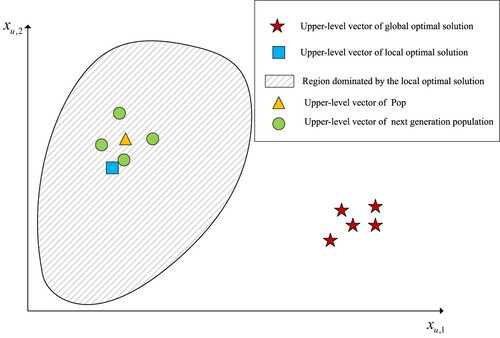
The purpose of the upper-level environment selection proposed in this paper is to update the upper-level population Pop, lower-level populations Archive and the lower-level reference points set RP. It is worth noting that Pop are the individuals with the best upper-level performance. In the next section, we will generate the upper-level vectors of offsprings around the upper-level vectors of Pop to speed up convergence and reduce computational overhead. However, it may cause the population to fall into local optimisation. As shown in Figure 3, there is a upper-level vector of a local optimal solution in the upper-level variable space and the region dominated by the local optimal solution is quite large. If the selection is based on the principle of convergence first, the upper-level vectors of Pop will converge to the local optimal upper-level vector with a high probability. If we continue to generate the upper-level vectors of offsprings near the upper-level vector of Pop at this time, individuals in Archive will completely fall into local optimisation. Therefore, we should select individuals to consist Pop based on the principle of diversity first, keeping the diversity of upper-level vectors of Pop and Archive as much as possible to avoid falling into local optimisation. The selection operator in MOEA/D-M2M is exactly the selection operator with diversity first.

Figure 3. The population fall into local optimisation.

MOEA/D-M2M is a variant of MOEA/D (Zhang & Li, 2007). Different from MOEA/D's method of transforming a multi-objective optimisation problem into multiple single objective optimisation problems, MOEA/D-M2M transforms a multi-objective optimisation problem into multiple multi-objective optimisation problems. Specifically, MOEA/D-M2M divides the candidate solutions into multiple sub-populations according to the diversity of them in the objective space, and then selects individuals in each sub-population according to convergence and diversity to form the next generation population. Therefore, the next generation population has good convergence while retaining excellent diversity. Such solutions are suitable for us to accelerate convergence and avoid the search falling into local optimisation.

The details of upper-level environment selection are shown in Algorithm 3. First of all, k reference weight vectors $\mathit{W}=\{{\mathit{\omega }}_{\mathbf{1}},\dots ,{\mathit{\omega }}_{\mathit{k}}\}$ are uniformly generated, and the size of sub-population (s) is set. Next, the best $n_u$ individuals are selected from R to update Pop according to the selection operator of MOEA/D-M2M, and the upper-level vectors of individuals in Pop are grouped and stored in $Pu=\{P{u}_1,\dots ,P{u}_k\}$ according to their matching relationship with $\mathit{W}$. Then, the individuals in R that have the same upper-level vectors as the individuals in Pop are eliminated. After that, we start updating the Archive. In the beginning, an empty set $A{r}_u$ is created to record the upper-level vectors corresponding to individuals that will be stored in the updated Archive. Then, for each reference weight vector ${\mathit{\omega }}_{\mathit{i}}$, do the following to fill $n_u=k\ast s$ different upper-level vectors into $A{r}_u$.

First, the set $P{u}_i$ of the upper-level vectors of the individuals associated with ${\mathit{\omega }}_{\mathit{i}}$ in Pop is assigned to $A{u}_i$. Next, duplicate upper-level vectors and the same upper-level vectors from $A{u}_i$ as in $A{r}_u$ are deleted. When the number of upper-level vectors in $A{u}_i$ is less than s, we need to supplement $A{u}_i$. If there are individuals associated with ${\mathit{\omega }}_{\mathit{i}}$ in R, the optimal individual $\hat{x}$ is selected according to the upper-level objective value; otherwise, $\hat{x}$ is picked out from R randomly. The upper-level vector of $\hat{x}$ is added into $A{u}_i$, and individuals with the same upper-level vector as $\hat{x}$ in R are deleted. After supplementing $A{u}_i$, $A{r}_u$ merges $A{u}_i$.

After $A{u}_i$ is filled with $n_u$ upper-level vectors, Archive is updated with individuals in Archive and SQ that have the same upper-level vectors as $A{r}_u$, and RP is updated with individuals in RP and RQ that have the same upper-level vectors as $A{r}_u$. So far, we have updated Archive and RP, and obtained mating pools $Pu=\{P{u}_1,\dots ,P{u}_k\}$ and $Au=\{A{u}_1,\dots ,A{u}_k\}$.

2.3. Offspring reproduction

After obtaining mating pools Pu and Au, offspring reproduction is executed, which is shown in Algorithm 4. For each $P{u}_i$, each upper-level vector ($P{u}_i^j$) in $P{u}_i$ and two randomly selected upper-level vectors ($A{u}_i^{randi1}$ and $A{u}_i^{randi2}$) in $A{u}_i$ generate a new upper-level vector ($Q_{u,(i-1)\ast k+j}$) through DE operator. Then, the dual populations lower-level search is executed to optimise the lower-level multi-objective task for $Q_{u,(i-1)\ast k+j}$.

2.4. Refine search

To ensure that each individual in Pop satisfies the lower-level optimality constraint, refine search is executed for upper-level vectors in Pop before the end of each round of upper-level search. It is worth noting that the proposed refine search is consistent with the dual populations lower-level search in design concept. While searching for better lower-level solutions, it prefers individuals that perform better in the upper-level objective space. The details of refine search are shown in Algorithm 5.

First, the upper-level vectors corresponding to the individuals in Pop are extracted without repetition as the upper-level vectors that need refine search, which are recorded as $X_u^{rs}$. For each upper-level vector $X_{u,i}^{rs}$ in $X_u^{rs}$, each corresponding individual in Pop and any two corresponding individuals in Archive generate a new lower-level offspring $of{f}_i$ through DE operator. Next, $of{f}_i$ and all corresponding individuals in Archive and RP are merged into r. Then, the best $n_l$ individuals are picked out from r using reference-point-based non-dominated sorting approach according to their lower-level objective value and denoted as rp. After that, individuals corresponding to $X_{u,i}^{rs}$ in RP are replaced by rp. If the number of lower-level non-dominated individuals in r is no less than $n_l$, the lower-level dominated members are eliminated from r; otherwise, r is updated by rp. Subsequently, individuals corresponding to $X_{u,i}^{rs}$ in Archive are replaced by r. After all vectors in $X_u^{rs}$ have completed the above operations, upper-level environment selection is executed to update Pop, Archive, Pu and Au. It should be noted that the number of individuals corresponding to an upper vector in Archive may exceed $n_l$, which needs to be reduced. For each upper-level vector with more than $n_l$ corresponding individuals in Archive, its corresponding individuals in Archive are sorted using reference-point-based non-dominated sorting approach according to their upper-level objective value. The best $n_l$ individuals are retained, while the others are eliminated.

2.5. Termination criteria

We adopt a hypervolume-based termination criterion proposed by Sinha et al. (2017) at both levels. At the lower-level, the maximum ($H_l^{max}$) and minimum ($H_l^{min}$) hypervolume are calculated according to the lower-level objective value of $R{P}_i$ in every generation from the previous ${\tau }_l$ generations (with the worst encountered lower-level objective value in the previous ${\tau }_l$ generations used as reference points). The $H_l$-metric is computed as follows: (2) $H_l=\frac{H_l^{max}-H_l^{min}}{H_l^{max}+H_l^{min}}.$(2) If $H_l\le {ϵ}_l$, then the lower-level optimisation task is terminated indicating adequate convergence. A similar measure is used for the upper-level termination as well, except that the upper-level objective value of Pop are used to compute the hypervolumes. We have used ${\tau }_l=10$, ${\tau }_u=10$, ${ϵ}_l=0.001$ and ${ϵ}_u=0.001$ in our study.

3. Experimental results and discussion

To empirically examine the performance of the proposed MOBEA-DPL, we evaluate MOBEA-DPL on the DS test problems proposed by Deb and Sinha (2009).

There are five test problems in the DS series. In DS1, DS2 and DS3, the dimension of both upper and lower-level problems can be increased by increasing the parameter K. The parameter γ can be adjusted to cause a small proportion of lower-level Pareto-optimal points to be responsible for the upper-level Pareto-optimal front. Besides, conflict between two levels of optimisation can be introduced by choosing $\tau =-1$. Moreover, the lower-level problem of DS1 is difficult to be solved to Pareto-optimality due to multi-modalities, and it can make an algorithm difficult to locate the true Pareto-optimal points of DS1 by adjusting parameter α. While the upper-level problem of DS2 has multi-modalities, thereby causing an algorithm difficulty in finding the upper-level Pareto-optimal front. DS3 is the most challenging of these three with following properties: first, the Pareto-optimal fronts for both the lower and upper levels lie on constraint boundaries, thereby requiring good constraint handling strategies to solve both problems optimally. Second, not all lower-level Pareto-optimal solutions qualify as upper-level Pareto-optimal solutions. Third, every lower-level front has an unequal contribution to the upper-level Pareto-optimal front. When it comes to DS4 and DS5, the problem complexity in converging to the appropriate lower and upper-level fronts can be increased by increasing K and L. Only one Pareto-optimal point from each participating lower-level problem qualifies to be on the upper-level front in DS4. DS5 has similar difficulties as in DS4, except that only a finite number of $x_u$ qualifies at the upper-level PF and that a consecutive set of lower-level Pareto-optimal solutions now qualify to be on the upper-level PF (Deb & Sinha, 2009).

In the remainder of this section, we first present a brief introduction to the experimental settings of all the compared algorithms. Then, the results from 21 runs of each algorithm for each test problem are presented. A comparative study of the computational expense required by different approaches is also provided.

3.1. Experimental settings

1. Genetic operators: In this paper, the DE (Vesterstrom & Thomsen, 2004; Vishwakarma & Sisaudia, 2020) is adopted in all algorithms in the experiments for offspring generation. The parameters of DE in all algorithms in the experiments are default values, which are set to $C_r=1$ and F = 0.5, while the expectation of number of bits doing mutation is set to proM = 1 and the distribution index of polynomial mutation is set to disM = 20. Such parameter setting is also adopted by Cai et al. (2022).

2. Population size: In all algorithms in the behaviour study of the MOBEA-DPL, the upper-level population size is set to $n_u=50$, while the lower-level population size is set to $n_l=50$. The number of reference weight vectors in upper-level environment selection is set to k = 10, and the size of sub-population is set to $s=n_u/k=5$. While in the comparisons of MOBEA-DPL with other approaches, $n_u$ is set to 20 for DS1-DS3, and 5 for DS4 and DS5. $n_l$ is set to 20 for DS1-DS3, and 40 for DS4 and DS5. These are the same as the settings in BLMOCC (Cai et al., 2022). k is set to 5.

3. The test problems: The parameters setting of the test problem is shown in Table 3. In order to shorten the running time, we set the parameter k of the control variable dimension in DS1, DS2 and DS3 to 5 in the behaviour study of the MOBEA-DPL, while other parameters related to the problem characteristics are consistent with Sinha et al. (2017). While in the comparisons of MOBEA-DPL with other approaches, all parameters are consistent with Cai et al. (2022).

Table 3. Benchmark functions used in the behaviour study of the MOBEA-DPL.

Benchmark problems	Parameters setting
DS1	K = 5 or $10,r=0.1,\alpha =1,\gamma =1,\tau =1$
DS2	K = 5 or $10,r=0.25,\gamma =4,\tau =-1$ or 1
DS3	K = 5 or $10,r=0.2,\tau =1$
DS4	K = 1, L = 9
DS5	K = 1, L = 9

3.2. Behaviour study of the MOBEA-DPL

In this section, there are three comparison algorithms. The first one, denoted as MOBEA-nl, considers the quality differences of sub-populations corresponding to different upper-level vectors as MOBEA-DPL, but loses sight of the fact that the lower-level non-dominated solutions may not remain non-dominated in the upper-level objective space, which uses an evolutionary many-objective optimization algorithm usingreference-point based nondominated sorting approach (NSGAIII) proposed by Jain and Deb (2014) as the optimiser for the lower-level search. Other parts of MOBEA-nl are consistent with MOBEA-DPL. Different from MOBEA-nl, the second one, denoted as MOBEA-nr, treats each upper-level vector in Archive equally when generating the upper-level vector of offspring. Each upper-level vector in Au and other two randomly selected vectors generate a new upper-level vector through DE operator, which ignores the quality differences of sub-populations corresponding to different upper-level vectors. Other parts of MOBEA-nr are consistent with the proposed MOBEA-DPL. The third algorithm is a combination of the first two, which is denoted as MOBEA-nrl. When generating the upper-level vectors of offsprings, MOBEA-nrl, like MOBEA-nr, only uses Au as the mating pool. In the lower-level search, NSGAIII is used as the optimiser like MOBEA-nl. Other parts of MOBEA-nrl are consistent with MOBEA-DPL.

3.2.1. Comparison results in IGD

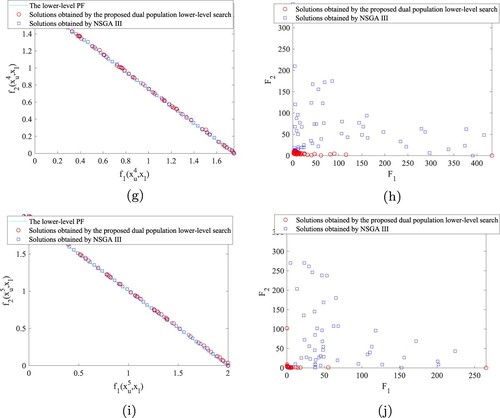
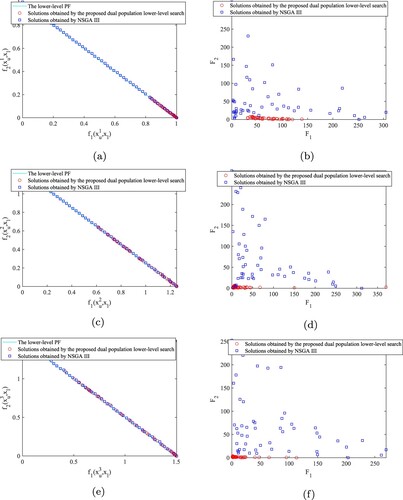
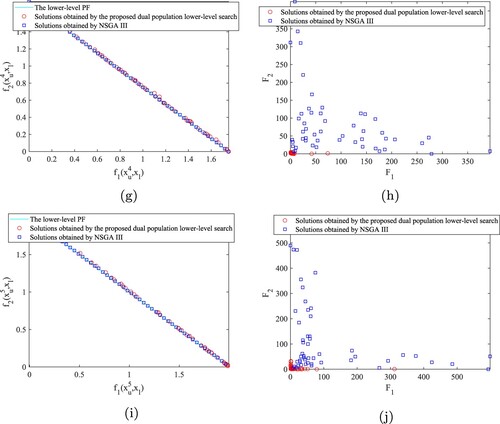
Table 4 presents the comparison results of the four algorithms in inverted generational distance (IGD) on problems proposed by Deb and Sinha, 2009 (the DS series), including the results of Wilcoxon rank-sum test calculated at a significance level of $\alpha =0.05$, where “+”, “=” and “−” indicate that the compared algorithm is better than, similar to and inferior to the proposed MOBEA-DPL, respectively. We can see that several comparison algorithms have no great difference in the quality of upper-level PF in the first three problems. This is because for DS1 and DS2, the entire lower-level PS can remain non-dominated in the upper-level objective space. Although not all lower-level Pareto-optimal solutions qualify as upper-level Pareto-optimal solutions (Deb & Sinha, 2009), the proportion of qualified ones is still relatively large, which is not enough to make a significant difference in the results. Therefore, MOBEA-nl and MOBEA-nrl using the usual lower-level search strategy can also obtain the lower-level most of non-dominated solutions with good upper-level performance. However, when it comes to DS4 and DS5, the algorithms with dual populations lower-level search strategy (i.e. MOBEA-DPL and MOBEA-nr) have obvious advantages. We uniformly take five points on the upper-level decision variable space (i.e. $x_u\in [1,2]$) of the two problems, which are $x_u^1=1$, $x_u^2=1.25$, $x_u^3=1.5$, $x_u^4=1.75$ and $x_u^5=2$. Then, we use the two different lower-level search strategies used in the comparison algorithms to solve the lower-level tasks corresponding to these five upper-level variables, and the results are shown in Figures 4 and 5. The left column subgraphs are the distributions of the solutions in the lower-level objective space, while the right column subgraphs are the distributions of the solutions in the upper-level objective space. We can see that although they are points on the same lower-level PF, their performance in the upper-level objective space are very different. NSGAIII in the experiment is the same as the lower-level search strategy of the existing algorithms, which only uses the lower-level objectives as the basis for the lower-level environment selection. They can find the solutions in the lower-level PS, but they cannot further screen the solutions in the lower-level PS. However, the proposed dual population lower-level search strategy not only searches the lower-level PS but also converges to those solutions with good upper-level performance in the lower-level PS. Therefore, with dual populations lower-level search strategy, MOBEA-DPL and MOBEA-nr obtain significantly better results in IGD, which proves the effectiveness of the proposed dual populations lower-level search.

Figure 4. Performance difference between two lower-level search strategies on DS4. (a) Non-dominated solutions of $\mathbf{f}(x_u^1,{\mathbf{x}}_{\mathbf{l}})$, where $x_u^1=1$. (b) The performance of non-dominated solutions of $\mathbf{f}(x_u^1,{\mathbf{x}}_{\mathbf{l}})$ in the upper-level objective space, where $x_u^1=1$. (c) Non-dominated solutions of $\mathbf{f}(x_u^2,{\mathbf{x}}_{\mathbf{l}})$, where $x_u^2=1.25$. (d) The performance of non-dominated solutions of $\mathbf{f}(x_u^2,{\mathbf{x}}_{\mathbf{l}})$ in the upper-level objective space, where $x_u^2=1.25$. (e) Non-dominated solutions of $\mathbf{f}(x_u^3,{\mathbf{x}}_{\mathbf{l}})$, where $x_u^3=1.5$. (f) The performance of non-dominated solutions of $\mathbf{f}(x_u^3,{\mathbf{x}}_{\mathbf{l}})$ in the upper-level objective space, where $x_u^3=1.5$. (g) Non-dominated solutions of $\mathbf{f}(x_u^4,{\mathbf{x}}_{\mathbf{l}})$, where $x_u^4=1.75$. (h) The performance of non-dominated solutions of $\mathbf{f}(x_u^4,{\mathbf{x}}_{\mathbf{l}})$ in the upper-level objective space, where $x_u^4=1.75$. (i) Non-dominated solutions of $\mathbf{f}(x_u^5,{\mathbf{x}}_{\mathbf{l}})$, where $x_u^5=2$. (j) The performance of non-dominated solutions of $\mathbf{f}(x_u^5,{\mathbf{x}}_{\mathbf{l}})$ in the upper-level objective space, where $x_u^5=2$.

Figure 5. Performance difference between two lower-level search strategies on DS5. (a) Non-dominated solutions of $\mathbf{f}(x_u^1,{\mathbf{x}}_{\mathbf{l}})$, where $x_u^1=1$. (b) The performance of non-dominated solutions of $\mathbf{f}(x_u^1,{\mathbf{x}}_{\mathbf{l}})$ in the upper-level objective space, where $x_u^1=1$. (c) Non-dominated solutions of $\mathbf{f}(x_u^2,{\mathbf{x}}_{\mathbf{l}})$, where $x_u^2=1.25$. (d) The performance of non-dominated solutions of $\mathbf{f}(x_u^2,{\mathbf{x}}_{\mathbf{l}})$ in the upper-level objective space, where $x_u^2=1.25$. (e) Non-dominated solutions of $\mathbf{f}(x_u^3,{\mathbf{x}}_{\mathbf{l}})$, where $x_u^3=1.5$. (f) The performance of non-dominated solutions of $\mathbf{f}(x_u^3,{\mathbf{x}}_{\mathbf{l}})$ in the upper-level objective space, where $x_u^3=1.5$. (g) Non-dominated solutions of $\mathbf{f}(x_u^4,{\mathbf{x}}_{\mathbf{l}})$, where $x_u^4=1.75$. (h) The performance of non-dominated solutions of $\mathbf{f}(x_u^4,{\mathbf{x}}_{\mathbf{l}})$ in the upper-level objective space, where $x_u^4=1.75$. (i) Non-dominated solutions of $\mathbf{f}(x_u^5,{\mathbf{x}}_{\mathbf{l}})$, where $x_u^5=2$. (j) The performance of non-dominated solutions of $\mathbf{f}(x_u^5,{\mathbf{x}}_{\mathbf{l}})$ in the upper-level objective space, where $x_u^5=2$.

Table 4. The comparison results of the IGD averages of the four algorithms running 21 times independently on DS series.

Pr. no. (var.)	MOBEA-DPL	MOBEA-nl	MOBEA-nr	MOBEA-nrl
DS1 $(5+5)$	1.93E−02	1.88E−02(=)	2.01E−02(=)	1.95E−02(=)
DS2 $(5+5)$	1.66E−02	1.76E−02(=)	1.81E−01(=)	1.84E−02(=)
DS3 $(5+5)$	2.15E−02	2.16E−02(=)	2.36E−02(−)	2.48E−02(−)
DS4 $(1+9)$	1.68E−01	6.33E−01(−)	1.65E−01(=)	5.96E−01(−)
DS5 $(1+9)$	1.82E−01	6.77E−01(−)	1.68E−01(+)	6.00E−01(−)

Note: The symbols “+”, “=” and “−” denote that the compared algorithm is better than, similar to and inferior to the proposed MOBEA-DPL, respectively, under the Wilcoxon's rank sum test with a 0.05 significance level.

3.2.2. Comparison results in FEs

Table 5 shows the minimum, maximum and average number of FE required for the upper and lower-level objectives from 21 runs of the compared algorithms. At the same time, Table 5 also gives the ratio of average FEs, where the numerator is the average FEs of the comparison algorithm and the denominator is the average FEs of MOBEA-DPL.

Table 5. The total function evolution by the compared algorithms and their statistical comparison results in 21 independent runs for benchmark problems.

		Best		Worst		Average		Ratio of average FEs
Pr. no. (var.)	Al. no.	Total UL FEs	Total LL FE	Total UL FEs	Total LL FEs	Total UL FEs	Total LL FEs	Total UL FEs	Total LL FEs
DS1 (5 + 5)	MOBEA-DPL	8.32E+05	7.56E+06	1.73E+06	1.59E+07	1.23E+06	1.11E+07	1	1
	MOBEA-nl	1.06E+05	8.87E+06	1.63E+05	1.35E+07	1.32E+05	1.08E+07	0.11	0.97
	MOBEA-nr	1.24E+06	1.10E+07	2.31E+06	2.05E+07	1.73E+06	1.54E+07	1.41	1.39
	MOBEA-nrl	1.30E+05	1.04E+07	2.46E+05	2.01E+07	1.77E+05	1.44E+07	0.14	1.30
DS2 (5 + 5)	MOBEA-DPL	1.53E+06	1.82E+07	5.10E+06	6.68E+07	2.83E+06	3.70E+07	1	1
	MOBEA-nl	1.33E+05	1.11E+07	3.10E+05	2.84E+07	1.88E+05	1.63E+07	0.07	0.44
	MOBEA-nr	2.08E+05	1.68E+06	7.55E+06	9.95E+07	3.60E+06	4.59E+07	1.27	1.24
	MOBEA-nrl	1.94E+05	1.50E+07	5.86E+05	5.30E+07	2.73E+05	2.18E+07	0.10	0.58
DS3 (5 + 5)	MOBEA-DPL	1.58E+05	1.11E+07	4.38E+05	3.06E+07	2.76E+05	1.93E+07	1	1
	MOBEA-nl	9.96E+04	1.03E+07	2.98E+05	3.11E+07	1.88E+05	1.96E+07	0.68	1.02
	MOBEA-nr	2.12E+05	1.57E+07	4.65E+05	3.26E+07	3.05E+05	2.18E+07	1.11	1.12
	MOBEA-nrl	1.24E+05	1.25E+07	2.82E+05	2.93E+07	1.83E+05	1.89E+07	0.66	0.98
DS4 (1 + 9)	MOBEA-DPL	2.79E+05	1.26E+06	7.47E+05	3.37E+06	4.60E+05	2.07E+06	1	1
	MOBEA-nl	2.52E+04	1.46E+06	6.38E+04	3.79E+06	3.71E+04	2.16E+06	0.08	1.04
	MOBEA-nr	3.02E+05	1.40E+06	6.68E+05	3.02E+06	4.64E+05	2.12E+06	1.01	1.02
	MOBEA-nrl	2.39E+04	1.40E+06	7.87E+04	4.69E+06	4.18E+04	2.46E+06	0.09	1.18
DS5 (1 + 9)	MOBEA-DPL	2.85E+05	1.29E+06	6.74E+05	3.06E+06	3.52E+05	1.59E+06	1	1
	MOBEA-nl	2.67E+04	1.54E+06	6.45E+04	3.70E+06	4.02E+04	2.32E+06	0.11	1.45
	MOBEA-nr	2.77E+05	1.27E+06	6.06E+05	2.78E+06	3.46E+05	1.58E+06	0.98	0.99
	MOBEA-nlr	2.58E+04	1.50E+06	7.88E+04	4.62E+06	4.11E+04	2.40E+06	0.12	1.51

Comparing MOBEA-DPL and MOBEA-nl, MOBEA-nr and MOBEA-nrl, respectively, we can see that the proposed dual population lower-level search not only increases the upper-level (UL) FEs on all the test problems but also increases the lower-level (LL) FEs on the test problems (i.e. DS1, DS2 and DS3) where all or most lower-level Pareto-optimal solutions qualify as upper-level Pareto-optimal solutions. As for the test problems (i.e. DS4 and DS5) where only a smaller part of lower-level Pareto-optimal solutions qualify as upper-level Pareto-optimal solutions, the proposed dual population lower-level search can reduce their lower-level FEs. The growth rate of upper-level FEs on all the test problems is between 1.47 and 12.7. In bilevel optimisation algorithms, the lower-level FEs are often more than one order of magnitude than the upper-level FEs, so the computational overhead is mainly to count the lower-level FEs. Therefore, the increase of upper-level FEs is acceptable. On DS1, DS2 and DS3, there are obvious differences in lower-level FEs. Due to the proposed dual population lower-level search, the lower-level FEs have increased slightly on DS1 and DS3, but more than doubled on DS2. This is because the upper-level task and lower-level task of DS2 are conflict (i.e. $\tau =-1$), which means that when dual population lower-level search selects individuals according to their upper-level objective value to form the next generation population, solutions far from the lower-level PF among the lower-level non-dominated solutions are preferred. Therefore, it leads to slower convergence and more lower-level FEs. When it comes to DS4 and DS5, the proposed dual population lower-level search can effectively find the upper-level Pareto-optimal solutions in the lower-level Pareto-optimal solutions, which makes each upper-level vector obtain the correct evaluation and avoid the search misled by the wrong evaluation, so MOBEA-DPL and MOBEA-nr have less lower-level FEs. However, only one Pareto-optimal point from each participating lower-level problem qualifies to be on the upper-level PF in DS4 (Deb & Sinha, 2009), which makes DS4 a more difficult problem than DS5. Without dual population lower-level search, MOBEA-nl and MOBEA-nrl are difficult to find better solutions on DS4, so premature convergence take place. Therefore, the reduction of lower-level FEs on DS4 is much less than that on DS5.

Comparing MOBEA-DPL and MOBEA-nr, MOBEA-nl and MOBEA-nrl, respectively, we can see that the proposed upper-level vector generation strategy has no effect on those problems with low-dimension upper-level decision space (i.e. DS4 and DS5, whose upper-level decision space dimension is only 1), because the upper-level vectors are easy to converge quickly in such a low-dimensional space. When it comes to problems with high-dimension upper-level decision space (i.e. DS1, DS2 and DS3, whose upper-level decision space dimension is 5), the situation is a little complicated. On DS1 and DS2, algorithms with the proposed upper-level vector generation strategy (i.e. MOBEA-DPL and MOBEA-nl) achieve smaller upper-level FEs and smaller lower-level FEs with a decrease of between 19% and 30%. However, MOBEA-DPL achieved 10% less upper-level FEs and 11% less lower-level FEs than MOBEA-nr on DS3, MOBEA-nl achieved 3% more upper-level FEs and 4% more lower-level FEs than MOBEA-nrl on DS3. That is because not all lower-level Pareto-optimal solutions qualify as upper-level Pareto-optimal solutions in DS3. With the proposed dual population lower-level search, MOBEA-nr can continuously improve the quality of the upper-level PF by converging the population to those qualified lower-level Pareto-optimal solutions. Therefore, even if the probability of generating a promising upper-level vector is low, MOBEA-nr can avoid premature convergence on DS3. However, with a low probability of generating a promising upper-level vector and without the proposed dual population lower-level search, MOBEA-nrl inevitably converges prematurely on DS3. With the proposed upper-level vector generation strategy, MOBEA-nl is more likely to generate promising upper-level vectors and continuously improve the upper-level PF, so MOBEA-nl also avoids premature convergence on DS3. MOBEA-nrl has obtained the worst IGD and the least FEs on DS3, which provide evidence for this claim.

Overall, the experimental results demonstrate that the proposed dual population lower-level search can effectively improve the quality of upper-level PF of problem where not all lower-level Pareto-optimal solutions qualify as upper-level Pareto-optimal solutions and greatly increased the computational overhead for problems with conflicting upper and lower-level objectives. In order to obtain a better solution, the overhead of computing resources is acceptable. In addition, the experimental results also show that the proposed upper-level vector generation strategy can effectively reduce the computational overhead for problems with high-dimension upper-level decision space. Thus, the proposed MOBEA-DPL is efficient and effective.

3.3. The comparisons of MOBEA-DPL with other approaches

In this section, we conduct experiments to compare the performance of MOBEA-DPL with a nested strategy (NS), a state-of-the-art hybrid bilevel evolutionary multi-objective optimisation (H-BLEMO) algorithm (Deb & Sinha, 2010) and a state-of-the-art cooperative coevolution with knowledge-based dynamic variable decomposition optimisation algorithm (BLMOCC) (Cai et al., 2022). The settings of test problems and comparison algorithms are the same as those in BLMOCC (Cai et al., 2022). It should be noted that we do not have the original codes of H-BLEMO and BLMOCC. We do not think we can reproduce their algorithms perfectly according to their papers. Therefore, we extract the data of IGD and FEs in the original BLMOCC. For IGD, 1000 reference points are uniformly sampled from the true PFs on all the problems, which is the same as that in BLMOCC. Similarly, the scale of the non-dominated solutions used to calculate IGD is also consistent with that in BLMOCC. Thus, it can be reflected for a fair comparison. Table 6 presents the comparison results of the mean and standard deviation values of IGD of MOBEA-DPL with other approaches on DS series, and the best mean results of individual test instances are highlighted, while the comparison results of FEs of MOBEA-DPL with other approaches are shown in Table 7.

Table 6. The comparison results of the mean and standard deviation values of IGD of MOBEA-DPL with other approaches on DS series.

Pr. no. (var.)	MOBEA-DPL	NS	H-BLEMO	BLMOCC
DS1 $(10+10)$	1.217E−02 (2.702E−03)	2.363E−01 (3.87E−02)	1.254E−01 (1.48E−01)	7.858E−02 (2.74E−04)
DS2 $(10+10)$	5.357E−02 (2.221E−02)	2.307E−01 (3.68E−04)	1.782E−01 (5.16E−02)	1.087E−01 (5.87E−03)
DS3 $(10+10)$	7.349E−02 (2.321E−02)	4.032E−01 (5.86E−03)	2.569E−01 (8.58E−02)	1.667E−01 (2.94E−02)
DS4 $(1+9)$	1.522E−02 (3.404E−03)	1.141E−01 (7.84E−04)	7.723E−02 (2.73E−03)	6.892E−02 (3.46E−03)
DS5 $(1+9)$	4.273E−02 (4.238E−02)	1.247E−01 (8.18E−04)	8.285E−02 (4.07E−03)	7.963E−02 (4.51E−03)

Table 7. The total function evolution by the compared algorithms and their statistical comparison results in 21 independent runs for benchmark problems.

	Best (MOBEA-DPL)		Worst (MOBEA-DPL)		Median (MOBEA-DPL)		Saving: $\frac{\mathrm{N}\mathrm{S}\left(\mathrm{M}\mathrm{e}\mathrm{d}\right)}{\mathrm{M}\mathrm{O}\mathrm{B}\mathrm{E}\mathrm{A}\text{-}\mathrm{D}\mathrm{P}\mathrm{L}\left(\mathrm{M}\mathrm{e}\mathrm{d}\right)}$		Saving: $\frac{\mathrm{H}\text{-}\mathrm{B}\mathrm{L}\mathrm{E}\mathrm{M}\mathrm{O}\left(\mathrm{M}\mathrm{e}\mathrm{d}\right)}{\mathrm{M}\mathrm{O}\mathrm{B}\mathrm{E}\mathrm{A}\text{-}\mathrm{D}\mathrm{P}\mathrm{L}\left(\mathrm{M}\mathrm{e}\mathrm{d}\right)}$		Saving: $\frac{\mathrm{B}\mathrm{L}\mathrm{M}\mathrm{O}\mathrm{C}\mathrm{C}\left(\mathrm{M}\mathrm{e}\mathrm{d}\right)}{\mathrm{M}\mathrm{O}\mathrm{B}\mathrm{E}\mathrm{A}\text{-}\mathrm{D}\mathrm{P}\mathrm{L}\left(\mathrm{M}\mathrm{e}\mathrm{d}\right)}$
Pr. no. (var.)	Total UL FEs	Total LL FE	Total UL FEs	Total LL FEs	Total UL FEs	Total LL FEs	Total UL FEs	Total LL FEs	Total UL FEs	Total LL FEs	Total UL FEs	Total LL FEs
DS1 $(10+10)$	1.478E+06	8.665E+06	2.828E+06	1.521E+07	2.102E+06	1.162E+07	0.357	2.523	0.040	0.247	0.018	0.088
DS2 $(10+10)$	1.883E+06	1.051E+07	3.587E+06	1.940E+07	2.448E+06	1.602E+07	0.398	2.844	0.045	0.288	0.021	0.10
DS3 $(10+10)$	9.543E+05	1.086E+07	1.865E+06	2.109E+07	1.370E+06	1.527E+07	0.774	2.819	0.081	0.288	0.038	0.101
DS4 $(1+9)$	1.346E+06	2.960E+06	2.476E+06	5.438E+06	1.910E+06	4.204E+06	0.188	2.400	0.026	0.324	0.017	0.178
DS5 $(1+9)$	8.950E+05	1.964E+06	2.707E+06	5.922E+06	1.561E+06	3.397E+06	0.249	3.784	0.035	0.502	0.023	0.266

We can see that the proposed MOBEA-DPL achieves the best IGD on all problems. The reason is that the proposed dual population lower-level search strategy and the refine search enable more upper-level non-dominated solutions to be found. However, the FEs required for the upper and lower-level objectives of MOBEA-DPL are still large. Compared with NS, although the lower-level FEs of MOBEA-DPL is reduced by more than half, it is still far more than that of algorithms with computational overhead reduction methods (i.e. H-BLEMO and BLMOCC). Therefore, the dual population lower-level search strategy and upper-level vector generation strategy proposed in this paper are complementary to the existing researches. Combined with the existing computational overhead reduction methods, MOBEA-DPL can obtain better quality upper-level PF and consumes less computing resources.

3.4. Application on a real-world optimisation problem

In this section, MOBEA-DPL is applied to the real-world decision-making problem we mentioned in the introduction, which is about the CEO making decisions considering the reactions of branch heads. A fuzzy version of this problem is addressed by Zhang et al. (2007), and a deterministic version of this problem can be mathematically formulated as follows: (3) $\begin{array}{rl}\underset{\begin{array}{c}{\mathbf{x}}_{\mathbf{u}}\in {\mathbb{R}}^2\\ {\mathbf{x}}_{\mathbf{l}}\in {\mathbb{R}}^3\end{array}}{max}& \mathbf{F}({\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}})=\left[\begin{array}{c}{x}_{u,1}+9x_{u,2}+10x_{l,1}+x_{l,2}+3x_{l,3}\\ 9x_{u,1}+2x_{u,2}+2x_{l,1}+7x_{l,2}+4x_{l,3}\end{array}\right]\\ \mathbf{s}\mathbf{.}\mathbf{t}\mathbf{.}& {\mathbf{x}}_{\mathbf{l}}\in \arg \underset{{\mathbf{x}}_{\mathbf{l}}\in {\mathbb{R}}^3}{max}\left\{\begin{array}{c}\mathbf{f}({\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}})=\left[\begin{array}{c}4x_{u,1}+6x_{u,2}+7x_{l,1}+4x_{l,2}+8x_{l,3}\\ 6x_{u,1}+4x_{u,2}+8x_{l,1}+7x_{l,2}+4x_{l,3}\end{array}\right]|\\ g_1({\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}})=3x_{u,1}-9x_{u,2}-9x_{l,1}-4x_{l,2}-61\le 0\\ g_2({\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}})=5x_{u,1}+9x_{u,2}+10x_{l,1}-x_{l,2}-2x_{l,3}-924\le 0\\ g_3({\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}})=3x_{u,1}+3x_{u,2}+x_{l,3}+5x_{l,3}-420\le 0\end{array}\right\},\\ & G_1({\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}})=3x_{u,1}+9x_{u,2}+9x_{l,1}+5x_{l,2}+3x_{l,3}-1039\le 0,\\ & G_2({\mathbf{x}}_{\mathbf{u}},{\mathbf{x}}_{\mathbf{l}})=-4x_{u,1}-2x_{u,2}+3x_{l,1}-3x_{l,2}+2x_{l,3}-94\le 0,\\ & x_{u,1},x_{u,2},x_{l,1},x_{l,2},x_{l,3}\ge 0,\end{array}$(3) where ${\mathbf{x}}_{\mathbf{u}}=(x_{u,1},x_{u,2})\in {\mathbb{R}}^2$ is the CEO's decision variables, and ${\mathbf{x}}_{\mathbf{l}}=(x_{l,1},x_{l,2},x_{l,3})\in {\mathbb{R}}^3$ are the branch heads' decision variables. The CEO aims to maximise the net profits and the quality of products produced in the company, while the objectives of the branch heads are to maximise both the worker satisfaction and their branch profits. They are all subject to constraints such as the requirements of material, marking cost, labour cost and working hours.

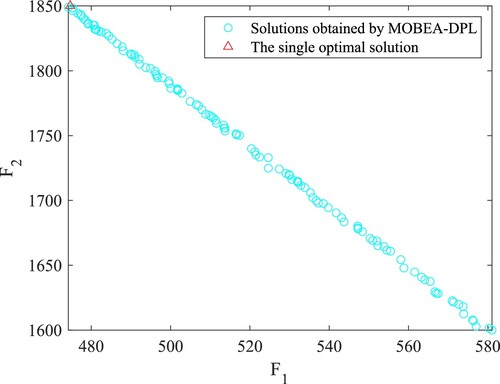
It is not possible to solve this problem analytically. Zhang et al. (2007) solved this problem by converting the two objectives into a single objective with the weighted sum approach for obtaining one optimal solution. Figure 6 shows the final non-dominated set obtained by MOBEA-DPL on this problem. The single optimal solution obtained by Zhang et al. (2007) has also been presented in Figure 6 (marked in triangle). It can be observed that MOBEA-DPL is able to well-approximate the whole PF, including the optimal solution obtained by Zhang et al. (2007). The results further verify the effectiveness of MOBEA-DPL for a real-world multi-objective bilevel optimisation problem.

Figure 6. The obtained PF of MOBEA-DPL on a practical problem. The point marked with a triangle is obtained by Zhang et al. (2007).

4. Conclusion

Multi-objective bilevel optimisation problems are difficult optimisation problems with two levels of multi-objective optimisation tasks. Both the nested structure of bilevel problems and the characteristics of multiple optimum solutions of multi-objective optimisation problems make the multi-objective bilevel optimisation problems computationally demanding and difficult to be solved.

Most of the existing researches focus on methods to reduce the computational overhead. Although the above algorithms can greatly reduce the computational overhead, they only use the lower-level objective value as the basis for environment selection in the lower-level search, and the result is to obtain a set of solutions evenly distributed on the lower-level PF. However, the upper-level performance of different optimal solutions may be very different, even they belong to the same lower-level problem. Not all lower-level Pareto-optimal solutions qualify as upper-level Pareto-optimal solutions. If the proportion of such points in the lower-level PS is further reduced, the lower-level search of the above algorithm is difficult to obtain these points, which may result in a poor quality upper-level PF. Therefore, we propose a MOBEA-DPL, which use two populations ($R{P}_i$ and $S{P}_i$) in the lower-level search. $R{P}_i$ always maintains non-dominance and diversity in the lower-level objective space throughout the lower-level search process, which provides $S{P}_i$ with convergence pressure from the lower level. $S{P}_i$ is consistent with $R{P}_i$ in the early stage of lower-level search. But in the later stage, $S{P}_i$ searches for the upper-level non-dominated solutions that is not dominated by $R{P}_i$ in the lower-level objective space. In this way, $S{P}_i$ not only meets the lower-level optimality constraints but also have a good performance in the upper-level objective space.

In addition, to improve the search efficiency, we set up the upper-level mating pool according to the performance of the current generation of individuals in the upper-level task. Compared with the previous practice of treating all upper-level vectors equally and ignoring the quality differences of sub-populations corresponding to different upper-level vectors, it is obviously more reasonable and efficient that the upper-level vector with higher quality sub-population should have more opportunities to produce offspring.

The proposed algorithm has been evaluated on five test problems with different kinds of complexities. The experimental results demonstrate that the proposed dual population lower-level search can effectively improve the quality of upper-level PF of problem where not all lower-level Pareto-optimal solutions qualify as upper-level Pareto-optimal solutions and greatly increased the computational overhead for problems with conflicting upper and lower-level objectives. In order to obtain a better solution, the overhead of computing resources is acceptable. In addition, the experimental results also show that the proposed upper-level vector generation strategy can effectively reduce the computational overhead for problems with high-dimension upper-level decision space. Thus, the proposed MOBEA-DPL is efficient and effective. Meanwhile, MOBEA-DPL is also applied to the real-world decision-making problem and successfully obtained the whole PF, including the optimal solution obtained by Zhang et al. (2007). It further verifies the effectiveness of MOBEA-DPL for a real-world multi-objective bilevel optimisation problem.

However, the FEs required for the upper and lower-level objectives of the proposed MOBEA-DPL are still large. In general, the dual population lower-level search strategy and upper-level vector generation strategy proposed in this paper are complementary to the existing researches. Combined with the existing computational overhead reduction methods, MOBEA-DPL can obtain better quality upper-level PF and consume less computing resources. In addition, due to the existence of extreme points and the reference-point-based non-dominated sorting approach used in the upper-level environment selection, the proposed MOBEA-DPL is difficult to obtain uniformly distributed points on the upper-level PF of problems DS4 and DS5. These problems need to be solved in the next research.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported in part by the National Natural Science Foundation of China (62172110), in part by the Natural Science Foundation of Guangdong Province (2022A1515010130), and in part by the Programme of Science and Technology of Guangdong Province (2021A0505110004).