Should PLS become factor-based or should CB-SEM become composite-based? Both!

ABSTRACT

This paper critically discusses a recent EJIS paper entitled “Will PLS have to become factor-based to survive and thrive?”, which laments that covariance-based structural equation modelling cannot handle composite models, postulates that PLS should become factor-based, and advocates the use of the PLSF-SEM method. We clarify that covariance-based structural equation modelling can handle composite models, e.g. using the so-called Henseler – Ogasawara specification, agree that PLS in its original form cannot consistently estimate the parameters of reflective measurement models, and reiterate that consistent PLS is a viable means to overcome this limitation. Finally, we study the performance of PLSF-SEM through scenario analyses. Based on our results, we conclude that PLSF-SEM is inferior to covariance-based structural equation modelling and consistent PLS in almost all respects. Therefore, we cannot currently recommend the use of PLSF-SEM, and it is up to future research to demonstrate potential advantages over existing structural equation modelling techniques.

KEYWORDS:

• PLS-SEM
• consistent PLS
• H–O specification
• reflective measurement
• formative constructs

1. Introduction

Structural equation modelling (SEM) is a versatile analytical tool for theory testing, which is widely applied in information systems (IS) and many other disciplines of business and social science. It relies on a representation of a theory in the form of a statistical model and compares the model-implied variance-covariance matrix with the variance-covariance matrix of the data at hand to judge the quality of the model. While there are many different SEM techniques, two types of SEM techniques prevail: covariance-based SEM (CB-SEM) and variance-based SEM. The most prominent variance- and covariance-based SEM technique are partial least squares (PLS) and maximum likelihood, respectively.

A recent issues and opinion piece published in this journal (Kock, 2024, further abbreviated as K24) opens a debate about the future of SEM in IS research. In essence, K24 identifies two major problems in the SEM context and proposes a solution. The first problem is that although composites play a pivotal role in research and society, CB-SEM cannot deal with composites, which renders composite models paradoxical. The second problem is that PLS, which actually deals with composite models, cannot consistently estimate reflective measurement models. The latter is also known as common factor model. Therefore, K24 argues that “PLS-based methods will have to become factor-based to survive and thrive in the context of SEM”. As a solution, K24 proposes factor-based PLS (PLSF-SEM; Kock, 2017, 2019a, 2019b). K24 regards PLSF-SEM as a suitable means to address most of the criticisms of PLS as expressed in a recent debate in the journal Communications of the Association of Information Systems (cf. Evermann & Rönkkö, 2023a, 2023b; Kock, 2023). K24 is not only an opinion piece, but also an advocacy paper for PLSF-SEM.

In our commentary, we would like to draw attention to the issues that are relevant for IS researchers: To what extent do the capabilities of SEM techniques such as CB-SEM and PLS satisfy the methodological needs of IS researchers? What are the actual benefits of using PLSF-SEM? Which SEM technique should be preferred in typical IS research situations? We show that the two problems that K24 raises have already been solved: CB-SEM can be used for structural equation models containing composites (cf. Grace & Bollen, 2008; Schuberth, 2023), and if a correction for attenuation is applied to PLS as is done in consistent PLS (PLSc; Dijkstra & Henseler, 2015a, 2015b), analysts can obtain consistent estimates for common factor models. Finally, we show through scenario analysis that PLSF-SEM is inferior to existing solutions in several respects. Since the adoption of premature techniques can harm the progress of science (Evermann & Rönkkö, 2023a), we recommend to stick to more established techniques, particularly CB-SEM or PLSc. Both of them can deal with models that contain composites and common factors.

2. SEM in IS research from a helicopter view

Theories of IS research are often expressed as relationships between theoretical constructs. To empirically test such theories, IS researchers strongly rely on SEM. An additional complexity arises from the fact that some constructs of IS research are best modelled as common factors, whereas other constructs are better modelled as composites (Yu et al., 2021). Therefore, as K24 implicitly notes – and we fully agree with this notion – SEM techniques only have a future for IS research if they can cope with both, common factors and composites.

Traditionally, CB-SEM and PLS were only capable of modelling theoretical constructs in a single way: CB-SEM modelled constructs as common factors (see e.g., Bollen, 1989), whereas PLS modelled constructs as composites (see e.g., Dijkstra, 2017; Sarstedt et al., 2016). Consequently, the way of how the theoretical constructs should be modelled dictated the choice of the SEM technique. The decision for or against a method was not to be made light-heartedly, because using the wrong model for one’s theoretical constructs can easily result in biased estimates and lead to erroneous conclusions (c.f. Jarvis et al., 2003; Sarstedt et al., 2016; Schuberth, Rosseel, et al., 2023).

In recent years, methodological research on SEM has made significant progress, so that the formerly strict relation between the SEM techniques and the way of modelling theoretical constructs has been relaxed (Henseler, 2021; Schuberth et al., in press; Schuberth, Zaza, et al., 2023). More specifically, the advent of the Henseler–Ogasawara specification (H–O specification, see Schuberth, 2023) allows to specify composites in CB-SEM with the same ease as common factors, and consistent PLS (PLSc, see Dijkstra & Henseler, 2015a, 2015b) makes it possible to obtain consistent estimates for common factor models using the iterative PLS algorithm. In the following subsection, we will discuss both developments in more detail.

2.1. Modeling composites with CB-SEM using the H–O specification

Specifying composites in CB-SEM is neither impossible nor paradoxical.¹ Although traditionally, CB-SEM has mainly been used for modelling common factors, researchers have also occasionally investigated its use for modelling composites (e.g., Dolan et al., 1999; Fan, 1997; Grace & Bollen, 2008; Hancock et al., 2013; Rose et al., 2019). Admittedly, all of these approaches have their limitations; they either require multiple estimation steps, are limited to exogenous constructs, require complex constraints, or work only with pre-specified weights. This means that none of these approaches can model composites as easily as PLS.

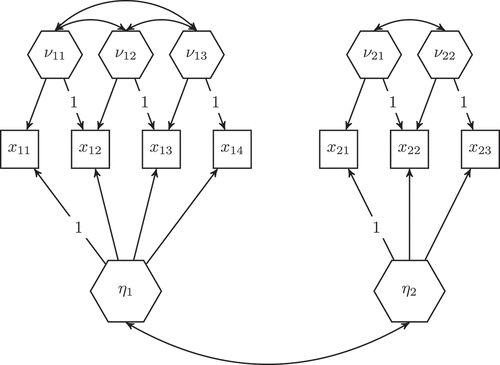
This situation changed with the development of the H–O specification, which allows researchers using CB-SEM to model composites with the same flexibility that they are accustomed from modelling common factors (Schuberth, 2023; Yu et al., 2023). It expresses the relationships between a composite and its components by means of composite loadings, not weights. The variances and covariances of a block of components are explained by a focal composite, i.e., the emergent variable, and a set of potentially correlated, but not fully linearly dependent composites that capture the remaining variances and covariances, i.e., the excrescent variables (Henseler, 2021; Yu et al., 2023). Note that the H–O specification models a composite in such a way that it accounts for the covariances between its components and other variables of the model (for an alternative that specifies composites without that characteristic, see the pseudo-indicator model proposed by Rose et al., 2019).

Figure 1 depicts a model consisting of two emergent variables, ${\eta }_1$ and ${\eta }_2$, and seven observed variables ($x_{11}$–$x_{14}$ and $x_{21}$–$x_{23}$). It also contains five excrescent variables, ${\nu }_{11}$, ${\nu }_{12}$, ${\nu }_{13}$, ${\nu }_{21}$, and ${\nu }_{22}$. The model is identified and has 6 degrees of freedom. In analogy to the kind of model studied in confirmatory factor analysis, which typically consists of correlated common factors, this model consists of correlated composites and is the underlying type of model studied in a confirmatory composite analysis (CCA, see Hubona et al., 2021; Schamberger et al., 2023; Schuberth et al., 2018a). Various estimators have been proposed for CCA: Next to maximum likelihood and other estimators of CB-SEM (Liu et al., 2022; Schamberger et al., 2023), also PLS (Henseler & Schuberth, 2020; Schuberth, 2021) or MAXVAR (Schuberth et al., 2018a) can be employed.

Figure 1. Specifying composites in CB-SEM.

2.2. Estimating models containing common factors with PLSc

It is well established in the literature that PLS can consistently estimate structural models that contain composites (Dijkstra, 2017). In contrast, when a structural equation model contains common factors, PLS estimates are known to be only consistent at large, i.e., only when both the number of indicators and the number of observations tend to infinity will consistent estimates be obtained (Hui & Wold, 1982). Therefore, drawing conclusions from structural equation models containing common factors that have been estimated by PLS can severely compromise a researcher’s conclusions (Evermann & Rönkkö, 2023a; Rönkkö & Evermann, 2013; Schuberth, 2021; Schuberth, Rosseel, et al., 2023; Schuberth, Schamberger, et al., 2023).

As a remedy, a consistent version of PLS, namely consistent PLS (PLSc) was introduced (Dijkstra, 1985; Dijkstra & Henseler, 2015b). In a first step, PLSc conducts the traditional PLS algorithm using Mode A to obtain weight estimates. Subsequently, PLSc applies a correction for attenuation to consistently estimate factor loadings and path coefficients. Consistent factor loading estimates of the indicators associated with a common factor ${\eta }_j$ are obtained as follows:

(1) ${\hat{\lambda }}_{\mathit{j}}={\hat{c}}_{\mathit{j}}{\stackrel{\mathbf{ˆ}}{\mathit{w}}}_{\mathit{j}}$(1)

where ${\stackrel{\mathbf{ˆ}}{\mathit{w}}}_{\mathit{j}}$ is the vector containing the PLS Mode A weight estimates. The correction factor ${\hat{c}}_{\mathit{j}}$ is obtained in such a way that the off-diagonal elements of the indicators’ empirical correlation matrix ${\mathit{S}}_{\mathit{jj}}$ are “reproduced as best as possible in a least squares sense” (Dijkstra & Henseler, 2015a):

(2) ${\hat{c}}_{\mathit{j}}=\sqrt{\frac{{\widehat{\mathit{w}{\mathit{ }}^{\mathrm{\prime }}}}_{\mathit{j}}({\mathit{S}}_{\mathit{jj}}-\mathrm{diag}({\mathit{S}}_{\mathit{jj}})){\hat{\mathit{w}}}_{\mathit{j}}}{{\widehat{\mathit{w}{\mathit{ }}^{\mathrm{\prime }}}}_{\mathit{j}}({\hat{\mathit{w}}}_{\mathit{j}}{\widehat{\mathit{w}{\mathit{ }}^{\mathrm{\prime }}}}_{\mathit{j}}-\mathrm{diag}({\hat{\mathit{w}}}_{\mathit{j}}{\widehat{\mathit{w}{\mathit{ }}^{\mathrm{\prime }}}}_{\mathit{j}})){\hat{\mathit{w}}}_{\mathit{j}}}}$(2)

Moreover, the reliability of the factor scores obtained by PLS Mode A weights can be estimated as ${\widehat{\rho }}_{\mathit{j}}={\widehat{c}}_{\mathit{j}}^2{(w\prime j{\widehat{w}}_{\mathit{j}})}^2$. In the literature, this reliability coefficient is also known as Dijkstra-Henseler’s ${\rho }_A$ (Dijkstra & Henseler, 2015a). Consequently, the correlation between PLS Mode A factor scores can be corrected for attenuation to obtain consistent common factor correlation estimates:

(3) $\widehat{\text{cor}}({\eta }_j,{\eta }_i)=\mathit{w}\prime \mathit{j}{S}_{\mathit{ji}}{\widehat{w}}_{\mathit{i}}\sqrt{{\widehat{\rho }}_{\mathit{j}}{\widehat{\rho }}_{\mathit{i}}}$(3)

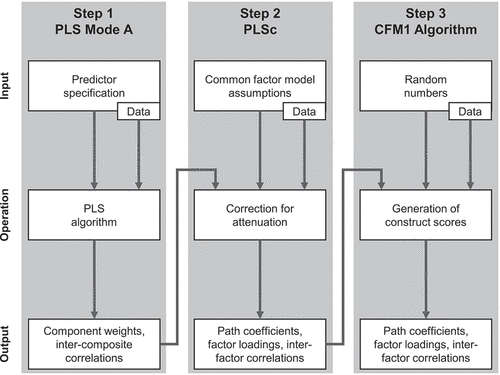
In the final step, these common factor correlations are used to consistently estimate the path coefficient by ordinary least squares or two-stage least squares in case of recursive or non-recursive structural models, respectively. Since PLSc applies the correction for attenuation for each construct separately, it can be applied to models containing both common factors and composites. In case of a composite, the respective reliability estimate is set to one and thus no correction for attenuation is applied. Figure 2 shows schematically the steps of PLSc.

Figure 2. Schematic illustration of PLSc (adapted from Schuberth et al., 2018b).

Nowadays, PLSc is well explored. For instance, its asymptotical properties have been derived (e.g., Dijkstra, 1985; Schuberth, Rosseel, et al., 2023), and its finite sample performance has been studied and compared to existing approaches (e.g., Aguirre-Urreta & Rönkkö, 2018; Dijkstra & Henseler, 2015a; Dijkstra & Schermelleh-Engel, 2014; Schuberth, Hubona, et al., 2023; Takane & Hwang, 2018; Yuan et al., 2020). Moreover, PLSc has been extended to deal with ordinal indicators (Schuberth et al., 2018b), to allow for correlated measurement errors within blocks of indicators (Rademaker et al., 2019), to overcome multicollinearity issues in the structural model (Jung & Park, 2018), and to handle outliers (Schamberger et al., 2020). Finally, various guidelines for applied IS researchers who want to use PLSc have been proposed (e.g., Benitez et al., 2020; Evermann & Rönkkö, 2023a; Henseler et al., 2016).

3. What about PLSF-SEM?

K24 strongly advocates another technique: PLSF-SEM. Arguably, PLSF-SEM addresses many criticisms brought forward against PLS (cf. Evermann & Rönkkö, 2023a). But is PLSF-SEM a viable methodological option for IS researchers? In this section we try to answer some basic questions about PLSF-SEM: What is PLSF-SEM? What are its capabilities? What benefits can it offer to IS researchers?

3.1. What is PLSF-SEM?

The working principle of PLSF-SEM can be summarised in a single sentence: PLSF-SEM takes the results of PLSc and tries to reproduce them. In other words, “as far as parameter estimation is concerned, [PLSF-SEM] is simply PLSc but slower and more difficult to understand” (Evermann & Rönkkö, 2023b, p. 763). Taking a more granular look at PLSF-SEM as is done in Figure 3, one could say that it consists of three steps that are performed in a sequence: PLS Mode A, PLSc, and the actual PLSF-SEM algorithm. In the third step, an iterative algorithm called CFM1 (Kock, 2022) mixes indicator data and random data in order to create factor scores. These factor scores are constructed in such a way that they reproduce the common factor correlations obtained from PLSc as close as possible (Kock, 2017).

Figure 3. The three steps toward PLSF-SEM.

All three steps take the data, the output of the previous step (if available), and some external input; perform an operation; and produce some output. However, the third step differs from the other two in two important ways: the (lack of) quality of the external input and the (lack of) novelty of the output. Whereas in the first two steps, the external input provides new information, the external input of the third step is either uninformative or bears the danger of incorporating inappropriate information. And while the first two steps produce output that represents new information, the third step produces output that has already been produced in Step 2. The equivalence of the output of Steps 2 and 3 is a logical consequence of the requirement that the inter-factor correlations produced by PLSF-SEM be equal to those produced by PLSc. This requirement “drives the iterative convergence process” (Kock, 2019b, p. 681).

Since PLSF-SEM merely reproduces the output of PLSc, the only added value of PLSF-SEM could be the factor scores it generates. But even this remaining possibility of added value is questionable. Factor scores serve as carriers of information. However, the information carried by PLSF-SEM factor scores is either known by design, known from a previous step, or untrustworthy. Information like the mean and variance of PLSF-SEM factor scores are known by design: Since they are standardised, they have a mean of 0 and a variance of 1. Information like path coefficients, inter-factor correlations, R2 values, variance inflation factors, factor loadings, construct reliabilities, item reliabilities, average variance extracted are all known or can be calculated from the output of Step 2, i.e., PLSc. Since these values are already available, there is no need to have the factor scores for their determination. K24 sees merits in the PLSF-SEM factor scores for the study and visualisation of interactions and other nonlinear effects. However, Dijkstra and Schermelleh-Engel (2014) could not find any obvious advantage of scores-based analyses of interactions and other nonlinear effects over CB-SEM (concretely, latent moderated structural equations, LMS, Klein & Moosbrugger, 2000), and surface plots of models with interaction effects require only a regression equation with estimated coefficients, not factor scores. Moreover, it remains unclear how researchers should deal with the fact that PLSF-SEM creates different factor scores with different random data, so that any analysis based on PLSF-SEM factor scores might not be reproducible. The approach taken by PLSF-SEM – holding the random number seed constant – is not a satisfactory solution, because the factor scores will still differ from one analysis to another if the model is built in a different order. In general, it cannot be ruled out that the random data contained in PLSF-SEM’s factor scores has undesired effects on the results of any more advanced analysis. Moreover, based on a comparison of PLSF-SEM, Thurstone and Bartlett factor scores conducted in Kock (2019a), K24 notes that “PLSF produced the highest quality estimates of correlation-preserving factors”. However, literature has been established that neither Bartlett factor scores nor Thurstone factor scores are correlation preserving, i.e., the correlations among the factor scores is different to the correlations among the factors (e.g., DiStefano et al., 2009; Skrondal & Laake, 2001). Against this background, we do not share the optimistic view on PLSF-SEM factor scores.

3.2. Can PLSF-SEM deal with common factors?

As the letter “F” in its name suggests, PLSF-SEM is devoted to structural equation models with common factors. K24 regards PLSF-SEM as the obvious solution for making PLS factor-based; it has “some advantages not only over classic PLS implementations, but also over covariance-based SEM approaches”. According to Kock (2019b, p. 682), one of PLSF-SEM’s main advantages is the “ability to generate estimates of the true factors”.

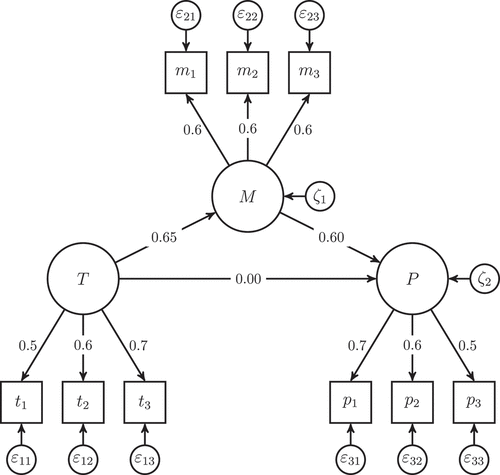
To assess PLSF-SEM’s ability to deal with common factors, we subject it to a scenario analysis. A scenario analysis has the advantage that the true parameter values are known (for the researcher, not for the method). In this way, we aim to answer the question of how PLSF-SEM performs in a certain research situation. For this purpose, we rely on the same population model as used in K24 (Figure 3) to illustrate the performance of PLSF-SEM relative to that of CB-SEM and PLS. This population model is depicted in Figure 4. However, while K24 drew a sample of $\mathit{N}=10,000$ from this population model, we make use of a dataset of the same size that functions exactly according to the population model. We use CB-SEM as implemented in the R package lavaan (version 0.6–14; Rosseel, 2012), PLS and PLSc as implemented in the R package cSEM (version 0.5.0; Rademaker & Schuberth, 2022), and PLSF-SEM with the Type CFM1 algorithm as implemented in WarpPLS (version 8.0; Kock, 2022). Among the available PLSF-SEM algorithms, the Type CFM1 algorithm is the only one documented in the user manual.

Figure 4. Population model with three common factors.

Table 1. Comparison of results for a structural equation model with common factors only.

Coefficient	True value	CB-SEM	PLSc	PLSF-SEM	PLS
${\lambda }_{\mathit{T}1}$	0.500	0.500	0.500	0.524	0.675
${\lambda }_{\mathit{T}2}$	0.600	0.600	0.600	0.614	0.762
${\lambda }_{\mathit{T}3}$	0.700	0.700	0.700	0.696	0.822
${\lambda }_{\mathit{M}1}$	0.600	0.600	0.600	0.598	0.757
${\lambda }_{\mathit{M}2}$	0.600	0.600	0.600	0.596	0.757
${\lambda }_{\mathit{M}3}$	0.600	0.600	0.600	0.590	0.757
${\lambda }_{\mathit{P}1}$	0.700	0.700	0.700	0.700	0.822
${\lambda }_{\mathit{P}2}$	0.600	0.600	0.600	0.612	0.762
${\lambda }_{\mathit{P}3}$	0.500	0.500	0.500	0.521	0.675
${\beta }_{\mathit{MT}}$	0.650	0.650	0.650	0.662	0.413
${\beta }_{\mathit{PM}}$	0.600	0.600	0.600	0.614	0.335
${\beta }_{\mathit{PT}}$	0.000	0.000	0.000	0.003	0.113
$R^2(\mathit{M})$	0.423	0.423	0.423	0.438	0.171
$R^2(\mathit{P})$	0.360	0.360	0.360	0.379	0.156
AVE($\mathit{T}$)	0.367	0.367	0.367	0.379	0.571
AVE($\mathit{M}$)	0.360	0.360	0.360	0.354	0.573
AVE($\mathit{P}$)	0.367	0.367	0.367	0.379	0.571
${\rho }_c$($\mathit{T}$)	0.630	0.630	0.630	0.644	0.799
${\rho }_c$($\mathit{M}$)	0.628	0.628	0.628	0.621	0.801
${\rho }_c$($\mathit{P}$)	0.630	0.630	0.630	0.643	0.799
SRMR	0.000	0.000	0.000	0.015	0.095

Table 1 reports the coefficients and the parameters retrieved from the four methods. Based on these values, at least three observations can be made regarding the performance of PLSF-SEM: First, the obtained values suggest that PLSF-SEM certainly deserves the qualifier “factor-based”. In contrast to traditional PLS, PLSF-SEM produces results that are much closer to the true values. Second, in contrast to CB-SEM and PLSc, PLSF-SEM cannot retrieve the true parameter values. Although the deviations are small, they are noticeable and non-negligible. The occurrence of these deviations indicates that PLSF-SEM is not Fisher consistent. Finally, the model estimated by PLSF-SEM shows some misfit (in terms of SRMR). This is surprising, because the population model works according to a common factor model. Although the degree of misfit is still much smaller than that of traditional PLS, it still means that PLSF-SEM is not able to identify a perfectly fitting model as such.

In order to assess PLSF-SEM’s ability to generate estimates of the true factors, we inspect the produced factor scores and compare them to their true values. Table 2 shows the scores of all three factors for the first five cases as well as the last case in our dataset. This table lists the factor scores from two different PLSF-SEM runs. The runs differ only with regard to the order in which the model was built by the modeller. Table 2 allows two important insights: First, the PLSF-SEM factor scores differ from one run to another, which means that the factor scores are determined differently without that the data or the model would have changed. The metrological uncertainty that we can witness here originates from factor indeterminacy (Rigdon et al., 2019). Factor indeterminacy can be defined as “the inability to determine uniquely the common and unique factor variables of the common factor model from the uniquely defined ‘observed variables’ because the number of observed variables is smaller than the number of common and unique factors” (Mulaik & McDonald, 1978, p. 177). Since the “estimates of the true factors” of PLSF-SEM are to a certain extent arbitrary, they should not be understood as estimates in the statistical sense. Second, the factor scores produced by PLSF-SEM can be quite far off from the true values. In the current case, the correlation between the PLSF-SEM factor scores and the true factor scores is approximately 0.7 (see the last row of Table 2), which means that the PLSF-SEM factor scores have about one half of their variance in common with the true factor scores. Notably, the PLSF-SEM factor scores deviate even more from the true scores than the composite scores generated by PLS. The correlation between PLS composite scores and the true factor scores is 0.803 for T and P, and 0.792 for M. Thus, at least for the illustrative model in K24 (Figure 3), PLSF-SEM factor scores cannot be regarded as an improvement over PLS composite scores.

Table 2. True factor scores and factor scores from two PLSF-SEM runs for three common factors.

	T			M			P
	True	PLSF-SEM		True	PLSF-SEM		True	PLSF-SEM
Case	Value	Run 1	Run 2	Value	Run 1	Run 2	Value	Run 1	Run 2
1	−0.368	−0.822	−0.655	−0.630	−1.181	−0.779	−0.897	−0.470	−0.970
2	−0.511	0.111	0.245	0.248	0.988	0.677	0.387	0.407	0.522
3	−1.414	−1.371	−0.164	−0.516	−1.073	−0.748	0.580	1.069	−0.387
4	1.562	1.949	0.820	−0.256	0.689	0.510	1.087	0.836	2.113
5	−0.432	0.047	0.422	−1.157	−0.769	−0.414	−0.872	−0.192	−0.881
⁝	⁝	⁝	⁝	⁝	⁝	⁝	⁝	⁝	⁝
10,000	−0.712	−0.841	−0.650	−1.515	−1.459	−1.583	−2.447	−1.615	−1.682
Correlation with
true scores		0.703	0.701		0.695	0.696		0.693	0.695

3.3. Can PLSF-SEM deal with composites?

According to K24, composites can play an important role not only in IS research, but also in many other fields of business and social science. A substantial body of methodological literature agrees with this assessment (cf. Diamantopoulos & Winklhofer, 2001; Petter et al., 2007; Rose et al., 2019; Yu et al., 2021) and regards composites as important way to model phenomena of interest. Thus, there is a need for statistical methods that can deal with composite models. Originally, PLS is a composite-based technique, and it can consistently estimate composite models (Dijkstra, 2017). PLSF-SEM should have inherited this characteristic.² But is PLSF-SEM a consistent estimator when structural equation models contain composites? And can PLSF-SEM retrieve the true composite scores?

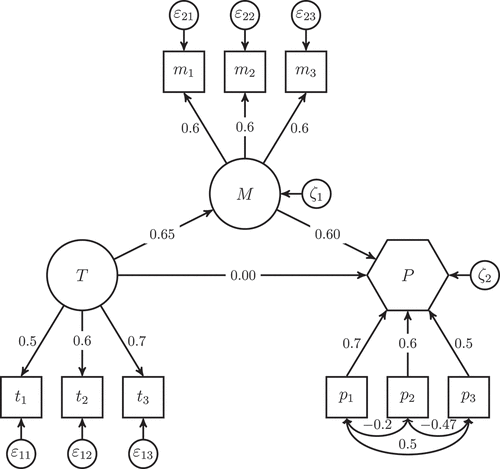
To assess PLSF-SEM’s ability to deal with composites, we subject it to another scenario analysis. In this case, we rely on a slightly modified population model as depicted in Figure 5. It differs from the previous population model with regard to the endogenous construct $\mathit{P}$: $\mathit{P}$ is now modelled as a composite, and instead of factor loadings, we now have weights with values of 0.7, 0.6., and 0.5. Again, we make use of a dataset comprising 10,000 observations that functions exactly according to the population model.

Figure 5. Population model with two common factors and one composite.

To estimate the model parameters, we use CB-SEM as implemented in the R package lavaan (version 0.6–14; Rosseel, 2012) in combination with the H–O specification (Yu et al., 2023), PLS (Mode A for the common factors, Mode B for the composite) and PLSc (Mode A with correction for attenuation for the common factors and Mode B for the composite) as implemented in the R package cSEM (version 0.5.0; Rademaker & Schuberth, 2022), and PLSF-SEM with the Type CFM1 algorithm as implemented in WarpPLS (version 8.0; Kock, 2022). Again, we report the results of two PLSF-SEM runs that differ with regard to the order in which the model was built. While lavaan and cSEM work without any problems, WarpPLS displays a warning message for the model. Since the warning message is uncritical³ and we do not see any obvious reason why PLSF-SEM should fail when the other methods work reliably, we continue with the PLSF-SEM analysis.

Figure 6 shows the model specification for PLSF-SEM as well as a selection of the results such as weights, loadings, path coefficients and R2 values. These values differ from the population values depicted in Figure 5. In particular, all values related to the composite $\mathit{P}$ are far off from their true values; this holds for the weights, the path coefficients, and the R2 value. Table 3 provides a detailed comparison of the results obtained for the four methods. It clearly shows that CB-SEM and PLSc are able to retrieve the correct values, whereas PLSF-SEM fails to do so. PLS is only able to reproduce the weights correctly. The clearest signal is emitted by the overall model fit as quantified by the SRMR: While the models estimated with CB-SEM and PLSc yield a perfect fit (SRMR = 0), the models estimated by PLS and PLSF-SEM show a substantial amount of misfit. In particular, the SRMR of 0.193 obtained from PLSF-SEM is far above any common threshold (see e.g., Hu & Bentler, 1999; Schermelleh-Engel et al., 2003).

Table 3. Comparison of results for a structural equation model with two common factors and a composite.

Coefficient	True	CB-SEM	PLSc	PLSF-SEM		PLS
	Value			Run 1	Run 2
${\lambda }_{\mathit{T}1}$	0.500	0.500	0.500	0.544	0.550	0.675
${\lambda }_{\mathit{T}2}$	0.600	0.600	0.600	0.646	0.656	0.762
${\lambda }_{\mathit{T}3}$	0.700	0.700	0.700	0.729	0.746	0.822
${\lambda }_{\mathit{M}1}$	0.600	0.600	0.600	0.648	0.650	0.757
${\lambda }_{\mathit{M}2}$	0.600	0.600	0.600	0.647	0.645	0.757
${\lambda }_{\mathit{M}3}$	0.600	0.600	0.600	0.642	0.645	0.757
$w_{\mathit{P}1}$	0.700	0.700	0.700	0.179	0.178	0.700
$w_{\mathit{P}2}$	0.600	0.600	0.600	$-$0.172	$-$0.171	0.600
$w_{\mathit{P}3}$	0.500	0.500	0.500	0.213	0.215	0.500
${\beta }_{\mathit{MT}}$	0.650	0.650	0.650	0.675	0.758	0.413
${\beta }_{\mathit{PM}}$	0.600	0.600	0.600	0.512	0.556	0.417
${\beta }_{\mathit{PT}}$	0.000	0.000	0.000	0.307	0.203	0.141
$R^2(\mathit{M})$	0.423	0.423	0.423	0.456	0.575	0.171
$R^2(\mathit{P})$	0.360	0.360	0.360	0.568	0.522	0.242
AVE($\mathit{T}$)	0.367	0.367	0.367	0.415	0.430	0.571
AVE($\mathit{M}$)	0.360	0.360	0.360	0.417	0.418	0.573
AVE($\mathit{P}$)	–	–	–	0.598	0.598	–
${\rho }_c$($\mathit{T}$)	0.630	0.630	0.630	0.677	0.690	0.799
${\rho }_c$($\mathit{M}$)	0.628	0.628	0.628	0.682	0.683	0.801
${\rho }_c$($\mathit{P}$)	–	–	–	0.403	0.403	–

Figure 6. Model with two common factors and a composite estimated with PLSF-SEM (WarpPLS 8.0 screenshot).

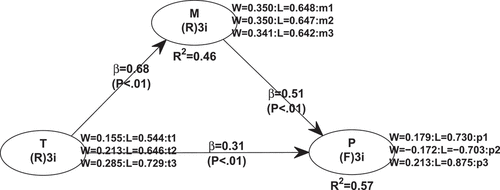
In order to assess PLSF-SEM’s ability to produce composite scores, we inspect the produced composite scores and compare them to the true values. Table 4 shows the scores of the composite $\mathit{P}$ for the first five cases as well as the last case in our dataset. Again, this table lists the composite scores from two different PLSF-SEM runs. The two runs differ only with regard to the order in which the model was built by the modeller. Table 4 allows two important insights: First, the composite scores produced by PLSF-SEM can be quite far off from the true values. In the current case, the correlation between the PLSF-SEM composite scores and the true composite scores is approximately 0.527, which means that the PLSF-SEM composite scores have less than one third of their variance in common with the true composite scores. This means that the composite scores generated by PLSF-SEM are even less valid than the factor scores generated by PLSF-SEM, although the components of the composite are not contaminated by random measurement error. PLSF-SEM’s inability to generate valid composite scores weighs even harder taking into account that CB-SEM and and PLSc are able to perfectly reproduce the true composite scores. Also for structural equation models containing composites, there appear to be substantial differences between the results obtained from two different PLSF-SEM runs. Consequently, PLSF-SEM cannot be regarded as a valid method for structural equation models containing composites (formative constructs), which poses a validity threat for extant and future studies that used or will use PLSF-SEM under such circumstances.

Table 4. Scores for the composite P obtained through different approaches.

Case	True	CB-SEM	PLSc	PLSF-SEM		PLS
	Value			Run 1	Run 2
1	0.783	0.783	0.783	0.261	0.259	0.783
2	$-$1.267	$-$1.267	$-$1.267	$-$0.063	$-$0.065	$-$1.267
3	1.117	1.117	1.117	$-$0.508	$-$0.507	1.117
4	0.007	0.007	0.007	$-$0.753	$-$0.749	0.007
5	$-$1.379	$-$1.379	$-$1.379	$-$1.046	$-$1.047	$-$1.379
⁝	⁝	⁝	⁝	⁝	⁝	⁝
10.000	$-$0.521	$-$0.521	$-$0.521	$-$0.509	$-$0.507	$-$0.521
Correlation with
true scores		1.000	1.000	0.526	0.527	1.000

3.4. A summative evaluation of PLSF-SEM

The starting point for our evaluation is the claims that have been made about PLSF-SEM. Kock (2017, p. 48) claims that PLSF-SEM is “a new method that generates estimates of both true composites and factors”. As our conceptual and scenario analyses have shown, this notion is erroneous in at least two ways. First, PLSF-SEM does not generate estimates of true factors. Since the obtained factor scores contain a substantial portion of random data, their values depend on the concrete random data used for this purpose. We found that the creation of factor scores is influenced by the order in which the structural equation model is built by the analyst. This makes the factor scores unreproducible. For estimates, this is undesirable. Second, PLSF-SEM does not generate estimates of true composites, leading to distorted results if a model contains a composite. This makes PLSF-SEM a clearly inferior method, since CB-SEM and PLSc are able to generate true composite scores without any problems. Finally, in contrast to what the term “new method” might suggest, PLSF-SEM does not provide any new insights; it simply tries to reproduce the results of an existing method, namely PLSc. Against this background, we cannot currently identify any advantages of PLSF-SEM that outweigh its weaknesses.

4. Implications

There is a good message for IS researchers who need a versatile technique to estimate structural equation models: There is still something to choose! Table 4 compiles what is known and what is not known about the four techniques mentioned by K24 with regard to possible model specifications, properties of the estimator, and available model assessment tools.

If researchers deal with a structural equation model that only consists of composites, they may use CB-SEM with the H–O specification or PLS using Mode B. Both techniques provide consistent estimates. First simulation results indicate that for correctly specified composite models, the two techniques have a very similar performance in terms of parameter recovery (Schuberth, Hubona, et al., 2023). However, CB-SEM is asymptotically efficient, offers more flexibility in modelling, and facilitates model comparisons. Thus, until the PLS literature demonstrates a use case where PLS outperforms CB-SEM with the H–O specification, there seems to be little reason to use PLS over CB-SEM.

If a structural equation model contains one or more common factors, it is indispensable to rely on a technique that has been designed for this purpose, e.g., CB-SEM or PLSc. Particularly for CB-SEM and PLSc, there is ample evidence that they consistently estimate structural equation models containing both composites and common factors. Unfortunately, the same does not hold true for PLSF-SEM. PLSF-SEM is characterised by the fact that it almost reproduces the parameter estimates of PLSc for common factor models, but cannot cope with composites. Because of this weakness, its lack of added value over PLSc, and its unclear characteristics, we can currently not identify any situation in which we would recommend the use of PLSF-SEM. Until the ambiguities surrounding PLSF-SEM are resolved and clear advantages of PLSF-SEM over existing techniques are demonstrated, IS researchers should not prematurely adopt PLSF-SEM. Instead, they rather should use CB-SEM or PLSc. First simulation results indicate that for correctly specified common factor models, the two techniques have a very similar performance in terms of parameter recovery (Schuberth, Hubona, et al., 2023). PLSc has the advantage of being a limited information estimator, meaning that misspecification in one part of the model has little effect on the rest of the model. However, CB-SEM is more efficient (Takane & Hwang, 2018), offers more flexibility in modelling (cf. Schuberth, Zaza, et al., 2023), facilitates model comparisons, and is less prone to chance correlations (see Rönkkö, 2014), making it the preferred technique in most research settings.

As Table 5 illustrates, among the SEM techniques discussed in K24, CB-SEM offers the largest amount of features and it is most well-understood. We therefore conclude that in most research settings, using CB-SEM is the most promising avenue. However, if CB-SEM does not produce results, PLSc could be a good alternative (Evermann & Rönkkö, 2023a; Schuberth, Zaza, et al., 2023).

Table 5. Comparing the suitability of CB-SEM, PLSc, PLSF-SEM, and PLS for IS research.

Characteristic	CB-SEM with ML	PLSc	PLSF-SEM	PLS-SEM
Model specification options
Recursive path models	possible (Jöreskog, 1970)	possible (Dijkstra & Henseler, 2015b)	possible (Kock, 2019b)	possible (Wold, 1974)
Non-recursive path models	possible (Wong & Law, 1999)	possible (Dijkstra & Henseler, 2015a)	possible (Kock, 2019a)	possible (Callaghan et al., 2007)
Common factor models	possible (Bollen, 1989)	possible (Dijkstra & Henseler, 2015b)	possible (Kock, 2019b)	not possible (Henseler et al., 2024)
Composite models	possible (Schuberth, 2023)	possible (Henseler, 2017)	not possible (this paper)	possible (Dijkstra, 2017)
Formative measurement	possible (Jöreskog & Goldberger, 1975)	possible (Henseler, 2017)	no evidence	not possible (Schuberth, Rosseel et al., 2023)
Error correlations	possible (Bollen, 1989)	possible within indicator blocks (Rademaker et al., 2019)	no evidence	no evidence
Parameter constraints	possible (Bollen, 1989)	no evidence	no evidence	no evidence
Model comparisons	possible (Bollen, 1989)	no evidence	no evidence	partially possible (Sharma et al., 2019)
Properties of the estimator
Consistency	yes (Bollen, 1989)	yes (Dijkstra & Henseler, 2015a)	no (this paper)	only for composites (Dijkstra, 2017)
Efficiency	asymptotic (Bollen, 1989)	no evidence	no evidence	no evidence
Optimization criterion	defined (Jöreskog, 1970)	undefined	undefined	undefined
Convergence	likely (Reinartz et al., 2009)	likely (Kock, 2019b)	likely (Kock, 2019b)	likely (Henseler, 2010)
Heywood cases	possible (Reinartz et al., 2009)	possible (Sharma et al., 2023)	unknown	not possible (Lohmöller, 1988)
Model assessment tools
Parametric model fit tests	available (Bollen, 1989)	not available	not available	not available
Non-parametric model fit tests	available (Bollen & Stine, 1992)	available (Dijkstra & Henseler, 2015a)	not available	available for composites (Schuberth, Rademaker et al., 2023)
Model fit indices	many available (Hu & Bentler, 1999)	few available (Henseler et al., 2016)	not available	few available (Henseler et al., 2014)
Information criteria	available (Bollen et al., 2014)	not available	not available	available for structural models (Sharma et al., 2019)
Parametric parameter tests	available (Bollen, 1989)	not available	not available	not available
Non-parametric parameter tests	available (Nevitt & Hancock, 2001)	available (Aguirre-Urreta & Rönkkö, 2018)	available (Kock, 2019b)	available (Chin, 1998)

5. Conclusion

IS research requires SEM techniques that can deal with both common factors and composites. To this end, it is desirable that PLS could also be used to estimate models containing common factors and CB-SEM could also be used to estimate models containing composites. Fortunately, methodological research has provided various developments of these two techniques. On the one hand, the PLS estimates can be corrected for attenuation bias in case of common factors using Cronbach’s alpha or Dijkstra-Henseler’s ${\rho }_A$ (Dijkstra & Henseler, 2015b; Yuan et al., 2020). On the other hand, specifications have been proposed for CB-SEM that allow for dealing with composites (Grace & Bollen, 2008; Rose et al., 2019; Schuberth, 2023; Yu et al., 2023).

Acknowledgements

The authors thank Iris Junglas, Senior Editor of the European Journal of Information Systems, for the invitation to write this commentary. They also thank Alexandra Elbakyan for her efforts in making science accessible. During the preparation of this work, the authors used DeepL in order to improve the readability and language of the manuscript. After using this tool, the authors reviewed and edited the content as needed and take full responsibility for the content of the publication.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

Jörg Henseler gratefully acknowledges financial support from FCT Fundação para a Ciência e a Tecnologia [Portugal], national funding through a research grant from the Information Management Research Center – MagIC/NOVA IMS [UIDB/04152/2020].

Notes

1. K24 (Figure 6) presents two unidentified composite models and uses them to illustrate an alleged “paradox of composite-based models”. However, unidentified models should not be used as a basis for interpretation. In particular, they do not allow for general statements about composite models or CB-SEM.

2. According to Kock (2017, p. 48), PLSF-SEM can deal with structural equation models that contain composites, because “factors and measurement errors are only adjusted in those cases where measurement error is assumed to exist”.

3. The displayed warning message is “At least one measurement error weight is greater than the related composite weight”. None of the leading textbooks on SEM regards this issue as problematic (cf. Bollen, 1989; Byrne, 2011; Kline, 2023; Schumacker & Lomax, 2004).