m-Bonacci graceful labeling

Abstract

We introduce new labeling called m-bonacci graceful labeling. A graph G on n edges is m-bonacci graceful if the vertices can be labeled with distinct integers from the set $\{0,1,2,\dots ,Z_{n,m}\}$ such that the derived edge labels are the first n m-bonacci numbers. We show that complete graphs, complete bipartite graphs, gear graphs, triangular grid graphs, and wheel graphs are not m-bonacci graceful. Almost all trees are m-bonacci graceful. We give m-bonacci graceful labeling to cycles, friendship graphs, polygonal snake graphs, and double polygonal snake graphs.

Keywords:

• m-Bonacci number
• graceful graph

1. Introduction

In 1964, Ringel conjectured that given a tree T with n vertices, the complete graph $K_{2n+1}$ can be decomposed into $2n+1$ edge-disjoint copies of T [12]. To address this problem, in 1966, Rosa introduced the concept of graceful labeling of graphs as β-valuations [13]. Rosa showed that Ringel’s conjecture holds if all the trees are graceful. From this, the famous Ringel-Kotzig conjecture was formed. The conjecture states that all trees are graceful, which is still open. Several researchers ([1, 5], to name a few) have worked on this conjecture and have some partial results.

Golumb in [7], introduced the term graceful. A graceful labeling of a graph $G=(V,E)$ on n edges is defined as follows: G is said to be graceful if there exists a function $f:\{0,1,2,\dots ,n\}\to V$ such that the function $g:E\to \{1,2,\dots ,n\}$ defined by $g(e=uv)=|f(u)-f(v)|$ is a bijection. In 1985, Lo defined edge graceful labeling by assigning labels to the edges of the graph G on p vertices and n edges, from the set $\{1,2,3,\dots ,n\}$ such that the derived vertex labeling is a bijection from V(G) to $\{0,1,2,\dots ,p-1\}$ [10]. Several researchers ([4, 14] to name a few) are working on in this edge graceful labeling.

In [9], Koh et al. defined a tree on n + 1 vertices to be a Fibonacci tree if the vertices can be labeled with the first n + 1 Fibonacci numbers so that the induced edge labeling should be the first n Fibonacci numbers, which were later called as Super-Fibonacci labeling (See [6] for more information). In [2], Bange et al. modified the definition of Koh et al. by relaxing the vertex labels to the set of distinct integers from $\{0,1,2,\dots ,F_n\},$ where F_n is the n-th Fibonacci number. A new group of graphs called Fibonacci graceful graphs was obtained from this definition. A graph on n edges is said to be Fibonacci graceful if there exists a vertex labeling with distinct elements from the set $\{0,1,2,\dots ,F_n\}$ such that the induced edge labels form a bijection on to the first n Fibonacci numbers. For all other types of graceful labeling, we refer the reader to [6].

In this paper, we extend the concept of Fibonacci graceful to m-bonacci graceful graphs by replacing the Fibonacci numbers with m-bonacci numbers.

The paper is arranged as follows. In Section 2, notations, definition of m-bonacci number and definition and example of m-bonacci graceful labeling are given. Some basic properties of m-bonacci graceful labeling is discussed in Section 3. In Section 4, we find some special graphs which are not m-bonacci graceful. In Section 5, m-bonacci graceful labeling of some special classes of graphs are given. We end the paper with a few concluding remarks.

2. Preliminaries

We refer the reader to [3] for basic concepts and definitions of graphs. By G(p, n), we denote a simple graph on p vertices and n edges. In this paper, we use the following definition for an m-bonacci number. The m-bonacci sequence ${\left\{Z_{n,m}\right\}}_{n\ge -(m-2)}$ is defined by $$Z_{i,m}=0,-(m-2)\le i\le 0,Z_{1,m}=1$$ and for $n\ge 2,$ $$Z_{n,m}=\sum _{i=n-m}^{n-1}{Z}_{i,m}$$ Each $Z_{i,m}$ is called an m-bonacci number. For example, when m = 5, the sequence is $${\left\{Z_{n,5}\right\}}_{n=-3}^{\infty }=\{0,0,0,0,1,1,2,4,8,16,31\dots \}$$ In [2], Bange et al. defined a new labeling called Fibonacci graceful labeling. We generalize the definition to any m. We define a new labeling called m-bonacci graceful labeling as follows:

Definition 1.

Let $G(p.n)$ be a graph on p vertices and n edges. G(p, n) is called m-bonacci graceful if there exists a labeling l of its vertices with distinct integers from the set $\{0,1,2,\dots ,Z_{n,m}\}$ which induces an edge labeling $l\prime$ defined by $l\prime (uv)=|l(u)-l(v)|,$ is a bijection onto the set $\{Z_{1,m},Z_{2,m},\dots ,Z_{n,m}\}.$

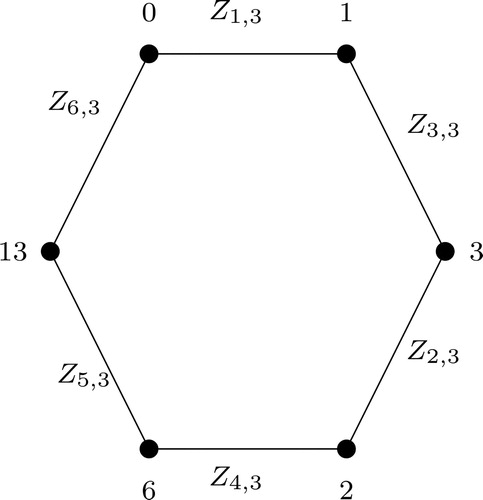
When m = 2, the above labeling is the Fibonacci graceful labeling. For m = 3, Figure 1 shows a 3-bonacci graceful labeling of C₆.

Figure 1. C₆ with tribonacci graceful labeling.

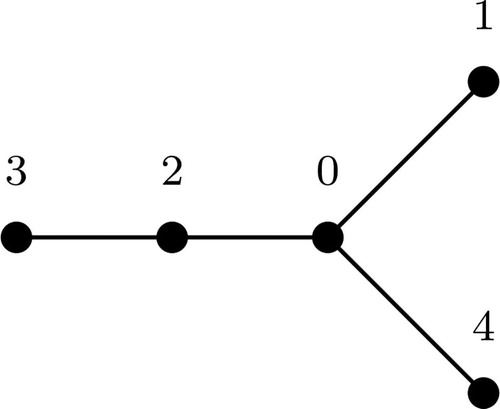
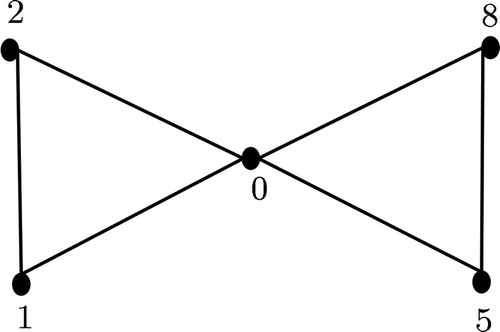
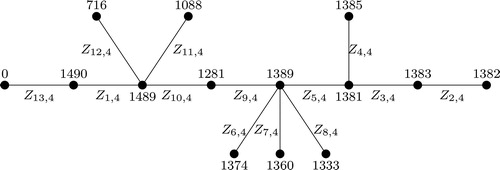
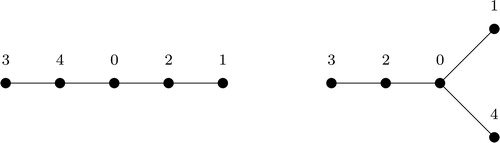
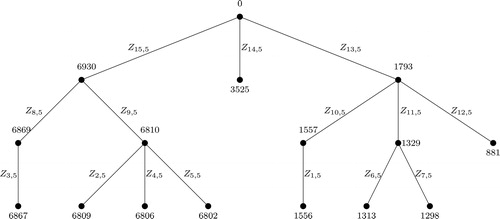
Note that, not all graphs are m-bonacci graceful. Also, if a graph G is m-bonacci graceful for some m, then it does not necessarily imply that G is m-bonacci graceful for all m. For example, consider the graph C₆. It was shown in [2], that C₆ is Fibonacci graceful and one can see from Figure 1 that C₆ is also 3-bonacci graceful. However, C₆ is not 4-bonacci graceful. Infact we show that (see Theorem 3) C₆ is m-bonacci graceful for all m ≥ 2 and $m\ne 4.$ We also give a labeling of the Butterfly graph (see Figure 4) such that it is Fibonacci graceful. But one can verify (see Proposition 1) that Butterfly graph is not m-bonacci graceful for all m ≥ 3. We also give an example of a tree (Figure 2) which is m-bonacci graceful for any m ≥ 3, whereas it is not Fibonacci graceful. The famous” Ringel-Kotzig conjecture” states that all trees are graceful. But, the conjecture does not hold for m-bonacci graceful labeling. Some trees are m-bonacci graceful for some m, whereas some trees are not m-bonacci graceful for any m. In Figure 3, one can see that T₁ is 3-bonacci graceful, whereas T₂ is not m-bonacci graceful for any m. In fact, we show that (Proposition 2) $K_{1,n},n\ge 3,$ is not m-bonacci graceful for any m. If a graph G is not graceful, it is not necessarily true that G is not m-bonacci graceful for any m. For example, Figure 4 shows that the butterfly graph is Fibonacci graceful. But in [13], Rosa showed that any Eulerian graph with edge count congruent to 1 or $2(\mathrm{mod}\hspace{0.5em}4)$ is not graceful. Thus, both the butterfly graph as well as C₆, are not graceful. We see that the butterfly graph is Fibonacci graceful (see Figure 4) but not m-bonacci graceful for all m ≥ 3 (see Proposition 1) and C₆ is m-bonacci graceful for all m ≥ 2 and $m\ne 4$ (see Proposition 1). Hence, we conclude the following.

Figure 2. m-bonacci graceful labeling for m ≥ 3.

Figure 3. $(a)T_1,(b)T_2.$

Figure 4. Fibonacci graceful labeling of Butterfly graph.

Observation 1.

The following are true.

• There exists a graph that is Fibonacci graceful but not m-bonacci graceful for allm ≥ 3

• There exists a graph that is m-bonacci graceful for allm ≥ 3 but not Fibonacci graceful

• There exists a graph that is graceful but not m-bonacci graceful for anym ≥ 2

• There exists a graph that is m-bonacci graceful for all$m\ge 5$ but not graceful.

3. Properties of m-bonacci graceful graphs

In this section, we study some basic properties of m-bonacci graceful graphs. From the definition, it is clear that, for a graph to be m-bonacci graceful, one of its edges must have the label $Z_{n,m},$ which is only possible when 0 and $Z_{n,m}$ are the labels for its incident vertices. Moreover, any vertex adjacent to the vertex labeled with 0 must have an m-bonacci number as its label. We first recall some well known properties of m-bonacci numbers [8, 11].

Lemma 1.

For $m\ge 2$, we have the following.

1. $2Z_{k,m}\ge Z_{k+1,m}$ for all $k\ge 1.$

2. If the sum of m m-bonacci numbers equals another m-bonacci number, then those m + 1 numbers must be consecutive.

3. The first $2m+1$ terms of the m-bonacci sequence are $Z_{i,m}=0,-(m-2)\le i\le 0,$ $Z_{1,m}=Z_{2,m}=1,$ $Z_{j,m}=2^{j-2},3\le j\le m+1,$ $Z_{m+2,m}=2^m-1.$

Based on the observations in Lemma 1, we deduce the following.

Corollary 1.

For $m\ge 2$, such that $0<n<m+1$ and t > 0, the following is true. $$\sum _{i=t+1}^{t+n}{\delta }_i{Z}_{i,m}\ne 0,{\delta }_i=\pm 1$$

Proof.

Let $0<n<m+1$ and t > 0. Then, we have $$\begin{array}{c}{Z}_{t+n,m}=\sum _{i=t+n-m}^{t+n-1}{Z}_{i,m}\\ >\sum _{i=t+1}^{t+n-1}{Z}_{i,m}(\text{since}\mathrm{}t>0,n<m+1)\end{array}$$ Hence, the result. □

We first observe that similar to Fibonacci graceful graphs [2] the labeling of an m-bonacci graceful graph need not be unique, i.e., the graph can have several distinct labeling.

Observation 2.

LetG(p, n) be an m-bonacci graceful graph for some$m\ge 2,$ with vertex labels from the set$\{a_1,a_2,\dots ,a_n\}.$ Then, replacing each vertex labelsa_i with$Z_{n,m}-a_i$ also gives an m-bonacci graceful labeling.

It was also observed in [2] that the cycle structure of Fibonacci graceful graphs is dependent on Fibonacci identities. We observe here that the result is also true for any m ≥ 3.

Lemma 2.

Let G(p, n) be an m-bonacci graceful graph and let C be a cycle of length k in G(p, n). Then there exists a sequence ${\left\{{\delta }_i\right\}}_{i=1}^k$ with ${\delta }_i=\pm 1$ for all $i=1,2,\dots ,k$ such that $$\sum _{i=1}^k{\delta }_i{Z}_{j_i,m}=0$$where ${\left\{Z_{j_i,m}\right\}}_{i=1}^k$ are the derived m-bonacci numbers for the edges of C.

The following corollary is a direct observation from the above Lemma and the fact (See Lemma 1) that if the sum of any m m-bonacci numbers is another m-bonacci number, then these numbers must be consecutive. The corollary gives an edge labeling for cycles of a particular length.

Corollary 2.

Let G be an m-bonacci graceful graph such that G has a cycle C of length $km-(k-2),1\le k\le 3$. Then, the edges of C must be labeled with m-bonacci numbers $Z_{j,m}$ for $i\le j\le i+km$, and $j\ne i+tm$ for $1\le t\le k-1$ for some $i\ge 1.$

Thus, from Lemma 2 and Corollary 2, we observe the following, which provides a condition for the edge labels for any cycle in an m-bonacci graceful graph.

Corollary 3.

Let G(p, n) be an m-bonacci graceful graph and C be a cycle in G(p, n). If $Z_{k,m}$ is the largest m-bonacci number appearing as an edge label of C, then $Z_{k-1,m},$ $Z_{k-2,m},$ $\dots ,$ $Z_{k-(m-1),m}$ should also appear as edge labels on C.

The following result gives conditions on the number of edges in any Eulerian m-bonacci graceful graph.

Theorem 1.

Let G(p, n) be an Eulerian m-bonacci graceful graph. Then, $$n\equiv 0,2,3,\dots ,m-1\text{or}m(\mathrm{mod}(m+1))$$

Proof.

Let G be an Eulerian m-bonacci graceful graph. Then, G can be decomposed into edge-disjoint cycles. From Lemma 2, it is clear that the sum of all the edge labels around any cycle is even and hence, $Z_{1,m}+Z_{2,m}+\cdots +Z_{n,m}$ is even. But by Lemma 1, $Z_{1,m}+Z_{2,m}+\cdots +Z_{n,m}$ is odd only when $n\equiv 1(\mathrm{mod}m+1)$ for m ≥ 2. Hence, the result. □

The following result gives a partial information about the cycles of any m-bonacci graceful graph.

Proposition 1.

Any m-bonacci graceful graph can have at most one cycle of length less than or equal to m. From this, we get that, for m ≥ 3, the only maximal outerplanar m-bonacci graceful graph is C₃.

Proof.

Let G be an m-bonacci graceful graph and let C be a cycle of G of length n such that $n\le m.$ Let the vertices of C be m-bonacci gracefully labeled with labels from the set $\left\{0\right\}\cup \{Z_{i,m}:2\le i\le n\}$ (since $n\le m,$ by Lemma 1, $Z_{i+1,m}-Z_{i,m}=Z_{i-1,m},1\le i\le n$). Suppose there exists another cycle $C\prime$ of length $t\le m$ in G whose vertices are labeled such that $Z_{k,m}$ with k > n is the largest edge label of $C\prime .$ Now, by Corollary 3, $Z_{k-1,m},$ $Z_{k-2,m},\dots ,Z_{k-(m-1),m}$ are also edge labels of $C\prime .$ Since $t\le m,Z_{k,m},$ $Z_{k-1,m},$ $Z_{k-2,m},\dots ,Z_{k-(m-1),m}$ are the only edge labels and the length of $C\prime$ is m. By Lemma 2, there exists a sequence $\left\{{\delta }_i\right\}$ with ${\delta }_i=\pm 1$ such that, (1) $$\sum _{i=1}^m{\delta }_i{Z}_{k-(i-1),m}=0$$(1) Note that, the labels are m consecutive m-bonacci numbers. By Corollary 1, Equation (1)(1) $$\sum _{i=1}^m{\delta }_i{Z}_{k-(i-1),m}=0$$(1) does not hold true. Thus, an m-bonacci graceful graceful graph can have a maximum of only one cycle of length less than or equal to m. Hence, the result. □

4. Forbidden graphs

In this section, we discuss some special graphs that are not m-bonacci graceful. We start this section with the tree graph. Except K₁ and K₂, any tree with the number of edges at most three cannot be m-bonacci gracefully labeled, as there does not exist enough integers between 0 and $Z_{n,m}$ to label n + 1 vertices.

In [2], Bange et al. proved that any graph which has a 3-edge connected subgraph is not Fibonacci graceful. One can observe that the result also holds when m ≥ 3. We omit the proof as it is similar to the proof given by Bange et al.

Theorem 2.

If G has a 3-edge connected subgraph, then G is not m-bonacci graceful for m ≥ 2.

The above result cannot be improved further as cycles are 2-edge connected, and most of them are m-bonacci graceful. The following corollary is a direct observation from Theorem 2.

Corollary 4.

The following graphs are not m-bonacci graceful for m ≥ 2.

• Complete graph $K_n,n\ge 4$

• The wheel graph $W_n,n\ge 3$

• The Generalized Petersen graph

• The Fence graph

• The Circular ladder graph

We now discuss the case for complete bipartite graphs. One can easily verify that both $K_{1,1}$ and $K_{2,2}$ are m-bonacci graceful for all m ≥ 3. $K_{1,1}$ is Fibonacci graceful but $K_{2,2}$ is not Fibonacci graceful. In the following result we show that complete bipartite graphs $K_{t,n}$ except for $K_{1,1}$ and $K_{2,2}$ are not m-bonacci graceful for m ≥ 2.

Proposition 2.

Complete bipartite graphs, except for $K_{1,1}$ and $K_{2,2}$, are not m-bonacci graceful for m ≥ 2.

Proof.

Let $t,n\ge 3.$ Then, $K_{t,n}$ is 3-edge connected. By Theorem 2, $K_{t,n}$ is not m-bonacci graceful for m ≥ 2.

$K_{1,n},$ $n\ge 2$ is not m-bonacci graceful. At most either $Z_{1,m}$ or $Z_{2,m}$ will appear as one of the edge labels (Note that, $Z_{1,m}=Z_{2,m}=1$).

Now, the only case left is $K_{2,n},$ $n\ge 3.$ Let u, v be the two vertices that are adjacent to other n vertices. Let l(u) = 0. Then, all the n vertices should be labeled with m-bonacci numbers. Since $n\ge 3,$ it is impossible to give a label to v distinct from other n + 1 vertices such that the graph is m-bonacci graceful. The proof is similar if a vertex from the other partite set with n vertices gets 0 as vertex label. □

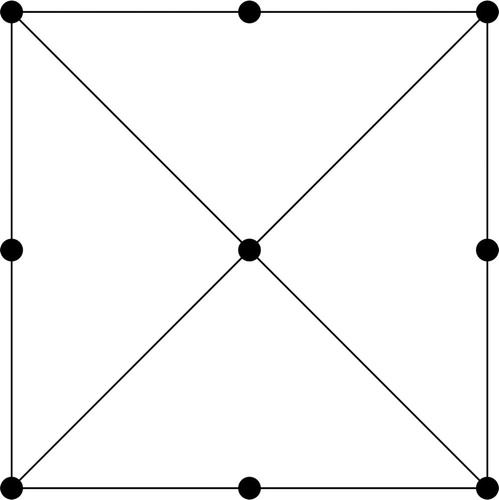
The following result shows that gear graphs are not m-bonacci graceful. Gear graph is obtained by replacing each edge in the perimeter of the wheel graph W_n by a path of length 2. We denote gear graphs by G_n. G_n has $2n+1$ vertices. G₄ is shown in Figure 5. G₃ is Fibonacci graceful but not m-bonacci graceful $\forall m\ge 3.$

Figure 5. Gear graph G₄.

Proposition 3.

Gear graphs $G_t,t\ge 4$ are not m-bonacci graceful for all m ≥ 2.

Proof.

Let G_t be a gear graph. Suppose G_t is m-bonacci graceful for some $m\ge 2$ and $t\ge 4.$ Recall that, a gear graph is a subdivision of wheel graph. Let v be the single universal vertex of G_t. Let u₁ and u₂ be the end vertices of the edge with $Z_{n,m}$ as edge label. Note that at least one of the vertices u₁ and u₂ is of degree greater than 2. Now, we have two different cases.

• Case 1: If either u₁ or u₂ is v, then we get three edge disjoint paths from u₁ to u₂. So we get a cycle which does not contain the edge with edge label $Z_{n-1,m}.$ This is a contradiction to Corollary 3.

• Case 2: If both $u_1,u_2\ne v,$ then $l(v)\ne 0.$ We have the following two subcases:

  m ≥ 3: Let u₁ be the vertex of degree 3. Let u₃ be the vertex of degree 3 such that u₂ is adjacent to u₃ and u₃ is adjacent to v. Now we have two cycles: $v{u}_1{u}_2{u}_{3}v$ and the outer perimeter cycle from u₂ to u₂. Note that, these two cycles have only two edges in common i.e., $u_1{u}_2$ and $u_2{u}_3.$ Also, the edge label of $u_1{u}_2$ is $Z_{n,m}$ and we get a cycle which does not contain either the edge with $Z_{n-1,m}$ as edge label or the edge with $Z_{n-2,m}$ as edge label. Thus for $m\ge 3,$ in either case, it is a contradiction to Corollary 3.

• m = 2: Without loss of generality, let v and u₁ are adjacent. Let u₃ be the vertex adjacent to u₂ and v. Let f_k denote the k-th Fibonacci number. Consider the cycle $C:$ $v{u}_3{u}_2{u}_{1}v.$ Since f_n is an edge label of C, by Corollary 3, $f_{n-1}$ must be an edge label of one of the edges of C. Now, by Lemma 2, we get that $f_{n-3}$ and $f_{n-4}$ are the remaining edge labels (otherwise it will give contradiction to Lemma 2). If the edge label of vu₃ is $f_{n-1},$ then by Corollary 3 and Lemma 2, the cycle of length four different from the cycle C, which has vu₃ as one of its edge, must have $f_{n-2},f_{n-4},f_{n-5}$ as edge labels. This is not possible (since $f_{n-4}$ is one of the edge labels of the cycle $C:$ $v{u}_3{u}_2{u}_{1}v$). The same contradiction arises for $f_{n-1}$ to be the edge label of vu₁. So, $f_{n-1}$ is the edge label of $u_2{u}_3.$ Without loss of generality, let $l\prime (v{u}_1)=f_{n-3}$ and $l\prime (v{u}_3)=f_{n-4},$ where $l\prime$ is the derived edge labeling. Now consider the cycles C₁ and C₂ which have vu₁ and vu₃ as one of its edges, respectively. Clearly, C₁ and C₂ does not share any edge (since we consider only $G_t,t\ge 4$). To satisfy Lemma 2 and Corollary 3, the only possible remaining edge labels of C₁ are $f_{n-2},f_{n-5},f_{n-6}.$ This implies that, the largest edge label in C₂ is $f_{n-4}.$ By Corollary 3, $f_{n-5}$ should be an edge label of one of the edges of C₂, which is not possible.

Thus, $G_t,t\ge 4,$ is not m-bonacci graceful for all $m\ge 2.$ □

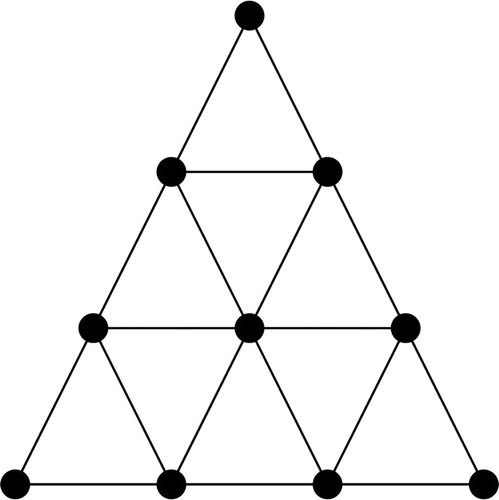
4.1. Triangular grid graph

Triangular grid graph is a graph with vertex set $V=\{(i,j,k):i+j+k=n,i,j,k\ge 0\}$ and two vertices $(i_1,j_1,k_1)$ and $(i_2,j_2,k_2)$ are adjacent if and only if $|i_1-i_2|+|j_1-j_2|+|k_1-k_2|=n.$ We denote such graphs by TG_n. The graph TG_n has $\frac{(n+1)(n+2)}{2}$ vertices and $\frac{3n(n+1)}{2}$ edges. Note that, when n = 0, TG_n is K₁ and when n = 1, TG_n is K₃. The graph TG₃ is given in Figure 6. In the following result, we show that $T{G}_n,n\ge 2,$ is not m-bonacci graceful $\forall m\ge 2.$

Figure 6. Triangular grid graph TG₃.

Proposition 4.

The triangular grid graph TG_n is not m-bonacci graceful for all $m\ge 2,n\ge 2.$

Proof.

Let m ≥ 3. Then, by Proposition 1, $T{G}_n,$ $n\ge 2,$ is not m-bonacci graceful. Let m = 2 and $N=\frac{3n(n+1)}{2}$ denote the number of edges in TG_n. Let f_k denote the k-th Fibonacci number. To the contrary, assume that there exists an n such that TG_n is Fibonacci graceful. Then, f_N is an edge label of some edge uv in TG_n. At most one vertex of u and v can have degree 2. Now, we have two cases.

• Case 1: If $deg(u),deg(v)\ne 2,$ then the edge uv lies in two different cycles. But, at most one of the two cycles can have $f_{N-1}$ as one of its edge labels. This is a contradiction to Corollary 3.

• Case 2: If deg(u) = 2, then let w be another vertex which is adjacent to both u and v in TG_n. By Lemma 2 and Corollary 3, $f_{N-1}$ and $f_{N-2}$ are the other two edge labels of the cycle uvwu. If $f_{N-1}$ is the edge label of vw, then another triangle which has vw as one of its edge labels can not have $f_{N-2}$ as one of its edge labels, which is a contradiction to Corollary 3. Hence, the edge label of uw and vw is $f_{N-1}$ and $f_{N-2}$ respectively. Now, consider the triangle vwtv, t is another vertex of TG_n adjacent to v and w. Now, by Lemma 2 and Corollary 3, the edge labels are $f_{N-3}$ and $f_{N-4}.$ Without loss of generality, let $f_{N-3}$ be the edge label of the edge vt. Now, the triangle different from vtwv and uvwu which has vt as one of its edge can not have $f_{N-4}$ as one of its edge labels, which is a contradiction to Corollary 3.

Hence, the result. □

5. m-Bonacci graceful graphs

In this section, we discuss some special graphs which are m-bonacci graceful. We start the section with cycles. We begin by answering for what values of n and m, C_n is m-bonacci graceful. The following theorem gives a characterization for all cycles C_n that are m-bonacci graceful. In [2], Bange et al found the values of n for which C_n is Fibonacci graceful. The following theorem is the generalization of the result to any m.

Theorem 3.

Let m ≥ 2. The cycle C_n with n vertices is m-bonacci graceful if and only if $n\equiv 0,2,3,$ $\dots ,m-1orm(\mathrm{mod}(m+1)).$

Proof.

Consider a cycle C_n of length n. Let $n\equiv 0,2,3,$ $\dots ,m-1orm(\mathrm{mod}(m+1)).$ Then, $n=k(m+1)+t$ for some $t\in \{0,2,3,\dots ,m\}.$ Let $v_1,v_2,\dots ,v_n$ be the vertices of C_n. We give a labeling for C_n as follows: (2) $$l(v_j)=\{\begin{array}{cc}0\hfill & j=1\hfill \\ Z_{n,m}\hfill & j=2\hfill \\ l(v_{j-1})-Z_{n-(j-2),m}\hfill & 3\le j\le m+1\hfill \end{array}$$(2) For $1\le i\le k,$ (3) $$l(v_{i(m+1)+j})=\{\begin{array}{cc}l(v_{i(m+1)})+Z_{n-i(m+1),m}\hfill & j=1\hfill \\ l(v_{i(m+1)+1})-Z_{n-(i(m+1)-1),m}\hfill & j=2\hfill \\ l(v_{i(m+1)+(j-1)})-Z_{n-(i(m+1)+(j-2)),m}\hfill & 3\le j\le m+1\hfill \end{array}$$(3) Here $l(v_2)=Z_{n,m}>l(v_3)>\cdots >l(v_{m+1})=l(v_m)-Z_{n-(m-1),m}=Z_{n-(m-2),m}>0.$ Again $l(v_{m+2})=Z_{n-(m-2),m}+Z_{n-(m+1),m}>l(v_{m+3})>\dots >l(v_{2(m+2)})>0.$ Here $l(v_{m+1})<l(v_{m+2})$ and $l(v_{m+3})=Z_{n-(m-2),m}+Z_{n-(m+1),m}-Z_{n-m,m}<Z_{n-(m-2),m}=l(v_{m+1}).$ Hence, all the labels are distinct and positive integers. Proceeding in the same way, we get that all the labels are distinct. The difference of each adjacent vertex label is distinct m-bonacci numbers (clear from the construction of labels). Hence, C_n is m-bonacci graceful.

Conversely, suppose C_n is m-bonacci graceful for some m. One can easily observe that by Theorem 1, C_n is not m-bonacci graceful if $n\equiv 1(\mathrm{mod}(m+1)).$ From Equations (2)(2) $$l(v_j)=\{\begin{array}{cc}0\hfill & j=1\hfill \\ Z_{n,m}\hfill & j=2\hfill \\ l(v_{j-1})-Z_{n-(j-2),m}\hfill & 3\le j\le m+1\hfill \end{array}$$(2) and (3)(3) $$l(v_{i(m+1)+j})=\{\begin{array}{cc}l(v_{i(m+1)})+Z_{n-i(m+1),m}\hfill & j=1\hfill \\ l(v_{i(m+1)+1})-Z_{n-(i(m+1)-1),m}\hfill & j=2\hfill \\ l(v_{i(m+1)+(j-1)})-Z_{n-(i(m+1)+(j-2)),m}\hfill & 3\le j\le m+1\hfill \end{array}$$(3) , C_n is graceful for $n\equiv 0,2,3,$ $\dots ,m-1orm(\mathrm{mod}(m+1)).$ Hence, the result. □

The following corollary gives the vertex label of particular vertices of C_n.

Corollary 5.

Let $C_n:$ $v_1{v}_2{v}_3\dots v_n{v}_1$ be an m-bonacci graceful cycle for some m ≥ 2, and labeled as given in Theorem 3. Then, $l(v_{i(m+1)})$ is an m-bonacci number for all $i\ge 1.$

Proof.

We prove this result by induction on i. By Theorem 3, we have the following: $$\begin{array}{c}l(v_{m+1})=Z_{n,m}-Z_{n-(m-1),m}-Z_{n-(m-2),m}-\cdots -Z_{n-1,m}\\ =Z_{n-m,m}\end{array}$$ Therefore, the result is true for i = 1. Assume that $l(v_{i(m+1)})$ is an m-bonacci number. Let $l(v_{i(m+1)})=Z_{s,m}$ for some s. By construction, it is easy to verify that $s=n-(i(m+1)-1).$ By Theorem 3, we have, (4) $$\begin{array}{c}l(v_{(i+1)(m+1)})=l(v_{i(m+1)})+Z_{n-i(m+1),m}-Z_{n-(i(m+1)-1),m}-Z_{n-(i(m+1)+1),m}\\ -Z_{n-(i(m+1)+2),m}-\cdots -Z_{n-(i(m+1)+m-1)),m}\\ =l(v_{i(m+1)})+Z_{n-(i(m+1)+m),m}-Z_{n-(i(m+1)-1),m}\\ =Z_{n-(i(m+1)+m),m}\end{array}$$(4) From Equation (4)(4) $$\begin{array}{c}l(v_{(i+1)(m+1)})=l(v_{i(m+1)})+Z_{n-i(m+1),m}-Z_{n-(i(m+1)-1),m}-Z_{n-(i(m+1)+1),m}\\ -Z_{n-(i(m+1)+2),m}-\cdots -Z_{n-(i(m+1)+m-1)),m}\\ =l(v_{i(m+1)})+Z_{n-(i(m+1)+m),m}-Z_{n-(i(m+1)-1),m}\\ =Z_{n-(i(m+1)+m),m}\end{array}$$(4) , $l(v_{(i+1)(m+1)})$ is an m-bonacci number. By induction, the result is true for all i. □

The next simple special class of graph is the tree. For any m, we can give graceful labeling to K₁ and K₂. For n = 4 and $m\ge 3,$ the only tree which cannot be m-bonacci gracefully labeled is $K_{1,4}.$ $K_{1,n}$ is not m-bonacci graceful for any $m\ge 2$ (refer Proposition 2). For m ≥ 3, except $K_{1,4}$ all trees with five edges are m-bonacci graceful.

The following theorem provides m-bonacci graceful labeling for any tree with edges more than 5. We omit the proof as it is similar to the proof given by Bange et al. Few examples are shown in the Figures 7–9.

Figure 7. 4-bonacci graceful labelling of a caterpillar.

Figure 8. m-bonacci graceful labelling of trees with 4 edges, $m\ge 3.$

Figure 9. 5-bonacci graceful labeling of a non-caterpillar.

Figure 10. Tribonacci graceful labeling of $F{r}_8^4.$

Theorem 4.

All trees T_n with $n\ge 6$, where n denotes the number of edges, except for $K_{1,n}$, are m-bonacci graceful for all m ≥ 2.

5.1. Friendship graph

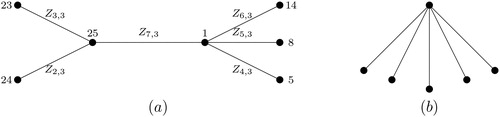
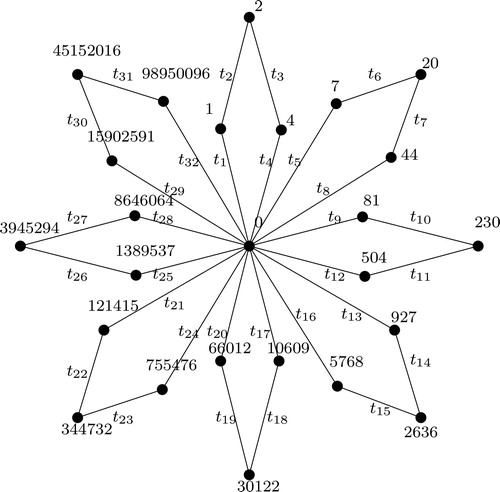
The Friendship graph $F{r}_n^t$ is obtained by joining n copies of C_t with a common vertex. An example of $F{r}_8^4$ is given in Figure 10. By Proposition 1, $F{r}_n^t,$ $n>1,$ $t\le m,$ is not m-bonacci graceful for all m ≥ 2. In the following result, we find values of t such that the Friendship graph $F{r}_n^t$ is m-bonacci graceful for all m ≥ 2.

Theorem 5.

Let m ≥ 2. The friendship graph $F{r}_n^{k(m+1)}$ is m-bonacci graceful for all k ≥ 1

Proof.

Let v be the common vertex with vertex label 0. We denote by $A_1,A_2,\dots ,A_n$ the distinct cycles in $F{r}_n^{k(m+1)}.$ Let the vertices of each A_i, $1\le i\le n,$ be $v,v_2^i,v_3^i,\dots ,v_{k(m+1)}^i$ in that order. We label the vertices of cycle A_i in a similar way as given in Theorem 3 with the starting label $l(v_2^i)=Z_{(n-(i-1))k(m+1),m}.$ By Corollary 5, $l(v_{k(m+1)}^i)$ is an m-bonacci number. The derived edge labels of A_i are: $Z_{(n-(i-1))k(m+1),m},Z_{(n-(i-1))k(m+1)-1,m},\dots ,Z_{(n-(i-1))k(m+1)-m,m}.$ Thus, the vertex labels and edge labels are distinct and hence the result. □

3-bonacci graceful labeling of $F{r}_8^4$ is shown in the Figure 10.

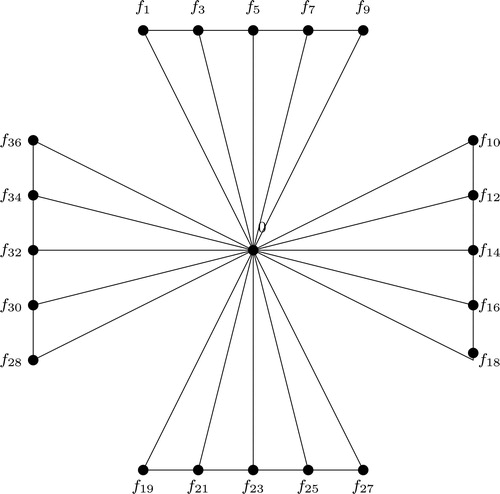
Another variant of Friendship graph denoted by $\overline{F}{r}_n^k$ is obtained by joining n copies of F_k with a common vertex, where F_k is a fan on k + 1 vertices. When k = 2, $\overline{F}{r}_n^k$ is nothing but $F{r}_n^3$ which is Fibonacci graceful. Thus, we take k > 2. Note that, by Proposition 1, the fan graph F_k for k > 2 and $\overline{F}{r}_n^k$ are not m-bonacci graceful for all $m\ge 3.$ The following result gives a Fibonacci graceful labeling of $\overline{F}{r}_n^k$ for $k\ge 2.$

Theorem 6.

The friendship graph $\overline{F}{r}_n^k$ is Fibonacci graceful for all $n\ge 1$ and $k\ge 2.$

Proof.

Let v be the common vertex and let $A_1,A_2,\dots ,A_n$ denote the n copies of the fan graph F_k respectively. Let the vertices of A_i be $u_{i1},u_{i2},\dots ,u_{ik}$ such that u_ij is adjacent with vertex v for all $1\le j\le k$ and u_ij is adjacent with vertex $u_{i(j+1)}$ for all $1\le j\le k-1.$ Label the vertex v as 0.

For $1\le j\le k,$ we label the vertices of A_i as follows: $$l(u_{ij})=\{\begin{array}{cc}{f}_{2(i-1)k-i+2j}\hfill & :i\text{odd}\hfill \\ f_{2(i-1)k-i+2(j-1)}\hfill & :i\text{even}\hfill \end{array}$$ Clearly, the vertex labels and edge labels are distinct. Thus, $\overline{F}{r}_n^k$ is Fibonacci graceful. □

A Fibonacci graceful labeling of $\overline{F}{r}_4^5$ is given in Figure 11.

Figure 11. Fibonacci graceful labeling of $\overline{F}{r}_4^5.$

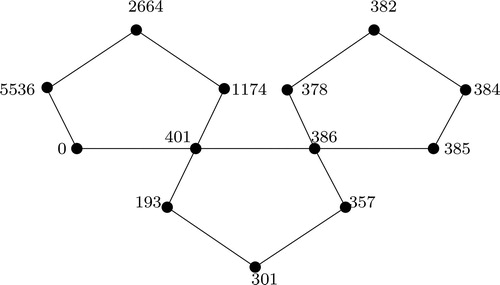
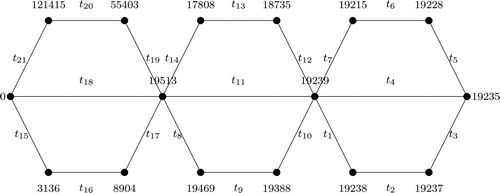
5.2. Polygonal snake graph

A polygonal snake graph is obtained from a path P_t by replacing each edge of P_t by C_n i.e., for each edge in the path P_t a cycle of length n is adjoined. It is denoted by $P{S}_{t,n}$ where t denotes the number of vertices of the path and n denotes the number of edges of the cycle C_n. Hence, $P{S}_{t,n}$ has $t(n-1)-(n-2)$ vertices and $n(t-1)$ edges. An example is shown in Figure 12.

Figure 12. 4-bonacci graceful labeling of $P{S}_{4,5}.$

Theorem 7.

The Polygonal snake graph $P{S}_{t,m+1}$ is m-bonacci graceful for all $t\ge 1$ and m ≥ 2.

Proof.

Let $P{S}_{t,m+1}$ denote the polygonal snake graph with $tm-(m-1)$ vertices and $N=(m+1)(t-1)$ edges and let $A_1,A_2,\dots ,A_{t-1}$ be the cycles of $P{S}_{t,m+1}$ in that order. Denote the vertices of A_i by $u_{i1},u_{i2},\dots ,u_{i(m+1)}$ for all $1\le i\le t-1.$ Note that, $u_{i(m+1)}=u_{(i+1)1}$ for all $1\le i\le t-2.$ We label the vertices of A₁ as follows: $$\begin{array}{c}l(u_{11})=0,l(u_{12})=Z_{N,m},\\ l(u_{1j})=l(u_{1(j-1)})-Z_{N-(j-2),m},3\le j\le m+1.\end{array}$$ Here, $l(u_{12})>l(u_{13})>\dots >l(u_{1(m+1)}).$ Thus, the vertex labels of A₁ are all distinct. Now, we have the following: (5) $$\begin{array}{c}l(u_{1(m+1)})=l(u_{1m})-Z_{N-(m-1),m}\\ =Z_{N,m}-\sum _{i=N-(m-1)}^{N-1}{Z}_{i,m}\\ =Z_{N-m,m}\end{array}$$(5) Thus, the derived edge labels are $Z_{N,m},Z_{N-1,m},\dots ,Z_{N-m,m}.$ We have $u_{i1}=u_{(i-1)(m+1)},2\le i\le t-1.$ We now label the vertices of $A_i,2\le i\le t-1$ inductively as follows: $$\begin{array}{c}l(u_{i2})=l(u_{i1})-Z_{N-(i-1)m-1,m}\\ l(u_{ij})=l(u_{i(j-1)})+Z_{N-(i-1)m-(j-1),m},3\le j\le m+1\end{array}$$ Clearly, for a given A_i, $2\le i\le t-1,$ (6) $$l(u_{i(m+1)})>l(u_{im})>l(u_{i(m-1)})>\cdots >l(u_{i2})$$(6) and for $2\le j\le m+1,$ we have the following: (7) $$\begin{array}{c}l(u_{ij})=l(u_{i(j-1)})+Z_{N-(i-1)m-(j-1),m}\\ =l(u_{i1})-Z_{N-(i-1)m-1,m}+M_1\end{array}$$(7) where, $$M_1=\sum _{a=N-(i-1)m-(j-1)}^{N-(i-1)m-2}{Z}_{a,m}$$

Since M₁ adds at most m – 1 consecutive m-bonacci numbers, from Equation (7)(7) $$\begin{array}{c}l(u_{ij})=l(u_{i(j-1)})+Z_{N-(i-1)m-(j-1),m}\\ =l(u_{i1})-Z_{N-(i-1)m-1,m}+M_1\end{array}$$(7) , we have $$l(u_{ij})<l(u_{i1}),2\le j\le m+1$$ Thus, all vertices of the polygon A_i for $2\le i\le t-1,$ have distinct labels. We now show that for any two A_p and A_q, $2\le p,q\le t-1,$ such that $p\ne q$ the vertex labels of A_p and A_q are all distinct. We first prove the following claim.

Claim: For $i\ge 2,$ we have $l(u_{i(m+1)})>l(u_{(i+1)(m+1)})$ and $l(u_{(i+1)2})>l(u_{im})$

From Equation (7)(7) $$\begin{array}{c}l(u_{ij})=l(u_{i(j-1)})+Z_{N-(i-1)m-(j-1),m}\\ =l(u_{i1})-Z_{N-(i-1)m-1,m}+M_1\end{array}$$(7) , we get that $l(u_{i1})>l(u_{i(m+1)})$ $\forall i\ge 2.$ Since $u_{i(m+1)}=u_{(i+1)1},$ we have $l(u_{i(m+1)})>l(u_{(i+1)(m+1)}).$ The only thing left to prove is $l(u_{(i+1)2})>l(u_{im}).$ We have that, (8) $$\begin{array}{c}l(u_{(i+1)2})=l(u_{(i+1)1})-Z_{N-im-1,m}(\text{vertex}\mathrm{}\text{labeling}\mathrm{}\text{of}\mathrm{}{A}_{i+1})\\ =l(u_{i(m+1)})-Z_{N-im-1,m}(\text{since}\mathrm{}{u}_{i(m+1)}=u_{(i+1)2})\\ =l(u_{i1})-Z_{N-(i-1)m-1,m}+\sum _{a=N-im}^{N-(i-1)m-2}{Z}_{a,m}-Z_{N-im-1,m}(\text{From Eq}.7)\end{array}$$(8) Also we have, (9) $$l(u_{im})=l(u_{i1})-Z_{N-(i-1)m-1,m}+\sum _{a=N-(i-1)m-(m-1)}^{N-(i-1)m-2}{Z}_{a,m}$$(9) From Equations (8)(8) $$\begin{array}{c}l(u_{(i+1)2})=l(u_{(i+1)1})-Z_{N-im-1,m}(\text{vertex}\mathrm{}\text{labeling}\mathrm{}\text{of}\mathrm{}{A}_{i+1})\\ =l(u_{i(m+1)})-Z_{N-im-1,m}(\text{since}\mathrm{}{u}_{i(m+1)}=u_{(i+1)2})\\ =l(u_{i1})-Z_{N-(i-1)m-1,m}+\sum _{a=N-im}^{N-(i-1)m-2}{Z}_{a,m}-Z_{N-im-1,m}(\text{From Eq}.7)\end{array}$$(8) and (9)(9) $$l(u_{im})=l(u_{i1})-Z_{N-(i-1)m-1,m}+\sum _{a=N-(i-1)m-(m-1)}^{N-(i-1)m-2}{Z}_{a,m}$$(9) , we get $l(u_{(i+1)2})-l(u_{im})=Z_{N-im,m}-Z_{N-im-1,m}>0$ since $N-im>2.$ Hence, $l(u_{(i+1)2})>l(u_{im})$ and the claim holds.

By claim and Equation (6)(6) $$l(u_{i(m+1)})>l(u_{im})>l(u_{i(m-1)})>\cdots >l(u_{i2})$$(6) , it is clear that the vertex labels of $A_2,A_3,\dots ,A_{t-1}$ are all distinct. We now show that the vertex labels of A₁ and A_i for $2\le i\le t-1$ are distinct. In A₁ we have, (10) $$l(u_{12})>l(u_{13})>\cdots >l(u_{1(m+1)})=l(u_{21})$$(10) We have from Equation (6)(6) $$l(u_{i(m+1)})>l(u_{im})>l(u_{i(m-1)})>\cdots >l(u_{i2})$$(6) , $l(u_{21})>l(u_{2j}),2\le j\le m+1.$ Hence, by the above claim and Equation (10)(10) $$l(u_{12})>l(u_{13})>\cdots >l(u_{1(m+1)})=l(u_{21})$$(10) , the vertex labels of $P{S}_{t,m+1}$ are all distinct from each other. By calculation, we get that $l(u_{i(m+1)})-l(u_{i1})=Z_{N-i(m+1),m}.$ By construction, other edge labels are distinct m-bonacci numbers. Hence, $P{S}_{t,m+1}$ is m-bonacci graceful. □

A 4-bonacci labeling of $P{S}_{4,5}$ is given in Figure 12.

5.3. Double polygonal snake graph

The double polygonal snake graph denoted by $D(P{S}_{t,n})$ is obtained from the path with edges $e_1,e_2,\dots e_{t-1}$ by adjoining two different cycles of length n to each e_i as the common edge for all $1\le i\le t-1.$

Note that, $D(P{S}_{t,n})$ has $(t-1)(2n-3)+1$ vertices and $(t-1)(2n-1)$ edges. An example of such a graph is given in Figure 13.

Figure 13. $D(P{S}_{4,3}).$

Theorem 8.

The double polygonal snake graph $D(P{S}_{t,m+1})$ is m-bonacci graceful for all m ≥ 2.

Proof.

The graph $D(P{S}_{t,m+1})$ has $(t-1)(2m-1)+1$ vertices and $N=(t-1)(2m+1)$ edges. Let A_i and B_i denote the two different cycles associated with edge e_i of the path P_t, $1\le i\le t-1.$ Let u_ij and w_ij denote the vertices of cycles A_i and B_i respectively, $1\le j\le m+1.$ For each i such that $1\le i\le t-1,$ we have $u_{i1}=w_{i1},u_{i(m+1)}=w_{i(m+1)}.$ We label the vertices of A₁ as follows: (11) $$\begin{array}{c}l(u_{11})=0,l(u_{12})=Z_{N,m},\\ l(u_{1j})=l(u_{1(j-1)})-Z_{N-(j-2),m},3\le j\le m+1\end{array}$$(11) Clearly the vertex labels are distinct as $l(u_{12})>l(u_{13})>\cdots >l(u_{1m})>l(u_{1(m+1)}).$ Also, we have the following: (12) $$\begin{array}{c}l(u_{1(m+1)})=l(u_{1m)})-Z_{N-(m-1),m}\\ =Z_{N,m}-\sum _{i=N-(m-1)}^{N-1}{Z}_{i,m}\\ =Z_{N-m,m}\end{array}$$(12) From Equations (11)(11) $$\begin{array}{c}l(u_{11})=0,l(u_{12})=Z_{N,m},\\ l(u_{1j})=l(u_{1(j-1)})-Z_{N-(j-2),m},3\le j\le m+1\end{array}$$(11) and (12)(12) $$\begin{array}{c}l(u_{1(m+1)})=l(u_{1m)})-Z_{N-(m-1),m}\\ =Z_{N,m}-\sum _{i=N-(m-1)}^{N-1}{Z}_{i,m}\\ =Z_{N-m,m}\end{array}$$(12) , the derived edge labels of the edges of A₁ are $Z_{N,m},Z_{N-1,m},\dots ,Z_{N-m,m}.$ We now label the vertices of B₁ as follows: (13) $$\begin{array}{c}l(w_{1m})=l(u_{1(m+1)})-Z_{N-m-1,m}\\ l(w_{1j})=l(w_{1(j+1)})-Z_{N-2m+(j-1),m},2\le j\le m-1\end{array}$$(13) We have, $l(u_{1(m+1)})>l(w_{1m})>l(w_{1(m-1)})>\cdots >l(w_{12})>l(w_{11})=l(u_{11}).$ Hence, the label of vertices of A₁ and B₁ are distinct. By the definition of $l(w_{12}),$ we have the following: (14) $$\begin{array}{c}l(w_{12})=l(w_{13})-Z_{N-2m+1,m}\\ =Z_{N-m,m}-\sum _{i=N-2m+1}^{N-m-1}{Z}_{i,m}\\ =Z_{N-2m,m}\end{array}$$(14) From Equations (13)(13) $$\begin{array}{c}l(w_{1m})=l(u_{1(m+1)})-Z_{N-m-1,m}\\ l(w_{1j})=l(w_{1(j+1)})-Z_{N-2m+(j-1),m},2\le j\le m-1\end{array}$$(13) and (14)(14) $$\begin{array}{c}l(w_{12})=l(w_{13})-Z_{N-2m+1,m}\\ =Z_{N-m,m}-\sum _{i=N-2m+1}^{N-m-1}{Z}_{i,m}\\ =Z_{N-2m,m}\end{array}$$(14) , the derived edge labels of B₂ are $Z_{N-m,m},Z_{N-m-1,m},\dots ,Z_{N-2m,m},$ where $Z_{N-m,m}$ is the edge label of the edge $e_1=u_{11}{u}_{1(m+1)}.$

We now label the vertices of A_i and B_i, $i\ge 2$ as follows: (15) $$\begin{array}{c}l(u_{i2})=l(u_{i1})-Z_{N-(i-1)(2m+1),m}\\ l(u_{ij})=l(u_{i(j-2)})+Z_{N-(i-1)(2m+1)-(j-2),m},3\le j\le m+1\\ l(w_{im})=l(u_{i(m+1)})+Z_{N-(i-1)(2m+1)-(m+(m-2)),m}\\ l(w_{ij})=l(u_{i(j+1)})+Z_{N-(i-1)(2m+1)-(m+(j-1)),m},3\le j\le m\end{array}$$(15) From Equation (15)(15) $$\begin{array}{c}l(u_{i2})=l(u_{i1})-Z_{N-(i-1)(2m+1),m}\\ l(u_{ij})=l(u_{i(j-2)})+Z_{N-(i-1)(2m+1)-(j-2),m},3\le j\le m+1\\ l(w_{im})=l(u_{i(m+1)})+Z_{N-(i-1)(2m+1)-(m+(m-2)),m}\\ l(w_{ij})=l(u_{i(j+1)})+Z_{N-(i-1)(2m+1)-(m+(j-1)),m},3\le j\le m\end{array}$$(15) , we have, $l(u_{i2})<l(u_{i3})<\cdots <l(u_{im})<l(u_{i(m+1)})<l(w_{im})<l(w_{i(m-1)})<\cdots <l(w_{i2}).$ The edge label of $u_{i1}{u}_{i(m+1)}$ is (16) $$\begin{array}{c}l(u_{i1})-l(u_{i(m+1)})=l(u_{(i-1)m})+Z_{N-(i-2)(2m+1)-(m-1),m}\\ -[l(u_{im})+Z_{N-(i-1)(2m+1)-(m-1),m}]\\ =Z_{N-m-(i-1)(2m+1),m}\end{array}$$(16) Similarly, we get that $l(u_{i1})-l(w_{i2})=Z_{N-2m-(i-1)(2m+1),m}.$ Thus, the derived edge labels are distinct m-bonacci numbers. The proof that the vertex labels are distinct is as same as that of Theorem 7. Hence, the result. □

A 3-bonacci graceful labeling of $D(P{S}_{4,4})$ is given in Figure 14.

Figure 14. 3-bonacci labeling of $D(P{S}_{4,4}).$

6. Conclusion

We defined new graceful labeling called m-bonacci graceful labeling and gave labeling for some special class of graphs. We also found some particular classes of graphs that are not m-bonacci graceful. It will be interesting to look into the m-bonacci graceful labeling of $G\ast H,$ where G and H may or may not be m-bonacci graceful and * is a graph operation.

Additional information

Funding

The second author wishes to acknowledge the fellowship received from Department of Science and Technology under INSPIRE fellowship (IF170077).