Asymptotic energy of connected cubic circulant graphs

Abstract

In this article, we compute the oblique asymptote of the energy function for all connected cubic circulant graphs. Moreover, we show that this oblique asymptote is an upper bound for the energies of two of the subclasses of Möbius ladder graphs and lower bound for the remaining four subclasses.

Keywords:

• Möbius ladder graph
• Prism graph
• energy of a graph
• asymptotic energy

AMS subject classification:

• 5C50
• 15A18
• 68R05
• 42A05

1. Introduction

The energy of a graph is the sum of the absolute values of the eigenvalues of adjacency matrix of the graph. The concept first appeared in 1978 in [7]. The term energy refers to molecular energy in quantum chemistry. The notation E(G) stands for the energy of the graph G. In this paper we mainly focus on the mathematical perspective of the energy functions of Möbius ladder graph and Prism graph rather than focusing their roles in quantum chemistry and molecular biology. The authors [3] derived the energy functions of all connected cubic circulant graphs that are represented by only two family of classes namely Möbius ladder and Prism graphs. The lower and upper boundaries for the energy of Möbius ladder and Prism graphs can be improved by knowing the oblique asymptote of the energy functions for connected cubic circulant graphs and this is the main motivation for the authors. In this section, we introduce briefly the structure of the connected cubic circulant graphs and their energy functions.

1.1. Energies of connected cubic circulant graphs

Let A be a matrix of order n. Then we say that A is a circulant matrix if $a_{i,j}=a_{1,j-i+1}$ for all $i,j\in \left\{1,2,\dots ,n\right\},$ where the subscripts are computed in modulo n, see [5]. We call G as a circulant graph, if G is isomorphic to a graph whose adjacency matrix is circulant.

The Möbius ladder graph L_n for $n\ge 4$ even is formed by an n-cyle graph such that each vertex is connected by an edge to the opposite vertex, see [6, 8]. Let $n\ge 3$ be odd integer. The prism graph P_n consists of 2n vertices such that $p_1,\dots ,p_n$ and $q_1,\dots ,q_n$ form two n-cyles and there exist an edge $(p_i,q_i)$ for $i=1,\dots ,n,$ see [8, 9].

The adjacency matrices of Möbius ladder and Prism graphs are both circulant. The first rows of their adjacency matrices [12] are $$\mathit{cir}{c}_n(0,1,\underset{n/2-2}{\underbrace{0,\dots ,0}},1,\underset{n/2-2}{\underbrace{0,\dots ,0}},1)\hspace{1em}\text{and}\hspace{1em}\mathit{cir}{c}_{2n}(\underset{n-1}{\underbrace{0,\dots ,0}},1,1,1,\underset{n-2}{\underbrace{0,\dots ,0}})$$ respectively.

A graph for which $E(G)\le 2(n-1)$ is called non-hyperenergetic. Another interesting invariant, known as the asymptotic energy, is the $\underset{n\to \infty }{\lim }E(G)$ [2, 10, 13].

Let $A=[a_0,a_1,\dots ,a_{n-1}]$ be a circulant matrix. The eigenvalues of A are given by ${\lambda }_k={\sum }_{j=0}^{n-1}{a}_j{w}^j,$ where $w=e^{\frac{2\pi ik}{n}}$ is the $n^{\text{th}}$ rooth of unity and $k=0,1,\dots ,n-1$ [5, 8]. The eigenvalues of the Möbius ladder graph are ${\lambda }_k=2\hspace{0.17em}\text{cos}\hspace{0.17em}\left(\frac{2\pi k}{n}\right)+{(-1)}^k,$ see [8]. The closed formula for the energy of the Möbius ladder graph is given in [3].

The family of all cubic, connected, and circulant graphs correspond to only two classes, namely the Prism graphs P_n where n is odd and $n\ge 3$ and the Möbius ladder graph L_n where n is even and $n\ge 4$ [1, 4]. In [12] (see p. 25) it was shown that for odd n, the adjacency matrix of $L_{2n}$ is column equivalent to the adjacency matrix of P_n. It turns out that finding the algebraic expressions for L_n is equivalent to finding algebraic expressions for all cubic, connected, and circulant graphs.

Let $n\ge 4$ be an even integer. Then the energy of L_n can be computed by one of the algebraic expressions that is stated in the following theorem. Note that the lower script” o” and” e” in q_o and q_e denote the odd and even integers respectively.

Theorem 1.1

([3]). If $n\ge 4$ is an integer, then $E\left(L_n\right)$ is given by $$E\left(L_n\right)=\{\begin{array}{cc}\frac{n}{3}+4\sqrt{3}\text{cot}\left(\frac{2\pi }{n}\right)\hfill & n=6q_o\hfill \\ \frac{n}{3}+2\sqrt{3}\text{cot}\left(\frac{\pi }{n}\right)\hfill & n=6q_e\hfill \\ \frac{n-2}{3}+4\text{csc}\left(\frac{\pi }{n}\right)\hspace{0.17em}\text{sin}\hspace{0.17em}\left(\frac{\pi }{3}+\frac{\pi }{3n}\right)\hfill & n=6q_o+2\hfill \\ \frac{n+16}{3}+4\hspace{0.17em}\text{sin}\hspace{0.17em}\left(\frac{(n-2)\pi }{6n}\right)\hfill & \hfill \\ \left(2\hspace{0.17em}\text{sin}\hspace{0.17em}\left(\frac{(n-2)\pi }{3n}\right)\text{csc}\left(\frac{\pi }{n}\right)-\hspace{0.17em}\text{sec}\hspace{0.17em}\left(\frac{\pi }{n}\right)\right)\hfill & n=6q_e+2\hfill \\ \frac{n-4}{3}+8\text{csc}\left(\frac{2\pi }{n}\right)\hspace{0.17em}\text{sin}\hspace{0.17em}\left(\frac{\pi }{3}+\frac{2\pi }{3n}\right)\hfill & n=6q_o+4\hfill \\ \frac{n+2}{3}+4\text{csc}\left(\frac{\pi }{n}\right)\hspace{0.17em}\text{cos}\hspace{0.17em}\left(\frac{\pi }{6}+\frac{\pi }{3n}\right)\hfill & n=6q_e+4\hfill \end{array}$$

In [12] (see p. 25) it was shown that for odd n, the adjacency matrix of $L_{2n}$ is column equivalent to the adjacency matrix of P_n. Therefore, by replacing n with 2n in the energy of L_n the following theorem was stated.

Theorem 1.2

([3]). If $n\ge 3$ is an integer, then $E\left(P_n\right)$ is given by $$E\left(P_n\right)=\{\begin{array}{cc}\frac{2n}{3}+2\sqrt{3}\text{cot}\left(\frac{\pi }{2n}\right)\hfill & n=3q_o\hfill \\ \frac{2n-2}{3}+4\text{csc}\left(\frac{\pi }{2n}\right)\hspace{0.17em}\text{sin}\hspace{0.17em}\left(\frac{\pi }{3}+\frac{\pi }{6n}\right)\hfill & n=3q_e+1\hfill \\ \frac{2n+2}{3}+4\text{csc}\left(\frac{\pi }{2n}\right)\hspace{0.17em}\text{cos}\hspace{0.17em}\left(\frac{\pi }{6}+\frac{\pi }{6n}\right)\hfill & n=3q_o+2\hfill \end{array}$$

2. Main result

The following theorem gives us the asymptotic energy of Möbius ladder.

Theorem 2.1.

Let L_n be a Möbius ladder graph for an even integer $n\ge 4$, the linear function ${\Psi }_n=n\left(\frac{2\sqrt{3}}{\pi }+\frac{1}{3}\right)$ is the oblique asymptote of $E\left(L_n\right).$

Proof.

Note that $E\left(L_n\right)={\sum }_{k=0}^{n-1}\left|2\hspace{0.17em}\text{cos}\hspace{0.17em}\left(\frac{2\pi k}{n}\right)+{(-1)}^k\right|,$ see [8]. This sum can be split as follows. $$E\left(L_n\right)=\sum _{k=1}^{\frac{n}{2}}\left|2\hspace{0.17em}\text{cos}\hspace{0.17em}\left(\frac{2\pi (2k-2)}{n}\right)+1\right|+\sum _{k=1}^{\frac{n}{2}}\left|2\hspace{0.17em}\text{cos}\hspace{0.17em}\left(\frac{2\pi (2k-1)}{n}\right)-1\right|$$ Let $h_1=f_1°g_1,$ where $f_1\left(x\right)=2\hspace{0.17em}\text{cos}\hspace{0.17em}\left(x\right)+1$ and $g_1\left(k\right)=\frac{2\pi (2k-2)}{n}.$ Notice that as k goes from 1 to $\frac{n}{2}$ the values of g₁ become $\left\{0,\frac{4\pi }{n},\frac{8\pi }{n},\dots ,2\pi -\frac{4\pi }{n}\right\}$ and the Riemann sum for h₁ is ${\sum }_{k=1}^{\frac{n}{2}}{h}_1\left(k\right)\frac{4\pi }{n},$ where $\frac{4\pi }{n}$ is the width of each subinterval. Moreover, as n goes to infinity the domain of h₁ becomes $[0,2\pi )$ and the limit of the Riemann sum is $$\underset{n\to \infty }{\lim }\frac{4\pi }{n}\sum _{k=1}^{\frac{n}{2}}\left|2\hspace{0.17em}\text{cos}\hspace{0.17em}\left(\frac{2\pi (2k-2)}{n}\right)+1\right|={\int }_0^{2\pi }\left|2\hspace{0.17em}\text{cos}\hspace{0.17em}\left(x\right)+1\right|dx$$ Let $h_2=f_2°g_2,$ where $f_2\left(x\right)=2\hspace{0.17em}\text{cos}\hspace{0.17em}\left(x\right)-1$ and $g_2\left(k\right)=\frac{2\pi (2k-1)}{n}.$ Notice that as k goes from 1 to $\frac{n}{2}$ the values of g₂ become $\left\{\frac{2\pi }{n},\frac{6\pi }{n},\dots ,2\pi -\frac{2\pi }{n}\right\}$ and the Riemann sum for h₂ is ${\sum }_{k=1}^{\frac{n}{2}}{h}_2\left(k\right)\frac{4\pi }{n},$ where $\frac{4\pi }{n}$ is the width of each subinterval. Moreover, as n goes to infinity the domain of h₂ becomes $(0,2\pi )$ and the limit of the Riemann sum is $$\underset{n\to \infty }{\lim }\frac{4\pi }{n}\sum _{k=1}^{\frac{n}{2}}\left|2\hspace{0.17em}\text{cos}\hspace{0.17em}\left(\frac{2\pi (2k-1)}{n}\right)-1\right|={\int }_0^{2\pi }|2\hspace{0.17em}\text{cos}\hspace{0.17em}\left(x\right)-1|dx$$ Therefore, if we denote the energy of $E\left(L_n\right)$ at infinity by $E\left(L_{\infty }\right),$ then $$\begin{array}{c}E\left(L_{\infty }\right)=\frac{n}{4\pi }({\int }_0^{2\pi }\left|2\hspace{0.17em}\text{cos}\hspace{0.17em}\left(x\right)+1\right|dx+{\int }_0^{2\pi }\left|2\hspace{0.17em}\text{cos}\hspace{0.17em}\left(x\right)-1\right|dx)\\ =\frac{n}{4\pi }\left(\frac{2}{3}\left(6\sqrt{3}+\pi \right)+\frac{2}{3}\left(6\sqrt{3}+\pi \right)\right)\\ =n\left(\frac{2\sqrt{3}}{\pi }+\frac{1}{3}\right)={\Psi }_n\approx 1.43599n\end{array}$$ which completes the proof. □

Remark 2.2.

Note that the constant, 1.43599, in ${\Psi }_n$ is one less than the constant of $E\left(\overline{Ci}(n,1)\right)$ computed in [10].

Remark 2.3.

Note that ${\Psi }_n\le 2(n-1)$ for all $n\ge 4$ which shows that Möbius ladders are non-hyperenergetic. This was also shown in [11], see Corollary 1.

Let $I_1=\left\{E\right(L_n^{6q_o}),E(L_n^{6q_e}\left)\right\}$ and $I_2=\left\{E\right(L_n^{6q_o+2}),E(L_n^{6q_o+4}),E(L_n^{6q_e+2}),E(L_n^{6q_e+4}\left)\right\}$ where the superscript denotes the class of each functions. The lower and the upper bounds of the energy functions of the Möbius ladder graph is given in the following theorem. Note that ${\Psi }_n$ divides the energy functions of $E\left(L_n\right)$ into two classes and it turns out that ${\Psi }_n$ is an upper bound for I₁ and a lower bound for I₂.

Theorem 2.4.

If n > 4, then the ordering of the energy functions of L_n is as follows. (1) $$E\left(L_n^{6q_o}\right)<E\left(L_n^{6q_e}\right)<{\Psi }_n<E\left(L_n^{6q_e+4}\right)<E\left(L_n^{6q_o+2}\right)<E\left(L_n^{6q_e+2}\right)<E\left(L_n^{6q_o+4}\right).$$(1)

Proof.

We will prove that each consecutive pair of inequalities in the ordering is true.

Case 1.

We first show that $E\left(L_n^{6q_o}\right)<E\left(L_n^{6q_e}\right).$ Note that $0<\hspace{0.17em}\text{tan}\hspace{0.17em}\left(\frac{\pi }{n}\right)<1$ for $n>4,$ so $0<1-{\hspace{0.17em}\text{tan}\hspace{0.17em}}^2\left(\frac{\pi }{n}\right)<1,$ hence $$2\left(\frac{1-{\hspace{0.17em}\text{tan}\hspace{0.17em}}^2\left(\frac{\pi }{n}\right)}{2\hspace{0.17em}\text{tan}\hspace{0.17em}\left(\frac{\pi }{n}\right)}\right)<\frac{1}{\hspace{0.17em}\text{tan}\hspace{0.17em}\left(\frac{\pi }{n}\right)}\mathrm{}\text{which}\mathrm{}\text{is}\mathrm{}\text{equivalent}\mathrm{}\text{to}\mathrm{}2\text{cot}\left(\frac{2\pi }{n}\right)<\text{cot}\left(\frac{\pi }{n}\right).$$ Therefore, $$E\left(L_n^{6q_o}\right)=\frac{n}{3}+4\sqrt{3}\text{cot}\left(\frac{2\pi }{n}\right)<\frac{n}{3}+2\sqrt{3}\text{cot}\left(\frac{\pi }{n}\right)=E\left(L_n^{6q_e}\right).$$

Case 2.

We will prove that $E\left(L_n^{6q_e}\right)<{\Psi }_n.$ Notice that for $x\in \left(0,\pi \right),$ we have $\text{cot}\left(x\right)<\frac{1}{x}.$ So if n > 4, then $\text{cot}\left(\frac{\pi }{n}\right)<\frac{n}{\pi },$ and this implies the following inequality which is what we want to establish. $$E\left(L_n^{6q_e}\right)=\frac{n}{3}+2\sqrt{3}\text{cot}\left(\frac{\pi }{n}\right)<n\left(\frac{2\sqrt{3}}{\pi }+\frac{1}{3}\right)={\Psi }_n$$

Case 3.

We show that ${\Psi }_n<E\left(L_n^{6q_e+4}\right)$ is valid for n > 4. We know from Theorem 1 that if $n=6q_e+4,$ then (2) $$E\left(L_n\right)=\frac{n+2}{3}+4\text{csc}\left(\frac{\pi }{n}\right)\hspace{0.17em}\text{cos}\hspace{0.17em}\left(\frac{\pi }{6}+\frac{\pi }{3n}\right)$$(2) For the simplicity of the estimation, let $p=\frac{\pi }{3n},$ then the algebraic expression $\text{csc}\left(\frac{\pi }{n}\right)\hspace{0.17em}\text{cos}\hspace{0.17em}\left(\frac{\pi }{6}+\frac{\pi }{3n}\right)$ reduces to $\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}\left(\frac{\pi }{3}-p\right)}{\hspace{0.17em}\text{sin}\hspace{0.17em}\left(3\left(\frac{\pi }{3}-p\right)\right)},$ and for all $p\in \left(0,\frac{\pi }{3}\right),$ we have the following estimation: $$\begin{array}{c}0<\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}\left(3\left(\frac{\pi }{3}-p\right)\right)}{\hspace{0.17em}\text{sin}\hspace{0.17em}\left(\frac{\pi }{3}-p\right)}=\left(3-4{\hspace{0.17em}\text{sin}\hspace{0.17em}}^2\left(\frac{\pi }{3}-p\right)\right)\\ =\left(1+2\hspace{0.17em}\text{cos}\hspace{0.17em}\left(\frac{2\pi }{3}-2p\right)\right)=(1-\hspace{0.17em}\text{cos}\hspace{0.17em}2p+\sqrt{3}\hspace{0.17em}\text{sin}\hspace{0.17em}2p)\\ =\left(2{\hspace{0.17em}\text{sin}\hspace{0.17em}}^{2}p+2\sqrt{3}\hspace{0.17em}\text{sin}\hspace{0.17em}p\hspace{0.17em}\text{cos}\hspace{0.17em}p\right)=2\hspace{0.17em}\text{sin}\hspace{0.17em}p(\hspace{0.17em}\text{sin}\hspace{0.17em}p+\sqrt{3}\hspace{0.17em}\text{cos}\hspace{0.17em}p)\\ <2p(p+\sqrt{3})=2p\frac{3-p^2}{\sqrt{3}-p}<2p\frac{3}{\sqrt{3}-p}\end{array}$$ Therefore, $\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}\left(\frac{\pi }{3}-p\right)}{\hspace{0.17em}\text{sin}\hspace{0.17em}\left(3\left(\frac{\pi }{3}-p\right)\right)}>\frac{1}{2}\left(\frac{\sqrt{3}}{3p}-\frac{1}{3}\right)=\frac{1}{2}\left(\frac{n\sqrt{3}}{\pi }-\frac{1}{3}\right),$ and this implies that $$E\left(L_n^{6q_e+4}\right)>\frac{n+2}{3}+2\left(\frac{n\sqrt{3}}{\pi }-\frac{1}{3}\right)=n\left(\frac{1}{3}+\frac{2\sqrt{3}}{\pi }\right)={\Psi }_n.$$

Case 4.

We show that $E\left(L_n^{6q_o+2}\right)>E\left(L_n^{6q_e+4}\right)$ holds for n > 4. Notice that if n > 4, then $\frac{\pi }{n}<\frac{\pi }{2}$ and $\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}\left(\frac{3\pi }{n}\right)}{\hspace{0.17em}\text{sin}\hspace{0.17em}\left(\frac{\pi }{n}\right)}=4{\hspace{0.17em}\text{cos}\hspace{0.17em}}^2\left(\frac{\pi }{n}\right)-1<3$ that is $\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}\left(\frac{\pi }{n}\right)}{\hspace{0.17em}\text{sin}\hspace{0.17em}\left(\frac{3\pi }{n}\right)}>\frac{1}{3}.$ Using the Theorem 1, we have the following estimation. $$\begin{array}{c}E\left(L_n^{6q_o+2}\right)-E\left(L_n^{6q_e+4}\right)=-\frac{4}{3}+\frac{4}{\hspace{0.17em}\text{sin}\hspace{0.17em}\left(\frac{\pi }{n}\right)}\left(\hspace{0.17em}\text{sin}\hspace{0.17em}\left(\frac{\pi }{3}+\frac{\pi }{3n}\right)-\hspace{0.17em}\text{sin}\hspace{0.17em}\left(\frac{\pi }{3}-\frac{\pi }{3n}\right)\right)\\ =-\frac{4}{3}+\frac{4\hspace{0.17em}\text{sin}\hspace{0.17em}\left(\frac{\pi }{3n}\right)}{\hspace{0.17em}\text{sin}\hspace{0.17em}\left(\frac{\pi }{n}\right)}>0\end{array}$$

Case 5.

We show that $E\left(L_n^{6q_e+2}\right)>E\left(L_n^{6q_o+2}\right)$ holds for n > 4. For simplicity, we let $p=\frac{\pi }{6}-\frac{\pi }{3n}.$ If n > 4, then ${\hspace{0.17em}\text{cos}\hspace{0.17em}}^2\left(p\right)>\frac{3}{4}$ and $\frac{1}{4\left(4{\hspace{0.17em}\text{cos}\hspace{0.17em}}^2\right(p)-1)}<\frac{1}{8},$ so $$\frac{{\hspace{0.17em}\text{cos}\hspace{0.17em}}^2\left(p\right)}{2\hspace{0.17em}\text{cos}\hspace{0.17em}\left(2p\right)+1}=\frac{1}{4}+\frac{1}{4\left(4{\hspace{0.17em}\text{cos}\hspace{0.17em}}^2\right(p)-1)}<\frac{1}{4}+\frac{1}{8}=\frac{3}{8}$$ Notice that $$\frac{{\hspace{0.17em}\text{cos}\hspace{0.17em}}^2\left(p\right)}{2\hspace{0.17em}\text{cos}\hspace{0.17em}\left(2p\right)+1}=\frac{{\hspace{0.17em}\text{cos}\hspace{0.17em}}^2\left(p\right)(2\hspace{0.17em}\text{cos}\hspace{0.17em}(2p)-1)}{4{\hspace{0.17em}\text{cos}\hspace{0.17em}}^2\left(2p\right)-1}=\frac{\hspace{0.17em}\text{cos}\hspace{0.17em}\left(2p\right)-\hspace{0.17em}\text{sin}\hspace{0.17em}\left(p\right)\hspace{0.17em}\text{sin}\hspace{0.17em}\left(3p\right)}{4{\hspace{0.17em}\text{cos}\hspace{0.17em}}^2\left(2p\right)-1}<\frac{3}{8}$$ Substituting $4{\hspace{0.17em}\text{cos}\hspace{0.17em}}^2\left(2p\right)-1=\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}\left(6p\right)}{\hspace{0.17em}\text{sin}\hspace{0.17em}\left(2p\right)}$ and multiplying both sides by 16 in above inequality yields that $$\begin{array}{c}\frac{16(\hspace{0.17em}\text{sin}\hspace{0.17em}(2p)\hspace{0.17em}\text{cos}\hspace{0.17em}(2p)-\hspace{0.17em}\text{sin}\hspace{0.17em}(p)\hspace{0.17em}\text{sin}\hspace{0.17em}(2p)\hspace{0.17em}\text{sin}\hspace{0.17em}(3p\left)\right)}{\hspace{0.17em}\text{sin}\hspace{0.17em}\left(6p\right)}=\frac{8\hspace{0.17em}\text{sin}\hspace{0.17em}\left(4p\right)}{\hspace{0.17em}\text{sin}\hspace{0.17em}\left(6p\right)}-\frac{8\hspace{0.17em}\text{sin}\hspace{0.17em}\left(p\right)\hspace{0.17em}\text{sin}\hspace{0.17em}\left(2p\right)}{\hspace{0.17em}\text{cos}\hspace{0.17em}\left(3p\right)}<6\\ 6+\frac{8\hspace{0.17em}\text{sin}\hspace{0.17em}\left(p\right)\hspace{0.17em}\text{sin}\hspace{0.17em}\left(2p\right)}{\hspace{0.17em}\text{cos}\hspace{0.17em}\left(3p\right)}>\frac{8\hspace{0.17em}\text{sin}\hspace{0.17em}\left(4p\right)}{\hspace{0.17em}\text{sin}\hspace{0.17em}\left(6p\right)}=4\left(\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}\left(p\right)}{\hspace{0.17em}\text{sin}\hspace{0.17em}\left(3p\right)}+\frac{\hspace{0.17em}\text{cos}\hspace{0.17em}\left(p\right)}{\hspace{0.17em}\text{cos}\hspace{0.17em}\left(3p\right)}\right)\\ 6+\frac{8\hspace{0.17em}\text{sin}\hspace{0.17em}\left(p\right)\hspace{0.17em}\text{sin}\hspace{0.17em}\left(2p\right)}{\hspace{0.17em}\text{cos}\hspace{0.17em}\left(3p\right)}-4\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}\left(p\right)}{\hspace{0.17em}\text{sin}\hspace{0.17em}\left(3p\right)}>4\frac{\hspace{0.17em}\text{cos}\hspace{0.17em}\left(p\right)}{\hspace{0.17em}\text{cos}\hspace{0.17em}\left(3p\right)}\end{array}$$ This inequality is equivalent to $E\left(L_n^{6q_e+2}\right)>E\left(L_n^{6q_o+2}\right)$ since $\text{cos}\hspace{0.17em}\left(p\right)=\hspace{0.17em}\text{sin}\hspace{0.17em}(\frac{\pi }{3}+\frac{\pi }{3n}),\hspace{0.17em}\text{cos}\hspace{0.17em}\left(3p\right)=\hspace{0.17em}\text{sin}\hspace{0.17em}\left(\frac{\pi }{n}\right),\hspace{0.17em}\text{sin}\hspace{0.17em}\left(3p\right)=\hspace{0.17em}\text{cos}\hspace{0.17em}\left(\frac{\pi }{n}\right),$ and $6=\frac{n+16}{3}-\frac{n-2}{3}.$

Case 6.

Proving $E\left(L_x^{6q_o+4}\right)>E\left(L_x^{6q_e+2}\right)$ is similar to previous case, hence it is omitted. □

Remark 2.5.

The proof of Theorem 2.4 can also be done by Taylor expansion for the difference of each consecutive energy functions.

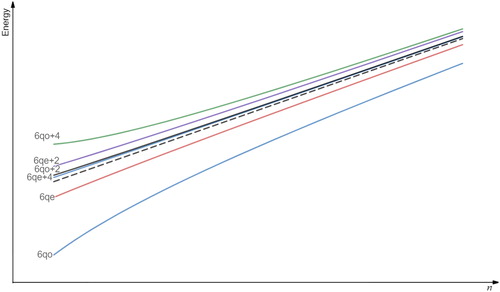
The graph of each energy functions in Theorem 1.1 along with the graph of ${\Psi }_x,$ when $x\in \mathbb{R}$ and x > 4 can be seen in Figure 1. The dash line is the graph of ${\Psi }_x.$ The ordering of the graphs from top to down are $6q_o+4,6q_e+2,6q_o+2,6q_e+4,6q_e,$ and $6q_o$ respectively. Since we are just interested in the discrete cases we immediately state the following corollary.

Figure 1. The asympthotic behaviour of the Möbius ladder graph.

Corollary 2.6.

If $n\ge 4$ is an even integer, then $$\frac{n}{3}+4\sqrt{3}\text{cot}\left(\frac{2\pi }{n}\right)\le E\left(L_n\right)\le \frac{n-4}{3}+8\text{csc}\left(\frac{2\pi }{n}\right)\hspace{0.17em}\text{sin}\hspace{0.17em}(\frac{\pi }{3}+\frac{2\pi }{3n}).$$ The ordering of the energy functions of prism graph is derived from Theorem 2.4, Theorem 1.1 and Theorem 1.2 as follows $$E\left(P_n^{3q_o}\right)<{\Psi }_{2n}=2{\Psi }_n<E\left(P_n^{3q_o+2}\right)<E\left(P_n^{3q_e+1}\right).$$ Therefore, someone can easily determine the boundaries of the energy of the prism graphs as given in the below corollary.

Corollary 2.7.

If $n\ge 3$ is an odd integer, then $$\frac{2n}{3}+2\sqrt{3}\text{cot}\left(\frac{\pi }{2n}\right)\le E\left(P_n\right)\le \frac{2n-2}{3}+4\text{csc}\left(\frac{\pi }{2n}\right)\hspace{0.17em}\text{sin}\hspace{0.17em}\left(\frac{\pi }{3}+\frac{\pi }{6n}\right)$$ One of the interesting results that is derived directly from Theorem 2.4 is the comparison of the energies of Möbius ladder graphs and prism graphs as given in the next corollary.

Corollary 2.8.

If $n\ge 3$ is integer, then the following holds

1. If $n=3q_o$, then $E\left(L_{2n}\right)<E\left(P_n\right)$

2. If $n=3q_o+2$ or $n=3q_e+1$, then $E\left(L_{2n}\right)>E\left(P_n\right).$

Disclosure statement

No potential conflict of interest was reported by the author(s).