Local edge coloring of graphs

Abstract

Let $G=(V,E)$ be a graph. A local edge coloring of G is a proper edge coloring $c:E\to \mathbb{N}$ such that for each subset S of E(G) with $2\le \left|S\right|\le 3,$ there exist edges $e,f\in S$ such that $|c(e)-c(f)|\ge n_s,$ where n_s is the number of copies of P₃ in the edge induced subgraph $〈S〉.$ The maximum color assigned by a local edge coloring c to an edge of G is called the value of c and is denoted by ${\chi }_{\ell }^{\prime }(c).$ The local edge chromatic number of G is ${\chi }_{\ell }^{\prime }(G)=\min \{{\chi }_{\ell }^{\prime }(c)\},$ where the minimum is taken over all local edge colorings c of G. In this article, we derive bounds and many results based on local edge coloring.

Keywords:

• Coloring
• edge coloring
• local coloring
• line graph

Mathematics Subject Classification:

• 05C15
• 05C69

1. Introduction

By a graph $G=(V,E),$ we mean a finite and undirected graph with neither loops nor multiple edges. The order and size of G are denoted by n and m, respectively. For graph theoretic terminology, we refer to Chartrand and Lesniak [1].

Graph coloring is one of the major areas in graph theory that have been well studied. Several variations of coloring have been introduced and studied by many researchers. For an excellent survey of various graph colorings and open problems, we refer to [2, 3]. A proper coloring of a graph G is an assignment of colors to the vertices(edges) of G in such a way that no two adjacent vertices (edges) receive the same color. The chromatic (edge chromatic) number $\chi (G)(\chi \prime (G))$ is the minimum number of colors required for a proper (edge) coloring of G.

Chartrand et al. introduced the following concept of local coloring and local chromatic number in [4, 5]. Li et al and Klav$\check{z}$ ar et al. recently proved many substantial results based on the local coloring of graphs in [6, 7]. Let us denote $\mathbb{N}[t]=\{1,2,\dots ,t\}.$ A local coloring of a graph G is a function $c:V(G)\to \mathbb{N}[t]$ such that for each $S\subseteq V(G),2\le \left|S\right|\le 3,$ there exist $u,v\in S$ with $|c(u)-c(v)|$ at least the number of edges in the subgraph induced by S. The maximum color assigned by c is the value ${\chi }_{\ell }^{}(c),$ and the local chromatic number of G is ${\chi }_{\ell }^{}(G)=\min \{{\chi }_{\ell }^{}(c):c$ is a local coloring of $G\}.$

Motivated by the concept of local coloring, we introduce the concept of local edge coloring and present several results. We need the following theorems.

Theorem 1.1.

[2] For every nonempty graph G, $\chi \prime (G)=\chi (L(G)).$

Theorem 1.2.

[8, 9] If G is a simple graph, then $\Delta (G)\le \chi \prime (G)\le \Delta (G)+1.$

Theorem 1.3.

[4] For every positive integer n, ${\chi }_{\ell }^{}(K_n)=\lfloor \frac{3n-1}{2}\rfloor .$

1.1. Local edge colorings of graphs

Definition 1.4.

For $k\ge 2,$ a k-local edge coloring of a graph G of edge size at least 2 is a function $c:E(G)\to \mathbb{N}$ having the property that for each set $S\subseteq E(G)$ with $2\le \left|S\right|\le k,$ there exist edges $e_1,e_2\in S$ such that $|c(e_1)-c(e_2)|\ge n_s,$ where n_s is the number of copies of P₃ in the edge induced subgraph $〈S〉.$ The maximum color assigned by a k-local edge coloring c to an edge of G is called the value of c and is denoted by ${\ell }_{c_k}^{\prime }(c).$ The k-local edge chromatic number of G is ${\ell }_{c_k}^{\prime }(G)=\min \{{\ell }_{c_k}^{\prime }(c)\},$ where the minimum is taken over all k- local edge coloring c of G.

Even though we have defined k-local edge coloring, in this paper, we confine ourselves to the study of 3-local edge colorings, which is simply called local edge coloring. Also, $\ell {\prime }_{ek}(c)$ and $\ell {\prime }_{ek}(G)$ are denoted by ${\chi }_{\ell }^{\prime }(c)$ and ${\chi }_{\ell }^{\prime }(G),$ respectively. A local edge coloring c with ${\chi }_{\ell }^{\prime }(c)={\chi }_{\ell }^{\prime }(G)$ is called a minimum local edge coloring of G. The following are a few elementary observations.

Observation 1.5.

A local edge coloringc is a proper edge coloring ofG satisfying the following conditions.

1. Any inducedP₄ contains at least two edgese, f such that$|c(e)-c(f)|\ge 2.$

2. AnyK₃ or an induced$K_{1,3}$ contains at least two edgese, f such that$|c(e)-c(f)|\ge 3.$

Observation 1.6.

For any graphG, $\chi \prime (G)\le {\chi }_{\ell }^{\prime }(G).$

Observation 1.7.

For any cycleC_n, $${\chi }_{\ell }^{\prime }(C_n)=\{\begin{array}{cc}3\hfill & \text{for}n>4\hfill \\ 4\hfill & \text{for}n=3.\hfill \end{array}$$

Observation 1.8.

For any pathP_n, $${\chi }_{\ell }^{\prime }(P_n)=\{\begin{array}{cc}3\hfill & \text{for}n>3\hfill \\ 2\hfill & \text{for}n=3.\hfill \end{array}$$

Observation 1.9.

It can be easily verified that any local edge coloring ofG is a local coloring ofL(G) and hence it follows that${\chi }_{\ell }^{\prime }(G)={\chi }_{\ell }(L(G)).$

Observation 1.10.

If$\chi \prime (G)={\chi }_{\ell }^{\prime }(G),$ then$\Delta (G)\le 4.$

The following theorem gives bounds for ${\chi }_{\ell }^{\prime }(G).$

Theorem 1.11.

For any graphG, $\lfloor \frac{3\Delta (G)-1}{2}\rfloor \le {\chi }_{\ell }^{\prime }(G)\le 2\chi \prime (G)-1.$

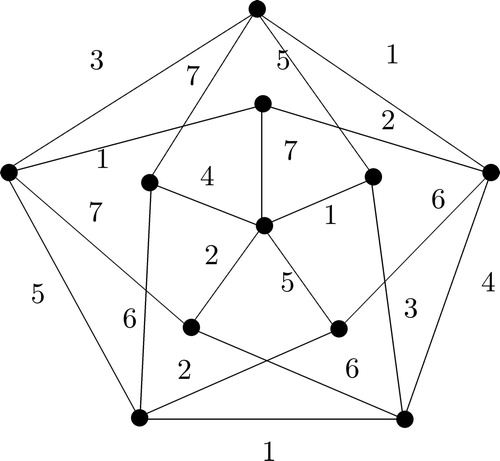
Example 1.12.

Let $G\cong C_n+2K_1$ be a graph with even parity $n\ge 6.$ Then, ${\chi }_{\ell }^{\prime }(G)=\lfloor \frac{3n-1}{2}\rfloor .$

Proof.

Consider the graph $G=C_n+2K_1$ with $n\ge 6$ and n is even. Let $V(G)=\{v_1,v_2,\dots ,v_n,u,v\}$ and let $E(G)={\cup }_{i=1}^n\{e_i^{\prime },e_i^{″}\}\cup {\cup }_{j=1}^{n-1}\left\{e_j\right\}\cup \left\{e_n\right\},$ where $e_j=v_j{v}_{j+1},e_n=v_1{v}_n,e_i^{\prime }=u{v}_i,$ and $e_i^{″}=v{v}_i.$

By Theorem 1.11, ${\chi }_{\ell }^{\prime }(G)\ge \lfloor \frac{3\Delta (G)-1}{2}\rfloor =\lfloor \frac{3n-1}{2}\rfloor =k$(say). Now consider the coloring $f:E(G)\to \mathbb{N}[k]$ defined as below $$f(e)=\{\begin{array}{cc}3\ell -2\hfill & \text{for}1\le \ell \le \frac{n}{2}\text{and}e\in \{e_{\ell }^{\prime },e_{\ell +1}^{″}\}\hfill \\ 3\ell -1\hfill & \text{for}1\le \ell \le \frac{n}{2}-1\text{and}e\in \{e_{\frac{n}{2}+\ell }^{\prime },e_{\frac{n}{2}+\ell +1}^{″}\}\hfill \\ k\hfill & \text{for}e\in \{e_n^{\prime },e_1^{″}\}\hfill \\ 3\hfill & \text{for}e\in {\cup }_{i=1}^n\left\{e_i\right\}\text{and}i\text{is}\text{odd}\hfill \\ 6\hfill & \text{for}e\in {\cup }_{i=1}^n\left\{e_i\right\}\text{and}i\text{is}\text{even}.\hfill \end{array}$$

Clearly, f satisfies the local edge coloring condition and which gives ${\chi }_{\ell }^{\prime }(G)\le k.$ □

Remark 1.13.

The lower bound for the Theorem 1.11 is sharp in star graph $K_{1,\Delta }$ and $Gr\ddot{o}t\mathit{zsch}$ graph in Figure 1.

Figure 1. $Gr\ddot{o}\text{tzsch}$ graph G for which ${\chi }_{\ell }^{\prime }(G)=7.$

Theorem 1.14.

Let G be any graph within the family of paths and cycles. Then, $\chi \prime (G)={\chi }_{\ell }^{\prime }(G)$ if and only if $G\in \{P_2,P_3,C_{2k+1},k\ge 2\}.$

Proof.

Clearly if $G\in \{P_2,P_3,C_{2k+1},k\ge 2\},$ then $\chi \prime (G)={\chi }_{\ell }^{\prime }(G).$ Conversely, consider a graph G with $\Delta (G)\le 2$ and $\chi \prime (G)={\chi }_{\ell }^{\prime }(G).$ If $\Delta (G)=1,$ then $G\cong P_2.$ If $\Delta (G)=2,$ then G is isomorphic to path P_n or cycle C_n. If $G\cong P_n,n\ge 4,$ then ${\chi }_{\ell }(G)=3\ne 2=\chi \prime (G).$ If $G\cong C_3,$ then ${\chi }_{\ell }(G)=4\ne 3=\chi \prime (G).$ Similarly, if $G\cong C_n,$ n is even, then ${\chi }_{\ell }(G)=3\ne 2=\chi \prime (G).$ Hence, if $G\in \{P_3,C_{2k+1},k\ge 2\},$ then $\chi \prime (P_3)={\chi }_{\ell }^{\prime }(P_3)=2$ and $\chi \prime (C_n)={\chi }_{\ell }^{\prime }(C_n)=3$ for n is odd and $n\ge 5.$ □

Theorem 1.15.

Let G be a graph with $\Delta (G)\ge 4$ and let Δ be even. If there exist two adjacent vertices u and v with $\mathrm{deg}(u)=\mathrm{deg}(v)=\Delta$, then ${\chi }_{\ell }^{\prime }(G)>\lfloor \frac{3\Delta (G)-1}{2}\rfloor .$

Proof.

Let $uv(=e)\in E(G)$ with $\mathrm{deg}(u)=\mathrm{deg}(v)=\Delta ,$ Δ be even. Then, the subgraph H of L(G) induced by the set of all edges incident with u and v is isomorphic to the graph consisting of two copies of $K_{\Delta }$ with exactly one common vertex. By Theorem 1.3, any local coloring c of even order complete graph is unique. Therefore, ${\chi }_{\ell }(H)>\lfloor \frac{3\Delta (G)-1}{2}\rfloor .$ By Observation 1.9, ${\chi }_{\ell }^{\prime }(G)>\lfloor \frac{3\Delta (G)-1}{2}\rfloor .$ □

Corollary 1.16.

If G is any even r-regular graph with $r\ge 4$, then ${\chi }_{\ell }^{\prime }(G)>\lfloor \frac{3r-1}{2}\rfloor .$

Example 1.17.

The Petersen graph $\mathbb{P}$ is local 5 edge colorable.

Proof.

Suppose ${\chi }_{\ell }^{\prime }(\mathbb{P})=4.$ This implies that $E(\mathbb{P})$ can be partitioned into matching $E_1\cup E_2\cup E_3\cup E_4.$ Let $\left|E_1\right|\ge \left|E_2\right|\ge \left|E_3\right|\ge \left|E_4\right|.$ Consider any local coloring $c:E(\mathbb{P})\to \mathbb{N}[4]$ and consider the labeling of $\mathbb{P}$ in Figure 2(i). Clearly $4\le \left|E_1\right|\le 5.$

Figure 2. Local edge coloring of Petersen graph $\mathbb{P}.$

Case 1: $\left|E_1\right|=4.$

Since $|E(\mathbb{P})|=15,\left|E_2\right|=\left|E_3\right|=4.$ Let $E_1=\{e_1,e_3,e_7,e_9\},E_2=\{e_2,e_5,e_6,e_8\},$ and $E_3=\{e_4,e_{10},e_{12},e_{13}\}.$ Let $B=\{(e_1,e_2,e_3),(e_2,e_1,e_5),(e_4,e_3,e_{13}),(e_1,e_{12},e_9),(e_{12},e_2,e_{13}),(e_7,e_{13},e_2)\}.$ In $E(\mathbb{P})-E_4,$ there exist two sets E_i and E_j such that the difference between the colors assigned to E_i and E_j is 1, which is a contradiction, since every element in B forms a path P₄ in $\mathbb{P}.$ The argument is similar for other possibilities of $E_i,1\le i\le 4,$ since $\mathbb{P}$ is both vertex and edge transitive. Hence, ${\chi }_{\ell }^{\prime }(\mathbb{P})>4.$

Case 2: $\left|E_1\right|=5.$

In $\mathbb{P},$ edges in outer cycle $\{e_1,e_2,e_3,e_4,e_5\}=B$(say) receive three colors in any local edge coloring assignment. Suppose $E_1=\{e_{11},e_{12},e_{13},e_{14},e_{15}\}.$ Clearly there exists an edge $e_i\in B$ adjacent to exactly two edges e_j and e_k in E₁ such that $|c(e_i)-c(e_j)|=|c(e_i)-c(e_k)|=1.$ This gives c is not a local edge coloring and ${\chi }_{\ell }^{\prime }(P)>4.$

Suppose $E_1=\{e_2,e_5,e_6,e_8,e_{14}\}$ consists of dotted edges in Figure 2(i). Now remaining 10 edges form a two-vertex disjoint cycle of order 5. Consider the 5-cycle $\{e_7,e_{13},e_3,e_4,e_{15}\}=C$(say) consists of darked edges in Figure 2(i) receive three colors in any local edge coloring assignment. Clearly there exists an edge $e_i\in C$ adjacent to exactly two edges e_j and e_k in E₁ such that $|c(e_i)-c(e_j)|=|c(e_i)-c(e_k)|=1.$ This gives c is not a local edge coloring and ${\chi }_{\ell }^{\prime }(\mathbb{P})>4.$ Similarly, we can give a contradiction if we choose any matching of size 5 in $\mathbb{P},$ since $\mathbb{P}$ is both vertex and edge transitive.

By cases 1 and 2, ${\chi }_{\ell }^{\prime }(\mathbb{P})>4$ and there is a local 5-edge coloring for $\mathbb{P}$ in Figure 2(ii). □

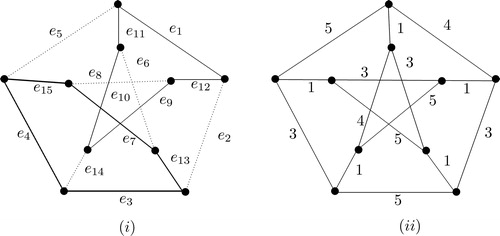
Example 1.18.

If $G\cong C_n\square K_2$ for $n\ge 3,$ then ${\chi }_{\ell }^{\prime }(G)=5.$

Proof.

Clearly $\Delta (G)=3.$ Consider the graph $G\cong C_3\square K_2$ as in Figure 3. Clearly by Theorem 1.11, ${\chi }_{\ell }^{\prime }(G)\ge 4.$ In G receives either {1, 2, 4} or {1, 3, 4} in outer cycle for any local 4-edge coloring. If assign such a coloring in C₃, then at least one of the dotted edges in Figure 3 does not receive any label in $\mathbb{N}[4]$ which gives ${\chi }_{\ell }^{\prime }(G)>4.$ By Theorem 1.11, ${\chi }_{\ell }^{\prime }(G)\le 5.$

Figure 3. Graph $C_3\square K_2$ and subgraph H of $C_n\square K_2$ for $n\ge 4.$

For $n\ge 4,$ the graph $H\cong P_4\square K_2$ is a subgraph of $G\cong C_n\square K_2.$ Consider the edge set of H as in Figure 3. Clearly by Theorem 1.11, ${\chi }_{\ell }^{\prime }(H)\ge 4.$ Let $f:E(G)\to \mathbb{N}[4]$ be a local coloring of H. If $f(e_1)=1,f(e_2)=3$ and $f(e_8)=4,$ then either $f(e_3)$ or $f(e_9)$ not belongs to $\mathbb{N}[4],$ since $\{e_8,e_2,e_9\}$ and $\{e_8,e_2,e_3\}$ forms a path P₄. The similar argument for if $f(e_1)=1,f(e_2)=2$ and $f(e_8)=4.$ If $f(e_1)=1,f(e_2)=4$ and $f(e_8)=3,$ then either $f(e_4)$ or $f(e_5)$ not belongs to $\mathbb{N}[4].$ The similar argument for if $f(e_1)=1,f(e_2)=4$ and $f(e_8)=2.$ If $f(e_1)=2,f(e_2)=4$ and $f(e_8)=1,$ then $f(e_4),f(e_7)\in \{3,4\}$ and $f(e_5)\notin \mathbb{N}[4].$ The similar argument for if $f(e_1)=3,f(e_2)=4$ and $f(e_8)=1.$ By all the above argument ${\chi }_{\ell }^{\prime }(G)>4$ and by Theorem 1.11, ${\chi }_{\ell }^{\prime }(G)\le 5.$ □

Corollary 1.19.

If $G\cong P_n\square K_2$ for $n\ge 4$, then ${\chi }_{\ell }^{\prime }(G)=5.$

1.2. Conclusion and scope

In this paper, we have introduced the concept of local edge chromatic number and have presented a few basic results.

If G is a connected graph with $\chi \prime (G)=k,$ then any k-edge coloring of G should use all the colors $1,2,\dots ,k.$ However, if G is a connected graph with ${\chi }_{\ell }^{\prime }(G)=k,$ then minimum local edge coloring of G need not use all the colors $1,2,\dots ,k.$ Any minimum edge local coloring certainly the colors 1 and k must be used. Motivated by the above observation, we propose the following new definition.

Definition 1.20.

A minimum local edge coloring c of G with ${\chi }_{\ell }^{\prime }(G)=k$ is called a local rainbow edge coloring if for each integer i, $1\le i\le k,$ there is an edge e of G for which c(e) = i. That is, c uses all of colors $1,2,\dots ,k.$ A graph G is called locally edge rainbow if every minimum local edge coloring of G is a local rainbow edge coloring.

Based on the definition 1.20, we pose the following problem.

Problem 1.21.

For every positive integerk, does there exists a locally edge rainbow graphG_k with${\chi }_{\ell }^{\prime }(G_k)=k.$

Conjecture 1.22.

Every 3-regular graph is not 4-local edge colorable.

Conjecture 1.23.

If G is 1-factorable, then ${\chi }_{\ell }^{\prime }(G)=2\Delta (G)-1.$

Problem 1.24.

Does there exist a graphG with$3\le \Delta (G)\le 4$ and$\chi \prime (G)={\chi }_{\ell }^{\prime }(G)$?

Acknowledgements

The third author is thankful to the management of Sri Sivasubramaniya Nadar College of Engineering, Chennai for the support. The authors express their sincere thanks to the referees for their valuable suggestions and comments which helped to improve the paper a lot.