?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.Abstract
We define a total k-labeling of a graph G as a combination of an edge labeling
and a vertex labeling
such that
if
and
if
where
The total k-labeling
is called an edge irregular reflexive k-labeling of G if every two different edges has distinct edge weights, where the edge weight is defined as the summation of the edge label itself and its two vertex labels. Thus, the smallest value of k for which the graph G has the edge irregular reflexive k-labeling is called the reflexive edge strength of G. In this paper, we study the edge irregular reflexive labeling of corona product of two paths and corona product of a path with isolated vertices. We determine the reflexive edge strength for these graphs.
1. Introduction
An edge irregular reflexive labeling is introduced by Ryan et al. [Citation25] and is inspired by the problems of an irregular assignment and an edge irregular total labeling. Let us start with a brief review of the origins and some background information of these labelings.
Chartrand et al. [Citation13] proposed a labeling problem in 1988, that is, determine the minimum value of parallel edges between every two vertices to ensure that a loopless multigraph has vertex irregularity. This problem is created as a consequence of Handshaking Lemma, i.e., no simple graph can have each distinct vertex degree, however, it is possible in multigraphs.
They defined this labeling problem as an edge k-labeling of a graph G such that the vertex weight is
for all vertices x,
with
where
the summation is over all vertices y adjacent to x. Such labeling is called irregular assignment and the irregularity strength of G, s(G) is known as the minimum k for which G has an irregular assignment using labels not greater than k. In other words, irregularity strength is interpreted as the minimum number of parallel edges, such that every vertex has a distinct degree in multigraph. For further results, see papers [Citation6, Citation14, Citation17, Citation23, Citation24]. For comprehensive survey of graph labelings, please refer [Citation15].
Bača et al. [Citation10] introduced a total k-labeling to be an edge irregular total k-labeling of a graph G if for every two different edges xy and
of G one has
The total edge irregularity strength, denoted by tes(G) is defined as the minimum k for which G has an edge irregular total k-labeling. Some other results on the total edge irregularity strength can be referred to [Citation2–5, Citation7, Citation11, Citation12, Citation21, Citation22, Citation26].
Therefore, Ryan et al. [Citation25] were subsequently combined these two labeling problems by allowing for the vertex labels representing as loops. They noticed that: (a) the vertex labels are even non-negative integers, which also representing the fact that each loop added 2 to the vertex degree; and (b) vertex label 0 is permissible as representing a loopless vertex.
Thus, they defined the edge irregular reflexive k-labeling as a combination of an edge labeling and a vertex labeling
in which labeling
is a total k-labeling of the graph G such that
if
and
if
where
The total k-labeling
is called an edge irregular reflexive k-labeling of G if for every two different edges xy,
of G one has
The smallest value of k for which such labeling exists is called the reflexive edge strength of G and is denoted by res(G). For more results of reflexive edge strength of graphs, see [Citation1, Citation8, Citation9, Citation16, Citation18–20, Citation27, Citation28].
This paper focuses on the edge irregular reflexive labeling of two classes of corona product of graphs, that is, corona product of two paths and corona product of a path with isolated vertices. All graphs considered here are simple, finite and undirected. At the end of this paper, we are able to determine the reflexive edge strength of these graphs with condition that they admit such labeling.
2. Significant lemma and conjecture
It is known that Lemma 1 is proved in [Citation25].
Lemma 1.
For every graph G,
The following conjecture is proved by Bača et al. [Citation9].
Conjecture 1.
Any graph G with maximum degree satisfies:
where r = 1 for
and zero otherwise.
3. Corona product of two paths
Suppose Pn is a path of order n and Pm is another path of order m. The corona product of two paths, denoted by is defined as a graph obtained by taking one copy of Pn (with n vertices) and n copies of Pm, and then joining the i-th vertex of Pn to every vertex of the i-th copy of Pm.
Therefore, the vertex set and edge set of are defined as
and
respectively.
The following theorem shows the edge irregular reflexive labeling on and its reflexive edge strength,
Theorem 1.
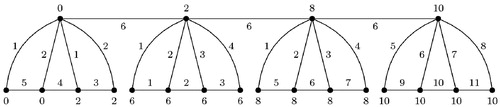
For and
Proof.
Note that the graph has
edges. By using Lemma 1, we obtain the following lower bound:
It clearly shows that k is odd only when n, or n,
otherwise, k is even.
Now, we prove that k is the upper bound for ), where n,
First, we define a total k-labeling
of
by labeling the vertex set and edge set.
All vertices xi and
are labeled with the even integers in the following ways.
otherwise,
if
For
otherwise,
if
The edges
and
are labeled as follows.
if j is odd, whereas
if j is even. For
otherwise,
if
For
otherwise,
if
The edges
are labeled as follows:
Evidently, all vertex labels and edge labels are at most k under the labeling thus, labeling
is a total k-labeling of
Next, we show the edge weights of all edges in
are distinct under the total k-labeling
For j odd,
whereas for j even,
For
For
and
For
For
and
For
We can see that the edge weights of all edges in are distinct integers from the set
in other words, every edge has a distinct weight. Thus, the total k-labeling
is an edge irregular reflexive k-labeling of
and k is the reflexive edge strength of
This completes the proof. □
and show the corresponding edge irregular reflexive k-labelings of and
4. Corona product of a path with isolated vertices
Assume Pn is a path of order n and mK1 is a disjoint union of m copies of isolated vertex. The corona product of a path with m copies of isolated vertex, denoted by is defined as a graph obtained by taking one copy of Pn (with n vertices) and n copies of mK1 by joining the i-th vertex of Pn to every vertex of the i-th copy of mK1. Note that
is also known as a subclass of caterpillars.
Therefore, the vertex set and edge set of are
and
respectively. The number of edges of
denoted by
is
Thus, according to Lemma 1,
(1)
(1)
We notice that k is odd when or
or
or n,
Otherwise, k is even.
The following lemmas show the reflexive edge strength of by distinguishing m into odd and even cases. First, we deal with
when m is odd.
Lemma 2.
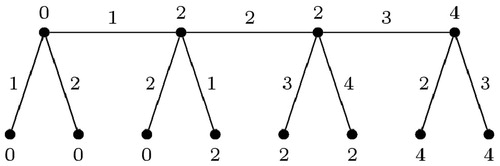
For and m odd,
Proof.
As a fact that has
edges. According to Lemma 1, the lower bound for
is shown as (1). Now, we prove that k is the upper bound for
when m is odd. We first define a total k-labeling
of
All vertices xi and
are labeled with the even integers in the following ways.
For
or
Otherwise,
The edges
and
are labeled as follows.
if
or
otherwise,
Next,
if
or
otherwise,
For
and
if
whereas
if
Next, for
or
For
Otherwise,
Evidently, all vertex labels and edge labels are at most k under the labeling thus, labeling
is a total k-labeling of
Next, we show the edge weights of all edges in
are distinct under the total k-labeling
For i = 1,
if
or
if
if
For i = 2,
when
if
otherwise,
if
when
if
otherwise,
if
For
and
if
or
or
if
or
Take note that
in (iii)(A) and (iii)(B).
For i = 1,
if
if
if
For
when
if
otherwise,
if
when
if
otherwise,
if
when
if
otherwise,
if
if
It clearly shows that the edge weights of all edges in are distinct integers from the set
which means that all edges have distinct weights. Thus, the total k-labeling
is an edge irregular reflexive k-labeling of
and k is the reflexive edge strength of
where m is odd. This completes the proof. □
and show the corresponding edge irregular reflexive 7-labeling of and edge irregular reflexive 8-labeling of
respectively.
In the next lemma, we deal with when m is even.
Lemma 3.
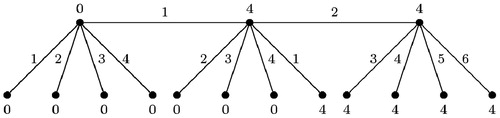
For and m even,
Proof.
Since the number of edges of is
by Lemma 1, we obtain the lower bound as shown in (1). Now, we prove that k is the upper bound for
when m is even. We first define a total k-labeling
of
All vertices xi and
are labeled as follows.
For
Then,
if
or
or
Next,
if
or
Otherwise,
The vertices
are labeled as follows.
For i = 3 and
The edges
and
are labeled as follows. .
For
if
or
otherwise,
Next,
if
or
or
otherwise,
For
if
otherwise,
Next,
if
otherwise,
For
For i = 3,
if
if
otherwise,
if
Clearly, all vertex labels and edge labels are at most k under the labeling thus, labeling
is a total k-labeling of
Using similar approach as in the proof of Lemma 2, we are able to find the edge weights of all edges in
and
Therefore, the results of edge weights are: (a) if i = 1, otherwise,
if
and (b)
if i = 1,
if i = 2,
if i = 3, otherwise,
if
We can see that the edge weights of all edges in are distinct integers from the set
in other words, every edge has a distinct weight. Thus, the total k-labeling
is an edge irregular reflexive k-labeling of
and k is the reflexive edge strength of
where m is even. This completes the proof. □
and show the corresponding edge irregular reflexive 4-labeling of and edge irregular reflexive 6-labeling of
respectively.
Combining Lemmas 2 and 3, we obtain the concluding result for the reflexive edge strength of corona product of path with mK1 as follows.
Theorem 2.
For and all positive integers m,
5. Conclusion
This paper has successfully determined the reflexive edge strength of corona product of graphs, that is, corona product of two paths and corona product of a path with isolated vertices, where these graphs have also proven to admit the edge irregular reflexive labeling. Moreover, these generalized results are not only strengthened the Conjecture 1, but also thoroughly replaced the weak and restricted results of the previous paper [Citation19]. Last but not least, this interesting study found a problem that worths for further investigation, that is:
Problem 1.
Determine the reflexive edge strength of corona product of a path Pn with m copies of complete graphs, i.e., where
and all positive integers m.
Acknowledgement
The authors would like to thank the referees for their valuable comments that improved the paper.
Disclosure statement
No potential competing interest was reported by the authors.
Additional information
Funding
References
- Agustin, I. H., Utoyo, I, Venkatachalam, M. (2020). Edge irregular reflexive labeling of some tree graphs. IOP Conf. Ser. J. Phy. Conf. Ser. 1543: 012008.
- Ahmad, A., Bača, M., Bashir, Y, Siddiqui, M. K. (2012). Total edge irregularity strength of strong product of two paths. Ars. Comb. 106: 449–459.
- Ahmad, A., Bača, M, Siddiqui, M. K. (2014). On edge irregular total labeling of categorical product of two cycles. Theory Comput. Syst. 54(1): 1–12.
- Ahmad, A., Siddiqui, M. K, Afzal, D. (2012). On the total edge irregular strength of zigzag graphs. Australasian J. Combin. 54: 141–149.
- Al-Mushayt, O., Ahmad, A, Siddiqui, M. K. (2012). On the total edge irregularity strength of hexagonal grid graphs. Australasian J. Combin. 53: 263–271.
- Amar, D, Togni, O. (1998). Irregularity strength of trees. Discrete Math. 190(1-3): 15–38.
- Anholcer, M, Palmer, C. (2012). Irregular labelings of circulant graphs. Discrete Math. 312(23): 3461–3466.
- Bača, M., Irfan, M., Ryan, J., Semaničová-Feňovčíková, A, Tanna, D. (2019). Note on edge irregular reflexive labelings of graphs. AKCE Int. J. Graphs Comb. 16(2): 145–157.
- Bača, M., Irfan, M., Ryan, J., Semaničová-Feňovčíková, A, Tanna, D. (2017). On the edge irregular reflexive labelings for the generalized friendship graphs. Mathematics 5(4): 67.
- Bača, M., Jendrol’, S., Miller, M, Ryan, J. (2007). On irregular total labelings. Discrete Math. 307(11-12): 1378–1388.
- Bača, M, Siddiqui, M. K. (2014). Total edge irregularity strength of generalized prism. Appl. Math. Comp. 235: 168–173.
- Brandt, S., Miškuf, J, Rautenbach, D. (2008). On a conjecture about edge irregular total labelings. J. Graph Theory 57(4): 333–343.
- Chartrand, G., Jacobson, M. S., Lehel, J., Oellermann, O. R., Ruiz, S, Saba, F. (1988). Irregular networks. Congr. Numer. 64: 187–192.
- Dinitz, J. H., Garnick, D. K, Gyárfás, A. (1992). On the irregularity strength of the m × n grid. J. Graph Theory 16(4): 355–374.
- Gallian, J. A. (2019). A dynamic survey of graph labeling. Electron. J. Comb. #DS6: 1–553.
- Guirao, J. L. G., Ahmad, S., Siddiqui, M. K, Ibrahim, M. (2018). Edge irregular reflexive labeling for the disjoint union of generalized Petersen graph. Mathematics 6(12): 304.
- Gyárfás, A. (1998). The irregularity strength of Km,m is 4 for odd m. Discrete Math. 71: 273–274.
- Ibrahim, M., Majeed, S, Siddiqui, M. K. (2020). Edge irregular reflexive labeling for star, double star and caterpillar graphs. TWMS J. App. Eng. Math. 10(3): 718–726.
- D. Indriati, Widodo, I. Rosyida, (2020). Edge irregular reflexive labeling on corona of path and other graphs. IOP Conf. Series: Journal of Physics: Conf. Series 1498: 012004.
- Irfan, M., Bača, M, Semaničová-Feňovčíková, A. On reflexive edge strength of generalized prism graphs. Electron. J. Graph Theory Appl. doi:10.3390/math5040067
- Ivančo, J, Jendrol', S. (2006). Total edge irregularity strength of trees. Discuss. Math. Graph Theory 26(3): 449–456.
- Jendrol’, S., Miškuf, J, Soták, R. (2010). Total edge irregularity strength of complete graphs and complete bipartite graphs. Discrete Math. 310(3): 400–407.
- Lehel, J. (1991). Facts and quests on degree irregular assignment. In: Graph Theory, Combinatorics and Applications; New York, USA: Wiley, pp. 765–782.
- Nierhoff, T. (2000). A tight bound on the irregularity strength of graphs. SIAM J. Discrete Math. 13(3): 313–323.
- Ryan, J., Munasinghe, B, Tanna, D. (2017) Reflexive irregular labelings, preprint.
- Siddiqui, M. K. (2012). On the edge irregularity strength of a categorical product of a cycle and a path. AKCE Int. J. Graphs Comb. 9(1): 43–52.
- Tanna, D., Ryan, J, Semaničová-Feňovčíková, A. (2017). Edge irregular reflexive labeling of prisms and wheels. Australasian J. Combin. 69(3): 394–401.
- Zhang, X., Ibrahim, M., Bokhary, S. A. H, Siddiqui, M. K. (2018). Edge irregular reflexive labeling for the disjoint union of gear graphs and prism graphs. Mathematics 6(9): 142.