Graphoidally independent infinite graphs

Abstract

A graphoidal cover of a graph G (not necessarily finite) is a collection ψ of paths in G, called ψ-edges, (not necessarily finite, not necessarily open) satisfying the following axioms: (GC-1) Every vertex of G is an internal vertex of at most one path in ψ, and (GC-2) every edge of G is in exactly one path in ψ. The pair $(G,\psi )$ is called a graphoidally covered graph. In a graphoidally covered graph $(G,\psi ),$ two distinct vertices u and v of G are ψ-adjacent if they are the ends of a finite open path in ψ. A graphoidally covered graph $(G,\psi )$ (or G) in which no two distinct vertices are ψ-adjacent is called ψ-independent and a graph G possessing a graphoidal cover ψ such that G is ψ-independent is called a graphoidally independent graph. This paper is an attempt to characterize graphoidally independent infinite graphs. In this paper we establish complete characterization of graphoidally independent infinite trees, infinite unicyclic graphs and infinite 2-edge connected graphs.

Keywords:

• Graphoidal cover of a graph
• graphoidally covered graphs
• graphoidally independent graphs

2010 MATHEMATICS SUBJECT CLASSIFICATION::

• 05C69

1. Introduction

Throughout this paper, unless specifically mentioned otherwise, notation and terminology in graph theory will be as in West [14], except that a graph could be infinite in which case the reader is referred to Ore [11].

The concept of graphoidal covers for finite graphs was first introduced by Acharya and Sampathkumar [1] in 1987 as a close variant of another emerging discrete structure called semigraphs [13]. Many interesting notions like graphoidal covering number [1], graphoidal labeling [10], graphoidal length [9], etc., based on graphoidal covers of a graph were introduced and are being studied extensively. In particular, the notion of graphoidal covering number of a graph has attracted many researchers and numerous work is present in the literature [4–7, 12]. A detailed treatment of graphoidal covers and graphoidally covered graphs is given in [8]. Later on in 1999, Acharya and Gupta [2] extended the notion of graphoidal covers to infinite graphs.

Given a graph $G=(V,E)$ (not necessarily finite) by a graphoidal cover of G we mean a collection ψ of non-trivial paths in G, which are not necessarily open and not necessarily finite, satisfying the following axioms: (GC-1) Every vertex of G is an internal vertex of at most one path in ψ, and (GC-2) Every edge of G belongs to exactly one path in ψ.

For a given graphoidal cover ψ of a graph G, the paths in ψ are called ψ-edges of G, and the ordered pair $(G,\psi )$ is called a graphoidally covered graph. In this definition, when G is infinite, a ψ-edge could possibly be infinite; in particular, it may be a one-way infinite path having one end-vertex or a two-way infinite path having no end-vertex. Further, a finite open ψ-edge has two distinct end-vertices. A closed ψ-edge is a cycle and has only one coincident end-vertex, which is specified by ψ.

The set of all graphoidal covers of G is denoted by ${\mathcal{G}}_G.$ Clearly, $E=:E(G),$ the edge set of G, is a graphoidal cover of G and is called the trivial graphoidal cover of G; a graphoidal cover that is not trivial will be referred to as being non-trivial.

An interesting theoretical motivation for studying graphoidally covered graphs is that every ear-decomposition of a finite 2-connected (2-edge connected) graph G (cf.: [14], p.146) is a graphoidal cover of G, thus, the notion of a graphoidal cover of any graph can also be looked upon as a generalization of the notion of an ear-decomposition of a finite 2-connected(2-edge connected) graph. Graphoidal cover of a graph can also be viewed as a collection of internally vertex disjoint paths covering the edge set of the graph and two vertices are adjacent when they are the endpoints of a path of the collection; hence, one may view the notion of graphoidal covers of a graph as a graph decomposition into internally vertex-disjoint paths of a graph, which not only holds for finite graphs but also for infinite graphs.

Definition 1.1.

In a graphoidally covered graph $(G,\psi ),$ two distinct vertices u and v of G are said to be ψ-adjacent if they are the ends of an open ψ-edge; a vertex is said to be self-ψ-adjacent if it is both the ‘initial’ and the ‘terminal’ end of a closed ψ-edge (i.e., a cycle in ψ).

A graphoidal cover ψ of a graph G is called a totally disconnecting graphoidal cover of G if no two distinct vertices in G are ψ-adjacent. Clearly, for a graphoidally covered graph $(G,\psi ),$ the graphoidal cover ψ is totally disconnecting graphoidal cover of G if ψ contains no open path of finite length i.e., every ψ-edge is either a one-way infinite path, a two-way infinite path or a cycle. A cycle or an infinite path are trivial examples of graphs G which admit a totally disconnecting graphoidal cover.

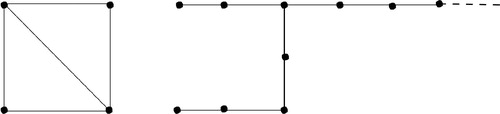
However, it is not necessary that every graph G (finite or infinite) possesses a totally disconnecting graphoidal cover. The graphs shown in Figure 1 cannot have any totally disconnecting graphoidal cover as it can be clearly seen that every graphoidal cover ψ of these graphs contains an open finite ψ-edge.

Figure 1. Examples of graphs which do not possess any totally disconnecting graphoidal cover.

Thus, a given graph G may or may not possess a totally disconnecting graphoidal cover. This gives rise to the following definition:

Definition 1.2.

[2] A graph G is said to be a graphoidally independent graph if G admits a totally disconnecting graphoidal cover ψ, and in this case, the corresponding graphoidally covered graph $(G,\psi )$ (or the graph G) is said to be ψ-independent.

A complete characterization of graphoidally independent finite graphs is given in [3] and the problem remains open for infinite graphs. In the next section we study graphoidally independent infinite graphs for which we shall need the following definitions, terminology and theorems.

Given a graph $G=(V,E)$ and a subset $F\subseteq E(G),$ By G – F, we mean a subgraph obtained by removing the edges of F from G. Given a graph G and a collection ψ of paths of G, by $V(\psi ),$ we mean the set of vertices lying on paths of ψ i.e. $V(\psi )={\cup }_{P\in \psi }V(P),$ and by $E(\psi ),$ we mean the set of edges of paths in ψ i.e. $E(\psi )={\cup }_{P\in \psi }E(P).$

Definition 1.3.

[2] Given any subgraph H of G, $P\in \psi$ is called H-forming if $E(H)\cap E(P)\ne \varphi .$

Definition 1.4.

[2] A free path in a graph is a maximal path each edge of which is a bridge.

Theorem 1.5.

[2] If $G=(V,E)$ is any graph having a graphoidal cover ψ such that G is ψ-independent then every free path in G has infinite length.

Definition 1.6.

[2] Given a graph $G=(V,E),$ by a hypercycle in G we mean a sequence $(x_1,P_1,x_2,\dots ,x_k,P_k,x_1),k\ge 2$ where x_i’s are distinct vertices and each P_i is either a cycle or an infinite path in G such that the following conditions are satisfied:

(HC1) for each $i\in \{1,2,\dots ,k\},x_i\in V(P_i)$ and x_i is the end-vertex of P_i, if P_i is a one-way infinite path.

(HC2) $x_{i+1}\in V(P_i)-\left\{x_i\right\}$ for each $i\in \{1,2,\dots ,k-1\}.$

(HC3) $V(P_i)\cap V(P_{i+1})=\left\{x_{i+1}\right\}$ for every $i\in \{1,2,\dots ,k-1\}.$

(HC4) $|i-j|\ge 2(\mathit{modulo} k)$ implies $V(P_i)\cap V(P_j)=\varphi .$

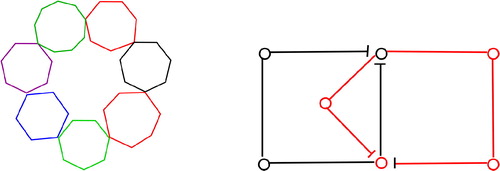
Here, k is called the length of the hypercycle. Further, a hypercycle is called a necklace block if each path P_i in its description is a cycle of G. Note that if k = 2 in this definition, then (HC3) implies that $V(C_1)\cap V(C_2)=\{x_1,x_2\}.$ Examples of necklace blocks are shown by the graphs in Figure 2.

Figure 2. Examples of Necklace Blocks for (i) k > 2, and (ii) $k=2.$

The following lemma proved in [2] provides some insight into the structure of graphoidally independent graphs.

Lemma 1.7.

[2] Let $G=(V,E)$ be any non-trivial connected graphoidally independent graph. Then the following are true:

1. To any nontrivial noncycle block $B^{*}$ in G there corresponds a hypercycle

$Z^{*}=(x_1,P_1,x_2,P_2,\dots ,x_k,P_k,x_1)$ such that

1. For each i, P_i is either a cycle or an infinite path.

2. $B^{*}\cap P_i=$ $\{\begin{array}{cc}{P}_i,& if{P}_{i}isa\mathit{cycle},\\ x_i-x_{i+1} \mathit{segment}of P_i,& if{P}_{i}isan\mathit{infinite}\mathit{path}.\end{array}$

3. x_i is the starting vertex of P_i, if P_i is a one-way infinite path.

4. $B^{*}$ is induced by the set X, where $$X=\underset{i=1}{\overset{k}{\cup }}(B^{*}\cap P_i)$$

5. G contains at most one nontrivial noncycle block.

In this paper we further explore the structure of infinite graphs which are graphoidally independent. Firstly, we provide two necessary conditions for a graph G to be graphoidally independent and then we prove that these two necessary conditions, although are not sufficient for a graph in general to be graphoidally independent, are sufficient for infinite tree and infinite unicyclic graph to be graphoidally independent. In this paper, we also characterize infinite 2-edge connected graphs which are graphoidally independent.

2. Results

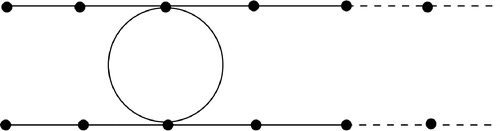
It follows from Theorem 1.5 that if a graph G is graphoidally independent, then every free path in G has infinite length. The graph given in Figure 3 shows that the converse is not true.

Figure 3. Example of an infinite graph having free paths of only infinite length yet not graphoidally independent.

Now we present another necessary condition for a graph to be graphoidally independent.

Proposition 2.1.

An infinite graphoidally independent graph can have at most one pendant vertex.

Proof.

Let G be a graphoidally independent infinite graph. Let if possible, G have more than one pendant vertex. Let u and v be two pendant vertices in G. Since G is graphoidally independent, there exists a graphoidal cover ψ of G such that G is ψ-independent i.e., all ψ-edges are either one-way infinite paths or two-way infinite paths or cycles in G. Let P be a shortest u-v path in G. Then all edges of P are contained in some ψ-edges. If $P\in \psi ,$ then P is a ψ-edge of finite length which is a contradiction. Thus $P\notin \psi .$ Let $\{P_1,P_2,\dots ,P_r\}$ be the set of P-forming ψ-edges. Let $P_i^{\prime }=P\cap P_i.$ Let the ordering of P_i’s be such that the last vertex of $P_i^{\prime }$ is the first vertex of $P_{i+1}^{\prime }.$ Then for each i, $|V(P_i^{\prime })\cap V(P_{i+1}^{\prime })|=1.$ Let $V(P_i)\cap V(P_{i+1})=\left\{u_{i+1}\right\}.$ Then $u_{i+1}$ must be end-vertex of at least one of P_i and $P_{i+1},$ say of $P_{i+1}.$ Also if no P_i has more than one end-vertex, $u_{i+2}\in P_{i+1}$ must be one of the internal vertices. Thus, $u_{i+1}$ is the end-vertex of $P_{i+1}$ and internal vertex of P_i in ψ. Therefore, in particular u_r is an end-vertex of P_r. This implies $P_r=P_r^{\prime },$ a u_r-v path. Thus, P_r is a ψ-edge of finite length. This contradicts the fact that G is ψ-independent. Hence G can have at most one pendant vertex. □

The converse of Proposition 2.1 is not true in general. The infinite graph G given in Figure 4 has no pendant vertex and is not a graphoidally independent graph.

Figure 4. Example of an infinite graph not having any pendant vertex yet not graphoidally independent.

By combining Theorem 1.5 and Proposition 2.1 we have the following theorem:

Theorem 2.2.

If an infinite graph G is graphoidally independent then the following holds:

1. G has at most one pendant vertex.

2. G has no free path of finite length.

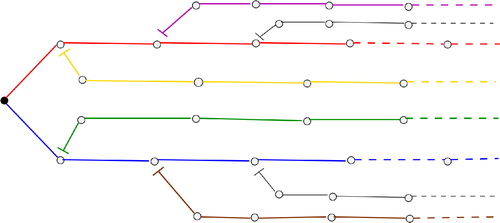
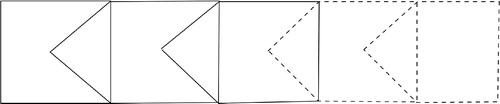
The converse of Theorem 2.2 is not true in general. The graph G shown in Figure 5 has no free path and no pendant vertex, and does not possess any graphoidal cover ψ such that G is ψ-independent.

Figure 5. Example of an infinite graph not having any pendant vertex or free path but still not graphoidally independent.

Nevertheless, in the next theorem we show that the conditions are sufficient in case of an infinite tree.

Theorem 2.3.

An infinite tree T is graphoidally independent if and only if T has at most one pendant vertex.

Proof.

By Proposition 2.1, the condition is necessary.

Conversely, suppose T is an infinite tree having at most one pendant vertex. We will show that there exists a graphoidal cover ψ of T such that T is ψ-independent and hence graphoidally independent.

Case (I): T has no pendant vertex.

Let P₀ be an arbitrarily chosen two-way infinite path in T. Let ${\psi }_0=\left\{P_0\right\}.$ Consider the subgraph $T_1=T-E(P_0).$ Let $V_1=\{v\in V(P_0):d_{T_1}(v)\ge 1\}.$ If $V_1=\varphi ,$ then T = P₀ itself and $\psi ={\psi }_0$ is the desired graphoidal cover of T. If $V_1\ne \varphi ,$ then for each $v\in V_1,$ let ${\psi }_1(v)$ denote a maximal set of edge-disjoint one-way infinite paths in T₁ each having v as an end-vertex. Further, let ${\psi }_1={\cup }_{v\in V_1}{\psi }_1(v).$ Consider the subgraph $T_2=T_1-E({\psi }_1).$ If $E(T_2)=\varphi ,$ then $\psi ={\psi }_0\cup {\psi }_1$ is the desired graphoidal cover. If not, we can iterate the process and obtain a sequence of sets of one-way infinite paths ${\psi }_0,{\psi }_1,{\psi }_2,\dots$ such that

1. ${\psi }_0=\left\{P_0\right\}.$

2. Each one-way infinite path in ψ_i has its end-vertex in $V({\psi }_{i-1}).$

3. ${\cup }_{i}E({\psi }_i)=E(T).$

4. $E({\psi }_i)\cap E({\psi }_j)=\varphi ,$ for $i\ne j.$

Let $\psi ={\psi }_0\cup \left\{\underset{i\ge 1}{\cup }{\psi }_i\right\}.$ Then by construction, ψ is a graphoidal cover of T consisting of one-way infinite paths and therefore no two vertices in T are ψ-adjacent. Thus, T is ψ-independent and hence graphoidally independent.

Case II: T has one pendant vertex.

Suppose T has a pendant vertex, namely w. We choose a one-way infinite path, say P₀, in T having w as an end-vertex. Let ${\psi }_0=\left\{P_0\right\}$ and w is the end-vertex of P₀ w.r.t. ψ₀. Consider the subgraph $T_1=T-E(P_0).$ Now proceeding exactly in the same way as in Case I, we obtain a graphoidal cover ψ of T such that T is ψ-independent and hence graphoidally independent. □

The graph shown in Figure 6 is an example of graphoidally independent infinite tree having no pendant vertex.

Figure 6. Example of a graphoidally independent infinite tree.

Next, we show that in case of an infinite unicyclic graph the two necessary conditions given by Theorem 2.2 together are sufficient as well for it to be graphoidally independent.

Theorem 2.4.

An infinite unicyclic graph G is graphoidally independent if and only if

1. G has at most one pendant vertex.

2. G has no free path of finite length.

Proof.

In view of Theorems 2.2, conditions are necessary.

Conversely, let G be an infinite unicyclic graph satisfying conditions (a) and (b). We shall show that there exists a graphoidal cover ψ of G such that G is ψ-independent and hence graphoidally independent. Let C be the unique cycle of G.

Case I: G has no pendant vertex.

Choose a vertex $w\in V(C).$ Let ${\psi }_0=\left\{C\right\}$ with w as the coincident end-vertex of C with respect to ψ₀. Consider the subgraph $G_1=G-E(C).$ Since G is connected, therefore there exists at least one vertex in V(C) whose degree in G₁ is at least one. Let $$V_1=\{v\in V(C):d_{G_1}(v)\ge 1\}.$$

Since G is unicyclic and has no pendant vertex, therefore for every $v\in V_1,$ every maximal path P having v as an end-vertex is an infinite free path and $V(P)\cap V(C)=\left\{v\right\}.$ For each $v\in V_1,$ let ${\psi }_1(v)$ denote a maximal set of edge-disjoint one-way infinite free paths in G₁, each having v as an end-vertex and let ${\psi }_1={\cup }_{v\in V_1}{\psi }_1(v).$ Now consider the subgraph $G_2=G_1-E({\psi }_1).$ Let $V_2=\{v\in V({\psi }_1):d_{G_2}(v)\ge 1\}.$ If $V_2=\varphi ,$ then $\psi ={\psi }_0\cup {\psi }_1$ is the desired graphoidal cover. If not, we can iterate the process and obtain a sequence of sets of one-way infinite paths ${\psi }_1,{\psi }_2,\dots$ such that

1. For each $i\ge 1,$ each one-way infinite path in ψ_i has its end-vertex in $V({\psi }_{i-1}).$

2. ${\cup }_{i}E({\psi }_i)=E(G)$

3. $E({\psi }_i)\cap E({\psi }_j)=\varphi ,$ for $i\ne j.$

Let $\psi ={\psi }_0\cup \left\{\underset{i\ge 1}{\cup }{\psi }_i\right\}.$ By construction, ψ is a graphoidal cover of G such that each ψ-edge is either a cycle or a one-way infinite path and therefore no two vertices in G are ψ-adjacent. Hence G is graphoidally independent.

Case II: G has a pendant vertex, say w₀.

Let P₀ be a one-way infinite free path emanating from w₀ such that $V(P_0)\cap V(C)\ne \varphi .$ Let $V(P_0)\cap V(C)=\left\{u\right\}$ and let ${\psi }_0=\{P_0,C\}$ where w₀ is the end-vertex of P₀ and u is the end-vertex of C. Let $S_0=P_0\cup C.$ Consider the subgraph $G_1=G-E(S_0).$ Let $V_1=\{v\in V(S_0):d_{G_1}(v)\ge 1\}.$ If $V_1=\varphi ,$ then $\psi ={\psi }_0$ is the desired graphoidal cover of G. If $V_1\ne \varphi ,$ then for each $v\in V_1,$ every maximal path P having v as an end-vertex is an infinite free-path and $V(P)\cap V(S_0)=\left\{v\right\}.$ Let ${\psi }_1(v)$ denote a maximal set of edge-disjoint one-way infinite free paths in G₁, each having v as an end-vertex and let ${\psi }_1={\cup }_{v\in V_1}{\psi }_1(v).$ Now consider the subgraph $G_2=G_1-E({\psi }_1).$ Let $V_2=\{v\in V({\psi }_1):d_{G_2}(v)\ge 1\}.$ If $V_2=\varphi ,$ then $\psi ={\psi }_0\cup {\psi }_1$ is the desired graphoidal cover. If not, we can iterate the process and obtain a sequence of sets of one-way infinite paths ${\psi }_1,{\psi }_2,\dots$ such that:

1. For each $i\ge 1,$ each one-way infinite path in ψ_i has its end-vertex in $V({\psi }_{i-1}).$

2. ${\cup }_{i}E({\psi }_i)=E(G)$

3. $E({\psi }_i)\cap E({\psi }_j)=\varphi ,$ for $i\ne j.$

Let $\psi ={\psi }_0\cup \left\{\underset{i\ge 1}{\cup }{\psi }_i\right\}.$ By construction, ψ is a graphoidal cover of G such that each ψ-edge is either a cycle or a one-way infinite path and therefore no two vertices in G are ψ-adjacent. Hence G is graphoidally independent. □

Remark 2.5.

The two necessary conditions stated in Theorem 2.2 for an infinite graph to be graphoidally independent are equivalent in case of an infinite tree. Firstly if every free path of an infinite tree is of infinite length then it cannot have more than one pendant vertex, otherwise the path between two pendant vertices will form a free path of finite length. Conversely if an infinite tree has at most one pendant vertex then the tree can not have a free path of finite length.

So far the infinite graphs considered in the above discussion have edge-connectivity one. The problem of characterizing graphoidally independent infinite graphs in general is a complex problem. So in the next section we target infinite 2-edge connected graphs, which are graphoidally independent.

3. Infinite 2-Edge connected graphoidally independent graphs

The following theorem provides a complete characterization of infinite 2-edge connected graphoidally independent graphs.

Theorem 3.1.

A 2-edge connected infinite graph G is graphoidally independent if and only if G satisfies one of the following:

1. G is a cycle-cactus.

2. G has exactly one nontrivial noncycle block which is a necklace block and every other block is a cycle in G.

Proof.

Necessity:

Since G is 2-edge connected, every block of G is non-trivial. Further since the 2-edge connected infinite graph G is graphoidally independent, G has a graphoidal cover ψ such that G is ψ-independent and each ψ-edge is a cycle.

Case 1: Each of the blocks is a cycle.

In this case G is a cycle-cactus and (a) is satisfied.

Case 2: G has a non-cycle block.

By Lemma 1.7, such a block is unique. Let $B^{*}$ be the unique non-cycle block of G. Since all ψ-edges are cycles, again by Lemma 1.7, $B^{*}$ must be the necklace block. Also since every other block is non-trivial, therefore must be a cycle. thus (b) is satisfied.

Sufficiency:

To prove the sufficiency part, suppose first that G satisfies condition (a) of the theorem. We will prove that there exists a graphoidal cover ψ of G such that G is ψ-independent. The following algorithm constructs such a graphoidal cover for G.

Step 1. Let B₀ be any cycle block of G and let u be any arbitrary vertex of B₀. Let $\{B_1,B_2,\dots ,B_k,\dots \}$ be the set of all cycle blocks of G having non-empty intersection with B₀. Condition (a) implies that for each i, $|V(B_i)\cap V(B_0)|=1$ and for all distinct $i,j\in \{1,2,\dots ,k,\dots \},|V(B_i)\cap V(B_j)|=\varnothing .$ Let $V(B_i)\cap V(B_0)=\left\{v_i\right\},$ for each i. Let ${\psi }_0=\{B_0,B_1,B_2,\dots ,B_k,\dots \}$ where u is the coincident end-vertex of B₀ and for each $i\in \{1,2,3\dots ,k\dots \},$ v_i is the coincident end-vertex of B_i w.r.t ψ₀. If $V(G)=V(B_0)\cup \{\underset{i}{\cup }V(B_i)\},$ then $\psi ={\psi }_0$ is a graphoidal cover of G and clearly G is ψ-independent as all ψ-edges are cycles.

Step 2. Let $V(G)\ne V(B_0)\cup \{\underset{i}{\cup }V(B_i)\}.$ Then, for every $i\in \{1,2,\dots ,k,\dots \},$ let $\{B_{i1},B_{i2},B_{i3},\dots ,B_{il},\dots \}$ be the set of all cycle blocks in G having non-empty intersection with B_i. Again due to condition (a) of the theorem, for each j ∈ {1, 2, 3,…, l,…}, | V (B_ij) ∩ V (B_i) | = 1 and let $V(B_{ij})\cap V(B_i)=\left\{v_{ij}\right\}.$ Let ${\psi }_1(i)=\{B_{i1},B_{i2},\dots ,B_{il},\dots \}$ where v_ij is the coincident end-vertex of B_ij for each $j\in \{1,2,\dots ,l,\dots \}$ with respect to ${\psi }_1(i)$ and let ${\psi }_1=\underset{i}{\cup }{\psi }_1(i).$ If $$V(G)=V(B_0)\cup \left\{\underset{i}{\cup }\left\{V(B_i)\cup \{\underset{j}{\cup }V(B_{ij})\}\right\}\right\}$$ then $\psi ={\psi }_0\cup {\psi }_1$ is the desired graphoidal cover of G. Otherwise, we repeat the procedure yielding a sequence of set of cycles ${\psi }_1,{\psi }_2,{\psi }_3,\dots .$ such that;

1. for $i\ge 1,$ all cycles in ψ_i have their end-vertices in cycles of ${\psi }_{i-1},$ and

2. ${\psi }_0\cup \left\{\underset{i\ge 1}{\cup }{\psi }_i\right\}$ covers all edges of G.

Thus, $\psi ={\psi }_0\cup \left\{\underset{i\ge 1}{\cup }{\psi }_i\right\}$ is a graphoidal cover of G each of whose ψ-edge is a cycle. Hence, G is ψ-independent.

Now, let G satisfy condition (b) of the theorem, viz., G has a necklace block, say B₀, and $$B_0=\{x_1,C_1,x_2,C_2,\dots ,x_k,C_k,x_1\},k\ge 2$$ where $C_i^{\prime }s$ are all cycles. Let ${\psi }_0=\{C_1,C_2,\dots ,C_k\}$ where x_i is the end-vertex of C_i for each $i\in \{1,2,\dots ,k\}.$ Let ${\mathcal{B}}_1$ be the set of all cycles having a vertex common with B₀. Then for each cycle $C\in {\mathcal{B}}_1,V(C)\cap V(B_0)$ is unique and let $V(C)\cap V(B_0)=\left\{v_{1c}\right\}.$ Further let ${\psi }_1=\underset{C\in {\mathcal{B}}_1}{\cup }C$ where $v_{1c}$ is the end-vertex of C for each $C\in {\mathcal{B}}_1.$ If $V(G)=V(B_0)\cup V({\mathcal{B}}_1)$ then $\psi ={\psi }_0\cup {\psi }_1$ is the desired graphoidal cover of G. If not, then we take the set of all cycles in G having a vertex common with cycles in ψ₁ and repeat the procedure. Continuing this way we obtain a sequence of set of cycles ${\psi }_0,{\psi }_1,{\psi }_2,\dots .$ such that:

1. for $i\ge 1,$ all cycles in ψ_i have their end-vertices in cycles of ${\psi }_{i-1},$ and

2. ${\psi }_0\cup \left\{\underset{i\ge 1}{\cup }{\psi }_i\right\}$ covers all edges of G.

Thus, $\psi ={\psi }_0\cup \left\{\underset{i\ge 1}{\cup }{\psi }_i\right\}$ forms a graphoidal cover of G each of whose ψ-edge is a cycle. Hence, G is ψ-independent. □

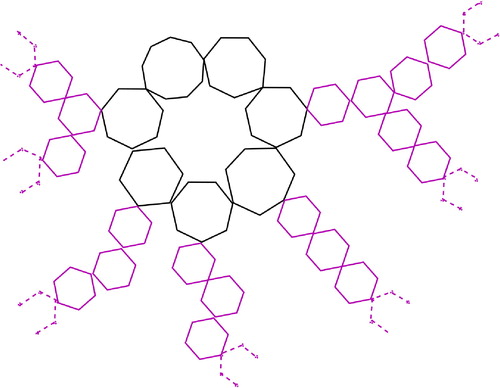
Figure 7 shows an examples of a 2-edge connected graphoidally independent graph.

Figure 7. Example of a 2-edge Connected Graphoidally Independent Graph.

4. Concluding remarks

In this paper we focused on the problem of characterizing infinite graphoidally independent graphs, We observed that a graphoidally independent graph G satisfies the following: (i) G has at most one pendant vertex, and (ii) all free paths in G are of infinite length. We also observed that in case of an infinite tree and infinite unicyclic graph, the two conditions are sufficient as well. The question arises:“Are the two necessary conditions sufficient for an infinite cactus to be graphoidally independent?” No, it is not true in case of cactus having more than one cycle. Consider the graph shown in Figure 8. So we have the following problems:

Figure 8. Example of an infinite cactus which is not graphoidally independent.

Problem 1. Characterize graphoidally independent infinite cacti.

Problem 2. Characterize graphoidally independent infinite graphs.

Acknowledgement

The work presented in this paper was initiated by Late Dr. B.D. Acharya and we dedicate this work to him.