Independent resolving sets in graphs

Abstract

Let $G=(V,E)$ be a connected graph. Let $W=\{w_1,w_2,\dots ,w_k\}$ be a subset of V with an order imposed on W. The k-vector $r(v|W)=(d(v,w_1),d(v,w_2),\dots ,d(v,w_k))$ is called the resolving vector of v with respect to W. The set W is called a resolving set if $r(v|W)\ne r(u|W)$ for any two distinct vertices $u,v\in V.$ In this paper we investigate the existence of independent resolving sets in Cartesian product and corona of graphs.

Keywords:

• Resolving set
• independent resolving set
• metric dimension
• corona
• Cartesian product

2010 Mathematical Subject Classification Number:

• 05C12

1. Introduction

By a graph $G=(V,E)$ we mean a finite, undirected connected graph with neither loops nor multiple edges. The order $\left|V\right|$ and the size $\left|E\right|$ of G are denoted by n and m respectively. For graph theoretic terminology we refer to Chartrand and Lesniak [3].

The distance d(u, v) between two vertices in G is the length of a shortest u-v path in G. Let $W=\{w_1,w_2,\dots ,w_k\}$ be an ordered subset of V and let $v\in V.$ Then the k-vector $(d(v,w_1),d(v,w_2),\dots ,d(v,w_k))$ is called the resolving vector of v with respect to W and is denoted by $r(v|W).$ The set W is called a resolving set of G if $r(u|W)\ne r(v|W)$ for any two distinct vertices u and v. The minimum cardinality of a resolving set of G is called the metric dimension of G and is denoted by $\mathit{dim}(G).$ The concept of resolving set was independently discovered by Harary and Melter [5] and Slater [8]. Slater used the terms locating set and location number. Harary and Malter used the term resolving set and metric dimension.

Many resolving parameters have been formulated and investigated by combining resolving property with another graph theoretic property such as connected, independent or acyclic. For a survey of conditional resolving sets we refer to [7].

The concept of independent resolving set was introduced and studied in [4]. A subset W of V which is both an independent set and a resolving set is called an independent resolving set. The minimum cardinality of an independent resolving set of G is called the independent metric dimension of G and is denoted by $\mathit{idim}(G).$ This parameter is denoted by ir(G) in [4]. Since ir(G) is used for irredundance number in the study of domination, we prefer to use idim(G) instead of $ir(G).$ Not all graphs have an independent resolving set and hence idim(G) is not defined for all graphs. The existence of independent resolving sets in some classes of graphs has been proved in [4]. A characterization of all graphs of order n for which $\mathit{idim}(G)\in \{1,n-2,n-1\}$ is given in [4].

Definition 1.1.

[6] Let $G_1=(V_1,E_1)$ and $G_2=(V_2,E_2)$ be two graphs. The Cartesian product $G_1\square G_2$ is the graph with vertex set $V_1\times V_2$ and (v₁, v₂) is adjacent to (w₁, w₂) if either v₁ = w₁ and $v_2{w}_2\in E_2$ or v₂ = w₂ and $v_1{w}_1\in E_1.$

Theorem 1.2.

[2] Let G be a connected graph of order n. Then dim(G) = 1 if and only if G is the path $P_n.$

Theorem 1.3.

[6] Let G₁ and G₂ be two connected graphs. Then the distance between two vertices (v₁, v₂) and (w₁, w₂) in $G_1\square G_2$ is given by $d((v_1,v_2),(w_1,w_2))=d_{G_1}(v_1,w_1)+d_{G_2}(v_2,w_2).$

Definition 1.4.

Let G be a connected graph of order n with $V(G)=\{v_1,v_2,\dots ,v_n\}.$ Let $H_1,H_2,\dots ,H_n$ be connected graphs. The generalized corona $H=G°(H_1,H_2,\dots ,H_n)$ is the graph obtained from G by joining v_i to all the vertices of $H_i.$

Theorem 1.5.

[1] Let G₁ and G₂ be two connected graphs and let $S\subseteq V(G_1\square G_2).$ Then every pair of vertices in a fixed row of $G_1\square G_2$ is resolved by S if and only if the projection of S onto G₁ resolves $G_1.$ Similarly every pair of vertices in a fixed column of $G_1\square G_2$ is resolved by S if and only if the projection of S onto G₂ resolves $G_2.$

In this article, we investigate the existence of independent resolving sets in generalized corona and Cartesian product of graphs.

2. Independent resolving sets in generalized corona

Metric dimension of corona product of graphs has been studied in Yeno et al. [9]. In this section we investigate the existence of independent resolving sets in generalized corona of graphs.

Let $H=G°(H_1,H_2,\dots ,H_n)$ be the generalized corona of G with $H_1,H_2,\dots ,H_n.$ The induced subgraph $H[V(H_i)\cup \{V_i\}]$ is denoted by $G_i.$

Definition 2.1.

Let $W_i=\{w_{i_1},w_{i_2},\dots ,w_{i_k}\}\subseteq V(H_i)$ and let $v\in V(H_i)-W_i.$ Then $r^{*}(v|W_i)=(d_{G_i}(v,w_{i_1}),d_{G_i}(v,w_{i_2}),\dots ,d_{G_i}(v,w_{i_k}))$ is called the resolving vector of v with respect to W_i in $G_i.$

Theorem 2.2.

The generalized corona $H=G°(H_1,H_2,\dots ,H_n)$ has an independent resolving set if and only if for each i with $1\le i\le n,$ one of the following holds.

1. $|V(H_i)|\le 3$ and if $|V(H_i)|=3,$ then $H_i\ne K_3.$

2. $|V(H_i)|\ge 4$ and there exists an independent set W_i in H_i such that $r^{*}(u|W_i)\ne r^{*}(v|W_i)$ for any two distinct vertices u, v in $V(H_i)-W_i.$

Proof.

Suppose H has an independent resolving set W. If $|V(H_i)|\ge 3$ and $W\cap V(H_i)=\varnothing ,$ then $r(u|W)=r(v|W)$ for any two distinct vertices in H_i which is a contradiction. Hence $W\cap V(H_i)\ne \varnothing .$ Now, suppose $H_i=K_3.$ Since W is independent, $|W\cap V(H_i)|=1$ and $r(u|W)=r(v|W)$ for the remaining two vertices of $H_i.$ Hence $H_i\ne K_3$ and (i) holds. Now, let $|V(H_i)|\ge 4$ and let $W_i=W\cap V(H_i).$ Suppose there exist two distinct vertices u, v in H_i such that $r^{*}(u|W_i)=r^{*}(v|W_i).$ Since $d(u,w)=d(v,w)$ for all $w\in W-W_i,$ it follows that $r(u|W)=r(v|W),$ which is a contradiction. Hence (ii) holds. Conversely suppose (i) or (ii) holds for each i. If $|V(H_i)|\le 3,$ let $W_i=\left\{w_{i_1}\right\}$ where $w_{i_1}\in V(H_i)$ and $\mathrm{deg}(w_{i_1})\ne 2.$ If $|V(H_i)|\ge 4,$ let W_i be as in (ii).

We claim that $W={\cup }_{i=1}^n{W}_i$ is an independent resolving set of H. Let u and v be two distinct vertices in $V(H)-W.$ If $u,v\in V(G),u=v_i$ and $v=v_j,$ then $d(u,w)<d(v,w)$ for all $w\in W_i.$ If $u\in V(G),u=v_i$ and $v\in H_i,$ then $d(u,w)<d(v,w)$ for all $w\in W_j$ for any $j\ne i.$ If $u\in V(G),u=v_i$ and $v\in H_j$ where $j\ne i,$ then $d(u,w)<d(v,w)$ for all $w\in W_i.$ If $u\in V(H_i),v\in V(H_j)$ and $j\ne i,$ then $d(u,w)<d(v,w)$ for all $w\in W_i.$ If $u,v\in V(H_i)$ and $|V(H_i)|=3,$ then $d(u,w_{i_1})\ne d(v,w_{i_1}).$ If $u,v\in V(H_i)$ and $|V(H_i)|\ge 4,$ then $r^{*}(u|W_i)\ne r^{*}(v|W_i)$ and $d(u,w)=d(v,w)$ for all $w\in W-W_i.$ Thus in all cases $r(u|W)\ne r(v|W).$ Hence W is an independent resolving set of H. □

Corollary 2.3.

Let G be a graph of order n and let $H=G°(H_1,H_2,\dots ,H_n).$ If each H_i is a path of order 2 or 3, then $\mathit{idim}(H)=n.$

Proof.

If each H_i is a path of order 2 or 3, then $W_i=\left\{v_{i_1}\right\},$ and W is an independent resolving set of H and $\left|W\right|=n.$ Hence $\mathit{idim}(H)\le n.$ Also if W is any independent resolving set of H, then $W\cap V(H_i)\ne \varnothing$ for all i. Hence $\left|W\right|\ge n,$ so that $\mathit{idim}(H)\ge n.$ Thus $\mathit{idim}(H)=n.$ □

Corollary 2.4.

Let G be a graph of order n and let $H=G°(H_1,H_2,\dots ,H_n).$ If $H_i=K_{r_i}$ for some i and $r_i\ge 3,$ then H does not have an independent resolving.

Proof.

Any resolving set W of H contains at least two vertices of H_i and hence W is not independent. □

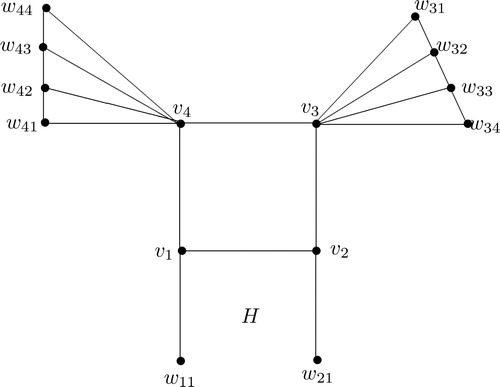
Example 2.5.

Let G = C₄ and let $H=G°(K_1,K_1,P_4,P_4).$ The graph H is given in Figure 1.

Figure 1. Graph H with $\mathit{idim}(H)=|V(G)|=4..$

Clearly $W=\{w_{31},w_{33},w_{41},w_{43}\}$ is a minimum independent resolving of H and hence $\mathit{idim}(H)=|V(G)|=4.$ This shows that the converse of Corollary 2.3 is not true.

Example 2.6.

Let $H=C_4°(H_1,H_2,H_3,H_4).$ If $H_1=H_2=H_3=H_4=K_1,$ then $\mathit{idim}(H)=2<|V(C_4)|.$ If $H_1=H_2=K_1,H_3=K_2$ and $H_4=P_4,$ then $\mathit{idim}(H)=3<|V(C_4)|.$ If $H_1=H_2=H_3=H_4=P_4,$ then $\mathit{idim}(H)=8>|V(C_4)|.$ Thus if G is a graph of order n and $H=G°(H_1,H_2,\dots ,H_n),$ then we can have idim(H) < n or idim(H) = n or $\mathit{idim}(H)>n.$ Hence the following problem arises naturally.

Problem 2.7.

Let G be a graph of order n and let $H=G°(H_1,H_2,\dots ,H_n).$ Characterize graphs H for which $\mathit{idim}(H)=|V(G)|=n.$

3. Independent resolving sets in Cartesian product

Cáceres et al. [1] have presented several results on the metric dimension of Cartesian product of graphs.

In this section, we investigate the existence of independent resolving sets in Cartesian product of two graphs. Let G₁ and G₂ be connected graphs of order r and s respectively. Let $V(G_1)=\{v_1,v_2,\dots ,v_r\}$ and $V(G_2)=\{w_1,w_2,\dots ,w_s\}.$ We denote the vertex (v_i, w_j) in $G_1\square G_2$ by $x_{ij}.$ It follows from Theorem 1.3 that $d(x_{ij},x_{kl})=d_{G_1}(v_i,v_k)+d_{G_2}(w_j,w_l).$

Consider the grid $G=P_r\square P_s.$ If $r=s=2,$ then $G=C_4,$ which does not have an independent resolving set. The following theorem shows that all the other grids have an independent resolving set.

Theorem 3.1.

Let $G=P_r\square P_s$ where $r\ge 2$ and $s\ge 3.$ Then $\mathit{idim}(G)=2.$

Proof.

Let $W=\{x_{11},x_{1s}\}.$ Since $s\ge 3,$ it follows that W is an independent set in G. $$\text{Now},\mathrm{ }r(x_{ij}|W)=(d(x_{ij},x_{11}),d(x_{ij},x_{1s}))$$ $$=(i+j-2,i-1+s-j)$$ Hence $r(x_{ij}|W)=r(x_{st}|W)$ if and only if $i+j=s+t$ and $i-j=s-t.$ Thus $r(x_{ij}|W)=r(x_{st}|W)$ if and only if x_ij = x_st and hence W is a resolving set of G. It follows from Theorem 1.2 that $\mathit{idim}(G)=2.$ □

The following theorem shows that if the independent metric dimension of Cartesian product of two graphs is 2, then one of the two graphs is a path.

Theorem 3.2.

Let G₁ and G₂ be connected graphs and let $G=G_1\square G_2.$ If $\mathit{idim}(G)=2,$ then G₁ or G₂ is a path.

Proof.

Let $W=\{x_{ij},x_{st}\}$ be an independent resolving set of G. We claim that i = s or $j=t.$ Suppose $i\ne s$ and $j\ne t.$ Let v_r be the neighbor of v_s in a shortest v_i-v_s path in G₁ and let w_k be the neighbor of w_t in a shortest w_j-w_t path in $G_2.$ Now, $d(x_{ij},x_{sk})=d_{G_1}(v_i,v_s)+d_{G_2}(w_j,w_k)=d_{G_1}(v_i,v_s)+d_{G_2}(w_j,w_t)-1.$ Also $d(x_{st},x_{sk})=d_{G_2}(w_t,w_k)=1.$ Hence $r(x_{sk}|W)=(d_{G_1}(v_i,v_s)+d_{G_2}(w_j,w_t)-1,1).$ $$\begin{array}{c}\text{Also}\mathrm{ }d(x_{ij},x_{rt})=d_{G_1}(v_i,v_r)+d_{G_2}(w_j,w_t)\\ =d_{G_1}(v_i,v_s)-1+d_{G_2}(w_j,w_t)\\ \text{and}\mathrm{ }d(x_{st},x_{rt})=d_{G_1}(v_s,v_r)=1.\end{array}$$ Hence $r(x_{rt}|W)=r(x_{sk}|W),$ which is a contradiction.

Thus i = s or $j=t.$ Hence $\left|W_1\right|=1$ or $\left|W_2\right|=1$ where W₁ and W₂ are the projections of W on G₁ and G₂ respectively. Hence it follows from Theorem 1.2 and Theorem 1.5 that G₁ or G₂ is a path. □

Theorem 3.3.

Let $G=P_m\square C_n$ where $m\ge 2$ and $n\ge 5.$

Then $\mathit{idim}(G)=\{\begin{array}{cc}2\hfill & \hspace{1em}\mathit{\text{if}}\mathrm{ }n\mathrm{ }\mathit{\text{is}}\mathrm{ }\mathit{\text{odd}}\hfill \\ 3\hfill & \hspace{1em}\mathit{\text{if}}\mathrm{ }n\mathrm{ }\mathit{\text{is}}\mathrm{ }\mathit{\text{even}}.\hfill \end{array}$

Proof.

Let $P_m=(v_1,v_2,\dots ,v_m)$ and $C_n=(w_1,w_2,\dots ,w_n,w_1).$ Let $G=P_m\square C_n$ and let $x_{ij}=(v_i,w_j).$ We consider two cases.

Case 1. n is odd.

Let $n=2k+1$ and let $W=\{x_{1k},x_{1n}\}.$ Since $n\ge 5,$ it follows that W is an independent set in G. We claim that W is a resolving set of G. Let $x_{ij}\in V(G).$ Then (1) $$\begin{array}{c}d(x_{ij},x_{1k})=d_{P_m}(v_i,v_1)+d_{C_n}(w_j,w_k)\\ =i-1+|j-k|\\ \text{Also}\mathrm{ }d(x_{ij},x_{1n})=d_{P_m}(v_i,v_1)+d_{C_n}(w_j,w_n)\\ =\{\begin{array}{cc}i-1+j\hfill & \hspace{1em}\text{if}\mathrm{ }j\le k\hfill \\ (i-1)+(n-j)\hfill & \hspace{1em}\text{if}\mathrm{ }j>k\hfill \end{array}\\ \text{Hence}\mathrm{ }r(x_{ij}|W)=\{\begin{array}{cc}(i-1+|j-k|,i-1+j)\hfill & \hspace{1em}\text{if}\mathrm{ }j\le k\hfill \\ (i-1)+|j-k|,i-1+n-j)\hfill & \hspace{1em}\text{if} j>k\hfill \end{array}\\ =\{\begin{array}{ll}(i-1+k-j,i-1+j)& \text{if}\mathrm{ }j\le k\\ (i-1+j-k),i-1+n-j)& \text{if} j>k\end{array}\hspace{1em}\end{array}$$(1) Now suppose $r(x_{ij}|W)=r(x_{st}|W).$ If $j\le k$ and $t>k,$ then $i-1+k-j=s-1+t-k$ and $i-1+j=s-1+n-t.$ From these two equations we get $2i=2s+1,$ which is a contradiction. A similar contradiction arises if $t\le k$ and $j>k.$ Hence it follows that either $j\le k$ and $t\le k$ or j > k and $t>k.$ In both these cases, (1)(1) $$\begin{array}{c}d(x_{ij},x_{1k})=d_{P_m}(v_i,v_1)+d_{C_n}(w_j,w_k)\\ =i-1+|j-k|\\ \text{Also}\mathrm{ }d(x_{ij},x_{1n})=d_{P_m}(v_i,v_1)+d_{C_n}(w_j,w_n)\\ =\{\begin{array}{cc}i-1+j\hfill & \hspace{1em}\text{if}\mathrm{ }j\le k\hfill \\ (i-1)+(n-j)\hfill & \hspace{1em}\text{if}\mathrm{ }j>k\hfill \end{array}\\ \text{Hence}\mathrm{ }r(x_{ij}|W)=\{\begin{array}{cc}(i-1+|j-k|,i-1+j)\hfill & \hspace{1em}\text{if}\mathrm{ }j\le k\hfill \\ (i-1)+|j-k|,i-1+n-j)\hfill & \hspace{1em}\text{if} j>k\hfill \end{array}\\ =\{\begin{array}{ll}(i-1+k-j,i-1+j)& \text{if}\mathrm{ }j\le k\\ (i-1+j-k),i-1+n-j)& \text{if} j>k\end{array}\hspace{1em}\end{array}$$(1) gives $i-j=s-t$ and $i+j=s+t.$ Hence i = s and $j=t,$ so that $x_{ij}=x_{st}.$ Thus W is a resolving set of G. Hence $\mathit{idim}(G)=2.$

Case 2. n is even.

Let $n=2k$ and let $W=\{x_{11},x_{mk},x_{mn}\}.$ Clearly W is an independent set in G. Now let $x_{ij},x_{st}\in V(G)$ and $x_{ij}\ne x_{st}.$ (2) $$\begin{array}{c}\text{Then}\mathrm{ }r(x_{ij}|W)=\{\begin{array}{ll}(i+j-2,m-i+k-j,m-i+j)& \text{if}\mathrm{ }j\le k\\ (i+n-j,m-i+j-k,m-i+n-j)& \text{if}\mathrm{ }j>k\end{array}\hspace{1em}\\ \hspace{1em}\end{array}$$(2) (3) $$\text{and}\mathrm{ }r(x_{st}|W)=\{\begin{array}{ll}(s+t-2,m-s+k-t,m-s+t)& \text{if}\mathrm{ }t\le k\\ (s+n-t,m-s+t-k,m-s+n-t)& \text{if}\mathrm{ }t>k\end{array}\hspace{1em}$$(3) Suppose $r(x_{ij}|W)=r(x_{st}|W).$ If $j\le k$ and $t\le k$ or j > k and $t>k,$ then it follows from (2)(2) $$\begin{array}{c}\text{Then}\mathrm{ }r(x_{ij}|W)=\{\begin{array}{ll}(i+j-2,m-i+k-j,m-i+j)& \text{if}\mathrm{ }j\le k\\ (i+n-j,m-i+j-k,m-i+n-j)& \text{if}\mathrm{ }j>k\end{array}\hspace{1em}\\ \hspace{1em}\end{array}$$(2) and (3)(3) $$\text{and}\mathrm{ }r(x_{st}|W)=\{\begin{array}{ll}(s+t-2,m-s+k-t,m-s+t)& \text{if}\mathrm{ }t\le k\\ (s+n-t,m-s+t-k,m-s+n-t)& \text{if}\mathrm{ }t>k\end{array}\hspace{1em}$$(3) that $i+j=s+t$ and $i-j=s-t.$ Hence i = s and $j=t,$ so that $x_{ij}=x_{st},$ which is a contradiction.

If $j\le k$ and $t>k,$ then $j<t.$ Also from (2)(2) $$\begin{array}{c}\text{Then}\mathrm{ }r(x_{ij}|W)=\{\begin{array}{ll}(i+j-2,m-i+k-j,m-i+j)& \text{if}\mathrm{ }j\le k\\ (i+n-j,m-i+j-k,m-i+n-j)& \text{if}\mathrm{ }j>k\end{array}\hspace{1em}\\ \hspace{1em}\end{array}$$(2) and (3)(3) $$\text{and}\mathrm{ }r(x_{st}|W)=\{\begin{array}{ll}(s+t-2,m-s+k-t,m-s+t)& \text{if}\mathrm{ }t\le k\\ (s+n-t,m-s+t-k,m-s+n-t)& \text{if}\mathrm{ }t>k\end{array}\hspace{1em}$$(3) we have $i+j-2=s+n-t$ and $m-i+k-j=m-s+t-k.$ Since $n=2k,$ adding these two equations, we get $m-2=m,$ which is a contradiction. A similar contradiction arises if j > k and $t\le k.$ Thus $r(x_{ij}|W)\ne r(x_{st}|W)$ and hence W is a resolving set of G. Thus $\mathit{idim}(G)\le 3.$

Now let $S=\{x_{ac},x_{bd}\}$ be an independent set in G. We claim that S is not a resolving set of G. We consider three cases.

Case i. $a\ne b$ and $c\le d.$

Let v_s be the vertex adjacent to b in a shortest a-b path in P_m and let w_t be the vertex adjacent to d in a shortest c-d path in $C_m.$ $$\begin{array}{c}\text{Then}\mathrm{ }r(x_{bt}|S)=r(x_{sd}|S)\\ =(d_{P_m}(v_a,v_b)+d_{C_n}(c,d)-1,1).\end{array}$$ Hence W_s is not a resolving set of G.

Case ii. a = b and $c\ne d.$

If $1<a<m,$ then $r(x_{(a+1)d}|S)=r(x_{(a-1)d}|S)=(d_{C_n}(w_c,w_d)+1,1).$ If a = 1 and $|c-d|<\frac{n}{2},$ then $$\begin{array}{c}r(x_{2d}|S)=r(x_{1(d+1)}|S)\\ =(1+d_{C_n}(w_c,w_d),1)\end{array}$$ If a = 1 and $|c-d|>\frac{n}{2},$ then $$r(x_{2d}|S)=r(x_{1(d-1)}|S)=(1+d_{C_n}(w_c,w_d),1).$$ If a = 1 and $|c-d|=\frac{n}{2},$ then $$r(x_{1(c+1)}|S)=r(x_{1(c-1)}|S)=(1,d_{C_n}(w_c,w_d)-1).$$ Thus S is not a resolving set of G. This proof is similar if $a=m.$

Case iii. $a\ne b$ and $c=d.$

In this case, $r(x_{a(c-1)}|S)=r(x_{a(c+1)}|S)=(1,|a-b|+1).$

Hence S is not a resolving set of G. Thus $\mathit{idim}(G)\ge 3$ and hence $\mathit{idim}(G)=3.$ □

Theorem 3.4.

Let $G=C_n\square C_n$ where $n\ge 5$ and n is odd. Then $\mathit{idim}(G)=3.$

Proof.

Let $(v_1,v_2,\dots ,v_n,v_1)$ and $(w_1,w_2,\dots ,w_n,w_1)$ be two copies of the cycle $C_n.$ We denote the vertex (v_i, w_j) in G by $x_{ij}.$

Let $n=2k-1$ and let $W=\{x_{11},x_{k1},x_{nk}\}.$ Then $$r(x_{ij}|W)=\{\begin{array}{cc}(i+j)-2,k-i+j-1,i+k-j)\hfill & \text{if}\mathrm{ }i,j\le k\hfill \\ (n-i-j+2,k+i-j+1,n-i+j-k)\hfill & \text{if}\mathrm{ }i,j>k\hfill \\ (i+n-j,k-i+n-j+1,i+j-k)\hfill & \text{if}\mathrm{ }i\le \mathit{k and j}>k\hfill \\ (j+n-i,k-i+n-j+1,i+j-k)\hfill & \text{if}\mathrm{ }j\le \mathit{k and i}>k.\hfill \end{array}$$ Now, suppose $r(x_{ij}|W)=r(x_{st}|W).$

If $i,j,s,t\le k$ or $i,j,s,t>k,$ then $i+j=s+t$ and $i-j=s-t.$ Hence $x_{ij}=x_{st}.$ If $i,j,s\le k$ and $t>k,$ then $j<t.$ Using the expressions for $r(x_{ij}|W)$ and $r(x_{st}|W)$ we get $2j=n+2$ and $2j=n+1,$ which is a contradiction. A similar contradiction arises in other cases. Thus $r(x_{ij}|W)=r(x_{st}|W)$ implies $x_{ij}=x_{st}.$ Hence W is a resolving set of G and $\mathit{idim}(G)\le 3.$ Also it follows from Theorem 3.2 that $\mathit{idim}(G)\ge 3.$ Hence $\mathit{idim}(G)=3.$ □

4. Conclusion and scope

Since a characterization of graphs which admit an independent resolving set is an unsolved problem, determining such graphs in various classes of graphs is a significant problem. In this paper we have initiated a study of this problem in corona and Cartesian product of graphs. Similar investigation for other graph classes is an interesting direction for further research.