Antimagic labeling of new classes of trees

Abstract

An antimagic labeling of a graph G with q edges is an injective mapping $f:E(G)\to \{1,2,\dots ,q\}$ such that the induced vertex label for each vertex is different, where the induced vertex label of a vertex u is ${\varphi }_f(u)=\sum _{e\in E(u)}f(e).$ Here, E(u) is the set of edges incident to the vertex u. In 1990, Hartsfield and Ringel conjectured that all trees except K₂ are antimagic. Still this conjecture is open. In this article, we prove that two recursive classes of trees called binomial tree B_k, $k\ge 2$ and Fibonacci tree F_h, $h\ge 2$ are antimagic. This result supports Hartsfield and Ringel conjecture.

Keywords:

• Graph labeling
• antimagic labeling
• binomial tree
• Fibonacci tree
• Hartsfield and Ringel conjecture

MATHEMATICS SUBJECT CLASSIFICATION:

• 05C78

1. Introduction

Hartsfield and Ringel [3] introduced antimagic labeling. Let $G=(V,E)$ be a simple graph without any isolated vertex and $f:E(G)\to \{1,2,\dots ,|E\left|\right\}$ is a bijective mapping. For each vertex u of G, the vertex sum ${\varphi }_f(u)=\sum _{e\in E(u)}f(e),$ where E(u) is the set of edges incident to u. If ${\varphi }_f(u)\ne {\varphi }_f(v)$ for any two distinct vertices $u,v\in V(G),$ then f is called antimagic labeling of G. A graph is called antimagic if it admits antimagic labeling. In 1990, Hartsfield and Ringel [3] conjectured that every tree except K₂ is antimagic. This conjecture is still open for over three decades now. Though several partial results supporting Hartsfield and Ringel conjecture have been proved, completely settling the conjecture appears to be hard.

Hartsfield and Ringel [3] proved that paths are antimagic. Shang [6] has proved that all spiders are antimagic. Chawathe and Krishna [1] proved that complete m-ary trees are antimagic. Kaplan et al. [4] showed that trees with at most one 2-degree vertex are antimagic. Recently, in 2014, Liang et al. [5] interestingly identified the class of trees with structural property admitting antimagic labeling. More precisely, Liang et al. [5] proved that if T is a tree with either $V_2(T)$ and $V-V_2(T)$ are both independent sets or $V_2(T)$ induces a path and every other vertex of T has an odd degree, then T is antimagic, where $V_2(T)$ is set of 2-degree vertices of the tree T. This result motivated us to identify the family of trees having the complementary structural property of the trees considered by Liang et al. [5]. That is, if $V_2(T)$ denotes the set of all 2-degree vertices of a tree T, then neither $V_2(T)$ and $V-V_2(T)$ are both independent sets nor $V_2(T)$ induces a path and every other vertex has an odd degree. In this article, we identify two new families of trees called binomial trees and Fibonacci trees satisfying the above complementary property.

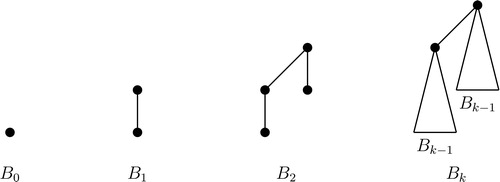
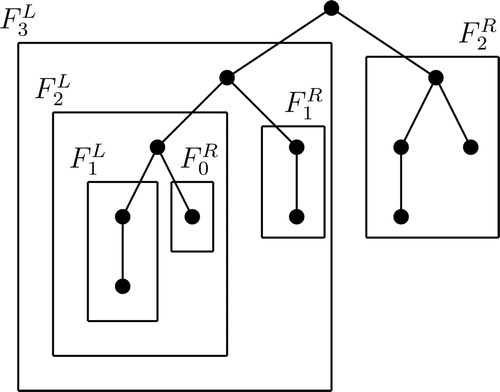
The binomial tree B_k is a rooted tree defined recursively. The binomial tree B₀ is a single node and B₁ is an edge. One of the pendent vertices of B₁ is considered as the root of B₁. The binomial tree B_k consists of two binomial trees $B_{k-1}$ that are linked together so that the root of one is the leftmost child of the root of the other. The root of the right copy of $B_{k-1}$ is the root of B_k (in Figure 1, the binomial trees B₀, B₁, B₂, and B_k are given).

Figure 1. Binomial trees.

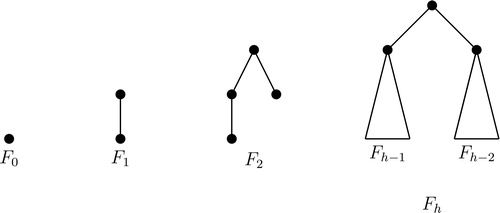
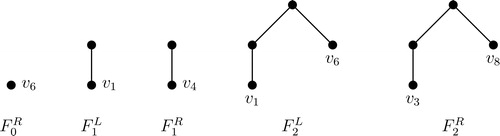
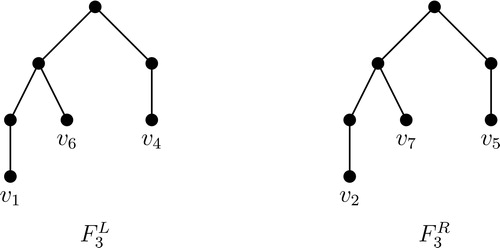
The Fibonacci tree F_h is a rooted tree of height h defined recursively. The Fibonacci tree F₀ is a single node and F₁ is an edge K₂. The Fibonacci tree F₂ is constructed by taking a copy of F₁; a copy of F₀; a new vertex considering it as the root of F₂ and making it adjacent to a vertex of F₁ and a vertex of F₀. For $h\ge 3$ the Fibonacci tree F_h is constructed by taking a copy of $F_{h-1};$ a copy of $F_{h-2};$ a new vertex considering it as the root of F_h and making it adjacent to the root vertex of $F_{h-1}$ and the root vertex of $F_{h-2}$ (in Figure 2, the Fibonacci trees F₀, F₁, F₂, and F_h are given).

Figure 2. Fibonacci trees.

Furthermore, in this article, we prove that binomial tree B_k, for all $k\ge 2$ and Fibonacci tree F_h, for all $h\ge 2$ are antimagic. These two results support Hartsfield and Ringel conjecture [3].

2. Binomial trees are antimagic

In this section, we prove that binomial trees are antimagic. As binomial tree B₀ is a single node and binomial tree B₁ is a K₂, B₀ and B₁ are not antimagic. In Theorem 1, we prove that all binomial trees B_k, $k\ge 2$ are antimagic.

Theorem 1.

The binomial tree B_k, for $k\ge 2$ is antimagic.

Proof.

Consider the binomial tree B_k. The binomial tree B_k is basically a rooted tree of height k having $2^k$ vertices. There are exactly kC_i vertices at level i, for $0\le i\le k.$ The binomial tree B_k has exactly $2^{k-i}$ vertices of degree i, for $1\le i\le k-1$ and exactly 2 vertices of degree k. We give the antimagic labeling of the binomial tree B_k, for $k\ge 2,$ using the following two steps.

• Step 1: Linear representation of the binomial tree

  Let $B_{k-1}^L$ and $B_{k-1}^R$ be the two copies of $B_{k-1}$ in B_k, called the left subtree and right subtree. Let $V(B_{k-1}^R)=\{v_1,v_2,\dots ,v_{2^{k-1}}\}.$ Arrange $V(B_{k-1}^R)$ into two rows. The top row consists of vertices $v_{2^{k-2}+1},v_{2^{k-2}+2},\dots ,v_{2^{k-1}}$ from right to left. The bottom row consists of vertices $v_1,v_2,\dots ,v_{2^{k-2}}$ from right to left.

  Let e_i be the edge joining v_i and $v_{2^{k-2}+i},$ where $1\le i\le 2^{k-2}.$ The edges e₁, e₂, $\cdots ,e_{2^{k-2}}$ are called vertical edges. Let $e_{2^{k-2}+i}$ be the edge joining $v_{2^{k-2}+2i-1}$ and $v_{2^{k-2}+2i},$ where $1\le i\le 2^{k-3}.$ The edges $e_{2^{k-2}+1},e_{2^{k-2}+2},\dots ,e_{2^{k-2}+2^{k-3}}$ are called horizontal edges.

  For $3\le j\le k-1$ and $1\le i\le 2^{k-j-1},$ let $e_{2^{k-2}+2^{k-3}+\cdots +2^{k-j}+i}$ be the edge joining $v_{2^{k-2}+1+(2i-2)(2^{j-2})}$ and $v_{2^{k-2}+1+(2i-1)(2^{j-2})}.$ The edges are called the right to left link edges.

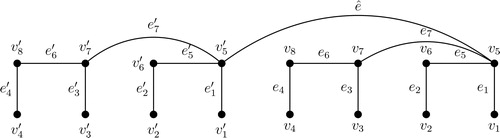
  Label the corresponding vertices and edges of $B_{k-1}^L$ as in $B_{k-1}^R,$ where the vertex v_i is replaced by $v_i^{\prime }$ for $1\le i\le 2^{k-1}$ and the edge e_i is replaced by $e_i^{\prime }$ for $1\le i\le 2^{k-1}-1.$ Let $\widehat{e}$ denote the edge joining the root $v_{2^{k-2}+1}$ of $B_{k-1}^R$ and the root $v_{2^{k-2}+1}^{\prime }$ of $B_{k-1}^L$ in B_k (The representation of vertices and edges of B₄ is shown in Figure 3).

  Figure 3. Representation of vertices and edges of B₄.

  

• Step 2: Defining antimagic labeling

  Consider the binomial tree $B_k,k\ge 2$ with its linear representation as described in Step 1. Define a function $f:E(B_k)\to \{1,2,\dots ,|E(B_k)\left|\right\}$ such that $f(e_i)=2i-1,$ $f(e_i^{\prime })=2i,$ for i, $1\le i\le 2^{k-1}-1$ and $f(\widehat{e})=2^k-1.$ Clearly, f is a bijection.

Claim: Induced vertex labels are distinct.

The induced vertex label is defined to be the sum of the labels of the edges incident with the vertex. Under the linear representation of binomial tree B_k, B_k has $2^{k-1}$ vertices $v_1,v_1^{\prime },v_2,v_2^{\prime },\dots ,v_{2^{k-2}},v_{2^{k-2}}^{\prime },$ each having degree one. For $1\le i\le 2^{k-2},$ the set of edges incident with the vertex v_i, $E(v_i)=\left\{e_i\right\}$ and with the vertex $v_i^{\prime },E(v_i^{\prime })=\left\{e_i^{\prime }\right\}.$

B_k has $2^{k-2}$ vertices $v_{2^{k-2}+(2^0+1)},$ $v_{2^{k-2}+(2^0+1)}^{\prime },v_{2^{k-2}+(2^0+1)+(2^1)(1)},$ $v_{2^{k-2}+(2^0+1)+(2^1)(1)}^{\prime },\dots ,$ $v_{2^{k-2}+(2^0+1)+(2^1)(2^{k-3}-1)},$ $v_{2^{k-2}+(2^0+1)+(2^1)(2^{k-3}-1)}^{\prime }$ each having degree two. For $0\le i\le 2^{k-3}-1,$ the set of edges incident with the vertex $v_{2^{k-2}+(2^0+1)+(2^1)(i)},$ $E(v_{2^{k-2}+(2^0+1)+(2^1)(i)})=\{e_{(2^0+1)+(2^1)(i)},e_{2^{k-2}+(2^0)+(2^0)(i)}\}$ and the set of edges incident with the vertex $v_{2^{k-2}+(2^0+1)+(2^1)(i)}^{\prime },$ $E(v_{2^{k-2}+(2^0+1)+(2^1)(i)}^{\prime })=\{e_{(2^0+1)+(2^1)(i)}^{\prime },e_{2^{k-2}+(2^0)+(2^0)(i)}^{\prime }\}.$

B_k has $2^{k-j}$ vertices $v_{2^{k-2}+(2^{j-2}+1)},$ $v_{2^{k-2}+(2^{j-2}+1)}^{\prime },$ $v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(1)},$ $v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(1)}^{\prime },\dots ,v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(2^{k-j-1}-1)},$ $v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(2^{k-j-1}-1)}^{\prime },$ each having degree j, where $3\le j\le k-1.$ For $3\le j\le k-1$ and $0\le i\le 2^{k-j-1}-1,$ the set of edges incident with the vertex $v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(i)},$ $E(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(i)})=\{e_{(2^{j-2}+1)+(2^{j-1})(i)},e_{2^{k-2}-2^{j-3}+1+(2^{j-2})+(2^{j-2})(i)},$ $e_{2^{k-2}+2^{k-3}-2^{j-4}+1+(2^{j-3})+(2^{j-3})(i)},\dots ,e_{2^{k-2}+2^{k-3}+\cdots +2^{k-j+1}-2^0+1+(2^1)+(2^1)(i)},$ $e_{2^{k-2}+2^{k-3}+\cdots +2^{k-j}+(2^0)+(2^0)(i)}\}$ and with the vertex $v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(i)}^{\prime },$ $E(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(i)}^{\prime })=\{e_{(2^{j-2}+1)+(2^{j-1})(i)}^{\prime },e_{2^{k-2}-2^{j-3}+1+(2^{j-2})+(2^{j-2})(i)}^{\prime },$ $e_{2^{k-2}+2^{k-3}-2^{j-4}+1+(2^{j-3})+(2^{j-3})(i)}^{\prime },\dots ,e_{2^{k-2}+2^{k-3}+\cdots +2^{k-j+1}-2^0+1+(2^1)+(2^1)(i)}^{\prime },$ $e_{2^{k-2}+2^{k-3}+\cdots +2^{k-j}+(2^0)+(2^0)(i)}^{\prime }\}.$

B_k has two vertices $v_{2^{k-2}+1}$ and $v_{2^{k-2}+1}^{\prime },$ each having degree k. The set of edges incident with the vertex $v_{2^{k-2}+1},$ $E(v_{2^{k-2}+1})=\{e_1,e_{1+2^{k-2}},e_{1+2^{k-2}+2^{k-3}},\dots ,e_{1+2^{k-2}+2^{k-3}+\cdots +2^1},\widehat{e}\}$ and with the vertex $v_{2^{k-2}+1}^{\prime },$ $E(v_{2^{k-2}+1}^{\prime })=\{e_1^{\prime },e_{1+2^{k-2}}^{\prime },e_{1+2^{k-2}+2^{k-3}}^{\prime },\dots ,e_{1+2^{k-2}+2^{k-3}+\cdots +2^1}^{\prime },\widehat{e}\}.$

The induced vertex label of v_i is ${\varphi }_f(v_i)=\sum _{e\in E(v_i)}f(e),$ where $1\le i\le 2^k.$

For $1\le i\le 2^{k-2},$ the induced vertex label of one degree vertex ${\varphi }_f(v_i)=f(e_i)$ and ${\varphi }_f(v_i^{\prime })=f(e_i^{\prime }).$ From the definition of f, it is clear that, (1) $${\varphi }_f(v_1)<{\varphi }_f(v_1^{\prime })<{\varphi }_f(v_2)<{\varphi }_f(v_2^{\prime })<\cdots <{\varphi }_f(v_{2^{k-2}})<{\varphi }_f(v_{2^{k-2}}^{\prime }).$$(1)

For $0\le i\le 2^{k-3}-1,$ the induced vertex label of two degree vertex ${\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(i)})=f(e_{(2^0+1)+(2^1)(i)})+f(e_{2^{k-2}+(2^0)+(2^0)(i)})$ and ${\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(i)}^{\prime })=f(e_{(2^0+1)+(2^1)(i)}^{\prime })+f(e_{2^{k-2}+(2^0)+(2^0)(i)}^{\prime }).$ From the definition of f, it follows that (2) $$\begin{array}{c}{\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(0)})<{\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(0)}^{\prime })<\\ {\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(1)})<{\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(1)}^{\prime })<\cdots <\\ {\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(2^{k-3}-1)})<{\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(2^{k-3}-1)}^{\prime }).\end{array}$$(2)

For $3\le j\le k-1$ and $0\le i\le 2^{k-j-1}-1,$ the induced vertex label of j degree vertex, ${\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(i)})=f(e_{(2^{j-2}+1)+(2^{j-1})(i)})+$ $f(e_{2^{k-2}-2^{j-3}+1+(2^{j-2})+(2^{j-2})(i)})+f(e_{2^{k-2}+2^{k-3}-2^{j-4}+1+(2^{j-3})+(2^{j-3})(i)})+\cdots +$ $f(e_{2^{k-2}+2^{k-3}+\cdots +2^{k-j+1}-2^0+1+(2^1)+(2^1)(i)})+f(e_{2^{k-2}+2^{k-3}+\cdots +2^{k-j}+(2^0)+(2^0)(i)});$ $${\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(i)}^{\prime })=f(e_{(2^{j-2}+1)+(2^{j-1})(i)}^{\prime })+f(e_{2^{k-2}-2^{j-3}+1+(2^{j-2})+(2^{j-2})(i)}^{\prime })+f(e_{2^{k-2}+2^{k-3}-2^{j-4}+1+(2^{j-3})+(2^{j-3})(i)}^{\prime })+\cdots +f(e_{2^{k-2}+2^{k-3}+\cdots +2^{k-j+1}-2^{j-j}+1+(2^1)+(2^1)(i)}^{\prime })+f(e_{2^{k-2}+2^{k-3}+\cdots +2^{k-j}+(2^0)+(2^0)(i)}^{\prime })$$

From the definition of f, it follows that (3) $$\begin{array}{c}{\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)})<{\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)}^{\prime })<{\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(1)})<\\ {\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(1)}^{\prime })<\cdots <{\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(2^{k-j-1}-1)})<\\ {\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(2^{k-j-1}-1)}^{\prime }).\end{array}$$(3)

The induced vertex label of k degree vertices ${\varphi }_f(v_{2^{k-2}+1})=f(e_1)+f(e_{1+2^{k-2}})+f(e_{1+2^{k-2}+2^{k-3}})+\cdots +f(e_{1+2^{k-2}+2^{k-3}+\cdots +2^1})+f(\widehat{e})$ and ${\varphi }_f(v_{2^{k-2}+1}^{\prime })=f(e_1^{\prime })+f(e_{1+2^{k-2}}^{\prime })+f(e_{1+2^{k-2}+2^{k-3}}^{\prime })+\cdots +f(e_{1+2^{k-2}+2^{k-3}+\cdots +2^1}^{\prime })+f(\widehat{e}).$ By the definition of f, it is clear that (4) $${\varphi }_f(v_{2^{k-2}+1})<{\varphi }_f(v_{2^{k-2}+1}^{\prime }).$$(4)

Therefore, from Equations (1)(1) $${\varphi }_f(v_1)<{\varphi }_f(v_1^{\prime })<{\varphi }_f(v_2)<{\varphi }_f(v_2^{\prime })<\cdots <{\varphi }_f(v_{2^{k-2}})<{\varphi }_f(v_{2^{k-2}}^{\prime }).$$(1) to (4)(4) $${\varphi }_f(v_{2^{k-2}+1})<{\varphi }_f(v_{2^{k-2}+1}^{\prime }).$$(4) it is clear that, for $1\le j\le k,$ the induced vertex labels of all j degree vertices are distinct.

From (1(1) $${\varphi }_f(v_1)<{\varphi }_f(v_1^{\prime })<{\varphi }_f(v_2)<{\varphi }_f(v_2^{\prime })<\cdots <{\varphi }_f(v_{2^{k-2}})<{\varphi }_f(v_{2^{k-2}}^{\prime }).$$(1) ) and (2(2) $$\begin{array}{c}{\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(0)})<{\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(0)}^{\prime })<\\ {\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(1)})<{\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(1)}^{\prime })<\cdots <\\ {\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(2^{k-3}-1)})<{\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(2^{k-3}-1)}^{\prime }).\end{array}$$(2) ), the maximum of one degree vertex label induced is ${\varphi }_f(v_{2^{k-2}}^{\prime })$ $=f(e_{2^{k-2}}^{\prime })$ and the minimum of two degree vertex label induced is ${\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(0)})=f(e_{(2^0+1)+(2^1)(0)})+f(e_{2^{k-2}+(2^0)+(2^0)(0)}).$ By the definition of f, $f(e_{2^{k-2}}^{\prime })<f(e_{2^{k-2}+(2^0)+(2^0)(0)}).$ Hence, (5) $${\varphi }_f(v_{2^{k-2}}^{\prime })<{\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(0)}).$$(5)

From (2(2) $$\begin{array}{c}{\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(0)})<{\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(0)}^{\prime })<\\ {\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(1)})<{\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(1)}^{\prime })<\cdots <\\ {\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(2^{k-3}-1)})<{\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(2^{k-3}-1)}^{\prime }).\end{array}$$(2) ) and (3(3) $$\begin{array}{c}{\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)})<{\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)}^{\prime })<{\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(1)})<\\ {\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(1)}^{\prime })<\cdots <{\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(2^{k-j-1}-1)})<\\ {\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(2^{k-j-1}-1)}^{\prime }).\end{array}$$(3) ), the maximum of two degree vertex label induced is ${\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(2^{k-3}-1)}^{\prime })=f(e_{(2^0+1)+(2^1)(2^{k-3}-1)}^{\prime })+f(e_{2^{k-2}+2^0+(2^0)(2^{k-3}-1)}^{\prime })$ and the minimum of three degree vertex label induced is ${\varphi }_f(v_{2^{k-2}+(2^1+1)+(2^2)(0)})$ $=f(e_{(2^1+1)})+f(e_{2^{k-2}-2^0+1+2^1})+f(e_{2^{k-2}+2^{k-3}+2^0}).$ By the definition of f, $f(e_{(2^0+1)+(2^1)(2^{k-3}-1)}^{\prime })<f(e_{2^{k-2}-2^0+1+2^1})$ and $f(e_{2^{k-2}+2^0+(2^0)(2^{k-3}-1)}^{\prime })<$ $f(e_{2^{k-2}+2^{k-3}+2^0}).$ Hence, (6) $${\varphi }_f({v\prime }_{2^{k-2}+(2^0+1)+(2^1)(2^{k-3}-1)})<{\varphi }_f(v_{2^{k-2}+(2^1+1)+(2^2)(0)}).$$(6)

From (3(3) $$\begin{array}{c}{\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)})<{\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)}^{\prime })<{\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(1)})<\\ {\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(1)}^{\prime })<\cdots <{\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(2^{k-j-1}-1)})<\\ {\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(2^{k-j-1}-1)}^{\prime }).\end{array}$$(3) ), for $3\le j\le k-2,$ the maximum of j degree vertex label induced is ${\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(2^{k-j-1}-1)}^{\prime })=$ $f(e_{2^{j-2}+1+2^{k-2}-2^{j-1}}^{\prime })+f(e_{2^{k-2}-2^{j-3}+1+(2^{j-2})+(2^{j-2})(2^{k-j-1}-1)}^{\prime })+$ $f(e_{2^{k-2}+2^{k-3}-2^{j-4}+1+(2^{j-3})+(2^{j-3})(2^{k-j-1}-1)}^{\prime })+\cdots +$ $f(e_{2^{k-2}+2^{k-3}+\cdots +2^{k-j+1}-2^{j-j}+1+(2^1)+(2^1)(2^{k-j-1}-1)}^{\prime })+$ $f(e_{2^{k-2}+2^{k-3}+\cdots +2^{k-j}+(2^0)+(2^0)(2^{k-j-1}-1)}^{\prime })$ and the minimum of j + 1 degree vertex label induced is ${\varphi }_f(v_{2^{k-2}+(2^{j-1}+1)+(2^j)(0)})=f(e_{2^{j-1}+1})+$ $f(e_{2^{k-2}-2^{j-2}+1+(2^{j-1})})+f(e_{2^{k-2}+2^{k-3}-2^{j-3}+1+(2^{j-2})})+\cdots +$ $f(e_{2^{k-2}+2^{k-3}+\cdots +2^{k-j}-2^0+1+(2^1)})+f(e_{2^{k-2}+2^{k-3}+\cdots +2^{k-j-1}+(2^0)}).$ By the definition of f, $f(e_{{2^{j-2}+1+2}^{k-2}-2^{j-1}}^{\mathrm{\prime }})<f(e_{2^{k-2}-2^{j-2}+1+2^{j-1}}),\mathrm{ }f(e_{2^{k-2}-2^{j-3}+1+2^{j-2}+(2^{j-2})(2^{k-j-1}-1)}^{\mathrm{\prime }})<f(e_{2^{k-2}+2^{k-3}-2^{j-3}+1+2^{j-2}}),\dots ,\mathrm{ }f(e_{2^{k-2}+2^{k-3}+\dots +2^{k-j}+2^0+(2^0)(2^{k-j-1}-1)}^{\mathrm{\prime }})<$ $f\left(e_{2^{k-2}+2^{k-3}+\dots +2^{k-j-1}+2^0}\right).$

Hence, for any $j,3\le j\le k-2,$ (7) $${\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(2^{k-j-1}-1)}^{\prime })<{\varphi }_f(v_{2^{k-2}+(2^{j-1}+1)+(2^j)(0)}).$$(7)

From (3(3) $$\begin{array}{c}{\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)})<{\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)}^{\prime })<{\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(1)})<\\ {\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(1)}^{\prime })<\cdots <{\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(2^{k-j-1}-1)})<\\ {\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(2^{k-j-1}-1)}^{\prime }).\end{array}$$(3) ) and (4(4) $${\varphi }_f(v_{2^{k-2}+1})<{\varphi }_f(v_{2^{k-2}+1}^{\prime }).$$(4) ), the maximum of k – 1 degree vertex label induced is ${\varphi }_f(v_{2^{k-2}+(2^{k-3}+1)}^{\prime })=f(e_{2^{k-3}+1}^{\prime })+f(e_{2^{k-2}-2^{k-4}+1+2^{k-3}}^{\prime })+f(e_{2^{k-2}+2^{k-3}-2^{k-5}+1+2^{k-4}}^{\prime })$ $+\cdots +f(e_{2^{k-2}+2^{k-3}+\cdots +2^2+2^1}^{\prime })+f(e_{2^{k-2}+2^{k-3}+\cdots +2^1+2^0}^{\prime })$ and the minimum of k degree vertex label induced is ${\varphi }_f(v_{2^{k-2}+1})=f(e_1)+f(e_{1+2^{k-2}})+$ $f(e_{1+2^{k-2}+2^{k-3}})+\cdots +f(e_{1+2^{k-2}+2^{k-3}+\cdots +2^1})+f(\widehat{e}).$ By the definition of f, we have, $f(e_{2^{k-3}+1}^{\prime })<f(e_{1+2^{k-2}}),f(e_{2^{k-2}-2^{k-4}+1+2^{k-3}}^{\prime })<f(e_{1+2^{k-2}+2^{k-3}}),\dots ,$ $f(e_{2^{k-2}+2^{k-3}+\cdots +2^1+2^0}^{\prime })<f(\widehat{e}).$ Hence, (8) $${\varphi }_f(v_{2^{k-2}+(2^{k-3}+1)}^{\prime })<{\varphi }_f(v_{2^{k-2}+1}).$$(8)

From Equations (5)(5) $${\varphi }_f(v_{2^{k-2}}^{\prime })<{\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(0)}).$$(5) to (8)(8) $${\varphi }_f(v_{2^{k-2}+(2^{k-3}+1)}^{\prime })<{\varphi }_f(v_{2^{k-2}+1}).$$(8) , we observe that, the minimum of the induced vertex labels of j degree vertex is greater than the maximum of the induced vertex label of j – 1 degree vertex, for $2\le j\le k-1.$ From Equations (1)(1) $${\varphi }_f(v_1)<{\varphi }_f(v_1^{\prime })<{\varphi }_f(v_2)<{\varphi }_f(v_2^{\prime })<\cdots <{\varphi }_f(v_{2^{k-2}})<{\varphi }_f(v_{2^{k-2}}^{\prime }).$$(1) to (4)(4) $${\varphi }_f(v_{2^{k-2}+1})<{\varphi }_f(v_{2^{k-2}+1}^{\prime }).$$(4) , for $1\le j\le k,$ the induced vertex labels of all j degree vertices are distinct.

Thus, all the induced vertex labels of B_k are distinct. Hence, the function ${\varphi }_f$ is injective.

From Step 2, it is clear that the function f defined in Step 2 is antimagic. Thus, the binomial tree B_k, for $k\ge 2$ is antimagic. □

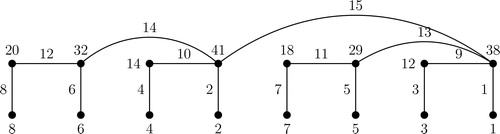
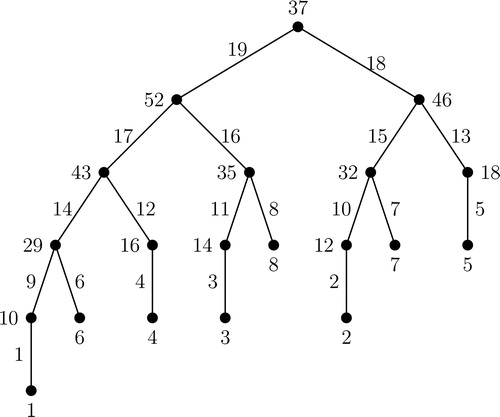
In Figure 4, the edge labels and the induced vertex labels of B₄ are shown as an illustration.

Figure 4. Edge labels with induced vertex labels of B₄.

3. Fibonacci trees are antimagic

In this section, we prove that Fibonacci trees are antimagic. As Fibonacci tree F₀ is a single node and Fibonacci tree F₁ is K₂, F₀ and F₁ are not antimagic. In Theorem 2, we prove that Fibonacci tree F_h is antimagic, for $h\ge 2.$

Theorem 2.

The Fibonacci tree F_h, for $h\ge 2$ is antimagic.

Proof.

Consider the Fibonacci tree F_h. Let n(h) denote the number of vertices in Fibonacci tree F_h. Observe that, F_h consists of vertices of degree either one or two or three. Let $d_i(h)$ denote the number of i degree vertices in F_h, for $1\le i\le 3.$ In Fibonacci tree F₂, $n(2)=4;$ $d_1(2)=2;$ $d_2(2)=2;$ $d_3(2)=0$ and in F₃, $n(3)=7;$ $d_1(3)=3;$ $d_2(3)=3;$ $d_3(3)=1.$ From the definition of Fibonacci tree F_h, we have, for $h\ge 4,n(h)=n(h-1)+n(h-2)+1;$ $d_1(h)=d_1(h-1)$+$d_1(h-2);$ $d_2(h)=d_2(h-1)+d_2(h-2)-1$ and $d_3(h)=d_3(h-1)+d_3(h-2)+2.$ Now we give the antimagic labeling of the Fibonacci tree F_h, for $h\ge 2,$ using the following two steps.

Step 1: Representation of Fibonacci tree

For the convenience of naming the vertices, we visualize the Fibonacci tree as given below.

In F_h, the left subtree $F_{h-1}$ is referred to as $F_{h-1}^L$ and the right subtree $F_{h-2}$ is referred to as $F_{h-2}^R.$ In general, in F_h, for j, $2\le j\le h-1,$ the left subtree of $F_{h-j+1}^L$ is referred as $F_{h-j}^L$ and the right subtree of $F_{h-j+1}^L$ is referred as $F_{h-j-1}^R$ (The representation of the left and right subtrees of F₄ are shown in Figure 5).

Figure 5. Representation of left and right sub-trees of F₄.

Observe that, in any Fibonacci tree F_h, for j, $2\le j\le h-1,$ the pendant vertices of $F_j^L$ are the pendant vertices of $F_{j-1}^L$ and the pendant vertices of $F_{j-2}^R.$

We name the vertices and the edges of F_h using the following vertex and edge naming procedure.

Vertex and edge naming procedure:

• In F₂, name the unique pendant vertex in $F_1^L$ as v₁ and name the unique pendant vertex in $F_0^R$ as v₂. In F₃, name the pendant vertex in $F_1^L$ as v₁ and name the pendant vertex in $F_0^R$ as v₃. Then, name the pendant vertex in $F_1^R$ as v₂.

• In F_h, for $h\ge 4,$ name the pendant vertex in $F_1^L$ as v₁ and in $F_0^R$ as $v_{1+d_1(h-1)}.$ Then, name the pendant vertex in $F_1^R$ as $v_{1+d_1(h-2)}.$ For each j, $2\le j\le h-2,$ in the increasing order of j, we name the pendant vertices of $F_j^L$ and $F_j^R$ recursively as given below.

• For each j, $2\le j\le h-3,$ consider the left subtree $F_j^L$ and its corresponding right subtree $F_j^R.$ By the representation of subtrees of Fibonacci tree, the pendant vertices of $F_j^L$ are the pendant vertices of $F_{j-1}^L$ and the pendant vertices of $F_{j-2}^R.$ Since all the pendant vertices of $F_{j-1}^L$ and $F_{j-2}^R$ are already named, it implies that all the pendant vertices of $F_j^L$ are also named. Thus for each pendant vertex in $F_j^L,$ if it is named as v_l in $F_j^L,$ then find its corresponding pendant vertex in $F_j^R$ and name it as $v_{l+d_1(h-j-1)}.$ Then, consider the left subtree $F_{h-2}^L$ and its corresponding right subtree $F_{h-2}^R.$ For each pendant vertex in $F_{h-2}^L,$ if it is named as v_l in $F_{h-2}^L,$ then find its corresponding pendant vertex in $F_{h-2}^R$ and name it as $v_{l+1}.$ Observe that, the pendant vertices of the left subtree $F_{h-1}^L$ are the pendant vertices of $F_{h-2}^L$ and the pendant vertices of $F_{h-3}^R.$ Since all the pendant vertices of $F_{h-2}^L$ and $F_{h-3}^R$ are already named, it implies that all the pendant vertices of $F_{h-1}^L$ are also named.

• In F_h, name the parent vertex of v₁ as $v_{d_1(h)+1}.$ Then, find the vertex v_k with least suffix k such that the parent of v_k is not named. Now name the parent of v_k as $v_{y+1},$ where v_y is the latest named parent vertex. Continue this process until we finally name the root vertex of F_h.

• Now, after naming all the vertices in F_h, the pendant vertices can be arranged as a sequence v₁, v₂,$\cdots ,v_{d_1(h)},$ where $d_1(h)$ is the number of one-degree vertices in F_h; the two-degree vertices in F_h can be arranged as a sequence $v_{d_1(h)+1},v_{d_1(h)+2},\dots ,v_{d_1(h)+d_2(h)-1}$ and $v_{n(h)}$ and the three-degree vertices in F_h can be arranged as a sequence $v_{d_1(h)+d_2(h)},v_{d_1(h)+d_2(h)+1},\dots ,v_{d_1(h)+d_2(h)+d_3(h)-1}.$

• For $1\le i<j\le n(h),$ the edge (v_i, v_j) is named as e_i.

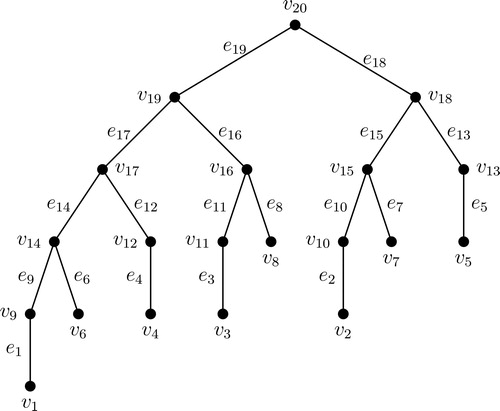
(The naming of the pendant vertices of F₅ is shown in step by step manner in Figures 6 and 7. The above description of vertices and edges of the Fibonacci tree F₅ are shown in Figure 8.)

Figure 6. Naming the pendant vertices of $F_0^R,F_1^L,F_1^R,F_2^L,F_2^R$ in F₅.

Figure 7. Naming the pendant vertices of $F_3^L,F_3^R$ in F₅.

Figure 8. Representation of vertices and edges of F₅.

Step 2: Defining antimagic labeling

Consider the Fibonacci tree F_h as described in Step 1. Define a function $f:E(F_h)\to \{1,2,\dots ,n(h)-1\}$ such that $f(e_i)=i,$ for i, $1\le i\le n(h)-1.$ Clearly, f is a bijection.

Claim: Induced vertex labels are distinct.

Under the representation of the Fibonacci tree, F_h, F_h has $d_1(h)$ vertices $v_1,v_2,v_3,\dots ,v_{d_1(h)}$ each having degree one. For $1\le i\le d_1(h),$ the set of edges incident with the vertex v_i, $E(v_i)=\left\{e_i\right\}.$

F_h has $d_2(h)$ vertices $v_{d_1(h)+1},v_{d_1(h)+2},\dots ,v_{d_1(h)+d_2(h)-1}$ and $v_{n(h)}$ each having degree 2. For $1\le i\le d_2(h)-1,$ the set of edges incident with the vertex $v_{d_1(h)+i},E(v_{d_1(h)+i})=\{e_i,e_{d_1(h)+i}\}$ and with the vertex $v_{n(h)},E(v_{n(h)})=\{e_{n(h)-2},e_{n(h)-1}\}.$

F_h has $d_3(h)$ vertices $v_{d_1(h)+d_2(h)},$ $v_{d_1(h)+d_2(h)+1},\dots ,v_{d_1(h)+d_2(h)+d_3(h)-1}$ each having degree 3. For $0\le i\le d_2(h-1)-2,$ the set of edges incident with the vertex $v_{d_1(h)+d_2(h)+i},$ $E(v_{d_1(h)+d_2(h)+i})=\{e_{d_2(h)+i},e_{d_1(h)+i+1},e_{d_1(h)+d_2(h)+i}\}.$ For $0\le i\le d_2(h-2)-2,$ the set of edges incident with the vertex $v_{d_1(h)+d_2(h)+d_2(h-1)-1+i},$ $E(v_{d_1(h)+d_2(h)+d_2(h-1)-1+i})=\{e_{d_1(h)+d_2(h-1)+i},$ $e_{d_1(h)+d_2(h)+i},e_{d_1(h)+d_2(h)+d_2(h-1)-1+i}\}.$ For $2\le j\le h-3$ and $0\le i\le d_2(h-j-1)-2,$ the set of edges incident with the vertex $v_{d_1(h)+d_2(h)+d_2(h-1)+\cdots +d_2(h-j)-j+i},E(v_{d_1(h)+d_2(h)+d_2(h-1)+\cdots +d_2(h-j)-j+i})=$ $\{e_{d_1(h)+d_2(h)+d_2(h-1)+\cdots +d_2(h-j+2)+d_2(h-j)-(j-1)+i},$ $e_{d_1(h)+d_2(h)+d_2(h-1)+\cdots +d_2(h-j+1)-(j-1)+i},e_{d_1(h)+d_2(h)+d_2(h-1)+\cdots +d_2(h-j)-j+i}\}.$

The induced vertex label of v_i, ${\varphi }_f(v_i)=\sum _{e\in E(v_i)}f(e),$ for $1\le i\le n(h).$ For $1\le i\le d_1(h),$ the induced vertex label of one degree vertex ${\varphi }_f(v_i)=f(e_i).$ From the definition of f, we can see that (1) $${\varphi }_f(v_1)<{\varphi }_f(v_2)<\cdots <{\varphi }_f(v_{d_1(h)}).$$(1)

For $1\le i\le d_2(h)-1,$ the induced vertex label of two degree vertex ${\varphi }_f(v_{d_1(h)+i})=f(e_i)+f(e_{d_1(h)+i})$ and ${\varphi }_f(v_{n(h)})=f(e_{n(h)-2})+f(e_{n(h)-1}).$ From the definition of f, we can see that (2) $${\varphi }_f(v_{d_1(h)+1})<{\varphi }_f(v_{d_1(h)+2})<\cdots <{\varphi }_f(v_{d_1(h)+d_2(h)-1})<{\varphi }_f(v_{n(h)}).$$(2)

For $0\le i\le d_2(h-1)-2,$ the induced vertex label of three degree vertex ${\varphi }_f(v_{d_1(h)+d_2(h)+i})=f(e_{d_2(h)+i})+f(e_{d_2(h)+i+1})+f(e_{d_1(h)+d_2(h)+i})$ and for $0\le i\le d_2(h-2)-2,$ ${\varphi }_f(v_{d_1(h)+d_2(h)+d_2(h-1)-1+i})=f(e_{d_1(h)+d_2(h-1)+i})+$ $f(e_{d_1(h)+d_2(h)+i})+f(e_{d_1(h)+d_2(h)+d_2(h-1)-1+i}).$ In general, for $2\le j\le h-3,$ ${\varphi }_f(v_{d_1(h)+d_2(h)+d_2(h-1)+\cdots +d_2(h-j)-j+i})=$ $f(e_{d_1(h)+d_2(h)+d_2(h-1)+\cdots +d_2(h-j+2)+d_2(h-j)-(j-1)+i})+$ $f(e_{d_1(h)+d_2(h)+d_2(h-1)+\cdots +d_2(h-j+1)-(j-1)+i})+f(e_{d_1(h)+d_2(h)+d_2(h-1)+\cdots +d_2(h-j)-j+i}),$ where $0\le i\le d_2(h-j-1)-2$. From the definition of f, it is follows that (3) $${\varphi }_f(v_{d_1(h)+d_2(h)})<{\varphi }_f(v_{d_1(h)+d_2(h)+1})<\cdots <{\varphi }_f(v_{d_1(h)+d_2(h)+d_3(h)-1}).$$(3)

Therefore, from Equations (1)(1) $${\varphi }_f(v_1)<{\varphi }_f(v_1^{\prime })<{\varphi }_f(v_2)<{\varphi }_f(v_2^{\prime })<\cdots <{\varphi }_f(v_{2^{k-2}})<{\varphi }_f(v_{2^{k-2}}^{\prime }).$$(1) to (3)(3) $$\begin{array}{c}{\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)})<{\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)}^{\prime })<{\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(1)})<\\ {\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(1)}^{\prime })<\cdots <{\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(2^{k-j-1}-1)})<\\ {\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(2^{k-j-1}-1)}^{\prime }).\end{array}$$(3) it is clear that, for $1\le j\le 3,$ the induced vertex labels of all j degree vertices are distinct.

Also, from the definition of f, we have,

${\varphi }_f(v_l)-{\varphi }_f(v_i)\ge 3,$ for $d_1(h)+d_2(h)\le i<l\le n(h)-1.$(4)

That is, the difference between any two vertices of degree three is at least 3.

From (1(1) $${\varphi }_f(v_1)<{\varphi }_f(v_1^{\prime })<{\varphi }_f(v_2)<{\varphi }_f(v_2^{\prime })<\cdots <{\varphi }_f(v_{2^{k-2}})<{\varphi }_f(v_{2^{k-2}}^{\prime }).$$(1) ) and (2(2) $$\begin{array}{c}{\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(0)})<{\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(0)}^{\prime })<\\ {\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(1)})<{\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(1)}^{\prime })<\cdots <\\ {\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(2^{k-3}-1)})<{\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(2^{k-3}-1)}^{\prime }).\end{array}$$(2) ), the maximum of one degree vertex label induced is ${\varphi }_f(v_{d_1(h)})=f(e_{d_1(h)})$ and the minimum of two degree vertex label induced is ${\varphi }_f(v_{d_1(h)+1})=f(e_1)+f(e_{d_1(h)+1}).$ As $f(e_{d_1(h)})<f(e_{d_1(h)+1}),$ we have, (5) $${\varphi }_f(v_{d_1(h)})<{\varphi }_f(v_{d_1(h)+1}).$$(5)

From (2(2) $$\begin{array}{c}{\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(0)})<{\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(0)}^{\prime })<\\ {\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(1)})<{\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(1)}^{\prime })<\cdots <\\ {\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(2^{k-3}-1)})<{\varphi }_f(v_{2^{k-2}+(2^0+1)+(2^1)(2^{k-3}-1)}^{\prime }).\end{array}$$(2) ) and (3(3) $$\begin{array}{c}{\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)})<{\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)}^{\prime })<{\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(1)})<\\ {\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(1)}^{\prime })<\cdots <{\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(2^{k-j-1}-1)})<\\ {\varphi }_f(v_{2^{k-2}+(2^{j-2}+1)+(2^{j-1})(2^{k-j-1}-1)}^{\prime }).\end{array}$$(3) ), the maximum of two degree vertex label induced is ${\varphi }_f(v_{d_1(h)+d_2(h)-1})=f(e_{d_2(h)-1})+f(e_{d_1(h)+d_2(h)-1})$ and the minimum of three degree vertex label induced is ${\varphi }_f(v_{d_1(h)+d_2(h)})=f(e_{d_2(h)})+f(e_{d_1(h)+1})+f(e_{d_1(h)+d_2(h)}).$ From the definition of f, $f(e_{d_2(h)-1}))<f(e_{d_2(h)})$ and $f(e_{d_1(h)+d_2(h)-1})<f(e_{d_1(h)+d_2(h)}).$ Hence, (6) $${\varphi }_f(v_{d_1(h)+d_2(h)-1})<{\varphi }_f(v_{d_1(h)+d_2(h)}).$$(6)

From Equations (1)(1) $${\varphi }_f(v_1)<{\varphi }_f(v_1^{\prime })<{\varphi }_f(v_2)<{\varphi }_f(v_2^{\prime })<\cdots <{\varphi }_f(v_{2^{k-2}})<{\varphi }_f(v_{2^{k-2}}^{\prime }).$$(1) to (6)(6) $${\varphi }_f({v\prime }_{2^{k-2}+(2^0+1)+(2^1)(2^{k-3}-1)})<{\varphi }_f(v_{2^{k-2}+(2^1+1)+(2^2)(0)}).$$(6) , we have, $${\varphi }_f(v_1)<{\varphi }_f(v_2)<\cdots <{\varphi }_f(v_{d_1(h)})<{\varphi }_f(v_{d_1(h)+1})<\cdots <{\varphi }_f(v_{d_1(h)+d_2(h)-1})<{\varphi }_f(v_{d_1(h)+d_2(h)})<\cdots <{\varphi }_f(v_{d_1(h)+d_2(h)+d_3(h)-1}).$$

Hence, the induced vertex labels of all the vertices of F_h are ordered and are distinct except the root vertex $v_{n(h)}.$

For the base case h < 5, it is easy to verify that ${\varphi }_f(v_{n(h)})\ne {\varphi }_f(v_i)$ for any $i,1\le i\le d_1(h)+d_2(h)+d_3(h)-1.$ For $5\le h\le 7,$ ${\varphi }_f(v_{d_1(h)+d_2(h)+d_2(h-1)-2})<{\varphi }_f(v_{n(h)})<{\varphi }_f(v_{d_1(h)+d_2(h)+d_2(h-1)-1}).$ Hence, ${\varphi }_f(v_{n(h)})\ne {\varphi }_f(v_i)$ for any $i,1\le i\le d_1(h)+d_2(h)+d_3(h)-1.$ Hence, for $2\le h\le 7,$ all the induced vertex labels of F_h are distinct. For $h\ge 8,$ we observe that, ${\varphi }_f(v_{d_1(h)+d_2(h)+1})\le {\varphi }_f(v_{n(h)})\le {\varphi }_f(v_{d_1(h)+d_2(h)+d_3(h)-4}).$ If ${\varphi }_f(v_{n(h)})\ne {\varphi }_f(v_{d_1(h)+d_2(h)+i}),$ for any $i,1\le i\le d_3(h)-4,$ then all the induced vertex labels of F_h are distinct.

Suppose, if ${\varphi }_f(v_{n(h)})={\varphi }_f(v_{d_1(h)+d_2(h)+i}),$ for some i, $1\le i\le d_3(h)-4,$ then we define a relabeling function $f\prime :E(F_h)\to \{1,2,\dots ,n(h)-1\}$ such that $f\prime (e_i)=f(e_i),$ for i, $1\le i\le n(h)-4.$ $f\prime (e_{n(h)-3})=n(h)-1=f(e_{n(h)-1});$ $f\prime (e_{n(h)-2})=f(e_{n(h)-2});$ $f\prime (e_{n(h)-1})=n(h)-3=f(e_{n(h)-3}).$ Clearly $f\prime$ is a bijection.

The induced vertex labels are given by $\varphi {\prime }_{f\prime }(v_i)=\sum _{e\in E(v_i)}f\prime (e),$ where $1\le i\le n(h).$ By the definition of $f\prime ,$ we have, ${\varphi }_{f\prime }^{\prime }(v_i)={\varphi }_f(v_i)$ for $i,1\le i\le n(h)-4$ and $\varphi {\prime }_{f\prime }(v_{n(h)-3})={\varphi }_f(v_{n(h)-3})+2;$ $\varphi {\prime }_{f\prime }(v_{n(h)-2})={\varphi }_f(v_{n(h)-2});$ $\varphi {\prime }_{f\prime }(v_{n(h)-1})={\varphi }_f(v_{n(h)-1})$ and $\varphi {\prime }_{f\prime }(v_{n(h)})={\varphi }_f(v_{n(h)})-2.$

From the definition of $\varphi \prime ,$ the induced vertex labels of one degree and two degree vertices are all distinct. From (4(4) $${\varphi }_f(v_{2^{k-2}+1})<{\varphi }_f(v_{2^{k-2}+1}^{\prime }).$$(4) ), we have, $\varphi {\prime }_{f\prime }(v_{n(h)-2})-\varphi {\prime }_{f\prime }(v_{n(h)-3})=$ ${\varphi }_f(v_{n(h)-2})-{\varphi }_f(v_{n(h)-3})-2\ge 1$ and $\varphi {\prime }_{f\prime }(v_{n(h)})-\varphi {\prime }_{f\prime }(v_{d_1(h)+d_2(h)+i-1})$ $={\varphi }_f(v_{n(h)})-2-\varphi {\prime }_{f\prime }(v_{d_1(h)+d_2(h)+i-1})=$ ${\varphi }_f(v_{d_1(h)+d_2(h)+i})-2-{\varphi }_f(v_{d_1(h)+d_2(h)+i-1})$ $\ge 1.$ Hence, the induced vertex labels of three degree vertices are distinct and the root vertex label do not coincide with any of the other induced vertex labels.

Therefore, all the induced vertex labels of F_h are distinct.

Hence from Step 2, it is clear that the function defined in Step 2 is antimagic. Hence the Fibonacci tree F_h, for $h\ge 2$ is antimagic. □

In Figure 9, antimagic labeling of F₅ is shown as an illustration.

Figure 9. Antimagic labeling of Fibonacci tree F₅.

4. Discussion

It appears that recursively defined trees (like binomial trees and Fibonacci trees) favors for defining antimagic labeling. Thus, we end the article with the following question.

What are the other well-defined recursive classes of trees having the complementary structural property of the trees considered by Liang et al. [5] that admit antimagic labeling?

Acknowledgment

The authors profoundly thank both the anonymous referees for their valuable comments in improving the presentation of the paper.

Additional information

Funding

The second author is thankful to the Department of Science and Technology for providing financial support through the DST INSPIRE Fellowship [grant number: IF160354].