Independent point-set domination in line graphs

Abstract

Line graph of a graph G is an intersection graph of the edge set E(G) of G. In this paper, we obtain a sharp upper bound on the diameter of graph G whose line graph is an ipsd graph (graph possessing an independent point-set dominating set) by establishing a fundamental relation between diameter of G and diameter of its line graph L(G). We prove that if for a graph G, the length $c_{\text{ind}}(G)$ of the longest induced cycle is greater than 5, then its line graph does not possess an ipsd-set. Further we characterize certain classes of graphs viz., trees, complete graphs and complete bipartite graphs whose line graphs possess an independent point set dominating set.

Keywords:

• Domination
• point-set domination
• independent set
• line graph

2010 MATHEMATICS SUBJECT CLASSIFICATION:

• 05C69

1. Introduction

Throughout this paper we consider simple, finite, undirected and connected graphs. For any graph G, the set V(G) (or, simply V) and E(G) (or, simply E) represents its vertex set and edge set respectively. For standard terminologies used in this paper we refer to books by F. Harary [5] and Chartrand [3].

In 1993, E. Sampathkumar and Pushpa Latha [10] introduced the notion of point-set domination in graphs.

Definition 1.1.

[10] A set $D\subseteq V$ is defined to be a point-set dominating set (or, in short, psd-set) of G if for every non-empty subset $S\subseteq V(G)\setminus D,$ there exists a vertex $v\in D$ such that the subgraph $〈S\cup \left\{v\right\}〉$ is connected.

This definition can be seen as a natural extension of the concept of domination by using the interpretation that a subset D of the vertex set V of G is a dominating set if and only if for every singleton subset {s} of $V(G)\setminus D,$ there exists a vertex d in D such that the induced subgraph $〈\left\{s\right\}\cup \left\{d\right\}〉$ is connected.

We first give some basic definitions and important results which will be useful in our further investigation.

Definition 1.2.

[7] In a graph G, a set $I\subset V$ is an independent set if no two vertices in I are adjacent i.e, $〈I〉\cong \overline{K_{\left|I\right|}}.$ The independence number $\alpha (G)$ is defined as $$\alpha (G)=\max \left\{\right|I|:I\text{is an independent set of}G\}$$

An independent set I of G of cardinality $\alpha (G)$ is called an α-set of G.

Definition 1.3.

In a graph G, a point-set dominating set $D\subseteq V(G)$ is said to be an independent point-set dominating set (or, in short, an ipsd-set) of G if D is an independent subset of V(G).

It is interesting to observe that not every graph possesses an ipsd-set, for example C₆. To observe that the cycle $C_6=(v_1,v_2,..,v_6)$ is not an ipsd graph, take any independent subset I of C₆. Without loss of generality, we can assume that $v_1\in I.$ Then $v_2,v_6\notin I.$ If $v_4\in I,$ then $v_3,v_5\notin I$ and $〈\{v_2,v_5,x\}〉$ is not connected for any $x\in I.$ If $v_4\notin I,$ then for the set $\{v_2,v_4,v_6\}$ in $V\setminus I,$ there is no element $x\in I$ such that $〈\{v_2,v_4,v_6,x\}〉$ is connected. Hence C₆ is not an ipsd-graph. Thus a graph need not possess an ipsd-set and hence the study of graphs which possess an ipsd-set is of importance. In [1, 2, 4, 10], an in-depth study has been done towards characterizing graphs which possess an ipsd-set.

Definition 1.4.

A graph is said to be an ipsd graph if it possesses an ipsd-set.

Theorem 1.5.

[10] If a graph G is an ipsd graph, then $\mathit{diam}(G)\le 4.$

Theorem 1.6.

[1] For any graph G, if there exists a vertex $w\in V(G)$ such that $V(G)\setminus N(w)$ is independent, then G is an ipsd graph.

Theorem 1.7.

[1] A tree T is an ipsd graph if and only if $\mathit{diam}(T)\le 4.$

Proposition 1.8.

[1] A cycle C_n ($n\ge 3$) is an ipsd graph if and only if $n\le 5.$

Derived graphs play an important role in graph theory. Line graph is one such well studied class of derived graphs and is historically very rich. Significance of study of line graphs is also due to the fact that there is a linear time algorithm to recognize line graphs and to reconstruct their original graphs [8, 9].

Definition 1.9.

Line graph L(G) of any graph G is a graph with vertex set $V(L(G))=E(G)$ and two vertices in $V(L(G))$ are adjacent if the corresponding edges in G are adjacent.

In this paper, we study the existence of an ipsd-set in line graph of a graph. When it comes to possessing an ipsd-set, there is no direct relation between a graph and its line graph, that is, line graph of an ipsd graph may or may not be an ipsd graph and vice-versa. For example, consider the path P₆ of length 5, the graph itself is not an ipsd graph while its line graph is an ipsd graph. Also, the complete graph K₆ is an ipsd graph but its line graph is not an ipsd graph (see Theorem 3.6). Further, if we take the star $K_{1,n},$ then both $K_{1,n}$ and $L(K_{1,n})$ are ipsd graphs, while if we consider cycle C_n $(n\ge 6),$ then both C_n and $L(C_n)$ fail to possess an ipsd-set. Thus it is of interest to study graphs whose line graphs are ipsd graphs.

Our immediate aim is to obtain upper bounds on the diameter, induced cycle number $c_{\text{ind}}(G)$ (maximum cardinality of an induced cycle of G) [6] and girth for graphs whose line graphs possess an independent point-set dominating set (i.e., ipsd-set). To exhibit the bound on the diameter of graph G, we establish a fundamental relation between diameter of G and diameter of its line graph L(G). We, further, characterize certain classes of graphs viz., trees, complete graphs and complete bipartite graphs whose line graphs possess an independent point set dominating set.

2. Necessary conditions for ipsd

In this section, we obtain some necessary conditions for a graph whose line graph is an ipsd graph. We begin with proving that diameter of such a graph can not exceed 5. The main ingredient to prove this result is a folklore result which exhibits a relation between diameter of G and diameter of L(G). For this purpose we introduce following notations.

Notation 2.1.

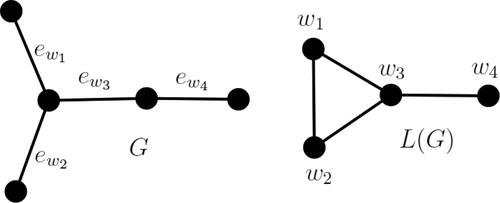
For any edge e in G, v_e will denote its corresponding vertex in L(G). For any vertex v in L(G), e_v will denote its corresponding edge in G.

Remark 2.2.

For any path $P_G=(u_1,u_2,\dots ,u_n)$ of vertices in G, the corresponding image in L(G) is a path of length n – 2 which we represent by $L(P_G)=(v_{e_1},v_{e_2},\dots ,v_{e_{n-1}}),$ where $e_i=u_i{u}_{i+1},$ for $i=1,2,\dots ,n-1.$ However for a path $Q_{L(G)}=(w_1,w_2,\dots ,w_n)$ of vertices in L(G), the corresponding inverse subgraph $〈\{e_{w_1},e_{w_2},\dots ,e_{w_n}\}〉$ of G, which we denote by $L^{-1}(Q_{L(G)}),$ may not be a path in the underlying graph G. In fact, in some cases $L^{-1}(Q_{L(G)})$ may fail to be a trail in G.

For example, refer Figure 1 with path $Q=(w_1,w_2,w_3,w_4).$

Figure 1. Graph G and its line graph L(G).

In the following result such an anomaly does not exist for paths in L(G) which are shortest in length.

Lemma 2.3.

In a graph G, if a path $P_{L(G)}$ is a geodesic of length k in L(G), then $L^{-1}(P_{L(G)})$ is a path of length k + 1 in G.

Proof.

Consider any geodesic $P_{L(G)}=(u=u_1,u_2,\dots ,u_{k+1}=v)$ of length k in L(G). We claim that $L^{-1}(P_{L(G)})=〈\{e_{u_1},e_{u_2},\dots ,e_{u_{k+1}}\}〉$ is a e_u-e_v path of length k + 1 in G. Suppose on the contrary, $L^{-1}(P_{L(G)})$ is not a path in G. Since $L^{-1}(P_{L(G)})$ is connected, there exists e_u-e_v path Q_G in $L^{-1}(P_{L(G)})$ of length at most k in G. But in that case $L(Q_G)$ is a u-v path of length at most k – 1 in L(G), a contradiction. Hence $L^{-1}(P_{L(G)})$ is a path in G consisting of k + 1 edges. Thus $L^{-1}(P_{L(G)})$ is a path of length k + 1 in G. □

Remark 2.4.

In the last theorem we observed that for any given graph G and any geodesic $P_{L(G)}$ of length k in L(G), the corresponding inverse subgraph $L^{-1}(P_{L(G)})$ is a path of length k + 1 in G. But $L^{-1}(P_{L(G)})$ need not be a geodesic in G. For example if we consider $G=(u_1,e_1,u_2,e_2,u_3,\dots ,u_5,e_5,u_1)$ to be a cycle of length 5. Then $L(G)=(v_{e_1},v_{e_2},\dots ,v_{e_5}).$ For the geodesic $P_{L(G)}=(v_{e_1},v_{e_2},v_{e_3})$ in L(G), $L^{-1}(P_{L(G)})=(u_1,u_2,u_3,u_4)$ is not a geodesic in G.

We now proceed to prove a fundamental result which provides bound for the diameter of L(G) in terms of the diameter of the graph G.

Theorem 2.5.

For any graph G, $\mathit{diam}(L(G))-1\le \mathit{diam}(G)\le \mathit{diam}(L(G))+1.$

Proof.

Let diam(G) = k. To prove the result, we will show that $k-1\le \mathit{diam}(L(G))\le k+1.$

We first show that $\mathit{diam}(L(G))\ge k-1.$ Let u and v be two vertices in G with $d(u,v)=k$ and $P_G=(u=u_1,e_1,u_2,e_2,\dots ,u_k,e_k,u_{k+1}=v)$ be u-v path in G of length k. Then corresponding path $L(P_G)=(v_{e_1},v_{e_2},\dots ,v_{e_k})$ is a path of length k – 1 in L(G). We claim that $d(v_{e_1},v_{e_k})=k-1.$ If $d(v_{e_1},v_{e_k})=l<k-1,$ then there exists a $v_{e_1}$-$v_{e_k}$ path (say) $Q_{L(G)}=(v_{e_1},w_1,w_2,\dots w_{l-1},v_{e_k})$ of length l in L(G). By Lemma 2.3, $L^{-1}(Q_{L(G)})$ is a path of length l + 1 in G from edge e₁ to e_k. Note that the vertex set of $L^{-1}(Q_{L(G)})$ contains u and v. Hence $L^{-1}(Q_{L(G)})$ contains a u-v sub-path (say) R (possibly $R=L^{-1}(Q_{L(G)})$) of length at most $l+1(<k),$ a contradiction to the fact that $d(u,v)=k.$ Thus, $\mathit{diam}(L(G))\ge k-1.$

Next we prove that $\mathit{diam}(L(G))\le k+1.$ Suppose, if possible, $\mathit{diam}(L(G))>k+1$ and let w₁, w₂ be two vertices in L(G) such that $d(w_1,w_2)=k+2.$ Also, let $e_{w_1}=x_1{x}_2$ and $e_{w_2}=y_1{y}_2$ be the corresponding edges in G. Since diam(G) = k, $d(x_1,y_1)\le k.$

Let $d(x_1,y_1)=k_0(\le k)$ and R_G be any shortest path from x₁ to y₁ of length k₀ in G. Then $S_G=〈\{x_2,y_2\}\cup V(R_G)〉$ is a $e_{w_1}$-$e_{w_2}$ path in G of length at most $k_0+2.$ But then $L(S_G)$ is an w₁-w₂ path in L(G) of length $k_0+1\le k+1<k+2,$ a contradiction to the fact that $d(w_1,w_2)=k+2.$ Hence the result follows. □

In Theorem 2.5, all inequalities are sharp. For example, if we take G = K₄, then diam(G) = 1 and $\mathit{diam}(L(G))=2.$ Likewise if we take G to be any path $P_{n+1}$ of length n, then diam(G) = n and $\mathit{diam}(L(G))=n-1.$ Also in case we take G isomorphic to any cycle C_n, then $\mathit{diam}(G)=\mathit{diam}(L(G))=n.$

The above fundamental result leads to a necessary condition for line graph of a graph to be an ipsd graph.

Theorem 2.6.

If line graph L(G) of graph G is an ipsd graph, then $\mathit{diam}(G)\le 5.$

Proof.

Proof follows immediately from Theorem 1.5 and Theorem 2.5. □

Remark 2.7.

Note that, since line graph of P₆ is an ipsd graph, the bound on diameter in Theorem 2.6 is sharp. Moreover, the condition in theorem is not sufficient, for example consider the cycle C₆.

Since line graphs are claw-free graphs (cf. [5]), following proposition about claw-free ipsd graphs will be quite useful in further investigation.

Proposition 2.8.

If G is a claw-free graph possessing an ipsd-set D, then $\alpha (V(G)\setminus D)\le 2$ and $|N(v)\cap D|\le 2$ for each $v\in V(G)\setminus D.$

Our next result throws light on the structure of the graphs whose line graphs are ipsd graphs, as regards the maximum length $c_{\mathit{ind}}(G)$ of an induced cycle in the graph.

Theorem 2.9.

If line graph L(G) of graph G is an ipsd graph, then $c_{\text{ind}}(G)\le 5.$

Proof.

Let L(G) be an ipsd graph and F be an ipsd-set of L(G). Let, if possible, $c_{\text{ind}}(G)\ge 6.$ Let $C=(u_1{e}_1{u}_2{e}_2\dots u_{n-1}{e}_{n-1}{u}_n{e}_n{u}_1)$ be a longest induced cycle in G. Since $c_{\text{ind}}(G)\ge 6,n\ge 6.$ If n > 6, then $V(L(G))\setminus F$ has at least three independent vertices from L(C). But since F is an ipsd-set of L(G), it induces the existence of an induced subgraph isomorphic to a claw, a contradiction to the fact that line graph L(G) is claw-free. Thus n = 6 and $C=(u_1{e}_1{u}_2{e}_2\dots u_5{e}_5{u}_6{e}_6{u}_1).$ Since F is independent, $|V(L(C))\cap F|\le 3.$ From Proposition 2.8, $\alpha (V(L(C))\setminus F)\le 2.$ Consequently, $|V(L(C))\cap F|=2.$

Without loss of generality, let $v_{e_1}\in V(L(C))\cap F.$ Then since $\alpha (V(L(C))\setminus F)\le 2,v_{e_4}\in V(L(C))\cap F.$ Since $\{v_{e_2},v_{e_5}\}$ is an independent set in $V(L(C))\setminus F$ and F is an ipsd-set of L(G), there exists $d\in F\setminus V(L(C))$ such that d is adjacent to both $v_{e_2}$ and $v_{e_5}.$ Then, e_d is adjacent to e₂ and e₅ in G. But then $e_d\in 〈V(C)〉,$ contradicting the assumption that C is an induced cycle in G. Hence our assumption is wrong and $c_{\text{ind}}(G)\le 5.$ □

Corollary 2.10.

If line graph L(G) of graph G is an ipsd graph, then $\mathit{girth}(G)\le 5.$

Proof.

Follows immediately from Theorem 2.9 and the fact that $\mathit{girth}(G)\le c_{\text{ind}}(G).$ □

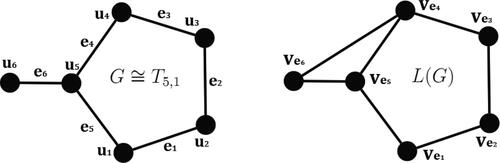
The next theorem characterizes graphs with girth 5 whose line graphs are ipsd graphs. We will show that cycle C₅ and tadpole $T_{5,1}$ are the only graphs with girth 5 whose line graphs are ipsd graphs.

Definition 2.11.

[11] A tadpole graph $T_{n,m}$ is a graph obtained by identifying a vertex of cycle C_n with an end vertex of path $P_{m+1}.$

Theorem 2.12.

For a graph G with girth 5, L(G) is an ipsd graph if and only if either $G\cong C_5$ or $G\cong T_{5,1}.$

Proof.

Necessity, let G be a graph with girth 5 such that L(G) is an ipsd graph. Let $C=(u_1,u_2,u_3,u_4,u_5,u_1)$ be any induced cycle of length 5 in G. If $G\cong C_5,$ then there is nothing to prove. Let $G\ncong C_5$ and F be an ipsd-set of L(G). Let $L(C)=(v_{e_1},v_{e_2},v_{e_3},v_{e_4},v_{e_5},v_{e_1})$ where $e_i=u_i{u}_{i+1}$ (addition in indices is addition modulo 5) for $i=1,2,\dots ,5.$ Since F is an independent set, $|F\cap V(L(C))|\le 2.$ Since F is ipsd-set of L(G) and C is an induced cycle of G, $|V(L(C))\cap F|=2.$ Without loss of generality assume that $V(L(C))\cap F=\{v_{e_1},v_{e_3}\}.$ Since $G\ncong C_5$ and G is connected, $(V(G)\setminus V(C))\cap N(V(C))\ne \varnothing .$

We claim that $(V(G)\setminus V(C))\cap N(V(C))\subset N(u_5).$ Suppose on the contrary, there exists $w\in (V(G)\setminus V(C))\cap N(V(C))$ such that $w\notin N(u_5).$ Then as girth(G) = 5, $w\in N(u_i)$ for exactly one $i\in \{1,2,3,4\}.$ If $w\in N(u_1),$ then we get an independent set $\{v_{e_{w{u}_1}},v_{e_2},v_{e_4}\}$ of cardinality 3 in $V(L(G))\setminus F,$ contradiction to Proposition 2.8. Hence $w\notin N(u_1).$ Similarly $w\notin N(u_4).$ If $w\in N(u_2),$ then $v_{e_{w{u}_2}}$ and $v_{e_4}$ are non-adjacent vertices in $V(L(G))\setminus F$ with no common neighborhood in F, contradiction to the fact that F is an ipsd-set. Hence $w\notin N(u_2).$ Likewise it can be proved that $w\notin N(u_3).$ But then $w\notin N(V(C)),$ a contradiction. Hence $(V(G)\setminus V(C))\cap N(V(C))\subset N(u_5).$

Next we claim that $d(u_5)=3.$ Suppose on the contrary, $d(u_5)\ge 4$ and $w_1,w_2\in N(u_5).$ Since F is independent set in L(G), at least one of $v_{e_{w_1{u}_5}}$ and $v_{e_{w_2{u}_5}}$ belongs to $V(L(G))\setminus F.$ Without loss of generality, let $v_{e_{w_1{u}_5}}\in V(L(G))\setminus F.$ But then $v_{e_2}$ and $v_{e_{w_1{u}_5}}$ are non-adjacent vertices in $V(L(G))\setminus F$ with no common neighborhood in F, contradiction to the fact that F is an ipsd-set. Thus $d(u_5)=3.$ Let $w\in N(u_5).$ Then $v_{e_{w{u}_5}}\in F.$ For otherwise, $v_{e_2}$ and $v_{e_{w{u}_5}}$ will form a pair of non-adjacent vertices in $V(L(G))\setminus F$ with no common neighborhood in F, a contradiction. Now to prove that $G\cong T_{5,1},$ it is enough to show that $|V(G)\setminus V(C_5)|=1,$ that is d(w) = 1. If there exists $x\in N(w)\setminus \left\{u_5\right\},$ then as $v_{e_{w{u}_5}}\in F$ and F is independent, it follows $v_{e_{xy}}\notin F.$ But then $\{v_{e_{xy}},v_{e_2}\}$ is an independent subset of $V(L(G))\setminus F$ with no common neighbourhood in F, a contradiction. Hence $|V(G)\setminus V(C_5)|=1$ and hence the result (Figure 2).

Figure 2. Graph $G\cong T_{5,1}$ and its line graph L(G).

Conversely, if $G\cong C_5,$ then $L(G)\cong C_5.$ By Proposition 1.8, L(G) is an ipsd graph and we are done in this case. Let $G\cong T_{5,1}$ and $C=(u_1,e_1,u_2,e_2,u_3,\dots ,u_5,e_5,u_1)$ be the cycle in G with pendant edge $e_6=\{u_5,u_6\}.$ Then $\{v_{e_1},v_{e_3},v_{e_6}\}$ is an ipsd-set for line graph L(G) of G. □

3. Characterization of some classes of graphs whose line graphs are ipsd graphs

In this section we consider some well known classes of graphs viz. trees, complete graphs, complete bipartite graphs, wheel graphs, grid graphs, $K_n\square K_2$ and $C_n\square K_2$ and characterize graphs in these classes, whose line graphs possess an ipsd-set. In this direction we first state two trivial observations which follow immediately from Theorem 1.7 and Proposition 1.8.

Observation 3.1.

1. Line graph $L(P_n)$ of a path P_n is an ipsd graph if and only if $n\le 6.$

2. Line graph $L(C_n)$ of a cycle C_n is an ipsd graph if and only if $n\le 5.$

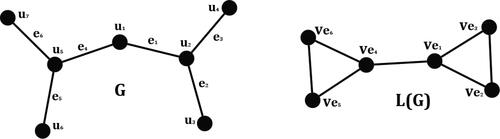
We now consider trees whose line graphs are ipsd graphs. From Theorem 2.6, we know that $\mathit{diam}(G)\le 5$ for every tree G whose line graph L(G) is an ipsd graph. But the condition is not sufficient in case of trees. There are trees G with $\mathit{diam}(G)\le 5$ whose line graph L(G) is not an ipsd graph. For example refer to tree G in Figure 3. For any independent set I of L(G), there exist two vertices u, v in $V\setminus I$ such that $d(u,v)=3>2$ (see Figure 3). Hence L(G) is not an ipsd graph.

Figure 3. Tree G with diameter 4.

Thus it is interesting to examine trees whose line graphs are ipsd graphs. Since line graph of a tree with diameter 2 is a complete graph and is, therefore, always an ipsd graph. For a tree G of diameter 3, the vertex v_e in L(G) corresponding to the edge e joining central vertices is a universal vertex in L(G) and therefore $\left\{v_e\right\}$ forms an ipsd-set of L(G). However, if we consider trees with diameter 4 or 5, then as pointed before, their line graphs may or may not possess an ipsd-set. Thus to characterize trees whose line graphs are ipsd, we need to focus on trees of diameter 4 and 5.

Theorem 3.2.

For a tree G with diameter 4, L(G) is an ipsd graph if and only if at most one vertex other than central vertex supports more than one pendant vertex.

Proof.

Let G be a tree of diameter 4 and w be the central vertex of G. Let F be an ipsd-set of L(G). Let, if possible, $u_1,u_2\in N(w)$ be such that each of them has more than one pendant neighbor. Let x₁, y₁ be two pendant neighbors of u₁ and x₂, y₂ be two pendant neighbors of u₂. Then at most one of $v_{u_1{x}_1},v_{u_1{y}_1}$ can belong to F. Similarly, at most one of $v_{u_2{x}_2},v_{u_2{y}_2}$ can belong to F. In each of the cases, we get two non adjacent vertices in $V(L(G))\setminus F$ with distance greater than 2, contrary to the assumption that F is a psd set of L(G) and hence the necessity follows.

Conversely, let G satisfy the given condition. If no vertex other than w supports more than one pendant vertex, then for any support vertex $u\in N(w),V(L(G))\setminus N(v_{wu})$ is an ipsd-set of L(G). If G has a vertex other than w, say u₀, which supports more than one pendant vertex, then $V(L(G))\setminus N(v_{w{u}_0})$ is an ipsd-set of L(G). □

Theorem 3.3.

Line graph L(G) of a tree G with diameter 5 is an ipsd graph if and only if every support vertex, except possibly, the two central vertices, has exactly one pendant neighbor.

Proof.

Let F be an ipsd-set of L(G). Let w₁, w₂ be the two central vertices of G. Let, if possible, there exist a support vertex $w\notin \{w_1,w_2\}$ which support more than one pendant vertex. Let x₁, x₂ be two distinct pendant neighbors of w. Then at least one of $v_{w{x}_1},v_{w{x}_2}$ must belong to $V(L(G))\setminus F,$ say $v_{w{x}_1}.$ Let $(u_0,u_1,w_1,w_2,w,x_1)$ be a diametrical path of L(G). But since F is psd set and $d(v_{w{x}_1},v_{u_1{u}_0})>2,d(v_{w{x}_1},v_{u_1{w}_1})>2,$ both of the adjacent vertices $v_{u_1{u}_0},v_{u_1{w}_1}$ must belong to F, which contradicts the fact that F is independent. Thus no vertex other than w₁, w₂ can support more than one pendant vertex and hence the necessity follows.

For converse part, suppose G satisfies given condition. Then $V(L(G))\setminus N_{L(G)}(v_{w_1{w}_2})$ is an independent psd set of L(G). Hence, the result. □

Theorem 3.4.

Line graph L(G) of a tree G is an ipsd graph if and only if one of the following conditions hold:

1. $1\le \mathit{diam}(G)\le 3$;

2. diam(G) = 4 and at most one vertex other than central vertex supports more than one pendant vertex;

3. diam(G) = 5 and every support vertex, except possibly, the two central vertices, has exactly one pendant neighbor.

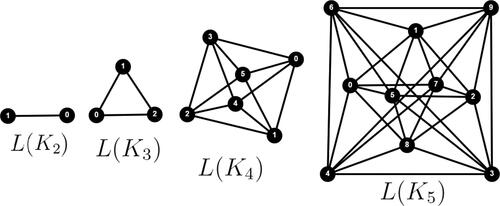
After completely characterizing trees whose line graphs are ipsd graphs, we next consider complete graphs. We will prove that line graph of a complete graph K_n is an ipsd graph if and only if $n\le 5.$ In Figure 4, line graphs of complete graphs $K_2,K_3,K_4$ and K₅ are illustrated. It is easy to check that the sets {0}, {0}, {0, 2} and {0, 2} are ipsd-sets of $L(K_2),L(K_3),L(K_4)$ and $L(K_5),$ respectively. Hence if $n\le 5,$ then $L(K_n)$ is an ipsd graph. Thus it remains to show that if n > 5, then $L(K_n)$ is not an ipsd graph. Following observations will be useful in proving this result.

Figure. 4. Line Graph of Complete Graphs K₂, K₃, K₄ and K₅.

Observation 3.5.

[3, 5] For complete graph K_n,

1. $\mathit{diam}(L(K_n))=2$ for $n\ge 4.$

2. $\alpha (L(K_n))=\lfloor \frac{n}{2}\rfloor .$

3. Every maximal independent set is maximum independent set of $L(K_n).$

4. For any α-set F of $L(K_n),\alpha (〈V(L(K_n))\setminus F〉)=\lfloor \frac{n}{2}\rfloor .$

Theorem 3.6.

Line graph of complete graph K_n is an ipsd graph if and only if $n\le 5.$

Proof.

Sufficiency follows immediately from above discussion. To prove necessity, let $L(K_n)$ be an ipsd graph and F be an ipsd-set of $L(K_n).$ Since every psd-set is a dominating set and every independent dominating set is a maximal independent set, by Observation 3.5, $\left|F\right|=\lfloor \frac{n}{2}\rfloor$ and $\alpha (〈V(L(K_n))\setminus F〉)=\lfloor \frac{n}{2}\rfloor .$ Also, by Proposition 2.8, $\alpha (〈V(L(K_n))\setminus F〉)\le 2.$ Thus $\lfloor \frac{n}{2}\rfloor \le 2$ and consequently, $n\le 5.$ □

Remark 3.7.

Note that for $n\le 5,$ every $\alpha (L(K_n))$-set of $L(K_n)$ will form an ipsd-set of $L(K_n).$

Theorem 3.8.

Line graph of a complete bipartite graph $K_{m,n}$ is an ipsd graph if and only if either $\min \{m,n\}=1$ or $m+n<6.$

Proof.

Let $L(K_{m,n})$ be an ipsd-graph and F be an ipsd-set of $L(K_{m,n}).$ Let $V(K_{m,n})=\{x_1,\dots ,x_m,y_1,\dots ,y_n\}$ and $E(K_{m,n})=\{x_i{y}_j:i=1,2,\dots m\text{and}$ $j=1,2,\dots n\}.$ If $\min \{m,n\}=1,$ then there is nothing to prove. Let $\min \{m,n\}>1$ and without loss of generality assume that $m\le n.$ To prove the theorem we need to show that $m+n<6.$ Suppose on the contrary, $m+n\ge 6.$ We have two possibilities:

Case 1. $m\ge 3.$ Then $n\ge 3.$ Without loss of generality assume that $v_{x_1{y}_1}\in F.$ Then as F is an independent set, $v_{x_1{y}_2},v_{x_1{y}_3},v_{y_1{x}_2},v_{y_1{x}_3}\in V(L(K_{m,n}))\setminus F.$ Again, since F is independent, at least one of $v_{x_3{y}_2},v_{x_3{y}_3}\in V(L(K_{m,n}))\setminus F.$ Then either $\{v_{x_1{y}_2},v_{y_1{x}_2},v_{x_3{y}_3}\}$ or $\{v_{x_1{y}_3},v_{y_1{x}_2},v_{x_3{y}_2}\}$ is an independent set in $V(K_{m,n})\setminus F,$ a contradiction to Proposition 2.8.

Case 2. m = 2. Then $n\ge 4.$ Without loss of generality we may assume that $v_{x_1{y}_1}\in F.$ Then $v_{x_1{y}_2},v_{x_1{y}_3},v_{x_1{y}_4},v_{y_1{x}_2}\in V(K_{m,n})\setminus F.$ Again, since F is independent set, at least two of $v_{x_2{y}_2},v_{x_2{y}_3},v_{x_2{y}_4}\in V(K_{m,n})\setminus F.$ Then in each possible case, we get at least two non adjacent vertices in $V(K_{m,n})\setminus F$ with no common neighbor in F, a contradiction.

Thus in both the possible cases, we arrive at a contradiction. Hence our assumption is wrong and $m+n<6.$ Hence the necessity.

Conversely, let G be a complete bipartite graph isomorphic to $K_{m,n}.$ If $\min \{m,n\}=1,$ then $L(K_{m,n})$ is a complete graph, which is trivially an ipsd graph. If $m+n<6,$ then every $\alpha (L(K_{m,n}))$-set will form an ipsd-set of $L(K_{m,n}).$ Hence the result follows. □

Definition 3.9.

A wheel graph W_n of order n + 1 is defined as graph join $K_1+C_n.$ In other words, a wheel graph contains a cycle C_n and a vertex (called root vertex) which is adjacent to every vertex of the cycle C_n.

Theorem 3.10.

Line graph of a wheel graph W_n is ipsd graph if and only if $n\le 4.$

Proof.

Let G be wheel graph W_n with w as root vertex and $C_n=(u_1,u_2,\dots ,u_n)$ as the underlying cycle. Let $L(W_n)$ be an ipsd graph and F be an ipsd-set of $L(W_n).$ Since C_n is induced cycle of W_n, by Theorem 2.9, $n\le 5.$ We claim that $n\le 4.$ If n = 5, then since F is independent, $|V(L(C_n))\cap F|\le 2.$ If $|V(L(C_n))\cap F|\le 1,$ then there exist two non adjacent vertices in $V(L(C_n))\setminus F$ without common neighbor in F, a contradiction. Therefore $|V(L(C_n))\cap F|=2$ and let $v_{u_1{u}_2},v_{u_4{u}_5}\in F.$ Then mutually non adjacent vertices $v_{u_1{u}_5},v_{u_2{u}_3},v_{w{u}_4}\in V(L(G))\setminus F,$ a contradiction to Proposition 2.8. Thus $n\le 4.$

Sufficiency, for $n\le 4,$ every α-set of $L(W_n)$ will form an ipsd-set of $L(W_n).$ □

Definition 3.11.

(Harary 1994, p. 22 [5]) The Cartesian graph product $G=G_1\square G_2$ of graphs G₁ and G₂ with disjoint point sets V₁ and V₂ and edge sets X₁ and X₂ is the graph with point set $V_1\times V_2$ and $u=(u_1,u_2)$ is adjacent with $v=(v_1,v_2)$ whenever u₁ = v₁ and u₂ is adjacent to v₂ in G₂ or u₁ is adjacent to v₁ in G₁ and u₂ = v₂.

Theorem 3.12.

Line graph of a grid $P_m\square P_n$ ($m\le n$) is an ipsd graph if and only if either m = 1 and $n\le 6$ or m = 2 and n = 2, 3.

Proof.

Necessity, let line graph of a grid $P_m\square P_n$ be an ipsd graph and F be an ipsd-set of $L(P_m\square P_n).$ If m = 1, then $P_m\square P_n\cong P_n$ and therefore $n\le 6$ and we are through. Let $m\ne 1.$ Then $n\ge m\ge 2.$ Let $V(L(P_m\square P_n))=\{(x_i,y_j)|x_i\in V(P_m),y_i\in V(P_n),i=1,2,\dots ,m\text{and}\mathrm{j}=1,2,\dots \mathrm{n}\}.$ If $m\ge 3,$ then since F is independent, at least one of $v_{(x_1,y_1)(x_1,y_2)},v_{(x_1,y_1)(x_2,y_1)}$ belongs to $V(L(P_m\square P_n))\setminus F$ and similarly at least one of $v_{(x_3,y_3)(x_2,y_3)},v_{(x_3,y_3)(x_3,y_2)}$ belongs to $V(L(P_m\square P_n))\setminus F.$ But in each possible combination, we get two non adjacent vertices in $V(L(P_m\square P_n))\setminus F$ with no common vertex in $L(P_m\square P_n),$ a contradiction. Hence m = 2. Then $n\ge 2.$ If $n\ge 4,$ then since F is independent, at least one of $v_{(x_1,y_1)(x_1,y_2)},v_{(x_1,y_1)(x_2,y_1)}$ belongs to $V(L(P_m\square P_n))\setminus F$ and similarly at least one of $v_{(x_2,y_4)(x_2,y_3)},v_{(x_2,y_4)(x_1,y_4)}$ belongs to $V(L(P_m\square P_n))\setminus F.$ But in each possible combination, we get two non adjacent vertices in $V(L(P_m\square P_n))\setminus F$ with distance greater than 2, a contradiction. Thus m = 2 and and n = 2, 3.

Conversely, If m = 1 and $n\le 6,$ then $L(P_m\square P_n)$ is a path of length at most 4 and is trivially an ipsd graph. Let m = 2 and n = 2, 3. If n = 2, then $L(P_m\square P_n)\cong C_4$ and trivially is an ipsd graph. If n = 3 and $V(L(P_2\square P_3))=\{(x_i,y_j)|x_i\in V(P_2),y_i\in V(P_3),i=1,2\text{and}\mathrm{j}=1,2,3\},$ then $\{v_{(x_1,y_1)(x_2,y_1)},v_{(x_1,y_2)(x_2,y_2)},v_{(x_1,y_3)(x_2,y_3)}\}$ will form an ipsd-set for $L(P_n\square P_m)$ and hence the result. □

Theorem 3.13.

$L(K_n\square K_2)$ ($n\ge 2$) is an ipsd graph if and only if n = 2, 3.

Proof.

Let $L(K_n\square K_2)$ be an ipsd graph. Let $V(K_n)=\{x_1,x_2,\dots ,x_n\}$ and $V(K_2)=\{y_1,y_2\}.$ $I=\{v_{(x_i,y_1)(x_i,y_2)},i=1,2,\dots ,n\}$ is a perfect matching of $L(K_n\square K_2)$ of cardinality n. Also by Observation 3.5, $L(K_n\square K_2)\setminus I$ has an independent set of cardinality $2\lfloor \frac{n}{2}\rfloor .$ These facts together with Proposition 2.8, imply that n < 4.

Conversely, $L(K_2\square K_2)$ is isomorphic to C₄ which is an ipsd graph. Now if n = 3, then $\{v_{(x_i,y_1)(x_i,y_2)}:i=1,2,3\}$ is an ipsd-set of $L(K_3\square K_2),$ hence the result. □

Theorem 3.14.

$L(C_n\square K_2)$ is an ipsd graph if and only if n = 3.

Proof.

Let $L(C_n\square K_2)$ be an ipsd graph. Let $V(C_n)=\{x_1,x_2,\dots ,x_n\}$ and $V(K_2)=\{y_1,y_2\}.$ $I=\{v_{(x_i,y_1)(x_i,y_2)},i=1,2,\dots ,n\}$ is a perfect matching of $L(C_n\square K_2)$ of cardinality n. Also since independence number of a cycle of order n is $\lfloor \frac{n}{2}\rfloor ,L(C_n\square K_2)\setminus I$ has an independent set of cardinality $2\lfloor \frac{n}{2}\rfloor .$ These facts together with Proposition 2.8, imply that n < 4.

Conversely, If n = 3, then $\{v_{(x_i,y_1)(x_i,y_2)}:i=1,2,3\}$ is an ipsd-set of $L(C_3\square K_2),$ hence the result. □

4. Conclusion

In this paper we have shown that for any graph G whose line graph is an ipsd graph, $\max \{\mathit{diam}(G),c_{\mathit{ind}}(G),\mathit{girth}(G)\}\le 5.$ We have completely characterized graphs G with girth(G) = 5 whose line graph is an ipsd graph. We have also obtained characterization in certain classes of graphs whose line graphs are ipsd graphs. It would be fascinating and challenging at the same time to obtain complete characterization of graphs whose line graphs are ipsd graphs.

Problem 1.

Characterize graphs G whose line graph is an ipsd graph.