?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.Abstract
A lexicographic product of graphs G and H, denoted by is defined as a graph with the vertex set
and an edge
presents in the product whenever
or (u1 = u2 and
). We investigate the sufficient conditions for vertex pancyclicity of lexicographic products of complete graphs Kn, paths Pn or cycles Cn with a general graph. We obtain that (i) if G1 is a traceable graph of even order and G2 is a graph with at least one edge, then
is vertex pancyclic; (ii) if G1 is hamiltonian and G2 is a graph with at least one edge, then
is vertex pancyclic.
1. Introduction
We consider a finite, undirected, simple graph G with the vertex set V(G) and the edge set E(G). The maximum degree of G is denoted by Most of the basic graph theory terminologies in this work follow from West’s textbook [Citation11]. An (s, t)-path of G is a path in G from vertex s to vertex t, denoted by P(s, t). Then, P(t, s) denotes the reversed path of P(s, t). The length of a path or cycle is the number of its edges. A path in G is a hamiltonian path or a spanning path if it contains all the vertices of G. A graph G is traceable if G contains a hamiltonian path. A cycle of G is a hamiltonian cycle if it contains all the vertices of G. A graph G is said to be hamiltonian if it contains a hamiltonian cycle. Otherwise, G is non-hamiltonian. A graph G of order n is said to be pancyclic if it contains a cycle of each length l for
A vertex of G is a k-vertex pancyclic if it is contained in a cycle of each length l for
and a graph G is a vertex k-pancyclic if all vertices of G are k-vertex pancyclic. We usually use pancyclic and vertex pancyclic instead of 3-vertex pancyclic and vertex 3-pancyclic, respectively. A graph G is said to be vertex even pancyclic if each vertex of G is contained in a cycle of each even length l for
In 1971, Bondy [Citation2] posed the metaconjecture which stated that almost any nontrivial sufficient condition on a graph which implies that the graph is hamiltonian also implies that the graph is pancyclic, otherwise there may be a simple family of exceptional graphs. There are several works supporting this metaconjecture (see [Citation10]). Apart from pancyclicity, there are a number of works show that those conditions also imply that the graph is vertex pancyclic. For instance, in 1960, Ore [Citation8] introduced degree sum condition which was stated that “for each pair of non-adjacent vertices u, v in G, ”and showed that if G is a graph satisfying the degree sum condition, then G is hamiltonian. Bondy [Citation3] showed that if G is graph satisfying the degree sum condition, then G is pancyclic or
In 1984, Xiaotao Cai [Citation5] considered the degree sum condition and proved that a graph G satisfying this condition is vertex 4-pancyclic or
(see [Citation10] for more examples).
Let G and H be two graphs. The cartesian product of graphs G and H, denoted by is defined as a graph with the vertex set
and an edge
presents in the cartesian product whenever u1 = u2 and
or symmetrically v1 = v2 and
The lexicographic product or graph composition of graphs G and H, denoted by is defined as a graph with the vertex set
and an edge
presents in the lexicographic product whenever
or (u1 = u2 and
). The double graph of a graph G is
From the definitions of the cartesian product and the lexicographic product of graphs G and H, we can see that and
Therefore, the vertex pancyclicity over
implies the vertex pancyclicity over
Here, we only consider vertex pancyclicity over
on the conditions that do not imply vertex pancyclic over
For cartesian products, they also have a bunch of works relating to the metaconjecture, i.e., almost any nontrivial condition on a cartesian product which implies that the cartesian product is hamiltonian also implies that the cartesian product is pancyclic (there may be a simple family of exceptional graphs).
Theorem 1.
[Citation9] If G is a 3-connected cubic graph, then is hamiltonian.
Theorem 2.
[Citation9] If G is an even 3-cactus, then is hamiltonian.
A cactus is a connected graph in which every block is a K2 or a cycle, where a block is a maximal 2-connected subgraph. A 3-cactus is a cactus with maximum degree 3. An even 3-cactus is a 3-cuctus in which all of its cycles are of even length.
Theorem 3.
[Citation1] If G is a connected graph, then is hamiltonian for
Theorem 4.
[Citation4] If G is a connected graph, then is hamiltonian for
Theorem 5.
[Citation4] Let G be a connected almost claw-free graph and be an even integer. Then,
is hamiltonian.
However, such conditions only imply that a cartesian product is vertex even pancyclic as follows.
Theorem 6.
[Citation6] If G is a 3-connected cubic graph, then is vertex even pancyclic.
Theorem 7.
[Citation6] If G is an even 3-cactus, then is vertex even pancyclic.
Theorem 8.
[Citation4] Let n be even and . If G is a 1-pendent cactus with
, then
is vertex even pancyclic.
A claw is a The vertex of degree 3 is its center. For a set
B is a dominating set if every vertex of G is in B or has a neighbor in B. A graph G is 2-dominated if the size of a minimum dominating set of G is at most 2. A graph G is called an almost claw-free graph if the set of center vertices of induced claws in G is independent and the neighborhood of each center vertex induces a 2-dominated subgraph. For a graph G, a vertex of degree 1 in G is called pendent if its neighbor is a vertex of degree at least 3 in G. A 1-pendent cactus is a cactus in which every vertex v has at most 1 pendent neighbor (v can have other non pendent neighbors).
Here, we notice that vertex pancyclicity over cartesian products is affected by the number of edges between each copy of a graph. This motivates us to consider lexicographic product that contains more edges.
For the pancyclicity of lexicographic products, there are a few results. In 2006, Kaiser and Kriesell [Citation7] investigated toughness conditions on a graph G that the lexicographic product of G and a graph is hamiltonian and also pancyclic in which stated that if G is 4-tough and H contains at least one edge, then is pancyclic. In addition, they showed the following theorem.
Theorem 9.
[Citation7] If G, H are graphs with at least one edge each, then either has no cycles, or it contains cycles of all lengths between the length of the shortest cycle and the length of the longest cycle.
The following theorem on vertex pancyclic will be used in this article.
Theorem 10.
[Citation5] Let G be a graph of order with
for distinct nonadjacent vertices u, v in G. Then, G is vertex 4-pancyclic unless n is even and
We know that a vertex pancyclic graph is hamiltonian. Then, a non-hamiltonian graph is not vertex pancyclic. Here, we provide the necessary condition for a graph to be hamiltonian as follows.
Theorem 11.
[Citation11] If G has a hamiltonian cycle, then for each nonempty set , the graph G – S has at most
components.
To study vertex pancyclicity over lexicographic products, we start by investigating the lexicographic product of Kn with a graph G in Subsection Citation2.Citation1. By Theorem 10, we obtain that is vertex pancyclic for
In Subsection Citation2.Citation2, we show that
is vertex pancyclic if G1 is a traceable graph of even order and G2 is a graph with at least one edge. Since G1 is traceble, we consider the lexicographic product of a path and G2 instead of the lexicographic product of G1 and G2. Furthermore, we directly show that if G1 and G2 are nontrivial traceable graphs, then
is vertex pancyclic. In Subsection Citation2.Citation3, we show that if G1 is hamiltonian and G2 is a graph with at least one edge, then
is vertex pancyclic. Since G1 is hamiltonian, we consider the lexicographic product of a cycle and G2 instead of the lexicographic product of G1 and G2.
2. Vertex pancyclicity of some lexicographic products
2.1. Complete Graphs
First of all, we investigate lexicographic products of complete graphs with a graph. Let Kn be a complete graph of order n and Ak be an empty graph of order k. Theorem 10 gives us the following theorem.
Theorem 12.
is vertex pancyclic for
and
Proof.
Let (x, y) be any vertex of Then,
Since
there are
such that
Then,
forms a cycle of length 3 containing (x, y).
Next, we can see that the order of is nk and
Let
such that
Then,
Since
is not isomorphic to a balance complete bipartite graph
by Theorem 10, we obtain that
is vertex 4-pancyclic. Thus, (x, y) is contained in a cycle of each length l for
Therefore,
is vertex pancyclic. □
Since Ak is a spanning subgraph of all graphs of order k, we obtain the following corollary.
Corollary 1.
Let and G be a graph. Then
is vertex pancyclic.
By Corollary 1, since C3 is a complete graph of order 3, we obtain the following corollary.
Corollary 2.
Let G be a graph. Then, is vertex pancyclic.
2.2. Paths
We start this section by considering the lexicographic product of a path P2 and any graph as follows.
Let and Ak be an empty graph of order k. Then,
is isomorphic to a balanced complete bipartite graph
with two partite sets, V1 and V2, where
and
Since a balanced complete bipartite graph is hamiltonian and also vertex even pancyclic for
(to prove that
is vertex even pancyclic, we can use the result that it is hamiltonian), we obtain that
is vertex even pancyclic for
Since Ak is a spanning subgraph of any graph of order k, we obtain the following remark.
Remark 1.
Let G be a nontrivial graph. Then, is vertex even pancyclic.
Now, we investigate the lexicographic product between P2 and a graph G as follows.
Theorem 13.
Let G be a nontrivial graph with at least one edge. Then, is vertex pancyclic.
Proof.
Let and
for
Since G contains at least one edge, assume that
Then,
and
are edges of
Let
If x = x1, then (x, y) is adjacent to both vertices (x2, y1) and (x2, y2). Thus,
is a cycle of length 3 containing (x, y). If x = x2, then (x, y) is adjacent to both vertices (x1, y1) and (x1, y2). Thus,
is a cycle of length 3 containing (x, y). Thus, each vertex of
is contained in a cycle of length 3.
Since is not isomorphic to any complete bipartite graph. Since
is of order
with
for any pair of distinct nonadjacent vertices u and v in
by Theorem 10, G is vertex 4-pancyclic.
Therefore, is vertex pancyclic. □
Now, we consider the lexicographic product of a path Pn for with a graph G.
Remark 2.
For any k and is non-hamiltonian.
Let and
Choose
Then,
Let H denote the graph
Then, H has k + 1 components,
and
By Theorem 11,
is non-hamiltonian.
From Remark 2, we can see that the lexicographic product of Pn and an empty graph is non-hamiltonian and not vertex pancyclic. We invertigate the condition of a graph G for to be vertex pancyclic and show that
is vertex pancyclic when n is even and G contains at least one edge. We start with the following lemmas.
Lemma 1.
Let . If u and v are on the different partite sets of a complete bipartite graph
, then there is a path P(u, v) in
of each odd length l for
Proof.
Let be a complete bipartite graph for
with partite sets V1 and V2. Assume that
and
For k = 2, let
and
We obtain that uv and
are paths P(u, v) of length 1 and 3, respectively.
For let
and
We can see that
is a subgraph of
induced by
Since a balanced complete bipartite graph is vertex even pancyclic,
contains a cycle of each even length l for
Let
be a cycle in
of even length l for some
Then, any two consecutive vertices of C contain in the different partite sets. Without loss of generality, let
and
We see that
if i is odd and
if i is even and
Then,
is a path P(u, v) in
of length l + 1. Note that l + 1 is an odd number. Since l is an arbitrary even number between 4 and
there exists a path P(u, v) in
of each odd length l for
In addition, uv and
are paths from u to v in
of length 1 and 3, respectively.
Therefore, there exists a path P(u, v) in of each odd length l for
□
Lemma 2.
Let be even and G be a nontrivial graph of order k. If
is a path and
, then
contains a path
of each length l for
Proof.
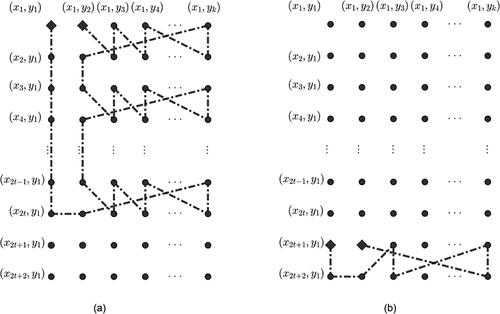
Let and
for
Since
vertices
and (x2, y2) form a clique of order 4. Then, there are paths
of length l for
We prove by the mathematical induction on n. For n = 2, let and
We can see that the subgraph induced by
in
is isomorphic to
Since
and
by Lemma 1, there exists a path
in
of each odd length l for
To show that there exists a path
of each length l for
we extend the path
of each length l for
as follows.
Join the vertex (x1, y1) with the vertex (x2, y2) of
(see ).
Join the vertex (x2, y1) of the edge
with the vertex (x2, y2) of
(see ).
Then, a path of each odd length l for
can be extended to a path
of each even length l for
by (a), and of each odd length l for
by (b). Thus, we obtain that there exists a path
of each length l for
For the induction step, let and suppose that the statement holds for all even n,
We show that the statement still holds for
Let
for
The set
induces a subgraph
of
By the induction hypothesis,
contains paths
of each length l for
In order to show that there exists a path
of each length l for
we preform three steps as follows.
We show that there is a path
of length
Let
for all
Consider each pair of vertex set
and
for all
We can see that the set
induces a subgraph
of
By Lemma 1, there is a path
of length
We connect such t paths,
for all
together to obtain a path
of length
By reversing path
there is a path
of length
(see ).
We show that there is a path
of length 2tk. From (i), there is
of length
and
is a path of length
(see ). Connecting
and
together yields a path
of length 2tk.
We show that there is a path
of each length l for
Let
be a path of length
By connecting
with
of length
from (i). We obtain a path
of length
(see ). Consider the set
The set
induces a subgraph
of
By the induction hypothesis,
contains a path
of each length l for
where each vertex of
contains in the set
(see ). Since
and
are adjacent to vertices
and
we replace the edge
of
by
of each length l for
and obtain a path
of each length l for
Therefore, there exist paths of each length l for
for n is an even number
□
By reversing path into
we also obtain that
contains a path
between
and
of each length l for
when n is even.
Theorem 14.
Let be even. If G is a graph with at least one edge, then
is vertex pancyclic.
Proof.
Let and
for
Since G contains at least one edge, without loss of generality, we assume that
We prove by the mathematical induction on n. For n = 2, Theorem 13 yileds that is vertex pancyclic.
For the induction step, let and suppose that the statement holds for all even n, where
We show that the statement still holds for
Let
for
The each set,
and
induces a subgraph
of
By the induction hypothesis, a vertex in the induced subgraph
is contained in a cycle of each length l for
Then, all vertices of
is contained in a cycle of each length l for
In order to show that
is vertex pancyclic, we show that each vertex of
is contained in a cycle of each length l for
Let (x, y) be a vertex of Without loss of generality, we assume that
We perform two steps as follows.
We show that there is a cycle of length
containing (x, y). By Lemma 2 and the reversing path, there is a path
of length
in the subgraph of
induced by
Moreover,
contains vertex (x, y). Since vertex
is adjacent to the two end verties of
we connect
to each end vertex of
Then, a cycle of length
containing (x, y) is obtained.
We show that there is a cycle of each length l for
containing (x, y). We can see that
is the subgraph of
induced by
By Lemma 2, there is a path
in
of each length l for
For the subgraph of
of
induced by
we obtain (from Lemma 2 and the reversing path) a path
of length
containing (x, y). Since
and
are adjacent to
and
respectively, we connect each end vertex of
to each end vertex of
together. Then, (x, y) is contained in a cycle of each length l for
Therefore, is vertex pancyclic for n is even. □
By Theorem 14, we obtain that is vertex pancyclic if n is even and G is a graph with at least one edge. Since a path Pn is a subgraph of traceable graphs of order n, we obtain the following corollary.
Corollary 3.
If G1 is a traceable graph of even order and G2 is a graph with at least one edge, then is vertex pancyclic.
Example 1.
Petersen graph is a graph of order 10 containing a hamiltonian path. By Corollary 3, the lexicographic product of this Petersen graph with a graph of at least one edge is vertex pancyclic.
Next, we investigate the lexicographic product of odd paths and a graph.
Theorem 15.
Let n > 2 be odd. If G is a graph of order with exactly one edge, then
is not vertex pancyclic.
Proof.
Let and
where
Assume that
Choose
Then,
Let H denote the graph
Then, H has
components,
for all
By Theorem 11,
is non-hamiltonian. Therefore,
is not vertex pancyclic. □
Therefore, if n is odd and G is a graph with the same condition as in Theorem 14, i.e.,G is a graph with at least one edge, then we cannot conclude anything about vertex pancyclic of
Now, we investigate the condition that provide vertex pancyclic over lexicographic products. We consider nontrivial traceable graphs G1 and G2 as follows.
Theorem 16.
If G1 and G2 are nontrivial traceable graphs, then is vertex pancyclic.
Proof.
Let G1 and G2 be traceable graphs of order n and m, respectively, for Let
and
be spanning paths in G1 and G2, respectively. Since G2 is a nontrivial traceable graph, G2 contains at least one edge.
If n is even, by Corollary 3, is vertex pancylic. Assume that n is odd. Let
and
be subgraphs of Pn. We can see that
and
are subgraphs of
By Theorem 14,
and
are vertex pancyclic. Then, each vertex of
is contained in a cycle of each length l for
We show that each vertex of is contained in a cycle of each length l for
Let (xi, yj) be a vertex of
for some
and
Case 1. Then, we consider the subgraph
Similar to the prove of Theorem 14, by reversing a path
of Lemma 2, there is a path
of length
containing vertex (xi, yj). Consider subgraph
of
This subgraph contains a path
where
Since each vertex of
is adjacent to vertices
and
we connect
with each end vertex of
respectively, for all
Then, (xi, yj) is contained in a cycle of length l for
Case 2. i = n. We consider the subgraph instead of
By Lemma 2, there is a path
of length
containing vertex (xi, yj). Consider subgraph
of the lexicographic product
It contains a path
where
By a similar argument as in case 1, we obtain that (xi, yj) is contained in a cycle of each length l for
Therefore, is vertex pancyclic. □
By Theorem 16, we obtain that is vertex pancyclic for all
even though n is an odd number, the following theorem is proved.
Corollary 4.
If G is a nontrivial traceable graph, then the double graph of G is vertex pancyclic.
2.3. Cycles
Theorem 17.
Let and Ak be an empty graph of order k. Then,
is hamiltonian.
Proof.
We see that is Cn which is hamiltonian. Assume that k > 1. Let
and
We can see that the path
in Cn forms the path
in
for each
Let
for
and
For
each pair of paths Pi and
is connected by the edge ei and the paths Pk and P1 are connected by the edge ek. A hamiltonian in
is
□
Since is a subgraph of
for any graph G of order k, we obtain the following corollaries.
Corollary 5.
If and G is a graph, then
is hamiltonian.
Corollary 6.
If G1 is hamiltonian and G2 is a graph, then is hamiltonian.
Corollary 6 does not hold for the cartesian product For counter example, let G2 be disconnected. Then,
is disconnected (and of course non-hamiltonian) although G1 is hamiltonian.
By Corollary 2, is vertex pancyclic for
Unfortunately, the lexicographic product of cycle Cn for
and empty graph Ak for
is not vertex pancyclic. For instance,
contains no cycle of length 5. Now, we investigate the condition of G that allows the product
to be vertex pancyclic.
Theorem 18.
Let . If G is a graph with exactly one edge, then
is vertex pancyclic.
Proof.
Let and
for
Since G contains exactly one edge, assume that
We can see that
is a spanning subgraph of
where
By Theorem 14,
is vertex pancyclic if n is even.
Assume that n is odd. Let and
We can see that
and
are subgraphs of
induced by
and
respectively. By Theorem 14,
and
are vertex pancyclic. Then, each vertex of
is contained in a cycle of each length l such that
We now apply Theorem 9 to show that each vertex is contained in a cycle of each length l such that
By Theorem 9 and Corollary 5, contains a cycle of each length l such that
Let
be a cycle in
of length l for some
for
and
We consider two cases as follows.
Case 1. does not form an edge in Cl. Then, Cl is a cycle in
Let (xs, yt) be a vertex of
where
and
If
for some
then (xs, yt) is contained in Cl. Assume that
for any α. We consider two subcases as follows.
Subcase 1.1. If for some
then
Since Cl is in
for any
and
This implies that
Since
Thus, we can replace
in Cl by (xs, yt). Therefore, (xs, yt) is contained in a cycle of length l.
Subcase 1.2. If for all
we translate cycle Cl to be
by defining an injective function. Let
We define an injective function
by
This function translates indices in each vertex
of the cycle Cl. The vertices with new indices are vertices of cycle
From this function, vertex
is translate into vertex
If
then
is contained in
Assume that
We can replace vertex
by vertex (xs, yt) as showed in Subcase 1.1. Hence, (xs, yt) is contained in a cycle of length l.
Case 2. forms an edge in Cl. Let S be a subgraph of G induced by the set
Then, S is a path
If k = 2, then
By Theorem 4,
is vertex pancyclic. Now, we assume that k > 2. Let
and
be subgraphs of
induced by
and
respectively. Then,
and
We can see that
We first show that all vertices of are contained in a cycle of length l. Since
forms an edge in Cl, Cl contains a vertex of
Then, there are vertices
and
contained in Cl for some
We translate cycle Cl into
as showed in Subcase 1.2, and obtain that all vertices in
are contained in a cycle of length l.
Next, we show that each vertex of is contained in a cycle of length l. Consider a cycle of maximum length in
The length of such cycles is at most 2n. Since the length of Cl is at least
and
for k > 2, the cycle Cl contains a vertex of
Let (xs, yt) be any vertex in
If
for some
then
Assume that
for any
If
for some
then
Similar to Subcase 1.1, we can replace vertex
by (xs, yt). Thus, (xs, yt) is in a cycle of length l. If
for all
then let
Similar to Subcase 1.2, we can translate cycle Cl into
Then, vertex
is translated into
If
then (xs, yt) is contained in
Otherwise, we can replace vertex
by (xs, yt) as shown in Subcase 1.1.
From these two cases, we conclude that each vertex is contained in a cycle of each length l for Therefore,
is vertex pancyclic. □
From Theorem 18, we can see that adding more edges into the graph G dose not affect vertex pancyclic property. Thus, we obtain the following corollary.
Corollary 7.
Let . If G is a graph with at least one edge, then
is vertex pancyclic.
If G1 is hamiltonian containing a spanning cycle Cn, then Cn is a subgraph of G1. We can extend Corollary 7 as follows.
Corollary 8.
If G1 is hamiltonian and G2 is a graph with at least one edge, then is vertex pancyclic.
3. Conclusion and discussion
This article obtain that is vertex pancyclic provided that
and
and
is vertex pancyclic for all positive integers n. However, the vertex pancyclicity of
can be obtained only for
is an even integer. If n = 1, then
Thus, the vertex pancyclicity of
depends on G. If
is an odd integer, then we can see from Theorem 15 that the vertex pancyclicity of
may depend on some conditions on n and k. Therefore, our future research will try to find the conditions which imply the vertex pancyclicity of the
when
is odd integer.
References
- Barnette, D, Rosenfeld, M. (1973). Hamiltonian circuits in certain prisms. Discrete Math 5: 389–394.
- Bondy, J. A. (1971). Pancyclic graph. In B. Rouge (eds.), Proceedings of the Second Louisiana Conference on Combinatorics, Graph Theory and Computing, Louisiana State University, Baton Rouge, LA, pp. 167–172.
- Bondy, J. A. (1971). Pancyclic graphs I. J. Combin. Theory Ser. B. 11(1): 80–84.
- Čada, R., Flandrin, E, Li, H. (2009). Hamiltonicity and pancyclicity of cartesian products of graphs. Discrete Math 309(22): 6337–6343.
- Cai, X.-T. (1984). On the panconnectivity of Ore graph. Sci. Sin. Ser. A. 27(7): 684–694.
- Goddard, W, Henning, M. A. (2001). Pancyclicity of the prism. Discrete Math. 234(1–3): 139–142.
- Kaiser, T, Kriesell, M. (2006). On the pancyclicity of lexicographic products. Graphs Combin. 22(1): 51–58.
- Ore, O. (1960). Note on Hamilton circuits. Amer. Math. Monthly 67(1): 55.
- Paulraja, P. (1993). A characterization of Hamiltonian prisms. J. Graph Theory 17(2): 161–171.
- Randerath, B., Schiermeyer, I., Tewes, M, Volkmann, L. (2002). Vertex pancyclic graphs. Discrete Appl. Math. 120(1–3): 219–237.
- West, D. B. (2001). Introduction to Graph Theory. 2nd ed. Hoboken, NJ: Prentice Hall.