Reduced non-zero component union graph of free semi-modules

Abstract

Let $\mathbb{M}$ be a finitely generated free semimodule over a semiring $\mathbb{S}$ with identity having the invariant basis number property. Let $\mathbb{B}=\{m_1,\dots ,m_k\}$ be a basis of $\mathbb{M}$ and let $a={\sum }_{i=1}^k{a}_i{m}_i\in \mathbb{M}.$ Then the skeleton of a with respect to $\mathbb{B}$ is defined as $S_{\mathbb{B}}(a)=\{m_i:a_i\ne 0 \text{and} 1\le i\le k\}.$ The reduced non-zero component union graph ${\Gamma }_U(\mathbb{M})$ of $\mathbb{M}$ with respect to $\mathbb{B},$ is the simple undirected graph with vertex set $V=\{a\in {\mathbb{M}}^{*} | a={\sum }_{i=1}^k{c}_i{m}_i,$ where at least one of the c_i’s is zero$\}$ and two distinct vertices $a,b\in V$ are adjacent if and only if $S_{\mathbb{B}}(a)\cup S_{\mathbb{B}}(b)=\mathbb{B}.$ In this paper, we show that the graph ${\Gamma }_U(\mathbb{M})$ is connected and find its domination number, clique number and chromatic number. In the case of finite semirings, we determine the order, size and degrees of vertices in ${\Gamma }_U(\mathbb{M}).$ Also, we give the characterization for planarity of ${\Gamma }_U(\mathbb{M}).$

Keywords:

• Modules
• semiring
• semimodule
• domination
• non-zero component graph

1991 Mathematics Subject Classification:

• 06F25
• 16Y60
• 05C10

1. Introduction

In recent years, the graphs derived from algebraic structures have become an interesting topic in the area of research. The advantage of studying graphs from algebraic structures is that one may realize some properties about algebraic structures through properties of derived graph structures and vice versa. Actually, the concept of a graph from a commutative ring was introduced by Beck [1] and later modified and named as zero-divisor graph by Anderson and Livingston [2]. Some of the well studied graphs from commutative rings are zero-divisor graph, total graph, comaximal graph, annihilating graph, unit graph, Cayley sum graph, generalized total graph and trace graph of matrices [3–8]. Any interested reader can refer the monograph [9] for complete literature on graphs from rings.

In the case of vector spaces, intersection graphs associated with subspaces of vector spaces were first studied in [10,11] and then Das [12–15] has introduced and investigated certain graphs associated with finite dimensional vector spaces. Recently, Bhuniya and Maity [16,17] have generalized some of the graphs from vector spaces to semimodules. From this, we intend to extend the study of the non-zero component union graph of a finite dimensional vector space [14] to a finitely generated free semimodule over a semiring with identity and having invariant basis number property.

2. Preliminaries

Let us recall certain notations and concepts which will be needed in the subsequent sections. By a graph $G=(V,E),$ we mean an undirected simple graph with V as the vertex set and E as the edge set. For a subset $A\subseteq V(G),〈A〉$ denotes the induced subgraph of G. For unspecified terms in graph theory, one may refer to [18]. Let $\mathbb{V}$ be a finite dimensional vector space of dimension k over a field $\mathbb{F}$ with $\mathbb{B}=\{m_1,m_2,\dots ,m_k\}$ as a basis. For $a\in \mathbb{V},$ let $a={\sum }_{i=1}^k{a}_i{m}_i.$ Now, the skeleton of $a\in \mathbb{V}$ with respect to $\mathbb{B}$ is defined as $S_{\mathbb{B}}(a)=\{m_i:a={\sum }_{i=1}^k{a}_i{m}_i,a_i\ne 0,1\le i\le k\}.$ The non-zero component union graph of $\mathbb{V}$ was introduced and studied by Das [14]. Actually, the non-zero component union graph $\Gamma ({\mathbb{V}}_{\mathbb{B}})$ of $\mathbb{V}$ is the simple undirected graph with vertex set ${\mathbb{V}}^{*}=\mathbb{V}\setminus \left\{0\right\}$ and two distinct vertices a and b are adjacent if and only if $S_{\mathbb{B}}(a)\cup S_{\mathbb{B}}(b)=\mathbb{B}.$ Note that $S_{\mathbb{B}}(c)=\mathbb{B} \forall c\in A=\{{\sum }_{i=1}^k{c}_i{m}_i:c_i\ne 0 \forall i(1\le i\le k)\}$ and so the vertices in A are adjacent to every other vertex in $\Gamma ({\mathbb{V}}_{\mathbb{B}}).$

Throughout this paper $\mathbb{S}$ is a commutative semiring with additive identity $0_{\mathbb{S}}$ and multiplicative identity $1_{\mathbb{S}}.$ Also $\mathbb{M}$ is a finitely generated and free semimodule over $\mathbb{S}$ with invariant basis number property. We take $\mathbb{B}=\{m_1,\dots ,m_k\}$ as a basis of $\mathbb{M},$ $k={\dim }_{\mathbb{S}}(\mathbb{M})$ (or $\mathit{ran}{k}_{\mathbb{S}}(\mathbb{M})$) and ${\mathbb{M}}^{*}=\mathbb{M}\setminus \left\{0_{\mathbb{M}}\right\}.$ If a semiring $\mathbb{S}$ is having invariant basis number property, then it follows that every vector of a finitely generated free semimodule $\mathbb{M}$ over $\mathbb{S}$ can be expressed uniquely as a linear combination of elements of $\mathbb{S}$ [19, Corollary 3.1]. i.e., if $\{m_1,m_2,\dots ,m_k\}$ is a basis of a free semimodule $\mathbb{M}$ over semiring $\mathbb{S},$ then every element $a\in \mathbb{M}$ can be expressed uniquely as $a=a_1{m}_1+a_2{m}_2+\dots +a_k{m}_k,$ where $a_i\in \mathbb{S}.$ We call a_i the ith component of a. One can refer Golan [20] for basic notions and results on semirings and semimodules.

In parallel to the definition of the non-zero component union graph of vector spaces, one can define the non-zero component union graph $\Gamma ({\mathbb{M}}_{\mathbb{B}})$ of a semi-module $\mathbb{M}.$ As observed earlier, elements in the set $\{{\sum }_{i=1}^k{c}_i{m}_i:c_i\ne 0 \forall i(1\le i\le k)\}$ are adjacent to every other vertex in $\Gamma ({\mathbb{M}}_{\mathbb{B}})$ of the non-zero component union graph of semi-modules. Due to this strong graph theoretical property, we delete these vertices and study about the non-zero component union graph in the case of finitely generated free semimodules. Hence we define, the reduced non-zero component union graph ${\Gamma }_U({\mathbb{M}}_{\mathbb{B}})$ of $\mathbb{M}$ with respect to the basis $\mathbb{B}$ as the simple undirected graph with vertex set $V=\{a\in {\mathbb{M}}^{*} | a={\sum }_{i=1}^k{c}_i{m}_i,$ where at least one of the c_i’s is zero$\}$ and two distinct vertices $a,b\in V$ are adjacent if and only if $S_{\mathbb{B}}(a)\cup S_{\mathbb{B}}(b)=\mathbb{B}.$ Here, for all $a\in V({\Gamma }_U({\mathbb{M}}_{\mathbb{B}})),$ we have $|S_{\mathbb{B}}(a)|\ge 1$ and $|S_{\mathbb{B}}(a)|<k.$ i.e., $1\le |S_{\mathbb{B}}(a)|\le k-1$ for all $a\in V({\Gamma }_U({\mathbb{M}}_{\mathbb{B}})).$

With the aim to extend the study on the non-zero component union graph to finitely generated free semimodules, in Section 3, first we observe that the properties of the graph ${\Gamma }_U({\mathbb{M}}_{\mathbb{B}})$ is independent on the choice of the basis $\mathbb{B}$ of $\mathbb{M}.$ Hence, we simply denote the reduced non-zero component union graph of $\mathbb{M}$ as ${\Gamma }_U(\mathbb{M}).$ Thereafter, we discuss certain basic properties like connectedness, diameter and girth of the reduced non-zero component union graph ${\Gamma }_U(\mathbb{M})$ of $\mathbb{M}.$ In Section 4, we find the domination number, clique number and chromatic number of ${\Gamma }_U(\mathbb{M}).$ In Section 5, we determine the degrees of the vertices in ${\Gamma }_U(\mathbb{M})$ and also obtain the order and size of ${\Gamma }_U(\mathbb{M})$ when the underlying semiring is finite. Finally, we obtain a characterization for ${\Gamma }_U(\mathbb{M})$ to be a chordal graph or planar graph.

3. Basic properties of ${\Gamma }_U(\mathbb{M})$

In this section, we obtain some basic properties of the graph ${\Gamma }_U(\mathbb{M})$ like connectedness, diameter and girth. Also we prove that when ${\Gamma }_U(\mathbb{M})$ is complete bipartite.

The following concerns about ${\Gamma }_U({\mathbb{M}}_{{\mathcal{B}}_1})$ and ${\Gamma }_U({\mathbb{M}}_{{\mathcal{B}}_2})$ with respect to two bases ${\mathcal{B}}_1$ and ${\mathcal{B}}_2$ of $\mathbb{M}$ of equal cardinality.

Theorem 3.1.

Let $\mathbb{M}$ be a finitely generated free semimodule over a semiring $\mathbb{S}$ with two bases ${\mathcal{B}}_1=\{m_1,\dots ,m_k\}$ and ${\mathcal{B}}_2=\{n_1,\dots ,n_k\}$ of $\mathbb{M}$. Then the graphs ${\Gamma }_U({\mathbb{M}}_{{\mathcal{B}}_1})$ and ${\Gamma }_U({\mathbb{M}}_{{\mathcal{B}}_2})$ are isomorphic.

Proof.

Define $\Phi :\mathbb{M}\to \mathbb{M}$ by $\Phi (c_1{m}_1+\cdots +c_k{m}_k)=c_1{n}_1+\cdots +c_k{n}_k.$ Clearly $\Phi$ is an $\mathbb{S}$-semimodule isomorphism on $\mathbb{M}$ such that $\Phi (m_i)=n_i$ for all $i\in \{1,2,\dots ,k\}.$ One can check that the restriction ${\Phi }^{\prime }:V({\Gamma }_U({\mathbb{M}}_{{\mathcal{B}}_1}))\to V({\Gamma }_U({\mathbb{M}}_{{\mathcal{B}}_2}))$ of $\Phi$ on ${\mathbb{M}}^{*}\setminus \{{\sum }_{i=1}^k{c}_i{m}_i:c_i\ne 0 \forall i\}$ is a graph isomorphism. □

Remark 3.2.

In view of Theorem 3.1, properties of ${\Gamma }_U({\mathbb{M}}_{\mathcal{B}})$ does not depend on the choice of the basis $\mathbb{B}$ for $\mathbb{M}.$ So one can take any basis of $\mathbb{M}$ to study ${\Gamma }_U({\mathbb{M}}_{\mathbb{B}})$ henceforth, we do not refer the basis $\mathbb{B}$ of $\mathbb{M}$ in the notation of the graph ${\Gamma }_U(\mathbb{M}).$ Also hereafter, we denote the skeleton of $a\in \mathbb{M}$ as S(a) without any reference to the basis $\mathbb{B}$ of $\mathbb{M}.$

Now, let us see some examples of ${\Gamma }_U(\mathbb{M}).$

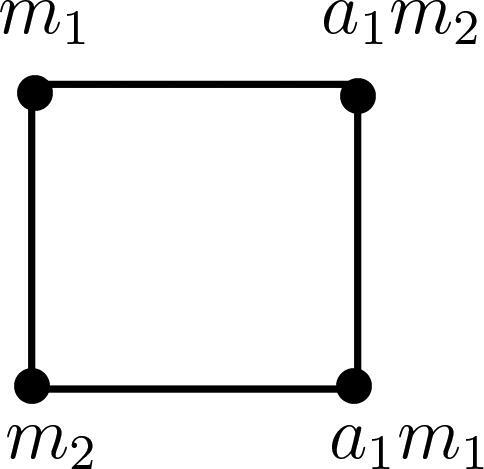
Example 3.3.

If $\dim (\mathbb{M})=1,$ then ${\Gamma }_U(\mathbb{M})$ is the null graph. If $\dim (\mathbb{M})=2$ and $\left|\mathbb{S}\right|=2,$ then ${\Gamma }_U(\mathbb{M})$ is the complete graph K₂ as given in Figure 1. When $\dim (\mathbb{M})=2$ and $\left|\mathbb{S}\right|=3,$ then ${\Gamma }_U(\mathbb{M})$ is the cycle C₄ as given in Figure 2. When $\dim (\mathbb{M})=3$ and $\left|\mathbb{S}\right|=2,$ then ${\Gamma }_U(\mathbb{M})$ is the graph given in Figure 3.

Figure 1. $\dim (\mathbb{M})=2;\left|\mathbb{S}\right|=2.$

Figure 2. $\dim (\mathbb{M})=2;\left|\mathbb{S}\right|=3.$

Figure 3. $\dim (\mathbb{M})=3;\left|\mathbb{S}\right|=2.$

Next, we investigate the connectedness and diameter of ${\Gamma }_U(\mathbb{M}).$

Lemma 3.4.

Let $\mathbb{M}$ be a finitely generated free semimodule over a semiring $\mathbb{S}$. If $\dim (\mathbb{M})=2$ and $\left|\mathbb{S}\right|\ge 2$, then ${\Gamma }_U(\mathbb{M})$ is connected.

Proof.

As observed in Example 3.3, ${\Gamma }_U(\mathbb{M})=K_2$ when $\dim (\mathbb{M})=2$ and $\left|\mathbb{S}\right|=2$ and so connected. So let us assume that $\left|\mathbb{S}\right|\ge 3.$

Assume that $\mathbb{B}=\{m_1,m_2\}$ be a basis of $\mathbb{M}.$ Let a and b be two distinct vertices in ${\Gamma }_U(\mathbb{M}).$ If a and b are adjacent in ${\Gamma }_U(\mathbb{M}),$ then $d(a,b)=1.$ Suppose a and b are not adjacent. Without loss of generality, one can assume that $S(a)\cup S(b)=\left\{m_1\right\}.$ Since $|S(a)|\ge 1$ and $|S(b)|\ge 1,$ we have $S(a)=\left\{m_1\right\}=S(b).$ Now, we choose a vertex $c\in V({\Gamma }_U(\mathbb{M}))$ such that $S(c)=\left\{m_2\right\}.$ Then $a-c-b$ is a path in ${\Gamma }_U(\mathbb{M})$ and so $d(a,b)=2.$ □

Theorem 3.5.

Let $\mathbb{M}$ be a finitely generated free semimodule over a semiring $\mathbb{S}.$ If $\dim (\mathbb{M})\ge 3,$ then ${\Gamma }_U(\mathbb{M})$ is connected with diameter 3.

Proof.

Assume that $\mathbb{B}=\{m_1,m_2,\dots ,m_k\}$ be a basis of $\mathbb{M}.$ Let a and b be two distinct vertices in ${\Gamma }_U(\mathbb{M}).$ If a and b are adjacent in ${\Gamma }_U(\mathbb{M}),$ then $d(a,b)=1.$ Otherwise, $S(a)\cup S(b)\subset \mathbb{B}.$ Since $a,b\in V({\Gamma }_U(\mathbb{M})),$ there exists $\mathcal{\ell }$ and r such that $a_{\mathcal{\ell }}\ne 0$ and $b_r\ne 0.$ This implies that $m_{\mathcal{\ell }}\in S(a)$ and $m_r\in S(b).$

Case (i). If $\mathcal{\ell }=r,$ then we take a vertex $c\in V({\Gamma }_U(\mathbb{M}))$ such that $c_{\mathcal{\ell }}=0$ and $c_i\ne 0$ for all $1\le i\le k,$ $i\ne \mathcal{\ell }.$ In this case, we have $S(c)=\mathbb{B}\setminus \left\{m_{\mathcal{\ell }}\right\}=\mathbb{B}\setminus \left\{m_r\right\}, S(a)\cup S(c)=\mathbb{B}$ and $S(c)\cup S(b)=\mathbb{B}.$ Hence $a-c-b$ is a path in ${\Gamma }_U(\mathbb{M})$ and so $d(a,b)=2.$

Case (ii). If $\mathcal{\ell }\ne r,$ then we choose vertices $c,d\in V({\Gamma }_U(\mathbb{M}))$ such that $c_{\mathcal{\ell }}=0,$ $c_i\ne 0$ for all $1\le i\le k,$ $i\ne \mathcal{\ell }$ and $d_r=0,$ $d_i\ne 0$ for all $1\le i\le k,$ $i\ne r.$ Now, we have $S(c)=\mathbb{B}\setminus \left\{m_{\mathcal{\ell }}\right\}, S(d)=\mathbb{B}\setminus \left\{m_r\right\}, S(a)\cup S(c)=\mathbb{B}, S(c)\cup S(d)=\mathbb{B}$ and $S(d)\cup S(b)=\mathbb{B}.$ Hence $a-c-d-b$ is a path in ${\Gamma }_U(\mathbb{M})$ and $d(a,b)=3.$

Thus ${\Gamma }_U(\mathbb{M})$ is connected and $\mathit{diam}({\Gamma }_U(\mathbb{M}))=3.$ □

In view of Lemma 3.4 and Theorem 3.5, we have the following corollary, which gives the diameter for ${\Gamma }_U(\mathbb{M}).$

Corollary 3.6.

Let $\mathbb{M}$ be a finitely generated free semimodule over a semiring $\mathbb{S}$ of dimension k. Then $$\mathit{diam}({\Gamma }_U(\mathbb{M}))=\{\begin{array}{c}3\mathrm{ } if k\ge 3;\hfill \\ 2\mathrm{ } if k=2 \text{and} \left|\mathbb{S}\right|\ge 3;\hfill \\ 1\mathrm{ } if k=2 \text{and} \left|\mathbb{S}\right|=2.\hfill \end{array}$$

If $\dim (\mathbb{M})\ge 3,$ then one can partition the vertex set of ${\Gamma }_U(\mathbb{M})$ into three sets $H_1, H_2$ and H₃ where

$H_1=\{{\sum }_{j=1}^k{c}_j{m}_j\hspace{0.17em}:\hspace{0.17em}\exists \mathit{\text{only}} \mathit{\text{one}} \mathit{i} \mathit{\text{such}} \mathit{\text{that}} {\mathit{c}}_{\mathit{i}}\ne 0 \mathit{\text{and}}\hspace{0.17em}{\mathit{c}}_{\mathit{j}}=0 \forall 1\le \mathit{j}\ne \mathit{i}\le \mathit{k}\}$

$H_2=\{{\sum }_{j=1}^k{c}_j{m}_j : \exists \mathit{\text{only}} \mathit{\text{one}} \mathit{i} \mathit{\text{such}} \mathit{\text{that}} {\mathit{c}}_{\mathit{i}}=0 \mathit{\text{and}} {\mathit{c}}_{\mathit{j}}\ne 0 \forall 1\le \mathit{j}\ne \mathit{i}\le \mathit{k}\}$ and $$H_3=V({\Gamma }_U(\mathbb{M}))\setminus (H_1\cup H_2).$$

In the remaining part of the paper, we make use of these sets and their induced subgraphs while studying about the graph ${\Gamma }_U(\mathbb{M}).$

Lemma 3.7.

Let $\mathbb{M}$ be a finitely generated free semimodule over a semiring $\mathbb{S}$ with $\dim (\mathbb{M})\ge 3.$ Let

$H_1=\{{\sum }_{j=1}^k{c}_j{m}_j : \exists \mathit{\text{only}} \mathit{\text{one}} \mathit{i} \mathit{\text{such}} \mathit{\text{that}} {\mathit{c}}_{\mathit{i}}\ne 0 \mathit{\text{and}} {\mathit{c}}_{\mathit{j}}=0\hspace{0.17em}\forall 1\le \mathit{j}\ne \mathit{i}\le \mathit{k}\}$

$H_2=\{{\sum }_{j=1}^k{c}_j{m}_j : \exists \mathit{\text{only}} \mathit{\text{one}} \mathit{i} \mathit{\text{such}} \mathit{\text{that}} {\mathit{c}}_{\mathit{i}}=0 \mathit{\text{and}} {\mathit{c}}_{\mathit{j}}\ne 0 \forall 1\le \mathit{j}\ne \mathit{i}\le \mathit{k}\}$ and $H_3=V({\Gamma }_U(\mathbb{M}))\setminus (H_1\cup H_2).$

Then H₁ is an independent set and every vertex of H₁ is adjacent to some vertices of H₂ only.

Proof.

Let $x,y\in H_1.$ By the definition of $H_1,$ $S(x)=\left\{m_{\mathcal{\ell }}\right\}$ and $S(y)=\left\{m_r\right\}$ for some $\mathcal{\ell }$ and r in $\{1,2,\dots ,k\}.$ Since $\dim (\mathbb{M})\ge 3,$ we have $S(x)\cup S(y)\subset \mathbb{B}$ and so x and y are not adjacent in ${\Gamma }_U(\mathbb{M}).$ Thus H₁ is an independent set in ${\Gamma }_U(\mathbb{M}).$

Let $x\in H_1$ and $y\in H_3.$ Then $S(x)=\left\{m_{\mathcal{\ell }}\right\}$ and $y={\sum }_{j=1}^k{y}_j{m}_j,$ there exists at least two components s and t such that $y_s=0,y_t=0$ and $s\ne t.$ Therefore $S(y)\subseteq \mathbb{B}\setminus \{m_s, m_t\}.$

If $\mathcal{\ell }=s,$ then $m_t\notin S(x)\cup S(y)$ and so $S(x)\cup S(y)\subset \mathbb{B}.$ Hence x and y are not adjacent in ${\Gamma }_U(\mathbb{M}).$ Similarly the assertion is true when $\mathcal{\ell }=t.$

If $\mathcal{\ell }\ne s$ and $\mathcal{\ell }\ne t,$ then $m_s,m_t\notin S(x)\cup S(y).$ Hence x is not adjacent to y. Therefore a vertex in H₁ is not adjacent to any of the vertices in $H_3.$

Let $x=c_{\mathcal{\ell }}{m}_{\mathcal{\ell }}\in H_1.$ Trivially $c_{\mathcal{\ell }}\ne 0.$ Let $y={\sum }_{j=1}^k{d}_j{m}_j \in H_2$ where $d_{\mathcal{\ell }}=0$ and $d_j\ne 0$ for all $1\le j\ne \mathcal{\ell }\le k.$ One can see that x and y are adjacent in ${\Gamma }_U(\mathbb{M}).$ □

Lemma 3.8.

Let $\mathbb{M}$ be a finitely generated free semimodule over a semiring $\mathbb{S}$ of dimension $k\ge 3$. Let

$H_2=\{{\sum }_{j=1}^k{c}_j{m}_j\hspace{0.17em}:\hspace{0.17em}\exists \text{only} \text{one} \mathrm{i} \text{such} \text{that} {\mathrm{c}}_{\mathrm{i}}=0 \text{and} {\mathrm{c}}_{\mathrm{j}}\ne 0 \forall 1\le \mathrm{j}\ne \mathrm{i}\le \mathrm{k}\}.$ Then $〈H_2〉$ is a complete k-partite graph in ${\Gamma }_U(\mathbb{M}).$

Proof.

Let $X_i=\{{\sum }_{j=1}^k{c}_j{m}_j : c_i=0 \text{and} c_j\ne 0 \forall 1\le j\ne i\le k\}\subset H_2$ for $1\le i\le k.$ Clearly $H_2={\cup }_{i=1}^k{X}_i.$ By definition, each X_i is an independent set in $〈H_2〉.$ Also further every vertex in X_i is adjacent to all the vertices in ${\cup }_{j=1,j\ne i}^k{X}_j$ and hence $〈H_2〉$ is a complete k-partite graph. □

In the following, we see that when ${\Gamma }_U(\mathbb{M})$ is complete bipartite.

Theorem 3.9.

Let $\mathbb{M}$ be a finitely generated free semimodule over a semiring $\mathbb{S}$. Then ${\Gamma }_U(\mathbb{M})$ is complete bipartite if and only if $\dim (\mathbb{M})=2.$

Proof.

Assume that ${\Gamma }_U(\mathbb{M})$ is a complete bipartite graph. Suppose $\dim (\mathbb{M})>2.$ This implies that there exist $x, y, z\in H_2$ such that $x_i=0, y_j=0$ and $z_{\mathcal{\ell }}=0$ for $i\ne j\ne \mathcal{\ell }.$ By the definition of $H_2,$ we have $S(x)=\mathbb{B}\setminus \left\{m_i\right\}, S(y)=\mathbb{B}\setminus \left\{m_j\right\}$ and $S(z)=\mathbb{B}\setminus \left\{m_{\mathcal{\ell }}\right\}.$ Now, the subgraph induced by $\{x, y, z\}$ of ${\Gamma }_U(\mathbb{M})$ is $K_3,$ which is a contradiction to ${\Gamma }_U(\mathbb{M})$ does not contain an odd cycle. Hence $\dim (\mathbb{M})=2.$

Conversely, assume that $\dim (\mathbb{M})=2$ and $\{m_1,m_2\}$ be a basis of $\mathbb{M}.$ Now, the vertex set of ${\Gamma }_U(\mathbb{M})$ is of the form $V({\Gamma }_U(\mathbb{M}))=A_1\cup A_2$ where $A_1=\{a_1{m}_1 : a_1\ne 0\}$ and $A_2=\{a_2{m}_2 : a_2\ne 0\}$ and $A_1\cap A_2=\varnothing .$ Clearly $S(a)=\left\{m_1\right\}$ for all $a\in A_1$ and $S(b)=\left\{m_2\right\}$ for all $b\in A_2.$ Therefore, by the adjacency of ${\Gamma }_U(\mathbb{M})$ we see that A₁ and A₂ are independent sets in ${\Gamma }_U(\mathbb{M})$ and also $S(a)\cup S(b)=\mathbb{B}$ for all $a\in A_1$ and $b\in A_2.$ Hence every vertex in A₁ is adjacent to every vertex in A₂ and so ${\Gamma }_U(\mathbb{M})$ is complete bipartite. □

In the following lemma, we see that when ${\Gamma }_U(\mathbb{M})$ is complete.

Lemma 3.10.

Let $\mathbb{M}$ be a finitely generated free semimodule over a semiring $\mathbb{S}$ of dimension k. Then ${\Gamma }_U(\mathbb{M})$ is complete if and only if $\dim (\mathbb{M})=2$ and $\left|\mathbb{S}\right|=2.$

Proof.

Assume that ${\Gamma }_U(\mathbb{M})$ is complete. Suppose $\dim (\mathbb{M})\ge 3.$ By Lemma 3.7, H₁ is an independent set with at least three elements, a contradiction to ${\Gamma }_U(\mathbb{M})$ is complete. Therefore $\dim (\mathbb{M})\le 2.$ Note that ${\Gamma }_U(\mathbb{M})$ is a null graph when $\dim (\mathbb{M})=1$ and so we have $\dim (\mathbb{M})=2.$ Suppose $\left|\mathbb{S}\right|\ge 3.$ Then there exists $a\in \mathbb{S}\setminus \{0,1\}$ and so m₁ is not adjacent to $a{m}_1,$ again a contradiction. Thus $\left|\mathbb{S}\right|=2.$

Conversely, assume that $\dim (\mathbb{M})=2$ and $\left|\mathbb{S}\right|=2.$ Then ${\Gamma }_U(\mathbb{M})$ is K₂ as seen in Figure 1. □

Now, we obtain the girth of the graph ${\Gamma }_U(\mathbb{M}).$

Theorem 3.11.

Let $\mathbb{M}$ be a finitely generated free semimodule over a semiring $\mathbb{S}$ of dimension k. Then $$gr({\Gamma }_U(\mathbb{M}))=\{\begin{array}{c}3\mathrm{ } if k\ge 3;\hfill \\ 4\mathrm{ } if k=2 \mathit{\text{and}} \left|\mathbb{S}\right|\ge 3;\hfill \\ \infty \mathrm{ }if k=2 \mathit{\text{and}} \left|\mathbb{S}\right|=2.\hfill \end{array}$$

Proof.

Let $\mathbb{B}=\{m_1,m_2,\dots ,m_k\}$ be a basis for $\mathbb{M}.$

• Case 1. Assume that $k\ge 3.$ Let a, b, c be the vertices in $V({\Gamma }_U(\mathbb{M}))$ such that $S(a)=\{m_1, m_2,\dots ,m_{k-1}\},S(b)=\{m_1,\dots ,m_{k-2}, m_k\},$ and $S(c)=\{m_1,\dots ,m_{k-3}, m_{k-1}, m_k\}.$ Then $〈\{a,b,c\}〉=K_3$ is an induced subgraph of ${\Gamma }_U(\mathbb{M})$ and so $gr({\Gamma }_U(\mathbb{M}))=3.$

• Case 2. Let k = 2 and $\left|\mathbb{S}\right|\ge 3.$ By Theorem 3.9, ${\Gamma }_U(\mathbb{M})$ is complete bipartite and hence $gr({\Gamma }_U(\mathbb{M}))=4.$

• Case 3. If k = 2 and $\left|\mathbb{S}\right|=2,$ then as observed in Example 3.3, ${\Gamma }_U(\mathbb{M})$ is K₂ and hence $gr({\Gamma }_U(\mathbb{M}))=\infty .$ □

4. Parameters of ${\Gamma }_U(\mathbb{M})$

In this section, we discuss certain graph parameters like the domination number, chromatic number and clique number of ${\Gamma }_U(\mathbb{M}).$ At last, we observe that ${\Gamma }_U(\mathbb{M})$ is weakly perfect.

Theorem 4.1.

Let $\mathbb{M}$ be a finitely generated free semimodule over a semiring $\mathbb{S}$ with $\dim (\mathbb{M})=k.$ Then $$\gamma ({\Gamma }_U(\mathbb{M}))=\{\begin{array}{cc}1\hfill & if \dim (\mathbb{M})=2 \mathit{and} \left|\mathbb{S}\right|=2;\hfill \\ 2\hfill & if \dim (\mathbb{M})=2 \mathit{and} \left|\mathbb{S}\right|\ge 3;\hfill \\ k\hfill & if \dim (\mathbb{M})\ge 3.\hfill \end{array}$$

Proof.

If $\dim (\mathbb{M})=2$ and $\left|\mathbb{S}\right|=2,$ then by Example 3.3, $\gamma ({\Gamma }_U(\mathbb{M}))=1.$

If $\dim (\mathbb{M})=2$ and $\left|\mathbb{S}\right|\ge 3,$ then by Theorem 3.9, ${\Gamma }_U(\mathbb{M})$ is complete bipartite and hence $\gamma ({\Gamma }_U(\mathbb{M}))=2.$

Let $\dim (\mathbb{M})=k\ge 3$ and $\mathbb{B}=\{m_1,\dots ,m_k\}$ be a basis for $\mathbb{M}.$ Consider $A=\{x_1,x_2,\dots ,x_k\}\subseteq V({\Gamma }_U(\mathbb{M})),$ where $x_i=m_1+m_2+\dots +m_{i-1}+m_{i+1}+\dots +m_k$ for $1\le i\le k.$ For any $a={\sum }_{i=1}^k{a}_i{m}_i\in V({\Gamma }_U(\mathbb{M}))\setminus A,$ we have at least one i such that $a_i\ne 0$ and so $S(a)\cup S(x_i)=\mathbb{B}.$ This implies a is adjacent to $x_i\in A.$ Hence A is a dominating set of ${\Gamma }_U(\mathbb{M}).$

Suppose $A\prime \subset A$ and $A\prime$ is a dominating set of ${\Gamma }_U(\mathbb{M}).$ Then there exists at least one i such that $x_i\in A$ and $x_i\notin A\prime .$ Now, let $b\in V({\Gamma }_U(\mathbb{M}))\setminus A\prime$ be such that $S(b)=\left\{m_i\right\}.$ Note that $S(b)\cup S(c)\subset \mathbb{B}$ for every $c\in A\prime$ and so b is not dominated by the vertices of $A\prime .$ This implies $A\prime$ is not a dominating set. Hence A is a minimal dominating set of ${\Gamma }_U(\mathbb{M}).$ To complete the proof, it remains to prove that no subset with less than k elements is a dominating set of ${\Gamma }_U(\mathbb{M}).$ From Lemma 3.7, every vertex in H₁ is adjacent to some vertices in H₂ only and therefore the vertices in H₁ can be dominated only by the vertices of H₂. Clearly $\left|H_1\right|\ge k$ and $\left|H_2\right|\ge k.$ Now, consider the subset $H_1^{\prime }=\{y_1=a_1{m}_1,y_2=a_2{m}_2\dots ,y_k=a_k{m}_k:a_i\ne 0 \text{for} 1\le i\le k\}$ of $H_1.$ By the adjacency of vertices in ${\Gamma }_U(\mathbb{M}),$ at least k vertices $z_i\in H_2$ with $S(z_i)=\mathbb{B}\setminus \left\{m_i\right\}$ for $1\le i\le k$ are needed to dominate the vertices of $H_1^{\prime }.$ Hence no subset with less than k elements is a dominating set in ${\Gamma }_U(\mathbb{M}).$ □

In the following theorem, we prove that ${\Gamma }_U(\mathbb{M})$ is weakly perfect.

Theorem 4.2.

Let $\mathbb{M}$ be a finitely generated free semimodule over a semiring $\mathbb{S}$ with $\dim (\mathbb{M})=k.$ Then the clique number and chromatic number of ${\Gamma }_U(\mathbb{M})$ are both equal to k and so ${\Gamma }_U(\mathbb{M})$ is weakly perfect.

Proof.

Let $\mathbb{B}=\{m_1,\dots ,m_k\}$ be a basis for $\mathbb{M}.$ Consider $A=\{x_1,x_2,\dots ,x_k\}\subseteq V({\Gamma }_U(\mathbb{M}))$ where $x_i=m_1+m_2+\dots +m_{i-1}+m_{i+1}+\dots +m_k.$ Clearly the induced subgraph $〈A〉$ is a complete subgraph of ${\Gamma }_U(\mathbb{M}).$ Suppose there exists $y\in V({\Gamma }_U(\mathbb{M}))$ and $y\notin A$ such that $〈A\cup \left\{y\right\}〉$ is a clique of ${\Gamma }_U(\mathbb{M}).$ Since y is adjacent to x_i for every i, we have that $S(y)=\mathbb{B}.$ This implies that $y\notin V({\Gamma }_U(\mathbb{M}))$ and thus A is a maximal clique of size k. Suppose $A\prime =\{y_1,y_2,\dots ,y_{k+1}\}$ be a clique of size k + 1. Since dimension of $\mathbb{M}$ is k, there exist $y_i,y_j\in A\prime$ such that they have zero in the same component. This implies $S(y_i)\cup S(y_j)\subset \mathbb{B}$ and so y_i is not adjacent to $y_j,$ which is a contradiction. Thus the clique number $\omega ({\Gamma }_U(\mathbb{M}))=k.$

For any graph G, we have $\omega (G)\le \chi (G)$ and hence $k\le \chi ({\Gamma }_U(\mathbb{M})).$ On the other hand, assign color 1 to all the vertices having zero in the first component and color 2 to the vertices having first component as non-zero and zero in the second component. Continuing in this way, we assign color k to all vertices having only k-th component as zero. By this way of coloring, one can see that the vertices receive the same color are not adjacent. Thus, we get a proper coloring for ${\Gamma }_U(\mathbb{M})$ and hence $\chi ({\Gamma }_U(\mathbb{M}))\le k.$ Thus $\chi ({\Gamma }_U(\mathbb{M}))=k.$ □

5. ${\Gamma }_U(\mathbb{M})$ over finite semirings

In this section, we discuss some basic properties of ${\Gamma }_U(\mathbb{M})$ where $\mathbb{M}$ is a finitely generated free semimodule over a finite semiring $\mathbb{S}.$ First, we obtain the degree of vertices in ${\Gamma }_U(\mathbb{M}).$

Theorem 5.1.

Let $\mathbb{M}$ be a finitely generated free semimodule over a finite semiring $\mathbb{S}$ with $\dim (\mathbb{M})=k$ and $\left|\mathbb{S}\right|=q$. Then, the degree of the vertex $a=a_1{m}_{i_1}+a_2{m}_{i_2}+\dots +a_r{m}_{i_r},$ where $a_{\mathcal{\ell }}\ne 0(1\le \mathcal{\ell }\le r<k)$ in the graph ${\Gamma }_U(\mathbb{M})$ is ${(q-1)}^{k-r}{q}^r-{(q-1)}^k.$

Proof.

Let $b=b_1{m}_1+b_2{m}_2+\dots +b_k{m}_k$ be adjacent to a. Clearly, $S(a)=\{m_{i_1},m_{i_2},\dots ,m_{i_r}\}$ and $S(b)\supseteq \mathbb{B}\setminus \{m_{i_1},m_{i_2},\dots ,m_{i_r}\}.$ Thus, all b_j’s except $j=i_1,i_2,\dots ,i_r$ must be non-zero and $b_{i_1},b_{i_2},\dots ,b_{i_r}$ can be any element in the semiring $\mathbb{S}.$ Therefore, the number of possibilities for b is equal to ${(q-1)}^{k-r}{q}^r$ which includes the elements (which are not vertices in ${\Gamma }_U(\mathbb{M})$) of the form ${\sum }_{i=1}^k{c}_i{m}_i:c_i\ne 0 \forall i.$ Note that there are ${(q-1)}^k$ elements which are of the form ${\sum }_{i=1}^k{c}_i{m}_i:c_i\ne 0 \forall i$ and they are not in $V({\Gamma }_U(\mathbb{M})).$ Hence the degree of the vertex $a=a_1{m}_{i_1}+a_2{m}_{i_2}+\dots +a_r{m}_{i_r},$ where $a_{\mathcal{\ell }}\ne 0$ for $1\le \mathcal{\ell }\le r<k$ is equal to ${(q-1)}^{k-r}{q}^r-{(q-1)}^k.$ □

From Theorem 5.1, we have the following characterization for ${\Gamma }_U(\mathbb{M})$ to be Eulerian.

Corollary 5.2.

Let $\mathbb{M}$ be a finitely generated free semimodule over a finite semiring $\mathbb{S}$ with $\dim (\mathbb{M})=k$ and $\left|\mathbb{S}\right|=q.$ Then ${\Gamma }_U(\mathbb{M})$ is Eulerian if and only if q is odd.

Theorem 5.3.

Let $\mathbb{M}$ be a finitely generated free semimodule over a finite semiring $\mathbb{S}$ with $\dim (\mathbb{M})=k$ and $\left|\mathbb{S}\right|=q.$ Then the following statements hold.

1. The minimum degree $\delta ({\Gamma }_U(\mathbb{M}))={(q-1)}^{k-1};$

2. The maximum degree $\Delta ({\Gamma }_U(\mathbb{M}))=(q-1)q^{k-1}-{(q-1)}^k;$

3. The number of vertices of minimum degree in ${\Gamma }_U(\mathbb{M})$ is $k(q-1);$

4. The number of vertices of maximum degree in ${\Gamma }_U(\mathbb{M})$ is $(\begin{array}{c}k\\ k-1\end{array}){(q-1)}^{k-1}.$

Proof.

1. From Theorem 5.1, the degree of the vertex $c_1{m}_{i_1}+c_2{m}_{i_2}+\dots +c_r{m}_{i_r},$ where c_i’s are non-zero is ${(q-1)}^{k-r}{q}^r-{(q-1)}^k.$ Thus the minimum degree corresponds to r = 1 and hence $\delta ({\Gamma }_U(\mathbb{M}))={(q-1)}^{k-1}.$

2. The maximum degree corresponds to $r=k-1$ and hence $\Delta ({\Gamma }_U(\mathbb{M}))=(q-1)q^{k-1}-{(q-1)}^k.$

3. Note that each vertex with exactly one component as non-zero is of minimum degree. Since $\left|\mathbb{S}\right|=q$ and $\mathbb{M}$ is k-dimensional, we get the number of vertices with exactly one component as non-zero in ${\Gamma }_U(\mathbb{M})$ is $k(q-1).$

4. Each vertex with exactly k – 1 components as non-zero is of maximum degree and the number of vertices with k – 1 components as non-zero in ${\Gamma }_U(\mathbb{M})$ is $(\begin{array}{c}k\\ k-1\end{array}){(q-1)}^{k-1}.$ □

In the view of Theorem 5.3, we have the following corollary.

Corollary 5.4.

Let $\mathbb{M}$ be a finitely generated free semimodule over a finite semiring $\mathbb{S}$ with $\dim (\mathbb{M})=k$ and $\left|\mathbb{S}\right|=q.$ Then the following hold.

1. ${\Gamma }_U(\mathbb{M})$ is a regular graph if and only if $k=2.$

2. ${\Gamma }_U(\mathbb{M})$ has no vertex of degree $|V({\Gamma }_U(\mathbb{M}))|-1$ except in the case k = 2 and $q=2.$

3. $\mathit{rad}({\Gamma }_U(\mathbb{M}))=\{\begin{array}{c}2\mathrm{ } if k\ge 3;\hfill \\ 2\mathrm{ } if k=2 \text{and} q\ge 3;\hfill \\ 1\mathrm{ } if k=2 \text{and} q=2.\hfill \end{array}$

4. ${\Gamma }_U(\mathbb{M})$ is self-centered if k = 2.

Proof.

1. Proof follows from the Theorem 5.3 (i) and (ii).

2. By Theorem 5.3 (ii), we have $\Delta ({\Gamma }_U(\mathbb{M}))=(q-1)q^{k-1}-{(q-1)}^k\ne (q^k-1)-{(q-1)}^k-1=|V({\Gamma }_U(\mathbb{M}))|-1$ except in the case k = 2 and $q=2.$

3. If k = 2 and $q=2,$ then by Corollary 3.6, $\mathit{rad}({\Gamma }_U(\mathbb{M}))$ is 1.

   From (ii), e(a) > 1 for all $a\in V({\Gamma }_U(\mathbb{M}))$ except in the case k = 2 and $q=2.$

   Suppose k = 2 and $q\ge 3.$ By Corollary 3.6, $\mathit{rad}({\Gamma }_U(\mathbb{M}))$ is 2.

   Suppose $k\ge 3.$ Now let $a=m_1+m_2+\dots +m_{k-1}\in V({\Gamma }_U(\mathbb{M})).$ Clearly $S(a)=\mathbb{B}\setminus \left\{m_k\right\}.$ For any $b\in V({\Gamma }_U(\mathbb{M})), d(a,b)=1$ if $m_k\in S(b).$ Suppose $m_k\notin S(b).$ Since $|S(b)|\ge 1,$ then there exists at least one $i\in \{1,2,\dots ,k-1\}$ such that $m_i\in S(b).$ Now we choose a vertex $c\in V({\Gamma }_U(\mathbb{M}))$ such that $c\in \mathbb{B}\setminus \left\{m_i\right\}.$ This gives a path $a-c-b$ in ${\Gamma }_U(\mathbb{M})$ and $d(a,b)=2.$ Therefore $e(a)=2.$ Hence radius of ${\Gamma }_U(\mathbb{M})$ is 2 when $k\ge 3.$

4. Follows from (iii) and Corollary 3.6. □

Theorem 5.5.

Let $\mathbb{M}$ be a finitely generated free semimodule over a finite semiring $\mathbb{S}$ with $\dim (\mathbb{M})=k$ and $\left|\mathbb{S}\right|=q.$ Then the number of vertices of ${\Gamma }_U(\mathbb{M})$ is $(q^k-1)-{(q-1)}^k$ and the number of edges of ${\Gamma }_U(\mathbb{M})$ is $\frac{{(q-1)}^k\left[{(q+1)}^k-2q^k+{(q-1)}^k\right]}{2}.$

Proof.

Note that $A=\{{\sum }_{i=1}^k{c}_i{m}_i:c_i\ne 0 \forall i\}$ contains ${(q-1)}^k$ elements and so number of vertices in ${\Gamma }_U(\mathbb{M})=\left|{\mathbb{M}}^{*}\right|-\left|A\right|=(q^k-1)-{(q-1)}^k.$ By Theorem 5.1, the degree of the vertex $c_1{m}_{i_1}+c_2{m}_{i_2}+\dots +c_r{m}_{i_r},$ ($c_i\ne 0$ for every i) is ${(q-1)}^{k-r}{q}^r-{(q-1)}^k.$ Now, there are $(\begin{array}{c}k\\ r\end{array}){(q-1)}^r$ vertices with exactly r components as non-zero in its basic representation. Since the sum of degrees of all vertices in ${\Gamma }_U(\mathbb{M})$ is 2m, we have $$\begin{array}{c}2m=\sum _{r=1}^{k-1}\left(\begin{array}{c}k\\ r\end{array}\right){(q-1)}^r({(q-1)}^{k-r}{q}^r-{(q-1)}^k)\\ =\sum _{r=1}^{k-1}\left(\begin{array}{c}k\\ r\end{array}\right){(q-1)}^r{(q-1)}^{k-r}{q}^r-\sum _{r=1}^{k-1}\left(\begin{array}{c}k\\ r\end{array}\right){(q-1)}^r{(q-1)}^k\\ ={(q-1)}^k\sum _{r=1}^k\left(\begin{array}{c}k\\ r\end{array}\right)q^r-{(q-1)}^k{q}^k\\ -{(q-1)}^k\sum _{r=1}^k\left(\begin{array}{c}k\\ r\end{array}\right){(q-1)}^r+{(q-1)}^k{(q-1)}^k\\ ={(q-1)}^k\left[{(q+1)}^k-1-q^k-q^k+1+{(q-1)}^k\right]\\ ={(q-1)}^k\left[{(q+1)}^k-2q^k+{(q-1)}^k\right]\end{array}$$ and hence $$m=\frac{{(q-1)}^k\left[{(q+1)}^k-2q^k+{(q-1)}^k\right]}{2}.$$ □

A chordal graph is a simple graph in which every cycle of length four and greater has a chord. In other words, a chordal graph is a graph possessing no chord less cycles of length four or greater. In the following theorem, we give a necessary and sufficient condition for ${\Gamma }_U(\mathbb{M})$ to be a chordal graph.

Theorem 5.6.

Let $\mathbb{M}$ be a finitely generated free semimodule over a finite semiring with $\dim (\mathbb{M})=k$ and $\left|\mathbb{S}\right|=q.$ Then ${\Gamma }_U(\mathbb{M})$ is chordal if and only if (k = 2 and q = 2) or (k = 3 and q = 2).

Proof.

Let $\mathbb{B}=\{m_1,m_2,\dots ,m_k\}$ be a basis of ${\Gamma }_U(\mathbb{M}).$ Assume that ${\Gamma }_U(\mathbb{M})$ is chordal.

Suppose $k\ge 4.$ Let $\Omega =\{m_2+m_3+\cdots +m_k,m_1+m_3+m_4+\cdots +m_k,m_2+m_4+m_5+\cdots +m_k,m_1+m_3+m_5+\cdots +m_k\}\subseteq V({\Gamma }_U(\mathbb{M})).$ Then the induced subgraph $〈\Omega 〉$ is C₄ and hence is a subgraph in ${\Gamma }_U(\mathbb{M}),$ a contradiction to ${\Gamma }_U(\mathbb{M})$ is chordal. Therefore $k\le 3.$

• Case (i) Suppose k = 3 and $q\ge 3.$ Let $x_1=m_1+m_2, x_2=m_1+m_3, x_3=a_1{m}_1+m_2$ and $x_4=a_1{m}_1+m_3,$ where $a_1\in \mathbb{S}\setminus \{0,1\}.$ Then the $〈\{x_1,x_2,x_3,x_4\}〉$ is C₄ in ${\Gamma }_U(\mathbb{M}),$ a contradiction. Hence $q=2.$

• Case (ii) Suppose k = 2 and $q\ge 3.$ Then, for $a_1\in \mathbb{S}\setminus \{0,1\},$ the vertices $m_1,m_2,a_1{m}_1,a_1{m}_2$ induce C₄ in ${\Gamma }_U(\mathbb{M}).$ Therefore $q=2.$

Converse follows from the Figures 1 and 3. □

Next, we obtain a characterization for the planarity of the graph ${\Gamma }_U(\mathbb{M}).$ This gives all finitely generated free semimodules over finite semirings for which ${\Gamma }_U(\mathbb{M})$ is planar. The following is a famous characterization for planar graphs and we make use of the same.

Theorem 5.7.

([18, Kuratowski]) A graph G is planar if and only if it contains no subdivision of K₅ or $K_{3,3}.$

Theorem 5.8.

Let $\mathbb{M}$ be a finitely generated free semimodule over a finite semiring with $\dim (\mathbb{M})=k$ and $\left|\mathbb{S}\right|=q.$ Then ${\Gamma }_U(\mathbb{M})$ is planar if and only if (k = 2 and $q\le 3$) or (k = 3 and q = 2).

Proof.

Let $\mathbb{B}=\{m_1,m_2,\dots ,m_k\}$ be a basis of ${\Gamma }_U(\mathbb{M}).$ Assume that ${\Gamma }_U(\mathbb{M})$ is planar.

• Claim 1. $k\le 3.$ Suppose $k\ge 4.$ Select $x_i(1\le i\le 6)$ such that $S(x_1)=\mathbb{B}\setminus \left\{m_k\right\}, S(x_2)=\mathbb{B}\setminus \left\{m_{k-1}\right\}, S(x_3)=\mathbb{B}\setminus \left\{m_{k-2}\right\},S(x_4)=\mathbb{B}\setminus \left\{m_{k-3}\right\}, S(x_5)=\mathbb{B}\setminus \{m_{k-2},m_k\}$ and $S(x_6)=\mathbb{B}\setminus \{m_{k-1},m_{k-3}\}.$ Then $\Omega =\{x_i : 1\le i\le 6\}$ is a subset of the vertex set of ${\Gamma }_U(\mathbb{M})$ and the subgraph induced by Ω contains $K_{3,3}.$ By Theorem 5.7, ${\Gamma }_U(\mathbb{M})$ is non-planar. Hence $k\le 3.$

• Claim 2. If k = 3, then q must be 2. Suppose $q\ge 3.$ By Lemma 3.8, we have $〈H_2〉$ is a complete k-partite graph in ${\Gamma }_U(\mathbb{M}).$ Clearly $\left|H_2\right|=k{(q-1)}^{k-1}$ and each partite set has ${(q-1)}^{k-1}$ vertices. Since $q\ge 3,$ $〈H_2〉$ contains $K_{3,3}$ as a subgraph in ${\Gamma }_U(\mathbb{M}).$ By Theorem 5.7, ${\Gamma }_U(\mathbb{M})$ is non-planar. Hence q = 2.

• Claim 3. If $k=2,$ then $q\le 3.$ Suppose $q\ge 4.$ Since k = 2, by Theorem 3.9, ${\Gamma }_U(\mathbb{M})$ is complete bipartite. The vertex set of ${\Gamma }_U(\mathbb{M})$ is of the form $V({\Gamma }_U(\mathbb{M}))=A_1\cup A_2$ and $A_1\cap A_2=\varnothing$ where $A_1=\{a_1{m}_1 : a_1\ne 0\}$ and $A_2=\{a_2{m}_2 : a_2\ne 0\}.$ Clearly $\left|A_1\right|=q-1$ and $\left|A_2\right|=q-1.$ Therefore ${\Gamma }_U(\mathbb{M})$ is $K_{q-1,q-1}$ with $q\ge 4$ and consequently $K_{3,3}$ is a subgraph of ${\Gamma }_U(\mathbb{M}),$ which is a contradiction. Hence $q\le 3.$

Conversely, assume that (k = 2 and $q\le 3$) or (k = 3 and q = 2).

Case 1. If k = 2 and $q=2,$ then by Figure 1, ${\Gamma }_U(\mathbb{M})=K_{1,1},$ a planar graph.

Case 2. If k = 2 and $q=3,$ then by Figure 2, ${\Gamma }_U(\mathbb{M})=K_{2,2},$ a planar graph.

Case 3. Assume that k = 3 and $q=2.$ A planar embedding of ${\Gamma }_U(\mathbb{M})$ is given in Figure 3. □

Next, we discuss about Hamiltonicity of ${\Gamma }_U(\mathbb{M})$ and we prove that ${\Gamma }_U(\mathbb{M})$ is Hamiltonian in some cases.

Remark 5.9.

Let $\mathbb{M}$ be a finitely generated free semimodule over a finite semiring $\mathbb{S}$ of dimension k and $\left|\mathbb{S}\right|=q.$ If $q=2,$ by Theorem 5.3, we have $\delta ({\Gamma }_U(\mathbb{M}))=1$ $\forall k$ and so ${\Gamma }_U(\mathbb{M})$ is non-Hamiltonian.

Lemma 5.10.

Let $\mathbb{M}$ be a finitely generated free semimodule over a finite semiring $\mathbb{S}$ of dimension k and $\left|\mathbb{S}\right|=q$. If k = 2 and $q\ge 3,$ then ${\Gamma }_U(\mathbb{M})$ is Hamiltonian.

Proof.

By the assumption, there is a basis $\mathbb{B}=\{m_1,m_2\}$ for ${\Gamma }_U(\mathbb{M}).$ Since k = 2 and $q\ge 3,$ by Theorem 3.9, we have ${\Gamma }_U(\mathbb{M})$ is complete bipartite. From the proof of the Theorem 5.8, we have ${\Gamma }_U(\mathbb{M})$ is $K_{q-1,q-1}.$ Hence ${\Gamma }_U(\mathbb{M})$ is Hamiltonian when k = 2 and $q\ge 3.$ □

We propose the following conjecture with regard to the Hamiltonian characterization of ${\Gamma }_U(\mathbb{M}).$

Conjecture 5.11.

Let $\mathbb{M}$ be a finitely generated free semimodule over a finite semiring $\mathbb{S}$ of dimension k and $\left|\mathbb{S}\right|=q$. If $k\ge 3$ and $q\ge 3,$ then ${\Gamma }_U(\mathbb{M})$ is Hamiltonian.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This research work is supported by CSIR Emeritus Scientist Scheme (No. 21 (1123)/20/EMR-II) of Council of Scientific and Industrial Research, Government of India through the second author. Also this research work is supported by Dr. M.G.R. Research scholarship by Manonmaniam Sundaranar University, India through the first author.