Binding number and path-factor critical deleted graphs

Abstract

A graph G is called a $P_{\ge k}$-factor deleted graph if G – e has a $P_{\ge k}$-factor for any $e\in E(G).$ A graph G is $(P_{\ge k},n)$-factor critical deleted if for every subset $V\prime \subseteq V(G)$ with $|V\prime |=n,$ the graph $G-V\prime$ is $P_{\ge k}$-factor deleted. Zhou, Bian and Pan [Discrete Appl. Math. (2021) in press] showed that an $(n+2)$-connected graph G is $(P_{\ge 3},n)$-factor critical deleted if its binding number $\mathit{bind}(G)>\frac{n+3}{2}.$ In this paper, we give a new binding number condition for $(P_{\ge 3},n)$-factor critical deleted graphs, which improves the above result.

Keywords:

• Path-factor
• $P_{\ge 3}$-factor
• binding number
• $P_{\ge 3}$-factor deleted graph
• $(P_{\ge 3},n)$-factor critical deleted graph

Mathematics Subject Classification:

• 05C38 05C70

1. Introduction

In this paper, we deal with only finite simple graph. For standard graph-theoretic notation not explained here, we refer to [4]. Given a vertex v in graph G, let $N_G(v)$ be the set of vertices adjacent to v in G and $d_G(v)=|N_G(v)|$ be the degree of v in G. For any subset $S\subseteq V(G),$ we define $N_G(S)$ by $N_G(S)=\underset{v\in S}{\cup }{N}_G(v),$ and let $G[S]$ denote the subgraph of G induced by S. Denote by $G-S:=G[V(G)\setminus S]$ the resulting graph after deleting the vertices of S from G. The concept of binding number was introduced by Woodall [14]. For a connected graph G, its binding number, denoted by bind(G), was defined as $$\mathit{bind}(G)=\min \left\{\frac{|N_G(X)|}{\left|X\right|}:\varnothing \ne X\subseteq V(G),N_G(X)\ne V(G)\right\}.$$

For a family of connected graphs $\mathcal{F},$ a spanning subgraph H of a graph G is called an $\mathcal{F}$-factor of G if each component of H is isomorphic to some graph in $\mathcal{F}.$ A spanning subgraph H of a graph G is called a $P_{\ge k}$-factor of G if every component of H is isomorphic to a path of order at least k. For example, a $P_{\ge 3}$-factor means a graph factor in which every component is a path of order at least three. A graph G is $P_{\ge k}$-factor deleted if for every edge $e\in E(G),$ G has a $P_{\ge k}$-factor that excludes e. A graph G is $(P_{\ge k},n)$-factor critical deleted if for every subset $V\prime \subseteq V(G)$ with $|V\prime |=n,$ the graph $G-V\prime$ is $P_{\ge k}$-factor deleted. Clearly, a $(P_{\ge k},0)$-factor critical deleted graph is a $P_{\ge k}$-factor deleted graph.

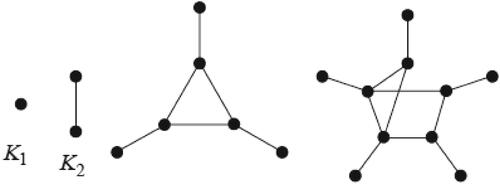
The concept of sun was introduced by Kaneko [6]. A graph H is called factor-critical if H – v has a 1-factor for each $v\in V(H).$ Let H be a factor-critical graph and $V(H)=\{v_1,v_2,\dots ,v_n\}.$ By adding new vertices $\{u_1,u_2,\dots ,u_n\}$ together with new edges $\{v_i{u}_i:1\le i\le n\}$ to H, the resulting graph is called a sun (e.g., see Figure 1). We also regard K₁ and K₂ as suns. A sun other than K₁ is called a big sun. Obviously, the order of a big sun is at least 6. A component of G is called a sun component if it is isomorphic to a sun. We denote by sun(G) the number of sun components in G. Recently, Kaneko [6] acquired a criterion for a graph to contain a $P_{\ge 3}$-factor, for which Kano, Katona and Király [7] presented a simpler proof.

Figure 1. Suns.

Theorem 1.1.

(Kaneko [6]) A graph G has a $P_{\ge 3}$-factor if and only if $\mathit{sun}(G-X)\le 2\left|X\right|$ for all $X\subseteq V(G).$

Since Tutte proposed the well-known Tutte 1-factor theorem [13], there are many results on graph factors [1–3, 5, 9, 16, 20], which can be found in the survey paper [12] and book [15].

In this paper, we mainly focus on the relationship between binding number and path factors, which were investigated by Kano & Tokushige [8], Nam [10], Zhou et al. [19], Robertshaw & Woodall [11] and Zhou & Sun [18].

Recently, Zhou, Bian and Pan [17] obtained a binding number condition for an $(n+2)$-connected graph to be $(P_{\ge 3},n)$-factor critical deleted.

Theorem 1.2.

(Zhou, Bian and Pan [17]) Let n be a nonnegative integer, and let G be an $(n+2)$-connected graph. If $\mathit{bind}(G)>\frac{3+n}{2}$, then G is $(P_{\ge 3},n)$-factor critical deleted.

In this paper, we also consider the binding number condition for an $(n+2)$-connected graph to be $(P_{\ge 3},n)$-factor critical deleted, which improves the result in the above Theorem.

Theorem 1.3.

Let n be a nonnegative integer. An $(n+2)$-connected graph G is $(P_{\ge 3},n)$-factor critical deleted if $$\mathit{bind}(G)>\{\begin{array}{cc}\frac{3}{2}\hspace{1em}\hfill & \text{if}n=0,\hfill \\ \frac{4+n}{3}\hspace{1em}\hfill & \text{if}n\ge 1.\hfill \end{array}$$

2. Proof of Theorem 1.3

For any $V\prime \subseteq V(G)$ with $|V\prime |=n,$ we write $G\prime =G-V\prime .$ To prove Theorem 1.3, it suffices to prove that $H:=G\prime -e$ contains a $P_{\ge 3}$-factor for any $e\in E(G\prime ).$ Suppose on the contrary that there exists an edge $e=xy\in E(G\prime )$ such that $H=G\prime -e$ has no $P_{\ge 3}$-factor. Then by Theorem 1.1, there exists a subset $X\subseteq V(H)$ such that (1) $$\mathit{sun}(H-X)\ge 2\left|X\right|+1.$$(1)

Claim 2.1.

$X\ne \varnothing .$

Proof.

Assume that $X=\varnothing .$ On one hand, since $\kappa (G\prime )\ge \kappa (G)-n=2,G\prime$ is a 2-connected graph and $|V(G\prime )|\ge 3.$ Thus H is a connected graph, and $\mathit{sun}(H)\le \omega (H)=1,$ where $\omega (H)$ denotes the number of connected components of H. On the other hand, it follows from (1) that $\mathit{sun}(H)=\mathit{sun}(H-X)\ge 2\left|X\right|+1=1.$ Hence, (2) $$\mathit{sun}(H)=1.$$(2)

Note that $|V(H)|=|V(G\prime )|\ge 3.$ Combining this with (2) implies that H is a big sun and $|V(H)|\ge 6.$ Let R be the factor-critical graph of H. Then $|V(R)|\ge 3$ and there exists $u\in V(R)$ such that $\omega (G\prime -\{u\})=\omega (H-\{u\})=2.$ Obviously, u is a cut-vertex of $G\prime ,$ contradicting to $\kappa (G\prime )\ge 2.$ □

Claim 2.2.

$\left|X\right|\ge 2$ and $\mathit{sun}(H-X)\ge 5.$

Proof.

On the contrary, from Claim 2.1, we assume that $\left|X\right|=1.$ Since G is $(n+2)$-connected, $\kappa (G\prime )\ge \kappa (G)-n=2.$ It follows that $G\prime -X$ is a connected graph, i.e., $\omega (G\prime -X)=1.$ Then by the definition of H, we have (3) $$\omega (H-X)=\omega (G\prime -X-e)\le \omega (G\prime -X)+1=2.$$(3)

On the other hand, according to (1), $$\omega (H-X)\ge \mathit{sun}(H-X)\ge 2\left|X\right|+1\ge 3,$$

contradicting to (3). Hence, $\left|X\right|\ge 2$ and $\mathit{sun}(H-X)\ge 2\left|X\right|+1\ge 5.$ □

Suppose that there exist a isolated vertices, b K₂’s and c big sun components $H_1,H_2,\dots ,H_c$ in H – X. We have $\mathit{sun}(H-X)=a+b+c.$ It follows from Claim 2.2 that (4) $$a+b+c=\mathit{sun}(H-X)\ge 2\left|X\right|+1\ge 5.$$(4)

Claim 2.3.

$x\notin X$ and $y\notin X.$

Proof.

Suppose on the contrary that $x\in X$ or $y\in X.$ It follows from (4) that $\mathit{sun}(G\prime -X)=\mathit{sun}(H-X)=a+b+c\ge 5.$ Set $Y=V(a{K}_1)\cup V(b{K}_2)\cup V(H_1)\cup \dots \cup V(H_c).$ Then $Y\ne \varnothing$ and $N_G(Y)\ne V(G).$ Thus, we obtain that $$\begin{array}{ccc}\frac{4+n}{3}\hfill & <\hfill & \mathit{bind}(G)\le \frac{|N_G(Y)|}{\left|Y\right|}\hfill \\ \hfill & \le \hfill & \frac{|V\prime |+\left|X\right|+2b+\sum _{i=1}^c|V(H_i)|}{a+2b+\sum _{i=1}^c|V(H_i)|}\hfill \\ \hfill & =\hfill & \frac{n+\left|X\right|+2b+\sum _{i=1}^c|V(H_i)|}{a+2b+\sum _{i=1}^c|V(H_i)|},\hfill \end{array}$$ which implies that (5) $$4a+2b+\sum _{i=1}^c|V(H_i)|+(a+2b+\sum _{i=1}^c|V(H_i)|-3)n<3\left|X\right|.$$(5)

In terms of (4), (5), $a\ge 0,b\ge 0,c\ge 0$ and $|V(H_i)|\ge 6,$ we can deduce that $$\begin{array}{ccc}3\left|X\right|\hfill & >\hfill & 4a+2b+\sum _{i=1}^c|V(H_i)|+(a+2b+\sum _{i=1}^c|V(H_i)|-3)n\hfill \\ \hfill & \ge \hfill & 2a+2b+6c+(a+2b+6c-3)n\hfill \\ \hfill & \ge \hfill & 2(a+b+c)+(a+b+c-3)n\hfill \\ \hfill & \ge \hfill & 2(a+b+c)\hfill \\ \hfill & \ge \hfill & 2(2|X|+1)\ge 4\left|X\right|+2,\hfill \end{array}$$ which implies that $\left|X\right|<-2,$ a contradiction. □

Next, we will consider the following two cases to complete the proof of Theorem 1.3.

• Case 1. $x\notin V(a{K}_1)$ and $y\notin V(a{K}_1).$

Using the following rules, we construct a set Z such that $Z\ne \varnothing$ and $N_G(Z)\ne V(G).$

• If $x\in V(b{K}_2)$ or $y\in V(b{K}_2),$ without loss of generality, we can assume that $x\in V(b{K}_2)$ and choose $Z=V(a{K}_1)\cup V(b{K}_2)\cup V(H_1)\cup \dots \cup V(H_c)\setminus \left\{x\right\}.$

• If $x\in V(H_1)\cup \dots \cup V(H_c)$ or $y\in V(H_1)\cup \dots \cup V(H_c),$ without loss of generality, we can assume that $x\in V(H_i).$ Let R_i be the factor-critical subgraph of H_i. Choose $Z=V(a{K}_1)\cup V(b{K}_2)\cup V(H_1)\cup \dots \cup V(H_c)\setminus \left\{z\right\},$ where $z\in V(R_i)\setminus \{x,y\}.$

• If $x\in V(G)\setminus (V\prime \cup X\cup V(a{K}_1)\cup V(b{K}_2)\cup V(H_1)\cup \dots \cup V(H_c))$ and $y\in V(G)\setminus (V\prime \cup X\cup V(a{K}_1)\cup V(b{K}_2)\cup V(H_1)\cup \dots \cup V(H_c)),$ choose $Z=V(a{K}_1)\cup V(b{K}_2)\cup V(H_1)\cup \dots \cup V(H_c).$

Then we can obtain that $$\begin{array}{ccc}\frac{4+n}{3}\hfill & <\hfill & \mathit{bind}(G)\le \frac{|N_G(Z)|}{\left|Z\right|}\hfill \\ \hfill & \le \hfill & \frac{|V\prime |+\left|X\right|+2b+\sum _{i=1}^c|V(H_i)|}{a+2b+\sum _{i=1}^c|V(H_i)|-1}\hfill \\ \hfill & =\hfill & \frac{n+\left|X\right|+2b+\sum _{i=1}^c|V(H_i)|}{a+2b+\sum _{i=1}^c|V(H_i)|-1},\hfill \end{array}$$ which implies that (6) $$4a+2b+\sum _{i=1}^c|V(H_i)|-4+(a+2b+\sum _{i=1}^c|V(H_i)|-4)n<3\left|X\right|.$$(6)

In terms of (4), (6), $a\ge 0,b\ge 0,c\ge 0$ and $|V(H_i)|\ge 6,$ we deduce that $$\begin{array}{ccc}3\left|X\right|\hfill & >\hfill & 4a+2b+\sum _{i=1}^c|V(H_i)|-4+(a+2b+\sum _{i=1}^c|V(H_i)|-4)n\hfill \\ \hfill & \ge \hfill & 4a+2b+6c-4+(a+2b+6c-4)n\hfill \\ \hfill & \ge \hfill & 2(a+b+c)-4+(a+b+c-4)n\hfill \\ \hfill & \ge \hfill & 2(a+b+c)-4\hfill \\ \hfill & \ge \hfill & 2(2|X|+1)-4\ge 4\left|X\right|-2,\hfill \end{array}$$ which implies that $\left|X\right|<2,$ a contradiction to Claim 2.2.

• Case 2. $x\in V(a{K}_1)$ or $y\in V(a{K}_1).$

Without loss of generality, we can assume that $x\in V(a{K}_1),$ which implies that $a\ge 1.$ Set $Z=V(a{K}_1)\cup V(b{K}_2)\cup V(H_1)\cup \dots \cup V(H_c)\setminus \left\{y\right\}.$ Then $Z\ne \varnothing$ and $N_G(Z)\ne V(G).$ We can obtain that (7) $$\mathit{bind}(G)\le \frac{|N_G(Z)|}{\left|Z\right|}\le \frac{|V\prime |+\left|X\right|+2b+\sum _{i=1}^c|V(H_i)|+1}{a+2b+\sum _{i=1}^c|V(H_i)|-1}=\frac{n+\left|X\right|+2b+\sum _{i=1}^c|V(H_i)|+1}{a+2b+\sum _{i=1}^c|V(H_i)|-1}.$$(7)

Subcase 2.1. n = 0.

According to the binding number condition and (7), we have $$\frac{3}{2}<\mathit{bind}(G)\le \frac{\left|X\right|+2b+\sum _{i=1}^c|V(H_i)|+1}{a+2b+\sum _{i=1}^c|V(H_i)|-1}.$$

This together with $a\ge 1$ and (4) implies that $$\begin{array}{ccc}2\left|X\right|\hfill & >\hfill & 3a+2b+\sum _{i=1}^c|V(H_i)|-5\hfill \\ \hfill & \ge \hfill & 3a+2b+6c-5\hfill \\ \hfill & \ge \hfill & 2(a+b+c)-4\hfill \\ \hfill & \ge \hfill & 2(2|X|+1)-4\ge 4\left|X\right|-2,\hfill \end{array}$$ which means $\left|X\right|<1,$ a contradiction to Claim 2.2.

Subcase 2.2. $n\ge 1.$

According to the binding number condition and (7), we have $$\frac{4+n}{3}<\mathit{bind}(G)\le \frac{n+\left|X\right|+2b+\sum _{i=1}^c|V(H_i)|+1}{a+2b+\sum _{i=1}^c|V(H_i)|-1}.$$

Together with $n\ge 1,a\ge 1,b\ge 0,c\ge 0,|V(H_i)|\ge 6$ and (4), we deduce that $$\begin{array}{ccc}3\left|X\right|\hfill & >\hfill & 4a+2b+\sum _{i=1}^c|V(H_i)|-7+(a+2b+\sum _{i=1}^c|V(H_i)|-4)n\hfill \\ \hfill & \ge \hfill & 4a+2b+6c-7+(a+2b+6c-4)n\hfill \\ \hfill & \ge \hfill & 2(a+b+c)-5+(a+b+c-4)n\hfill \\ \hfill & \ge \hfill & 2(2|X|+1)-5+n\hfill \\ \hfill & \ge \hfill & 4\left|X\right|-3+n\ge 4\left|X\right|-2,\hfill \end{array}$$ which implies that $\left|X\right|<2,$ also a contradiction to Claim 2.2.

This completes the proof of Theorem 1.3. □

3. Remarks

In this paper, we obtain a new binding number condition to guarantee an $(n+2)$-connected graph to be $(P_{\ge 3},n)$-factor critical deleted. We think the lower bound c of binding number could be improved to some extent. Furthermore, it should satisfy the following property. $$c>\{\begin{array}{cc}\frac{n+9}{7}\hspace{1em}\hfill & \text{if}0\le n\le 8,\hfill \\ \frac{n+4}{5}\hspace{1em}\hfill & \text{if}n\ge 9.\hfill \end{array}$$

If $0\le n\le 8,$ we construct an $(n+2)$-connected graph $G=K_{n+2}\vee (4K_2),$ where $\vee$ means “join”. Then $\mathit{bind}(G)=\frac{|N_G(4K_2-\left\{x\right\})|}{|4K_2-\{x\left\}\right|}=\frac{n+9}{7},$ where $x\in V(4K_2).$ Note that $\frac{n+9}{7}<\frac{n+4}{3}$ if $1\le n\le 8,$ and $\frac{n+9}{7}<\frac{3}{2}$ if n = 0. Set $e\in E(4K_2),V\prime =V(K_n)\subseteq V(K_{n+2}),G\prime =G-V\prime$ and $H=G\prime -e.$ For $X=V(K_{n+2})\setminus V\prime ,$ we can deduce that $\mathit{sun}(H-X)=5>2\left|X\right|=4.$ By Theorem 1.1, H does not contain a $P_{\ge 3}$-factor. Hence, $G\prime$ is not a $P_{\ge 3}$-factor deleted graph, i.e., G is not a $(P_{\ge 3},n)$-factor critical deleted graph.

If $n\ge 9,$ we also construct an $(n+2)$-connected graph $G=K_{n+2}\vee (K_2\cup 3K_1).$ Then $\mathit{bind}(G)=\frac{|N_G(K_2\cup 3K_1)|}{|K_2\cup 3K_1|}=\frac{n+4}{5}<\frac{n+4}{3}.$ Set $e\in E(K_2),V\prime =V(K_n)\subseteq V(K_{n+2}),G\prime =G-V\prime$ and $H=G\prime -e.$ For $X=V(K_{n+2})\setminus V\prime ,$ we can deduce that $\mathit{sun}(H-X)=5>2\left|X\right|=4.$ By Theorem 1.1, H does not contain a $P_{\ge 3}$-factor. Hence, $G\prime$ is not a $P_{\ge 3}$-factor deleted graph, which implies that G is not a $(P_{\ge 3},n)$-factor critical deleted graph.

Additional information

Funding

This work is supported by the National Natural Science Foundation of China (Grant Nos. 11871239 and 11971196).