Full article: On minimum revised edge Szeged index of bicyclic graphs

Formulae display: $MathJax Logo$ ?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.

Abstract

The revised edge Szeged index $S z_{e}^{*} (G)$ of a graph G is defined as $S z_{e}^{*} (G) = \sum_{e = u v \in E (G)} (m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2}),$ where $m_{u} (e)$ and $m_{v} (e)$ are, respectively, the number of edges of G lying closer to vertex u than to vertex v and the number of edges of G lying closer to vertex v than to vertex u, and $m_{0} (e)$ is the number of edges equidistant to u and v. In the paper, we show the sharp lower bound of revised edge Szeged index regarding bicyclic graphs. Moreover, all extremal graphs are characterized.

Keywords:

AMS SUBJECT CLASSIFICATION:

1. Introduction

All graphs considered in this paper are finite, undirected and simple. We refer the readers to [Citation4] for terminology and notations. Let C_n denote the cycle on n edges and S_m denote the star on m edges. For $u, v \in V (G), d (u, v)$ denotes the distance between u and v in G. The Wiener index of a connected graph G is defined as follows: $W (G) = \sum_{{u, v} \subseteq V (G)} d (u, v) .$

This topological index has been extensively studied in the mathematical literature, see [Citation10, Citation14, Citation15, Citation30].

Let e = uv be an edge of G, the sets $N_{0} (e), N_{u} (e)$ and $N_{v} (e)$ are the set of vertices equidistant from u and v, the set of vertices whose distance to vertex u is smaller than the distance to vertex v and the set of vertices closer to v than u, respectively. The number of vertice of $N_{u} (e), N_{v} (e)$ and $N_{0} (e)$ are denoted by $n_{u} (e), n_{v} (e)$ and $n_{0} (e),$ respectively. Evidently, $n_{u} (e) + n_{v} (e) + n_{0} (e) = | G | .$ For a tree T, its Wiener index can be defined alternatively as: $W (T) = \sum_{e = u v \in E (T)} n_{u} (e) n_{v} (e) .$

Motivated the above formula, Gutman [Citation12] introduced a graph invariant, named as the Szeged index as an extension of the Wiener index and defined by $S z (G) = \sum_{e = u v \in E (G)} n_{u} (e) n_{v} (e) .$

In [Citation25], Randić noticed that the Szeged index neglects the vertices with equal distance to the two endpoints of some edge. Hence he put forward a modified version of the Szeged index as revised Szeged index, which is defined as $S z^{*} (G) = \sum_{e = u v \in E (G)} (n_{u} (e) + \frac{n_{0} (e)}{2}) (n_{v} (e) + \frac{n_{0} (e)}{2}) .$ So far, many results explored the relationship (difference or quotient) between Szeged index (resp. revised Szeged index) and Wiener index; see, [Citation3, Citation6, Citation8, Citation9, Citation19, Citation22, Citation23, Citation33, Citation34]. There are a lots results with the bounds and applications of Szeged indices, refer to [Citation1, Citation2, Citation7, Citation17, Citation18, Citation20, Citation24, Citation26, Citation29, Citation31, Citation32].

Given an edge $e = u v \in E (G),$ the distance between the edge e and the vertex w, denoted by d(e, w), is defined as $d (e, w) = \min {d (u, w), d (v, w)} .$ Based on the definition, the three subsets of E(G) are proposed as $M_{u} (e) = {f \in E (G) : d (u, f) < d (v, f)}, M_{v} (e) = {f \in E (G) : d (u, f) > d (v, f)}, M_{0} (e) = {f \in E (G) : d (u, f) = d (v, f)} .$ Put $m_{u} (e) = | M_{u} (e) |, m_{v} (e) = | M_{v} (e) |$ and $m_{0} (e) = | M_{0} (e) | .$ Then, the edge Szeged index [Citation13], and revised edge Szeged index [Citation11] of G are defined as follows: $\begin{matrix} S z_{e} (G) = \sum_{e = u v \in E (G)} m_{u} (e) m_{v} (e), \\ S z_{e}^{*} (G) = \sum_{e = u v \in E (G)} (m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2}) . \end{matrix}$

Results on edge Szeged index can be found in [Citation5, Citation16, Citation27, Citation28]. In [Citation11], they determined the n-vertex unicyclic graphs with the largest and the smallest revised edge Szeged indices. In [Citation21], they identified those graphs whose revised edge Szeged index is maximal among bicyclic graphs. In the paper, we show the sharp lower bound of revised edge Szeged index regarding bicyclic graphs and characterize extremal graphs.

Theorem 1.1.

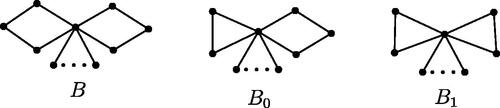
Let G be a connected bicyclic graph of size $m \geq 17$ . Then $S z_{e}^{*} (G) \geq \frac{1}{2} m^{2} + \frac{47}{4} m - 30$ with equality if and only if $G ≅ B$ , where B is depicted in .

Figure 1. These graphs are used in Theorem 1.1 and Theorem 3.1.

2. Some Lemmas

Note that $m_{u} (e) + m_{v} (e) + m_{0} (e) = m,$ it is deduced that $\begin{matrix} S z_{e}^{*} (G) = \sum_{e = u v \in E (G)} (m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2}) \\ = \sum_{e = u v \in E (G)} (\frac{m + m_{u} (e) - m_{v} (e)}{2}) (\frac{m - m_{u} (e) + m_{v} (e)}{2}) \\ = \sum_{e = u v \in E (G)} \frac{m^{2} - {(m_{u} (e) - m_{v} (e))}^{2}}{4} \\ = \frac{m^{3}}{4} - \frac{1}{4} \sum_{e = u v \in E (G)} (m_{u} (e) - m_{v} (e))^{2} . \end{matrix}$

Set $δ (e) = | m_{u} (e) - m_{v} (e) |,$ where e = uv, we get a normal version of revised edge Szeged index (1) $S z_{e}^{*} (G) = \frac{m^{3}}{4} - \frac{1}{4} \sum_{e \in E (G)} δ {(e)}^{2} .$ (1)

In the section, some elementary results are listed, which will be useful in the sequel.

Lemma 2.1.

Let $e \in E (G)$ . Then $δ (e) \leq m - 1$ and equality holds only if e is a pendant edge.

We now mark $G ≅ G_{1} \cdot G_{2},$ where $G_{1} \cdot G_{2}$ is the graph obtained from the G₁ and G₂ by identifying two vertices. Set w be the common vertex of G₁ and G₂. Obviously, w is a cut vertex of G. For every $e = u v \in E (G_{1}),$ w belongs to one of the three sets $N_{u} (e), N_{v} (e), N_{0} (e) .$ Since every path connecting u(v) and each vertex in $V (G_{2})$ is via w, all edges of G₂ must contained in one of the three sets $M_{u} (e), M_{v} (e), M_{0} (e)$ (the same with w). Therefore, the contribution of G₂ to the item $(m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2})$ completely relies on the size of G₂, that is, changing the structure of G₂ cannot alter the value $\sum_{e = u v \in E (G_{1})} (m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2}) .$ Since the contribution of the pendant edge to $(m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2})$ is the smallest, we have the following lemma.

Lemma 2.2.

Let $G (≇ S_{m})$ be a connected graph of size m. Then $S z_{e}^{*} (G_{1} \cdot S_{m}) < S z_{e}^{*} (G_{1} \cdot G),$ where the common vertex of $G_{1} \cdot S_{m}$ is the center vertex of S_m.

Let $S_{m, r} ≅ S_{m - r} \cdot C_{r},$ where the common vertex w of $S_{m - r} \cdot C_{r}$ is the center vertex of $S_{m - r},$ we called w is the center vertex of $S_{m, r} .$

Lemma 2.3.

[Citation11] For $m \geq 5$ , let G be an $m -$ edges unicyclic graph. Then $S z_{e}^{*} (G) \geq {\begin{matrix} \frac{1}{2} m^{2} + \frac{23}{4} m - 15, m \geq 15, \\ \frac{3}{4} m^{2} + \frac{5}{4} m - \frac{15}{4}, m \leq 15. \end{matrix}$ with equality if and only if $G ≅ S_{m, 3}$ for $m \leq 14, G ≅ S_{m, 3}$ or $S_{m, 4}$ for m = 15, and $G ≅ S_{m, 4}$ for $m \geq 16 .$

Lemma 2.4.

Let H₁ be a connected graph of size m₁ and H₂ be an unicyclic graphs of sizze $m_{2} .$ Then $S z_{e}^{*} (H_{1} \cdot H_{2}) \geq S z_{e}^{*} (H_{1} \cdot S_{m_{2}, 3})$ for $m_{1} + m_{2} \leq 14, S z_{e}^{*} (H_{1} \cdot H_{2}) \geq S z_{e}^{*} (H_{1} \cdot S_{m_{2}, 3}) = S z_{e}^{*} (H_{1} \cdot S_{m_{2}, 4})$ for $m_{1} + m_{2} = 15$ , and $S z_{e}^{*} (H_{1} \cdot H_{2}) \geq S z_{e}^{*} (H_{1} \cdot S_{m_{2}, 4})$ for $m_{1} + m_{2} \geq 16$ , where the common vertex of $H_{1} \cdot S_{m_{2}, 3} (H_{1} \cdot S_{m_{2}, 4})$ is the center vertex of $S_{m_{2}, 3} (S_{m_{2}, 4}) .$

Proof.

If $m_{1} + m_{2} \leq 14 .$ Then, by Lemma 2.3, we get $\begin{matrix} S z_{e}^{*} (H_{1} \cdot H_{2}) = \sum_{e = u v \in E (H_{1} \cdot H_{2})} (m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2}) \\ = \sum_{e \in E (H_{1})} (m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2}) + \sum_{e \in E (H_{2})} (m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2}) \\ = \sum_{e \in E (H_{1})} (m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2}) + S z_{e}^{*} (S_{m_{1}} \cdot H_{2}) - (m_{1} - 1) \frac{1}{2} (m - \frac{1}{2}) \\ \geq \sum_{e \in E (H_{1})} (m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2}) + S z_{e}^{*} (S_{m_{1}} \cdot S_{m_{2}, 3}) - (m_{1} - 1) \frac{1}{2} (m - \frac{1}{2}) \\ = \sum_{e \in E (H_{1})} (m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2}) + \sum_{e \in E (S_{m_{2}, 3})} (m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2}) \\ = S z_{e}^{*} (H_{1} \cdot S_{m_{2}, 3}) . \end{matrix}$ Samely, if $m_{1} + m_{2} = 15,$ then $S z_{e}^{*} (H_{1} \cdot H_{2}) \geq S z_{e}^{*} (H_{1} \cdot S_{m_{2}, 3}) = S z_{e}^{*} (H_{1} \cdot S_{m_{2}, 4}),$ and if $m_{1} + m_{2} \geq 16,$ then $S z_{e}^{*} (H_{1} \cdot H_{2}) \geq S z_{e}^{*} (H_{1} \cdot S_{m_{2}, 4}) .$ □

3. Proof of Theorem 1.1

A Θ-graph is a graph that connecting two fix vertices by three internally disjoint paths. If the corresponding three paths have the lengths a, b, c with $a \leq b \leq c,$ we denote it by $Θ (a, b, c) .$ Let $G_{m}^{1}$ be the set of m-edge bicyclic connected graphs with exactly two cycles. Let $G_{m}^{2}$ be the set of m-edge bicyclic connected graphs with three cycles. That is if $G \in G_{m}^{2},$ then it has a Θ graph as its subgraph, which is called the brace of G.

From Lemma 2.4, we deduce the following conclusion.

Theorem 3.1.

Let $G \in G_{m}^{1}$ . If $m \geq 16$ , then $S z_{e}^{*} (G) \geq \frac{1}{2} m^{2} + \frac{47}{4} m - 30$ with equality only if $G ≅ B$ ; If m = 15, then $S z_{e}^{*} (G) \geq \frac{1035}{4}$ with equality only if $G ≅ B, B_{0}, B_{1}$ , where $B, B_{0}, B_{1}$ is depicted in ; If $6 \leq m \leq 14$ , then $S z_{e}^{*} (G) \geq m^{2} + \frac{11}{4} m - \frac{15}{2}$ with equality only if $G ≅ B_{1} .$

Proof.

Since $G \in G_{m}^{1},$ there are two unicyclic graphs H₁ and H₂ such that $G = H_{1} \cdot H_{2} .$ Assume that $| E (H_{1}) | = m_{1}, | E (H_{2}) | = m_{2} .$ In view of Lemma 2.4, we get $\begin{matrix} S z_{e}^{*} (G) = S z_{e}^{*} (H_{1} \cdot H_{2}) \geq S z_{e}^{*} (H_{1} \cdot S_{m_{2}, 3}) \\ \geq S z_{e}^{*} (S_{m_{1}, 3} \cdot S_{m_{2}, 3}) = S z_{e}^{*} (B_{1}), for m \leq 14; \end{matrix}$ $\begin{matrix} S z_{e}^{*} (G) = S z_{e}^{*} (H_{1} \cdot H_{2}) \geq S z_{e}^{*} (H_{1} \cdot S_{m_{2}, 3}) = S z_{e}^{*} (H_{1} \cdot S_{m_{2}, 4}) \\ \geq S z_{e}^{*} (S_{m_{1}, 3} \cdot S_{m_{2}, 3}) = S z_{e}^{*} (S_{m_{1}, 3} \cdot S_{m_{2}, 4}) = S z_{e}^{*} (S_{m_{1}, 4} \cdot S_{m_{2}, 4}) \\ = S z_{e}^{*} (B_{1}) = S z_{e}^{*} (B_{0}) = S z_{e}^{*} (B), for m = 15; \end{matrix}$

$S z^{*} (G) = S z^{*} (H_{1} \cdot H_{2}) \geq S z^{*} (H_{1} \cdot S_{m_{2}, 4}) \geq S z^{*} (S_{m_{1}, 4} \cdot S_{m_{2}, 4}) = S z_{e}^{*} (B),$ for $m \geq 16 .$

Clearly, $S z_{e}^{*} (B) = \frac{1}{2} m^{2} + \frac{47}{4} m - 30$ and $S z_{e}^{*} (B_{1}) = m^{2} + \frac{11}{4} m - \frac{15}{2} .$ Therefore, the proof is complete. □

Lemma 3.2.

Let $G \in G_{m}^{2}$ with brace $Θ (2, 2, 2)$ . If $m \geq 6$ , then $S z_{e}^{*} (G) \geq \frac{1}{2} m^{2} + \frac{55}{4} m - 48$ and equality holds only if $G ≅ B_{2}$ , where B₂ is depicted in .

Figure 2. These graphs are used in Lemma 3.2, Lemma 3.3 and Lemma 3.4.

Proof.

Suppose that x₁ and x₂ are the vertices with degree 3 and $x_{3}, x_{4}, x_{5}$ are the vertices with degree 2 in $Θ (2, 2, 2)$ of G. In view of Lemma 2.2, we have that each edge in the pendant tree of each x_i is a pendant edge. Let l_i be the number of pendant edges of x_i. Assume that $l_{1} \geq l_{2}, l_{3} \geq l_{4} \geq l_{5}$ by symmetry. G₁ is the graph from G by transferring l₂ pendant edges from x₂ to x₁. It is checked that $\begin{matrix} \sum_{e \in E (G_{1})} δ^{2} (e) - \sum_{e \in E (G)} δ^{2} (e) \\ = δ^{2} (x_{1} x_{3}) - δ^{2} (x_{1} x_{3}) + δ^{2} (x_{1} x_{4}) - δ^{2} (x_{1} x_{4}) + δ^{2} (x_{1} x_{5}) - δ^{2} (x_{1} x_{5}) \\ + δ^{2} (x_{2} x_{3}) - δ^{2} (x_{2} x_{3}) + δ^{2} (x_{2} x_{4}) - δ^{2} (x_{2} x_{4}) + δ^{2} (x_{2} x_{5}) - δ^{2} (x_{2} x_{5}) \\ = {(l_{1} + l_{2} + l_{4} + l_{5} + 2 - l_{3} - 1)}^{2} - {(l_{1} + l_{4} + l_{5} + 2 - l_{2} - l_{3} - 1)}^{2} \\ + {(l_{1} + l_{2} + l_{3} + l_{5} + 2 - l_{4} - 1)}^{2} - {(l_{1} + l_{3} + l_{5} + 2 - l_{2} - l_{4} - 1)}^{2} \\ + {(l_{1} + l_{2} + l_{3} + l_{4} + 2 - l_{5} - 1)}^{2} - {(l_{1} + l_{3} + l_{4} + 2 - l_{2} - l_{5} - 1)}^{2} \\ + {(l_{1} + l_{2} + l_{3} + 1 - l_{4} - l_{5} - 2)}^{2} - {(l_{1} + l_{3} + 1 - l_{2} - l_{4} - l_{5} - 2)}^{2} \\ + {(l_{1} + l_{2} + l_{4} + 1 - l_{3} - l_{5} - 2)}^{2} - {(l_{1} + l_{4} + 1 - l_{2} - l_{3} - l_{5} - 2)}^{2} \\ + {(l_{1} + l_{2} + l_{5} + 1 - l_{3} - l_{4} - 2)}^{2} - {(l_{1} + l_{5} + 1 - l_{2} - l_{3} - l_{4} - 2)}^{2} \\ = 24 l_{1} l_{2} \geq 0. \end{matrix}$

It follows that $S z_{e}^{*} (G_{1}) \leq S z_{e}^{*} (G)$ and equality holds only if $G_{1} ≅ G .$

G₂ is the graph from G₁ by moving l₅ pendant edges from x₅ to x₃. It is deduced that $\begin{matrix} \sum_{e \in E (G_{2})} δ^{2} (e) - \sum_{e \in E (G_{1})} δ^{2} (e) \\ = {(l_{3} + l_{5} + 1 - l_{1} - l_{4} - 2)}^{2} - {(l_{3} + 1 - l_{1} - l_{4} - l_{5} - 2)}^{2} \\ + {(l_{1} + l_{3} + l_{5} + 2 - l_{4} - 1)}^{2} - {(l_{1} + l_{3} + l_{5} + 2 - l_{4} - 1)}^{2} \\ + {(l_{1} + l_{3} + l_{4} + l_{5} + 2 - 1)}^{2} - {(l_{1} + l_{3} + l_{4} + 2 - l_{5} - 1)}^{2} \\ + {(l_{1} + l_{3} + l_{5} + 1 - l_{4} - 2)}^{2} - {(l_{1} + l_{3} + 1 - l_{4} - l_{5} - 2)}^{2} \\ + {(l_{3} + l_{5} + 2 - l_{1} - l_{4} - 1)}^{2} - {(l_{3} + l_{5} + 2 - l_{1} - l_{4} - 1)}^{2} \\ + {(l_{3} + l_{4} + l_{5} + 2 - l_{1} - 1)}^{2} - {(l_{3} + l_{4} + 2 - l_{1} - l_{5} - 1)}^{2} \\ = 16 l_{3} l_{5} \geq 0. \end{matrix}$

By means of EquationEq. (1)(1) $S z_{e}^{*} (G) = \frac{m^{3}}{4} - \frac{1}{4} \sum_{e \in E (G)} δ {(e)}^{2} .$ (1) , $S z_{e}^{*} (G_{2}) \leq S z_{e}^{*} (G_{1})$ with equality only if $G_{2} ≅ G_{1} .$ G₃ denotes the graph from G₂ by shifting l₄ pendant edges from x₄ to x₃. So $S z_{e}^{*} (G_{3}) \leq S z_{e}^{*} (G_{2})$ by symmetry, and equality holds only if $G_{3} ≅ G_{2} .$

G₄ is the graph from G₃ by transferring l₁ pendant edges from x₁ to x₃. Clearly, $G_{4} ≅ B_{2} .$ Moreover, $\begin{matrix} \sum_{e \in E (G_{4})} δ^{2} (e) - \sum_{e \in E (G_{3})} δ^{2} (e) \\ = {(l_{1} + l_{3} + 1 - 2)}^{2} - {(l_{3} + 1 - l_{1} - 2)}^{2} + {(l_{1} + l_{3} + 2 - 1)}^{2} - {(l_{1} + l_{3} + 2 - 1)}^{2} \\ + {(l_{1} + l_{3} + 2 - 1)}^{2} - {(l_{1} + l_{3} + 2 - 1)}^{2} + {(l_{1} + l_{3} + 1 - 2)}^{2} - {(l_{1} + l_{3} + 1 - 2)}^{2} \\ + {(l_{1} + l_{3} + 2 - 1)}^{2} - {(l_{3} + 2 - l_{1} - 1)}^{2} + {(l_{1} + l_{3} + 2 - 1)}^{2} - {(l_{3} + 2 - l_{1} - 1)}^{2} \\ = 4 l_{1} (3 l_{3} + 1) \geq 0. \end{matrix}$

Using EquationEq. (1)(1) $S z_{e}^{*} (G) = \frac{m^{3}}{4} - \frac{1}{4} \sum_{e \in E (G)} δ {(e)}^{2} .$ (1) , we get $S z_{e}^{*} (G_{4}) \leq S z_{e}^{*} (G_{3}),$ and equality holds only if $G_{4} ≅ G_{3} .$ Moreover, $S z_{e}^{*} (G_{4}) = S z_{e}^{*} (B_{2}) = \frac{1}{2} m^{2} + \frac{55}{4} m - 48 .$ Hence the proof is finished. □

Lemma 3.3.

Let $G \in G_{m}^{2}$ with brace $Θ (1, 2, 2)$ . If $5 \leq m \leq 8$ , then $S z_{e}^{*} (G) \geq m^{2} + \frac{15}{4} m - \frac{27}{2}$ with equality only if $G ≅ B_{3}$ ; If m = 9, then $S z_{e}^{*} (G) \geq \frac{405}{4}$ with equality only if $G ≅ B_{3}, B_{4}$ , where B₃, B₄ is depicted in ; If $m \geq 10$ , then $S z_{e}^{*} (G) \geq \frac{3}{4} m^{2} + \frac{29}{4} m - \frac{99}{4}$ with equality only if $G ≅ B_{4} .$

Proof.

Let x₁ and x₂ be two vertices with degree 3 and x₃, x₄ are three vertices with degree 2 in $Θ (1, 2, 2)$ of G. In view of Lemma 2.1, we have that each edge in the pendant tree of each x_i is a pendant edge. Let l_i be the number of pendant edges of x_i. Suppose $l_{1} \geq l_{2}, l_{3} \geq l_{4}$ from symmetry. G₁ is the graph from G by moving l₂ pendant edges from x₂ to x₁. Moreover, we arrive at $\begin{matrix} \sum_{e \in E (G_{1})} δ^{2} (e) - \sum_{e \in E (G)} δ^{2} (e) \\ = {(l_{1} + l_{2} + 2 - 2)}^{2} - {(l_{1} + 2 - l_{2} - 2)}^{2} \\ + {(l_{1} + l_{2} + l_{4} + 2 - l_{3} - 1)}^{2} - {(l_{1} + l_{4} + 2 - l_{3} - 1)}^{2} \\ + {(l_{1} + l_{2} + l_{3} + 2 - l_{4} - 1)}^{2} - {(l_{1} + l_{3} + 2 - l_{4} - 1)}^{2} \\ + {(l_{4} + 2 - l_{3} - 1)}^{2} - {(l_{2} + l_{4} + 2 - l_{3} - 1)}^{2} \\ + {(l_{3} + 2 - l_{4} - 1)}^{2} - {(l_{2} + l_{3} + 2 - l_{4} - 1)}^{2} \\ = 8 l_{1} l_{2} \geq 0. \end{matrix}$

Using EquationEq. (1)(1) $S z_{e}^{*} (G) = \frac{m^{3}}{4} - \frac{1}{4} \sum_{e \in E (G)} δ {(e)}^{2} .$ (1) , we show $S z^{*} (G_{1}) \leq S z^{*} (G)$ with equality only if $G ≅ G_{1} .$

Let G₂ deonte the graph from G₁ by shifting l₄ pendant edges from x₄ to x₃. Then, $\begin{matrix} \sum_{e \in E (G_{2})} δ^{2} (e) - \sum_{e \in E (G_{1})} δ^{2} (e) \\ = {(l_{1} + 2 - 2)}^{2} - {(l_{1} + 2 - 2)}^{2} \\ + {(l_{3} + l_{4} + 1 - l_{1} - 2)}^{2} - {(l_{3} + 1 - l_{1} - l_{4} - 2)}^{2} \\ + {(l_{1} + l_{3} + l_{4} + 2 - 1)}^{2} - {(l_{1} + l_{3} + 2 - l_{4} - 1)}^{2} \\ + {(l_{3} + l_{4} + 1 - 2)}^{2} - {(l_{3} + 1 - l_{4} - 2)}^{2} \\ + {(l_{3} + l_{4} + 2 - 1)}^{2} - {(l_{3} + 2 - l_{4} - 1)}^{2} \\ = 16 l_{3} l_{4} \geq 0. \end{matrix}$

Combining with EquationEq. (1)(1) $S z_{e}^{*} (G) = \frac{m^{3}}{4} - \frac{1}{4} \sum_{e \in E (G)} δ {(e)}^{2} .$ (1) , $S z^{*} (G_{2}) \leq S z^{*} (G_{1})$ with equality only if $G_{2} ≅ G_{1} .$

G₃ is the new graph obtained from G₂ by moving l₁ pendant edges from x₁ to x₃. Hence, $G_{3} ≅ B_{4} .$ Furthermore, $\begin{matrix} \sum_{e \in E (G_{3})} δ^{2} (e) - \sum_{e \in E (G_{2})} δ^{2} (e) \\ = {(2 - 2)}^{2} - {(l_{1} + 2 - 2)}^{2} \\ + {(l_{1} + l_{3} + 1 - 2)}^{2} - {(l_{3} + 1 - l_{1} - 2)}^{2} \\ + {(l_{1} + l_{3} + 2 - 1)}^{2} - {(l_{1} + l_{3} + 2 - 1)}^{2} \\ + {(l_{1} + l_{3} + 1 - 2)}^{2} - {(l_{3} + 1 - 2)}^{2} \\ + {(l_{1} + l_{3} + 2 - 1)}^{2} - {(l_{3} + 2 - 1)}^{2} \\ = l_{1} (l_{1} + 8 l_{3} - 4) . \end{matrix}$

Note that $\sum_{e \in E (G_{3})} δ^{2} (e) \geq \sum_{e \in E (G_{2})} δ^{2} (e)$ with $l_{3} \geq 1 .$ So $S z_{e}^{*} (G_{3}) \leq S z_{e}^{*} (G_{2})$ by EquationEq. (1)(1) $S z_{e}^{*} (G) = \frac{m^{3}}{4} - \frac{1}{4} \sum_{e \in E (G)} δ {(e)}^{2} .$ (1) , and equality holds only if $G_{3} ≅ G_{2} .$ Clearly, $G_{2} ≅ B_{3}$ with $l_{3} = 0 .$ In addition, $S z_{e}^{*} (B_{3}) = m^{2} + \frac{15}{4} m - \frac{27}{2}, S z_{e}^{*} (B_{4}) = \frac{3}{4} m^{2} + \frac{29}{4} m - \frac{99}{4} .$ Our proof is finished. □

Lemma 3.4.

Let $G \in G_{m}^{2}$ with brace $Θ (1, 2, 3)$ . If $m \geq 6$ , then $S z_{e}^{*} (G) \geq \frac{3}{4} m^{2} + \frac{35}{4} m - \frac{59}{2}$ and equality holds only if $G ≅ B_{5}$ , where B₅ is depicted in .

Proof.

Assume that x₁ and x₂ are two vertices with degree 3 and $x_{3}, x_{4}, x_{5}$ are three vertices with degree 2 of $Θ (1, 2, 3)$ in G. In view of Lemma 2.1, we have that each edge in the pendant tree of each x_i is a pendant edge. Let l_i be the number of pendant edges of x_i. Assume that $l_{1} + l_{4} \geq l_{2} + l_{5}$ from symmetry. G₁ denotes the graph from G by transferring l₂ pendant edges from x₂ and l₅ pendant edges of x₅ to x₁ and x₄, respectively. We deduce that $\begin{matrix} \sum_{e \in E (G_{1})} δ^{2} (e) - \sum_{e \in E (G)} δ^{2} (e) \\ = {(l_{1} + l_{2} + l_{4} + l_{5} + 2 - 2)}^{2} - {(l_{1} + l_{4} + 2 - l_{2} - l_{5} - 2)}^{2} \\ + {(l_{1} + l_{2} + l_{4} + l_{5} + 3 - l_{3} - 1)}^{2} - {(l_{1} + l_{4} + 3 - l_{3} - 1)}^{2} \\ + {(3 - l_{3} - 1)}^{2} - {(l_{2} + l_{5} + 3 - l_{3} - 1)}^{2} \\ + {(l_{1} + l_{2} + l_{3} + 3 - l_{4} - l_{5} - 1)}^{2} - {(l_{1} + l_{2} + l_{3} + 3 - l_{4} - l_{5} - 1)}^{2} \\ + {(l_{1} + l_{2} + l_{3} + 3 - l_{4} - l_{5} - 1)}^{2} - {(l_{1} + l_{2} + l_{3} + 3 - l_{4} - l_{5} - 1)}^{2} \\ + {(l_{1} + l_{2} + l_{4} + l_{5} + 2 - 2)}^{2} - {(l_{1} + l_{4} + 2 - l_{2} - l_{5} - 2)}^{2} \\ = 10 (l_{2} + l_{5}) (l_{1} + l_{4}) \geq 0. \end{matrix}$

Combining with EquationEq. (1)(1) $S z_{e}^{*} (G) = \frac{m^{3}}{4} - \frac{1}{4} \sum_{e \in E (G)} δ {(e)}^{2} .$ (1) , $S z_{e}^{*} (G_{1}) \leq S z_{e}^{*} (G)$ and equality holds only if $G ≅ G_{1} .$

G₂ denotes the graph obtained from G₁ by moving l₄ pendant edges from x₄ to x₁. Then, we have $\begin{matrix} \sum_{e \in E (G_{2})} δ^{2} (e) - \sum_{e \in E (G_{1})} δ^{2} (e) \\ = {(l_{1} + l_{4} + 2 - 2)}^{2} - {(l_{1} + l_{4} + 2 - 2)}^{2} \\ + {(l_{1} + l_{4} + 3 - l_{3} - 1)}^{2} - {(l_{1} + l_{4} + 3 - l_{1} - 1)}^{2} \\ + {(3 - l_{3} - 1)}^{2} - {(3 - l_{3} - 1)}^{2} \\ + {(l_{1} + l_{3} + l_{4} + 3 - 1)}^{2} - {(l_{1} + l_{3} + 3 - l_{4} - 1)}^{2} \\ + {(l_{1} + l_{3} + l_{4} + 3 - 1)}^{2} - {(l_{1} + l_{3} + 3 - l_{4} - 1)}^{2} \\ + {(l_{1} + l_{4} + 2 - 2)}^{2} - {(l_{1} + l_{4} + 2 - 2)}^{2} \\ = 8 l_{4} (l_{1} + l_{3} + 2) \geq 0. \end{matrix}$

Using EquationEq.(1)(1) $S z_{e}^{*} (G) = \frac{m^{3}}{4} - \frac{1}{4} \sum_{e \in E (G)} δ {(e)}^{2} .$ (1) , $S z_{e}^{*} (G_{2}) \leq S z_{e}^{*} (G_{1})$ with equality only if $G_{2} ≅ G_{1} .$

G₃ is the graph obtained from G₂ by shifting l₃ pendant edges from x₃ to x₁. Clearly, $G_{3} ≅ B_{5} .$ Moreover, $\begin{matrix} \sum_{e \in E (G_{3})} δ^{2} (e) - \sum_{e \in E (G_{2})} δ^{2} (e) \\ = {(l_{1} + l_{3} + 2 - 2)}^{2} - {(l_{1} + 2 - 2)}^{2} + {(l_{1} + l_{3} + 3 - 1)}^{2} - {(l_{1} + 3 - l_{3} - 1)}^{2} \\ + {(l_{1} + l_{3} + 3 - 1)}^{2} - {(l_{1} + l_{3} + 3 - 1)}^{2} + {(l_{1} + l_{3} + 2 - 2)}^{2} - {(l_{1} + 2 - 2)}^{2} \\ + {(3 - 1)}^{2} - {(3 - l_{3} - 1)}^{2} + {(l_{1} + l_{3} + 3 - 1)}^{2} - {(l_{1} + l_{3} + 3 - 1)}^{2} \\ = l_{3} (8 l_{1} + l_{3} + 12) \geq 0. \end{matrix}$ Identifying with EquationEq.(1)(1) $S z_{e}^{*} (G) = \frac{m^{3}}{4} - \frac{1}{4} \sum_{e \in E (G)} δ {(e)}^{2} .$ (1) , $S z_{e}^{*} (G_{3}) \leq S z_{e}^{*} (G_{2})$ and equality holds with only if $G_{3} ≅ G_{2} .$

In addition, $S z_{e}^{*} (B_{5}) = S z^{*} (G_{3}) = \frac{3}{4} m^{2} + \frac{35}{4} m - \frac{59}{2} .$ We complete the proof. □

Theorem 3.5.

Let $G \in G_{m}^{2}$ with brace $Θ (a, b, c)$ . If $m \geq 22$ , then $S z_{e}^{*} (G) \geq \frac{1}{2} m^{2} + \frac{55}{4} m - 48$ with equality only if $G ≅ B_{2}$ ; If $10 \leq m \leq 21$ , then $S z_{e}^{*} (G) \geq \frac{3}{4} m^{2} + \frac{29}{4} m - \frac{99}{4}$ with equality only if $G ≅ B_{4}$ ; If m = 9, then $S z_{e}^{*} (G) = \frac{405}{4}$ with equality only if $G ≅ B_{3}, B_{4}$ ; If $5 \leq m \leq 8$ , then $S z_{e}^{*} (G) \geq m^{2} + \frac{15}{4} m - \frac{27}{2}$ with equality only if $G ≅ B_{3} .$

Proof.

Let $P_{a + 1}, P_{b + 1}, P_{c + 1}$ be the three paths of $Θ (a, b, c)$ in G. Mark x and y the two vertices with degree 3 of $Θ (a, b, c) .$ In order to complete the proof, we take the following three cases.

Case 1. $3 \leq a \leq b \leq c .$
We choose all edges with at least one end of x and y in $Θ (a, b, c) .$ e = xz denotes one of the six edges. Note that $m_{z} (e) \geq 2, m_{0} (e) = 3, m_{x} (e) \leq m - 5$ for $a = b = c = 3,$ and $m_{z} (e) \geq 3, m_{0} (e) \geq 1, m_{x} (e) \leq m - 4$ otherwise, then we have $δ (e) \leq m - 7 .$ This fact also holds for other five edges. So $\sum_{e = u v \in E (G)} δ^{2} (e) \leq 6 {(m - 7)}^{2} + (m - 6) {(m - 1)}^{2} < m^{3} - 2 m^{2} - 55 m + 192,$ for $m \geq 6 .$ Consisting with EquationEq.(1)(1) $S z_{e}^{*} (G) = \frac{m^{3}}{4} - \frac{1}{4} \sum_{e \in E (G)} δ {(e)}^{2} .$ (1) , the Case is true.
Case 2. $2 = a \leq b \leq c . .$
Subcase 2.1. $2 = a = b = c .$

The Subcase follows from Lemma 3.2.

Subcase 2.2. $2 = a = b, 3 \leq c .$

Take four edges of the paths $P_{a + 1}$ and $P_{b + 1} .$ Set one edge of them as e = xz, clearly, $δ (e) \leq m - 6 .$ Choose the two edges of the path $P_{c + 1}$ satisfying incident with x or y. Put down one of them as e = xw, obviously, $δ (e) \leq m - 5 .$ Hence $\sum_{e = u v \in E (G)} δ^{2} (e) \leq 4 {(m - 6)}^{2} + 2 {(m - 5)}^{2} + (m - 6) {(m - 1)}^{2} < m^{3} - 2 m^{2} - 55 m + 192.$

By means of EquationEq. (1)(1) $S z_{e}^{*} (G) = \frac{m^{3}}{4} - \frac{1}{4} \sum_{e \in E (G)} δ {(e)}^{2} .$ (1) , the Subcase is true.

Subcase 2.3. $2 = a, 3 \leq b \leq c$

Using the similar discussion of Subcase 2.2, the Subcase is also true.

Case 3. $1 = a \leq b \leq c . .$
Subcase 3.1. $1 = a, 2 = b = c .$

From Lemma 3.3, we deduce that if $m \geq 22,$ then $S z_{e}^{*} (B_{2}) < S z_{e}^{*} (B_{4});$ If $10 \leq m \leq 21,$ then $S z_{e}^{*} (B_{4}) < S z_{e}^{*} (B_{2});$ If m = 9, then $S z_{e}^{*} (B_{3}) = S z_{e}^{*} (B_{4}) < S z_{e}^{*} (B_{2});$ If m = 6, 7, 8, then $S z_{e}^{*} (B_{3}) < S z_{e}^{*} (B_{4}) < S z_{e}^{*} (B_{2});$ If m = 5, then $B_{3} ≅ B_{4} .$ Consequently, the Subcase is true.

Subcase 3.2. $1 = a, 2 = b, 3 = c .$

The Subcase follows from Lemma 3.4.

Subcase 3.3. $1 = a, 2 = b, 4 \leq c .$

Take the five edges that are with at least one end of x and y in $Θ (1, 2, c) .$ Set one edge e = xy, then $δ (e) \leq m - 7 .$ set e = xz from one of the other four edges, obviously, $δ (e) \leq m - 5 .$ In addition, take the two edges from the middle of $P_{c + 1} .$ e = uv denotes one of the two edges. we get $δ (e) \leq m - 6 .$ Hence $\sum_{e = u v \in E (G)} δ^{2} (e) \leq {(m - 7)}^{2} + 4 {(m - 5)}^{2} + 2 {(m - 6)}^{2} + (m - 7) {(m - 1)}^{2} < m^{3} - 2 m^{2} - 55 m + 192,$ for $m \geq 3.$ The Subcase is true by EquationEq.(1)(1) $S z_{e}^{*} (G) = \frac{m^{3}}{4} - \frac{1}{4} \sum_{e \in E (G)} δ {(e)}^{2} .$ (1) .

Subcase 3.4. $1 = a, 3 \leq b \leq c .$

Choose the five edges that are with at least one end of x and y of $Θ (1, b, c) .$ If e = xy, then $δ (e) \leq m - 7 .$ e = xz denotes one of other four edges, then $δ (e) \leq m - 4 .$ Take two edges from the middle of $P_{b + 1}, P_{c + 1} .$ Let e = uv be one of them. Then $δ (e) \leq m - 6 .$ Hence $\sum_{e = u v \in E (G)} δ^{2} (e) \leq {(m - 7)}^{2} + 4 {(m - 4)}^{2} + 2 {(m - 6)}^{2} + (m - 7) {(m - 1)}^{2} < m^{3} - 2 m^{2} - 55 m + 192.$ Together with EquationEq. (1)(1) $S z_{e}^{*} (G) = \frac{m^{3}}{4} - \frac{1}{4} \sum_{e \in E (G)} δ {(e)}^{2} .$ (1) , the Subcase is true.

Therefore, we finish the proof. □

From Theorem 3.1 and Theorem 3.5, we not only show the Theorem 1.1, but also obtain a strengthening result.

Theorem 3.6.

Let G be a bicyclic graph G with size $m (m \geq 5)$ . Then $S z_{e}^{*} (G) \geq {\begin{matrix} \frac{1}{2} m^{2} + \frac{47}{4} m - 30, & if m \geq 17, and ‘ =^{’} holds iff G ≅ B, \\ \frac{3}{4} m^{2} + \frac{29}{4} m - \frac{99}{4}, & if 13 \leq m \leq 16, and' =^{'} holds iff G ≅ B_{4}, \\ m^{2} + \frac{11}{4} m - \frac{15}{2}, & if 7 \leq m \leq 12, and' =^{'} holds iff G ≅ B_{4}, \\ 45, & if m = 6, and' =^{'} holds iff G ≅ B_{1}, B_{3}, \\ \frac{121}{4}, & if m = 5, and' =^{'} holds iff G ≅ B_{3} . \end{matrix}$

Acknowledgements

M. Liu is supported by National Natural Science Foundation of China (No. 11961040), Innovation ability improvement project of colleges and universities in Gansu Province (No. 2019A-037), Tianyou Youth Talent Lift Program of Lanzhou Jiaotong University. S. Ji is supported Shandong Provincial Natural Science Foundation of China (No. ZR2019MA012).

Disclosure statement

No potential conflict of interest was reported by the authors.

Data availability

The data used to support the findings of this study are available from the corresponding author upon request.

Additional information

Funding

M. Liu is supported by National Natural Science Foundation of China (No.11961040), Innovation ability improvement project of colleges and universities in Gansu Province (No.2019A-037), Tianyou Youth Talent Lift Program of Lanzhou Jiaotong University. S. Ji is supported Shandong Provincial Natural Science Foundation of China(No. ZR2019MA012).

References

Aouchiche, M, Hansen, P. (2010). On a conjecture about the Szeged index. Eur. J. Combin. 31(7): 1662–1666.
Google Scholar
Azari, M. (2017). Some variants of the Szeged index under rooted product of graphs. MMN 17(2): 761–775.
Google Scholar
Bonamy, M., Knor, M., Lužar, B., Pinlou, A, Škrekovski, R. (2017). On the difference between the Szeged and Wiener index. Appl. Math. Comput. 312: 202–213.
Google Scholar
Bondy, J. A, Murty, U. S. R. (2008). Graph Theory. Berlin: Springer-Verlag.
Google Scholar
Cai, X, Zhou, B. (2010). Edge Szeged index of Unicyclic graphs. MATCH Commun. Math. Comput. Chem. 63: 133–144.
Web of Science ®Google Scholar
Chen, L., Li, X, Liu, M. (2014). The (revised) Szeged index and the Wiener index of a nonbipartite graph. Euro. J. Comb. 36: 237–246.
Web of Science ®Google Scholar
Chen, L., Li, X, Liu, M. (2014). Tricyclic graphs with maximal revised Szeged index. Discr. Appl. Math. 177: 71–79.
Google Scholar
Chen, L., Li, X., Liu, M, Gutman, I. (2012). On a relation between the Szeged index and the Wiener index for bipartite graphs. Trans. Comb. 1(4): 43–49.
Google Scholar
Črepnjak, M, Tratnik, N. (2017). The Szeged index and the Wiener index of partial cubes with applications to chemical graphs. Appl. Math. Comput. 309: 324–333.
Web of Science ®Google Scholar
Dobrynin, A. A., Entringer, R, Gutman, I. (2001). Wiener index of trees: theory and applications. Acta Appl. Math. 66(3): 211–249.
Web of Science ®Google Scholar
Dong, H., Zhou, B, Trinajstić, C. (2011). A novel version of the edge-Szeged index. Croat. Chem. Acta 84: 543–545.
Google Scholar
Gutman, I. (1994). A formula for the Wiener number of trees and its extension to graphs containing cycles. Graph Theory Notes N. Y. 27: 9–15.
Google Scholar
Gutman, I, Ashrafi, A. R. (2008). The edge version of the Szeged index. Croat. Chem. Acta 81: 263–266.
Web of Science ®Google Scholar
Gutman, I., Klavžar, S, Mohar, B. (1997). Fifty years of the Wiener index. MATCH Commun. Math. Comput. Chem 35: 1–259.
Google Scholar
Gutman, I., Yeh, Y. N., Lee, S. L, Luo, Y. L. (1993). Some recent results in the theory of the Wiener number. Indian J. Chem. 32A: 651–661.
Google Scholar
Khalifeh, M. H., Yousefi-Azari, H., Ashrafi, A. R, Gutman, I. (2008). The edge Szeged index of product graphs. Croat. Chem. Acta 81: 277–281.
Web of Science ®Google Scholar
Khadikar, P., Kale, P., Deshpande, N., Karmarkar, S, Agrawal, V. (2000). Szeged indices of hexagonal chains. MATCH Commun. Math. Comput. Chem. 43: 7–15.
Google Scholar
Khadikar, P., Karmarkar, S., Agrawal, V. K., Singh, J., Shrivastava, A., Lukovits, I, Diudea, M. V. (2005). Szeged index-Applications for drug modeling. LDDD 2(8): 606–624.
Google Scholar
Li, S, Zhang, H. (2017). Proofs of three conjectures on the quotients of the (revised) Szeged index and the Wiener index and beyond. Discr. Math. 340(3): 311–324.
Web of Science ®Google Scholar
Li, X, Liu, M. (2013). Bicyclic graphs with maximal revised Szeged index. Discr. Appl. Math. 161(16–17): 2527–2531.
Google Scholar
Liu, M, Chen, L. (2016). Bicyclic graphs with maximal edge revised Szeged index. Discr. Appl. Math. 215: 225–230.
Google Scholar
Nadjafi-Arani, M. J., Khodashenas, H, Ashrafi, A. R. (2011). On the differences between Szeged and Wiener indices of graphs. Discr. Math. 311(20): 2233–2237.
Google Scholar
Nadjafi-Arani, M. J., Khodashenas, H, Ashrafi, A. R. (2012). Graphs whose Szeged and Wiener numbers differ by 4 and 5. Math. Comput. Model. 55(3–4): 1644–1648.
Google Scholar
Pisanski, T, Randić, M. (2010). Use of the Szeged index and the revised Szeged index for measuring network bipartivity. Discr. Appl. Math. 158(17): 1936–1944.
Web of Science ®Google Scholar
Randić, M. (2002). On generalization of Wiener index for cyclic structures. Acta Chim. Slov. 49: 483–496.
Web of Science ®Google Scholar
Simić, S., Gutman, I, Baltić, V. (2000). Some graphs with extremal Szeged index. Math. Slovaca 50: 1–15.
Google Scholar
Tratnik, N. (2017). The edge-Szeged index and the PI index of benzenoid systems in linear time. MATCH Commun. Math. Comput. Chem. 77: 393–406.
Web of Science ®Google Scholar
Vukičević, D. (2009). Note on the graphs with the greatest edge-Szeged index. MATCH Commun. Math. Comput. Chem. 61: 673–681.
Google Scholar
Wang, S. (2017). On extremal cacti with respect to the Szeged index. Appl. Math. Comput. 309: 85–92.
Google Scholar
Wiener, H. (1947). Structural determination of paraffin boiling points. J. Am. Chem. Soc. 69(1): 17–20.
PubMed Web of Science ®Google Scholar
Xing, R, Zhou, B. (2011). On the revised Szeged index. Discr. Appl. Math. 159(1): 69–78.
Google Scholar
Žerovnik, J. (1999). Szeged index of symmetric graphs. J. Chem. Inf. Comput. Sci. 39(1): 77–80.
Google Scholar
Zhang, H., Chen, J, Li, S. (2017). On the quotients between the (revised) Szeged index and Wiener index of graphs. Discr. Math. Theor. Comput. Sci. 19(1): 12–25.
Google Scholar
Zhang, H., Li, S, Zhao, L. (2016). On the further relation between the (revised) Szeged index and Wiener index. Discr. Appl. Math. 206: 152–164.
Google Scholar

On minimum revised edge Szeged index of bicyclic graphs

Abstract

1. Introduction

2. Some Lemmas

3. Proof of Theorem 1.1

Acknowledgements

Disclosure statement

Data availability

References

Information for

Open access

Opportunities

Help and information

On minimum revised edge Szeged index of bicyclic graphs

Abstract

1. Introduction

2. Some Lemmas

3. Proof of Theorem 1.1

Acknowledgements

Disclosure statement

Data availability

Additional information

Funding

References

Related research

To cite this article:

Download citation

Your download is now in progress and you may close this window

Login or register to access this feature

Information for

Open access

Opportunities

Help and information

Keep up to date