On the products of group vertex magic graphs

Abstract

Let $G=(V(G);E(G))$ be a simple undirected graph and let A be an additive Abelian group with identity 0. A mapping $l:V(G)\to A\setminus \left\{0\right\}$ is said to be a A-vertex magic labeling of G if there exists a μ in A such that $w(v)=\sum _{u\in N(v)}l(u)=\mu$ for any vertex v of G. If G admits such a labeling, then it is called an A-vertex magic graph. If G is A-vertex magic for any non-trivial Abelian group A, then G is called a group vertex magic graph. In this paper, we consider A-vertex magic and group vertex magic labeling of different products of graphs.

Keywords:

• A-vertex magic
• group vertex magic
• tensor product
• lexicographic product

1. Introduction

The concept of group vertex magic graphs was motivated by the V₄ magic labeling for edges, which was introduced by Lee [5] and it was proved that “A tree T is V₄-magic if and only if all its vertices have odd degrees”. Here, V₄ denotes the famous Klein’s four group. Low and Lee [6] extended the study of V₄-magic labeling for the product graphs by considering an arbitrary Abelian group instead of V₄. By getting motivated by this concept, analogously the concept of group vertex magic graphs was introduced and studied in [3]. Also, in [3], the authors have obtained a characterization of all A-vertex magic trees of diameter up to 4, where the group A is V₄. In [4], Kollaran et al. have characterized the trees of diameter 5, which are V₄ vertex magic. In this paper, we use group elements to label the vertices of a graph and we have extended the study of group vertex magicness of a graph by considering an arbitrary Abelian group. It is interesting to use the ideas of algebraic structure in graph theory. Here, we focus on group vertex magicness of join and tensor product of graphs, and we carefully use the remarkable theorems from group theory, namely Cauchy’s theorem, Sylow’s first theorem and fundamental theorem of finite Abelian groups in a fruitful way.

All graphs considered in this paper are simple finite graphs, and A denotes an Abelian group, not necessarily finite. For a graph G, we use V(G) (or simply V) for the vertex set of G. The open neighbourhood N(v) of a vertex v is the set of all vertices adjacent to v in G. For basic graph-theoretic ideas, we refer to Bondy and Murty [1]. Let R be a commutative ring with unity, we denote the multiplicative group of all units in R by U(R). For concepts in group theory, we refer to Herstein [2].

2. Main results

In this section we discuss the A-vertex magicness of join of two graphs.

Definition 1.

[3] A mapping $l:V(G)\to A\setminus \left\{0\right\}$ is said to be a A-vertex magic labeling of G if there exist a μ in A such that $w(v)=\sum _{u\in N(v)}l(u)=\mu$ for any vertex v of G. The element μ is called the magic constant of the labeling l. A graph G that admits such a labeling is called an A-vertex magic graph. If G is A-vertex magic graph for any non-trivial Abelian group A, then G is called a group vertex magic graph.

Theorem 1.

A graph G is ${\mathbb{Z}}_p$-vertex magic for all primes p if and only if G is A-vertex magic for all finite Abelian groups A.

Proof.

Let A be any non-trivial Abelian group. Assume that G is ${\mathbb{Z}}_p$-vertex magic, for all primes p. By Cauchy’s theorem, A has a subgroup isomorphic to ${\mathbb{Z}}_p,$ for some prime number p. Hence G is A-vertex magic for all finite Abelian groups A. The converse part is trivial. □

Observation 1.

A graph G is ${\mathbb{Z}}_2$ magic if and only if degree of every vertex in G is of same parity.

We prove the following theorem which is analogous to Lemma 1 in [7].

Theorem 2.

Let l be a A-vertex magic labeling of a graph G. Then

$\sum _{v\in V(G)}deg(v)l(v)=n\mu ,$ where n is the number of vertices of G and μ is the magic constant.

Proof.

For each vertex $v\in V(G),$ we have $w(v)=\mu .$ Clearly, $\sum _{v\in V(G)}w(v)=n\mu .$ This sum counts the label of v exactly deg(v) times. Thus, the equation holds. □

The following theorem is a generalisation of Theorem $2.6,2.7$ and $2.9(i)$ in [3].

Theorem 3.

Let $G=K_{n_1,n_2,\dots ,n_k}$ be a complete k-partite graph. Then G is A-vertex magic, where $\left|A\right|>2.$

Proof.

Let $V_1,V_2,\dots ,V_k$ be a partition of V(G) with $\left|V_j\right|=n_j.$ Let $v_i^j\in V_j,$ where $i=1,2,\dots ,n_j.$

Case 1.

p divides o(A), where p is an odd prime.

By Cauchy’s theorem, A has an element a of order p. If n_j is odd, then define $l:V\to A\setminus \left\{0\right\}$ by $$l(v_i^j)=\{\begin{array}{cc}a\hfill & \hspace{1em}\text{if}\mathrm{ }i\mathrm{ }\text{is}\mathrm{ }\text{odd}\hfill \\ -a\hfill & \hspace{1em}\text{if}\mathrm{ }i\text{is even}.\hfill \end{array}$$

If n_j is even, then define $$l(v_i^j)=\{\begin{array}{cc}2a\hfill & \hspace{1em}\text{if}\mathrm{ }i=1\hfill \\ a\hfill & \hspace{1em}\text{if}\mathrm{ }i>1\text{and}\mathrm{ }i\mathrm{ }\text{is}\mathrm{ }\text{odd}\hfill \\ -a\hfill & \hspace{1em}\text{if}\mathrm{ }i\text{is even}.\hfill \end{array}$$

Thus $w(v)=(k-1)a,$ for all $v\in V(G).$

Case 2.

4 divides o(A).

By Sylow’s first theorem and fundamental theorem of finite Abelian groups, A has a subgroup isomorphic to either ${\mathbb{Z}}_4$ or V₄. Suppose A has a subgroup isomorphic to ${\mathbb{Z}}_4.$ If n_j is odd, then $$l(v_i^j)=\{\begin{array}{cc}a\hfill & \hspace{1em}\text{if}\mathrm{ }i\mathrm{ }\text{is}\mathrm{ }\text{odd}\hfill \\ 3a\hfill & \hspace{1em}\text{if}\mathrm{ }i\text{is even}.\hfill \end{array}$$

If n_j is even, then $$l(v_i^j)=\{\begin{array}{cc}2a\hfill & \hspace{1em}\text{if}\mathrm{ }i=1\hfill \\ a\hfill & \hspace{1em}\text{if}\mathrm{ }i>1\mathrm{ }\text{and}\mathrm{ }i\mathrm{ }\text{is}\mathrm{ }\text{odd}\hfill \\ 3a\hfill & \hspace{1em}\text{if}\mathrm{ }i\mathrm{ }\text{is}\mathrm{ }\text{even},\hfill \end{array}$$ where o(a) = 4. Then $w(v)=(k-1)a,$ for all $v\in V(G).$

Suppose A has a subgroup isomorphic to $V_4=\{0,a,b,c\}.$ If n_j is odd, then $l(v_i^j)=a,$ for all i. If n_j is even, then $$l(v_i^j)=\{\begin{array}{cc}b\hfill & \hspace{1em}\text{if}\mathrm{ }i=1\hfill \\ \mathrm{c}\hfill & \hspace{1em}\text{if}\mathrm{ }i=2\hfill \\ a\hfill & \hspace{1em}\text{otherwise}.\hfill \end{array}$$

Thus $w(v)=(k-1)a,$ for all $v\in V(G).$

Case 3.

A is an infinite Abelian group.

In this case, either A contains an element of finite order or A contains a subgroup isomorphic to $\mathbb{Z}.$ Hence, the labeling defined in Case 1 or Case 2 is a magic labeling. □

Corollary 1.

Let $G=K_{n_1,n_2,\dots ,n_k}$ be a complete k-partite graph with each partite size of same parity. Then G is group vertex magic.

Proof.

By Observation 1 and Theorem 3, we get the required result. □

The above corollary is a generalization of Theorem $2.9(ii)$ in [3].

Theorem 4.

Let G₁ and G₂ be graphs. If the graph $G_1+G_2$ is A-vertex magic, then G₁ and G₂ are A-vertex magic.

Proof.

Let us assume that $G_1+G_2$ is A-vertex magic and the corresponding magic labeling is l. Now, define $l^{\prime }:V(G_1)\to A\setminus \left\{0\right\}$ by $l^{\prime }(v)=l(v).$ Let $v_1,v_2\in V(G_1).$ Since $w(v_1)=w(v_2)$ in $G_1+G_2,$ we have $$\begin{array}{cc}\sum _{v\in N(v_1)\cap V(G_1)}l(v)+\sum _{v\in V(G_2)}l(v)\hfill & =\sum _{v\in N(v_2)\cap V(G_1)}l(v)+\sum _{v\in V(G_2)}l(v).\hfill \\ \mathit{Hence}\sum _{v\in N(v_1)\cap V(G_1)}l(v)\hfill & =\sum _{v\in N(v_2)\cap V(G_1)}l(v).\hfill \\ \mathit{Now},\sum _{v\in N(v_1)}{l}^{\prime }(v)\hfill & =\sum _{v\in N(v_2)}{l}^{\prime }(v).\hfill \end{array}$$

Since v₁ and v₂ are arbitrary vertices in G₁, it follows that G₁ is A-vertex magic. By a similar argument, we get G₂ is A-vertex magic. □

Theorem 5.

Let G be an arbitrary r-regular graph with n vertices. Then the graph $G+K_m{}^c$ is A-vertex magic, where $\left|A\right|>2,m>1.$

Proof.

Let $V(G)=\{v_1,v_2,\dots ,v_n\}$ and $V(K_m{}^c)=\{u_1,u_2,\dots ,u_m\}.$ Let $a\in V_4\setminus \left\{0\right\}$ or ${\mathbb{Z}}_t\setminus \left\{0\right\},$ where t is an odd prime or t = 4.

Case 1.

ra = na

Assume that ra = na = e. If $a\in {\mathbb{Z}}_t$ and A has a subgroup isomorphic to ${\mathbb{Z}}_t,$ then define $l:V(G+K_m{}^c)\to A\setminus \left\{0\right\}$ by $l(v_i)=a,$ for all i, where o(a) = t and if m is odd, then $$l(u_j)=\{\begin{array}{cc}2a\hfill & \hspace{1em}\text{if}\mathrm{ }j=1\hfill \\ -a\hfill & \hspace{1em}\text{if}\mathrm{ }j=2,3\hfill \\ a\hfill & \hspace{1em}\text{if}\mathrm{ }j>2\mathrm{ }\text{and}\mathrm{ }j\mathrm{ }\text{is}\mathrm{ }\text{even}\hfill \\ -a\hfill & \hspace{1em}\text{if}\mathrm{ }j>3\mathrm{ }\text{and}\mathrm{ }j\text{is odd}.\hfill \end{array}$$

If m is even, then $$l(u_j)=\{\begin{array}{cc}a\hfill & \hspace{1em}\text{if}\mathrm{ }j\text{is}\mathrm{ }\text{odd}\hfill \\ -a\hfill & \hspace{1em}\text{if}\mathrm{ }j\text{is even}.\hfill \end{array}$$

Thus, $w(v)=e,$ for all $v\in V(G+K_m{}^c).$

If $a\in V_4$ and A has a subgroup isomorphic to $V_4=\{0,a,b,c\},$ then define $l:V\to A\setminus \left\{0\right\}$ by $l(v_i)=a,$ for all i and if m is odd, then $$l(u_j)=\{\begin{array}{cc}a\hfill & \hspace{1em}\text{if}\mathrm{ }j=1\hfill \\ b\hfill & \hspace{1em}\text{if}\mathrm{ }j=2\hfill \\ c\hfill & \hspace{1em}\text{if}\mathrm{ }j=3\hfill \\ a\hfill & \hspace{1em}\text{otherwise}.\hfill \end{array}$$

If m is even, then $l(u_j)=a.$ Thus $w(v)=e,$ for all $v\in V(G+K_m{}^c).$

Case 2.

$ra\ne na$

Since $ra\ne na,$ let $d=na-ra\ne 0.$ Suppose $a\in {\mathbb{Z}}_t.$ Now, define $l:V(G+K_m{}^c)\to A\setminus \left\{0\right\}$ by $l(v_i)=a,$ for all i and if m is odd, then $$l(u_j)=\{\begin{array}{cc}d\hfill & \hspace{1em}\text{if}\mathrm{ }j\text{is}\mathrm{ }\text{odd}\hfill \\ -d\hfill & \hspace{1em}\text{if}\mathrm{ }j\text{is even}.\hfill \end{array}$$

If m is even, then $$l(u_j)=\{\begin{array}{cc}d+b\hfill & \hspace{1em}\text{if}\mathrm{ }j=1\hfill \\ -b\hfill & \hspace{1em}\text{if}\mathrm{ }j=2\hfill \\ -d\hfill & \hspace{1em}\text{if}\mathrm{ }j>1\mathrm{ }\text{and}\mathrm{ }j\mathrm{ }\text{is}\mathrm{ }\text{odd}\hfill \\ d\hfill & \hspace{1em}\text{if}\mathrm{ }j>2\mathrm{ }\text{and}\mathrm{ }j\mathrm{ }\text{is}\mathrm{ }\text{even},\hfill \end{array}$$ where $d\ne -b$ in ${\mathbb{Z}}_t.$ Thus $w(v)=na,$ for all $v\in V(G+K_m{}^c).$

Suppose $a\in V_4.$ Assume that $d=na-ra,$ where $d\in V_4\setminus \left\{0\right\}.$ Let $g\in V_4\setminus \left\{0\right\}$ and $d\ne g.$ Define $l:V\to A\setminus \left\{0\right\}$ by $l(v_i)=a,$ for all i and if m is even, then $$l(u_j)=\{\begin{array}{cc}d+g\hfill & \hspace{1em}\text{if}\mathrm{ }j=1\hfill \\ g\hfill & \hspace{1em}\text{if}\mathrm{ }j=2\hfill \\ d\hfill & \hspace{1em}\text{otherwise}.\hfill \end{array}$$

If m is odd, then $l(u_j)=d$ for all j. Thus, w(v) = na, for all $v\in V(G+K_m{}^c).$

Case 3.

A is an infinite Abelian group.

In this case, either A contains an element of finite order or A contains a subgroup isomorphic to Z. Hence, the labeling defined in Case 1 or Case 2 is a magic labeling. □

A simple calculation gives following.

Proposition 1.

Let G be any graph and $C_n=(v_1,v_2,\dots ,v_n,v_1)$ If l is an A-vertex magic labeling of $G+C_n$, then $l(v_i)=l(v_j)$, where $j=i+4(\text{mod}n).$

Theorem 6.

The graph $G=C_n+K_m$ is A-vertex magic, where $\left|A\right|>2$ if and only if

1. n = 3 or

2. n = 4 or

3. $n=4m_1+2$, where $m_1=2^k,k\ge 0.$

Proof.

Let $V(G)=V(C_n)\cup V(K_m)$ be a partition of the vertex set of G, where $V(C_n)=\{v_1,v_2,\dots ,v_n\}$ and $V(K_m)=\{u_1,u_2,\dots ,u_m\}.$ Assume that G is A-vertex magic. Let $a,b,c,d,e\in A\setminus \left\{0\right\},$ not necessarily distinct. Now, $w(u_j)={\sum }_{k=1}^{n}l(v_k)+{\sum }_{k=1}^{m}l(u_k)-l(u_j),$ for all $j\in \{1,2,\dots ,m\}.$ For any i, j, $w(u_i)=w(u_j),$ which implies $l(u_i)=l(u_j).$ Therefore, l takes fixed value on $V(K_m).$

Case 1.

n is odd and $n\ge 5.$

In this case by Proposition 1, we have $l(v_1)=l(v_2)=\cdots =l(v_n).$ Assume that $l(v_i)=a$ and $l(u_j)=b,$ for all i, j. Then $w(v_i)=2a+mb$ and $w(u_j)=(m-1)b+na$ for all i, j, which implies $b=(n-2)a.$ In the group ${\mathbb{Z}}_{n-2},$ we have b = 0, which is a contradiction.

Case 2.

n is even and $n=4m_1,m_1>1.$ From Proposition 1, it is enough to label $v_1,v_2,v_3,$ and v₄ as follows $$l(v_i)=\{\begin{array}{cc}a\hfill & \hspace{1em}\text{if}\mathrm{ }i=1\hfill \\ b\hfill & \hspace{1em}\text{if}\mathrm{ }i=2\hfill \\ \mathrm{c}\hfill & \hspace{1em}\text{if}\mathrm{ }i=3\hfill \\ d\hfill & \hspace{1em}\text{if}\mathrm{ }i=4\hfill \end{array}$$

and $l(u_j)=e,$ for all $j\in \{1,2,\dots ,m\}.$ Then $b+d=a+c$ and $w(u_j)=2m_1(a+c)+(m-1)e,$ which implies $(2m_1-1)(a+c)=e.$ In the group ${\mathbb{Z}}_{2m_1-1},$ we have $e=0,$ which is a contradiction.

Case 3.

$n=4m_1+2$ and $m_1\ne 2^k,k\ge 0.$

In this case by Proposition 1, we have $l(v_1)=l(v_3)=l(v_5)=\cdots =l(v_{n-1})$ and $l(v_2)=l(v_4)=l(v_6)=\cdots =l(v_n).$ Now, it follows that $l(v_1)=a,l(v_2)=b$ and $l(u_1)=c$ (say). $$w(v_i)=\{\begin{array}{cc}2b+mc\hfill & \hspace{1em}\text{if}\mathrm{ }i\mathrm{ }\text{is}\mathrm{ }\text{odd}\hfill \\ 2a+mc\hfill & \hspace{1em}\text{if}\mathrm{ }i\mathrm{ }\text{is}\mathrm{ }\text{even},\hfill \end{array}$$ where $i=1,2,\dots ,n$ and $w(u_j)=\frac{n}{2}(a+b)+(m-1)c.$ Since $w(u_j)=w(v_1)=w(v_2),$ we have $4m_1(a+b)=2c.$ By prime factorization, $m_1=2^r{p}_1^{l_1}\cdots p_k^{l_k},$ where $p_i^{\prime }s$ are odd prime, for all $i=1,2,\dots ,k.$ In the group ${\mathbb{Z}}_t,$ we have c = 0, where $t=p_1^{l_1}\dots p_k^{l_k},$ which is a contradiction.

Now, let us prove the converse part.

Case 1.

Assume that n = 3. Then the graph $C_3+K_m\cong K_{m+3}$ is regular. Therefore, the graph $C_3+K_m$ is A-vertex magic graph.

Case 2.

Assume that n = 4. Define $l:V\to A\setminus \left\{0\right\}$ by $$l(v_i)=\{\begin{array}{cc}a\hfill & \hspace{1em}\text{if}\mathrm{ }i=1,4\hfill \\ b\hfill & \hspace{1em}\text{if}\mathrm{ }i=2,3\hfill \end{array}$$

and $l(u_j)=a+b,$ for all $j\in \{1,2,\dots ,m\},$ where $a\ne -b.$ Hence $w(v)=(m+1)(a+b),$ for all $v\in V(G).$

Case 3.

Assume that $n=4m_1+2$ and $m_1=2^k,k\ge 0.$

If p is an odd prime and it divides o(A), then by Cauchy’s theorem A has an element a of order p. Define $l:V\to A\setminus \left\{0\right\}$ by $$l(v)=\{\begin{array}{cc}4m_{1}a\hfill & \hspace{1em}\text{if}\mathrm{ }v\in V(K_m)\hfill \\ a\hfill & \hspace{1em}\text{if}\mathrm{ }v\in V(C_n).\hfill \end{array}$$

Hence, $w(v)=2a+m(4m_{1}a)$ for all $v\in V(G).$

If 4 divides o(A), then by Sylow’s first theorem and fundamental theorem of finite Abelian groups, A has a subgroup isomorphic to either ${\mathbb{Z}}_4$ or V₄. If A has a subgroup isomorphic to ${\mathbb{Z}}_4,$ then define $l:V\to {\mathbb{Z}}_4\setminus \left\{0\right\}$ by $$l(v_i)=\{\begin{array}{cc}a\hfill & \hspace{1em}\text{if}\mathrm{ }i\mathrm{ }\text{is}\mathrm{ }\text{odd}\hfill \\ 3a\hfill & \hspace{1em}\text{if}\mathrm{ }i\mathrm{ }\text{is}\mathrm{ }\text{even}\hfill \end{array}$$ and $l(u_j)=2a,$ for all $j\in \{1,2,\dots ,m\},$ where o(a) = 4. Then $w(v_i)=2(m+1)a$ and $w(u_i)=2(m-1)a,$ clearly $w(v_i)=w(u_j)$ for all i, j. If A has a subgroup isomorphic to $V_4=\{0,a,b,c\},$ then define $l:V\to V_4\setminus \left\{0\right\}$ by $$l(v_i)=\{\begin{array}{cc}a\hfill & \hspace{1em}\text{if}\mathrm{ }i\mathrm{ }\text{is}\mathrm{ }\text{odd}\hfill \\ b\hfill & \hspace{1em}\text{if}\mathrm{ }i\mathrm{ }\text{is}\mathrm{ }\text{even}\hfill \end{array}$$

and $l(u_j)=c,$ for all $j\in \{1,2,\dots ,m\}.$ Then w(v) = mc, for all $v\in V(G).$ □

Proposition 2.

Let G be a graph. If $P_n+G$ is A-vertex magic, where $\left|A\right|>2$ then $n\le 3.$

Proof.

Let $V(P_n)=\{v_1,v_2,\dots ,v_n\}.$ Assume that $P_n+G$ is A-vertex magic and n > 3. Since $w(v_1)=w(v_3),$ which implies $l(v_4)=0,$ which is a contradiction. □

Theorem 7.

The graph $G=P_n+K_m$ is A-vertex magic, where $\left|A\right|>2$ if and only if $n\le 3.$

Proof.

Let $V(P_n)=\{v_1,v_2,\dots ,v_n\}$ and $V(K_m)=\{u_1,u_2,\dots ,u_m\}.$ The necessity follows from Proposition 2. Now, let us prove the sufficiency.

Case 1.

n = 3.

Define $l:V\to A\setminus \left\{0\right\}$ by $l(u_j)=a,$ for all $j\in \{1,2,\dots ,m\},l(v_1)=a+b,\mathrm{ }l(v_2)=a$ and $l(v_3)=-b,$ where $a,b\in A$ and $a\ne -b.$ Then $w(v)=(m+1)a,$ for all $v\in V(G).$

Case 2.

n = 2.

In this case the graph $P_2+K_m\cong K_{m+2}$ is regular and hence it is A-vertex magic. □

Theorem 8.

The graph $G=P_n+K_m{}^c$ is A-vertex magic, where $\left|A\right|>2$ if and only if $n\le 3.$

Proof.

Let $V(P_n)=\{v_1,v_2,\dots ,v_n\}$ and $V(K_m{}^c)=\{u_1,u_2,\dots ,u_m\}.$ The necessity follows from Proposition 2. Now, let us prove the sufficiency. Let $a,b\in A\setminus \left\{0\right\}$ and $a\ne -b.$

Case 1.

n = 3.

Suppose m is odd. Define $l:V\to A\setminus \left\{0\right\}$ by $$l(u_j)=\{\begin{array}{cc}a+b\hfill & \hspace{1em}\text{if}\mathrm{ }j\text{is}\mathrm{ }\text{odd}\hfill \\ -(a+b)\hfill & \hspace{1em}\text{if}\mathrm{ }j\text{is}\mathrm{ }\text{even}\hfill \end{array}$$

$l(v_1)=a,l(v_2)=a+b$ and $l(v_3)=b.$ Thus $w(v)=2(a+b),$ for all $v\in V(G).$

Suppose m is even. Define $l:V\to A\setminus \left\{0\right\}$ by $$l(u_j)=\{\begin{array}{cc}a\hfill & \hspace{1em}\text{if}\mathrm{ }j=1\hfill \\ b\hfill & \hspace{1em}\text{if}\mathrm{ }j=2\hfill \\ -a\hfill & \hspace{1em}\text{if}\mathrm{ }j>1\mathrm{ }\text{and}\mathrm{ }j\mathrm{ }\text{is}\mathrm{ }\text{odd}\hfill \\ a\hfill & \hspace{1em}\text{if}\mathrm{ }j>2\mathrm{ }\text{and}\mathrm{ }j\mathrm{ }\text{is}\mathrm{ }\text{even}\hfill \end{array}$$

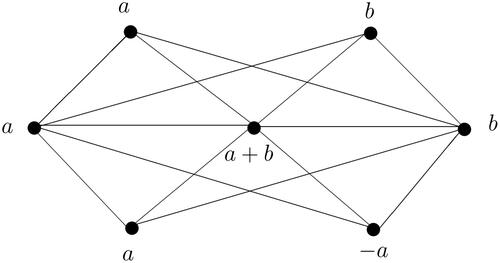
$l(v_1)=a,l(v_2)=a+b$ and $l(v_3)=b.$ An A-vertex magic labeling of $P_3+K_4{}^c$ is given in Figure 1.

Figure 1. A-vertex magic labeling of $P_3+K_4{}^c.$

Thus $w(v)=2(a+b),$ for all $v\in V(G).$

Case 2.

n = 2.

Suppose m is odd. Define $l:V\to A\setminus \left\{0\right\}$ by $$l(u_j)=\{\begin{array}{cc}a\hfill & \hspace{1em}\text{if}\mathrm{ }j\text{is}\mathrm{ }\text{odd}\hfill \\ -a\hfill & \hspace{1em}\text{if}\mathrm{ }j\text{is}\mathrm{ }\text{even}\hfill \end{array}$$ and $l(v_i)=a,$ for all i. Thus $w(v)=2a,$ for all $v\in V(G).$

Suppose m is even. Define $l:V\to A\setminus \left\{0\right\}$ by $$l(u_j)=\{\begin{array}{cc}a+b\hfill & \hspace{1em}\text{if}\mathrm{ }j=1\hfill \\ -b\hfill & \hspace{1em}\text{if}\mathrm{ }j=2\hfill \\ -a\hfill & \hspace{1em}\text{if}\mathrm{ }j>1\mathrm{ }\text{and}\mathrm{ }j\mathrm{ }\text{is}\mathrm{ }\text{odd}\hfill \\ a\hfill & \hspace{1em}\text{if}\mathrm{ }j>2\mathrm{ }\text{and}\mathrm{ }j\mathrm{ }\text{is}\mathrm{ }\text{even},\hfill \end{array}$$

$l(v_i)=a,$ for all i. Thus $w(v)=2a,$ for all $v\in V(G).$ □

Theorem 9.

The graph $G=P_n+C_m$ is A-vertex magic, where $\left|A\right|>2$ if and only if $n\le 3$ and

1. m = 3 or

2. m = 4 or

3. $m=4m_1+2$, where $m_1=2^k,k\ge 0.$

Proof.

Let $P_n=(v_1,v_2,\dots ,v_n)$ and $C_m=(u_1,u_2,\dots ,u_m,u_1).$ Assume that G is A-vertex magic. Let $a_i\in A\setminus \left\{0\right\},$ where $i=1,2,\dots ,7$ and not necessary distinct. By Proposition 2, we have $n\le 3.$

Suppose n = 2, then by Theorem 6, we get the required result.

Assume that n = 3.

Case 1.

m is odd, m > 3.

In this case by Proposition 1, we have $l(u_1)=l(u_2)=\cdots ,=l(u_m).$ Assume that $l(u_j)=a_1,l(v_1)=a_2,l(v_2)=a_3$ and $l(v_3)=a_4.$ Then $w(v_1)=a_3+m{a}_1$ and $w(u_j)=2a_1+2a_3,$ which implies, $(m-2)a_1=a_3.$ In the group ${\mathbb{Z}}_{m-2}$ we have $a_3=0,$ which is a contradiction.

Case 2.

m is even and $m=4m_1,m_1>1.$ From Proposition 1, it is enough to label $u_1,u_2,u_3,$ and u₄ as follows $$l(u_j)=\{\begin{array}{cc}{a}_1\hfill & \hspace{1em}\text{if}\mathrm{ }j=1\hfill \\ a_2\hfill & \hspace{1em}\text{if}\mathrm{ }j=2\hfill \\ a_3\hfill & \hspace{1em}\text{if}\mathrm{ }j=3\hfill \\ a_4\hfill & \hspace{1em}\text{if}\mathrm{ }j=4\hfill \end{array}$$

$l(v_1)=a_5,l(v_2)=a_6$ and $l(v_3)=a_7.$ Then $a_1+a_3=a_2+a_4$ and $a_6=a_5+a_7.$ Since $w(v_1)=w(u_1),$ which implies $a_6=(2m_1-1)(a_1+a_3).$ In the group ${\mathbb{Z}}_{2m_1-1},$ we have $a_6=0,$ which is contradiction.

Case 3.

$m=4m_1+2$ and $m_1\ne 2^k,k\ge 0.$

In this case by Proposition 1, we have $l(u_1)=l(u_3)=l(u_5)=\cdots =l(u_{n-1})$ and $l(u_2)=l(u_4)=l(u_6)=\cdots =l(u_n).$ Assume that $l(u_1)=a_1,l(u_2)=a_2$ and $l(v_1)=a_3,l(v_2)=a_4,l(v_3)=a_5.$ $$w(u_j)=\{\begin{array}{cc}2a_2+2a_4\hfill & \hspace{1em}\text{if}\mathrm{ }j\text{is}\mathrm{ }\text{odd}\hfill \\ 2a_1+2a_4\hfill & \hspace{1em}\text{if}\mathrm{ }j\text{is}\mathrm{ }\text{even},\hfill \end{array}$$ where $j=1,2,\dots ,m$ and $w(v_i)=\frac{m}{2}(a_1+a_2)+a_4.$ Since $w(v_i)=w(u_1)=w(u_2),$ we have $4m_1(a_1+a_2)=2a_4.$ By prime factorization, $m_1=2^r{p}_1^{l_1}\cdots p_k^{l_k},$ where p_i’s are odd prime, for all $i=1,2,\dots ,k.$ In the group ${\mathbb{Z}}_t,$ we have $a_4=0,$ where $t=p_1^{l_1}\dots p_k^{l_k},$ which is a contradiction.

To prove converse part, assume that n = 2, then by Theorem 6, we get the required result.

Now, assume that n = 3.

Case 1.

m = 3

Then by Theorem 7, we get the required result.

Case 2.

m = 4

Define $l:V\to A\setminus \left\{0\right\}$ by $$l(u_j)=\{\begin{array}{cc}{a}_1+a_2\hfill & \hspace{1em}\text{if}\mathrm{ }j=1,2\hfill \\ -a_2\hfill & \hspace{1em}\text{if}\mathrm{ }j=3,4\hfill \end{array}$$

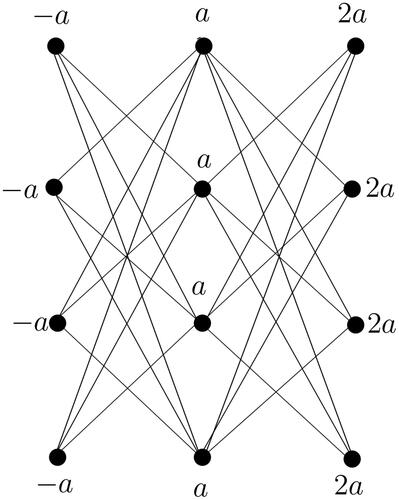
$l(v_1)=a_1+a_2,l(v_2)=a_1,$ and $l(v_3)=-a_2,$ where $a_1\ne -a_2.$ Thus $w(v)=3a_1,$ for all $v\in V(G).$ An A-vertex magic labeling of $P_3+C_4$ is given in Figure 2.

Figure 2. A-vertex magic labeling of $P_3+C_4.$

Case 3.

$m=4m_1+2$ and $m_1=2^k,k\ge 0.$

If p is an odd prime and it divides o(A), then define $l:V\to A\setminus \left\{0\right\}$ by $l(u_j)=a,$ for all j, $l(v_1)=4m_{1}a+b,l(v_2)=4m_{1}a$ and $l(v_3)=-b,$ where o(a) = p and $4m_{1}a\ne -b.$ Then $w(v)=2a+8m_{1}a,$ for all $v\in V(G).$

If 4 divides o(A), then A has a subgroup isomorphic to either ${\mathbb{Z}}_4$ or V₄. If A has a subgroup isomorphic to ${\mathbb{Z}}_4,$ then define $l:V\to {\mathbb{Z}}_4\setminus \left\{0\right\}$ by $$l(u_j)=\{\begin{array}{cc}a\hfill & \hspace{1em}\text{if}\mathrm{ }j\text{is}\mathrm{ }\text{odd}\hfill \\ 3a\hfill & \hspace{1em}\text{if}\mathrm{ }j\text{is}\mathrm{ }\text{even}\hfill \end{array}$$

$l(v_1)=a,l(v_2)=2a$ and $l(v_3)=a,$ where o(a) = 4. Thus $w(v)=2a,$ for all $v\in V(G).$ If A has a subgroup isomorphic to $V_4=\{0,a,b,c\},$ then define $l:V\to V_4\setminus \left\{0\right\}$ by $$l(u_j)=\{\begin{array}{cc}a\hfill & \hspace{1em}\text{if}\mathrm{ }j\text{is}\mathrm{ }\text{odd}\hfill \\ b\hfill & \hspace{1em}\text{if}\mathrm{ }j\text{is}\mathrm{ }\text{even}\hfill \end{array}$$

$l(v_1)=a,l(v_2)=c$ and $l(v_3)=b.$ Thus w(v) = 0, for all $v\in V(G).$ □

3. Group vertex magic labeling of product of graphs

In this section, we deal with tensor and lexicographic product of graphs which are group vertex magic.

Definition 2.

[6, 8] The tensor product $G\otimes H$ of graphs G and H is a graph such that the vertex set of $G\otimes H$ is the product $V(G)\times V(H)$ and vertices (g, h) and $(g\prime ,h\prime )$ are adjacent in $G\otimes H$ if and only if g is adjacent to $g\prime$ in G and h is adjacent to $h\prime$ in H.

Also, one can find several graph products in [8].

Theorem 10.

Let A be an Abelian group, underlying a commutative ring R. If there exist A-vertex magic labelings $l_1:V(G_1)\to A\cap U(R)$ and $l_2:V(G_2)\to A\cap U(R)$ for graphs G₁ and G₂ respectively, then $G_1\otimes G_2$ is A-vertex magic.

Proof.

Let us assume that the magic constant of G₁ under the labeling l₁ is a and the magic constant of G₂ under the labeling l₂ is b. Let $u\in V(G_1)$ and $v\in V(G_2).$ Define $l:V(G_1\otimes G_2)\to A\cap U(R)$ by $l((u,v))=l_1(u)·l_2(v).$ Assume that $N(u)=\{u_1,u_2,\dots ,u_k\}$ and $N(v)=\{v_1,v_2,\dots ,v_m\}.$ Then $N((u,v))=\{(u_i,v_j):i=1,2,\dots ,k$ and $j=1,2,\dots ,m\}.$ Now, $$\begin{array}{cc}w((u,v))\hfill & =\sum _{j=1}^m\sum _{i=1}^{k}l((u_i,v_j))\hfill \\ \hfill & =\sum _{i=1}^k{l}_1(u_i)·\sum _{j=1}^m{l}_2(v_j)\hfill \\ \hfill & =a·b.\hfill \end{array}$$

Since (u, v) is arbitrary, $w((u,v))=a·b,$ for all $(u,v)\in V(G_1\otimes G_2).$ □

Theorem 11.

The graph $P_n\otimes K_m$ is A-vertex magic, where $\left|A\right|>2$ and m > 1 if and only if

1. n = 2 or

2. n = 3.

Proof.

Let $V(P_n\otimes K_m)=\{(v_i,u_j)\}$ where $i\in \{1,2,\dots ,n\},j\in \{1,2,\dots ,m\}.$ Assume that $n\ge 4$ and $P_n\otimes K_m$ is A-vertex magic. Since $w((v_1,u_j))=w((v_3,u_j)),$ which implies ${\sum }_{k=1}^{m}l((v_4,u_k))-l((v_4,u_j))=0.$ That is, sum of any m – 1 distinct elements of $\{l((v_4,u_1)),\dots ,l((v_4,u_m))\}$ equal to 0, which implies $l((v_4,u_1))=\cdots =l((v_4,u_m)).$ Therefore, the graph $P_n\otimes K_m$ is not ${\mathbb{Z}}_p$ vertex magic, where p is prime and $p>m-1.$

Conversely, assume that n = 2. In this case the graph $P_2\otimes K_m$ is regular and hence A-vertex magic.

Now, assume that n = 3. If p is an odd prime and it divides o(A), then define $l:V\to A\setminus \left\{0\right\}$ by $$l((v_i,u_j))=\{\begin{array}{cc}-a\hfill & \hspace{1em}\text{if}\mathrm{ }i=1\hfill \\ a\hfill & \hspace{1em}\text{if}\mathrm{ }i=2\hfill \\ 2a\hfill & \hspace{1em}\text{if}\mathrm{ }i=3,\hfill \end{array}$$ where o(a) = p. Thus $w((v_i,u_j))=(m-1)a,$ for all i, j. 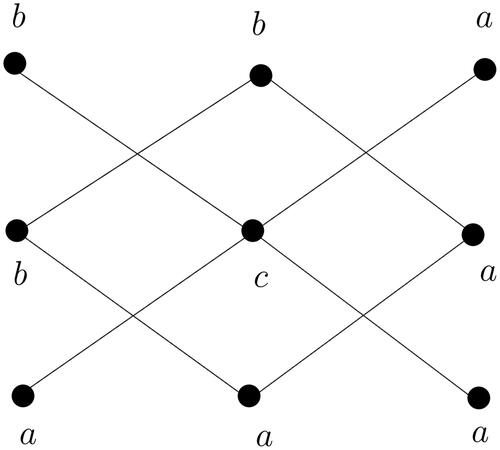A ${\mathbb{Z}}_p$-vertex magic labeling of $P_3\otimes K_4,$ where p is an odd prime is given in Figure 3.

Figure 3. A-vertex magic labeling of $P_3\otimes K_4.$

Suppose not, then 4 divides o(A). If A has a subgroup isomorphic to ${\mathbb{Z}}_4,$ then define $l:V\to {\mathbb{Z}}_4\setminus \left\{0\right\}$ by $$l((v_i,u_j))=\{\begin{array}{cc}3a\hfill & \hspace{1em}\text{if}\mathrm{ }i=1\hfill \\ a\hfill & \hspace{1em}\text{if}\mathrm{ }i=2\hfill \\ 2a\hfill & \hspace{1em}\text{if}\mathrm{ }i=3,\hfill \end{array}$$ where o(a) = 4. Thus $w((v_i,u_j))=(m-1)a,$ for all i, j.

If A has a subgroup isomorphic to $V_4=\{0,a,b,c\},$ then define $l:V\to V_4\setminus \left\{0\right\}$ by $$l((v_i,u_j))=\{\begin{array}{cc}b\hfill & \hspace{1em}\text{if}\mathrm{ }i=1\hfill \\ a\hfill & \hspace{1em}\text{if}\mathrm{ }i=2\hfill \\ c\hfill & \hspace{1em}\text{if}\mathrm{ }i=3.\hfill \end{array}$$

Thus $w((v_i,u_j))=(m-1)a,$ for all i, j. □

Theorem 12.

The graph $P_n\otimes P_m$ is A-vertex magic, when $\left|A\right|>2$ if and only if $m,n\le 3.$

Proof.

Let $V(P_n\otimes P_m)=\{(v_i,u_j)\}$ where $i\in \{1,2,\dots ,n\},j\in \{1,2,\dots ,m\}.$ Assume that $n\ge 4$ or $m\ge 4$ and $P_n\otimes P_m$ is A-vertex magic. Without loss of generality, assume that $m\ge 4.$ Now, consider the path $\{(v_1,u_1),(v_2,u_2),$ $(v_1,u_3),(v_2,u_4)\}.$ Since $w((v_1,u_1))=w((v_1,u_3)),$ which implies $l((v_2,u_4))=0,$ which is clearly not possible.

Conversely,

Case 1.

n = 2.

Suppose that m = 2. Then the graph $P_2\otimes P_2$ is regular and hence A-vertex magic. Suppose that m = 3. Define $l:V\to A\setminus \left\{0\right\}$ by $$l((v_i,u_j))=\{\begin{array}{cc}a+b\hfill & \hspace{1em}\text{if}\mathrm{ }j=1\hfill \\ a\hfill & \hspace{1em}\text{if}\mathrm{ }j=2\hfill \\ -b\hfill & \hspace{1em}\text{if}\mathrm{ }j=3\hfill \end{array}$$

and $a\ne -b.$ Thus $w(v)=a,$ for all $v\in P_2\otimes P_3.$

Case 2.

n = 3.

In this case it is enough to verify only for m = 3. If p is an odd prime and p divides o(A). Define $l:V\to A\setminus \left\{0\right\}$ by $$l((v_i,u_j))=\{\begin{array}{cc}-a\hfill & \hspace{1em}\text{if}\mathrm{ }i=j=1\hfill \\ 2a\hfill & \hspace{1em}\text{if}\mathrm{ }i=j=2\hfill \\ a\hfill & \hspace{1em}\text{otherwise},\hfill \end{array}$$ where o(a) = p. Thus $w(v)=2a,$ for all $v\in V(G).$

If 4 divides o(A) and A has a subgroup isomorphic to ${\mathbb{Z}}_4,$ then define $l:V\to {\mathbb{Z}}_4\setminus \left\{0\right\}$ by $$l((v_i,u_j))=\{\begin{array}{cc}3a\hfill & \hspace{1em}\text{if}\mathrm{ }i=j=1\hfill \\ 2a\hfill & \hspace{1em}\text{if}\mathrm{ }i=j=2\hfill \\ a\hfill & \hspace{1em}\text{otherwise},\hfill \end{array}$$ where a is generator of ${\mathbb{Z}}_4.$ Thus $w(v)=2a,$ for all $v\in V(G).$

If A has a subgroup isomorphic to $V_4=\{0,a,b,c\},$ then define $l:V\to V_4\setminus \left\{0\right\}$ by $$l((v_i,u_j))=\{\begin{array}{cc}b\hfill & \hspace{1em}\text{if}\mathrm{ }i=j=1\mathrm{ }\text{and}\mathrm{ }i\ne j,\mathrm{ }\text{where}\mathrm{ }i,j\in \{1,2\}\hfill \\ c\hfill & \hspace{1em}\text{if}\mathrm{ }i=j=2\hfill \\ a\hfill & \hspace{1em}\text{otherwise}.\hfill \end{array}$$

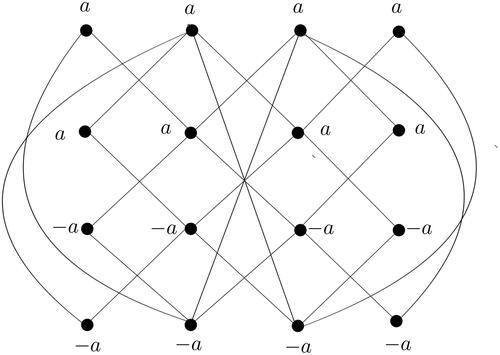
Thus $w(v)=c,$ for all $v\in V(G).$ A V₄-vertex magic labeling of $P_3\otimes P_3$ is given in Figure 4. □

Figure 4. V₄-vertex magic labeling of $P_3\otimes P_3.$

Theorem 13.

The graph $P_n\otimes C_m$ is group vertex magic if and only if (i) $n\le 3$ (or) (ii) n > 3 and $m\equiv 0(\mathit{mod} 4).$

Proof.

Let $V(P_n\otimes C_m)=\{(v_i,u_j)\}$ where $i\in \{1,2,\dots ,n\},j\in \{1,2,\dots ,m\}.$ Assume that $P_n\otimes C_m$ is group vertex magic. Suppose $m\cancel{\equiv }0(\mathit{mod} 4)$ and n > 3. Since $w((v_1,u_j))=w((v_3,u_j)),$ which implies $l((v_4,u_{j-1}))+l((v_4,u_{j+1}))=0.$ Thus, we have $l((v_4,u_j))+l((v_4,u_{(j+2)(\mathit{mod}\mathrm{ }m)}))=0.$ Further, if m is odd, then $l((v_4,u_1))=l((v_4,u_2))=\cdots =l((v_4,u_m)).$ If m is even, then $l((v_4,u_1))=l((v_4,u_3))=\cdots =l((v_4,u_{m-1}))$ and $l((v_4,u_2))=l((v_4,u_4))=\cdots =l((v_4,u_m)).$ Therefore, the graph $P_n\otimes C_m$ is not ${\mathbb{Z}}_p$ vertex magic, where p is an odd prime.

The converse part is given in three cases,

Case 1.

n = 2.

Then the graph $P_2\otimes C_m\cong 2C_m$ if m is even. If m is odd, then $P_2\otimes C_m\cong C_{2m},$ both are regular and hence group vertex magic.

Case 2.

n = 3

If p divides $o(A),$ where p is an odd prime, then define $l:V\to A\setminus \left\{0\right\}$ by $$l((v_i,u_j))=\{\begin{array}{cc}a\hfill & \hspace{1em}\text{if}\mathrm{ }i=1,3\hfill \\ 2a\hfill & \hspace{1em}\text{if}\mathrm{ }i=2,\hfill \end{array}$$ where o(a) = p. Thus $w((v_i,u_j))=4a,$ for all i, j.

Suppose 2 divides $o(A),$ then define $l:V\to A\setminus \left\{0\right\}$ by $l((v_i,u_j))=a,$ for all i, j, where o(a) = 2. Then $w((v_i,u_j))=0,$ for all i, j.

Case 3.

n > 3 and $m=4m_1,m_1\ge 1.$

Define $l:V\to A\setminus \left\{0\right\}$ by $$l((v_i,u_j))=\{\begin{array}{cc}a\hfill & \hspace{1em}\text{if}\mathrm{ }j\equiv 1,2(\mathit{mod} 4)\hfill \\ -a\hfill & \hspace{1em}\text{if}\mathrm{ }j\equiv 3,0(\mathit{mod} 4),\hfill \end{array}$$

where $k\in \{1,2,\dots ,m\}.$ Thus $w((v_i,u_j))=0,$ for all i, j. A group vertex magic labeling of $P_3\otimes C_4$ is given in Figure 5. □

Figure 5. group vertex magic labeling of $P_4\otimes C_4$.

Remark 1.

From Theorem 13, $P_n\otimes C_m$ admits A-vertex magic labeling, for $A={\mathbb{Z}}_2$, but from Theorem 11, 12 the graphs $P_n\otimes K_m$ and $P_n\otimes P_m$ fails to admit A-vertex magic labeling, when $A={\mathbb{Z}}_2.$

Definition 3.

[9] The lexicographic product or graph composition $G[H]$ of graphs G and H is a graph such that the vertex set of $G[H]$ is the product $V(G)\times V(H)$ and any two vertices (g, h) and $(g\prime ,h\prime )$ are adjacent in $G[H]$ if and only if either g is adjacent with $g\prime$ in G or $g=g\prime$ and h is adjacent with $h\prime$ in H.

Theorem 14.

Let A be an Abelian group, underlying a commutative ring R. If G₁ is r-regular graph and there exists an A-vertex magic labeling $l_2:V(G_2)\to A\cap U(R)$ for graph G₂, then the lexicographic product $G_1[G_2]$ is A-vertex magic.

Proof.

Let us assume the magic constant of l₂ is a and $\sum _{w\in V(G_2)}{l}_2(w)=b.$ Let $c\in A\setminus \left\{0\right\}\cap U(R).$ Define $l:V(G_1[G_2])\to A\cap U(R)$ by $l((u,v))=c·l_2(v).$ Assume that $N(u)=\{u_1,\dots ,u_r\}$ and $N(v)=\{v_1,\dots ,v_k\}.$ Then $N((u,v))=\{(u,v_j):j=1,\dots ,k\}\cup \{(u_i,w):i=1,\dots ,r$ and $w\in V(G_2)\}.$ Now, $$\begin{array}{cc}w((u,v))\hfill & =\sum _{j=1}^{k}l((u,v_j))+\sum _{w\in V(G_2)}\sum _{i=1}^{r}l((u_i,w))\hfill \\ \hfill & =c·a+r(c·b).\hfill \end{array}$$

Since (u, v) is arbitrary, $w((u,v))=c·a+r(c·b),$ for all $(u,v)\in V(G_1[G_2]).$ □

Theorem 15.

Let G be any simple graph on n vertices. The graph $G[K_m{}^c]$ is A-vertex magic, where $\left|A\right|>2$ if and only if m > 1.

Proof.

Let $V(G)=\{v_1,v_2,\dots ,v_n\}$ and $V(K_m{}^c)=\{u_1,u_2,\dots ,u_m\}.$ Assume that $G[K_m{}^c]$ is A-vertex magic and m = 1. Then $G[K_1{}^c]\cong G,$ but G need not be A-vertex magic.

Conversely, assume that $m\ge 2.$

Suppose m is odd. Define $l:V(G[K_m{}^c])\to A\setminus \left\{0\right\}$ by $$l(v_i,u_j)=\{\begin{array}{cc}a+b\hfill & \hspace{1em}\text{if}\mathrm{ }j=1\hfill \\ -b\hfill & \hspace{1em}\text{if}\mathrm{ }j=2\hfill \\ -a\hfill & \hspace{1em}\text{if}\mathrm{ }j>1\mathrm{ }\text{and}\mathrm{ }j\mathrm{ }\text{is}\mathrm{ }\text{odd}\hfill \\ a\hfill & \hspace{1em}\text{if}\mathrm{ }j>2\mathrm{ }\text{and}\mathrm{ }j\text{is}\mathrm{ }\text{even},\hfill \end{array}$$ where $a\ne -b.$ Thus $w(v)=0,$ for all $v\in V(G[K_m{}^c]).$

Suppose m is even. Define $l:V(G[K_m{}^c])\to A\setminus \left\{0\right\}$ by $$l(v_i,u_j)=\{\begin{array}{cc}a\hfill & \hspace{1em}\text{if}\mathrm{ }j\text{is}\mathrm{ }\text{odd}\hfill \\ -a\hfill & \hspace{1em}\text{if}\mathrm{ }j\text{is even}.\hfill \end{array}$$

Thus $w(v)=0,$ for all $v\in V(G[K_m{}^c]).$ □

Remark 2.

In the above theorems wherever it is required to label the vertices of G using an infinite Abelian group, we follow the technique mentioned in case 3 of Theorem 3.

4. Conclusion and scope

In this paper, we have studied the A-vertex magicness for various graph operations namely, join, tensor and lexicographic product. In this direction one can investigate A-vertex magicness for other graph products.

Acknowledgements

The first author would like to thank K. Ayyanar for the support and fruitful discussions.

Additional information

Funding

The work of Mr S. Balamoorthy is supported by a Junior Research Fellowship from CSIR-UGC, India (UGC-Ref.No.:1085/(CSIR-UGC NET JUNE 2019)).