On the distance spectra of m-generation n-prism graph

Abstract

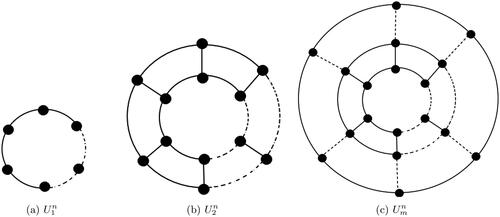
The distance matrix of a simple connected graph G is $D(G)=(d_{ij}),$ where d_ij is the length of a shortest path between the ith and jth vertices of G. Eigenvalues of D(G) are called the distance eigenvalues of G. The m-generation n-prism graph or (m, n)-prism graph can be defined in an iterative way where $(1,n)$-prism graph is an n-vertex cycle. In this paper, we first find the number of zero eigenvalues of the distance matrix of a (m, n)-prism graph. Next, we find some quotient matrix that contains m nonzero distance eigenvalues of a (m, n)-prism graph. Our next result gives the rest of the nonzero distance eigenvalues of a (m, n)-prism graph in terms of distance eigenvalues of a cycle. Finally, we find the characteristic polynomial of the distance matrix of a (m, n)-prism graph. Applying this result, we provide the explicit distance eigenvalues of a $(3,n)$-prism graph.

Keywords:

• Distance matrix
• distance eigenvalues
• path
• cycle
• prism graph

2000 Mathematics Subject Classification::

• 05C50

1. Introduction

Consider an n-vertex undirected, connected and simple graph $G=(V,E),$ where $V=\{1,2,3,\dots ,n\}$ is the vertex set and E is the edge set. The distance matrix of G, is denoted by D(G), is an n × n matrix $(d_{ij}),$ where d_ij is the distance between the ith and jth vertices in G. The matrix D(G) is symmetric, non-negative and irreducible. A cycle graph of n vertices is denoted by C_n, and a path graph of n vertices is denoted by P_n. The m-generation n-prism graph or (m, n)-prism graph can be defined in an iterative way. Let $(1,n)$-prism graph be an n-vertex cycle. Then, (m, n)-prism graph can be obtained from $(m-1,n)$-prism graph as follows: Every outermost vertex in $(m-1,n)$-prism graph gives birth to a new vertex, and all the n new vertex form a new cycle, then connect each new vertex with its corresponding mother vertex by an edge. 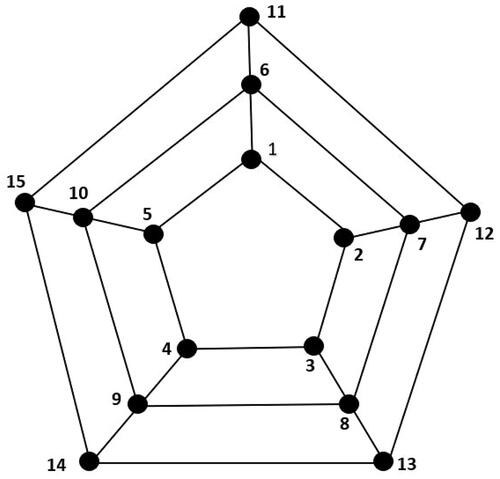We denote the (m, n)-prism graph by $U_m^n.$ For construction of $U_m^n,$ reader may see Figure 1. Clearly, the number of vertices of $U_m^n$ is mn. By J_n, we denote the n × n matrix with all entries one and by j_n we denote the $n\times 1$ column vector with all entries one. The Kronecker product of two matrices $A=(a_{ij})$ of size m × n and B of size $p\times q,$ denoted by $A\otimes B,$ is defined to be the mp × nq partition matrix $(a_{ij}B).$ For matrices M, N, P and Q of suitable sizes, $MN\otimes PQ=(M\otimes P)(N\otimes Q).$ Suppose a real symmetric matrix A can be partitioned as $(\begin{array}{cccc}{A}_{11}& A_{12}& \cdots & A_{1m}\\ \cdots & \cdots & \cdots & \cdots \\ A_{m1}& A_{m2}& \cdots & A_{mm}\end{array}),$ where each A_ij is a block of A. The matrix $Q=(q_{ij})$ of order m × m is called a quotient matrix of A, where q_ij is the average row sum of the block A_ij. If the row sum of each block A_ij is a constant, then the partition is called equitable.

Figure 1. Construction of $U_m^n.$

The distance matrix of a graph was introduced in [1] to the study of problem involves finding appropriate addresses so that a message can efficiently transfer through a series of loops from its origin to its destination. Balaban et al. [2] proposed the use of distance spectral radius, which is the largest eigenvalue of the distance matrix, as a molecular descriptor, while Gutman and Medeleanu [3] successfully used it to infer the extent of branching and model boiling points of alkanes. The distance spectral radius is a useful molecular descriptor in QSPR modeling as demonstrated by Consonni and Todeschini [4,5]. In [6], Graham and Lovász discussed the characteristic polynomial of distance matrix of a tree. Ruzieh and Powers [7] found all the eigenvalues and eigenvectors of the distance matrix of the path P_n. In [8], Fowler et al. found all the distance eigenvalues of the cycle C_n. Lin et al. [9] characterized connected graphs whose distance eigenvalues satisfies some properties. In [10], Atik and Panigrahi found the distance spectrum of some distance regular graphs, including the well-known Johnson graphs. In [11], authors found the bounds of the distance and distance signless Laplacian eigenvalues for any general graph. Aalipour et al. [12] determined the distance spectra of some graphs, including distance regular graphs, double odd graphs, Doob graphs and characterized strongly regular graphs as having more positive than negative distance eigenvalues. Alazemi et al. [13] characterized some distance-regular graphs in terms of number of distinct distance eigenvalues. In [14], Lu and Huang obtained the distance spectrum of B(n, k) which is a subgraph of the Boolean lattice. Pirzada et al. [15] worked on spectral spread of generalized distance matrix of a graph. A few more recent works related to spectra of distance matrix researchers may follow [16–18]. For extensive research, work on distance spectra can be found in the survey [19] and in the most recent survey [20]. In this paper, we first find the lower bound of the number of zero eigenvalues of the distance matrix of m-generation n-prism graph $U_m^n$ and later we prove that this bound is exact. Next, we find some quotient matrix of $D(U_m^n)$ corresponding to an equitable partition. We prove that this quotient matrix will contain m nonzero eigenvalues $D(U_m^n).$ Our next result gives the rest of the nonzero eigenvalues of $D(U_m^n).$ Applying these results, we find the characteristic polynomial of distance matrix of $U_m^n.$ As an immediate application of these results, we provide the explicit distance eigenvalues of $U_3^n.$

Next, we state some of the earlier useful results. The following is a well-known result on equitable partition of matrices.

Theorem 1.1.

[21] Let Q be a quotient matrix of a square matrix A corresponding to an equitable partition. Then the spectrum of A contains the spectrum of Q.

Explicit eigenvalues of P_n and C_n can be found from the following results.

Theorem 1.2.

[7] The distance eigenvalues ${\lambda }_i, i=1,2,\dots ,n$, of the path P_n with n > 2 are as follows:

1. 1. ${\lambda }_1=1/(\cosh \theta -1)$, where θ is the positive solution of $\tanh (\theta /2)\tanh (n\theta /2)=1/n.$

2. ${\lambda }_i=1/(\hspace{0.17em}\cos \hspace{0.17em}\theta -1)$, where (a) θ is the one of the $[(n-1)/2]$ solutions of $\tanh (\theta /2)\tanh (n\theta /2)=-1/n$ in the interval $(0,\pi )$, or (b) $\theta =(2m-1)\pi /n$ for $m=1,2,\dots ,[n/2].$

Theorem 1.3.

[8] The characteristic polynomial of $D(C_n)$, the distance matrix of an n-vertex cycle C_n, is given by $$\begin{array}{c}p(t)=t^{p-1}\left(t-\frac{n^2}{4}\right)\prod _{j=1}^p\left(t+{\csc }^2\left(\frac{\pi (2j-1)}{n}\right)\right), \mathrm{ }\text{if}\mathrm{ }n=2p.\hfill \\ p(t)=\left(t-\frac{n^2-1}{4}\right)\prod _{j=1}^p\left(t+\frac{1}{4}{\hspace{0.17em}\text{sec}\hspace{0.17em}}^2\left(\frac{\pi j}{n}\right)\right)\prod _{j=1}^p\left(t+\frac{1}{4}{\csc }^2\left(\frac{\pi (2j-1)}{2n}\right)\right), \text{if}\mathrm{ }n=2p+1.\hfill \end{array}$$

Theorem 1.4.

[22] Let T be a weighted tree on n vertices with edge weights ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_{n-1}$. Let D be the distance matrix of T. Then, for any real number x, $$\begin{array}{c}\det (D+xJ)={(-1)}^{n-1}{2}^{n-2}\left(\prod _{i=1}^{n-1}{\alpha }_i\right)\left(2x+\sum _{i=1}^{n-1}{\alpha }_i\right)\hfill \end{array}$$

Theorem 1.5.

[23] Suppose that A and B are square matrices of order n and m, respectively. Let ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n$ be the eigenvalues of A and ${\mu }_1,{\mu }_2,\dots ,{\mu }_m$ be the eigenvalues of B. Then, the eigenvalues of $A\otimes B$ are ${\lambda }_i{\mu }_j; i=1,2,\dots ,n; j=1,2,\dots ,m.$

Theorem 1.6.

[24] If $A,B\in M_{m,n}(F)$, then $$\begin{array}{c}\mathit{Rank}(A+B)\le \mathit{Rank}(A)+\mathit{Rank}(B)\hfill \end{array}$$

Equality holds if and only if $\mathit{range}(A)\cap \mathit{range}(B)=\left\{0\right\}$ and $\mathit{range}(A^T)\cap \mathit{range}(B^T)=\left\{0\right\}.$

2. Full D-spectrum of some graphs

We first discuss the number of zero eigenvalues of $D(U_m^n).$

Theorem 2.1.

The distance matrix of $U_m^n$ is having zero as an eigenvalue with multiplicity at least $mn-m-n+1$ and $mn-m-\frac{n}{2}$ according as n is odd and even, respectively.

Proof.

By a suitable ordering of vertices (as shown in Figure 2) we get the distance matrix of $U_m^n$ as (1) $$D(U_m^n)=\left[\begin{array}{ccccc}D(C_n)& D(C_n)+J_n& D(C_n)+2J_n& \cdots & D(C_n)+(m-1)J_n\\ D(C_n)+J_n& D(C_n)& D(C_n)+J_n& \cdots & D(C_n)+(m-2)J_n\\ D(C_n)+2J_n& D(C_n)+J_n& D(C_n)& \cdots & D(C_n)+(m-3)J_n\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ D(C_n)+(m-1)J_n& D(C_n)+(m-2)J_n& D(C_n)+(m-3)J_n& \cdots & D(C_n)\end{array}\right]$$(1) (2) $$\begin{array}{c}=\left[\begin{array}{ccccc}D(C_n)& D(C_n)& D(C_n)& \cdots & D(C_n)\\ D(C_n)& D(C_n)& D(C_n)& \cdots & D(C_n)\\ D(C_n)& D(C_n)& D(C_n)& \cdots & D(C_n)\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ D(C_n)& D(C_n)& D(C_n)& \cdots & D(C_n)\end{array}\right]+\left[\begin{array}{ccccc}0& J_n& 2J_n& \cdots & (m-1)J_n\\ J_n& 0& J_n& \cdots & (m-2)J_n\\ 2J_n& J_n& 0& \cdots & (m-3)J_n\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ (m-1)J_n& (m-2)J_n& (m-3)J_n& \cdots & 0\end{array}\right]\\ =J_m\otimes D(C_n)+D(P_m)\otimes J_n.\end{array}$$(2)

Figure 2. $U_3^5.$

We have from Theorem 1.3, the number of zero eigenvalues of $D(C_n)$ is 0 and $\frac{n}{2}-1$ according as n is odd and even, respectively. Also, for a symmetric matrix, the number of zero eigenvalues is equal to nullity. So, the rank of $D(C_n)=n$ if n is odd and the rank of $D(C_n)=\frac{n}{2}+1$ if n is even. Again by Theorem 1.2, we get the rank of $D(P_m)$ is m. Now by applying Theorem 1.5, we get the rank of $J_m\otimes D(C_n)$ is n and $\frac{n}{2}+1$ if n is odd and even, respectively, and the rank of $D(P_m)\otimes J_n$ is m. Thus, from Equation (2)(2) $$\begin{array}{c}=\left[\begin{array}{ccccc}D(C_n)& D(C_n)& D(C_n)& \cdots & D(C_n)\\ D(C_n)& D(C_n)& D(C_n)& \cdots & D(C_n)\\ D(C_n)& D(C_n)& D(C_n)& \cdots & D(C_n)\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ D(C_n)& D(C_n)& D(C_n)& \cdots & D(C_n)\end{array}\right]+\left[\begin{array}{ccccc}0& J_n& 2J_n& \cdots & (m-1)J_n\\ J_n& 0& J_n& \cdots & (m-2)J_n\\ 2J_n& J_n& 0& \cdots & (m-3)J_n\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ (m-1)J_n& (m-2)J_n& (m-3)J_n& \cdots & 0\end{array}\right]\\ =J_m\otimes D(C_n)+D(P_m)\otimes J_n.\end{array}$$(2) , we get $$\begin{array}{ccc}\mathit{Rank}(D(U_m^n))\hfill & \le \hfill & \mathit{Rank}(J_m\otimes D(C_n))+\mathit{Rank}(D(P_m)\otimes J_n)\hfill \\ \hfill & =\hfill & \{\begin{array}{cc}n+m, \hfill & \mathrm{ }\text{when}\mathrm{ }n\mathrm{ }\text{is}\mathrm{ }\text{odd}\hfill \\ \hfill & \hfill \\ \frac{n}{2}+m+1, \hfill & \mathrm{ }\text{when}\mathrm{ }n\text{is even}.\hfill \end{array}\hfill \end{array}$$

Now, we consider the matrix $J_m+D(P_m).$ Then, by considering all edge weight 1 of P_m and applying Theorem 1.4, we get the determinant of $J_m+D(P_m)$ is nonzero. So, the rank of $J_m+D(P_m)$ is m. Then, we have (3) $$\begin{array}{c}R\mathit{ank}(J_m+D(P_m))\le \mathit{Rank}(J_m)+\mathit{Rank}(D(P_m))\\ \Rightarrow m\le 1+m\end{array}$$(3)

Thus, the rank additivity does not hold in (16). So, by applying Theorem 1.6, we get there is some nonzero vector y such that $y\in (\mathit{range}(J_m)\cap \mathit{range}(D(P_m)).$ Then, there exist some vectors x₁ and x₂ such that $y=J_m{x}_1=D(P_m)x_2.$ Let k be the constant row sum of $D(C_n).$ We consider the nonzero vectors $X_1=\frac{1}{k}{x}_1\otimes j_n$ and $X_2=\frac{1}{n}{x}_2\otimes j_n.$ Then, $$\begin{array}{ccc}(J_m\otimes D(C_n))X_1\hfill & =\hfill & \frac{1}{k}(J_m\otimes D(C_n))(x_1\otimes j_n)\hfill \\ \hfill & =\hfill & \frac{1}{k}((J_m{x}_1)\otimes (D(C_n)j_n)=\frac{1}{k}(y\otimes (k{j}_n))=(y\otimes j_n)\hfill \end{array}$$

Similarly, we have $$\begin{array}{c}(D(P_m)\otimes J_n)X_2=(y\otimes j_n)\hfill \end{array}$$

Thus, we get a nonzero vector $y\otimes j_n$ such that $(y\otimes j_n)\in (\mathit{range}(J_m\otimes D(C_n))\cap \mathit{range}(D(P_m)\otimes J_n).$ So, the rank additivity does not hold in (13). Then, we have $$\begin{array}{ccc}\mathit{Rank}(D(U_m^n))\hfill & <\hfill & \mathit{Rank}(J_m\otimes D(C_n))+\mathit{Rank}(D(P_m)\otimes J_n)\hfill \\ \hfill & =\hfill & \{\begin{array}{cc}n+m, \hfill & \mathrm{ }\text{when}\mathrm{ }n\mathrm{ }\text{is}\mathrm{ }\text{odd}\hfill \\ \hfill & \hfill \\ \frac{n}{2}+m+1, \hfill & \mathrm{ }\text{when}\mathrm{ }n\text{is even}.\hfill \end{array}\hfill \end{array}$$

Hence, the number of zero eigenvalues which is the nullity of $D(U_m^n)$ is at least $mn-m-n+1$ and $mn-m-\frac{n}{2}$ according as n is odd and even, respectively. □

Our next result shows some quotient matrix of $D(U_m^n)$ corresponding to an equitable partition. From this quotient matrix, we find m nonzero eigenvalues of $D(U_m^n).$

Theorem 2.2.

The eigenvalues of $nD(P_m)+\frac{n^2}{4}{J}_m$ and the eigenvalues of $nD(P_m)+\frac{n^2-1}{4}{J}_m$ are also some nonzero eigenvalues of the distance matrix of $U_m^n$ according as n is even and odd, respectively.

Proof.

We consider the partition of $D(U_m^n)$ as in Equation (1)(1) $$D(U_m^n)=\left[\begin{array}{ccccc}D(C_n)& D(C_n)+J_n& D(C_n)+2J_n& \cdots & D(C_n)+(m-1)J_n\\ D(C_n)+J_n& D(C_n)& D(C_n)+J_n& \cdots & D(C_n)+(m-2)J_n\\ D(C_n)+2J_n& D(C_n)+J_n& D(C_n)& \cdots & D(C_n)+(m-3)J_n\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ D(C_n)+(m-1)J_n& D(C_n)+(m-2)J_n& D(C_n)+(m-3)J_n& \cdots & D(C_n)\end{array}\right]$$(1) . We note that each row sum of $D(C_n)$ is constant and is equal to $\frac{n^2}{4}$ and $\frac{n^2-1}{4}$ according as n is even and odd, respectively. Then, the considered partition of $D(U_m^n)$ is equitable. Now if n is even, then the corresponding quotient matrix is $$\begin{array}{ccc}{Q}_1\hfill & =\hfill & \left[\begin{array}{ccccc}\frac{n^2}{4}& \frac{n^2}{4}+n& \frac{n^2}{4}+2n& \cdots & \frac{n^2}{4}+(m-1)n\\ & & & & \\ \frac{n^2}{4}+n& \frac{n^2}{4}& \frac{n^2}{4}+n& \cdots & \frac{n^2}{4}+(m-2)n\\ & & & & \\ \frac{n^2}{4}+2n& \frac{n^2}{4}+n& \frac{n^2}{4}& \cdots & \frac{n^2}{4}+(m-3)n\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ \frac{n^2}{4}+(m-1)n& \frac{n^2}{4}+(m-2)n& \frac{n^2}{4}+(m-3)n& \cdots & \frac{n^2}{4}\end{array}\right]\hfill \\ \hfill & \hfill & \hfill \\ \hfill & =\hfill & \left[\begin{array}{ccccc}\frac{n^2}{4}& \frac{n^2}{4}& \frac{n^2}{4}& \cdots & \frac{n^2}{4}\\ & & & & \\ \frac{n^2}{4}& \frac{n^2}{4}& \frac{n^2}{4}& \cdots & \frac{n^2}{4}\\ & & & & \\ \frac{n^2}{4}& \frac{n^2}{4}& \frac{n^2}{4}& \cdots & \frac{n^2}{4}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ \frac{n^2}{4}& \frac{n^2}{4}& \frac{n^2}{4}& \cdots & \frac{n^2}{4}\end{array}\right]+\left[\begin{array}{ccccc}0& n& 2n& \cdots & (m-1)n\\ & & & & \\ n& 0& n& \cdots & (m-2)n\\ & & & & \\ 2n& n& 0& \cdots & (m-3)n\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ (m-1)n& (m-2)n& (m-3)n& \cdots & 0\end{array}\right]\hfill \\ \hfill & \hfill & \hfill \\ \hfill & =\hfill & \frac{n^2}{4}{J}_m+nD(P_m)\hfill \end{array}$$

Similarly, we get if n is odd, then the quotient matrix of $D(U_m^n)$ corresponding to the equitable partition of (1) is given by $$\begin{array}{c}{Q}_2=\frac{n^2-1}{4}{J}_m+nD(P_m).\hfill \end{array}$$

Then, by Theorem 1.1, we get the eigenvalues of $nD(P_m)+\frac{n^2}{4}{J}_m$ and the eigenvalues of $nD(P_m)+\frac{n^2-1}{4}{J}_m$ are also some eigenvalues of the distance matrix of $U_m^n$ according as n is even and odd, respectively. Finally, considering all edge weights 1 for the tree P_m in Theorem 1.4, we conclude that the determinants of both the matrices Q₁ and Q₂ are nonzero. Hence, eigenvalues of Q₁ and Q₂ are nonzero eigenvalues of $D(U_m^n)$ according as n is even and odd, respectively. □

Some of the nonzero eigenvalues of $D(U_m^n)$ are still remaining. The following result provides these nonzero eigenvalues.

Theorem 2.3.

Let λ be a nonzero eigenvalue of $D(C_n)$ other than the constant row sum. Then $m\lambda$ is an eigenvalue of $D(U_m^n).$

Proof.

We note that if k is a constant row sum of $D(C_n)$ then j_n is an eigenvector of $D(C_n)$ corresponding to the eigenvalue k. Let x be an eigenvector of $D(C_n)$ corresponding to the nonzero eigenvalue λ. Then as $D(C_n)$ is symmetric, all of its independent eigenvectors are orthogonal. Then, $j_n^{T}x=0,$ so that J_nx = 0. Then, from Equation (2)(2) $$\begin{array}{c}=\left[\begin{array}{ccccc}D(C_n)& D(C_n)& D(C_n)& \cdots & D(C_n)\\ D(C_n)& D(C_n)& D(C_n)& \cdots & D(C_n)\\ D(C_n)& D(C_n)& D(C_n)& \cdots & D(C_n)\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ D(C_n)& D(C_n)& D(C_n)& \cdots & D(C_n)\end{array}\right]+\left[\begin{array}{ccccc}0& J_n& 2J_n& \cdots & (m-1)J_n\\ J_n& 0& J_n& \cdots & (m-2)J_n\\ 2J_n& J_n& 0& \cdots & (m-3)J_n\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ (m-1)J_n& (m-2)J_n& (m-3)J_n& \cdots & 0\end{array}\right]\\ =J_m\otimes D(C_n)+D(P_m)\otimes J_n.\end{array}$$(2) , we get $$\begin{array}{ccc}D(U_m^n)(j_m\otimes x)\hfill & =\hfill & (J_m\otimes D(C_n)+D(P_m)\otimes J_n)(j_m\otimes x)\hfill \\ \hfill & =\hfill & (J_m{j}_m)\otimes (D(C_n)x)+(D(P_m)j_m)\otimes (J_{n}x)\hfill \\ \hfill & =\hfill & (m{j}_m)\otimes (\lambda x)+(D(P_m)j_m)\otimes (0)\hfill \\ \hfill & =\hfill & m\lambda (j_m\otimes x).\hfill \end{array}$$

Hence, we get $m\lambda$ is an eigenvalue of $D(U_m^n)$ corresponding to the eigenvector $j_m\otimes x.$ □

Remark 2.1.

We claim that the nonzero eigenvalues of $D(U_m^n)$ obtained from Theorem 2.2 and Theorem 2.3 are different. Assume that μ is an eigenvalue of $nD(P_m)+k{J}_m$ corresponding to the eigenvector y, where $k=\frac{n^2}{4}$ or $k=\frac{n^2-1}{4}$ according as n is even and odd, respectively. We note that this k is the constant row sum of $D(C_n)$ according as n is even and odd, respectively. Let λ be an nonzero eigenvalue of $D(C_n)$ other than k corresponding to the eigenvector x. Now we have $$\begin{array}{ccc}(J_m\otimes D(C_n)+D(P_m)\otimes J_n)(y\otimes j_n)\hfill & =\hfill & J_{m}y\otimes D(C_n)j_n+D(P_m)y\otimes J_n{j}_n\hfill \\ \hfill & =\hfill & J_{m}y\otimes k{j}_n+D(P_m)y\otimes n{j}_n\hfill \\ \hfill & =\hfill & k{J}_{m}y\otimes j_n+nD(P_m)y\otimes j_n\hfill \\ \hfill & =\hfill & (k{J}_m+nD(P_m))y\otimes j_n\hfill \\ \hfill & =\hfill & \mu (y\otimes j_n).\hfill \end{array}$$

This shows that $y\otimes j_n$ is an eigenvector of $D(U_m^n)$ corresponding to the eigenvalue μ. Also, from the proof of Theorem 2.3, we get $m\lambda$ is an eigenvalue of $D(U_m^n)$ corresponding to the eigenvector $j_m\otimes x.$

If possible let $\mu =m\lambda$, then for some scalar c we have $y\otimes j_n=c(j_m\otimes x)$. Then, this gives all components of x are equal which is impossible as $j_n^{T}x=0$. Hence, the nonzero eigenvalues of $D(U_m^n)$ obtained from Theorem 2.2 and Theorem 2.3 are different.

Theorem 2.4.

The characteristic polynomial of the distance matrix of $U_m^n$ is given by $$\begin{array}{c}P(t)=t^{mn-m-\frac{n}{2}}\det \left(t{I}_m-\frac{n^2}{4}{J}_m-nD(P_m)\right)\prod _{j=1}^{\frac{n}{2}}\left(t+m{\csc }^2\left(\frac{\pi (2j-1)}{n}\right)\right), \text{if}\mathrm{ }n\text{is even}. \hfill \\ p(t)=t^{mn-m-n+1}\det \left(t{I}_m-\frac{n^2-1}{4}{J}_m-nD(P_m)\right)\prod _{j=1}^{\frac{n-1}{2}}\left(t+m\frac{1}{4}{\hspace{0.17em}\text{sec}\hspace{0.17em}}^2\left(\frac{\pi j}{n}\right)\right)\prod _{j=1}^{\frac{n-1}{2}}\left(t+m\frac{1}{4}{\csc }^2\left(\frac{\pi (2j-1)}{2n}\right)\right),\hfill \\ \text{if}\mathrm{ }n\text{is odd}.\hfill \end{array}$$

Proof.

From the Theorems 2.2, 2.3, 1.3 and from Remark 2.1, the number of nonzero eigenvalues of $D(U_m^n)$ is at least equal to $$\begin{array}{c}\{\begin{array}{cc}n+m-1, \hfill & \mathrm{ }\text{when}\mathrm{ }n\mathrm{ }\text{is}\mathrm{ }\text{odd}\hfill \\ \hfill & \hfill \\ \frac{n}{2}+m, \hfill & \mathrm{ }\text{when}\mathrm{ }n\text{is even}.\hfill \end{array}\hfill \end{array}$$

Thus, the number of zero eigenvalues is at most $mn-m-n+1$ and $mn-m-\frac{n}{2}$ according as n is odd and even, respectively. Then, from Theorem 2.1, we get the number of zero eigenvalues of $D(U_m^n)$ is exactly $mn-m-n+1$ and $mn-m-\frac{n}{2}$ according as n is odd and even, respectively. Hence, the characteristic polynomial of $D(U_m^n)$ is $$\begin{array}{c}P(t)=t^{mn-m-\frac{n}{2}}\det \left(t{I}_m-\frac{n^2}{4}{J}_m-nD(P_m)\right)\prod _{j=1}^{\frac{n}{2}}\left(t+m{\csc }^2\left(\frac{\pi (2j-1)}{n}\right)\right), \text{if}\mathrm{ }n\text{is even}. \hfill \\ p(t)=t^{mn-m-n+1}\det \left(t{I}_m-\frac{n^2-1}{4}{J}_m-nD(P_m)\right)\prod _{j=1}^{\frac{n-1}{2}}\left(t+m\frac{1}{4}{\hspace{0.17em}\text{sec}\hspace{0.17em}}^2\left(\frac{\pi j}{n}\right)\right)\prod _{j=1}^{\frac{n-1}{2}}\left(t+m\frac{1}{4}{\csc }^2\left(\frac{\pi (2j-1)}{2n}\right)\right),\hfill \\ \text{if}\mathrm{ }n\text{is odd}.\hfill \end{array}$$ □

Now, by applying Theorem 2.4, one can find the explicit eigenvalues of $D(U_m^n).$ As an example, we provide the explicit distance eigenvalues of $U_3^n.$

Theorem 2.5.

Distance eigenvalues of $U_3^n$ are as follows:

When n is even:

$-2n,\frac{n}{8}\left(3n+8\pm \sqrt{9n^2+80n+192}\right),-3{\csc }^2(\frac{\pi (2j-1)}{n})$ for $j=1,2,\dots ,\frac{n}{2}$ together with zero with multiplicity $\frac{5n-6}{2}.$

When n is odd:

$-2n,\frac{1}{8}\left(3n^2+8n-3\pm \sqrt{9n^4+80n^3+174n^2-80n+9}\right),-\frac{3}{4}{\hspace{0.17em}\text{sec}\hspace{0.17em}}^2\left(\frac{\pi j}{n}\right),-\frac{3}{4}{\csc }^2(\frac{\pi (2j-1)}{2n})$ for $j=1,2,\dots ,\frac{n-1}{2}$ together with zero with multiplicity $2n-2.$

Proof.

We have eigenvalues of $\frac{n^2}{4}{J}_3-nD(P_3)=\left[\begin{array}{ccc}\frac{n^2}{4}& \frac{n^2}{4}+n& \frac{n^2}{4}+2n\\ & & \\ \frac{n^2}{4}+n& \frac{n^2}{4}& \frac{n^2}{4}+n\\ & & \\ \frac{n^2}{4}+2n& \frac{n^2}{4}+n& \frac{n^2}{4}\end{array}\right]$ are $-2n$ and $\frac{n}{8}\left(3n+8\pm \sqrt{9n^2+80n+192}\right).$

Also, the eigenvalues of $\frac{n^2-1}{4}{J}_3-nD(P_3)=\left[\begin{array}{ccc}\frac{n^2-1}{4}& \frac{n^2-1}{4}+n& \frac{n^2-1}{4}+2n\\ & & \\ \frac{n^2-1}{4}+n& \frac{n^2-1}{4}& \frac{n^2-1}{4}+n\\ & & \\ \frac{n^2-1}{4}+2n& \frac{n^2-1}{4}+n& \frac{n^2-1}{4}\end{array}\right]$ are $-2n$ and

$\frac{1}{8}\left(3n^2+8n-3\pm \sqrt{9n^4+80n^3+174n^2-80n+9}\right).$ Hence, applying Theorem 2.4, we get the desired result. □

Acknowledgement

The authors are thankful to the anonymous referees for various comments and suggestions.

Additional information

Funding

The authors would like to thank the Department of Science and Technology, India, for the financial support (start-up research grant (SRG/2019/000839)).