On the D-differential of a graph

Abstract

Let $G=(V(G),E(G))$ be a graph of order n(G). For a subset S of V(G), the boundary of S is defined as $B(S)=N(S)\setminus S,$ where N(S) is the open neighborhood of S. The external private neighborhood set of v with respect to S is defined as $\mathit{epn}(v,S)=\{u\in V(G)\setminus S|N(u)\cap S=\left\{v\right\}\}.$ For a subset S of V(G), the D-differential of S is defined as ${\partial }_D(S)=2|B(S)|-\left|S_w\right|,$ where $S_w=\{v\in S|\mathit{epn}(v,S)\ne \varnothing \}.$ In this paper, we introduce the concept of D-differential of a graph G, which is defined as ${\partial }_D(G)=\max \{{\partial }_D(S)|S\subseteq V(G)\}.$ We present several lower and upper bounds of D-differential of a graph. We construct a Gallai-type theorem for the D-differential ${\partial }_D(G)$ and double Roman domination number ${\gamma }_{dR}(G),$ which states that ${\partial }_D(G)+{\gamma }_{dR}(G)=2n(G).$ Thus, we can utilize a relation between D-differential and double Roman domination number. The concept of D-differential can be a framework to find double Roman domination number of graphs. Actually, we determine the double Roman domination number of middle graphs.

Keywords:

• Differential
• double Roman domination
• middle graph
• D-differential

2010 MATHEMATICS SUBJECT CLASSIFICATION:

• 05C69

1. Introduction

Let $G=(V(G),E(G))$ be a simple graph. The order $|V(G)|$ of G is denoted by n(G). The open neighborhood of $v\in V(G)$ is $N(v)=\{w\in V(G)|vw\in E(G)\}$ and its closed neighborhood is $N[v]=N(v)\cup \left\{v\right\}.$ The degree of a vertex v is denoted by deg(v), i.e., $\mathit{deg}(v)=|N(v)|.$ The maximum degree of G is denoted by $\Delta (G).$ For a subset S of V(G), the open neighborhood of S is $N(S)={\cup }_{v\in S}N(v),$ its closed neighborhood is $N[S]=N(S)\cup S,$ and the boundary of S is $B(S)=N(S)\setminus S.$ The differential of a subset S of V(G) is defined as $\partial (S)=|B(S)|-\left|S\right|,$ and the differential of a graph G is defined to be $\partial (G)=\mathit{max}\{\partial (S)|S\subseteq V(G)\}.$ The theory of differential of a graph has been studied in [1, 2, 5, 11, 12, 14]. In particular, Bermudo et al. [3] observed that the differential is related to the Roman domination number. Recently, it has been observed that the study of domination-related parameters can be approached through variants of differential. For example, the perfect differential [6], the strong differential [7], the 2-packing differential [8] and the quasi-total strong differential [9] are related to the perfect Roman domination number, the Italian domination number, the unique response Roman domination number and the quasi-total Italian domination number, respectively. The purpose of this paper is to define a variant of differential related to the double Roman domination number, which is inspired by [7]. We organize our paper following the methodology of [7].

Lewis et al. [11] motivated the definition of differential from the following game. You are allowed to buy as many tokens as you like, at a cost of one dollar each. Suppose that you buy k tokens. You then place the tokens on some subset S of k vertices of a graph G. For each vertex of G which has no token on it, but is adjacent to a vertex with a token on it, you receive one dollar. Your objective is to maximize your profit, that is, the total value received minus the cost of the tokens bought. Clearly, $\partial (S)=|B(S)|-\left|S\right|$ is the profit obtained with the placement S, and the maximum profit equals $\partial (G).$

Now, we introduce a variant of the differential game. Given a subset S of V(G) and $v\in S,$ the external private neighborhood set of v with respect to S is defined as $\mathit{epn}(v,S)=\{u\in V(G)\setminus S|N(u)\cap S=\left\{v\right\}\}.$ A subset S_w of S is defined to be $\{v\in S|\mathit{epn}(v,S)\ne \varnothing \}.$ We denote $S\setminus S_w$ by S_s.

As another version of the differential game, we suggest a game, which is called D-differential game with refund. You are allowed to buy as many tokens as you like, say k tokens, at a cost of two dollars each. You then place the tokens on some subset S of k vertices of a graph G. For each vertex of G which has no token on it, but is adjacent to a vertex with a token on it, you receive two dollars. You will get a refund of two dollars for each token placed in a vertex with no external private neighbor with respect to S, and you will get a refund of one dollar for each token placed in a vertex with external private neighbor with respect to S. In this game, we define the D-differential of S as the profit obtained with the placement S, which is ${\partial }_D(S)=2|B(S)|-\left|S_w\right|.$ The maximum profit equals the D-differential of G as to be ${\partial }_D(G)=\mathit{max}\{{\partial }_D(S)|S\subseteq V(G)\}.$ We define a ${\partial }_D(G)$-set as a subset S of V(G) with $\left|S\right|={\partial }_D(G).$

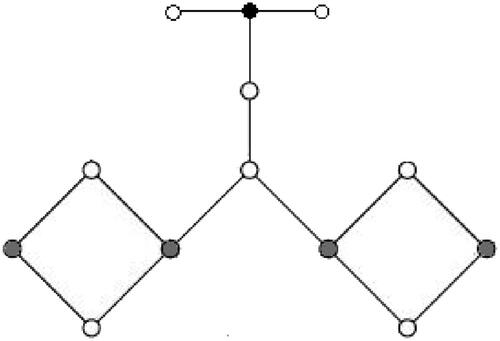
Let G be the graph given in Figure 1, and let S be the set of black and gray vertices in G. In the D-differential game with refund, if we place a token on each vertex of S, then we get a refund of nine dollars because of four gray vertices and one block vertex. Thus, the total profit of placement S equals ${\partial }_D(S)=2|B(S)|-\left|S_w\right|=16-1=15.$ Note that the maximum profit equals ${\partial }_D(G)={\partial }_D(S)=15.$

Figure 1. A graph G with ${\partial }_D(G)=15.$

A function $f:V(G)\to \{0,1,2,3\}$ is a double Roman dominating function (DRDF) on G if (i) if f(v) = 0, then v must have at least two neighbors assigned 2 under f or one neighbor w with f(w) = 3, (ii) if f(v) = 1, then v must have at least one neighbor w with $f(w)\ge 2.$ The double Roman domination number ${\gamma }_{dR}(G)$ equals the minimum weight $\sum _{v\in V(G)}f(v)$ of a DRDF on G.

A subset I of V(G) is an independent set if any two vertices of I are not adjacent. The independence number $\alpha (G)$ is the maximum cardinality among independent sets of G. A subset C of V(G) is a vertex cover if every edge of G is incident with at least one vertex in C. The vertex cover number $\beta (G)$ is the minimum cardinality among vertex covers of G. The following is a well-known theorem.

Theorem 1.1

(Gallai’s theorem). For a graph G, $$\alpha (G)+\beta (G)=n(G).$$

Motivated by the Gallai’s theorem, we construct a Gallai-type theorem for the D-differential ${\partial }_D(G)$ and double Roman domination number ${\gamma }_{dR}(G),$ which states that ${\partial }_D(G)+{\gamma }_{dR}(G)=2n(G).$ By our Gallai-type theorem, we derive general bounds from known result on the double Roman domination number.

In [10], Hamada and Yoshimura defined the middle graph of a graph. The middle graph M(G) of a graph G is the graph defined by $V(M(G))=V(G)\cup E(G)$ and two vertices $v,w\in V(M(G))$ are adjacent in M(G) if (i) $v,w\in E(G)$ and v, w are adjacent in G or (ii) $v\in V(G),w\in E(G)$ and v, w are incident in G.

Based on our Gallai-type theorem, we prove that the double Roman domination number of middle graph M(G) of a graph G is $2n(G)-\alpha \prime (G),$ where $\alpha \prime (G)$ is the matching number of G.

The rest of the paper is organized as follows. In Section 2, we present some necessary terminology and notation. In Section 3, we prove a Gallai-type theorem for the D-differential and double Roman domination number. In Section 4, we provide general bounds and results on the D-differential. In Section 5, we determine double Roman domination number of middle graphs.

2. Preliminaries

In this section, we begin by stating some notation. We denote two adjacent vertices (or edges) x and y by $x\sim y.$ If a vertex v is incident with an edge e, then we denote it by v – e.

The distance d(u, v) between two vertices u and v of a connected graph is the length of shortest walk between u and v in G. The eccentricity ecc(v) of a vertex v is the maximum distance from v to other vertices of G.

A subset D of V(G) is a dominating set of G if every vertex of $V(G)\setminus D$ has a neighbor in D. The domination number $\gamma (G)$ is the minimum cardinality of a dominating set of G. A subset D of V(G) is a 2-dominating set of G if every vertex of $V(G)\setminus D$ has at least two neighbors in D. The 2-domination number ${\gamma }_2(G)$ is the minimum cardinality of a 2-dominating set of G. A 2-dominating set D with $\left|D\right|={\gamma }_2(G)$ is called a ${\gamma }_2(G)$-set.

Given a DRDF f of a graph G, let $(V_0^f,V_1^f,V_2^f,V_3^f)$ be the ordered partition of V(G) such that $V_i^f=\{v\in V(G)|f(v)=i\}.$ Simply, we denote $(V_0^f,V_1^f,V_2^f,V_3^f)$ by $(V_0,V_1,V_2,V_3).$

Proposition 2.1

([4]). In a DRDF of weight ${\gamma }_{dR}(G)$, no vertex needs to be assigned the value 1.

Let T be a tree. A leaf of T is a vertex of degree one. A support vertex is a vertex adjacent to a leaf. The set of support vertices in T is denoted by $\mathcal{S}(T).$ The set of leaves in T is is denoted by $\mathcal{L}(T).$ We write $K_{1,n-1}$ for the star of order $n\ge 3.$ A matching in a graph G is a set of pairwise nonadjacent edges. The maximum number of edges in a matching of a graph G is called the matching number of G and denoted by $\alpha \prime (G).$ The union of graphs G and H is the graph $G\cup H$ with vertex set $V(G)\cup V(H)$ and edge set $E(G)\cup E(H).$

3. A Gallai-type theorem for the D-differential and double roman domination number

In this section, we establish a Gallai-type theorem, which states the relationship between the D-differential and the double Roman domination number.

Lemma 3.1.

For a graph G, there exists a ${\partial }_D(G)$-set which is a dominating set of G.

Proof.

Let S be a ${\partial }_D(G)$-set such that $\left|S\right|$ is maximum among ${\partial }_D(G)$-sets. If S is a dominating set of G, then we are done. Now suppose to the contrary that S is not a dominating set of G.

Let $v\in V(G)\setminus S$ such that $N(v)\cap S=\varnothing ,$ and let $S\prime =S\cup \left\{v\right\}.$ We divide our consideration into two cases.

Case 1.

$\mathit{epn}(v,S\prime )=\varnothing .$ Then $S_w^{\prime }\subseteq S_w$ and $B(S\prime )=B(S),$ which implies that ${\partial }_D(S\prime )\ge {\partial }_D(S)={\partial }_D(G).$ Thus, $S\prime$ is a ${\partial }_D(G)$-set with $|S\prime |>\left|S\right|,$ a contradiction.

Case 2.

$\mathit{epn}(v,S\prime )\ne \varnothing .$ Then $S_w^{\prime }\subseteq S_w\cup \left\{v\right\}$ and $|N(v)\setminus N[S]|\ge 1,$ which implies that ${\partial }_D(S\prime )\ge 2|B(S)|+2|N(v)\setminus N[S]|-\left|S_w\right|-1\ge 2|B(S)|-\left|S_w\right|={\partial }_D(S)={\partial }_D(G).$ Thus, $S\prime$ is a ${\partial }_D(G)$-set with $|S\prime |>\left|S\right|,$ a contradiction. □

Theorem 3.2

(Gallai-type theorem for the D-differential and double Roman domination number). For a graph G, $${\gamma }_{dR}(G)+{\partial }_D(G)=2n(G).$$

Proof.

By Lemma 3.1, there exists a ${\partial }_D(G)$-set S which is a dominating set of G. Then the function $f=(V(G)\setminus S,\varnothing ,S_s,S_w)$ is a DRDF of G, which implies that ${\gamma }_{dR}(G)\le w(f)=2\left|S_s\right|+3\left|S_w\right|.$ Thus, it follows from ${\partial }_D(G)=2(n(G)-|S|)-\left|S_w\right|=2n(G)-2\left|S_s\right|-3\left|S_w\right|$ that ${\gamma }_{dR}(G)\le 2n(G)-{\partial }_D(G).$

To prove that ${\gamma }_{dR}(G)\ge 2n(G)-{\partial }_D(G),$ let $f=(V_0,\varnothing ,V_2,V_3)$ be a ${\gamma }_{dR}(G)$-function. For $S:=V_2\cup V_3,$ it is easy to see that $S_s=V_2$ and $S_w=V_3.$ Thus, ${\partial }_D(G)\ge {\partial }_D(S)=2|V(G)\setminus (V_2\cup V_3)|-\left|V_3\right|=2n(G)-2\left|V_2\right|-3\left|V_3\right|=2n(G)-{\gamma }_{dR}(G).$ □

4. General bounds for the D-differential

In this section, we present various bounds on the D-differential. First of all, we derive some result from known bounds of the double Roman domination number.

Theorem 4.1

([4]). For a connected graph G of order $n(G)\ge 3,$ $${\gamma }_{dR}(G)\le \frac{5}{4}n(G).$$

By Theorems 3.2 and 4.1, we get the following theorem.

Theorem 4.2.

For a connected graph G of order $n(G)\ge 3,$ $${\partial }_D(G)\ge \frac{3}{4}n(G).$$

Theorem 4.3

([4]). For any graph G, $$2\gamma (G)\le {\gamma }_{dR}(G)\le 3\gamma (G).$$

By Theorems 3.2 and 4.3, we get the following theorem.

Theorem 4.4.

For any graph G, $$2n(G)-3\gamma (G)\le {\partial }_D(G)\le 2n(G)-2\gamma (G).$$

It follows from [4] that, for any graph G, $2\gamma (G)={\gamma }_{dR}(G)$ if and only if $\gamma (G)={\gamma }_2(G).$ The following is an immediate consequence.

Corollary 4.5.

For any graph G, ${\partial }_D(G)=2n(G)-2\gamma (G)$ if and only if $\gamma (G)={\gamma }_2(G).$

Theorem 4.6

([1]). For any graph G, $${\gamma }_{dR}(G)\le 2{\gamma }_2(G).$$

By Theorems 3.2 and 4.6, we get the following theorem.

Theorem 4.7.

For any graph G, $${\partial }_D(G)\ge 2n(G)-2{\gamma }_2(G).$$

The following result describes the structure of ${\partial }_D(G)$-sets for graphs with ${\partial }_D(G)=2n(G)-2{\gamma }_2(G).$

Proposition 4.8.

For any graph G, ${\partial }_D(G)=2n(G)-2{\gamma }_2(G)$ if and only if there exists a ${\partial }_D(G)$-set S such that S is a dominating set and $S_w=\varnothing .$

Proof.

Assume that ${\partial }_D(G)=2n(G)-2{\gamma }_2(G).$ Since $S_w=\varnothing$ for every ${\gamma }_2(G)$-set S, ${\partial }_D(G)=2n(G)-2{\gamma }_2(G)=2|B(S)|={\partial }_D(S).$ This implies that S is a ${\partial }_D(G)$-set satisfying the required conditions.

Conversely, assume that there exists a ${\partial }_D(G)$-set S such that S is a dominating set and $S_w=\varnothing .$ Then S is a 2-dominating set. Thus, ${\partial }_D(S)=2|B(S)|\le 2(n(G)-{\gamma }_2(G)).$ By Theorem 4.7, we have ${\partial }_D(G)=2n(G)-2{\gamma }_2(G).$ □

The following result describes the structure of ${\partial }_D(G)$-sets for graphs with ${\partial }_D(G)=2n(G)-3\gamma (G).$

Proposition 4.9.

For any graph G, ${\partial }_D(G)=2n(G)-3\gamma (G)$ if and only if every $\gamma (G)$-set S is a ${\partial }_D(G)$-set with $S_s=\varnothing .$

Proof.

Assume that ${\partial }_D(G)=2n(G)-3\gamma (G),$ and let S be a $\gamma (G)$-set. Since $|B(S)|=n(G)-\gamma (G),{\partial }_D(G)\ge {\partial }_D(S)=2|B(S)|-\left|S_w\right|=2(n(G)-\gamma (G))-(|S|-|S_s|)=2n(G)-3\gamma (G)+\left|S_s\right|,$ which implies that S is a ${\partial }_D(G)$-set with $S_s=\varnothing .$

Conversely, assume that every $\gamma (G)$-set S is a ${\partial }_D(G)$-set with $S_s=\varnothing .$ Then ${\partial }_D(G)={\partial }_D(S)=2|B(S)|-\left|S\right|=2n(G)-3\gamma (G).$ □

Next, we present bounds in terms of order and maximum degree.

Theorem 4.10

([13]). For a connected graph of order $n(G)\ge 2,$ $${\gamma }_{dR}(G)\ge \frac{3n(G)}{\Delta (G)+1}.$$

Moreover, if the equality holds, $G\in \{P_n,C_n\}$ or ${\gamma }_{dR}(G)=3\gamma (G).$

Theorem 4.11.

For a connected graph of order $n(G)\ge 2,$ $$2\Delta (G)-1\le {\partial }_D(G)\le \frac{2\Delta (G)-1}{\Delta (G)+1}n(G).$$

Proof.

The upper bound comes from Theorems 3.2 and 4.10. The lower bound is derived from the fact that ${\partial }_D(G)\ge {\partial }_D(\{u\})=2\Delta (G)-1$ for a vertex u with $\mathrm{deg}(u)=\Delta (G).$ □

The graphs for which ${\partial }_D(G)=\frac{2\Delta (G)-1}{\Delta (G)+1}n(G)$ are characterized by Theorem 4.10. Now we characterize the trees attaining the lower bound in Theorem 4.11.

We define that a tree T belongs to the family $\mathcal{T}$ if T satisfies the following conditions: for each $v\in V(T)$ with $\mathrm{deg}(v)=\Delta (T)$

• (C1) $v\in \mathcal{S}(T)$ and $\mathit{ecc}(v)\le 2,$

• (C2) $\mathrm{deg}(u)\le 2$ for any $u\in N(v),$

• (C3) deg(u) = 1 for any $u\in V(T)\setminus N[v].$

Define $LN(v)=N(v)\cap \mathcal{L}(T).$

Lemma 4.12.

Let $T\in \mathcal{T}$ of order $n(T)\ge 3$ and $v\in V(T)$ with $\mathrm{deg}(v)=\Delta (T)$. Then there exists a ${\partial }_D(T)$-set S such that $v\in S_w.$

Proof.

Suppose to the contrary that $v\notin S_w$ for every ${\partial }_D(T)$-set S. Fix a ${\partial }_D(T)$-set S. If $|LN(v)|\ge 2,$ then ${\partial }_D((S\setminus LN(v))\cup \{v\})\ge {\partial }_D(S),$ a contradiction. If $|LN(v)|=1,$ then there exists $u\in N(v)\cap \mathcal{S}(T)$ such that deg(u) = 2. Take $S\prime =(S\setminus (LN(v)\cup \left\{u\right\}))\cup \left\{v\right\}\cup LN(u).$ Then ${\partial }_D(S\prime )\ge {\partial }_D(S),$ a contradiction. This completes the proof. □

Theorem 4.13.

Let T be a tree of order $n(T)\ge 3$. Then ${\partial }_D(T)=2\Delta (T)-1$ if and only if $T\in \mathcal{T}.$

Proof.

Assume that ${\partial }_D(T)=2\Delta (T)-1.$ Let $v\in V(T)$ with $\mathrm{deg}(v)=\Delta (T).$ If $v\notin \mathcal{S}(T),$ then ${\partial }_D(T)\ge {\partial }_D(V(T)\setminus N(v))=2\Delta (T),$ a contradiction. Thus, $v\in \mathcal{S}(T).$ If $\mathit{ecc}(v)\ge 3,$ then there exists a vertex $u\in V(T)$ such that $d(v,u)\ge 2$ and $\mathit{deg}(u)\ge 2.$ So, ${\partial }_D(\{v,u\})\ge 2\Delta (T),$ a contradiction. Thus, the condition (C1) follows.

Suppose that there exists $u\in N(v)$ with $\mathit{deg}(u)\ge 3.$ Then ${\partial }_D(\{v,u\})\ge 2\Delta (T),$ a contradiction. Thus, the condition (C2) follows.

The condition (C3) follows from $\mathit{ecc}(v)\le 2$ in (C1) and (C2). Thus, $T\in \mathcal{T}.$

Conversely, assume that $T\in \mathcal{T}.$ By Theorem 4.11, it suffices to show ${\partial }_D(T)\le 2\Delta (T)-1.$ It follows from Lemma 4.12 that there exists a ${\partial }_D(T)$-set S such that $v\in S_w$ and $\mathit{deg}(v)=\Delta (T).$ Take S of the minimum cardinality among these sets. If $N(v)\cap S=\varnothing ,$ then it follows from (C1), (C2) and (C3) that $|N(x)\cap S|\le 1$ for $x\in N(v).$ So, ${\partial }_D(T)\le {\partial }_D(\{v\})=2\Delta (T)-1.$

Now, Suppose that $N(v)\cap S\ne \varnothing .$ Let $x\in N(v)\cap S.$ Then ${\partial }_D(S\setminus \{x\})\ge {\partial }_D(S)$ and $|S\setminus \{x\left\}\right|<\left|S\right|,$ a contradiction. This completes the proof. □

Finally, we characterize the extreme cases on the trivial bound of D-differential.

Theorem 4.14.

For a graph G of order $n(G)\ge 2$, the following statements hold.

1. $0\le {\partial }_D(G)\le 2n(G)-3.$

2. ${\partial }_D(G)=0$ if and only if G is an empty graph.

3. ${\partial }_D(G)=1$ if and only if either $G\cong P_2$ or $G\cong P_2\cup H$, where H is an empty graph with $n(H)=n(G)-2.$

4. ${\partial }_D(G)=2$ if and only if $G\cong P_2\cup P_2\cup H$, where H is an empty graph with $n(H)=n(G)-4.$

5. ${\partial }_D(G)=2n(G)-3$ if and only if $\Delta (G)=n(G)-1.$

6. ${\partial }_D(G)=2n(G)-4$ if and only if $\gamma (G)={\gamma }_2(G)=2.$

Proof.

1. It follows from ${\partial }_D(\varnothing )=0$ that ${\partial }_D(G)\ge 0.$ By Lemma 3.1, we take a ${\partial }_D(G)$-set S such that S is a dominating set. If $\left|S\right|=1,$ then ${\partial }_D(S)=2|B(S)|-\left|S_w\right|=2(n(G)-1)-1=2n(G)-3.$ If $\left|S\right|\ge 2,$ then ${\partial }_D(S)=2|B(S)|-\left|S_w\right|\le 2(n(G)-2).$ Thus, ${\partial }_D(G)\le 2n(G)-3.$

2. If ${\partial }_D(G)=0,$ then $2deg(u)-1={\partial }_D(\{u\})\le {\partial }_D(G)=0$ for each $u\in V(G).$ This implies that $\Delta (G)=0.$

   Conversely, assume that G is an empty graph. Then any subset S of V(G) has $B(S)=\varnothing$ and $S_w=\varnothing .$ Thus, ${\partial }_D(G)=0.$

3. Assume that ${\partial }_D(G)=1.$ If $\Delta (G)\ge 2,$ then $3\le 2deg(u)-1={\partial }_D(\{u\})\le {\partial }_D(G)$ for a vertex u with $\mathit{deg}(u)=\Delta (G),$ a contradiction. Thus, $\Delta (G)=1.$ If G is connected, then $G\cong P_2.$ If G is disconnected, then (ii) implies that $G\cong P_2\cup H,$ where H is an empty graph with $n(H)=n(G)-2.$

   Conversely, assume that either $G\cong P_2$ or $G\cong P_2\cup H,$ where H is an empty graph with $n(H)=n(G)-2.$ Then it is easy to see that ${\partial }_D(G)=1.$

4. Assume that ${\partial }_D(G)=2.$ By the same argument in (iii), we have $\Delta (G)=1,$ which implies that $G\cong P_2\cup P_2\cup H,$ where H is an empty graph with $n(H)=n(G)-4.$

   Conversely, assume that $G\cong P_2\cup P_2\cup H,$ where H is an empty graph with $n(H)=n(G)-4.$ Then it is easy to see that ${\partial }_D(G)=2.$

5. By Lemma 3.1, we take a ${\partial }_D(G)$-set S such that S is a dominating set. As mentioned in the proof of (i), if the cardinality of S is at least two, then ${\partial }_D(S)\le 2n(G)-4.$ Assume that ${\partial }_D(G)=2n(G)-3.$ Then a ${\partial }_D(G)$-set S is a singleton, which implies that $\Delta (G)=n(G)-1.$

   Conversely, assume that $\Delta (G)=n(G)-1.$ From the proof of (i), we deduce that ${\partial }_D(G)=2n(G)-3.$

6. Assume that ${\partial }_D(G)=2n(G)-4.$ By (i) and (v), we have $\Delta (G)\le n(G)-2$ and so $\gamma (G)\ge 2.$ By Lemma 3.1, we take a ${\partial }_D(G)$-set S such that S is a dominating set. Then $2n(G)-4={\partial }_D(S)=2|B(S)|-\left|S_w\right|=2n(G)-2\left|S_s\right|-3\left|S_w\right|,$ which implies that $\left|S_s\right|=2$ and $\left|S_w\right|=0.$ Since ${\gamma }_2(G)\ge \gamma (G),$ we have $\gamma (G)={\gamma }_2(G)=2.$

Conversely, assume that $\gamma (G)={\gamma }_2(G)=2.$ By Corollary 4.5, we have ${\partial }_D(G)=2n(G)-4.$ □

5. Double Roman domination number of middle graphs

In this section, we show that the double Roman domination number of the middle graph of a graph G can be determined by the matching number of G. For $v\in V(G),$ we denote $\{e\in E(G)|e-v\}$ by $N_M(v).$ For $e\in E(G),$ we denote $\{x\in V(G)\cup E(G)|x-e \text{or} x\sim e\}$ by $N_M(e).$

Theorem 5.1.

For a graph G, $${\gamma }_{dR}(M(G))=2n(G)-\alpha \prime (G).$$

Proof.

Note that $n(M(G))=n(G)+|E(G)|.$ By Theorem 3.2, it suffices to prove that ${\partial }_D(M(G))=2|E(G)|+\alpha \prime (G).$

Let S be a ${\partial }_D(M(G))$-set. For $e=vw\in E(G),$ suppose that $e,v,w\in S,$ and let $S\prime =S\setminus \left\{e\right\}.$ It follows from $N_M(v)\cup N_M(w)\supset N_M(e)\setminus \{v,w\}$ that $|B(S\prime )|=|B(S)|+1.$ Since v, w may have a private neighbor with respect to $S\prime ,\left|S{\prime }_w\right|\le \left|S_w\right|+2.$ Thus, we have ${\partial }_D(S\prime )\ge {\partial }_D(S),$ which implies that $S\prime$ is also a ${\partial }_D(M(G))$-set.

From now on, assume that there is no case that $e,v,w\in S$ for any edge e = vw. We proceed by proving five claims.

Claim 1.

There exists no pair of a vertex $v\in S$ and an edge $e\in S$ such that they are incident in G.

Suppose that there exists a pair of v, e with v – e, and let $S\prime =S\setminus \left\{v\right\}.$ Then $|B(S\prime )|=|B(S)|+1$ and $\left|S{\prime }_w\right|\le \left|S_w\right|+1,$ which implies that ${\partial }_D(S\prime )>{\partial }_D(S),$ a contradiction.

Claim 2.

There exists no pair of two vertex $v_1,v_2\in S$ such that they are adjacent in G.

Suppose that there exists a pair of v₁, v₂ with $v_1\sim v_2,$ and let $S\prime =(S\setminus \{v_1,v_2\})\cup \left\{v_1{v}_2\right\}.$ Then $|B(S\prime )|=|B(S)|+1$ and $\left|S{\prime }_w\right|\le \left|S_w\right|+1,$ which implies that ${\partial }_D(S\prime )>{\partial }_D(S),$ a contradiction.

Claim 3.

There exists a ${\partial }_D(M(G))$-set $S\prime$ such that $S\prime \subseteq E(G).$

If there exists a vertex $v\in S,$ then it follows from Claims 1 and 2 that $(N_M(v)\cup N(v))\cap S=\varnothing .$ Suppose that there exists a vertex $z\in N(v)$ such that z is not adjacent to any edge of S in M(G). Replace S by $S\prime :=(S\setminus \{v\})\cup \left\{vz\right\}.$ Then $|B(S\prime )|\ge |B(S)|+1$ and $S{\prime }_w\setminus \left\{vz\right\}\subseteq S_w\setminus \left\{v\right\},$ which implies that ${\partial }_D(S\prime )>{\partial }_D(S),$ a contradiction.

Now, assume that each vertex in N(v) is adjacent to some edge of S in M(G), and let $S\prime =S\setminus \left\{v\right\}.$ Then $|B(S\prime )|=|B(S)|.$ Let $e\in S\prime$ be an edge incident to a vertex in N(v). Whether or not e belongs to $S{\prime }_w$ is independent of edges in $N_M(v)\cap N_M(e).$ So, $S{\prime }_w=S_w,$ which implies that $S\prime$ is also a ${\partial }_D(M(G))$-set. Since S is finite, we obtain a ${\partial }_D(M(G))$-set $S\prime$ such that $S\prime \subseteq E(G)$ by repeating this process.

Claim 4.

The elements of S consist of disjoint edges of G.

Suppose that there exists a pair of $e_1,e_2\in E(G)$ with $e_1\sim e_2,$ and let $e_1=vw,e_2=wu.$ Consider $S\prime =(S\setminus \{e_1\})\cup \left\{v\right\}.$ By the same argument in the proof of Claim 3, if there exists a vertex $q\in N(v)$ such that q is not adjacent to any edge of S in M(G), then this induces a contradiction. Thus, each vertex in N(v) is adjacent to some edge of S in M(G), and let $S″=S\prime \setminus \left\{v\right\}.$ Then $|B(S″)|=|B(S\prime )|$ and $S\prime {\prime }_w=S{\prime }_w,$ which implies that $S″$ is also a ${\partial }_D(M(G))$-set. Since S is finite, we obtain a ${\partial }_D(M(G))$-set S₁ such that S₁ consists of disjoint edges by repeating this process.

Claim 5.

The cardinality of S is the matching number of G.

For a set D of disjoint edges, if an edge e can be added in D such that $D\prime :=D\cup \left\{e\right\}$ is disjoint, then ${\partial }_D(D\prime )>{\partial }_D(D),$ since $|B(D\prime )|\ge |B(D)|+2$ and $\left|D{\prime }_w\right|=\left|D_w\right|+1.$ For any two maximum matchings S₁ and S₂, we have $|B(S_1)|=|B(S_2)|=|E(G)|+\alpha \prime (G),$ which implies ${\partial }_D(S_1)={\partial }_D(S_2).$

Therefore, for a maximum matching S, ${\partial }_D(S)=2|B(S)|-\left|S_w\right|=2(|E(G)|+\alpha \prime (G))-\alpha \prime (G).$ □

Acknowledgment

The author would like to thank the anonymous reviewers for their comments.

Disclosure statement

No potential conflict of interest was reported by the author.

Additional information

Funding

This research was supported by Basic Science Research Program through the National Research Foundation of Korea funded by the Ministry of Education (2020R1I1A1A01055403).