Restrained Italian reinforcement number in graphs

Abstract

A restrained Italian dominating function (RID-function) on a graph $G=(V,E)$ is a function $f:V\to \{0,1,2\}$ satisfying: (i) $f(N(u))\ge 2$ for every vertex $u\in V(G)$ with $f(u)=0$, where $N(u)$ is the set of vertices adjacent to u; (ii) the subgraph induced by the vertices assigned 0 under f has no isolated vertices. The weight of an RID-function is the sum of its function value over the whole set of vertices, and the restrained Italian domination number is the minimum weight of an RID-function on G. In this paper, we initiate the study of the restrained Italian reinforcement number $r_{rI}(G)$ of a graph G defined as the cardinality of a smallest set of edges that we must add to the graph to decrease its restrained Italian domination number. We begin by showing that the decision problem associated with the restrained Italian reinforcement problem is NP-hard for arbitrary graphs. Then several properties as well as some sharp bounds of the restrained Italian reinforcement number are presented.

KEYWORDS:

• Restrained Italian domination
• restrained Italian reinforcement
• NP-hardness

1 Introduction

For definitions and notations not given here we refer to [9]. We consider simple graphs G with vertex set $V=V(G)$ and edge set $E=E(G)$. The order of G is $n=n(G)=\left|V\right|$. The open neighborhood of a vertex v, denoted $N(v)$ (or $N_G(v)$ to refer to G) is the set $\{u\in V(G)\mid uv\in E\}$ and its closed neighborhood is the set $N[v]=N_G[v]=N(v)\cup \left\{v\right\}$. The degree of a vertex $v\in V$ is $d(v)=d_G(v)=|N(v)|$. The maximum and minimum degree in G are denoted by $\Delta =\Delta (G)$ and $\delta =\delta (G)$, respectively. A vertex of degree one is called a leaf and its neighbor is called a support vertex.

As usual, the path (cycle, complete graph, complete p -partite graph, respectively) of order n is denoted by $P_n$ ($C_n$, $K_n,K_{n_1,n_2,\dots ,n_p}$, respectively). A star of order $n\ge 2$ is the graph $K_{1,n-1}.$A tree T is a double star if it contains exactly two vertices that are not leaves. A double star with respectively p and q leaves attached at each support vertex is denoted by $D{S}_{p,q}.$

For a subset $S\subseteq V$, the subgraph induced by S in G is denoted as G[S]. A subset $S\subseteq V$ is a dominating set of G if every vertex in $V\setminus S$ has a neighbor in S. The domination number $\gamma (G)$ is the minimum cardinality of a dominating set of G. In 1990, Kok and Mynhardt [11] introduced the reinforcement number $r(G)$ of a graph G as the minimum numbers of edges that have to be added to the graph G in order to decrease the domination number. However, it was assumed that $r(G)=0$ for all graphs G with domination number one. Since then, the concept of reinforcement has been defined and studied for several other domination parameters, such as Roman domination [10], total Roman domination [1], Italian domination [8], double Roman domination [3] and rainbow domination [2, 14].

The concept of Italian domination has been introduced in 2016 by Chellali et al. [6] as a new variation of Roman domination but called differently, Roman $\left\{2\right\}$-domination. An Italian dominating function (ID-function, for short) on a graph G is a function $f:V\to \{0,1,2\}$ having the property that $f(N(u))\ge 2$ for each vertex u with $f(u)=0$. The weight of an ID-function f is the sum $w(f)=\sum _{v\in V(G)}f(v)$. It is worth noting that since then several variations of Italian domination have been defined, see for example, [4, 5, 12, 16].

In 2021, Samadi, Alishahi, Masoumi and Mojdeh [13] defined the restrained Italian dominating function (RID-function, for short) as an ID-function f satisfying in addition the property that the subgraph induced by the vertices assigned 0 under f has no isolated vertices. The restrained Italian domination number ${\gamma }_{rI}(G)$ is the minimum weight of an RID-function on a graph G, and an RID-function of G with weight ${\gamma }_{rI}(G)$ is called a ${\gamma }_{rI}(G)$-function. Any RID-function f on G can be simply referred to as $f=(V_0,V_1,V_2)$, where $V_i=\{v\in V(G):f(v)=i\}$ for $i\in \{0,1,2\}$.

In this paper, we are interested in starting the study of the restrained Italian reinforcement number $r_{rI}(G)$ of a graph G defined as the cardinality of a smallest set of edges $F\subseteq E(\overline{G})$ such that ${\gamma }_{rI}(G+F)<{\gamma }_{rI}(G),$ where $\overline{G}$ denotes the complement graph of G. In the case that there is no subset of edges F with ${\gamma }_{rI}(G+F)<{\gamma }_{rI}(G)$, we define $r_{rI}(G)=0$. Since for any nontrivial connected graph G, ${\gamma }_{rI}(G)\ge 2,$ we deduce that $r_{rI}(G)=0$ for all nontrivial connected graphs with $r_{rI}(G)=2$. Moreover, we say that a subset $E^{\prime }\subseteq E(\overline{G})$ is an $r_{rI}(G)$-set if $\left|E^{\prime }\right|=r_{rI}(G)$ and ${\gamma }_{rI}(G+E^{\prime })<{\gamma }_{rI}(G)$.

In the rest of this paper, we show that the decision problem corresponding to the problem of computing $r_{rI}$ $(G)$ is NP-hard for an arbitrary graph G. Then various properties of the restrained Italian reinforcement number are presented and some sharp bounds on it are established. In addition, the restrained Italian reinforcement number is determined for some families of graphs.

We close this section by showing that any $r_{rI}(G)$-set of a connected graph G with ${\gamma }_{rI}(G)\ge 3$ can decrease the restrained Italian domination number of G by at most two.

Proposition 1.

Let G be a connected graph with ${\gamma }_{rI}(G)\ge 3$. If F is an $r_{rI}(G)$-set, then $${\gamma }_{rI}(G)-2\le {\gamma }_{rI}(G+F)\le {\gamma }_{rI}(G)-1.$$

Both bounds are sharp.

Proof.

By assumption, ${\gamma }_{rI}(G+F)<{\gamma }_{rI}(G),$ whence the upper bound. To show the lower bound, let us assume that ${\gamma }_{rI}(G+F)\le {\gamma }_{rI}(G)-3$. Let f be a ${\gamma }_{rI}(G+F)$-function and let $uv\in F$ such that $0\in \{f(u),f(v)\}$. If such an edge does not exist, then f is an RID-function of G leading to the contradiction ${\gamma }_{rI}(G)\le {\gamma }_{rI}(G+F).$ Hence we suppose that uv exists. Let $F^{\ast }=F-\left\{uv\right\}.$ Without loss of generality, suppose that $f(u)=0$. If $f(v)=1$, then u has a neighbor w with label 1 in $G+F^{\ast }$ and the function g defined on $G+F^{\ast }$ by $g(w)=2$ and $g(x)=f(x)$ otherwise, is an RID-function of $G+F^{\ast }$ yielding ${\gamma }_{rI}(G+F^{\ast })\le {\gamma }_{rI}(G+F)+1\le {\gamma }_{rI}(G)-2,$ contradicting the choice of F. Hence assume that $f(v)\ne 1$.

First let $f(v)=2$. If u has a neighbor w in $G+F^{\ast }$ with $f(w)\ge 1$, then the function g defined by $g(w)=2$ and $g(x)=f(x)$ otherwise, is an RID-function of $G+(F-\{uv\})$ yielding as above to the contradiction ${\gamma }_{rI}(G+F^{\ast })<{\gamma }_{rI}(G)$. Hence we assume that each neighbor of u in $G+F^{\ast }$ is assigned 0 under f. Let $u_1,\dots ,u_k$ be the neighbors of u in $G+F^{\ast }$. If $k=1$ and $u_1$ has a neighbor assigned 0 other than u, then the function $g(u)=1$ and $g(x)=f(x)$ otherwise, is an RID-function of $G+F^{\ast }$ yielding ${\gamma }_{rI}(G+F^{\ast })\le {\gamma }_{rI}(G+F)+1<{\gamma }_{rI}(G),$a contradiction. If $k=1$ and $u_1$ has no neighbor assigned 0 other than u, then the function $g(u)=g(u_1)=1$ and $g(x)=f(x)$ otherwise, is an RID-function of $G+F^{\ast }$ and thus ${\gamma }_{rI}(G+F^{\ast })\le {\gamma }_{rI}(G+F)+2<{\gamma }_{rI}(G),$a contradiction. Hence, assume that $k\ge 2$. If some $u_i$ has no neighbor assigned 0 other than u, then the function $g(u_i)=2$ and $g(x)=f(x)$ otherwise, is a RID-function of $G+F^{\ast }$ yielding again ${\gamma }_{rI}(G+F^{\ast })<{\gamma }_{rI}(G)$. Hence we assume that for each i, $u_i$ has at least two neighbors assigned 0 under f. In this case, the function $g(u)=1$ and $g(x)=f(x)$ otherwise, is an RID-function of $G+F^{\ast }$ and thus ${\gamma }_{rI}(G+F^{\ast })<{\gamma }_{rI}(G).$

Finally, assume that $f(v)=0$. Since F is an $r_{rI}(G)$-set, we can assume, without loss of generality, that all neighbors of u in $G+F^{\ast }$ have positive labels under f. Now, if v has a neighbor with weight 0 in $G+F^{\ast }$, then the function $g(u)=1$ and $g(x)=f(x)$ otherwise, is an RID-function of $G+F^{\ast }$ while if v has no neighbor with weight 0 in $G+F^{\ast }$, then the function $g(u)=g(v)=1$ and $g(x)=f(x)$ otherwise, is an RID-function of $G+F^{\ast }.$ Both situations yield the contradiction ${\gamma }_{rI}(G+F^{\ast })<{\gamma }_{rI}(G).$ Consequently, ${\gamma }_{rI}(G+F)\ge {\gamma }_{rI}(G)-2.$

The cycle $C_4$ is a simplest example of a graph for which the upper bound of Proposition 1 is attained, while the sharpness of the lower bound can be seen for the cycle $C_6.$ ▪

2 NP-hardness result

Our aim in this section, is to show that the decision problem associated with the Restrained Italian reinforcement is NP-hard. Consider the following decision problem.

Restrained Italian Reinforcement problem (RI-reinforcement)

Instance: A nonempty graph G and a positive integer k.

Question: Is $r_{rI}(G)\le k$ ?

We show the NP-hardness of the RI-reinforcement problem by transforming the well-known 3-SAT problem to it in polynomial time. Recall that the 3-SAT problem specified below was proven to be NP- complete in [7].

3-SAT problem

Instance: A collection $\mathcal{C}=\{C_1,C_2,\dots ,C_m\}$ of clauses over a finite set U of variables such that $\left|C_j\right|=3$ for every $j\in \{1,2,\dots ,m\}.$

Question: Is there a truth assignment for U that satisfies all the clauses in $\mathcal{C}$?

Theorem 2.

The RI-reinforcement problem is NP-complete for arbitrary graphs.

Proof.

Let $U=\{u_1,u_2,\dots ,u_n\}$ and $\mathcal{C}=\{C_1,C_2,\dots ,C_m\}$ be an arbitrary instance of 3-SAT problem. We will construct a graph G and a positive integer k such that $\mathcal{C}$ is satisfiable if and only if $r_{rI}(G)\le k$.

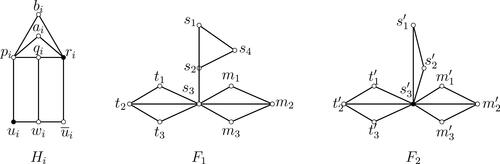
For each $i\in \{1,2,\dots ,n\},$ we associate to each variable $u_i\in U$a copy of the graph $H_i$ as illustrated in Figure 1. For each $j\in \{1,2,\dots ,m\}$, we associate to each clause $C_j=\{x_j,y_j,z_j\}\in \mathcal{C}$a single vertex $c_j$ by adding the edge-set $E_j=\{c_j{x}_j,c_j{y}_j,c_j{z}_j\}$. Finally, we add the graph F depicted in Figure 1 by connecting vertices $s_1,s_1^{\prime }$ to every vertex $c_j$. Clearly, the resulting graph G is of order $8n+m+19$ and size $11n+5m+27$ and thus G can be constructed in polynomial time. Set $k=1$. Figure 2 provides an example of the resulting graph when $U=\{u_1,u_2,u_3,u_4\}$ and $\mathcal{C}=\{C_1,C_2,C_3\}$, where $C_1=\{u_1,u_2,{\overline{u}}_3\}$, $C_2=\{{\overline{u}}_1,u_2,u_4\}$ and $C_3=\{{\overline{u}}_2,u_3,u_4\}$.

Figure 1: The graphs $H_i$ and $F=F_1\cup F_2$.

Figure 2: An instance of the restrained Italian reinforcement number problem resulting from an instance of 3-SAT. Here $k=1$ and ${\gamma }_{rI}(G)=22$, where the bold vertex p means there is a RIDF f with $f(p)=2$.

Figure 3: A graph G of order 9 and $r_{rI}(G)=4$.

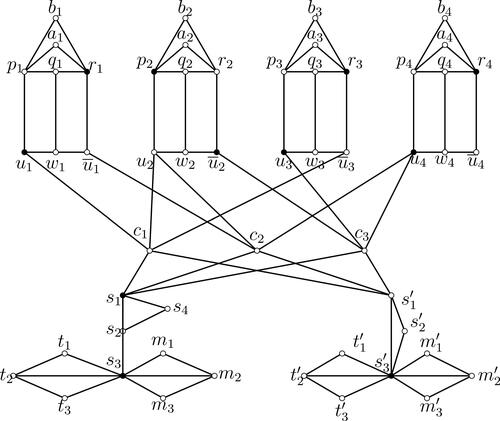
It is easy to see that for every ${\gamma }_{rI}(G)$-function f we have $\sum _{v\in V(H_i)}f(v)\ge 4$ for each $i\in \{1,2,\dots ,n\}$ . Moreover, to restrained Italian dominate vertices of $V(F)$, we need ${\sum }_{j=1}^{m}f(c_j)+f(V(F))\ge 6$. Therefore, ${\gamma }_{rI}(G)=w(f)\ge 4n+6$. The equality is obtained since one can easily construct an RID-function of G with weight $4n+6$ (you can follow the example of the function given on the resulting graph of Figure 2). Consequently, ${\gamma }_{rI}(G)=4n+6$.

In the sequel, we shall show that $\mathcal{C}$ is satisfiable if and only if $r_{rI}(G)=1$. Assume that $\mathcal{C}$ is satisfiable and let $t:U\to \{T,F\}$ be a satisfying mapping for $\mathcal{C}$. We construct a subset D of vertices of G as follows. If $t(u_i)=T$, then put the vertices $u_i$ and $r_i$ in D; while if $t(u_i)=F$, then put the vertices $\overline{u_i}$ and $p_i$ in D. Hence $\left|D\right|=2n$. Now, define the function g on $V(G)$ by $g(x)=2$ for every $x\in D,g(s_1)=1,g(s_3)=g(s_3^{\prime })=2$ and $g(y)=0$ for the remaining vertices. It is easy to check that g is an RID-function of $G+s_4{s}_3$ of weight $4n+5<{\gamma }_{rI}(G)=4n+6$, and therefore $r_{rI}(G)=1$.

Conversely, suppose that $r_{rI}(G)=1$. Then, there is an edge $e=uv\in E(\overline{G})$ such that ${\gamma }_{rI}(G+e)<4n+6$. Let $f=(V_0,V_1,V_2)$ be a ${\gamma }_{rI}(G+e)$-function. Whatever be the added edge e, we have $f(H_i)\ge 4$, and thus vertices u and v cannot both belong to $V(H_i)$ (for otherwise ${\gamma }_{rI}(G+e)\ge 4n+6$). Consequently, we can consider the following situations.

Either $u,v\in \{c_1,c_2,\dots ,c_m\}$ or $u\in V(H_i)$ for some i and $v\in \left\{c_j\right\}\cup V(F)$ for some j. In this case, as seen above, one can check that $\omega (f)\ge 4n+6$, a contradiction. The same can be observed when $u\in \{c_1,c_2,\dots ,c_m\}$ and $v\in V(F).$ Therefore, let $u,v\in V(F)$. Since $r_{rI}(G)=1$ and $f(H_i)\ge 4$, we must have ${\sum }_{j=1}^{m}f(c_j)+f(V(F))<6.$ Since also whatever the added edge e, we have $f(V(F))\ge 5,$ we deduce that $f(V(F))=5.$ In particular, we have $f(s_1^{\prime })=0,$ $f(s_1)\le 1$ and ${\sum }_{j=1}^{m}f(c_j)=0$. In addition, we note that if $\{u_i,\overline{u_i}\}\subseteq V_2$ or $\{u_i,\overline{u_i}\}\cap V_1\ne \varnothing$ for some i, then $f(H_i)\ge 5$ which leads to the contradiction ${\gamma }_{rI}(G+e)\ge 4n+6$. Thus, $\left|\{u_i,\overline{u_i}\}\cap V_2\right|\le 1$ and $\{u_i,\overline{u_i}\}\cap V_1=\varnothing$ for every $i\in \{1,\dots ,n\}$. Therefore each vertex $c_j$ must have a neighbor in $\{u_i,\overline{u_i}\}$ for some i which is assigned a 2. In this case, let $t:U\to \{T,F\}$ be a mapping defined by (1) $$t(u_i)=\{\begin{array}{cc}T\hfill & \text{if}f(u_i)=2\hfill \\ F\hfill & \text{otherwise}\hfill \end{array}$$(1) for $i\in \{1,\dots ,n\}$. We will show that t is a satisfying truth assignment for $\mathcal{C}$. It is sufficient to show that every clause in $\mathcal{C}$ is satisfied by t. Consider arbitrary clause $C_j\in \mathcal{C}$ for some $j\in \{1,\dots ,m\}$. If $c_j$ is dominated by $u_i$, then $f(u_i)=2$ and so $t(u_i)=T$. If $c_j$ is dominated by $\overline{u_i}$, then $f(\overline{u_i})=2$ and so $t(u_i)=F$ and $t(\overline{u_i})=T$. Hence, in either case the clause $C_j$ is satisfied. The arbitrariness of j shows that all clauses in $\mathcal{C}$ are satisfied by t, that is, $\mathcal{C}$ is satisfiable. This completes the proof of the theorem. ▪

3 Exact values

In this section we determine the restrained Italian reinforcement number of some classes of graphs including paths, cycles and complete p-partite graphs for any integer $p\ge 2$. It is useful to recall some results that we will use later. As observed in [13], for every connected graph G of order $n\ge 2,$ $2\le {\gamma }_{rI}(G)\le n.$A characterization of all connected graphs of order n with ${\gamma }_{rI}(G)\in \{2,3,n\}$ was provided by Samadi et al. [13] as follows.

Proposition 3

([13]).

For any connected graph G of order n, ${\gamma }_{rI}(G)=n$ if and only if $G\in \{K_1,K_{1,n-1}(n\ge 2),C_4,C_5,P_4,P_5,P_6\}$.

Let H be a complete bipartite graph of order $n\ge 3$ with partite sets X and Y, such that $\left|X\right|\le \left|Y\right|,$ $\left|X\right|\in \{1,2\}$ and $\left|Y\right|\ge 2$. Let $\Omega$ be the family of all connected graphs G obtained from H by adding some edges among the vertices in Y such that $\delta (G[Y])\ge 1$.

Proposition 4

([13]).

For any connected graph G of order $n\ge 2$, ${\gamma }_{rI}(G)=2$ if and only if $G\in \Omega \cup \left\{P_2\right\}$.

Let $\Psi$ consist of all graphs G satisfying one of the following:

1. $\Delta (G)=n-1$ and G has a unique vertex of degree one.

2. G is obtained from a graph H with $\delta (H)\ge 1$ by adding two vertices x and y by joining x to all $V(H)$ and joining y to at least one vertex of $V(H)$ but not to all $V(H).$

Finally, for two graphs H and R with $|V(H)|=3$ and $\delta (R)\ge 1$, let G be the graph obtained from H and R by joining each vertex of R to at least two vertices of H so that the resulting graph is connected. Let $\Theta$ be the family of all such resulting graphs G.

Proposition 5

([13]).

For any connected graph G, ${\gamma }_{rI}(G)=3$ if and only if $G\in \Psi \cup (\Theta \setminus \Omega ).$

Moreover, exact values of the restrained Italian domination number have been established by Volkmann [15] for paths, cycles, complete p-partite graphs.

Proposition 6

([15]).

Let $P_n$ be a path of order $n\ge 4$. Then ${\gamma }_{rI}(P_n)=\frac{2n+3+r}{3}$, where $n\equiv r (\text{mod} 3)$ for $r\in \{1,2,3\}$.

Proposition 7

([15]).

Let $C_n$ be a cycle of order $n\ge 3$. Then ${\gamma }_{rI}(C_n)=\frac{2n+3+r}{3}$, when $n\equiv r (\text{mod} 3)$ for $r\in \{1,2\}$ and ${\gamma }_{rI}(C_n)=\frac{2n}{3}$, when $n\equiv 0 (\text{mod} 3)$.

Proposition 8

([15]).

1. ${\gamma }_{rI}(K_{m,n})=4$ for $m,n\ge 2$

2. If $K_{n_1,n_2,\dots ,n_p}$ is the complete p-partite graph such that $p\ge 3$ and $n_1\le n_2\le \cdots \le n_p$, then ${\gamma }_{rI}(K_{1,n_2,\dots ,n_p})={\gamma }_{rI}(K_{2,n_2,\dots ,n_p})=2$ and ${\gamma }_{rI}(K_{n_1,n_2,\dots ,n_p})=3$ for $n_1\ge 3$.

We are now ready to establish the restrained Italian reinforcement number for paths, cycles and complete p-partite graphs.

Proposition 9.

For $n\ge 3$, $r_{rI}$ $(P_n)=1$.

Proof.

Let $P_n:=x_1{x}_2\dots x_n$ and let $n\equiv r (\text{mod} 3)$ for $r\in \{0,1,2\}$. If $n\equiv 0 (\text{mod} 3)$, then the function g defined by $g(x_{3i+1})=2$ for $0\le i\le (n-3)/3$ and $g(x)=0$ otherwise, is an RID-function of $P_n+x_n{x}_{n-2}$ of weight $\frac{2n}{3}.$ If $n\equiv 2 (\text{mod} 3)$, then the function g defined by $g(x_n)=2$, $g(x_{3i+1})=2$ for $0\le i\le (n-5)/3$ and $g(x)=0$ otherwise, is an RID-function of $P_n+x_n{x}_{n-2}$ of weight $\frac{2n+2}{3}.$ Finally, if $n\equiv 1 (\text{mod} 3)$, then the function g defined by $g(x_1)=1$, $g(x_{3i+2})=2$ for $0\le i\le (n-4)/3$ and $g(x)=0$ otherwise, is an RID-function of $P_n+x_n{x}_{n-2}$ of weight $\frac{2n+1}{3}.$ In either case, by Proposition 6, ${\gamma }_{rI}(P_n+x_n{x}_{n-2})<{\gamma }_{rI}(P_n)$ and thus $r_{rI}(P_n)=1.$ ▪

Proposition 10.

For $n\ge 4$, $$r_{rI}(C_n)=\{\begin{array}{cc}2\hfill & \text{if}n\equiv 0 (\text{mod} 3)\hfill \\ 1\hfill & \text{otherwise}.\hfill \end{array}$$

Proof.

Assume that $C_n:=(x_1{x}_2\dots x_n)$ be a cycle on n vertices. If $n\equiv r\hspace{1em}(\mathrm{mod}3)$ where $r\in \{1,2\}$, then by a similar argument to that used in the proof of Proposition 9, we can see that $r_{rI}(C_n)=1$. Hence we assume that $n\equiv 0\hspace{1em}(\mathrm{mod}3)$. First, since the function g defined by $g(x_{n-2})=1$, $g(v_{3i+1})=2$ for $0\le i\le (n-6)/3$ and $g(x)=0$ otherwise, is an RID-function of $C_n+\{x_1{x}_{n-1},x_1{x}_{n-3}\}$ of weight $(2n-3)/3={\gamma }_{rI}(C_n)-1$ (Proposition 7), we deduce that $r_{rI}(C_n)\le 2$.

To prove the inverse inequality, we need only to show that adding an arbitrary edge e cannot decrease ${\gamma }_{rI}(C_n).$ Note that for any edge $e\in \overline{C_n}$, ${\gamma }_{rI}(C_n+e)\le {\gamma }_{rI}(C_n)$. Let e be an arbitrary edge in $\overline{C_n}$ and let f be a ${\gamma }_{rI}(C_n+e)$-function. Assume first that there are three consecutive vertices $x_i,x_{i+1},x_{i+2}$ such that $f(x_i)=f(x_{i+1})=f(x_{i+2})=0$, say for $i=1$. Then the edge e must connect $x_2$ to some vertex assigned 2, say $x_j$, with $j\notin \{1,3\}.$ Moreover, to dominate $x_1$ and $x_3$, we must also have $f(x_4)=f(x_n)=2$. Consider the cycles $C^{\prime }:=(x_2{x}_3\dots x_j)$ of order $j-1$ and $C^{″}:=(x_2{x}_j\dots x_n{x}_1)$ of order $n-j+3.$ Let $j-1\equiv t_1\hspace{1em}(\mathrm{mod}3)$ and $n-j+3\equiv t_2\hspace{1em}(\mathrm{mod}3).$ Notice that $t_1=0$ and $t_2=2;$ $t_1=2$ and $t_2=0$ or $t_1=t_2=1.$ Assume that $j-1\equiv 0\hspace{1em}(\mathrm{mod}3)$ (the case $n-j+3\equiv 0\hspace{1em}(\mathrm{mod}3)$ is similar). Then $n-j+3\equiv 2\hspace{1em}(\mathrm{mod}3),$ and since the restrictions of f on $V(C^{\prime })$ and $V(C^{″})$ are RID-functions, we deduce from Proposition 7, that $$\begin{array}{cc}{\gamma }_{rI}(C_n+e)\hfill & =f(V(C^{\prime }))+f(V(C^{″}))-2\hfill \\ \ge {\gamma }_{rI}(C^{\prime })+{\gamma }_{rI}(C^{″})-2\hfill & \hfill \\ =\frac{2(j-1)}{3}+\frac{2(n-j+3)+3+2}{3}-2\hfill & \hfill \\ =\frac{2n+3}{3}>{\gamma }_{rI}(C_n).\hfill & \hfill \end{array}$$

Assume now that $t_1=t_2=1.$ Then, as above, it follows by Proposition 7 that $$\begin{array}{cc}{\gamma }_{rI}(C_n+e)\hfill & =f(V(C^{\prime }))+f(V(C^{″}))-2\hfill \\ \ge {\gamma }_{rI}(C^{\prime })+{\gamma }_{rI}(C^{″})-2\hfill & \hfill \\ =\frac{2(j-1)+3+1}{3}+\frac{2(n-j+3)+3+1}{3}-2\hfill & \hfill \\ =\frac{2n+6}{3}>{\gamma }_{rI}(C_n).\hfill & \hfill \end{array}$$

In either case, we get a contradiction. Next suppose there are three consecutive vertices $x_i,x_{i+1},x_{i+2}$ such that $f(x_i)+f(x_{i+1})+f(x_{i+2})=1$, say for $i=1$. If $f(x_2)=1$, then $f(x_1)=f(x_3)=0$ and each of $x_1$ and $x_3$ must be adjacent to a vertex assigned 2 as well as to a vertex assigned 0. This is possible only if $e=x_1{x}_3$ and so $G=(C_n+e)-x_2$ is a cycle on $n-1$ vertices, where the restriction of f to G is an RID-function. It follows that ${\gamma }_{rI}(C_n+e)=f(V(G))+1\ge {\gamma }_{rI}(G)+1,$ and by Proposition 7, we obtain ${\gamma }_{rI}(C_n+e)\ge \frac{2(n-1)+3+2}{3}+1>{\gamma }_{rI}(C_n)$, a contradiction Hence we can assume that $f(x_2)=0$. Without loss of generality, let $f(x_1)=1$ and $f(x_3)=0$. To dominate $x_2$, the edge e must connect $x_2$ to a vertex with a positive weight, say $x_j$, such that $j\ne 1.$ Likewise for $x_3$ we must have $f(x_4)=2$. Now, consider the cycles $C^{\prime }:=(x_2{x}_3\dots x_j)$ of order $j-1$ and the path $P^{\prime }:=x_j\dots x_n{x}_1$ of order $n-j+2.$ Let $j-1\equiv t_1\hspace{1em}(\mathrm{mod}3)$ and $n-j+2\equiv t_2\hspace{1em}(\mathrm{mod}3).$ Notice that $t_1=0$ and $t_2=1;$ $t_1=1$ and $t_2=3$ or $t_1=t_2=2.$ Notice also that the restrictions of f on $V(C^{\prime })$ and $V(P^{\prime })$ are RID-functions, and thus ${\gamma }_{rI}(C_n+e)=f(V(C^{\prime }))+f(V(P^{\prime }))-2\ge {\gamma }_{rI}(C^{\prime })+{\gamma }_{rI}(P^{\prime })-2.$ Now using Propositions 7 and 6, we get as before a contradiction. Finally, let $f(x_i)+f(x_{i+1})+f(x_{i+2})\ge 2$ for each $1\le i\le n$ where the sum in indices is taken modulo n. Then we have $${\gamma }_{rI}(G+e)=\frac{1}{3}\sum _{i=1}^n(f(x_i)+f(x_{i+1})+f(x_{i+2}))\ge \frac{2n}{3}={\gamma }_{rI}(G).$$

Thus ${\gamma }_{rI}(G+e)={\gamma }_{rI}(G).$ Consequently, $r_{rI}(C_n)=2$, and the proof is complete. ▪

Proposition 11.

For integers $1\le p\le q$, $$r_{rI}(K_{p,q})=\{\begin{array}{ccc}1\hfill & \text{if}\hfill & p=1,2,3.\hfill \\ p-2\hfill & \text{if}\hfill & p\ge 4.\hfill \end{array}$$

Proof.

Let $X=\{u_1,u_2,\dots ,u_p\}$ and $Y=\{v_1,v_2,\dots ,v_q\}$ be the partite sets of $K_{p,q}$. If $p=1$, then the function g defined by $g(u_1)=2$, $g(v_1)=g(v_2)=0$ and $g(x)=1$ otherwise, is an RID-function of $K_{1,q}+v_1{v}_2$ of weight $n-1$ and we deduce from Proposition 3 that $r_{rI}(K_{1,q})=1$. If $p=2$, then the function g defined by $g(u_1)=2$ and $g(x)=0$ otherwise, is an RID-function of $K_{2,q}+u_1{u}_2$ of weight 2 and we conclude from Proposition 8 that $r_{rI}(K_{2,q})=1$. If $p=3$, then the function g defined by $g(u_1)=2,g(u_2)=1$ and $g(x)=0$ otherwise, is an RID-function of $K_{3,q}+u_1{u}_3$ of weight 2 and by Proposition 8, we have $r_{rI}(K_{3,q})=1$.

Let $p\ge 4$. First we observe that the function g defined by $g(u_1)=2,g(u_2)=1$ and $g(x)=0$ otherwise, is an RID-function of $K_{p,q}+\{u_1{u}_i\mid 3\le i\le p\}$ of weight 3 and thus by Proposition 8, $r_{rI}(K_{p,q})\le p-2$. We next show that $r_{rI}(K_{p,q})\ge p-2$. Let F be an $r_{rI}(K_{p,q})$-set. Then $2\le {\gamma }_{rI}(K_{p,q}+F)\le 3$. If ${\gamma }_{rI}(K_{p,q}+F)=2$, then by Proposition 4 we must have $\Delta (K_{p,q}+F)\ge p+q-2$ and this implies that $\left|F\right|\ge p-2$. Hence assume that ${\gamma }_{rI}(K_{p,q}+F)=3$. By Proposition 5, $K_{p,q}+F\in \Psi \cup (\Theta \setminus \Omega )$. If $K_{p,q}+F\in \Psi$, then $\Delta (K_{p,q}+F)\ge p+q-2$ and thus $\left|F\right|\ge p-2$. Hence suppose that $K_{p,q}+F\in \Theta \setminus \Omega$ and let x, y, z be the vertices of H (see the construction of graphs in Family $\Theta$). If $|X\cap \{x,y,z\left\}\right|=3$ (the case $|Y\cap \{x,y,z\left\}\right|=3$ is similar), then each vertex in $X-\{x,y,z\}$ must be adjacent to at least to two vertices in $\{x,y,z\}$ implying that $\left|F\right|\ge 2(p-3)\ge p-2$. Also, if $|X\cap \{x,y,z\left\}\right|=2$ (the case $|Y\cap \{x,y,z\left\}\right|=2$ is similar), then each vertex in $X-\{x,y,z\}$ must be adjacent to at least to one vertex in $\{x,y,z\}$ implying that $\left|F\right|\ge p-2$. In any case, we conclude that $r_{rI}(K_{3,q})=p-2$ and the proof is complete. ▪

Proposition 12.

Let $K_{n_1,n_2,\dots ,n_p}$ be the complete p-partite graph such that $p\ge 3$ and $3\le n_1\le n_2\le \dots \le n_p$. Then $r_{rI}(K_{n_1,n_2,\dots ,n_p})=n_1-1$.

Proof.

Let $X_1=\{u_1,\dots ,u_{n_1}\}$, $X_2=\{v_1,\dots ,v_{n_2}\},\dots ,X_p$ be the partite sets of $K_{n_1,n_2,\dots ,n_p}$. Assume F is an $r_{rI}(K_{n_1,n_2,\dots ,n_p})$-set. Then ${\gamma }_{rI}(K_{n_1,n_2,\dots ,n_p}+F)=2$, and by Proposition 4 we must have $\Delta (K_{n_1,n_2,\dots ,n_p}+F)\ge n_1+\dots +n_p-2$ implying that $\left|F\right|\ge n_1-1$. On the other hand, the function g defined by $f(u_1)=f(v_1)=1$ and $f(x)=0$ otherwise, is an RID-function of $K_{n_1,n_2,\dots ,n_p}+\{u_i{u}_1\mid 2\le i\le n_1\}$ yielding $r_{rI}(K_{n_1,n_2,\dots ,n_p})\le \left|F\right|=n_1-1$. Consequently, $r_{rI}(K_{n_1,n_2,\dots ,n_p})=n_1-1$. ▪

4 Sufficient conditions for graphs G to have small $r_{rI}(G)$

In this section, we study graphs with small restrained Italian reinforcement number. We begin with the following lemma.

Lemma 13.

If G is a connected graph of order $n\ge 3$ with ${\gamma }_{rI}(G)=n$, then $r_{rI}(G)=1$.

Proof.

By Proposition 3, $G\in \{K_{1,n-1}(n\ge 3),C_4,C_5,P_4,P_5,P_6\}$. If G is a star $K_{1,n-1}(n\ge 3)$ with center u and leaves $u_1,\dots ,u_{n-1}$, then the function g defined by $g(u)=2$, $g(u_1)=g(u_2)=0$ and $g(x)=1$ otherwise, is an RID-function of $G+\left\{u_1{u}_2\right\}$ of weight $n-1$. Therefore ${\gamma }_{rI}(G)=1$. If $G\in \{C_4,C_5,P_4,P_5,P_6\}$, then the desired result follows from Propositions 9 and 10. ▪

Proposition 14.

Let G be a connected graph of order $n\ge 3$ with ${\gamma }_{rI}(G)\ge 3$. Then $r_{rI}(G)=1$ if and only if ${\gamma }_{rI}(G)=n$ or G has a function $f=(V_0,V_1,V_2)$ of weight less than ${\gamma }_{rI}(G)$ such that one of the following conditions holds.

1. $G[V_0]$ has at most two isolated vertices and $\sum _{x\in N(v)}f(x)\ge 2$ for each vertex $v\in V_0$.

2. $G[V_0]$ has no isolated vertices and there is exactly one vertex $v\in V_0$ such that either $\sum _{x\in N(v)}f(x)\le 1$ if $V_2\ne \varnothing$ or $\sum _{x\in N(v)}f(x)=1$ if $V_2=\varnothing$.

Proof.

If ${\gamma }_{rI}(G)=n$, then by Lemma 13 we have $r_{rI}(G)=1$. Hence suppose that ${\gamma }_{rI}(G)<n$, and let $f=(V_0,V_1,V_2)$ be a function on G with weight less than ${\gamma }_{rI}(G)$ satisfying (i) or (ii). Since $\omega (f)\le n-2$, we have $\left|V_0\right|\ge 2$. If $\left|V_2\right|\ge 1$, then let $u\in V_2$ and if $V_1\ne \varnothing$, then let $V_1=\{w_1,\dots ,w_t\}$. Now, if (ii) holds and $V_2\ne \varnothing$, then f is an RID-function of $G+uv$, while if (ii) holds and $V_2=\varnothing$, then we may assume that $w_1\notin N(v)$ and so f is an RID-function of $G+w_{1}v$. Assume now that (i) holds. If $G[V_0]$ has two isolated vertices w, v, then f is an RID-function of $G+\left\{wv\right\}$ and if $G[V_0]$ has exactly one isolated vertex, say w, then f is an RID-function of $G+\left\{wz\right\}$, where z is any vertex in $V_0-\left\{w\right\}$. Hence in either case $r_{rI}(G)=1$.

Conversely, let $r_{rI}(G)=1$ and suppose that $\left\{uv\right\}$ is an $r_{rI}(G)$-set. If ${\gamma }_{rI}(G)=n$, then we are done. Hence assume that ${\gamma }_{rI}(G)\le n-1$ and let f be a ${\gamma }_{rI}(G+\{uv\})$-function. Notice that vertices u and v cannot be assigned both positive value under f (otherwise, f is an RID-function of G). Without loss of generality, assume that $f(u)=0$. If $f(v)=0$, then f satisfies (i). Hence assume that $f(v)\ge 1$. If $\sum _{x\in N_G(u)}\ge 2$, then f is an RID-function of G. Hence $\sum _{x\in N_G(u)}f(x)\le 1$. If $f(v)=2$, then clearly f satisfies (ii). Assume that $f(v)=1$. Then we deduce from $2\le \sum _{x\in N_{G+uv}(u)}=f(v)+\sum _{x\in N_G(u)}f(x)\le 2$ that $\sum _{x\in N_G(u)}f(x)=1$ and thus f satisfies (ii). This completes the proof. ▪

Proposition 15.

Let G be a connected graph of order $n\ge 3$ with ${\gamma }_{rI}(G)\ge 3$ having a ${\gamma }_{rI}(G)$-function $f=(V_0,V_1,V_2)$ such that $\left|V_1\right|=1$. Then $r_{rI}(G)\le 1$.

Proof.

If ${\gamma }_{rI}(G)=n$, then by Lemma 13, we have $r_{rI}(G)=1$. Thus suppose that ${\gamma }_{rI}(G)<n.$ Then $V_0\ne \varnothing .$ Let f be a ${\gamma }_{rI}(G)$-function such that $\left|V_1\right|=1$. Let $V_1^f=\left\{v\right\}$ and let $N(v)=\{v_1,\dots ,v_t\}$. Notice that because of $\left|V_1\right|=1,$ for each i, either $f(v_i)=2$ or $v_i$ has a neighbor assigned 2. If $f(v_i)=2$ for some i, then no edge join v to $V_0$ and thus for any $w\in V_0$ the function g defined on $G+\left\{vw\right\}$ by $g(v)=0$ and $g(x)=f(x)$ otherwise, is an RID-function of $G+\left\{wv\right\}$ of weight $\omega (f)-1$. Hence we can assume that no $v_i$ is assigned 2. In that case, for any $w\in V_2$ the function g defined on $G+\left\{vw\right\}$ by $g(v)=0$ and $g(x)=f(x)$ otherwise, is an RID-function of $G+\left\{wv\right\}$ of weight $\omega (f)-1$. Therefore, in either case we have $r_{rI}(G)=1$. ▪

Proposition 16.

Let G be a connected graph of order $n\ge 3$ with ${\gamma }_{rI}(G)\ge 3$. If $\delta (G)=1$, then $r_{rI}(G)\le 3$.

Proof.

Clearly, if ${\gamma }_{rI}(G)=n$, then the result is immediate by Lemma 13. Hence we assume that ${\gamma }_{rI}(G)<n$, and let $f=(V_0,V_1,V_2)$ be a ${\gamma }_{rI}(G)$-function. Note that $V_0\ne \varnothing$ because ${\gamma }_{rI}(G)<n$. Let u be a support vertex of G and $u_1,\dots ,u_t$ be the leaf neighbors of u. By definition we have $f(u_i)\ge 1$ for each $i=1,\dots ,t$. Let $w\in V_0-\left\{u\right\}$. If $f(u)=2$, then the function g defined on $G+w{u}_1$ by $g(u_1)=0$ and $g(x)=f(x)$ otherwise, is an RID-function of $G+w{u}_1$ with weight $\omega (f)-1$. Hence assume that $f(u)=1$. Since G is not a star, there is a vertex v with positive label such that $v\notin \{u,u_1,\dots ,u_t\}$. Define the function g on $G+\{w{u}_1,v{u}_1\}$ by $g(u_1)=0$ and $g(x)=f(x)$ otherwise. Clearly, g is an RID-function of $G+\{w{u}_1,v{u}_1\}$ with weight $\omega (f)-1$. Finally let $f(u)=0$. If $f(u_1)=2$, then the function g defined on $G+uz$, where $z\in (V_1\cup V_2)-\left\{u_1\right\}$, by $g(u_1)=1$ and $g(x)=f(x)$ otherwise, is an RID-function of $G+\left\{uz\right\}$ with weight $\omega (f)-1$. Assume that $f(u_1)=1$. Then u has a neighbor v other than $u_1$ with $f(v)\ge 1$. If $f(v)=2$, then the function g on $G+\left\{v{u}_1\right\}$ defined by $g(u_1)=0$ and $g(x)=f(x)$ otherwise, is an RID-function of $G+\left\{v{u}_1\right\}$ with weight $\omega (f)-1$. Hence let $f(v)=1$. Since $\left|V_0\right|\ge 2$ and $d_G(u_1)=1$, $(V_1\cup V_2)-\{u_1,v\}$ is not empty. Let $v^{\prime }\in (V_1\cup V_2)-\{u_1,v\}$. Then the function g defined above is an RID-function on the graph G by adding to it the edges $v{u}_1,u_1{v}^{\prime }$ and possibly the edge $u{v}^{\prime }$ (if it does not exist). Consequently, $r_{rI}(G)\le 3$. ▪

Proposition 17.

Let G be a connected graph of order $n\ge 3$ with ${\gamma }_{rI}(G)\ge 3$. If G has at least two leaves, then $$r_{rI}(G)\le 2.$$

This bound is sharp for a double star $D{S}_{p,q}(q\ge p\ge 3)$.

Proof.

If ${\gamma }_{rI}(G)=n$, then the result follows from Lemma 13. Hence, we assume that ${\gamma }_{rI}(G)<n$, and let $f=(V_0,V_1,V_2)$ be a ${\gamma }_{rI}(G)$-function. Clearly, $V_0\ne \varnothing$. Let $w\in V_0$, and let $u_1$ and $v_1$ be two leaves of G whose support vertices are u and v, respectively (possibly $u=v$). By definition $f(u_1),f(v_1)\ge 1$. If $f(u)\ge 1$ (the case $f(v)\ge 1$ is similar), then the function g defined on $G+\{u_1{v}_1,u_{1}w\}$ by $g(u_1)=0$ and $g(x)=f(x)$ otherwise, is an RID-function of $G+\{u_1{v}_1,u_{1}w\}$ of weight $\omega (f)-1$. Hence, assume that $f(u)=f(v)=0$. Since G is not a star, we have $(V_1\cup V_2)-\{u_1,v_1\}\ne \varnothing$. Let $z\in (V_1\cup V_2)-\{u_1,v_1\}$. Define the function g on $G+\{u_{1}z,v_{1}z\}$ by $g(z)=\min \{2,f(z)+1\}=2$, $g(u_1)=g(v_1)=0$ and $g(x)=f(x)$ otherwise. Clearly, g is an RID-function of $G+\{u_{1}z,v_{1}z\}$ with weight $\omega (f)-1$. Therefore, in either case we have $r_{rI}(G)\le 2$. ▪

Corollary 18 .

For any tree T of order $n\ge 3$, $r_{rI}(T)\le 2.$

We know that $r_{rI}(P_2)=0$ and $r_{rI}(T)=1$ if T is a tree of order at least three belonging to $\{K_{1,n-1},P_4,P_5,P_6\}.$ It would be very interesting to characterize all trees T such that $r_{rI}(T)=1.$

5 Bounds on $r_{rI}(G)$

In this section, we present basic properties of the retrained Italian reinforcement number and derive some sharp upper bounds for this parameter. For any ${\gamma }_{rI}(G)$-function f and a vertex $v\in V_1\cup V_2$, we denote the set of vertices u in $N(v)\cap V_0$ with $\sum _{x\in N(u)}f(x)=2$ by $N_{ϵ}(v)$. Set $ϵ(v)=|N_{ϵ}(v)|$.

Proposition 19.

Let G be a connected graph of order $n\ge 4$ with ${\gamma }_{rI}(G)\ge 3.$ If $f=(V_0,V_1,V_2)$ is a ${\gamma }_{rI}(G)$-function with $V_2\ne \varnothing$, then $$r_{rI}(G)\le \min \{ϵ(v)\mid v\in V_2\}.$$

Proof.

Let $f=(V_0,V_1,V_2)$ be a ${\gamma }_{rI}(G)$-function with $V_2\ne \varnothing$. If $ϵ(v)=0$ for some vertex $v\in V_2,$ then reassigning v the value 1 instead of 2 provides an RID-function of weight less than ${\gamma }_{rI}(G)$ which leads to a contradiction. Hence $ϵ(v)\ge 1$ for every $v\in V_2.$ Let u be a vertex in $V_2$ such that $ϵ(u)=\min \{ϵ(v)\mid v\in V_2\}$ and let $N_{ϵ}(u)=\{u_1,\dots ,u_{ϵ}\}$. Since ${\gamma }_{rI}(G)\ge 3$, there exits a vertex $w\in (V_1\cup V_2)-\left\{u\right\}$. Let $F=\{wx\mid x\in N_{ϵ}(u)\}$ and define the function g by $g(u)=1$ and $g(x)=f(x)$ otherwise. Clearly, g is an RID-function of $G+F$ of weight less than ${\gamma }_{rI}(G)$ and so $r_{rI}(G)\le \min \{ϵ(v)\mid v\in V_2\}$. ▪

We observe that for any ${\gamma }_{rI}(G)$-function $f=(V_0,V_1,V_2)$, every vertex u of $V_2$ can have at most $d_G(u)$ neighbors in $V_0$. Whence the following corollary.

Corollary 20.

Let G be a connected graph with ${\gamma }_{rI}(G)\ge 3$ and $f=(V_0,V_1,V_2)$a ${\gamma }_{rI}(G)$-function with $\left|V_2\right|\ge 1$. Then $r_{rI}(G)\le \Delta .$

Proposition 21.

Let G be a connected graph with ${\gamma }_{rI}(G)\ge 3$ containing a path $v_1{v}_2{v}_3{v}_4{v}_5$ in which $d_G(v_i)=2$ for $i\in \{2,3,4\}$. Then $r_{rI}(G)\le 2$.

Proof.

If ${\gamma }_{rI}(G)=n$, then the result is immediate from Lemma 13. Hence, we assume that ${\gamma }_{rI}(G)<n$, and let $f=(V_0,V_1,V_2)$ be a ${\gamma }_{rI}(G)$-function. If $2\in \{f(v_2),f(v_3),f(v_4)\}$, then the result follows from Proposition 19. Hence, we assume that $2\notin$ $\{f(v_2),f(v_3),f(v_4)\}$. This implies that $f(v_3)\ne 0$, and thus $f(v_3)=1$. Therefore, $f(v_2)=f(v_4)=1$, because $d_G(v_2)=d_G(v_4)=2$. Define the function g by $g(v_3)=0$ and $g(x)=f(x)$ otherwise. It is easy to see that for any $w\in V_0$, g is an RID-function on $G+v_{3}w$ of weight $\omega (f)-1$. In either case, $r_{rI}(G)\le 2$. ▪

Proposition 22.

Let G be a connected graph of order $n\ge 4$ with ${\gamma }_{rI}(G)\ge 3$ and let $f=(V_0,V_1,V_2)$a ${\gamma }_{rI}(G)$-function with $V_1\ne \varnothing$. Then $$r_{rI}(G)\le 2+\min \{ϵ(v)\mid v\in V_1\}.$$

Proof.

Let $f=(V_0,V_1,V_2)$ be a ${\gamma }_{rI}(G)$-function with $V_1\ne \varnothing$. If ${\gamma }_{rI}(G)=n$, then the result follows from Lemma 13. Hence we assume that ${\gamma }_{rI}(G)<n$. Clearly, $V_0\ne \varnothing$. Let $v\in V_0$, and let u be a vertex in $V_1$ such that $ϵ(u)=\min \{ϵ(w)\mid w\in V_1\}.$ Let $N_{ϵ}(u)=\{u_1,\dots ,u_{ϵ}\}$ when $ϵ(u)\ge 1$ and let $V_1-\left\{u\right\}=\{z_1,\dots ,z_k\}$.

First assume that $N(u)\cap V_0=\varnothing$. If $V_2\ne \varnothing$ and $w\in V_2$, then consider the function g defined by $g(u)=0$ and $g(x)=f(x)$ otherwise. One can check that g has weight $\omega (f)-1$ and it is an RID-function on the graph $G^{\prime }$ obtained from G by adding the edge vu and possibly the edge uw if $uw\notin E(G).$ Hence we can assume that $V_2=\varnothing$. Now, if $\sum _{x\in N(u)}f(x)\ge 2$, then the function g defined on $G+\left\{vu\right\}$ by $g(u)=0$ and $g(x)=f(x)$ otherwise, is an RID-function of weight $\omega (f)-1$. Moreover, if $\sum _{x\in N(u)}f(x)=0$, then the function g defined on $G+\{z_{1}u,z_{2}u\}$ by $g(u)=0$ and $g(x)=f(x)$ otherwise, is an RID-function of weight $\omega (f)-1$. Finally, if $\sum _{x\in N(u)}f(x)=1$, then since ${\gamma }_{rI}(G)\ge 3$, there is a vertex $z\in V-N[u]$ with $f(z)=1$. In this case, the function g defined on $G+\{vu,zu\}$ by $g(u)=0$ and $g(x)=f(x)$ otherwise, is an RID-function of weight $\omega (f)-1$. All of the above situations lead to $r_{rI}(G)\le 2,$ and the result is valid.

For the sequel, we can assume that $N(u)\cap V_0\ne \varnothing$. If $V_2\ne \varnothing$ and $w\in V_2$, then the function g defined on $G_1=G+\{w{u}_1,\dots ,w{u}_{ϵ},wu\}$ by $g(u)=0$ and $g(x)=f(x)$ otherwise, is an RID-function of $G_1$ of weight $\omega (f)-1$. Hence assume that $V_2=\varnothing$. Since ${\gamma }_{rI}(G)\ge 3$, we have $\left|V_1\right|\ge 3$ and thus for any vertex $u_i$, there exists a vertex $u_i^{\prime }\in V_1$ such that $u_i{u}_i^{\prime }\notin E(G)$. Now, if $\sum _{x\in N(u)}f(x)\ge 2$, then the function g on $G_2=G+\{u_i{u}_i^{\prime }\mid 1\le i\le ϵ(u)\}$ defined by $g(u)=0$ and $g(x)=f(x)$ otherwise, is an RID-function of $G_2$ of weight $\omega (f)-1$. If $\sum _{x\in N(u)}f(x)=0$, then the function g on $G_3=G+\{z_{1}u,z_{2}u,u_i{u}_i^{\prime }\mid 1\le i\le ϵ(u)\}$ by $g(u)=0$ and $g(x)=f(x)$ otherwise, is an RID-function of $G_3$ of weight $\omega (f)-1$. Finally, assume that $\sum _{x\in N(u)}f(x)=1$. Without loss of generality, assume that $z_2\notin N[u]$ and let $F=\{z_{2}u,u_i{u}_i^{\prime }\mid 1\le i\le ϵ(u)\}.$ By defining the function g on $G+F$ as before, we can see that g is an RID-function of $G+F$ of weight $\omega (f)-1$. Consequently, in either case we get $r_{rI}(G)\le ϵ(u)+2=2+\min \{ϵ(v)\mid v\in V_1\}$. This completes the proof. ▪

Applying Propositions 19 and 22 we obtain the next result.

Corollary 23.

For any graph G of order $n\ge 4$, we have $$r_{rI}(G)\le \lfloor \frac{n}{2}\rfloor .$$

Moreover, the bound is sharp.

Proof.

It suffices to show $r_{rI}(G)\le \frac{n}{2}$. If ${\gamma }_{rI}(G)=2$, then $r_{rI}(G)=0$ and the result is valid. If ${\gamma }_{rI}(G)=n$, then by Lemma 13, $r_{rI}(G)=1$ and the desired result follows. Hence we assume that $3\le {\gamma }_{rI}(G)<n$, and let $f=(V_0,V_1,V_2)$ be a ${\gamma }_{rI}(G)$-function. Assume first that $\left|V_2\right|\ge 1$. If $ϵ(u)\le \frac{n}{2}$ for some $u\in V_2$, then the result is immediate by Proposition 19. Hence we assume that $ϵ(u)\ge \frac{n}{2}+1$ for each $u\in V_2$. It follows that $\left|V_2\right|=1$ and $V_1\ne \varnothing$ (since ${\gamma }_{rI}(G)\ge 3$). Let $V_2=\left\{u\right\}$ and $v\in V_1$. One can easily seen that $ϵ(v)\le \frac{n}{2}-3$ and the result follows from Proposition 22.

Assume now that $V_2=\varnothing$. Then $\left|V_1\right|\ge 3$. Let $V_1=\{v_1,\dots ,v_t\}$. If $ϵ(u)\le \frac{n}{2}-2$ for some $u\in V_1$, then the result is immediate by Proposition 22. Hence we assume that $ϵ(v_i)\ge \frac{n}{2}-1$ for each $u\in V_1$. Let $V_0^{\prime }={\cup }_{i=1}^t{N}_{ϵ}(v_i)$. Since each vertex in $V_0^{\prime }$ is adjacent to exactly two vertices in $V_1$, we conclude that $$2(n-|V_1|)=2\left|V_0\right|\ge 2\left|V_0^{\prime }\right|\ge (\frac{n}{2}-1)\left|V_1\right|,$$and this implies that $\left|V_1\right|\le 3$. Thus $\left|V_1\right|=3$. Since $ϵ(v_1)\ge \frac{n}{2}-1$, we have $|V(G)-N[v_1]|\le \frac{n}{2}$. Let $F=\{v_{1}x\mid x\in V(G)-N[v_1]\}$. Clearly, ${\gamma }_{rI}(G)=2$ and thus $r_{rI}(G+F)\le \frac{n}{2}$.

To show the sharpness, consider the graph G illustrated in Figure 4. It is easy to see that ${\gamma }_{rI}(G)=3$ and the function f on G defined by $f(u)=f(v)=f(w)=1$ and $f(x)=0$ otherwise, is the only ${\gamma }_{rI}(G)$-function. We deduce from Corollary 23 that $r_{rI}(G)\le 4=\lfloor \frac{n}{2}\rfloor$. Now let F be an $r_{rI}(G)$-set. Then ${\gamma }_{rI}(G+F)=2$ and so $G\in \Omega$ (see Proposition 4). If $X=\left\{x\right\}$ then we must have $d_{G+F}(x)=8$ that implies $\left|F\right|\ge 4$. If $X=\{x,y\}$, then we must have $d_{G+F}(x),d_{G+F}(y)=7$ implying that $\left|F\right|\ge 6$. Thus $\left|F\right|\ge 4=\lfloor \frac{n}{2}\rfloor$. Consequently, $r_{rI}(G)=4=\lfloor \frac{n}{2}\rfloor$. ▪

Figure 4: A graph G with $r_{rI}(G)=\Delta +2$.

Corollary 24.

For any graph G of order $n\ge 3$ with ${\gamma }_{rI}(G)\ge 3$, we have $$r_{rI}(G)\le \Delta +2.$$

The equality holds only if $\left|V_1\right|=\frac{2n}{\Delta +2}$. Moreover, this bound is sharp.

Proof.

The bound is trivial by Propositions 19 and 22. Now let the equality hold and let $f=(V_0,V_1,V_2)$ be a ${\gamma }_{rI}(G)$-function. If $\left|V_2\right|\ge 1$, then by Proposition 19 we have $r_{rI}(G)\le \Delta$, a contradiction. Hence we assume that $V_2=\varnothing$. If there is a vertex $u\in V_1$ such that $ϵ(u)<\Delta$, then Proposition 22 leads to $r_{rI}(G)\le \Delta +1$, a contradiction again. Therefore, $ϵ(u)=\Delta$ for each $u\in V_1$. This implies that every vertex assigned 0 is adjacent to exactly two vertices in $V_1$. By double counting the edges between $V_1$ and $V_0$ we get $\left|V_1\right|\Delta =2(n-|V_1|)$ or equivalently ${\gamma }_{rI}(G)=\left|V_1\right|=\frac{2n}{\Delta +2}$.

To show the sharpness of the bound, consider the graph G depicted in Figure 4. Clearly, G is a cubic graph of order 10 with ${\gamma }_{rI}(G)=4$ (for instance, the function f defined by $f(x_i)=1$ for $i=1,2,3,4$, and $f(x)=0$ otherwise, is a ${\gamma }_{rI}(G)$-function). Now let F be an $r_{rI}(G)$-set, and let $g=(V_0,V_1,V_2)$ be a ${\gamma }_{rI}(G+F)$-function. If $V_2\ne \varnothing$ and $u\in V_2$, then u must dominate all vertices in $V_0$, that is $d_{G+F}(u)\ge 8$ which yields $\left|F\right|\ge 5=\Delta +2$. Hence let $V_2=\varnothing$. Then we have $\left|V_1\right|\le 3$ and thus we have at least 14 edges between $V_1$ and $V_2.$ Since G is cubic, we deduce that $\left|F\right|\ge 5=\Delta +2$. Therefore $r_{rI}(G)=\left|F\right|\ge \Delta +2$, and the equality follows from Corollary 24. ▪