?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.Abstract
For a graph with
and
, a perfect double Italian dominating function is a function
having the property that
, for every vertex
with
. The weight of a perfect double Italian dominating function f is the sum
and the minimum weight of a perfect double Italian dominating function on G is the perfect double Italian domination number
of G. We initiate the study of perfect double Italian dominating functions. We check the
of some standard graphs and evaluate with γdI of such graphs. The perfect double Italian dominating functions versus perfect double Roman dominating functions are perused. The NP-completeness of this parameter is verified even when it is restricted to bipartite graphs. Finally, we characterize the graphs G of order n with
.
2010 Mathematics Subject Classification:
1 Introduction
Throughout this paper, we suppose that, G is a simple finite graph with vertex set and edge set
. We use [Citation23] as a reference for terminologies and notations which are not explicitly defined here. Let
be a graph. For
, we use the notation
to denote u and v are adjacent. The open neighborhood of a vertex
is the set
G
. The closed neighborhood of a vertex
is
. The open neighborhood of a set
is the set
. The closed neighborhood of a set
is the set
. Also when we write
, we mean the set
. We denote the degree of v by
. By
and
, we denote the maximum degree and minimum degree of a graph G, respectively. The distance between two vertices u and v is denoted by d(u, v). We write Kn, Pn and Cn for the complete graph, path and cycle of order n, respectively (see [Citation23]).
A vertex is pendant if it is of degree one. An edge is said to be pendant if one of its vertices is a pendant vertex. For a graph G, when we use the notation G + e, we mean that e is added as an edge to the G with the end points in G. Let G be a graph with . The Mycielski graph
of G is a simple graph with vertices
where
is an independent set, N(w) = U and
[Citation23]. In this section we show that conjecture 3 is true for the families of Mycielski graphs.
A set in a graph G is called a dominating set if
. The domination number
of G is the minimum cardinality of a dominating set in G, and a dominating set of G of cardinality
is called a γ-set of G. A dominating set S of a graph G is called a perfect dominating set if each vertex of G – S is dominated by exactly one vertex in S. The minimum cardinality of a perfect dominating set of G is the perfect domination number
. Perfect domination number and several variations on perfect dominating sets have received much attention in the literature; see some discussions in [Citation12], or see the survey in [Citation16].
Given a graph G and a positive integer , assume that
is a function, and suppose that
is the ordered partition of V induced by g, where
for
. So we can write
.
A Roman dominating function (an RDF) on G is a function such that if f(v) = 0 for some
, then there exists a vertex
for which f(w) = 2. The weight of a Roman dominating function is the sum
, and the minimum weight of a Roman dominating function on a graph G is called the Roman domination number of G, denoted by
[Citation7, Citation12, Citation21].
Already, some researchers worked on perfect Roman dominating set, for example see [Citation8, Citation15, Citation19]. As defined in [Citation15] a function is called a perfect Roman dominating function (or briefly, PRDF) if every vertex
is adjacent to exactly one vertex v for which
. The minimum weight of any PRDF of G is called the perfect Roman domination number
of G.
An Italian dominating function (Roman {2}-dominating function) is a function such that for every vertex
, with f(v) = 0, either there is at leaset one vertex
with f(u) = 2, or there are at least two vertices
with
, see [Citation6, Citation14].
Recently, Haynes et al [Citation13], introduced the concept of perfect Italian domination in graphs and trees and this concept was further discussed in [Citation4, Citation22].
As defined [Citation4, Citation13], a perfect Italian dominating function (PID-function) of a graph G is a function satisfying the condition that for every v in V with f(v) = 0, we have
. The perfect Italian domination number of G denoted
is the minimum weight of a PID-function of G.
Beeler et al. [Citation5] have defined double Roman domination as follows.
A double Roman dominating function (abbreviated DRD-function) on a graph G is a function such that the following conditions are met:
if f(v) = 0, then vertex v must have at least two neighbors in V2 or one neighbor in V3.
if f(v) = 1, then vertex v must have at least one neighbor in
.
The weight of a double Roman dominating function f on G is the sum , and the minimum weight of wf for every double Roman dominating function f on G is called double Roman domination number of G. We denote this number with
and a double Roman dominating function of G with weight
is called a
-function of G, see also [Citation11, Citation17].
The concept of perfect double Roman dominating function of a graph G, abbreviated PDRD-function, is introduced in [Citation10]. As defined in [Citation10], a function is a perfect double Roman dominating function (PDRD-function) if it is a DRD-function on G and if f(u) = 0, then u is either adjacent to exactly two vertices in V2 and no vertex in V3 or adjacent to exactly one vertex in V3 and no vertex in V2, and if f(u) = 1, then u is adjacent to exactly one vertex in V2 and no vertex in V3. The perfect double Roman domination number, denoted
, is the minimum weight of a PDRD-function of G.
Recently, Mojdeh and Volkmann [Citation18] defined double Italian (Roman {3}-)dominating functions as follows:
For a graph G, a double Italian (Roman {3}-)dominating function is a function having the property that for every vertex
, if
, then
. Formally, a double Italian dominating function
has the property that for every vertex
, with f(v) = 0, there exist at least either three vertices in
or one vertex in
and one vertex in
or two vertices in
or one vertex in
and for every vertex
, with f(v) = 1, there exist at least either two vertices in
or one vertex in
. The weight of a double Italian dominating function is the sum
, and the minimum weight of a double Italian dominating function f is the double Italian domination number, denoted by
, see also [Citation2, Citation3, Citation20].
Now we define a variant of perfect (Roman, Italian, double Roman) dominating function, namely, perfect double Italian dominating function (or perfect Roman {3}-dominating function). Hereafter we use the double Italian instead of Roman {3} and perfect double Italian instead of perfect Roman {3}. Also, by of G, we mean the perfect double Italian domination number of a graph G.
Definition 1.
A perfect double Italian dominating function (abbreviated, PDIDF or PDID-function) is a function having the property that,
for any vertex
, if f(v) = 0, then v is either adjacent to at least 3 and at most 4 vertices in V1 and no vertex in
, or is adjacent to at least 1 vertex and at most 2 vertices in V1 and exactly one vertex in V2 and no vertex in V3, or is adjacent to at most one vertex in V1 and exactly one vertex in V3 and no vertex in V2, or is adjacent to two vertices in V2 and no vertex in
, and
if f(v) = 1, then v either is adjacent to at least 2 vertices and at most 3 vertices in V1 and no vertex in
, or is adjacent to at most one vertex of V1 and exactly one vertex in V2 and no vertex in V3, or is adjacent to exactly one vertex in V3 and no vertex in
.
The weight of a perfect double Italian dominating function f is the sum and the minimum weight of a perfect double Italian dominating function on G is the perfect double Italian domination number (abbreviated, PDIDN or PDID number) of G, denoted by
.
We immediately have, for
As we remark on definition of PDIDF and definition of PDRDF, one of the differences between them is the neighborhood of any vertex in . Under any PDRDF, a vertex in V0 (V1) is adjacent to only two vertices of V2 or only one vertex in V3 (only one vertex in V2) while under any PDIDF f, a vertex v in V0 (V1) has the property,
. In addition, for any PDRDF f on a graph G, if
for vertex
, then f is a PDIDF on G. There are several examples of graphs G for which
. For instance consider cycles Cn for
([Citation1] and Observation 3). Also see Theorem 9 for other such examples.
We proceed as follows. In Section 2, we present some known results on the PDID number and show that for a family of graphs G. In Section 3, the PDID versus PDRD are studied. By patterning the paper [Citation1] for NP-completeness, we show that PDID is NP-complete even when restricted to bipartite graphs in Section 4. Finally, we characterize the graph G of order n with
in Section 5.
2 Specific values of perfect double Italian domination
In this section, we study the of some standard graph G and peruse the PDID number versus DID number. By the Definition 1, it is well known that, for any graph G
.
We start by graph path Pn. In [Citation18] it has been checked.
Observation 1.
([Citation18, Observation 4]) Let . Then
If we assign value 3 to the vertices vi, for any path Pn and assign 2 to vn for
, and 0 otherwise, then these assignments denote that each vertex of Pn is perfect double Italian dominated. Therefore
Now from Observation 1 we have.
Corollary 2.
Let . Then
Since assigning 1 to each vertex of Cn gives a and using Observation 6 of [Citation18] we observe that
and therefore.
Observation 3.
For a cycle Cn, .
Proposition 4.
For any complete bipartite graph we have.
,
for
,
, for
,
for
.
Proof.
The function f devotes value 3 to the center vertex of
and 0 otherwise, is a PDIDF of
.
The function f devotes value 2 to the vertices of the partite set with two vertices of
and 0 otherwise, is a PDIDF of
.
The function f devotes value 1 to the vertices of the partite set with three vertices of
, value 2 to one vertex of the other partite set and 0 otherwise, is a PDIDF of
.
The function f devotes value 3 to one vertex of each partite set and 0 otherwise, is a PDIDF of
. Now using Proposition 8 of [Citation18] and this fact that
, the results are observed.□
We have similar result for complete r-partite graphs for .
Proposition 5.
Let be the complete r-partite graph with
and
.
If
, then
,
If
, then
,
If
and
, then
,
If
and r = 3, then
.
Proof.
The function f devotes value 3 to the vertex of the first partite set and 0 otherwise is a PDIDF of G.
The function f devotes value 2 to the vertices of the first partite set and 0 otherwise is a PDIDF of G.
The function f devotes value 1 to the one vertex of the four partite sets and 0 otherwise is a PDIDF of G.
For checking the results in items 1–3, use Proposition 9 of [Citation18].
The function f devotes value 2 to the one vertex of each partite set and 0 otherwise is a PDIDF of G.
On the other hands we cannot assign value 2 to the one vertex of two partite sets and 1 to the one vertex of another, or 3 to the one vertex of one partite set and 2 to another partite set and 0 otherwise. Because the first assignments is not a PDIDF of G and the second assignments is not a DIDF of G. Therefore for item 4,
and the equality holds.□
In [Citation9], it was shown that.
Proposition 6.
[Citation9, Proposition 5.1] Let T be a tree of order n. If there exists three vertices u, v and w such that the induced subgraph with
, where w is adjacent to exactly one leaf or deg(w) = 2 and
for every γdR-function and
-function of T, then
.
Since any PDIDF of a graph G is a DIDF of G, we deduce that , in particular for trees T,
. It is easy to check that the tree T offered in Proposition 6 has the property
. As well, in what follows we show a family of trees T, and graphs G which have property that the
and
. See , T1
, blue label denote the
and red label denote the
.
Also we have the following proposition for the relation between PDIDF and DIDF which is also right for the relation between PDRDF and DRDF.
Proposition 7.
Let T be a tree of order n. If there exists five vertices vi, () such that the induced subgraph
with
, where vi, (
) is of degree 2 and
for every γdI-function and
-function of T, then
.
Proof.
If f assigns weight 2 to v3 and weight 0 to v2, v4, this is a double Italian domination but is not the case for perfect double Italian domination and any -function f assigns weight
and
, or
and
, (
). Thus,
. See , blue label denote the
and red label denote the
. □
The ; trees T1 and T2 are examples of Propositions 6 and 7, respectively, where the blue labels denote the and the red labels denote the
for
.
In , (T1 and T2) we show that . Maybe finding graphs G whose double Italian domination number and perfect double Italian domination number are different is not without grace. In the , we intend to present a construction of T1 as an example of a graph G with this property that
and propose its generalization as a problem.
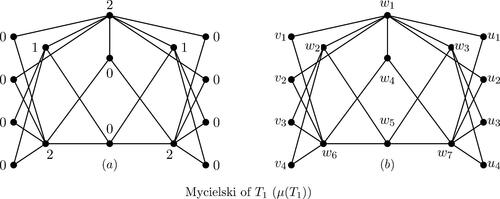
The graph G () is a Mycielski construction of T1.
Proposition 8.
Let G be the Mycielski of T1 (). Then
.
Proof.
In , the assignments denote the . Now consider and let f be a
function. If
and
, then, since
and
(, T1), we deduce
. Let
and
. The following must be definite.
. The same way
. For these eight summations, the minimum values that maybe assigned, are
. In this case, for PDI dominating, we have to assign the value at least 2 to the vertices w4 and w5. Thus
. If
or
, then the best possible are
and
, or
and
. In this case, also for PDI dominating, we have to assign the value at least 2 to the vertices w4 or w5. Again we have
. The other possible assignments trivially show that
. Therefore the result is observed. □
We end this section with a problem.
Problem.
For tree T supposed in Propositions 6 and 7, maybe have .
3 PDID versus PDRD
We want to make a comparison between perfect double Italian domination and perfect double Roman domination of a graph G. From definitions of PDRD-function, PDID-function and Observation 3 and Proposition 4.7 of [Citation4], we deduce .
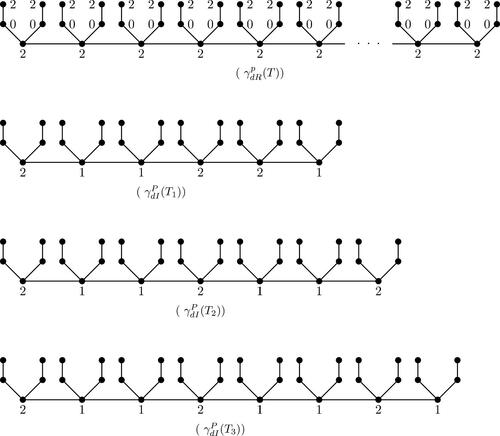
In [Citation18] authors showed that for any tree T (Theorem 5 of [Citation18]). Here we show that, it is not necessary the equality hold for
and
. In addition, we show that the difference between them tends to be infinite. For this, consider the .
In the figure we have three sets of vertices. The first category is pendant vertices, the second category is support vertices, and the third category is vertices that are neither leaves nor supports. In any -function f of trees T in the vertices of the first and third categories must be assigned 2 under f, and the second category must be assigned value 0 under f. In any
-function, g of trees T in , vertices of the first category should be assigned 2 under g, vertices of the second category should be assigned 0 under g and there are two cases for assigning to vertices of the third category.
Case 1. Let T be a tree such as T1 where the order of the third category is
. In this case for the vertex vi in the third category, we define
Case 2. Let T be a tree such as T2 or T3 where the order of the third category is
. In this case for the vertex vi in the third category, we define
This shows that.
Theorem 9.
For any positive integer r, there exist a tree T such that .
Proof.
If T is a tree such as T1 in where the order of the third category is , then
, and
.
If T is a tree such as T2 in where the order of the third category is , then
, and
.
If T is a tree such as T3 in where the order of the third category is , then
, and
.
Therefore, for even r we construct a tree such as T2 and for odd r we construct a tree such as T1 or T3. □
denotes a family of trees T such that . We can have as a problem
Problem.
Maybe characterize the trees T for which ?
4 Complexity and computational results
In this section, our aim is to study the complexity of the perfect double Italian domination of graphs and the following decision problem, to which we shall refer as PDIDP: In [Citation1] Ahangar et al. showed that the double Roman domination problem is NP-complete even when restricted to bipartite and planar graphs. Here we use similar method for showing that the perfect double Italian domination problem is NP-complete even when restricted to bipartite graphs. The details of the proof due to the proof of NP-completeness of DRD problem of [Citation1] and NP-completeness of DID problem of [Citation18]. Consider the following decision problem.
Perfect double Italian domination problem, PDIDP.
INSTANCE: Graph , and a positive integer
.
QUESTION: Does G have a perfect double Italian domination of weight at most k?
We show that the NP-completeness results by reducing the well-known NP-complete problem,
Exact-3-Cover (X3C), to PDID.
EXACT 3-COVER ().
INSTANCE: A finite set X with and a collection C of 3-element subsets of X.
QUESTION: Is there a sub-collection of C such that every element of X appears
in exactly one element of ?
Theorem 10.
PDID is NP-Complete for bipartite graphs.
Proof.
It is clear that PDID Problem belongs to since we can check in polynomial time that a function
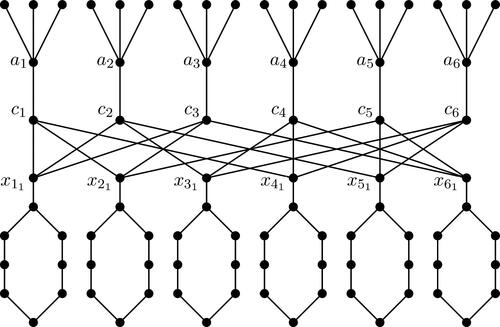
has weight at most k and is a Perfect double Italian dominating function. Now we have to show, how to transform any instance of X3C into an instance G of PDID so that, the solution one of them is equivalent to the solution of the other one. Let
and
be an arbitrary instance of X3C. For each
, we build a graph Hi obtained from a path
by adding the edge
. For each
, we build a star
centered at aj for which one leaf is labeled cj. Let
. Now to obtain a graph G, we add edges
if
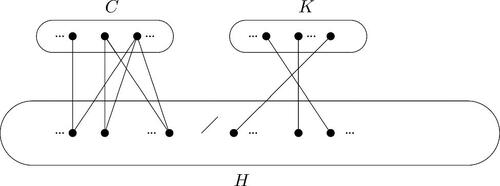
. It is clear that G is bipartite (for example, see ). Set
. Let H be the subgraph of G induced by the union of the
. Observe that for every PDIDF f on G,
to perfect double Italian dominate all vertices on each cycle
. Moreover, since Hi has a perfect double Italian domination number equal to 9, we can assume that
. More precisely, if
, then we may assume, without loss of generality, that
and
. Also, if
, then clearly at least one vertex of Hi (including
) is not perfect double Italian dominated. In this case, we may assume that vertices of Hi are assigned as follows so that only
is not Perfect double Italian dominated:
and
.
Suppose that the instance X, C of has a solution
. We construct a perfect double Italian dominating function f on G of weight k. For every Cj, assign the value 1 to cj if
and 0 if
. Assign 3 to every aj and 0 to each leaf neighbor of aj. Finally, for every i, assign 2 to
, and 0 to the remaining vertices of Hi. Since
exists,
, the number of
with weight 1 is q, having disjoint neighborhoods in
, where every
has one neighbors assigned 1 and one neighbor assigned 2. Hence, it is straightforward to see that f is a perfect double Italian dominating function with weight
.
Conversely, let be a perfect double Italian dominating function of G with weight at most k. Clearly, each star needs a weight of at least 3, and so we may assume, without loss of generality, that
and all its leaves are assigned 0. Since
in (G), it follows that each vertex cj may be assigned the value 0. Moreover, as mentioned above, for each i,
. We may assume that the vertices of Hi are assigned the values given in the second paragraph depending on whether
or
. Let p be the number of His having weight 9. Hence
. Now, if
for some j, then cj serves to perfect double Italian dominate some vertex
, and in that case
(since
. Let y be the number of
assigned 1. Then
, implies that
. On the other hand, since each cj has exactly three neighbors in
, we must have
. Combining these two inequalities, we arrive at p = 0 and y = q. Consequently,
is an exact cover for C. □
5 Characterization
In this section, we want to characterize the graphs whose PDID numbers are given. We bring up three categories in terms of PDID number.
.
where
.
.
5.1 

In [Citation18], the characterization has been performed so far.
Let G be a graph of order , with
. Then G is connected and
([Citation18] Observation 7). Since any vertex of label 0 is adjacent to a vertex of wight 3, it is clear that this devoting give us a PDIDF of G of weight 3. Therefore we have.
Observation 11.
Let G be a graph of order . Then
if and only if
.
Let G be a connected graph of order , with
. Then Proposition 10 of [Citation18] denotes
and any vertex of label 0 is adjacent to two vertices of wight 2, or at most four and at least three vertices of weight 1, and every vertex of label 1 has at most three and at least two neighborhoods of weight 1. It is obvious, this devoting presents a PDIDF of G of weight 4. Therefore we have.
Observation 12.
Let G be a connected graph of order . Then
if and only if
.
Now we characterize graphs G for which .
For characterizing the graphs G of order with
, we construct the families of graphs as follows:
. There is a path
such that
, where
and every vertex of H is adjacent to exactly 2 vertices of P and for P = P3, we must have
.
.
and there exists a vertex
such that for every
, x is adjacent to one or two vertices of C3, a is not adjacent to any vertex of C3 and for every
, x is adjacent to all vertices of C3.
.
, where
for each
and if
, then all vertices in A has a common neighbor in
.
. G contains a subgraph H of order at least two and the vertices
such that uis form a
with center u4 and there exists a vertex x in H for which
for
and
.
.
, where
such that every vertex of H is adjacent to 3 or 4 vertices in C.
.
, where
, each vertex of H is adjacent to exactly 3 or 4 vertices in
and if
and
, then there exists some vertex
such that
and
.
Theorem 13.
Let G be a connected graph of order . Then
if and only if
.
Proof.
If , then it is clear that
. Conversely, let
be a
-function of G. By definition,
. Hence
.
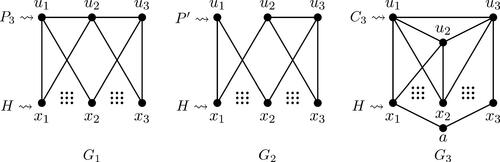
0. In the case of , there exist two vertices u1, u2 with assigned 1 and one vertex u3 with assigned 3. Therefore in this case, u3 is adjacent to every vertex of
, implying that
and so
, a contradiction to that
. Similarly, if
, we also have a contradiction.
In the case of
, there exist two vertices u1, u2 with assigned 2 and one vertex u3 with assigned 1, see Figures G1 and G2. Therefore, if
, then
.
In the case of
, there exist three vertices
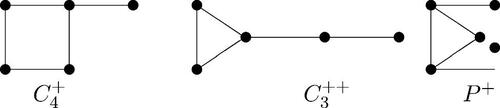
with assigned 1 and one vertex u4 with assigned 2. By the definition, it is easy to check that the induced subgraph by uis is either
or C4, or
. If the induced subgraph by uis is
, then by putting
, we imply that
(see Figure G3). If the induced subgraph by uis is C4, then we have
. If the induced subgraph by uis is
, then we have
.
For the case of
. It is straightforward that,
. □
5.2 

In this section, we investigate graphs G for which is equal to the order of G. Observations 1 and 3 shows that
for
and
. For this approach, we construct the following families of graphs.
. G is a graph obtained from H and K, such that
, with
, every vertex in H is adjacent to exactly one vertex in K and
for each
.
.
, where K is a complete graph,
, and every vertex of H is adjacent to exactly two vertices in
and
for any
.
. G = Cn or
such that
and for each u of degree three, there exists
such that
.
. There exist three graphs H, C, K such that
such that
and the set of vertices H, C and K satisfy the condition (i) and exactly one of the two conditions (ii) and (iii).
For any
, and
.
For any
, if
, then
.
For any
, if
, then
.
. There exist two graphs H and K of orders z and 2z, respectively, where
, such that
, where H, K and C satisfy in the following properties:
Every vertex in K is adjacent to exactly one vertex in H.
Every vertex in H is adjacent to at least one vertex in K.
where for each
.
If for some i,
, then there are
indices like js, such that
.
For each
.
For each
.
.
, where
, and for
, for
. Or
and
.
.
where
, and for
, or
, or
, and for
, or
, such that:
For
, one of the following holds:
If
, then
.
If
, then
and
.
If
, then
.
If
, then
, and exactly one of
or
holds.
If
, and
, then
.
If
, then
.
For
, one of the followings holds:
If
, then
.
If
, then
and
.
If
, then
.
Theorem 14.
Let G be a connected graph of order n. Then if and only if
.
Proof.
If , then it is easy to see that
.
Conversely, let be a
-function of G. By definition,
, and since
. So, there exist the following cases.
Case 1.
. So
. Therefore, there must be existed two graphs H and K such that
, with
. We assign the value 0 to the vertices of H and the value 3 to the vertices of K. Therefore, in this case,
.
Case 2.
. Then
. Therefore, every vertex with value 0 is adjacent to two vertices with value 2, and the vertices with value 2 are independent. In this case,
.
Case 3.
. So
. Hence all vertices are assigned with the value 1. Therefore,
.
Case 4.
, that is
and
. So every vertex V0 must be adjacent to only one vertex in V3 or adjacent to only two vertices in V2. Let H be the induced subgraph of V0, C be the induced subgraph of V2, and K be the induced subgraph of V3. Therefore, in this case,
.
Case 5.
and
and hence
. Therefore each vertex of weight 0 is adjacent to only one vertex of weight 3 and each vertex of weight 3 is adjacent to at least one vertex of weight 3. If a vertex of weight 3 is adjacent to
vertices, of weight 0, then each of t – 2 other vertices of weight 3 must have only one neighbor vertex of weight 0. Any vertex of weight 1 is not adjacent to a vertex of weight 3. If
is a set of vertices of weight 0 and
where x is a vertex of weight 3 and
, and if C is an induced subgraph of the vertices of weight 1, then
. Therefore, in this case,
.
Case 6.
and
and hence
. Thus any vertex of weight 0 is adjacent to two vertices of weight 2. The vertices of of weight 2 should not be adjacent together. Every vertex of weight 1 must be adjacent to a vertex of weight 2 or adjacent together. Therefore, in this case,
.
Case 7.
for any
. So every vertex in V0 must be adjacent to only three or four vertices of V1, or only two vertices of V1 and one vertex of V2, or only one vertex of V1 and one vertex of
, or only two vertices of V2, or only one vertex of V3.
Also every vertex of V1 must be adjacent to only two or three vertices of V1, or only one vertex of V1 and one vertex of V2, or only one vertex of . Therefore,
. □
5.3 

In this section, we characterize graphs G for which where n is the order of G. For
and
, the proof is straightforward and they are left.
Theorem 15.
Let G be a graph of order n. Then
if and only if
.
if and only if
.
if and only if
or
.
Theorem 16.
Let G be a graph of order n. Then if and only if one of the followings holds:
.
, or
.
.
Proof.
Let be a
-function f of G with
. Then
and
. Therefore
. It is well known that
, otherwise there exists a vertex v of weight zero with
, and for
, or
we will have
. On the other hand, if
, then we must have
. Now we may consider some cases.
Case 1.
and
, or
and
, or
and
. Then
if and only if
.
Case 2.
and
. Then
if and only if
, or
.
Case 3.
and
. Then
if and only if
. □
Theorem 17.
Let G be a graph of order n. Then if and only if one of the followings holds:
or
.
, or
.
.
.
.
Proof.
Let be a
-function f of G with
. Then
and
. Therefore
. It is well known that
, and for
, or
and
, or
, and
, or
, and
, and
, we will have
. On the other hand, if
, then we must only have
, because the other value for
is impossible.
Now we may consider some cases.
Case 1.
and
. Then,
if and only if
, or
.
Case 2.
and
, or
and
.
if and only if
, or
.
Case 3.
. Then
if and only if
.
Case 4.
and
. Then
if and only if
.
Case 5.
and
or
and
. Then
if and only if
. □
Theorem 18.
Let G be a graph of order n. Then if and only if one of the followings holds:
, where
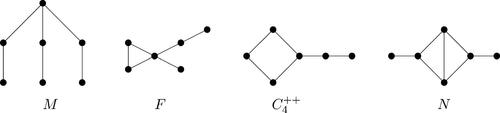
.
Z
, where
where
and
are the bellow graphs.
, where
where P+ is the bellow graph.
, where
.
Proof.
Let be a
-function f of G with
. Then
and
. Therefore
. It is well known that
, and for
, or
and
, or
, and
, or
, and
, or
, and
, or
, and
, we will have
. On the other hand, if
, then we must only have
, because of the other value for
is impossible. Now we may consider some cases.
Case 1.
and
, or
and
, or
, and
. Then
if and only if
, where
.
Case 2.
and
. Then,
if and only if
, where
.
Case 3.
and
, or
and
, or
and
, or
and
. Then,
if and only if
, where
.
Case 4.
and
, or
and
, or
and
, or
and
, or
and
, or
and
. Then,
if and only if
, where
. □
Theorem 19.
Let G be a graph of order n. Then if and only if one of the followings holds:
, where
or
where K is a graph of order 3 and size at most 1.
, where
.
, where
.
.
Proof.
Let be a
-function f of G with
. Then
. It is well known that
, and for
, or
and
, or
, and
, or
, and
, or
, and
, or
, and
, or
, and
, we will have
. On the other hand, if
, then we must only have
, because of the other value for
is impossible. Now we may consider some cases.
Case 1.
and
, or
and
, or
, and
, or
and
. Then,
if and only if
, where
or
where K is a graph of order 3 and size at most 1.
Case 2.
and
. Then,
if and only if
, where
.
Case 3.
, or
and
, or
, and
, or
, and
. Then,
if and only if
, where
.
Case 4.
, or
and
, or
, and
, or
, and
, or
, and
. Then,
if and only if
. □
We end the paper with the following problem.
Problem.
Characterize the graph G for which, .
Acknowledgments
The second author (Parvin Jalilolghadr) has been supported by “the University of Mazandaran,” when she was visiting the University of Mazandaran as a Post Doctoral Researcher. We are grateful to the anonymous referee for their useful comments on this paper that improved its presentation.
References
- Ahangar, H. A., Chellali, M., Sheikholeslami, S. M. (2017). On the double Roman domination in graphs. Discrete Appl. Math. 232: 1–7.
- Azvin, F., Jafari Rad, N. (2021). Bounds on the double Italian domination number of a graph. Discuss. Math. Graph Theory.
- Azvin, F., Jafari Rad, N., Volkmann, L. (2021). Bounds on the outer-independent double Italian domination number. Commun. Comb. Optim. 6(1): 123–136.
- Banerjeea, S., Henning, M. A., Pradhan, D. (2021). Perfect Italian domination in cographs. Appl. Math. Comput. 391: 125703.
- Beeler, R. A., Haynes, T. W., Hedetniemi, S. T. (2016). Double Roman domination. Discrete Appl. Math. 211: 23–29.
- Chellali, M., Haynes, T. W., Hedetniemi, S. T., McRaee, A. A. (2016). Roman {2}-domination. Discrete Appl. Math. 204: 22–28.
- Cockayne, E. J., Dreyer, P. A., Hedetniemi, S. M., Hedetniemi, S. T. (2004). Roman domination in graphs. Discrete Math. 278: 11–22.
- Darkooti, M., Alhevaz, A., Rahimi, S., Rahbani, H. (2019). On perfect Roman domination number in trees: complexity and bounds. J. Comb. Optim. 38: 712–720.
- Egunjobi, A. T., (2019). Perfect double Roman domination of trees. MSc Electronic theses and dissertations. East Tennessee State University, USA. https://dc.etsu.edu/etd/3576
- Egunjobi, A. T., Haynes, T. W. (2020). Perfect double Roman domination of trees. Discrete Appl. Math. 284(30): 71–85.
- Hao, G., Volkmann, L., Mojdeh, D. A. (2020). Total double Roman domination in graphs. Commun. Comb. Optim. 5(1): 27–39.
- Haynes, T. W., Hedetniemi, S. T., Slater, P. J. (1998). Fundamentals of Domination in Graphs. New York: Marcel Dekker, Inc.
- Haynes, T. W., Henning, M. A. (2019). Perfect Italian domination in trees. Discrete Appl. Math. 260: 164–177.
- Henning, M. A., Klostermeyer, W. F. 2017. Italian domination in trees. Discrete Appl. Math. 217: 557–564.
- Henning, M. A., Klostermeyer, W. F., MacGillivray, G. (2018) Perfect Roman domination in trees. Discrete Appl. Math. 236: 235–245.
- Klostermeyer, W. F. (2015). A taxonomy of perfect domination. J. Discrete Math. Sci. Cryptogr. 18: 105–116.
- Mojdeh, D. A., Mansouri, Zh. (2020). On the independent double Roman domination in graphs. Bull. Iran. Math. Soc. 46: 905–915.
- Mojdeh, D. A., Volkmann, L. (2020). Roman {3}-domination (double Italian domination). Discrete Appl. Math. 283: 555–564.
- Paleta, L. M., Jamil, F. P. (2020). More on perfect roman domination in graphs. Eur. J. Pure Appl. Math. 13(3): 529–548.
- Shao, Z., Mojdeh, D. A., Volkmann, L. (2020). Total Roman {3}-domination in graphs. Symmetry 12: 268.
- Stewart, I. (1999). Defend the Roman Empire!. Sci. Am. 281(6):136–139.
- Varghese, J., Lakshmanan, A. (2019). Perfect Italian domination number of graphs. arXiv. 1910.12260v1 [math.CO]. 27.
- West, D. B. (2001). Introduction to Graph Theory. 2nd ed. Upper Saddle River, NJ: Prentice-Hall.