Sudoku number of graphs

Abstract

We introduce a concept in graph coloring motivated by the popular Sudoku puzzle. Let $G=(V,E)$ be a graph of order n with chromatic number $\chi (G)=k$ and let $S\subseteq V.$ Let ${\mathcal{C}}_0$ be a k-coloring of the induced subgraph $G[S].$ The coloring ${\mathcal{C}}_0$ is called an extendable coloring if ${\mathcal{C}}_0$ can be extended to a k-coloring of G. We say that ${\mathcal{C}}_0$ is a Sudoku coloring of G if ${\mathcal{C}}_0$ can be uniquely extended to a k-coloring of G. The smallest order of such an induced subgraph $G[S]$ of G which admits a Sudoku coloring is called the Sudoku number of G and is denoted by $sn(G).$ In this paper we initiate a study of this parameter. We first show that this parameter is related to list coloring of graphs. In Section 2, basic properties of Sudoku coloring that are related to color dominating vertices, chromatic numbers and degree of vertices, are given. Particularly, we obtained necessary conditions for ${\mathcal{C}}_0$ being extendable, and for ${\mathcal{C}}_0$ being a Sudoku coloring. In Section 3, we determined the Sudoku number of various families of graphs. Particularly, we showed that a connected graph G has sn(G) = 1 if and only if G is bipartite. Consequently, every tree T has sn(T) = 1. We also proved that $sn(G)=|V(G)|-1$ if and only if G = K_n. Moreover, a graph G with small chromatic number may have arbitrarily large Sudoku number. In Section 4, we proved that extendable partial coloring problem is NP-complete. Extendable coloring and Sudoku coloring are nice tools for providing a k-coloring of G.

KEYWORDS:

• Chromatic number
• extendable coloring
• Sudoku coloring

2010 AMS SUBJECT CLASSIFICATION:

• 05C78
• 05C69

1 Introduction

By a graph $G=(V,E)$ we mean a finite undirected connected simple graph of order $n=\left|V\right|$ and size $m=\left|E\right|.$ For notations and concepts not defined here we refer to the book [1].

We introduce a concept in graph coloring which is motivated by the popular Sudoku puzzle. Let V denote the 81 cells consisting of 9 rows, 9 columns and nine 3 × 3 subsquares. Let G be the graph with vertex set V in which each of the rows, columns and the nine 3 × 3 subsquares are complete graphs. Clearly $\chi (G)=9$ and the solution of a Sudoku puzzle gives a proper vertex coloring of G with nine colors. A Sudoku puzzle corresponds to a proper vertex coloring $\mathcal{C}$ of an induced subgraph H of G using at most 9 colors with the property that $\mathcal{C}$ can be uniquely extended to a 9-coloring of G. This motivates the following definition.

Definition 1.1.

Let G be a connected graph of order n with chromatic number $\chi (G)=k\ge 2$. Let $S\subset V$ and let $G[S]$ be the induced subgraph of G. Let ${\mathcal{C}}_0$ be a proper k-coloring of $G[S]$. We also call ${\mathcal{C}}_0$a partial coloring of G. The coloring ${\mathcal{C}}_0$ is called an extendable coloring of $G[S]$ if ${\mathcal{C}}_0$ can be extended to a k-coloring for G. We say ${\mathcal{C}}_0$ is a Sudoku coloring of G if ${\mathcal{C}}_0$ can be uniquely extended to a proper k-coloring of G. The smallest order of such an induced subgraph $G[S]$ of G which admits a Sudoku coloring is called the Sudoku number of G and is denoted by sn(G).

Cooper and Kirkpatrick [2] have considered the same concept and introduced several parameters using critical sets. However, in this paper, we adopted different approach and proof techniques.

The natural questions that arises in the context of Sudoku puzzle is “What is the lowest number of clues in a Sudoku puzzle?”. It was long suspected that the number is 17 and in [8], the authors have proved that there is no 16-clue Sudoku puzzle. Thus the Sudoku number for the standard Sudoku puzzle is 17 (see also [7]).

We need the following definitions.

Definition 1.2.

[1] Let $G=(V,E)$ be a graph with chromatic number k. The graph G is uniquely colorable if the partition $\{V_1,V_2,\dots ,V_k\}$ of V induced by any k-coloring of G is unique up to a permutation.

The concept of list coloring was independently studied by Erdős et al. [4] and Vizing [9].

Definition 1.3.

Given a graph G and a set L(v) of colors for each vertex v, which is called a list or color-list of v, a list coloring is a coloring of G such that the vertex v is colored by a color in the list $L(v).$ If G admits a list coloring for a given list L, then G is called list colorable or L-colorable.

Scheduling problem is one of the classical applications of graph colorings. If the graph associated with an instance of the problem has chromatic number k, then k is the minimum number of timeslots required for a scheduling and each color class represents a time slot. Thus for implementation of a scheduling, the knowledge of the chromatic number alone is not sufficient and we need a k-coloring of G. Extendable coloring and Sudoku coloring are nice tools for providing a k-coloring of G.

In this paper we formulate Sudoku coloring as a list coloring problem and determine the Sudoku number of several classes of graphs.

2 Extension: a list coloring problem

Let ${\mathcal{C}}_0$ be an extendable coloring of G. Then for each uncolored vertex v there are some possible colors that can be used to color the vertex v. The set of all possible colors for v is a color-list of v. The problem of extending ${\mathcal{C}}_0$ to a k-coloring of G is equivalent to a list coloring problem.

In this paper, we use $\left\{i\right|1\le i\le k\}$ as the color set for a graph G if $\chi (G)=k$.

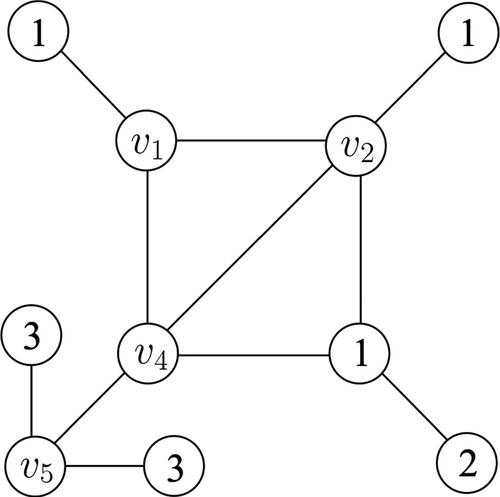
Example 2.1.

The partial coloring ${\mathcal{C}}_0$ for the graph given in Figure 1(a) is an extendable coloring. Also two extensions of ${\mathcal{C}}_0$ to a 3-coloring of G are given in Figure 1(b, c). Thus ${\mathcal{C}}_0$ is an extendable coloring, but not a Sudoku coloring.

Fig. 1 An extendable coloring with at least two extensions.

Example 2.2.

Consider the partial coloring ${\mathcal{C}}_0$ for the graph given in Figure 2.

Fig. 2 A coloring which is not extendable.

Clearly $L(v_4)=L(v_1)=L(v_2)=\{2,3\}$ and $G[\{v_1,v_2,v_4\}]=K_3.$ Hence G is not L-colorable and so ${\mathcal{C}}_0$ is not an extendable coloring.

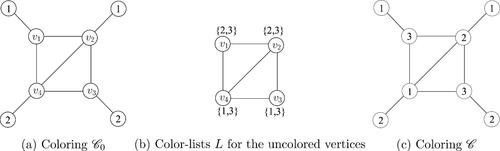
Example 2.3.

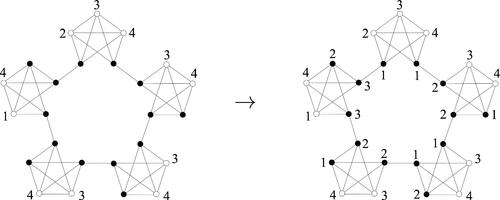
Consider the partial coloring ${\mathcal{C}}_0$, which involves 2 colors, for the graph given in Figure 3(a).

Fig. 3 A Sudoku coloring and its unique extension.

Clearly $L(v_2)=L(v_1)=\{2,3\}$ and $L(v_3)=L(v_4)=\{1,3\}$. So we have Figure 3(b). Let $\mathcal{C}$ be an extension of ${\mathcal{C}}_0$ to a 3-coloring of G. If v₂ is assigned color 3, then the color list of the two adjacent vertices v₃ and v₄ becomes $\left\{1\right\}.$ Hence the color for v₂ is 2. Now the colors to be assigned to the remaining vertices are uniquely determined and hence the coloring $\mathcal{C}$ given in Figure 3(c) is the unique extension of ${\mathcal{C}}_0$. Thus ${\mathcal{C}}_0$ is a Sudoku coloring of G.

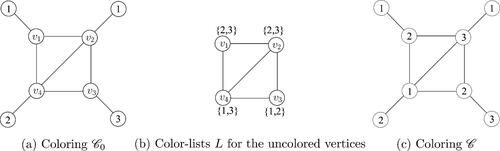
Example 2.4.

The partial coloring ${\mathcal{C}}_0$, which involves 3 colors, for the graph given in Figure 4(a) is a Sudoku coloring.

Fig. 4 A Sudoku coloring and its unique extension.

The argument is similar to Example 2.3. We omit here.

We now present a few results on list coloring of paths and cycles, which are used in the next section.

Lemma 2.1.

Let $L(x_i)$ be a list of colors of a vertex x_i in the path $P_n=x_1{x}_2\cdots x_n,1\le i\le n$. If $|L(x_i)|\ge 2$ for each i, then there are at least two list colorings of P_n.

Proof.

We color x_i in natural order starting at i = 1. When x_i, $1\le i\le n-1$, has been colored, then there is at least one color in $L(x_{i+1})$ can be assigned to $x_{i+1}$. So we have a list coloring for P_n. Since there are two choices for coloring x₁, we have the lemma. □

Lemma 2.2.

Suppose that there exists a list coloring of the cycle $C_n=x_1{x}_2\cdots x_n{x}_1$ such that the list of colors for each vertex x_i satisfies the following conditions:

1. $|L(x_i)|\ge 2$;

2. $L(x_i)\subseteq \{1,2,3\}$.

Then there are at least two list colorings of C_n.

Proof.

To show this lemma, we may assume a weaker condition that $|L(x_i)|=2$ for each i. Suppose $L(x_i)$ are the same for all i, $1\le i\le n$. Since C_n admits a list coloring, it follows that n is even. Now we are going to show that there exist two list colorings.

Now we assume that not all $L(x_i)$ are same. Then there exist two adjacent vertices whose lists are different. Hence we may assume without loss of generality that $L(x_1)=\{1,2\}$ and $L(x_n)=\{1,3\}.$ Let k be the least positive integer such that $2\le k\le n$ and $L(x_k)\ne L(x_1).$ If $k=n,$ then we assign color 3 to x₁ and by Lemma 2.1 we get two list colorings for the path $C_n-x_n.$ Suppose $k\le n-1.$ Let $\varphi$ be a list coloring of $C_n.$ Let $P=x_1{x}_2\cdots x_{k-1}$ and $Q=x_k{x}_{k+1}\cdots x_n.$ We claim that there exists a list coloring of C_n different from $\varphi .$ We consider two cases.

1. Let $L(x_k)=\{1,3\}.$

   1. Suppose $\varphi (x_n)=\varphi (x_k)=3.$ Then by interchanging the colors of the vertices of P, we get another list coloring of $C_n.$

   2. Suppose $\varphi (x_n)=\varphi (x_k)=1.$ Then P is an odd path and $\varphi (x_1)=\varphi (x_{k-1})=2.$ Now recolor x_k with color 3. By Lemma 2.1 we get a list coloring of the path Q and this gives a list coloring of C_n different from $\varphi .$

   3. Suppose $\varphi (x_n)$ and $\varphi (x_k)$ are distinct. Without loss of generality, let $\varphi (x_n)=1$ and $\varphi (x_k)=3.$ Then $\varphi (x_1)=2$ and $\varphi (x_{k-1})=\{\begin{array}{cc}2\hfill & \hspace{1em}\text{if }k-1\text{ is odd}\hfill \\ 1\hfill & \hspace{1em}\text{ if }k-1\text{is even}.\hfill \end{array}$

      If k – 1 is odd we recolor x_k by color 1 and by Case A2, we get a list coloring of C_n different from $\varphi .$ If k – 1 is even, we swap the colors 1 and 2 for P and then recolor x_k by 3. Similarly we recolor the inverse path $Q^{-1}=x_n{x}_{n-1}\cdots x_k$ and obtain a list coloring different from $\varphi .$

2. $L(x_k)=\{2,3\}.$

   If $\varphi (x_k)=\varphi (x_n)=3,$ the proof is similar to that of Case A1. Suppose $\varphi (x_k)\ne \varphi (x_n).$

   1. Suppose $\varphi (k_n)=1.$ Using Lemma 2.1, we get a list coloring of the path $R=x_n{x}_{n-1}\cdots x_1$ in which x_n is assigned color 3. Since the color assigned for x₁ is 1 or 2, this coloring is also a list coloring of C_n different from $\varphi .$

   2. Suppose $\varphi (x_n)=3$ and $\varphi (x_k)=2.$ Consider a list coloring of the path $x_k{x}_{k+1}\cdots x_n{x}_1{x}_2\cdots x_{k-1}$ in which x_k is colored 3. Since the color assigned to $x_{k-1}$ is 1 or 2, this is also a list coloring of C_n which is different from $\varphi .$

Thus there exist two list colorings of $C_n.$ □

We now proceed to present basic properties of Sudoku coloring.

Observation 2.3.

Let G be a connected graph with $\chi (G)\ge 3$. Let ${\mathcal{C}}_0=\{V_1,V_2,\dots ,V_r\}$ be a Sudoku coloring defined on an induced subgraph $G[S]$, for some $S\subset V(G)$. If $r\le k-2,$ then at least two new color classes are created in the extension process and hence the extension is not unique. Therefore, $r=k-1$ or k.

Let ${\mathcal{C}}_0$ be an extendable coloring of $G[S]$ and let $W=V(G)\setminus S.$ Let $w_1\in W$ be the first vertex to be colored in the extension process. Let ${\mathcal{C}}_1$ be the coloring on $G[S\cup \{w_1\}].$ Let w₂ be the next vertex to be colored and let ${\mathcal{C}}_2$ be the resulting coloring of $G[S\cup \{w_1,w_2\}].$ Continuing this process we get a sequence of colorings ${\mathcal{C}}_0,{\mathcal{C}}_1,{\mathcal{C}}_2,\dots$, ${\mathcal{C}}_t$ where $t=\left|W\right|$ and ${\mathcal{C}}_t$ is the required extension of ${\mathcal{C}}_0$ to a k-coloring of G. In the extension process, we update the color-list of the vertices as follows. If a vertex w is assigned color i, then L(w) is replaced by the empty set $\varnothing$ and the color i is removed from the list of all neighbors of w.

Definition 2.1.

Let G be a graph with $\chi (G)=k\ge 3.$ Let ${\mathcal{C}}_0=\{V_1,V_2,\dots ,V_{k-1}\}$ be an extendable coloring of $G[S]$ and let $w\in W=V\setminus S.$ The vertex w is called a color dominating vertex if w is adjacent to at least one vertex in each color class $V_i,1\le i\le k-1.$

Observation 2.4.

If w is a color dominating vertex, then in the extension process, k is the unique color assigned to w.

Definition 2.2.

Let G be a graph with $\chi (G)=k\ge 3.$ Let ${\mathcal{C}}_0=\{V_1,V_2,\dots ,V_k\}$ be an extendable coloring of $G[S]$ and let $w\in V\setminus S.$ The vertex w is called a near-color dominating vertex if there exists a unique color class V_j such that v is not adjacent to any vertex in $V_j.$

Observation 2.5.

If w is a near-color dominating vertex, then in the extension process, j is the unique color that can be assigned to w.

Example 2.5.

Consider the Sudoku coloring ${\mathcal{C}}_0$ of the graph in Figure 3. There is no color or near-color dominating vertex.

Example 2.6.

Let $C_{13}=v_1{v}_2\cdots v_{13}{v}_1$ be the 13-cycle. Let ${\mathcal{C}}_0=\{V_1,V_2,V_3\}$ be a coloring of $C_{13}[S]$, where $S=\left\{v_i\right|1\le i\le 13,i\text{ is odd}\},V_1=\{v_1,v_5,v_9\},V_2=\{v_3,v_7,v_{11}\}$ and $V_3=\left\{v_{13}\right\}$. Here every vertex w in $V\setminus S$ is a near-color dominating vertex and can be assigned a unique color. Thus ${\mathcal{C}}_0$ is a Sudoku coloring of C₁₃ and the unique extension $\mathcal{C}$ is given by $\mathcal{C}=(\{V_1\cup \left\{v_{12}\right\},V_2,V_3\cup \{v_2,v_4,v_6,v_8,v_{10}\})$.

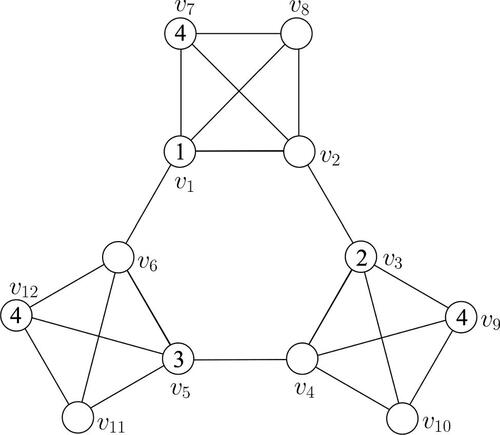
Example 2.7.

Consider the partial coloring ${\mathcal{C}}_0$ for the graph $C_6(K_4)$ given in Figure 5.

Fig. 5 A Sudoku coloring for $C_6(K_4)$.

Clearly ${\mathcal{C}}_0=\left\{\right\{v_1\},\{v_3\},\{v_5\},\{v_7,v_9,v_{12}\left\}\right\}.$ The vertex v₆ is a near-color dominating vertex for ${\mathcal{C}}_0$ and receives the color 2. Hence ${\mathcal{C}}_1=\left\{\right\{v_1\},\{v_3,v_6\},\{v_5\},\{v_7,v_9,v_{12}\left\}\right\}.$ Now v₁₁ is a near-color dominating vertex for ${\mathcal{C}}_1.$ (Note that v₁₁ is not a near-color dominating vertex for ${\mathcal{C}}_0$). The unique color for v₁₁ is 1. Hence ${\mathcal{C}}_2=\left\{\right\{v_1,v_{11}\},\{v_3,v_6\},\{v_5\},\{v_7,v_9,v_{12}\left\}\right\}.$ Proceeding like this we get $$\begin{array}{c}{\mathcal{C}}_3=\left\{\right\{v_1,v_{11}\},\{v_3,v_6\},\{v_5,v_2\},\{v_7,v_9,v_{12}\left\}\right\},\\ {\mathcal{C}}_4=\left\{\right\{v_1,v_{11}\},\{v_3,v_6,v_8\},\{v_5,v_2\},\{v_7,v_9,v_{12}\left\}\right\},\\ {\mathcal{C}}_5=\left\{\right\{v_1,v_{11},v_4\},\{v_1,v_6,v_8\},\{v_5,v_2\},\{v_7,v_9,v_{12}\left\}\right\}\\ \text{and}{\mathcal{C}}_6=\left\{\right\{v_1,v_{11},v_4\},\{v_1,v_6,v_8\},\{v_5,v_2,v_{10}\},\{v_7,v_9,v_{12}\left\}\right\}\end{array}$$

${\mathcal{C}}_6$ is the unique extension of ${\mathcal{C}}_0$ to a 4-coloring of G. Also $W=V\setminus S=\{v_6,v_{11},v_2,v_8,v_4,v_{10}\}$ where the vertices in W are listed in the order in which colors are assigned in the extension process.

The above examples illustrate the significant role of color dominating vertex and near-color dominating vertex in the extension process of a Sudoku coloring. The following concept provides another tool in this regard.

Definition 2.3.

Let G be a graph with $\chi (G)=k\ge 3.$ Let ${\mathcal{C}}_0=\{V_1,V_2,\dots ,V_k\}$ be an extendable coloring defined on $G[S]$ for some $S\subset V$. Suppose L is the corresponding list of the vertex set $V\setminus S$. The vertex $w\in V\setminus S$ is called an i-attractive vertex if w satisfies the following conditions.

1. The chromatic number of the subgraph induced by the closed neighborhood $N[w]$ is k.

2. There exists a color $i\in \{1,2,\dots ,k\}$ such that $i\notin L(v)$ for all $v\in N(w)$, the neighborhood of w.

Clearly if w is an i-attractive vertex, then in any extension of ${\mathcal{C}}_0$, the vertex w is assigned color i. In solving a Sudoku puzzle, this condition is very often used in determining the entry in a cell. But there may be no such vertex in some cases. Please see Example 2.4.

Lemma 2.6.

Let G be a graph with $\chi (G)=k\ge 3$. Suppose ${\mathcal{C}}_0$ is an extendable coloring of $G[S]$ for $S\subset V(G)$. If there is a pendant vertex $v\notin S$, then ${\mathcal{C}}_0$ is not a Sudoku coloring.

Proof.

Let $\mathcal{C}$ be an extension of ${\mathcal{C}}_0$ to G – v. Let u be the unique neighbor of v and let i be the color assigned to u. Then v can be assigned any of the colors from the set $\{1,2,\dots ,k\}\setminus \left\{i\right\}.$ Thus, ${\mathcal{C}}_0$ has more than one extension and hence the result follows. □

Lemma 2.7.

Let G be a graph with $\chi (G)=k\ge 3$. Suppose ${\mathcal{C}}_0$ is an extendable coloring of $G[S]$ for $S\subset V(G)$. If there is an edge xy for which $x,y\notin S$ such that $\mathrm{deg}(x)\le k-1$ and $\mathrm{deg}(y)\le k-1$, then ${\mathcal{C}}_0$ is not a Sudoku coloring of G.

Proof.

Let $\mathcal{C}$ be the extension of ${\mathcal{C}}_0$ to $G-\{x,y\}$. Now the lists of available colors of x and y are $\left\{i\right|1\le i\le k\}\setminus \{\mathcal{C}(u)|u\in N(x)\setminus \{y\left\}\right\}$ and $\left\{i\right|1\le i\le k\}\setminus \{\mathcal{C}(v)|v\in N(y)\setminus \{x\left\}\right\}$, respectively. By assumption, both of these lists contain at least 2 colors. Thus, ${\mathcal{C}}_0$ can be extended to at least 2 different colorings for G. □

3 Sudoku numbers for some graphs

Theorem 3.1.

Let G be a connected graph of order n. Then sn(G) = 1 if and only if G is a bipartite graph.

Proof.

Let G be a connected bipartite graph. Since the bipartition (V ₁, V ₂) is uniquely determined, if one vertex of G is assigned color 1, then the 2-coloring of G is uniquely determined. Thus, sn(G) = 1.

Conversely, suppose $sn(G)=1.$ Then there exists a vertex v of G such that the 1-coloring $\mathcal{C}$ of $K_1=\left\{v\right\}$ determines a χ-coloring of G. If $\chi (G)\ge 3,$ then $\chi (G-v)\ge 2$ and any extension of $\mathcal{C}$ to a χ-coloring of G is not unique, which is a contradiction. Thus $\chi (G)=2$ and G is bipartite. □

Corollary 3.2.

Every tree T has sn(T) = 1.

In what follows, we only consider graph G with $\chi (G)\ge 3$.

Theorem 3.3.

Let G be a uniquely colorable graph and let $\chi (G)=t.$ Then $sn(G)=t-1$.

Proof.

Let $\mathcal{C}=\{V_1,V_2,\dots ,V_t\}$ be the unique t-coloring of G. Let $u_i\in V_i$ and let $S=\{u_1,u_2,\dots ,u_{t-1}\}.$ Let ${\mathcal{C}}_0$ be a coloring of $G[S]$ in which u_i is assigned the color i. Clearly ${\mathcal{C}}_0$ is uniquely extendable to a t-coloring of G. Hence, $sn(G)\le t-1.$

Now, let $S\subseteq V(G)$ and $\left|S\right|\le t-2.$ Clearly $\chi (G-S)\ge 2.$ Hence for any coloring of $G-S,$ its extension to a χ-coloring of G is not unique. Hence $sn(G)\ge t-1$ and the theorem follows. □

Corollary 3.4.

Let G be a complete t-partite graph with $t\ge 3$, then $sn(G)=t-1$.

In the following theorem we obtain a characterization of connected graphs with order n having Sudoku number n – 1.

Theorem 3.5.

Let G be a connected graph of order n. Then $sn(G)=n-1$ if and only if G = K_n.

Proof.

Suppose $sn(G)=n-1$. Let $\chi (G)=k$ and let $\varphi =\{V_1,V_2,\dots ,V_k\}$ be a k-coloring of G. Then each color class V_i has at least one vertex, say v_i, which is adjacent to at least one vertex in V_j, $j\ne i$. Otherwise, there is a $(k-1)$-coloring for G. Let $S=\{v_1,v_2,\dots ,v_k\}$. We claim that the induced subgraph $G[S]$ is complete. Without loss of generality, suppose v₁ and v₂ are not adjacent. Let $w_1\in N(v_1)\cap V_2$ and $w_2\in N(v_2)\cap V_1$. Let $\psi =\varphi {|}_{V\setminus \{v_1,v_2\}}$ or equivalently ψ is obtained from $\varphi$ by uncoloring v₁ and v₂. Clearly, v₁ can be colored only with color 1 and v₂ can be colored only with color 2. Thus, ψ is a Sudoku coloring of G and $sn(G)\le n-2$, which is a contradiction. Hence, $G[S]$ is complete.

Now, suppose $S\ne V$. Since G is connected, there exists a vertex $u\in V\setminus S$ such that u is adjacent to a vertex $v_i\in S$, for some i. Suppose $u\in V_j,i\ne j$. Then $\eta =\varphi {|}_{V\setminus \{v_i,v_j\}}$ is a Sudoku coloring of G, which is again a contradiction. Hence, S = V and G = K_n. The converse follows from Corollary 3.4. □

In the following theorem, we determine the Sudoku number of cycles. This result is given in [2] and for the scope of completeness, we include its proof.

Theorem 3.6.

For $n\ge 3,$ $$sn(C_n)=\{\begin{array}{cc}1\hfill & \text{ if }n\text{ is even},\hfill \\ \frac{n+1}{2}\hfill & \text{otherwise}.\hfill \end{array}$$

Proof.

The case n is even follows from Theorem 3.1. So we assume that n is odd. Hence $\chi (C_n)=3$.

The case n = 3 is obvious. For $n\ge 5$, let $C_n=v_1{v}_2\cdots v_n{v}_1$. Let $S=\left\{v_j\right|1\le j\le n-2,j\text{ is odd}\}\cup \{v_{n-1}\}$. Define a coloring $\mathcal{C}$ for $C_n[S]$ by $\mathcal{C}(v_i)=1$ for $i\equiv 1\hspace{1em}(\mathrm{mod}4),\mathcal{C}(v_j)=2$ for $j\equiv 3\hspace{1em}(\mathrm{mod}4)$ and $\mathcal{C}(v_{n-1})=3$. This can be uniquely extended to a 3-coloring of C_n since we must have $\mathcal{C}(v_k)=3$ for even $k\cancel{=}n-1$ and $\mathcal{C}(v_n)=2$. Thus, $\mathcal{C}$ is a Sudoku coloring of C_n. Since $C_n[S]$ is of order $\frac{n+1}{2}$, we have $sn(C_n)\le \frac{n+1}{2}$.

Suppose there is an extendable coloring $\varphi$ of $G[S]$ with $\left|S\right|\le \frac{n-1}{2}.$ Then $|V(G)\setminus S|\ge \frac{n+1}{2}$. By pigeonhole principle, there is a K₂ subgraph which satisfies the condition of Lemma 2.7. Thus $\varphi$ is not a Sudoku coloring. Hence $sn(C_n)=\frac{n+1}{2}$. □

For $m\ge 2$ and $1\le i\le m$, let G_i be a simple graph with an induced subgraph H. An amalgamation of $G_1,\dots ,G_m$ over H is the simple graph obtained by identifying the vertices of H of each G_i so that the obtained new graph contains a subgraph H induced by the identified vertices. This subgraph H is called the common core of the amalgamation of $G_1,\dots ,G_m$. Suppose G is a graph with a proper subgraph K_r, $r\ge 1$. Let $A(mG,K_r)$ be the amalgamation of $m\ge 2$ copies of G over K_r. Note that there may be many non-isomorphic $A(mG,K_r)$ graphs. When r = 1, the graph is also known as one-point union of graphs. Note that $A(m{K}_2,K_1)\cong K_{1,m}$ and $A(m{K}_3,K_1)$ is the friendship graph f_m, $m\ge 2$.

Theorem 3.7.

For $m\ge 2,n\ge 3$ and $1\le r<n$, if $G=A(m{K}_n,K_r)$, then $sn(G)=m(n-r-1)+r-1$.

Proof.

Note that $|V(G)|=r+m(n-r)$ and $\chi (G)=n$. Let $K\cong K_r$ be the common core of G and let G_i be the i-th copy of K_n.

Choose one vertex in K, say x₀, and choose one vertex in each $G_i-K$, say x_i. Let $S=V(G)\setminus \left\{x_i\right|0\le i\le m\}$. Then $\left|S\right|=m(n-r-1)+r-1$.

Now color the vertices of $K-x_0$ from 1 to r – 1; those of $G_1-x_1$ from r + 1 to n – 1 and those of $G_i-x_i$ ($2\le i\le m$) from r + 2 to n, arbitrary. Note that, if $n=r+1$, then we do not perform the last two assignments. Clearly, this coloring can be extended to an n-coloring of G uniquely. Thus, $sn(G)\le m(n-r-1)+r-1$.

Suppose there is an extendable coloring $\varphi$ of $G[S]$ with $\left|S\right|<m(n-r-1)+r-1$. Then $|V(G)\setminus S|\ge m+2$. Considering the m + 1 subgraphs, K and $G_i-K,1\le i\le m$, by pigeonhole principle, there is an edge xy in either K or $G_i-K$ for i, for which x and y have not been colored.

Let $\widehat{\varphi }$ be an extension of $\varphi$. Then $\widehat{\varphi }(x)\ne \widehat{\varphi }(y)$. For convenience, we assume $\widehat{\varphi }(x)=1$ and $\widehat{\varphi }(y)=2$.

1. Suppose $x,y\in V(G_i-K)$ for some i. Since $\chi (G_i)=n,\{\widehat{\varphi }(v)|v\in V(G_i)\setminus \{x,y\}\}=\{j|3\le j\le n\}$. Now, if we swap the colors of x and y, then we get another extension of $\varphi$ for all i. Hence $\varphi$ is not a Sudoku coloring.

2. Suppose $x,y\in V(K)$. Similar to Case 1, we will obtain that $\{\widehat{\varphi }(v)|v\in V(G_i)\setminus \{x,y\}\}=\{j|3\le j\le n\}$ for all i. Again, we may swap the colors of x and y to obtain another extension of $\varphi$. Hence $\varphi$ is not a Sudoku coloring.

Thus, $sn(G)=m(n-r-1)+r-1$. □

Corollary 3.8.

For $m\ge 2,sn(f_m)=m$.

A tadpole graph T(n, m) is obtained from a cycle C_n and a P_m by identifying a vertex of C_n to an end vertex of P_m.

Theorem 3.9.

For $n\ge 3$ and $m\ge 2$, $$sn(T(n,m))=\{\begin{array}{cc}1\hfill & \text{ if }n\text{ even,}\hfill \\ \lfloor \frac{n+m}{2}\rfloor \hfill & \text{ if }n\text{ odd}.\hfill \end{array}$$

Proof.

Let $C_n=v_1{v}_2\cdots v_n{v}_1$ and $P_m=u_1{u}_2\cdots u_m$ with v₁ = u₁. Also let $G=T(n,m)$. The case n is even follows from Theorem 3.1. So, following we assume n is odd.

Suppose m is even. Let $S=\left\{v_i\right|2\le i\le n-1,i\text{ is even}\}\cup \{u_j|2\le j\le m,j\text{ is even}\}$ Define a coloring $\mathcal{C}$ on $G[S]$ by $$\begin{array}{c}\mathcal{C}(u_j)=\{\begin{array}{cc}2\hfill & \text{ if }j\equiv 2\hspace{1em}\left(\mathrm{mod}4\right)\hfill \\ 3\hfill & \text{ if }j\equiv 0\hspace{1em}\left(\mathrm{mod}4\right)\hfill \end{array}\hspace{1em}\text{ and }\\ \mathcal{C}(v_i)=\{\begin{array}{cc}3\hfill & \text{ if }i\equiv 2\hspace{1em}\left(\mathrm{mod}4\right)\hfill \\ 2\hfill & \text{ if }i\equiv 0\hspace{1em}\left(\mathrm{mod}4\right)\hfill \end{array}\end{array}$$

Now, we can extend this coloring $\mathcal{C}$ to a unique 3-coloring of T(n, m) with $\mathcal{C}(v_n)=3,2$ depending on whether $n\equiv 1$ or $3\hspace{1em}(\mathrm{mod}4)$, and $\mathcal{C}(v)=1$ for each remaining vertex v. Thus, $sn(T(n,m))\le \frac{n+m-1}{2}=\lfloor \frac{n+m}{2}\rfloor$.

Suppose there is an extendable coloring $\varphi$ of $G[S]$ with $\left|S\right|\le \frac{n+m-3}{2}.$ Then $|V(G)\setminus S|\ge \frac{n+m+1}{2}$. By Lemma 2.6 we may assume that $v_m\in S$. Now, consider $\frac{n+m-1}{2}$ subsets $\{u_{2j},u_{2j+1}\},1\le j\le (m-2)/2$; $\{v_{2i},v_{2i+1}\},1\le i\le (n-1)/2$; and $\left\{v_1\right\}$. By pigeonhole principle, there is a K₂ in G – S which satisfies the condition of Lemma 2.7. Thus $\varphi$ is not a Sudoku coloring. Thus $sn(T(n,m))=\lfloor \frac{n+m}{2}\rfloor$.

Suppose m is odd. Let $S=\left\{v_i\right|2\le i\le n-1,i\text{ is even}\}\cup \{u_j|1\le j\le m,j\text{ is odd}\}.$ Define a coloring $\mathcal{C}$ on $G[S]$ by $$\begin{array}{c}\mathcal{C}(u_j)=\{\begin{array}{cc}1\hfill & \text{ if }j\equiv 1\hspace{1em}\left(\mathrm{mod}4\right)\hfill \\ 3\hfill & \text{ if }j\equiv 3\hspace{1em}\left(\mathrm{mod}4\right)\hfill \end{array}\hspace{1em}\text{ and }\\ \mathcal{C}(v_i)=\{\begin{array}{cc}3\hfill & \text{ if }i\equiv 2\hspace{1em}\left(\mathrm{mod}4\right)\hfill \\ 2\hfill & \text{ if }i\equiv 0\hspace{1em}\left(\mathrm{mod}4\right)\hfill \end{array}\end{array}$$

Now, we can extend this coloring $\mathcal{C}$ to a unique 3-coloring of T(n, m) with $\mathcal{C}(v_n)=3,2$ depending on whether $n\equiv 1$ or $3\hspace{1em}(\mathrm{mod}4)$, $\mathcal{C}(v_i)=1$ for each remaining vertex v_i and $\mathcal{C}(u_j)=2$ for each remaining vertex u_j. Thus, $sn(T(n,m))\le \frac{n+m}{2}=\lfloor \frac{n+m}{2}\rfloor$.

Suppose there is an extendable coloring $\varphi$ of $G[S]$ with $\left|S\right|\le \frac{n+m-2}{2}$, then $|V(G)\setminus S|\ge \frac{n+m}{2}$. By Lemma 2.6 we may assume that $v_m\in S$. Now, consider $\frac{n+m}{2}-1$ edges $u_{2j-1}{u}_{2j},1\le j\le (m-1)/2$; and $v_{2i}{v}_{2i+1},1\le i\le (n-1)/2$. By pigeonhole principle, there is an edge xy in G – S. If $xy\ne u_1{u}_2$, then by Lemma 2.7 $\varphi$ is not a Sudoku coloring. Now let $xy=u_1{u}_2$. We may additionally assume that no edge of the graph $G-u_1$ lies in G – S.

If $v_n\notin S$, then the path $v_n{u}_1{u}_2$ lies in G – S. We extend $\varphi$ to $G-\{v_n,u_1,u_2\}$. Then the color-list of $v_n,u_1,u_2$ are of at least 2 colors. By Lemma 2.1, $\varphi$ can be extended to at least two 3-colorings of G. Thus $\varphi$ is not a Sudoku coloring.

If $v_n\in S$, then $v_2\notin S$ by the additional condition. This is the same case as the above case.

Thus, $sn(T(n,m))=\frac{n+m}{2}$. □

A lollipop graph L(n, m) is obtained from a K_n and a path P_m by identifying a vertex of K_n to an end vertex of P_m. Note that $T(3,m)=L(3,m)$.

Theorem 3.10.

For $n\ge 4$ and $m\ge 2,sn(L(n,m))=n+m-3$.

Proof.

Let the vertices of K_n be $v_i,1\le i\le n$ and $P_m=u_1{u}_2\cdots u_m$ with v₁ = u₁. Obviously $\chi (L(n,m))=n$.

Let $G=L(n,m)$. Let $S=\left\{v_i\right|3\le i\le n\}\cup \{u_j|2\le j\le m\}$. Then $\left|S\right|=n+m-3$. Define $\mathcal{C}(v_i)=i,3\le i\le n,\mathcal{C}(u_j)=2$ for even j and $\mathcal{C}(u_j)=1$ for odd j, where $2\le j\le m$. If we extend $\mathcal{C}$, then v₁ = u₁ must be colored by 1 and v₂ by 2. So $\mathcal{C}$ is a Sudoku coloring. Hence $sn(G)\le n+m-3$.

Let $\varphi$ be an extendable coloring of $G[S]$, for some $S\subset V(G)$ with $\left|S\right|<n+m-3$. In other words $|V(G)\setminus S|\ge 3$. Let x, y, z be three vertices in $V(G)\setminus S$. We extend $\varphi$ to $G-\{x,y,z\}$ first.

Suppose x = u_i, $2\le i\le m$. Then the color-list of x contains at least n – 2 colors. Thus $\varphi$ has at least two extensions.

Suppose x, y, z are in K_n. Without loss of generality let x = v₂ and y = v₃. Hence $\varphi$ is not a Sudoku coloring by Lemma 2.7.

Thus $sn(G)=n+m-3$. □

Let $C_{2n}(K_m)$ be a graph obtained from a 2n-cycle $C_{2n}$ by identifying every alternate edge of $C_{2n}$ with an edge of a distinct complete graph K_m. Thus, $C_{2n}(K_m)$ contains n copies of complete subgraph K_m such that the edges not belong to any K_m are alternate edges of $C_{2n}$. If $C_{2n}=x_1{x}_2\cdots x_{2n-1}{x}_{2n}{x}_1$, then $x_{2i-1}{x}_{2i}$ is an edge of the i-th complete graph K_m, $1\le i\le n$. We will denote the i-th complete graph K_m by Kⁱ. When we remove the vertices $x_{2i-1}$ and $x_{2i}$ from the Kⁱ, then the resulting subgraph $H^i\cong K_{m-2}$.

Theorem 3.11.

For $n\ge 2,m\ge 3,sn(C_{2n}(K_m))=n(m-2)$.

Proof.

Keep the notation defined above. Color any m – 3 vertices of each Hⁱ by $\left\{j\right|4\le j\le m\},1\le i\le n$. For even n, color $x_{4j+1}$ by 1 and $x_{4j+3}$ by 2 for $0\le j\le (n-2)/2$. For odd n, color $x_{4j+1}$ by 1; $x_{4j+3}$ by 2 for $0\le j\le (n-3)/2$ and $x_{2n-1}$ by 3.

Clearly, this is a proper coloring for the subgraph of $C_{2n}(K_m)$ induced by the colored vertices. To extend this coloring to the whole graph, all $x_{2j}$’s must be colored by 1, 2, or 3 uniquely. After that, the color of the last uncolored vertex in each Hⁱ is also fixed. Thus, $sn(C_{2n}(K_m))\le n(m-2)$.

Suppose there is an extendable coloring $\varphi$ of $C_{2n}(K_m)[S]$ with $\left|S\right|\le n(m-2)-1$. Then at least $2n+1$ vertices of $C_{2n}(K_m)$ have not been colored under $\varphi$. By pigeonhole principle, at least one Kⁱ, say i = 1 for convenience, contains at least three uncolored vertices, say u, v, w. We extend $\varphi$ to be an m-coloring of $C_{2n}(K_m)-\{u,v,w\}$. Now, the color-lists of u, v, w are the same and are of size 3. By Lemma 2.2, $\varphi$ is not a Sudoku coloring. Thus $sn(C_{2n}(K_m))=n(m-2)$. □

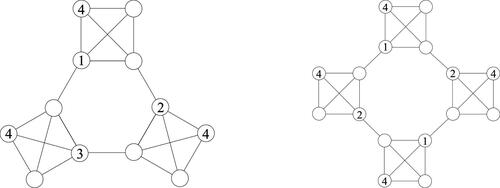
Example 3.1.

Two Sudoku colorings for $C_6(K_4)$ and $C_8(K_4)$ are given in Figure 6.

Fig. 6 Sudoku colorings of $C_6(K_4)$ and $C_8(K_4)$.

Keep the notation of defining the graph $C_{2n}(K_m)$. Let $C_{2n}(K_m^{-})$ be the graph obtained from $C_{2n}(K_m)$ by removing the n edges $x_{2i-1}{x}_{2i},1\le i\le n$. Thus $C_{2n}(K_m^{-})$ is an $(m-1)$-regular graph.

Theorem 3.12.

For $n\ge 2$ and $m\ge 4,sn(C_{2n}(K_m^{-}))=(m-3)n+1$.

Proof.

Let $G=C_{2n}(K_m^{-})$. Let $y_{i,j},1\le j\le m-2$, be the vertices of Hⁱ, $1\le i\le n$. Note that $\chi (G)=m-1$. We shall first show that $sn(G)\le (m-3)n+1$.

Suppose n is even. Define a partial coloring $\mathcal{C}$ on $C_{2n}(K_m^{-})$ by $\mathcal{C}(y_{i,j})=j+1$ for $1\le i\le n$ and $2\le j\le m-2,\mathcal{C}(y_{1,1})=2$. To extend $\mathcal{C}$ as an $(m-1)$-coloring, the odd path $x_2{x}_3{y}_{2,1}{x}_4\cdots x_{2n-1}{y}_{n,1}{x}_{2n}{x}_1$ must be colored alternatively by 1,2 starting from x₂ and ending at x₁. So $\mathcal{C}$ is a Sudoku coloring for G.

Suppose n is odd. Define a partial coloring $\mathcal{C}$ on $C_{2n}(K_m^{-})$ by $\mathcal{C}(y_{i,j})=j+1$ for $1\le i\le n-1$ and $2\le j\le m-2,\mathcal{C}(y_{1,1})=2,\mathcal{C}(y_{n,j})=j+1$ for $3\le j\le m-2$ (no this case if m = 4), and $\mathcal{C}(y_{n,2})=1$. To extend $\mathcal{C}$ as an $(m-1)$-coloring, the even path $x_2{x}_3{y}_{2,1}{x}_4\cdots x_{2n-1}{y}_{n,1}{x}_{2n}{x}_1)$ must be colored alternatively by 1,2 starting from x₂ and ending at $x_{2n-3}$. And then the last 6 vertices $y_{n-1,1},x_{2n-2},x_{2n-1},y_{n,1},x_{2n},x_1$ must be colored by 1, 2, 3, 2, 3,1, respectively. So $\mathcal{C}$ is a Sudoku coloring for G.

So we have $sn(C_{2n}(K_m^{-}))\le (m-3)n+1$ for both cases of n.

Suppose there is an extendable coloring $\varphi$ of $G[S]$ with $\left|S\right|\le (m-3)n$. Let the extension of $\varphi$ be ψ. Then at least 3n vertices of G have not been colored under $\varphi$.

1. Suppose $y_{i,j_1}$ and $y_{i,j_2}$ have not been colored under $\varphi$, for some i, $1\le j_1<j_2\le m-2$. Then $\psi (y_{i,j_1})\ne \psi (y_{i,j_2})$. Now we may exchange the colors of $y_{i,j_1}$ and $y_{i,j_2}$ to obtain another $(m-1)$-coloring for G. Thus $\varphi$ is not a Sudoku coloring for G.

2. Suppose at most one $y_{i,j}$ is uncolored by $\varphi$, for each i. In other word, at most 3 vertices of each $K^i-x_{2i-1}{x}_{2i}$ have not been colored. By pigeonhole principle, exactly three vertices of $K^i-x_{2i-1}{x}_{2i}$ have not been colored for each i. That is, $x_{2i-1},y_{i,j_i}$ and $x_{2i}$ have not been colored, for some j_i. All uncolored vertices induce a 3n-cycle C. The color-list of each vertex containing exactly two colors. By Lemma 2.2, $\varphi$ is not a Sudoku coloring for G.

Thus, $sn(C_{2n}(K_m^{-}))=(m-3)n+1$. □

Example 3.2.

A Sudoku coloring for $C_{10}(K_5^{-})$ and its extension are given in Figure 7.

Fig. 7 A Sudoku coloring and its extension for $C_{10}(K_5^{-})$.

Let G₁ = K₃ with vertices $x_1,y,z$. For $i\ge 2$, let G_i be obtained from $G_{i-1}$ by adding a vertex x_i adjacent to two adjacent vertices of $G_{i-1}$ (to form a new triangle) so that G_i is a 2-connected plane graph whose faces are triangles. Note that for $i\ge 3$, G_i is not unique. Consequently, every maximal outerplanar graph of order n + 2 is a possible G_n, $n\ge 1$. A fan graph F_n, $n\ge 2$, is obtained from $P_n=v_1{v}_2\cdots v_n$ by joining a vertex u to every vertex of P_n. Thus, F_n is a possible $G_{n-1}$.

Theorem 3.13.

For $i\ge 1$, let G_i be defined as above. Then $sn(G_i)=2$.

Proof.

Since $\chi (G_i)=3$, we have $sn(G_i)\ge 2$ for $i\ge 1$. Let $S=\{y,z\}$ and $G_i[S]$ has a coloring $\mathcal{C}(y)=1,\mathcal{C}(z)=2$. This coloring can be extended to a unique 3-coloring of G_i since we must color x₁ by 3 and for $i\ge 2$, we must color x_i by exactly one of 1, 2, or 3 which is different to the colors assigned to its two neighbors. So, $sn(G_i)\le 2$. Thus, $sn(G_i)=2$. □

Corollary 3.14.

Every fan graph (and maximal outerplanar graph) G has sn(G) = 2.

A wheel graph W_n, $n\ge 3$ of order n + 1 is obtained from an n-cycle $C_n=v_1{v}_2\cdots v_n{v}_1$ by joining a vertex u to every vertex of C_n. In each of these graphs, the maximum degree vertex is called the core of the graph.

Theorem 3.15.

For $n\ge 3,sn(W_n)=2$ if n is even, $sn(W_3)=3$ and $sn(W_n)=\frac{n+1}{2}$ if $n\ge 5$ is odd.

Proof.

Since W_n is not bipartite, $sc(W_n)\ge 2$.

Suppose n even. It is known that $\chi (W_n)=3$. Let $S=\{u,v_1\}$, then $W_n[S]$ has a coloring $\mathcal{C}(u)=1,\mathcal{C}(v_1)=2$. This coloring can be uniquely extended to a 3-coloring of W_n since we must have $\mathcal{C}(v_i)=2$ for remaining odd i, and $\mathcal{C}(v_i)=3$ for even i. So, $sn(W_n)\le 2$. Hence $sn(W_n)=2$.

Suppose n is odd. It is known that $\chi (W_n)=4$. The case W₃ = K₄ follows from Corollary 3.4. We assume $n\ge 5$. Let $S=\{v_i | 1\le i\le n,n\text{ is odd}\}$. Now, $W_n[S]$ has a coloring $\mathcal{C}(v_n)=4,\mathcal{C}(v_i)=2$ for $i\equiv 1\hspace{1em}(\mathrm{mod}4),i\ne n$ and $\mathcal{C}(v_i)=3$ for $i\equiv 3\hspace{1em}(\mathrm{mod}4),i\ne n$. This coloring can be uniquely extended to a 4-coloring of W_n since we must have $\mathcal{C}(u)=1,\mathcal{C}(v_i)=4$ for even $i\le n-3$, and $\mathcal{C}(v_{n-1})=2$ if $n\equiv 1\hspace{1em}(\mathrm{mod}4)$ while $\mathcal{C}(v_{n-1})=3$ if $n\equiv 3\hspace{1em}(\mathrm{mod}4)$. So, $sn(W_n)\le \frac{n+1}{2}$.

Suppose there is an extendable coloring $\varphi$ of $W_n[S]$ with $\left|S\right|\le \frac{n-1}{2}$. Since C_n is Hamiltonian, the number of components of $C_n-(S\setminus \{u\})$ is most $\left|S\right|\le \frac{n-1}{2}$. Since $C_n-(S\setminus \{u\})$ contains $\frac{n+1}{2}$ vertices, there is a K₂ subgraph in $C_n-(S\setminus \{u\})$. By Lemma 2.7, $\varphi$ is not a Sudoku coloring. Hence, $sn(W_n)=\frac{n+1}{2}$. □

4 Complexity for deciding extendable coloring

We now proceed to prove that for a given partial coloring $\varphi$ of a graph G with $\chi (G)=k$, the problem of deciding whether $\varphi$ is an extendable coloring is NP-complete.

The following is a classical result on graph colorings due to Grötzsch [6].

Theorem 4.1.

Any triangle-free planar graph is 3-colorable.

Extendable Partial Coloring Problem (EPCP)

Instance: A graph G with $\chi (G)=k$ and a partial coloring $\varphi$ of G.

Question: Can $\varphi$ be extended to a k-coloring of G?

Garey et al. [5] have proved that 3-colorability of planar graphs with maximum degree at most four is NP-complete. Using this, Dalley [3] proved that 3-colorability of 4-regular planar graphs is NP-complete. Also by Theorem 4.1, any triangle-free planar graph is 3-colorable. Hence the following problem is NP-complete.

3-colorability of 4-regular planar graphs having a triangle T (3C4PG)

Instance: A 4-regular planar graph G having a triangle T.

Question: Can G be colored with 3 colors?

Theorem 4.2.

EPCP is NP-complete.

Proof.

The proof is by reduction from 3C4PG. Let G be a 4-regular planar graph having a triangle T. We construct an instance of EPCP. Let $H=G+O_2$ and let $V(O_2)=\{u,v\}$. Let $\varphi$ be a partial coloring of H which assigns color 4 to u and v, and colors 1, 2, and 3 to the vertices of T. Since color 4 cannot be used for any vertex of G in an extension of $\varphi$, it follows that $$ is an extendable coloring of H if and only if G is 3-colorable. Hence EPCP is NP-complete. □

5 Conclusion and scope

The standard Sudoku graph is the Cartesian product $K_9\square K_9$ together with nine more copies of K₉ corresponding to the nine 3 × 3 subsquares. Hence determining the Sudoku number of $K_n\square K_n$ is an interesting problem for further investigation. If G is a disconnected graph with c components, then $sn(G)\ge c$. Investigation of Sudoku number of disconnected graphs is another interesting direction for further research.

Acknowledgments

The authors are thankful to Stijn Cambie and Bernardo Anibal Subercaseaux Roa for their helpful suggestions in proving Theorems 3.5 and 4.2, respectively.