On the metric dimension of bipartite graphs

Abstract

For an ordered subset $W=\{w_1,w_2,\dots ,w_k\}$ of vertices and a vertex v in a connected graph G, the ordered k-vector $r(v|W)=(d(v,w_1),d(v,w_2),\dots ,d(v,w_k))$ is called the representation of v with respect to W, where $d(v,w_i)$ is the distance between v and w_i, for $1\le i\le k$. The set W is called a resolving set of G if $r(u|W)\ne r(v|W)$, for every pair $u,v\in V(G)$. The minimum positive integer k for which G has a resolving set of cardinality k is the metric dimension of G, denoted as dim(G). A resolving set of G of cardinality dim(G) is a metric basis of G. For a bipartite graph G, projection is defined as a graph with the vertices of one of the partite sets, where two vertices are adjacent if they have at least one common neighbor in the other partite set. In this paper, we investigate the relation between the metric dimension of a bipartite graph and its projections. Furthermore, we present some realization results for the bounds on the metric dimension of a bipartite graph.

KEYWORDS:

• Distance
• resolving set
• metric dimension
• bipartite graph
• projection

2010 AMS SUBJECT CLASSIFICATION:

• 05C12

1 Introduction

The study of locating the vertices in a connected graph based on a distance parameter is a crucial idea for keeping track of graph-structured networks. To monitor a network efficiently, the goal is to distinguish every pair of vertices with respect to a set with minimum number of vertices. The concept of metric dimension fulfills the requirements of our goal to oversee a network.

In this paper, we consider simple, finite, and connected graphs. The distance d(u, v) between two vertices u and v in a connected graph G is the length of a shortest u – v path in G. For an ordered subset $W=\{w_1,w_2,\dots ,w_k\}$ of vertices and a vertex v in a connected graph G, the ordered k-vector $r(v|W)=(d(v,w_1),d(v,w_2),\dots ,d(v,w_k))$ is called the representation of v with respect to W. The set W is called a resolving set of G if distinct vertices have distinct representations. A minimum resolving set is a metric basis of G and its cardinality is the metric dimension of G, denoted as dim(G). P. J. Slater [12] pioneered this concept in the name of locating set. Independently, Harary and Melter [9] introduced the same concept, but coined as resolving set. Garey and Johnson [8] shown that finding the metric dimension of general graphs is an NP-complete problem. For a non-trivial connected graph G of order n, $1\le \dim (G)\le n-1$. Chartrand et al. [5] characterized all graphs with metric dimensions of $1,n-1$, or n – 2. Caceres et al. [4] investigated the metric dimension of Cartesian product of graphs. For the past few decades, this study has enormous growth. For some more previous investigations on this topic, refer [1, 3, 6, 10, 11].

In general, it is difficult to determine the metric dimension of an arbitrary graph. Finding exact values or reliable bounds for the metric dimension of particular classes of graphs has been the focus of a lot of research. Bipartite graph is one among the interesting graphs which can be modeled for two different sets of entities and their connections.

A bipartite graph G(V, E) is a graph whose vertex set V can be partitioned into two subsets V₁ and V₂ such that $V=V_1\cup V_2$ and each edge of G joins a vertex of V₁ to a vertex of V₂.

Baca et al. [1] determined the metric dimension of k-regular bipartite graphs G(n, n), where $k=n-1$ or $k=n-2$ and n is the number of vertices in each partite set. Since the problem of finding the metric dimension of a graph is NP-complete even when restricted to bipartite graphs [7], this paper studies the metric dimension of bipartite graphs.

Let G(V, E) be a bipartite graph with the partite sets V₁ and V₂. For the purpose of convenience, we assume that $U=V_1$ and $S=V_2$. This results that $V=U\cup S$ and $U\cap S=\varnothing$.

Definition 1.1

([2]). Let $G(U,S,E)$ be a bipartite graph with $\left|U\right|=n_1,\left|S\right|=n_2$ and $|E(G)|=m$. We define a graph $G\prime (U,E\prime )$ as the projection of the bipartite graph G for the vertex set U with respect to the vertex set S, where $V(G\prime )=U$ and $u_i{u}_j\in E(G\prime )$ if $N(u_i)\cap N(u_j)\ne \varnothing$, for $u_i,u_j\in U$.

For a bipartite graph G, projection made it simple to evaluate the metric dimension of G, by taking into account fewer vertices than the original graph. In particular, a bipartite graph is compressed into a new graph called projection with fewer vertices.

A bipartite graph $G(U,S,E)$ will always provide two projections. One for the vertex set U with respect to the vertex set S, denoted as $G\prime (U)$ and the other one for the vertex set S with respect to the vertex set U, denoted as $G\prime (S)$.

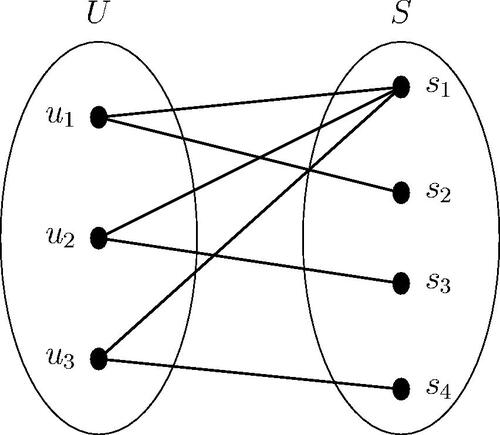
Consider the bipartite graph $G(U,S,E)$ with the partite sets $U=\{u_1,u_2,u_3\}$ and $S=\{s_1,s_2,s_3,s_4\}$ shown in Figure 1.

Fig. 1 Bipartite graph $G(U,S,E).$

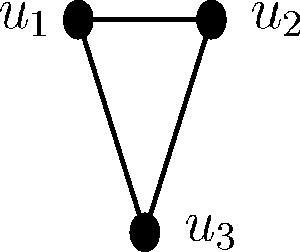
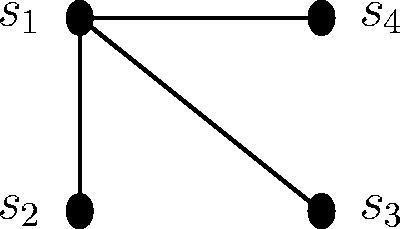
The projection $G\prime (U)$ of the bipartite graph G for the vertex set U with respect to the vertex set S and the projection $G\prime (S)$ of the bipartite graph G for the vertex set S with respect to the vertex set U are the graphs in Figures 2 and Figure 3, respectively.

Fig. 2 The projection $G\prime (U)$.

Fig. 3 The projection $G\prime (S)$.

2 The metric dimension of a bipartite graph and its projections

In this section, we establish some bounds on the metric dimension of bipartite graphs through projection.

The following lemma states that the relation between the distances of two vertices in a bipartite graph and its projection.

Lemma 2.1.

Let $G(U,S,E)$ be a connected bipartite graph. If $G\prime$ is the projection of G for the vertex set U with respect to the vertex set S, then $d_G(u_i,u_j)=2d_{G\prime }(u_i,u_j)$, for $u_i,u_j\in U$.

Proof.

We can rewrite the statement of this lemma as “If $G\prime$ is the projection of G for the vertex set U with respect to the vertex set S, then $d_G(u_i,u_j)=2x$ if and only if $d_{G\prime }(u_i,u_j)=x$, for $u_i,u_j\in U$ and $x\ge 0$.”

(If) Let $G\prime$ be the projection of a bipartite graph $G(U,S,E)$ for the vertex U with respect to the vertex set S.

We proceed by induction on the distance $d_{G\prime }(u_i,u_j)=x$.

Let $d_{G\prime }(u_i,u_j)=1$. Since $G\prime$ is the projection of the bipartite graph G, there exists a vertex $s_{ij}\in S$ such that $u_i{s}_{ij},u_j{s}_{ij}\in E(G)$. Thus, $d_G(u_i,u_j)=2$. This proves the base case. Assume that $d_G(u_i,u_l)=2(x-1)$, for $u_i,u_l\in U$ provided $d_{G\prime }(u_i,u_l)=x-1$. Let $d_{G\prime }(u_i,u_j)=x$. Choose a vertex $u_{j\prime }\in N_{G\prime }(u_j)$ such that $d_{G\prime }(u_i,u_{j\prime })=x-1$. Our assumption results that $d_G(u_i,u_{j\prime })=2(x-1)$. Let P be a shortest path from u_i to $u_{j\prime }$ of length $2(x-1)$ in G. Since $u_j{u}_{j\prime }\in E(G\prime )$, there exists a vertex $\mathrm{(}\text{HTML translation failed}\mathrm{)}$ such that $u_{j\prime }{s}_{jj\prime },u_j{s}_{jj\prime }\in E(G)$. P being a shortest path from u_i to $u_{j\prime }$ in G, we have $s_{jj\prime }\notin P$. Thus, P along with the edges $u_{j\prime }{s}_{jj\prime }$ and $s_{jj\prime }{u}_j$ forms a shortest path from u_i to u_j of length 2x in G.

(Only if) Let u_i and u_j be two vertices in G such that $d_G(u_i,u_j)=2x$.

Claim : $d_{G\prime }(u_i,u_j)=x$.

Suppose that $d_{G\prime }(u_i,u_j)<x$. Without loss of generality, let $d_{G\prime }(u_i,u_j)=x-1$. Let $Q=u_i=u_{ij}^1,u_{ij}^2,\dots ,u_{ij}^{(x)}=u_j$ be a shortest $u_i-u_j$ path of length $x-1$ in $G\prime$. Then the bipartite graph G yields at least $x-1$ distinct vertices of S say $s_1,s_2,\dots ,s_{x-1}$ such that for every pair $u_{ij}^l,u_{ij}^{(l+1)}$ of Q, there exists a vertex s_l with $u_{ij}^l{s}_l,u_{ij}^{(l+1)}{s}_l\in E(G)$, for $1\le l\le x-1$. This results a $u_i-u_j$ path of length $2(x-1)$ in G, which is a contradiction. In a similar manner, we reach a contradiction for $d_{G\prime }(u_i,u_j)>x$. Therefore, the result follows. □

Theorem 2.2.

Let $G(U,S,E)$ be a connected bipartite graph. Then $\mathit{dim}(G)\le \mathit{dim}(G_1)+\mathit{dim}(G_2)$, where G₁ and G₂ are the projections of G for the vertex set U with respect to the vertex set S and for the vertex set S with respect to the vertex set U respectively.

Proof.

Let G₁ and G₂ be the projections of a bipartite graph $G(U,S,E)$ for the vertex set U with respect to the vertex set S and for the vertex set S with respect to the vertex set U, respectively. Let $W_1=\{u_1,u_2,\dots ,u_k\}$ and $W_2=\{s_1,s_2,\dots ,s_l\}$ be minimum resolving sets of G₁ and G₂ respectively. Set $W=\{u_1,u_2,\dots ,u_k,s_1,s_2,\dots ,s_l\}$. Since G is bipartite, we have $d_G(u,u_i)\ne d_G(s,u_i)$, for $u\in U\setminus W,s\in S\setminus W$ and for all $u_i\in W_1$. Hence, it remains to prove that $r(u_s|W)\ne r(u_t|W)$, for $u_s,u_t\in U\setminus W$. The projection G₁ ensures that for a pair of vertices $u_s,u_t\in U\setminus W$, there is a vertex $u_r\in W_1$ such that $d_{G_1}(u_s,u_r)\ne d_{G_1}(u_t,u_r)$. This consequences that $2d_{G_1}(u_s,u_r)\ne 2d_{G_1}(u_t,u_r)$. By Lemma 2.1, $d_G(u_s,u_r)\ne d_G(u_t,u_r)$. Since $W_1\subset W$, u_r resolves u_s and u_t in G. Therefore, W resolves U in G. Similarly, it can be proved that the vertices of $W_2\subset W$ resolves S in G. This completes the proof. □

Theorem 2.3.

Let $G(U,S,E)$ be a connected bipartite graph. Then $\mathit{dim}(G)\ge \min \{\mathit{dim}(G_1),\mathit{dim}(G_2)$}, where G₁ and G₂ are the projections of G for the vertex set U with respect to the vertex set S and for the vertex set S with respect to the vertex set U respectively.

Proof.

Let G₁ and G₂ be the projections of a bipartite graph $G(U,S,E)$ for the vertex set U with respect to the vertex set S and for the vertex set S with respect to the vertex set U respectively. Without loss of generality, assume that $\mathit{dim}(G_1)\le \mathit{dim}(G_2)$. Let W₁ be a minimum resolving set of G₁ of cardinality k. Since G is a bipartite graph, by Lemma 2.1, we have $d_G(u_i,u_j)=2d_{G\prime }(u_i,u_j)$, for $u_i,u_j\in U$. This results that W₁ resolves the vertices of U in G. We consider the following three cases.

Case 1: Assume, to the contrary that $W=W_1\setminus \left\{w\right\}$, where $w\in W_1$ forms a minimum resolving set of G. Then W resolves V(G). In particular, $r_G(w|W)\ne r_G(v|W)$, for all $v\in V(G)\setminus \left\{w\right\}$. This follows that $d_G(w,w_i)\ne d_G(v,w_i)$, for $v\in U\setminus \left\{w\right\}$ and for some $w_i\in W$. Lemma 2.1 ensures that $d_{G_1}(w,w_i)\ne d_{G_1}(v,w_i)$, for some $w_i\in W$. However, W forms a resolving set of G₁, which is a contradiction.

Case 2: Suppose $W\subset S$ is a minimum resolving set of G such that $\left|W\right|<\left|W_1\right|$. Let $W=\{s_1,s_2,\dots ,s_{k-1}\}$. Then $r_G(u_p|W)\ne r_G(u_q|W)$, for all $u_p,u_q\in U,1\le p<q\le n_1$. This consequences that $d_G(u_p,s_i)\ne d_G(u_q,s_i)$, for some $s_i\in W$. In fact, for every $s_i\in W$, there exists a vertex $u_i\in U$ such that $u_i{s}_i\in E(G)$ to obtain $d_G(u_i,u_p)\ne d_G(u_i,u_q)$, for all $i,1\le i\le k-1$. By Lemma 2.1, we have $d_{G_1}(u_i,u_p)\ne d_{G_1}(u_i,u_q)$. This generates a minimum resolving set $\{u_1,u_2,\dots ,u_{k-1}\}$ of G₁ of cardinality less than k, which is a contradiction.

Case 3 : Suppose W is a minimum resolving set of G which intersects both U and S such that $\left|W\right|<\left|W_1\right|$. Let $W=\{u_1,u_2,\dots ,u_r,s_1,s_2,\dots ,s_{k-r-1}\}$, where $u_i\in U,s_j\in S$. Let $u_p,u_q\in U\setminus W,1\le p<q\le n_1$ be the vertices of U resolved by the vertices of $W\cap S$ in G. This consequences that $d_G(u_p,s_i)\ne d_G(u_q,s_i)$, for some $s_i\in W$. As discussed in case 2, for every $s_i\in W$, we can associate a vertex $u_i^{\prime }\in U$ such that $u_i^{\prime }{s}_i\in E(G)$ with $d_G(u_i^{\prime },u_p)\ne d_G(u_i^{\prime },u_q)$, for $1\le i\le k-r-1$. By Lemma 2.1, we have $d_{G_1}(u_i^{\prime },u_p)\ne d_{G_1}(u_i^{\prime },u_q)$. This produces a resolving set $\{u_1,u_2,\dots ,u_r,u_1^{\prime },u_2^{\prime },\dots ,u_{k-r-1}^{\prime }\}$ of G₁ of cardinality less than k, which is a contradiction.

In each case, there is no resolving set W of G such that $\left|W\right|<\left|W_1\right|$. Hence, we conclude that $\mathit{dim}(G)\ge \min \{\mathit{dim}(G_1),\mathit{dim}(G_2)\}$. □

Next, we provide some realizable results corresponds to the Theorem 2.3.

A bipartite graph $G(U,S,E)$ with $\left|U\right|=n_1$ and $\left|S\right|=n_2$ is called a chain graph if there exists an ordering $u_1,u_2,\dots ,u_{n_1}$ of U and an ordering $s_1,s_2,\dots ,s_{n_2}$ of S such that $N(u_1)\supseteq N(u_2)\supseteq N(u_3)\supseteq \cdots \supseteq N(u_{n_1})$ and $N(s_1)\subseteq N(s_2)\subseteq N(s_3)\subseteq \cdots \subseteq N(s_{n_2})$.

Proposition 2.4.

Let $G(U,S,E)$ be a connected bipartite chain graph with an ordering $u_1,u_2,\dots ,u_{n_1}$ of U and an ordering $s_1,s_2,\dots ,s_{n_2}$ of S such that $N(u_1)\supseteq N(u_2)\supseteq N(u_3)\supseteq \cdots \supseteq N(u_{n_1})$ and $N(s_1)\subseteq N(s_2)\subseteq N(s_3)\subseteq \cdots \subseteq N(s_{n_2})$. Let $G\prime$ be the projection for one of the partite sets with respect to the other. Then $(i)$ $\mathit{dim}(G)>\mathit{dim}(G\prime )$, whenever there exist $u,v\in V(G)\setminus V(G\prime )$ such that $\mathrm{(}\text{HTML translation failed}\mathrm{)}$, (ii) $\mathit{dim}(G)=\mathit{dim}(G\prime )$, otherwise.

Proof.

Without loss of generality, let $G\prime$ be the projection of G for the vertex set U with respect to the vertex set S. Since G is connected, we have $N(u_1)=S$. As a result, $G\prime$ is a complete graph on n₁ vertices and $\mathit{dim}(G\prime )=n_1-1$. Let $W\prime =V(G\prime )\setminus \left\{u_1\right\}$ be a minimum resolving set of $G\prime$. Suppose there exist two vertices $u,v\in V(G)\setminus V(G\prime )$ with $N(u)=N(v)$. Then $r(u|W\prime )=r(v|W\prime )$. Hence, $W\prime$ will not be a resolving set of G. Thus, to resolve G, it is necessary to add u or v into $W\prime$. This follows that $\mathit{dim}(G)>\mathit{dim}(G\prime )$. On the hand, if there is an ordering $s_1,s_2,\dots ,s_{n_2}$ of S such that $N(s_1)\subset N(s_2)\subset N(s_3)\subset ,\dots ,\subset N(s_{n_2})$, then there exist two vertices $s_i,s_j\in S$ with $N(s_i)\subset N(s_j)$, for $1\le i<j\le n_2$. Let $u_j\in N(s_j)\setminus N(s_i)$. Since $N(u_1)=S$, we have $u_j\ne u_1$. However, $u_j\in W\prime$ which resolves s_i and s_j. Hence, $W\prime$ is a minimum resolving set of G. Therefore, the result follows. □

In a connected graph G, two vertices u and v are said to be distance similar if $d(u,x)=d(v,x)$ for all $x\in V(G)\setminus \{u,v\}$. The set S of all vertices $u,v\in V(G)$ such that $d(u,x)=d(v,x)$ for all $x\in V(G)\setminus \{u,v\}$ is called a distance similar equivalence class in G.

Observation 2.5. If S is a distance similar equivalence class in a connected graph G with $\left|S\right|\ge 2$, then every resolving set of G contains at least $\left|S\right|-1$ vertices of S.

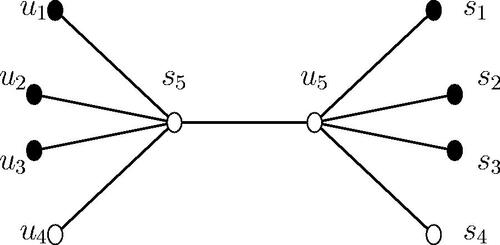
The bipartite graph G in Figure 4, has the partite sets $U=\{u_1,u_2,u_3,u_4,u_5\}$ and $S=\{s_1,s_2,s_3,s_4,s_5\}$. Since there are two distance similar equivalence classes $U\setminus \left\{u_5\right\}$ and $S\setminus \left\{s_5\right\}$ in G, every resolving set of G should contain the vertices of both the sets U and S.

Fig. 4 Bipartite graph $G(U,S,E)$ with its resolving set $\{u_1,u_2,u_3,s_1,s_2,s_3\}$.

As a result, it is interesting to learn about the bipartite graphs that are resolved by a subset of one of the partite sets. The following result guarantees the existence of a bipartite graph with a resolving set as a subset of one of the partite sets.

Let G be a graph. For a vertex $v\in V(G)$, we define $P_v=\{u\in N(v)|\mathrm{deg}(u)=1\}$. That is, P_v is the set of all pendent vertices adjacent to v. Moreover, if $\left|P_v\right|>1$, then P_v forms a distance similar equivalence class of G.

Theorem 2.6.

Let $G(U,S,E)$ be a bipartite graph. If $\left|P_u\right|>1$, for each $u\in U$, then there is a resolving set W of G such that $W\subseteq S$.

Proof.

Suppose $W\cap U\ne \varnothing$, for every resolving set W of G. Let $W\prime$ be a resolving set of G such that $W\prime \cap U=\{u_1,u_2,\dots ,u_r\}$, where $1\le r\le n_1$. Since $\left|P_u\right|>1$, for all $u\in U$, each $P_{u_i}$, for $1\le i\le r$ forms a distance similar equivalence class of G. By Observation 2.5, $W\prime$ contains at least $\left|P_{u_i}\right|-1$ vertices of $P_{u_i}$ those distinguishes the representation of u_i from others. Moreover, none of the vertices u_i will resolve the vertices of $N(u_i)$. This consequences that $W\prime \setminus \{u_1,u_2,\dots ,u_r\}$ is a resolving set of G, which is a contradiction. This completes the proof of the desired result. □

For a connected graph G of order n and diameter d, $\mathit{dim}(G)\le n-d$ [5]. In the following theorem, we provide the existence of a bipartite graph with $\mathit{dim}(G)=n-d$.

Theorem 2.7.

There exists a bipartite graph G of order n and diameter d such that $\mathit{dim}(G)=n-d$, for each pair $d,n\in N$, for $1\le d\le n-1$.

Proof.

Let d and n be positive integers with $1\le d\le n-1$. For d = 1, the complete graph K₂ is the only graph with the desired property. Suppose that $2\le d\le n-1$. Let G be the graph obtained from a star graph $H=K_{1,n-d}$ of order $n-d+1$ and a path $P:v_1,v_2,v_3,\dots ,v_{d-1}$ of order $d-1$ by joining the vertex of degree n – d say u in H to $v_{d-1}$. Then G is a bipartite graph of order n and diameter d. Since the n – d pendent vertices of $K_{1,n-d}$ forms a distance similar equivalence class of order n – d, by Observation 2.5, every resolving set of G contains at least $n-d-1$ pendent vertices of $K_{1,n-d}$. Therefore, $\dim (G)\ge n-d-1$. Let $W=V(K_{1,n-d})\setminus \{u,v\}$, where $u,v\in V(K_{1,n-d})$ and $u\ne v$. Then $r(v|W)=r(v_{d-1}|W)=(2,2,2,\dots ,2)$. This consequences that $\mathit{dim}(G)\ge n-d$. However, adding the vertex v or $v_{d-1}$ to W will results a minimum resolving set for G. Therefore, $\mathit{dim}(G)=n-d$. □

3 Conclusion and scope

The problem of finding the metric dimension of a bipartite graph is NP-complete [7]. This paper initiates the approach of determining the metric dimension of a bipartite graph using projection. A fascinating area for future research is similar investigation for other graph classes using projection.

Acknowledgments

The authors sincerely thank all of the anonymous reviewers for their valuable comments in improving the presentation of the paper.

Disclosure statement

The authors declare that there are no conflicts of interest.