On singularity and properties of eigenvectors of complex Laplacian matrix of multidigraphs

Abstract

In this article, we associate a Hermitian matrix to a multidigraph G. We call it the complex Laplacian matrix of G and denote it by $L_{\mathrm{}\mathbb{C}}(G)$. It is shown that the complex Laplacian matrix is a generalization of the Laplacian matrix of a graph. But, unlike the Laplacian matrix of a graph, the complex Laplacian matrix of a multidigraph may not always be singular. We obtain a necessary and sufficient condition for the complex Laplacian matrix of a multidigraph to be singular. For a multidigraph G, if $L_{\mathrm{}\mathbb{C}}(G)$ is singular, we say G is $L_{\mathrm{}\mathbb{C}}$-singular. We generalize some properties of the Fiedler vectors of undirected graphs to the eigenvectors corresponding to the second smallest eigenvalue of $L_{\mathrm{}\mathbb{C}}$-singular multidigraphs.

KEYWORDS:

• Multidigraph
• complex adjacency matrix
• complex Laplacian matrix
• spectrum
• Fiedler vector

AMS SUBJECT CLASSIFICATION:

• 05C50
• 05C05
• 15A18

1 Introduction

Throughout this article, we consider multidigraphs without self-loops. By a multidigraph, we mean a digraph (directed graph), where multiple directed edges between pairs of vertices are allowed, e.g. [8]. Two vertices in a multidigraph are said to be adjacent if there is at least one directed edge between them. Treating each undirected edge as equivalent to two oppositely oriented directed edges with the same end vertices, the class of all undirected graphs may be viewed as a subclass of the class of multidigraphs.

The adjacency matrix and the Laplacian matrix are among some of the most popular matrices associated with a graph. Let $G=(V(G),E(G))$ be a graph (undirected) on vertex set $V(G)=\{1,2,\dots ,n\}$. The adjacency matrix A(G) of G is an n × n matrix whose ijth entry is 1, if the vertices i and j are adjacent; and 0, otherwise. The Laplacian matrix L(G) of a graph G is defined as $L(G)=D(G)-A(G)$, where D(G) is the diagonal degree matrix of G. It is known that L(G) is positive semidefinite and 0 is one eigenvalue of L(G) afforded by the eigenvector $\mathbf{1}$, the vector of all ones. The Laplacian spectrum of a graph, in particular, the second smallest Laplacian eigenvalue of a graph has received much attention in the last three decades (see the survey articles by Merris and Mohar, e.g. [20, 21] and the references therein). Let $0={\lambda }_1(G)\le {\lambda }_2(G)\le \cdots \le {\lambda }_n(G)$ be the eigenvalues of L(G) arranged in nondecreasing order. Fiedler [10] proved that ${\lambda }_2(G)>0$ if and only if the graph G is connected. Observing ${\lambda }_2(G)$ as a quantitative measure of connectivity, Fiedler named it the algebraic connectivity of G and denoted by a(G). Subsequently, the algebraic connectivity has received much more attention, see [1] and the references therein. Relationship between the graph structure and the eigenvectors corresponding to its algebraic connectivity (popularly known as Fiedler vectors) has also been established, e.g. [4, 11–13, 18–20].

Let G be a graph and $x=(x_k),$ $k=1,2,\dots ,n,$ be a Fiedler vector of G. A vertex i in G is called a characteristic vertex with respect to x, if x_i = 0 and there is a vertex j adjacent to i such that $x_j\ne 0$. An edge {i, j} in G is called a characteristic edge with respect to x if $x_i{x}_j<0$. It is known that if G is a tree, then G has either exactly one characteristic vertex or exactly one characteristic edge with respect to x. Let G be a connected graph and x be a Fielder vector. If $V_x^{+}=\{i\in V(G):x_i\ge 0\}$ and $V_x^{-}=\{i\in V(G):x_i\le 0\}$, then it is known that the subgraphs induced by $V_x^{+}$ and $V_x^{-}$ are connected. We call x_i the valuation of vertex i with respect to the vector x. For a connected graph G, a vertex i is said to be a cut vertex of G if G – i (the graph obtained be deleting the vertex i from G) is disconnected. A block of a connected graph G is a maximal connected subgraph of G which does not have a cut vertex. The following results classify connected graphs into two distinct classes based on their Fiedler vectors.

Theorem 1.

(Fiedler [11]) Let G be a connected graph and $x=(x_k)$ be a Fiedler vector of G. Let i be a cut vertex of G and $G_1,G_2,\dots ,G_r$ be components of G – i. Then one of the following cases occur.

1. If $x_i>0$, then exactly one of the components $G_s,s=1,2,\dots ,r,$ contains a vertex with negative valuation. Moreover, x_i < x_j for all vertices j in the remaining components.

2. If x_i = 0 and there is a component containing both positively and negatively valuated vertices, then there is exactly one such component. All vertices in all other components have zero valuation.

3. If x_i = 0 and no component contains both positively and negatively valuated vertices, then each component contains either only positively valuated vertices, only negatively valuated vertices, or only zero valuated vertices.

Theorem 2.

(Fiedler [11]) Let G be a connected graph and $x=(x_k)$ be a Fiedler vector of G. Then exactly one of the following cases occurs.

1. There is a single block B₁ in G which contains both positively and negatively valuated vertices. Each other block has either vertices with positive valuation only, vertices with negative valuation only, or vertices with zero valuation only. Every path P which contains at most two cut points in each block, which starts in B₁ and contains just one vertex i in B₁ has the property that the valuations at cut points contained in P form either an increasing, decreasing, or a zero sequence along this path according to whether $x_i>0, x_i<0\text{ or }{x}_i=0.$ In the last case, all vertices in P have valuation zero.

2. No block of G contains both positively and negatively valuated vertices. There exists a unique vertex i which has valuation zero and is adjacent to a vertex with a non-zero valuation. This vertex i is a cut vertex. Each block contains (with the exception of i) either vertices with positive valuation only, vertices with negative valuation only, or vertices with zero valuation only. Every path P, which starts at i and contains at most two cut vertices in each block, has the property that the valuations at the cut vertices contained in P form either an increasing, decreasing, or zero sequence along P. Every path containing both positively and negatively valuated vertices passes through i.

On the other hand, the study of Laplacian spectrum of multidigraphs is very limited. Let G be a multidigraph. Then the Laplacian matrix of G is defined as $L(G)=D(G)-A(G)$, where D(G) is the diagonal matrix whose diagonal entries are the outdegrees of the respective vertices of G and A(G) is the adjacency matrix of G. (Note: In this case, the ijth entry of A(G) is equal to the number of directed edges from vertex i to vertex j in G.) It is known that the number of spanning trees oriented toward a vertex i of a multidigraph G is precisely the first cofactor of L(G) belonging to its iith entry, e.g. [6]. Unlike the case of a graph, the Laplacian matrix of a multidigraph G is not positive semidefinite and not even symmetric. But, 0 is always an eigenvalue of L(G) afforded by the eigenvector $\mathbf{1}$. Agaev and Chebotarev [2] described essentially cyclic digraphs (meaning, a digraph whose Laplacian spectrum contains nonreal eigenvalues) with ring structure. Chebotarev and Agaev [7] presented some basic results concerning the construction and study of distributed control system in terms of the Laplacian spectrum of digraphs. Su et al. [24] listed the Laplacian eigenvalues of some digraphs obtained from the wheel digraph by deleting some edges.

Let $\mathtt{i}$ denote $\sqrt{-1}$, the imaginary unit. Bapat et al. [3] were the first to consider a digraph with complex arc weights. They considered the arc weights to be of unit modulus and defined an adjacency matrix and a Laplacian matrix which are always Hermitian. In the same article, the authors gave many combinatorial results relating the Laplacian matrix and the digraph structure. Subsequently, Kalita [15] considered the 3-colored digraphs (these are digraphs with edge weights 1 or –1 or $\mathtt{i}$) containing exactly one nonsingular cycle, and studied the smallest Laplacian eigenvalue and the corresponding eigenvectors of such digraphs. Later Kalita [16] investigated the monotonicity properties of the first eigenvectors of nonsingular connected weighted digraphs along certain paths. Dong and Lin [9] introduced the concept of general complex weighted digraphs and gave some results establishing the relationship between the Laplacian matrix and the structure of its corresponding digraph. A complex unit gain graph is a graph where each orientation of an edge is given a complex unit, which is the inverse of the complex unit assigned to the opposite direction. Further, the eigenvalue bounds for the adjacency and Laplacian matrices are obtained by Reff [22].

Recently, Barik and Sahoo [5] introduced a new Hermitian matrix associated with a multidigraph (named as complex adjacency matrix) and obtained some interesting spectral properties of a multidigraph with respect to the complex adjacency matrix. The complex adjacency matrix of a multidigraph is defined as follows.

Definition 3.

(Barik and Sahoo [5]) Let $G=(V,E)$ be a multidigraph with $V=\{1,2,\dots ,n\}$. Let b_ij and f_ij denote the number of directed edges from j to i and from i to j, respectively. Then the complex adjacency matrix $A_{\mathrm{}\mathbb{C}}(G)$ of G is an n × n matrix $A_{\mathrm{}\mathbb{C}}(G)=[a_{ij}]$ whose rows and columns are indexed by V and the ijth entry is given by $$a_{ij}=\left(\frac{f_{ij}+b_{ij}}{2}\right)+\left(\frac{f_{ij}-b_{ij}}{2}\right)\mathtt{i}.$$

Note that if $A_{\mathrm{}\mathbb{C}}(G)=[a_{ij}]$ is a complex adjacency matrix of a multidigraph G, then each $a_{ij}\in \mathbb{W}$ where $\mathbb{W}=\{\frac{a}{2}+\frac{b}{2}\mathtt{i}:a,b\in \mathbb{Z},a\ge |b|\ge 0\text{ and }2|(a-b)\}$. Denote ${\mathbb{W}}_{+}=\mathbb{W}\backslash \left\{0\right\}$.

In [5], it is shown that the complex adjacency matrix of a multidigraph is a generalization of the adjacency matrix of a graph. A multidigraph is said to be bipartite if its underlying undirected simple graph is bipartite. It is well known that a graph is bipartite if and only if the adjacency spectrum of the graph is symmetric about origin. In the same paper the authors showed that unlike the graph case, the symmetric about origin property of a multidigraph does not necessarily imply that the multidigraph is bipartite. They provided a necessary condition for a multidigraph G to satisfy the above property. Sahoo [23] characterized a few interesting spectral properties of simple directed graphs corresponding to the complex adjacency matrix. Using the complex adjacency matrix, we define the complex Laplacian matrix for a multidigraph.

Definition 4.

Let G be a multidigraph on n vertices and $A_{\mathrm{}\mathbb{C}}(G)=[a_{ij}]$ be the complex adjacency matrix of G. Let $D_{\mathrm{}\mathbb{C}}(G)$ be a diagonal matrix whose diagonal entries are given by $d_{ii}={\sum }_{j=1}^n\left|a_{ij}\right|$. Then the matrix defined as $$L_{\mathrm{}\mathbb{C}}(G)=D_{\mathrm{}\mathbb{C}}(G)-A_{\mathrm{}\mathbb{C}}(G)$$is called the complex Laplacian matrix of G.

Thus, $L_{\mathrm{}\mathbb{C}}(G)$ is Hermitian and by Geršgorin disc theorem, it is also positive semidefinite (see [14]). Let ${\sigma }_{L_{\mathrm{}\mathbb{C}}}(G)=({\lambda }_1(G),{\lambda }_2(G),\dots ,{\lambda }_n(G)),$ where ${\lambda }_1(G)\le {\lambda }_2(G)\le \dots \le {\lambda }_n(G)$ are the eigenvalues of $L_{\mathrm{}\mathbb{C}}(G)$ arranged in non-decreasing order. Note that the complex Laplacian matrix of a graph is same as its Laplacian matrix (considering each edge as two oppositely oriented directed edges). Therefore, it can be thought of as a generalization of the Laplacian matrix of a graph to that of a multidigraph. In the recent years, Laplacian spectral properties of (complex) weighted digraphs are studied and many applications are found (see for reference [15–17]). In all these references, the modulus of each entry of the Laplacian matrix is one. So the complex Laplacian matrix defined here is a more general one.

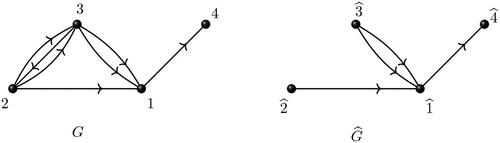
Example 5.

Consider the two multidigraphs G and $\widehat{G}$ as shown in Figure 1. The complex Laplacian matrices of these multidigraphs are given by $$\begin{array}{c}{L}_{\mathrm{}\mathbb{C}}(G)=\left[\begin{array}{cccc}2\sqrt{2}& -\frac{1}{2}+\frac{1}{2}\mathtt{i}& -1+\mathtt{i}& -\frac{1}{2}-\frac{1}{2}\mathtt{i}\\ -\frac{1}{2}-\frac{1}{2}\mathtt{i}& \frac{1+\sqrt{5}}{\sqrt{2}}& -\frac{3}{2}-\frac{1}{2}\mathtt{i}& 0\\ -1-\mathtt{i}& -\frac{3}{2}+\frac{1}{2}\mathtt{i}& \frac{2+\sqrt{5}}{\sqrt{2}}& 0\\ -\frac{1}{2}+\frac{1}{2}\mathtt{i}& 0& 0& \frac{1}{\sqrt{2}}\end{array}\right],\\ L_{\mathrm{}\mathbb{C}}(\widehat{G})=\left[\begin{array}{cccc}2\sqrt{2}& -\frac{1}{2}+\frac{1}{2}\mathtt{i}& -1+\mathtt{i}& -\frac{1}{2}-\frac{1}{2}\mathtt{i}\\ -\frac{1}{2}-\frac{1}{2}\mathtt{i}& \frac{1}{\sqrt{2}}& 0& 0\\ -1-\mathtt{i}& 0& \sqrt{2}& 0\\ -\frac{1}{2}+\frac{1}{2}\mathtt{i}& 0& 0& \frac{1}{\sqrt{2}}\end{array}\right].\end{array}$$

Fig. 1 A $L_{\mathrm{}\mathbb{C}}$-nonsingular multidigraph and a $L_{\mathrm{}\mathbb{C}}$-singular multidigraph.

From numerical computation, we have $$\begin{array}{c}{\sigma }_{L_{\mathrm{}\mathbb{C}}}(G)=(0.0094,0.7835,3.3485,4.6778)\text{ and }\\ {\sigma }_{L_{\mathrm{}\mathbb{C}}}(\widehat{G})=(0,0.7071,1.0171,3.9326).\end{array}$$

From Example 5, it is evident that 0 is not always the smallest eigenvalue of $L_{\mathrm{}\mathbb{C}}(G)$ unlike in case of the undirected graphs. We call a multidigraph G as $L_{\mathrm{}\mathbb{C}}$-singular if 0 is an eigenvalue of $L_{\mathrm{}\mathbb{C}}(G)$. So we arrive at the question: “which multidigraphs are $L_{\mathrm{}\mathbb{C}}$-singular?”. In Section 2, we completely describe all multidigraphs which are $L_{\mathrm{}\mathbb{C}}$-singular. In particular, we show that any multi-directed tree (a multidigraph G whose underlying graph is a tree) is $L_{\mathrm{}\mathbb{C}}$-singular. For a $L_{\mathrm{}\mathbb{C}}$-singular graph G, we consider the second smallest complex Laplacian eigenvalue and the corresponding eigenvectors of $L_{\mathrm{}\mathbb{C}}(G)$. As a generalization of Theorem 1 and Theorem 2, we prove results relating to the eigenvectors corresponding to the second smallest eigenvalue of $L_{\mathrm{}\mathbb{C}}(G)$ and the structure of a multidigraph G. It is also proved that in case of a multi-directed tree, the modulus of the components of eigenvectors corresponding to the second smallest eigenvalue retain the monotonicity property similar to that of a Fiedler vector of a tree. These results appear in the Section 3 of the article.

Following notations are being used in the rest of the paper. The zero vector is denoted by $\mathbf{0}$. We choose $\arg (0)=0$, as a convention. By $x=(x_k)$, we mean a column vector of appropriate order whose kth component is x_k. The transpose and conjugate transpose of a matrix A are denoted by A^T and $A^{*}$, respectively.

2 $L_{\mathrm{}\mathbb{C}}$-singular multidigraphs

Let G be a multidigraph on vertices $1,2,\dots ,n$. We associate a weighted digraph $G_{\mathrm{w}}$ with G in the following way. The digraph $G_{\mathrm{w}}$ has the same set of vertices as that of G. Let i and j be vertices in G. Denote the number of directed edges from i to j (the forward edges) by f_ij and the number of directed edges from j to i (the backward edges) by b_ij. Then there is a directed edge (i, j) from i to j in $G_{\mathrm{w}}$ with weight $$w_{ij}=\left(\frac{f_{ij}+b_{ij}}{2}\right)+\left(\frac{f_{ij}-b_{ij}}{2}\right)\mathtt{i},$$whenever w_ij is nonzero. This directed edge is denoted by $i\stackrel{w_{ij}}{\to }j$. Note that a directed edge $i\to j$ with weight w_ij in $G_{\mathrm{w}}$ is treated equivalent to the directed edge $j\to i$ with weight $\overline{w_{ij}}$. Notice that, the weights of an associated weighted digraph belong to the set $$\mathbb{W}=\{\frac{a}{2}+\frac{b}{2}\mathtt{i}:a,b\in \mathbb{Z},a\ge |b|\ge 0\text{ and }2|(a-b)\}$$ and we are not considering an edge with weight $0+0\mathtt{i}$ in $G_{\mathrm{w}}$. Further, an edge (i, j) of weight $m+n\mathtt{i}$ in $G_{\mathrm{w}}$ means that there are m + n directed edges from i to j and m – n directed edges from j to i in the multidigraph G and $A(G_{\mathrm{w}})=A_{\mathrm{}\mathbb{C}}(G)$.

The modular graph of G, denoted by $\left|G\right|$, is the weighted undirected graph obtained from $G_{\mathrm{w}}$ by replacing each of its edge weights by their modulus. That is, if $i\stackrel{w_{ij}}{\to }j$ in $G_{\mathrm{w}}$ for some $w_{ij}\in {\mathbb{W}}_{+}$, then the edge {i, j} in $\left|G\right|$ has weight $\left|w_{ij}\right|$. Observe that the adjacency matrix of $\left|G\right|$ is $A(|G|)=|A_{\mathrm{}\mathbb{C}}(G)|$, where by $|A_{\mathrm{}\mathbb{C}}(G)|$ we mean the entry-wise modulus of $A_{\mathrm{}\mathbb{C}}(G)$.

Example 6.

Consider the graph G in Figure 1. Its associated weighted digraph $G_{\mathrm{w}}$ and the modular graph $\left|G\right|$ are shown in Figure 2. Since in G there are two directed edges from vertex 2 to vertex 3 and one directed edge from vertex 3 to vertex 2, the weight of the directed edge from 2 to 3 in $G_{\mathrm{w}}$ is $\frac{3}{2}+\frac{\mathtt{i}}{2}$. Observe that the orientation of the directed edge between vertices 1 and 2 in G is altered in $G_{\mathrm{w}}$. So, we assign the directed edge from 1 to 2 in $G_{\mathrm{w}}$ with weight $\frac{1}{2}-\frac{\mathtt{i}}{2}$.

Fig. 2 Associated weighted digraph $G_{\mathrm{w}}$ and the modular graph $\left|G\right|$ of the graph G in Figure 1.

It is worth mentioning that in case of an undirected graph G, the Laplacian matrix L(G) can be expressed as $L(G)=M(G)M{(G)}^T$, where M(G) is the vertex-edge incidence matrix of G. Below we define a similar kind of matrix for a multidigraph in terms of its associated weighted digraph.

Definition 7.

Let G be a multidigraph on vertices $1,2,\dots ,n$ and $G_{\mathrm{w}}$ be its associated weighted digraph. Suppose that the edge set of $G_{\mathrm{w}}$ consists of the edges $e_1,e_2,\dots ,e_m$. Then the complex incidence matrix $M_{\mathrm{}\mathbb{C}}(G)=[{\stackrel{⌣}{m}}_{i,e_j}]$ of the multidigraph G is an n × m matrix, whose rows and columns are indexed by the vertices and edges of $G_{\mathrm{w}}$. Further, if e_j is the weighted directed edge between the vertices u and v of $G_{\mathrm{w}}$ such that $u\stackrel{w_{uv}}{\to }v$ for some $w_{uv}\in {\mathbb{W}}_{+}$, then $${\stackrel{⌣}{m}}_{i,e_j}=\{\begin{array}{cc}\sqrt{w_{uv}}\hfill & \text{ if }i=u,\hfill \\ -\sqrt{{\overline{w}}_{uv}}\hfill & \text{ if }i=v,\hfill \\ 0\hfill & \text{ otherwise,}\hfill \end{array}$$where $\sqrt{z}$ is the principal square root of the complex number z.

Observe that $L_{\mathrm{}\mathbb{C}}(G)=M_{\mathrm{}\mathbb{C}}(G)M_{\mathrm{}\mathbb{C}}{}^{\ast }(G)$. Thus, for a vector x of size n, we have (1) $$x^{\ast }{L}_{\mathrm{}\mathbb{C}}(G)x=\sum _{i\stackrel{w_{ij}}{\to }j}{\left|x_i\sqrt{{\overline{w}}_{ij}}-x_j\sqrt{w_{ij}}\right|}^2.$$(1)

Note that the complex incidence matrix defined for a multidigraph here is a generalization of the incidence matrix defined in [3] for a weighted digraph.

By an i₁-i_k-walk (denoted by $W_{[i_1,i_k]}$) in a multidigraph G, we mean a sequence of corresponding vertices $i_1,i_2,\dots ,i_k$ in $G_{\mathrm{w}}$ such that for $1\le p\le k-1$, we have $i_p\stackrel{w_{i_p{i}_{p+1}}}{\to }{i}_{p+1}$ in $G_{\mathrm{w}}$ for some $w_{i_p{i}_{p+1}}\in {\mathbb{W}}_{+}$. We call $$R(W_{[i_1,i_k]})=\frac{{\overline{w}}_{i_1{i}_2}{\overline{w}}_{i_2{i}_3}\cdots {\overline{w}}_{i_{k-1}{i}_k}}{w_{i_1{i}_2}{w}_{i_2{i}_3}\cdots w_{i_{k-1}{i}_k}}$$as the ratio-weight of the walk $W_{[i_1,i_k]}$, where each $w_{i_p{i}_{p+1}}\in {\mathbb{W}}_{+}$. By $\mathbf{n}=({\mathbf{n}}_k)$, we denote the vector of size n with ${\mathbf{n}}_1=1$ and for $k=2,3,\dots ,n,{\mathbf{n}}_k={\mathbf{n}}_i\frac{\sqrt{{\overline{w}}_{ik}}}{\sqrt{w_{ik}}}$ when $i\stackrel{w_{ik}}{\to }k,$ $w_{ik}\in {\mathbb{W}}_{+}$. For the graph in Figure 1, the ratio-weight of the walk 2-3-1-4 is $$\frac{(\frac{3}{2}-\frac{1}{2}\mathtt{i})(1-\mathtt{i})(\frac{1}{2}-\frac{1}{2}\mathtt{i})}{(\frac{3}{2}+\frac{1}{2}\mathtt{i})(1+\mathtt{i})(\frac{1}{2}+\frac{1}{2}\mathtt{i})}=\frac{-2-6\mathtt{i}}{-2+6\mathtt{i}}=\frac{1}{5}(-4+3\mathtt{i}).$$

A multidigraph G is said to be connected if $\left|G\right|$ is a connected weighted graph (that is, the underlying graph of G is connected). Our next result gives a necessary condition for the complex Laplacian matrix of a connected multidigraph to be singular.

Lemma 8.

Let G be a connected multidigraph on vertices $1,2,\dots ,n$. If G is $L_{\mathrm{}\mathbb{C}}$-singular, then the ratio-weights of all 1-i-walks are same for each $i=2,\dots ,n$. Furthermore, if G is $L_{\mathrm{}\mathbb{C}}$-singular, then 0 is a simple eigenvalue afforded by the eigenvector n.

Proof.

Suppose that G is $L_{\mathrm{}\mathbb{C}}$-singular and for $x\ne 0,$ assume that $L_{\mathrm{}\mathbb{C}}(G)x=0$. Then from equation (1)(1) $$x^{\ast }{L}_{\mathrm{}\mathbb{C}}(G)x=\sum _{i\stackrel{w_{ij}}{\to }j}{\left|x_i\sqrt{{\overline{w}}_{ij}}-x_j\sqrt{w_{ij}}\right|}^2.$$(1) , we have $$0=x^{\ast }{L}_{\mathrm{}\mathbb{C}}(G)x=\sum _{i\stackrel{w_{ij}}{\to }j}{\left|x_i\sqrt{{\overline{w}}_{ij}}-x_j\sqrt{w_{ij}}\right|}^2,$$which implies that $x_i\sqrt{{\overline{w}}_{ij}}-x_j\sqrt{w_{ij}}=0.$ So $x_j=x_i\frac{\sqrt{{\overline{w}}_{ij}}}{\sqrt{w_{ij}}}$ when $i\stackrel{w_{ij}}{\to }j,$ for $w_{ij}\in {\mathbb{W}}_{+}$. Therefore, n is an eigenvector of $L_{\mathrm{}\mathbb{C}}(G)$ corresponding to the eigenvalue 0. If there are two different walks from vertex 1 to vertex i, then by calculating the values of x_i along these two walks and squaring them, we get that the ratio-weights along both these 1-i-walks are same. Hence, the ratio-weights of all 1-i-walks are same for each $i=2,\dots ,n$.

Further, if x_i = 0 for some i, then x_j = 0 when $i\stackrel{w_{ij}}{\to }j,$ for $w_{ij}\in {\mathbb{W}}_{+}$. Since G is connected, we arrive at $x=\mathbf{0}$, which is a contradiction. Hence, 0 is a simple eigenvalue of $L_{\mathrm{}\mathbb{C}}(G)$ afforded by the eigenvector n. □

The following is an interesting remark about the eigenvector of $L_{\mathrm{}\mathbb{C}}(G)$ corresponding to the eigenvalue 0.

Remark 9.

Suppose that G is a $L_{\mathrm{}\mathbb{C}}$-singular multidigraph on vertices $1,2,\dots ,n$ and $\mathbf{n}=({\mathbf{n}}_k)$ is an eigenvector of $L_{\mathrm{}\mathbb{C}}(G)$ corresponding to the eigenvalue 0 with ${\mathbf{n}}_1=1$. Further, if $G_{\mathrm{w}}$ is the associated weighted digraph of G and for $i,j\in V(G)$, if $i\stackrel{w_{ij}}{\to }j$ in $G_{\mathrm{w}}$, then the corresponding components of n satisfy the condition $$\arg ({\mathit{n}}_j)=\arg ({\mathit{n}}_i)+\arg ({\overline{w}}_{ij}).$$

This is true since ${\mathbf{n}}_i\sqrt{{\overline{w}}_{ij}}-{\mathbf{n}}_j\sqrt{w_{ij}}=0$ implies ${\mathbf{n}}_j=\frac{{\overline{w}}_{ij}}{\left|w_{ij}\right|}{\mathbf{n}}_i$.

Let G be a multidigraph and $\left|G\right|$ be its modular graph. Then the Laplacian matrix of $\left|G\right|$ is given by $$L(|G|)=D(|G|)-A(|G|)=D(G)-|A_{\mathrm{}\mathbb{C}}(G)|,$$where $A(|G|)$ is the weighted adjacency matrix of $\left|G\right|$. Let ${\sigma }_L(|G|)$ denote the spectrum of $L(|G|)$. The following result provides a necessary and sufficient condition for a multidigraph to be $L_{\mathrm{}\mathbb{C}}$-singular in terms of the Laplacian spectrum of the corresponding modular graph.

Lemma 10.

Let G be a connected multidigraph and $\left|G\right|$ be its modular graph. Then G is $L_{\mathrm{}\mathbb{C}}$-singular if and only if the complex Laplacian spectrum of G and the Laplacian spectrum of $\left|G\right|$ are the same.

Proof.

Let G be a $L_{\mathrm{}\mathbb{C}}$-singular connected multidigraph on vertices $1,2,\dots ,n$. Then 0 is a simple eigenvalue of $L_{\mathrm{}\mathbb{C}}(G)$ afforded by the eigenvector n. Let S be the diagonal matrix where $s_{ii}=n_i$, for each $i=1,2,\dots ,n$. Clearly $S^{\ast }S=I_n$. Suppose that $S^{\ast }{L}_{\mathrm{}\mathbb{C}}(G)S=[b_{ij}]$, where $b_{ij}={\overline{\mathbf{n}}}_i{l}_{ij}{\mathbf{n}}_j.$ Suppose that there is a weighted directed edge $i\stackrel{w_{ij}}{\to }j$ in $G_{\mathrm{w}}$, for some $i,j\in V(G)$. Without loss of generality, assume that the vertex i lies on a path from 1 to j and 1-i-walk contains a sequence of corresponding vertices $1,2,\dots ,i-1,i$ in $G_{\mathrm{w}}$ such that for $1\le p\le i-1$, we have $p\stackrel{w_{p,p+1}}{\to }p+1$ in $G_{\mathrm{w}}$. Then, $$\begin{array}{c}{b}_{ij}=\left(\frac{\sqrt{w_{12}}\dots \sqrt{w_{i-1,i}}}{\sqrt{{\overline{w}}_{12}}\dots \sqrt{{\overline{w}}_{i-1,i}}}\right)\\ \hspace{1em}(-w_{ij})\left(\frac{\sqrt{{\overline{w}}_{12}}\dots \sqrt{{\overline{w}}_{i-1,i}}\sqrt{{\overline{w}}_{ij}}}{\sqrt{w_{12}}\dots \sqrt{w_{i-1,i}}\sqrt{w_{ij}}}\right)=-w_{ij}\frac{\sqrt{{\overline{w}}_{ij}}}{\sqrt{w_{ij}}}=-\left|w_{ij}\right|\end{array}$$and b_ii = l_ii for all $i=1,2,\dots ,n$. That is, $S^{\ast }{L}_{\mathrm{}\mathbb{C}}(G)S=L(|G|).$ Hence ${\sigma }_{L_{\mathrm{}\mathbb{C}}}(G)={\sigma }_L(|G|).$ The converse is trivial. □

The weight of a cycle multidigraph is defined as the product of the weights of all directed edges of the associated weighted cycle digraph, where all the edges are oriented either clockwise or anticlockwise (every weighted cycle digraph can be converted to one such cycle digraph). Let $G=(V,E)$ be a multidigraph and $H=(V_1,E_1)$ be such that $V_1\subset V$ and $E_1\subset E.$ Let $G_{\mathrm{w}}$ and $H_{\mathrm{w}}$ be the associated weighted digraphs of G and H, respectively. For $i,j\in V_1$, if $i\stackrel{w_{i,j}}{\to }j$ is a directed edge in $H_{\mathrm{w}}$ for $w_{ij}\in {\mathbb{W}}_{+}$ implies that $i\stackrel{w_{i,j}}{\to }j$ is also a directed edge in $G_{\mathrm{w}}$, then we call H as a sub-multidigraph of G. Our next result gives a necessary and sufficient condition for the complex Laplacian spectrum of G and the Laplacian spectrum of $\left|G\right|$ to be the same in terms of weights of cycle sub-multidigraphs of G.

Theorem 11.

Let G be a multidigraph on vertices $1,2,\dots ,n$ and $\left|G\right|$ be its modular graph. Then the complex Laplacian spectrum of G and the Laplacian spectrum of $\left|G\right|$ are same if and only if the weight of every cycle sub-multidigraph of G is positive. Further, if ${\sigma }_{L_{\mathrm{}\mathbb{C}}}(G)={\sigma }_L(|G|)$ and y is an eigenvector of $L(|G|)$ corresponding to the eigenvalue λ, then there exists an eigenvector x of $L_{\mathrm{}\mathbb{C}}(G)$ corresponding to λ such that $\left|x\right|=\left|y\right|$.

Proof.

Let λ be an eigenvalue of $L(|G|)={[c_{ij}]}_{n\times n}$ with a corresponding eigenvector $y=(y_k)$. Now from $L(|G|)y=\lambda y$, we have $$c_{ii}{y}_i+\sum _{\stackrel{j=1}{j\ne i}}^n{c}_{ij}{y}_j=\lambda y_i,\text{ for }i=1,\dots ,n.$$

Let $L_{\mathrm{}\mathbb{C}}(G)={[l_{ij}]}_{n\times n}$. Notice that $|L_{\mathrm{}\mathbb{C}}(G)|=D(|G|)-A(|G|)$, where in the term $|L_{\mathrm{}\mathbb{C}}(G)|$ entry-wise modulus of the matrix is considered. Hence, we have $c_{ij}=-\left|l_{ij}\right|=l_{ij}{\mathtt{e}}^{\mathtt{i}(\arg ({\overline{l}}_{ij})+\pi )}$, for $i\ne j$; and c_ii = l_ii, for $i=1,2,\dots ,n$. Thus, $$l_{ii}{y}_i+\sum _{\stackrel{j=1}{j\ne i}}^n{l}_{ij}{y}_j{\mathtt{e}}^{\mathtt{i}(\arg ({\overline{l}}_{ij})+\pi )}=\lambda y_i.$$

Since $y\ne \mathbf{0}$, without loss of generality suppose that $y_1\ne 0$. Consider a vector $x=(x_k)$ such that $x_1=\left|y_1\right|$. For $j\ne 1$, if there exists $i\stackrel{w_{ij}}{\to }j$ in $G_{\mathrm{w}}$ such that $y_i\ne 0$, then $$x_j=\{\begin{array}{cc}\left|y_j\right|{\mathtt{e}}^{\mathtt{i}(\arg (x_i)+\arg ({\overline{w}}_{ij}))},\hfill & \text{if }{y}_i{y}_j>0,\hfill \\ \left|y_j\right|{\mathtt{e}}^{\mathtt{i}(\arg (x_i)+\arg ({\overline{w}}_{ij})+\pi )},\hfill & \text{if }{y}_i{y}_j<0,\hfill \\ 0,\hfill & \text{if }{y}_j=0.\hfill \end{array}$$

Otherwise, if y_k = 0 for all k adjacent to j, then consider a directed path from 1 to j in $G_{\mathrm{w}}$ passing through some i, $i\stackrel{w_{ij}}{\to }j$ in $G_{\mathrm{w}}$. Let us assume that the directed path is $1\stackrel{w_{12}}{\to }2\cdots l\stackrel{w_{l,l+1}}{\to }l+1\cdots i\stackrel{w_{ij}}{\to }j$ such that $y_l\ne 0$ and $y_{l+1}=\cdots =y_i=0$. Then $$x_j=\{\begin{array}{cc}\left|y_j\right|{\mathtt{e}}^{\mathtt{i}(\arg (x_l)+\arg ({\overline{w}}_{l,l+1})+\cdots +\arg ({\overline{w}}_{ij}))},\hfill & \text{if }{y}_l{y}_j>0,\hfill \\ \left|y_j\right|{\mathtt{e}}^{\mathtt{i}(\arg (x_l)+\arg ({\overline{w}}_{l,l+1})+\cdots +\arg ({\overline{w}}_{ij})+\pi )},\hfill & \text{if }{y}_l{y}_j<0,\hfill \\ 0,\hfill & \text{if }{y}_j=0.\hfill \end{array}$$

Next we check the uniqueness of x_j. If G is a multi-directed tree, then clearly x_j is unique. For $i\stackrel{w_{ij}}{\to }j$ in $G_{\mathrm{w}}$, let there be another directed path from i to j in $G_{\mathrm{w}}$ as $i\stackrel{w_{i,i+1}}{\to }i+1\cdots i+m\stackrel{w_{i+m,j}}{\to }j$, such that the sub-multidigraph induced by vertices $[i,i+1,\dots ,i+m,j]$ forms a cycle multidigraph.

If $y_i{y}_j>0$, then along $i\stackrel{w_{ij}}{\to }j$ we have $$x_j=\left|y_j\right|{\mathtt{e}}^{\mathtt{i}(\arg (x_i)+\arg ({\overline{w}}_{ij}))},$$and along the directed path $i\stackrel{w_{i,i+1}}{\to }i+1\cdots i+m\stackrel{w_{i+m,j}}{\to }j$, irrespective of signatures of $y_{i+1},\dots ,y_{i+m}$, we have $$x_j=\left|y_j\right|{\mathtt{e}}^{\mathtt{i}(\arg (x_i)+\arg ({\overline{w}}_{i,i+1})+\cdots +\arg ({\overline{w}}_{i+m,j}))}.$$

Clearly, x_j gets unique valuation if and only if ${\mathtt{e}}^{\mathtt{i}(\arg ({\overline{w}}_{i,i+1})+\cdots +\arg ({\overline{w}}_{i+m,j})+\arg ({\overline{w}}_{ji}))}=1,$ that is, the weight of the cycle $[i,i+1,\dots ,i+m,j]$ is positive.

Similarly, the other cases $y_i{y}_j<0$ and y_i = 0 also gives the same conclusion as above. Hence it is clear that x_j for $j=1,2,\dots ,n$ gets unique valuation if and only if the weight of every cycle which contains j is positive. Now, it is easy to observe that x is an eigenvector of $L_{\mathrm{}\mathbb{C}}(G)$ corresponding to the eigenvalue λ and $\left|x\right|=\left|y\right|.$ Hence the proof. □

Remark 12.

Note that if G is a (multi)graph, then weight of every cycle in G is positive and for each walk in G the ratio-weight is always 1. Therefore, for a (multi)graph G, 0 is always an eigenvalue of $L_{\mathrm{}\mathbb{C}}(G)$ with the corresponding eigenvector $\mathbf{1}$.

As a consequence of Lemma 10 and Theorem 11, we provide a necessary and sufficient for a multidigraph to be $L_{\mathrm{}\mathbb{C}}$-singular, which is the main result of this section.

Theorem 13.

Let G be a multidigraph on n vertices. Then G is $L_{\mathrm{}\mathbb{C}}$-singular if and only if the weight of every cycle sub-multidigraph of G is positive.

The following is an immediate corollary of Theorem 13 for the case of multi-directed trees.

Corollary 14.

All multi-directed trees are $L_{\mathrm{}\mathbb{C}}$-singular.

3 Eigenvectors of a $L_{\mathrm{}\mathbb{C}}$-singular multidigraph corresponding to the second smallest eigenvalue

In this section, we generalize some results on the Fiedler vectors of a graph to that of multidigraphs, whenever the multidigraph is $L_{\mathrm{}\mathbb{C}}$-singular. Let G be a $L_{\mathrm{}\mathbb{C}}$-singular multidigraph on vertices $1,2,\dots ,n$ and $0={\lambda }_1\le {\lambda }_2\le \cdots \le {\lambda }_n$ be the eigenvalues of $L_{\mathrm{}\mathbb{C}}(G)$. Suppose that $x=(x_k)$ is an eigenvector of $L_{\mathrm{}\mathbb{C}}(G)$ corresponding to the second smallest eigenvalue λ₂ with $\arg (x_1)=0$ (if required, permute the vertices of G so that $x_1\ne 0$). We know that, if G is $L_{\mathrm{}\mathbb{C}}$-singular, then 0 is a simple eigenvalue afforded by the eigenvector $\mathbf{n}=({\mathbf{n}}_k)$. Let us partition the vertex set V(G) of G into three disjoint sets using the eigenvectors n and x as follows. $$\begin{array}{c}{V}_x^{+}=\{i\in V:x_i\ne 0\text{ and }\arg (x_i)=\arg ({\mathit{n}}_i)\},\\ V_x^{-}=\{i\in V:x_i\ne 0\text{ and }\arg (x_i)=\arg ({\mathit{n}}_i)+\pi \},\text{ and }\\ V_x^0=\{i\in V:x_i=0\}.\end{array}$$

Then we have the following observation on the structure of G.

Lemma 15.

Let G be a $L_{\mathrm{}\mathbb{C}}$-singular multidigraph on vertices $1,2,\dots ,n$ and $x=(x_k)$ be an eigenvector of $L_{\mathrm{}\mathbb{C}}(G)$ corresponding to the second smallest eigenvalue λ₂. If $i\in V_x^0$ and i is adjacent to a vertex in $V_x^{+}$ (resp. $V_x^{-}$), then i must also be adjacent to a vertex in $V_x^{-}$ (resp. $V_x^{+}$).

Proof.

Since $(L_{\mathrm{}\mathbb{C}}(G)-{\lambda }_2{I}_n)x=0$ and x_i = 0 for the vertex i, we have $$\sum _{\stackrel{j\in V(G)}{i\stackrel{w_{ij}}{\to }j}}{w}_{ij}{x}_j=0.$$

Assume that for every vertex j adjacent to i, we have either $j\in V_x^0$ or $j\in V_x^{+}$. We have $$\sum _{\stackrel{j\in V(G)}{i\stackrel{w_{ij}}{\to }j}}{w}_{ij}{x}_j=\sum _{\stackrel{j\in V_x^{+}}{i\stackrel{w_{ij}}{\to }j}}{w}_{ij}\left|x_j\right|e^{\mathtt{i}\arg (x_j)}=\sum _{\stackrel{j\in V_x^{+}}{i\stackrel{w_{ij}}{\to }j}}{w}_{ij}\left|x_j\right|e^{\mathtt{i}\arg ({\mathit{n}}_j)}.$$

Now, since $\mathbf{n}=({\mathbf{n}}_k)$ is an eigenvector of $L_{\mathrm{}\mathbb{C}}(G)$ corresponding to the eigenvalue 0 with ${\mathbf{n}}_1=1$, then from Remark 9, for every $i\stackrel{w_{ij}}{\to }j$ in $G_{\mathrm{w}}$, we have $\arg ({\mathbf{n}}_j)=\arg ({\mathbf{n}}_i)+\arg ({\overline{w}}_{ij}).$ Hence, $$\begin{array}{c}\sum _{\stackrel{j\in V_x^{+}}{i\stackrel{w_{ij}}{\to }j}}{w}_{ij}\left|x_j\right|e^{\mathtt{i}\arg ({\mathit{n}}_j)}\\ \hspace{1em}=\sum _{\stackrel{j\in V_x^{+}}{i\stackrel{w_{ij}}{\to }j}}{w}_{ij}\left|x_j\right|e^{\mathtt{i}(\arg ({\mathit{n}}_i)+\arg ({\overline{w}}_{ij}))}=e^{\mathtt{i}\arg ({\mathit{n}}_i)}\sum _{\stackrel{j\in V_x^{+}}{i\stackrel{w_{ij}}{\to }j}}\left|w_{ij}\right|\left|x_j\right|.\end{array}$$

Since there exists at least one vertex j adjacent to i such that $j\in V_x^{+},$ we have $$\sum _{\stackrel{j\in V(G)}{i\stackrel{w_{ij}}{\to }j}}{w}_{ij}{x}_j\ne 0,$$a contradiction. Thus, if $i\in V_x^0$ and i is adjacent to a vertex in $V_x^{+}$, then i must also be adjacent to a vertex in $V_x^{-}$ and vice versa. Hence the proof. □

Let G be a $L_{\mathrm{}\mathbb{C}}$-singular multidigraph and $x=(x_k)$ be an eigenvector of $L_{\mathrm{}\mathbb{C}}(G)$ corresponding to the second smallest eigenvalue λ₂. We say a vertex i in a multidigraph G as a characteristic vertex with respect to the eigenvector x if x_i = 0, and there is a vertex j adjacent to i such that $x_j\ne 0$. A multi-directed edge² between two vertices i and j in G is said to be a characteristic edge of G with respect to x if either $i\in V_x^{+}$ and $j\in V_x^{-}$ or $i\in V_x^{-}$ and $j\in V_x^{+}$. A block of a connected multi-directed graph G is a maximal connected sub-multidigraph of G with no cut vertices. The following result is a generalization of Theorem 1 for graphs to that of multidigraphs.

Theorem 16.

Let G be a $L_{\mathrm{}\mathbb{C}}$-singular connected multidigraph and $x=(x_k)$ be the eigenvector of $L_{\mathrm{}\mathbb{C}}(G)$ corresponding to the second smallest eigenvalue λ₂. Let i be a cut vertex of G and let $G_1,G_2,\dots ,G_r$ be components of G – i. Then one of the following cases occurs.

1. If $i\in V_x^{+}$ (resp. $i\in V_x^{-}$), then exactly one of the components $G_s,s=1,2,\dots ,r,$ contains vertices from $V_x^{-}$ (resp. $V_x^{+}$). Additionally, $\left|x_i\right|<\left|x_j\right|$ for every vertex j in the remaining components.

2. If x_i = 0 and there is a component containing vertices from both $V_x^{+}$ and $V_x^{-}$, then there is exactly one such component. All vertices in all other components have zero valuation.

3. If x_i = 0 and no component contains vertices from both $V_x^{+}$ and $V_x^{-}$, then each component G_s contains vertices either only from $V_x^{+}$, only from $V_x^{-}$, or only from $V_x^0$.

Proof.

Let $x=(x_k)$ be the eigenvector of $L_{\mathrm{}\mathbb{C}}(G)$ and $y=(y_k)$ be the eigenvector of $L(|G|)$ corresponding to second smallest eigenvalue λ₂, such that $\left|x\right|=\left|y\right|.$ To prove (i), it is sufficient to prove the case $i\in V_x^{+}$ (if $i\in V_x^{-}$, then we can simply multiply the vector x with –1 and get $i\in V_x^{+}$). Let $i\in V_x^{+}.$ That is, $x_i\ne 0$ and $\arg (x_i)=\arg ({\mathbf{n}}_i)$, where $\mathbf{n}=({\mathbf{n}}_k)$ is the eigenvector of $L_{\mathrm{}\mathbb{C}}(G)$ corresponding to the eigenvalue 0. If there is no vertex contained in $V_x^{-}$, then it is easy to observe that $x^{*}\mathbf{n}\ne 0,$ which is a contradiction to the fact that x and n are orthogonal vectors. So, $V_x^{-}$ is non-empty. For $s=1,2,\dots ,r,$ let $\left|G_s\right|$ be the component of $\left|G\right|-i$ corresponding to the component G_s of G – i. Since $x_i\ne 0$, we must have $y_i\ne 0.$ Assume that $y_i>0.$ Then from Theorem 1, exactly one of the components $\left|G_s\right|,s=1,\dots ,r,$ contains a vertex with negative valuation. Without loss of generality, assume that the component $\left|G_1\right|$ contains a vertex with negative valuation and every vertex in $\left|G_2\right|\cup \left|G_3\right|\cup \cdots \cup \left|G_r\right|$ is of positive valuation. To complete the proof, we show that every vertex in $G_2\cup G_3\cup \cdots \cup G_r$ must be contained in $V_x^{+}$. Let $i+1\in V(G_2)$ such that $i\stackrel{w_{i,i+1}}{\to }i+1$. Then $i+1\in V(|G_2|)$ and $y_{i+1}>0.$ Since $y_i{y}_{i+1}>0,$ from Theorem 11, we have $$x_{i+1}=\left|y_{i+1}\right|{\mathtt{e}}^{\mathtt{i}(\arg (x_i)+\arg ({\overline{w}}_{i,i+1}))}$$and $${\mathit{n}}_{i+1}={\mathtt{e}}^{\mathtt{i}(\arg ({\mathit{n}}_i)+\arg ({\overline{w}}_{i,i+1}))}.$$

Clearly, $\arg (x_{i+1})=\arg ({\mathbf{n}}_{i+1})$ and hence $i+1\in V_x^{+}.$ Similarly, we can prove that $i+1\in V_x^{+}$ if $y_i<0.$ By proceeding this way, we can conclude that every vertex in $G_2\cup G_3\cup \dots \cup G_r$ is contained in $V_x^{+}$. It is easy to observe from Theorem 1 that, $\left|x_i\right|<\left|x_j\right|$ for every vertex j in $G_2\cup G_3\cup \dots \cup G_r$.

To prove (ii), let x_i = 0 and there is a component containing vertices from both $V_x^{+}$ and $V_x^{-}$. Assume that the vertices $l\in V_x^{+}$ and $m\in V_x^{-}$ are contained in the component $G_1.$ Then from the construction of x in Theorem 11, it is easy to see that $y_l{y}_m<0.$ That is, the component $\left|G_1\right|$ contains both positively and negatively valuated vertices. Since $\left|x\right|=\left|y\right|$, proof follows from Theorem 1(ii).

Proof of (iii) follows immediately from Theorem 1(iii) and the fact that there is no component in G – i that contains vertices from both $V_x^{+}$ and $V_x^{-}$. □

Now we prove the main result of this section by using Lemma 15 and Theorem 16. This result is a generalization of Theorem 2 for graphs to that of multidigraphs.

Theorem 17.

Let G be a $L_{\mathrm{}\mathbb{C}}$-singular connected multidigraph and $x=(x_k)$ be the eigenvector of $L_{\mathrm{}\mathbb{C}}(G)$ corresponding to the second smallest eigenvalue λ₂. Then exactly one of the following cases occurs.

1. There is exactly one block B₁ of G, which contains vertices from both $V_x^{+}$ and $V_x^{-}$. Each other block in G has vertices either from $V_x^{+}$ only, $V_x^{-}$ only, or $V_x^0$ only. Every induced multi-directed path P which contains at most two cut vertices in each block, starts at B₁, and contains just one vertex in B₁ has the property that the absolute values of the corresponding entries in x of cut vertices form either an increasing or zero sequence along the path P.

2. No block of G contains vertices from both $V_x^{+}$ and $V_x^{-}$. There exists a unique cut vertex i which is a characteristic vertex of G. Each block contains vertices (except i) either from $V_x^{+}$ only, $V_x^{-}$ only, or $V_x^0$ only. Every induced path P which contains at most two cut vertices in each block and starts at i, has the property that the absolute values of the corresponding entries in x of cut vertices form either an increasing or zero sequence along the path P.

Proof.

If G has only one block, then it should contain vertices from $V_x^{+}$ and $V_x^{-}$. In this case we are done. Otherwise, suppose that B₁ is a block of G which contains vertices from both $V_x^{+}$ and $V_x^{-}$. Let B₂ be a block different from B₁ and i be the cut vertex that separates the blocks B₁ and $B_2.$ If $i\in V_x^{+}$ (respectively, $i\in V_x^{-}$), then Theorem 16(i) follows that every vertex in B₂ must be contained in $V_x^{+}$ (respectively, $i\in V_x^{-}$). If $i\in V_x^0$, then it follows from Theorem 16(ii) that every vertex in B₂ must be contained in $V_x^0$.

Let P be an induced multi-directed path of G starting at B₁ and containing exactly one vertex i of B₁, and not containing more than two cut vertices in each block of G. Let $i,i+1,\dots ,i+r$ be the cut vertices of G contained in P which are ordered along the path P. If $i\in V_x^{+}$, then by Theorem 1 we have, $i+1\in V_x^{+}$ and $\left|x_i\right|<\left|x_{i+1}\right|$. Since $i,i+1,\dots ,i+r$ are also the cut vertices of G, we can repeatedly apply Theorem 16 for the vertices $i+1,i+2,\dots ,i+r$ and conclude that $\left|x_i\right|<\left|x_{i+1}\right|<\cdots <\left|x_{i+r}\right|$. Similarly, if $i\in V_x^{-},$ then we can prove $\left|x_i\right|<\left|x_{i+1}\right|<\cdots <\left|x_{i+r}\right|$. If $i\in V_x^0$, then it follows from Theorem 16(ii) that every vertex in P has zero valuation. Hence the proof of (i) is completed.

To prove (ii), observe from Theorem 16 that there does not exist more than one block of G containing vertices from both $V_x^{+}$ and $V_x^{-}$. Thus, let us assume that there is no block of G that contains vertices from both $V_x^{+}$ and $V_x^{-}$. Therefore, there exists a vertex $i\in V_x^0$, which is adjacent to a vertex of non-zero valuation. From Lemma 15, i is adjacent to some vertices of $V_x^{+}$ as well as $V_x^{-}$. Since there is no block of G that contains vertices from both $V_x^{+}$ and $V_x^{-}$, it gives that i is a cut vertex. From Theorem 16(iii), i is the only vertex in $V_x^0$ that is adjacent to vertices of $V_x^{+}$ and $V_x^{-}$. Hence, each block of G contains vertices (except i) either from $V_x^{+}$ only, $V_x^{-}$ only, or $V_x^0$ only.

Let P be an induced multi-directed path of G starting at i. Since each block of G contains vertices (except i) either from $V_x^{+}$ only, $V_x^{-}$ only, or $V_x^0$ only, it follows that, if P contains a vertex of $V_x^{+}$ (respectively, $V_x^{-}$), then all vertices of P, except i, must be from $V_x^{+}$ (respectively, $V_x^{-}$). Let $i+1,i+2,\dots ,i+r$ be cut vertices of G contained in P which are ordered along the path P. If $i+1\in V_x^{+}$ or $i+1\in V_x^{-}$, then by using Theorem 16(i), we can conclude that $i<\left|i+1\right|<\cdots <\left|i+r\right|$. If $i+1\in V_x^0$, then by using Theorem 16(iii), we can conclude that all vertices of P must be in $V_x^0$. This completes the proof. □

Let T be a multi-directed tree and λ₂ be the second smallest eigenvalue of $L_{\mathrm{}\mathbb{C}}(T)$ afforded by the eigenvector x. Our next result follows immediately from the above result and shows that the absolute values of the components of x exhibit the monotonicity property similar to the Fiedler vectors of a graph.

Lemma 18.

Let T be a multi-directed tree on vertices $1,\dots ,n$ and $T_{\mathrm{w}}$ be its associated weighted directed tree. Let $x=(x_k)$ be an eigenvector of $L_{\mathrm{}\mathbb{C}}(T)$ corresponding to its second smallest eigenvalue λ₂. Then one of the following cases occur.

1. No entry of x is zero. In this case, there is a unique characteristic edge in T whose corresponding weighted edge in $T_{\mathrm{w}}$ is $i\stackrel{w_{ij}}{\to }j$. Further, along any walk in T that starts at i and does not contain j (and starts at j and does not contain i), the absolute values of the corresponding entries in x increase.

2. x contains some zero entries. In this case, the sub-multidigraph of T induced by the zero vertices (vertices whose corresponding entries in x are zeros) is connected. There is a unique vertex i such that it is a characteristic vertex. Further, along any walk in T that starts at v, the absolute values of the corresponding entries in x form either an increasing or a zero sequence.

The following example illustrates Theorem 17.

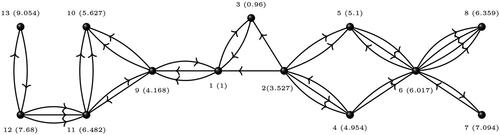
Example 19.

Consider a multidigraph G as shown in Figure 3. Observe that weight of every cycle sub-multidigraph of G is positive and hence G is $L_{\mathrm{}\mathbb{C}}$-singular. From MATLAB computation, the complex Laplacian spectrum of G is $$\begin{array}{c}(0, 0.1518, 0.6376, 1.0331, 1.3419, 2.175, 2.6145, 2.9943,\\ \hspace{1em}3.3609, 5.5367, 5.9741, 6.6080, 9.1005).\end{array}$$

Fig. 3 A multidigraph G showing Case (i) of Theorem 17.

Further, we compute the eigenvectors n and x corresponding to 0 and the second smallest eigenvalue of $L_{\mathrm{}\mathbb{C}}(G)$ (which is 0.1518 here), respectively. $$\mathit{n}=\left[\begin{array}{c}1\\ 0.7071+0.7071\mathtt{i}\\ 1\\ 0.8944+0.4472\mathtt{i}\\ 1\\ 0.9487-0.3162\mathtt{i}\\ 0.9487-0.3162\mathtt{i}\\ 0.4472-0.8944\mathtt{i}\\ 0.9487-0.3162\mathtt{i}\\ 0.4472-0.8944\mathtt{i}\\ 0.9487-0.3162\mathtt{i}\\ 0.8944+0.4472\mathtt{i}\\ 0.8944+0.4472\mathtt{i}\end{array}\right]\text{ and }x=\left[\begin{array}{c}1\\ -2.4940-2.4940\mathtt{i}\\ -0.9606\\ -4.4309-2.2154\mathtt{i}\\ -5.1001\\ -5.7087+1.9029\mathtt{i}\\ -6.7301+2.2434\mathtt{i}\\ -2.8437+5.6874\mathtt{i}\\ 3.9546-1.3182\mathtt{i}\\ 2.5167-5.0334\mathtt{i}\\ 6.1499-2.0500\mathtt{i}\\ 6.8689+3.4344\mathtt{i}\\ 8.0978+4.0489\mathtt{i}\end{array}\right]$$

By the definition of $V_x^{+}$ and $V_x^{-}$, we have $V_x^{+}=\{1,9,10,11,12,13\}$ and $V_x^{-}=\{2,3,4,5,6,7,8\}$. For G, the absolute values of entries of x are shown in Figure 3 near the corresponding vertices (rounded to three decimal places). Observe that there is exactly one block (block containing vertices 1, 2, and 3) that contains vertices from both $V_x^{+}$ and $V_x^{-}$. As we travel away from that block, the absolute values of the cut vertices strictly increases.

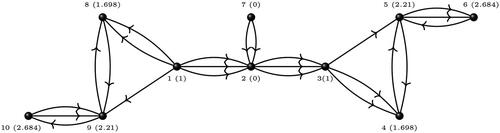
Next, for Case (ii) of Theorem 17 we consider a multidigraph G as shown in Figure 4. From MATLAB computation, the complex Laplacian spectrum of G is $$\begin{array}{c}(0, 0.2794, 0.7421, 1.5464, 1.6213, 3.3681, 4.5791, 4.5829,\\ \hspace{1em}5.0464, 8.3577).\end{array}$$

Fig. 4 A multidigraph G showing Case (ii) of Theorem 17.

The eigenvectors n and x of $L_{\mathrm{}\mathbb{C}}(G)$ corresponding to the eigenvalues 0 and 0.2794, respectively, are given below. $$\mathit{n}=\left[\begin{array}{c}1\\ 0.7071-0.7071\mathtt{i}\\ -\mathtt{i}\\ -0.7071-0.7071\mathtt{i}\\ -0.7071-0.7071\mathtt{i}\\ -0.8944-0.4472\mathtt{i}\\ 1\\ 0.7071-0.7071\mathtt{i}\\ 0.7071-0.7071\mathtt{i}\\ 0.8944-0.4472\mathtt{i}\end{array}\right]\text{ and }x=\left[\begin{array}{c}1\\ 0\\ \mathtt{i}\\ 1.2004+1.2004\mathtt{i}\\ 1.5625+1.5625\mathtt{i}\\ 2.4007+1.2003\mathtt{i}\\ 0\\ 1.2004-1.2004\mathtt{i}\\ 1.5625-1.5625\mathtt{i}\\ 2.4007-1.2003\mathtt{i}\end{array}\right]$$

Using n and x we can classify vertices of G into three disjoint sets as, $V_x^{+}=\{1,8,9,10\}, V_x^{-}=\{3,4,5,6\}$ and $V_x^0=\{2,7\}$. Vertex 2 is the only vertex that is in $V_x^0$ and adjacent to a non-zero valuated vertex. Observe that each block contains vertices (except 2) either from $V_x^{+}$ only, $V_x^{-}$ only, or $V_x^0$ only. Also notice that as we move away from vertex 2, the absolute values of the corresponding entries in x of cut vertices form either an increasing or zero sequence.

Acknowledgments

The authors are thankful to the anonymous referees for a careful reading of the article and the encouraging comments made in the report.

Additional information

Funding

The corresponding author acknowledges SERB, Government of India, for financial support through grant (MTR/2017/000080). The second author acknowledges the financial support from UGC, Government of India.

Notes

2 By a multi-directed edge between two vertices i and j in a multidigraph, we mean all the directed edges between i and j.