Number of cycles of small length in a graph

Abstract

Let G be a simple undirected graph. In this article, we obtain an explicit formula for the number of 8-cycles in G in terms of the entries of its adjacency matrix. We provide new formulae to find the number of cycles of length 4, 5 and 6 in G. When the girth of G is 10 (resp. 12), an explicit formula for the number of cycles of length 10 (resp. 12) is given. New formulae to find the number of paths of length 3, 4 and 5 in G are also obtained.

Keywords:

• Graph
• adjacency matrix
• walk
• path
• cycle
• girth

AMS SUBJECT CLASSIFICATION:

• 05C50
• 05C38
• 15A15

1 Introduction

Throughout this article we consider only simple undirected graphs. Let G be a graph with vertex set $V(G)=\{v_1,v_2,\dots ,v_n\}$ and edge set E(G). If two vertices v_i and v_j are adjacent in G, we denote it by $v_i\sim v_j$. The edge between v_i and v_j is denoted by $[v_i,v_j]$. In graph G, a walk of length k is a sequence of vertices and edges $[v_1,e_1,v_2,\dots ,e_k,v_{k+1}]$, where e_i is the edge between the vertices v_i and $v_{i+1}$, for $i=1,2,\dots ,k$. If $v_1=v_{k+1}$, then the walk is called as a closed walk. A walk in which all vertices are distinct is called a path and a closed path is called a cycle. The length of a shortest cycle in a graph G is called the girth of the graph and is denoted by g.

The adjacency matrix of G, is defined as the n × n matrix $A(G)=[a_{ij}]$, where a_ij = 1, if v_i and v_j are adjacent in G and 0 otherwise. The spectrum of G is defined as $\sigma (G)=({\lambda }_1(G),{\lambda }_2(G),\dots ,{\lambda }_n(G)),$ where ${\lambda }_1(G)\le {\lambda }_2(G)\le \dots \le {\lambda }_n(G)$ are the eigenvalues of A(G) arranged in non-decreasing order. We write A in place of A(G) when it is clear from the context. It is well known that the ij-entry of A^k is the number of walks from v_i to v_j of length k in G for $k=1,2,\dots$. We denote the ij-entry of A^k by $a_{ij}^{(k)}$. By a k-path (/k-walk/k-cycle), we mean a path (/walk/cycle) of length k. Since every 2-walk with distinct vertices is a 2-path, the number of paths of length 2 in G is $\sum _{i\ne j}{a}_{ij}^{(2)}$. Similarly, since every closed walk of length 3 is a 3-cycle, the number of 3-cycles in a simple graph G is $\frac{1}{6}tr(A^3)$. The following question arises naturally.

“Can we find similar formulae for the number of cycles and paths of higher length in terms of entries of the adjacency matrix of a given graph?”

Counting number of cycles of length equal to the girth or slightly larger is a fundamental problem of interest in information theory, particularly in the analysis and design of low-density parity-check codes, see [12, 16, 18, 20, 24]. For two graphs of the same girth, the one with the fewer cycles of length equal to the girth or girth plus two, might be the preferable. Although there are several algorithms to find the cycles and paths of given length in a graph (see [1–3, 11, 12, 14, 15, 17, 19, 23]), a combinatorial approach is useful to find the number of cycles or paths of small length.

Blake and Lin [4] computed the number of cycles of length equal to girth g in bi-regular bipartite graphs as a function of the spectrum of the graph, and the number and the degree of the vertices in each partition. In [10], the number of cycles of length $g+2,\dots ,2g-2$, in bi-regular bipartite graphs in terms of the spectrum and vertex degrees have been obtained by Dehghan and Banihashemi. Further, the authors computed the number of 4-cycles in irregular bipartite graphs with g = 4, and 6-cycles in half-regular bipartite graphs with g = 6, in terms of the spectrum and vertex degrees. The results are stated below.

Theorem 1

(Dehghan and Banihashemi [10]). Let G be an irregular bipartite graph on n vertices and $\sigma (G)=({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n)$. Then the number of 4-cycles in G is $$\frac{1}{8}\left[\sum _{i=1}^n{\lambda }_i^4-\sum _{i\in V(G)}{d}_i\left(2d_i-1\right)\right],$$where d_i is the degree of the vertex v.

Theorem 2

(Dehghan and Banihashemi [10]). Let G be a half-regular bipartite graph with girth 6 and vertex set $V(G)=U\cup W$, where $U=\{u_1,u_2,\dots ,u_l\}$ and $W=\{w_1,w_2,\dots ,w_m\}$. Let the degree of every vertex $u_i\in U$ be r and the degree of vertex $w_i\in W$ be d_i, $i=1,2,\dots ,m$. Then the number of 6-cycles in G is $\frac{1}{12}\left[{\sum }_{i=1}^{l+m}{\lambda }_i^6-nr(1+3(r-1)+2(r-1)(r-2))-\sum _{w_i\in W}(d_i(3d_i-2)+2d_i(d_i-1)(d_i-2))-\sum _{w_i\in W}6d_i(d_i-1)(r-1)-\sum _{w_i\in W}3d_i(d_i+r-2)\right],$ where $\sigma (G)=({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_{l+m})$.

In addition, Dehghan and Banihashemi [10] also mentioned that if $g\ge 8$, then even for half-regular bipartite graphs, it is impossible to calculate the number of cycles of length greater than or equals to g using only the spectrum of the graph and its vertex degrees. In case of irregular bipartite graphs, if $g\ge 6$, then it is not possible to find the number of cycles of length greater than or equals to g in terms of the spectrum of the graph and its vertex degrees. In this article, we provide formulae for the number of cycles of length 4, 5, 6, and 8 in a simple graph G in terms of the entries of its adjacency matrix. For a graph G having girth 8, 10, or 12, we provide formulae to calculate the number of cycles of length equal to girth in terms of the entries of its adjacency matrix.

On the other hand, in 1971, formulae for the number of 4-cycles and 5-cycles in a simple graph were given by Harary and Manvel [13] as described below.

Theorem 3

(Harary and Manvel [13]). Let G be a graph with n vertices with adjacency matrix A. Then

(i) the number of 4-cycles in G = $\frac{1}{8}\left[tr(A^4)-2m-\sum _{i\ne j}{a}_{ij}^{(2)}\right]$, where m denote the number of edges in G,

(ii) the number of 5-cycles in G = $\frac{1}{10}\left[tr(A^5)-5tr(A^3)-5{\sum }_{i=1}^n{d}_i{a}_{ii}^{(3)}\right]$.

Later in 2003, an explicit formula for the number of 6-cycles in a simple graph was given by Chang and Fu [7].

Theorem 4

(Chang and Fu [7]). Let G be a graph of order n. Then the number of 6-cycles in a graph G is $\frac{1}{12}\left[tr(A^6)-6tr(A^4)+5tr(A^3)-4tr(A^2)-3{\sum }_{i,j=1}^n{a}_{ij}^{(3)}+12{\sum }_{i,j=1}^n{a}_{ij}^{(2)}-3{\sum }_{i=1}^n{[a_{ii}^{(3)}]}^2+9\sum _{i\ne j}{a}_{ij}^{(2)}(a_{ij}^{(2)}-1)a_{ij}-6\sum _{i\ne j}{a}_{ij}^{(2)}(a_{ij}^{(2)}-1)(a_{ij}^{(2)}-2)-2{\sum }_{i=1}^n{a}_{ii}^{(2)}(a_{ii}^{(2)}-1)(a_{ii}^{(2)}-2)\right].$

Recently, Movarraei and Boxwala [21] gave an explicit formula for the number of 7-cycles in a graph. All the proofs were done based on the idea of subtracting the number of closed walks of length k, which are not k-cycles, from the number of closed walks of length k, that is, $tr(A^k)$. This can be simply written as, the number of k-cycles in a simple graph G is equal to $\frac{1}{2k}[tr(A^k)-W_k]$, where W_k represents the number of closed walks of length k which are not k-cycles. By following the same method, we obtain an explicit formula for the number of 8-cycles in a simple graph.

In a similar way, formulae to calculate the exact number of paths of length 3, 4, 5, and 6 in a graph G have been provided in recent years. Movarraei and Shikare [22] provided formulae to calculate the number of paths of length 3 and 4 in a graph.

Theorem 5

(Movarraei and Shikare [22]). Let G be a graph with vertex set $\{v_1,v_2,\dots ,v_n\}$ and d_i be the degree of vertex v_i. Then

(i) the number of 3-paths in $G=\sum _{i\ne j}{a}_{ij}^{(2)}(d_i-a_{ij}-1)$ and

(ii) the number of 4-paths in $G=\sum _{i\ne j}\left[a_{ij}^{(4)}-2a_{ij}^{(2)}(d_i-a_{ij})\right]-{\sum }_{i=1}^n\left[(2d_i-1)a_{ii}^{(3)}+6(\begin{array}{c}{d}_i\\ 3\end{array})\right]$.

The following explicit formula for the number of paths of length 5 was given by Boxwala and Movarraei [5].

Theorem 6

(Boxwala and Movarraei [5]). Let G be a graph with vertex set $\{v_1,v_2,\dots ,v_n\}$ and d_i be the degree of vertex v_i. Then the number of paths of length 5 in G is $\begin{array}{c}\sum _{i\ne j}{a}_{ij}^{(5)}-2\sum _{i\ne j}{a}_{ij}^{(4)}+2{\sum }_{i=1}^n{a}_{ii}^{(3)}(d_i-2)+4\sum _{i\ne j}{a}_{ij}^{(2)}-2\sum _{i\ne j}{a}_{ij}^{(2)}(d_i-a_{ij}-1)-4\sum _{i\ne j}{a}_{ij}^{(2)}(\begin{array}{c}{d}_i-a_{ij}-1\\ 2\end{array})+6\sum _{i\ne j}{a}_{ij}(\begin{array}{c}{a}_{ij}^{(2)}\\ 2\end{array})-2\sum _{i\ne j}{a}_{ii}^{(3)}{a}_{ij}^{(2)}-2{\sum }_{i=1}^n{a}_{ii}^{(3)}(\begin{array}{c}{d}_i-2\\ 2\end{array})-\\ 2{\sum }_{i=1}^n(a_{ii}^{(4)}-a_{ii}^{(2)}-2(\begin{array}{c}{d}_i\\ 2\end{array})-{\sum }_{j\ne i,j=1}^n{a}_{ij}^{(2)})(d_i-2)-\sum _{i\ne j}{a}_{ij}-3tr(A^4)+6tr(A^3)+3tr(A^2).\end{array}$

In the next section of this article, we provide new formulae to calculate the exact number of paths of length 3, 4, and 5 in a graph G. These new formulae have relatively less number of terms compared to the existing ones given in [22] and [5].

The organization of the remaining sections of the article is as follows: In Section 2, we obtain an explicit formula for the number of 8-cycles in G and provide new formulae to find the number of cycles of length 4, 5 and 6 in G. Further, new formulae to find the number of paths of length 3, 4 and 5 in G are obtained. In Section 3, we give an explicit formula for the number of cycles of length 10 (resp. 12) in terms of the spectrum and entries of its adjacency matrix when the girth of G is 10 (resp. 12).

2 Number of 8-cycles in a graph

Let G be a graph with vertex set $\{v_1,v_2,\dots ,v_n\}$ and d_i be the degree of vertex v_i. The number of k-cycles in a graph G is equal to $\frac{1}{2k}[tr(A^k)-W_k]$, where W_k represents the number of closed walks of length k which are not k-cycles. By following this method, we obtain an explicit formula for the number of 8-cycles in a simple graph G. First we calculate the number of closed 8-walks, which are not 8-cycles in G.

Lemma 7.

Let G be a graph with n vertices, m edges and $A=[a_{ij}]$ be the adjacency matrix of G. Then the number of closed 8-walks, which are not 8-cycles in G is $\begin{array}{c}{W}_8=2m+28{\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 2\end{array})+44tr(A^3)+72{\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 3\end{array})+52{\sum }_{i=1}^n{a}_{ii}^{(3)}(d_i-2)+2\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(2)}\\ 2\end{array})(32a_{ij}{d}_i+48d_i-124a_{ij}-63)+16\sum _{i\ne j}(\begin{array}{c}{d}_i-1-a_{ij}\\ 2\end{array})(a_{ij}^{(2)})\\ +48{\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 4\end{array})+120\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(2)}\\ 3\end{array})+64\sum _{i\ne j\ne k\ne l}{a}_{ij}{a}_{ik}{a}_{il}{a}_{jk}{a}_{kl}(a_{ij}^{(2)}-1)+128{\sum }_{i=1}^n(\begin{array}{c}\frac{1}{2}{a}_{ii}^{(3)}\\ 2\end{array})+48\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(2)}\\ 4\end{array})+32\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(2)}\\ 2\end{array})(\begin{array}{c}{d}_i-2-a_{ij}\\ 2\end{array})+64\sum _{i\ne j}(\begin{array}{c}\frac{1}{2}{a}_{ii}^{(3)}\\ 2\end{array})a_{ij}+16\sum _{i\ne j\ne k}(\begin{array}{c}{a}_{ij}^{(2)}\\ 2\end{array})(\begin{array}{c}{a}_{ik}^{(2)}\\ 2\end{array})\\ +8\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(3)}-a_{ij}(d_i+d_j-1)\\ 2\end{array})(2d_i-3a_{ij}-2)+8\sum _{i\ne j}[a_{ij}^{(3)}-a_{ij}(d_i+d_j-1)]a_{ij}^{(2)}(a_{ii}^{(3)}+a_{ij})+4\sum _{i\ne j}[a_{ij}^{(3)}-a_{ij}(d_i+d_j-1)](d_i+3-a_{ij})+8\sum _{i\ne j}[a_{ij}^{(3)}-a_{ij}(d_i+d_j-1)]a_{ij}(d_i-2)(d_j-2)-\\ 22\sum _{i\ne j\ne k\ne l}{a}_{ij}{a}_{ik}{a}_{il}{a}_{jk}{a}_{jl}{a}_{kl}-8\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(2)}\\ 2\end{array})(d_i-2-a_{ij})(d_j-2-a_{ij})-8\sum _{i\ne j}{a}_{ii}^{(3)}{a}_{ij}^{(2)}{a}_{ij}(d_j-2)-4\sum _{i\ne j}{a}_{ii}^{(3)}{a}_{ij}{a}_{jj}^{(3)}-48\sum _{i\ne j}[a_{ij}^{(3)}-a_{ij}(d_i+d_j-1)](\begin{array}{c}{a}_{ij}^{(2)}\\ 2\end{array})a_{ij}-24\sum _{i\ne j\ne k}[a_{ij}^{(3)}-a_{ij}(d_i+d_j-1)]a_{ik}^{(2)}{a}_{ik}{a}_{kj}.\end{array}$

Proof.

To calculate W₈, we first find all possible subgraphs of G in which there is a closed 8-walk that covers each edge of the subgraph at least once. Note that there is only one connected graph on 2 vertices, two connected graphs on 3 vertices, and six connected graphs on 4 vertices (drawn in Table 1, Cases 1 to 9). Observe that all these nine graphs have a closed 8-walk that covers each edge at least once.

Table 1 Closed 8-walks which are not 8-cycles.

Case	Subgraph	ni	Fi= Number of such subgraphs in G	$w_i=n_i{F}_i$
1		2	m	$2F_1$
2		28	${\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 2\end{array})$	$28F_2$
3		168	$\frac{1}{6}tr(A^3)$	$168F_3$
4		32	$\frac{1}{2}\sum _{i\ne j}(a_{ij}^{(3)}-a_{ij}(d_i+d_j-1))$	$32F_4$
5		72	${\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 3\end{array})$	$72F_5$
6		64	$\frac{1}{2}{\sum }_{i=1}^n{a}_{ii}^{(3)}(d_i-2)$	$64F_6$
7		264	$\frac{1}{4}\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(2)}\\ 2\end{array})$	$264F_7$
8		464	$\frac{1}{2}\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(2)}\\ 2\end{array})a_{ij}$	$464F_8$
9		528	$\frac{1}{24}\sum _{i\ne j\ne k\ne l}{a}_{ij}{a}_{ik}{a}_{il}{a}_{jk}{a}_{jl}{a}_{kl}$	$528F_9$
10		16	$\sum _{i\ne j}(\begin{array}{c}{d}_i-1-a_{ij}\\ 2\end{array})(a_{ij}^{(2)})$	$16F_{10}$
11		48	${\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 4\end{array})$	$48F_{11}$
12		112	$\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(2)}\\ 2\end{array})(d_i-2-a_{ij})$	$112F_{12}$
13		96	$\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(2)}\\ 2\end{array})a_{ij}(d_i-3)$	$96F_{13}$
14		48	$\frac{1}{2}\sum _{i\ne j\ne k}{a}_{ij}^{(2)}{a}_{ij}{a}_{ik}{a}_{jk}(d_k-2)-F_6-12F_9$	$48F_{14}$
15		192	$\frac{1}{2}\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(2)}\\ 3\end{array})$	$192F_{15}$
16		8	$\frac{1}{2}\sum _{i\ne j}[a_{ij}^{(3)}-a_{ij}(d_i+d_j-1)](d_i-1-a_{ij})-F_6$	$8F_{16}$
17		64	$\frac{1}{2}\sum _{i\ne j}[a_{ij}^{(3)}-a_{ij}(d_i+d_j-1)]a_{ij}^{(2)}{a}_{ij}-4F_8$	$64F_{17}$
18		128	$\frac{1}{2}\sum _{i\ne j\ne k\ne l}{a}_{ij}{a}_{ik}{a}_{il}{a}_{jk}{a}_{kl}(a_{ij}^{(2)}-1)-12F_9$	$128F_{18}$
19		320	${\sum }_{i=1}^n(\begin{array}{c}\frac{1}{2}{a}_{ii}^{(3)}\\ 2\end{array})-2F_8$	$320F_{19}$
20		96	$\frac{1}{2}\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(2)}\\ 4\end{array})$	$96F_{20}$
21		32	$\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(2)}\\ 2\end{array})(\begin{array}{c}{a}_{ii}^{(2)}-2-a_{ij}\\ 2\end{array})$	$32F_{21}$
22		16	$\frac{1}{2}\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(2)}\\ 2\end{array})(d_i-2-a_{ij})(d_j-2-a_{ij})-3F_{15}$	$16F_{22}$
23		96	$\frac{1}{6}\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(3)}-a_{ij}(d_i+d_j-1)\\ 2\end{array})-\frac{1}{3}{F}_8-\frac{1}{3}{F}_{12}-\frac{4}{3}{F}_{19}$	$96F_{23}$
24		96	$\frac{1}{2}\sum _{i\ne j}[a_{ij}^{(3)}-a_{ij}(d_i+d_j-1)](\begin{array}{c}{a}_{ij}^{(2)}\\ 2\end{array})a_{ij}-12F_9-2F_{18}$	$96F_{24}$
25		48	$\frac{1}{2}\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(3)}-a_{ij}(d_i+d_j-1)\\ 2\end{array})a_{ij}-6F_9-6F_{15}-F_{18}$	$48F_{25}$
26		48	$\frac{1}{2}\sum _{i\ne j\ne k}[a_{ij}^{(3)}-a_{ij}(d_i+d_j-1)]a_{ik}^{(2)}{a}_{ik}{a}_{kj}-F_6-6F_8-F_{13}-2F_{17}-F_{18}-4F_{19}$	$48F_{26}$
27		64	$\sum _{i\ne j}(\begin{array}{c}\frac{1}{2}{a}_{ii}^{(3)}\\ 2\end{array})a_{ij}-6F_8-F_{13}-4F_{19}$	$64F_{27}$
28		32	$\frac{1}{2}\sum _{i\ne j}{a}_{ii}^{(3)}{a}_{ij}^{(2)}{a}_{ij}(d_j-2)-2F_6-4F_8-24F_9-2F_{13}-2F_{14}-2F_{18}$	$32F_{28}$
29		32	$\frac{1}{8}\sum _{i\ne j}{a}_{ii}^{(3)}{a}_{ij}{a}_{jj}^{(3)}-3F_3-6F_8-6F_9-F_{18}-4F_{19}$	$32F_{29}$
30		16	$\sum _{i\ne j\ne k}(\begin{array}{c}{a}_{ij}^{(2)}\\ 2\end{array})a_{ik}^{(2)}-8F_8-2F_{12}-F_{13}-2F_{17}$	$16F_{30}$
31		16	$\frac{1}{2}\sum _{i\ne j}[a_{ij}^{(3)}-a_{ij}(d_i+d_j-1)]a_{ij}(d_i-2)(d_j-2)-12F_9-2F_{14}-F_{17}$	$16F_{31}$
32		32	$\frac{1}{2}\sum _{i\ne j\ne k}(\begin{array}{c}{a}_{ij}^{(2)}\\ 2\end{array})(\begin{array}{c}{a}_{ik}^{(2)}\\ 2\end{array})-12F_9-3F_{15}-3F_{18}-2F_{24}-2F_{25}$	$32F_{32}$
33		32	$\frac{1}{4}\sum _{i\ne j}[a_{ij}^{(3)}-a_{ij}(d_i+d_j-1)]a_{ij}^{(2)}{a}_{ii}^{(3)}-F_6-6F_8-24F_9-F_{13}-F_{14}-3F_{17}-6F_{18}-4F_{19}-4F_{24}-2F_{26}-\frac{1}{2}{F}_{28}-2F_{29}$	$32F_{33}$
34		16	$\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(3)}-a_{ij}(d_i+d_j-1)\\ 2\end{array})(d_i-a_{ij})-4F_8-3F_{12}-F_{13}-F_{14}-2F_{17}-2F_{18}-16F_{19}-2F_{22}-12F_{23}-2F_{26}-2F_{28}-F_{30}$	$16F_{34}$

It is also easy to check that among all 21 connected graphs on 5 vertices, there are exactly 10 graphs having a closed 8-walk that covers each edge at least once (drawn in Table 1, Cases 10 to 19). Similarly, among all 112 connected graphs on 6 vertices (see [9]), there are exactly 12 graphs with a closed 8-walk that covers each edge at least once (refer to Table 1, Cases 20 to 31).

Next we look for such graphs on 7 vertices. Note that if there is an edge e that is not contained in any cycle, then e occurs at least two times in a closed walk. Therefore, no tree on 7 vertices has a closed 8-walk that covers each edge at least once. Now, if a graph on 7 vertices has a 3-cycle, then there are 4 vertices which need to be connected using at most 5 edges. It is easy to see that there is only one such graph exists, which is shown in Case 33 of Table 1. Similarly, it can be seen that if a graph on 7 vertices has a cycle of length 4, 5, or 6, then the graph structure will be as shown in cases 32, 33, and 34 of Table 1, respectively. There does not exist a graph on 7 vertices that has a 7-cycle and a closed 8-walk.

Hence, there are 34 graphs in which there is a closed 8-walk that covers each edge of the graph at least once. In each case, we calculate all possible closed 8-walks, which covers all edges, and denote it by n_i, $i=1,2,\dots ,34$ (refer Table 1). The label at each vertex of the graphs in the table represents the number of closed 8-walks from that vertex to itself. For each case, we find a formula that gives the number of such subgraphs in G, and denote it by F_i, $i=1,2,\dots ,34$. We calculate $w_i=n_i{F}_i$. Finally, the number of closed 8-walks which are not 8-cycles are obtained by adding all w_i’s, that is, $W_8={\sum }_{i=1}^{34}{w}_i$. For better understanding, we have calculated and kept n_i, F_i and w_i in tabular form in Table 1 rather than writing step by step. □

The following is the main result of this section which follows immediately from the above Lemma.

Theorem 8.

Let W₈ be the expression as given in Lemma 7. Then the number of 8-cycles in a graph G with adjacency matrix A is $\frac{1}{16}[tr(A^{(8)})-W_8]$, where W₈ is the number of closed 8-walks which are not 8-cycles.

Example 9.

In K₈, we have $\begin{array}{c}{w}_1=56,w_2=4704,w_3=9408,w_4=26880,w_5=20160,w_6=53760,w_7=55440,w_8=194880,w_9=36960,w_{10}=53760,w_{11}=13440,w_{12}=376320,w_{13}=322560,w_{14}=161280,w_{15}=107520,w_{16}=26880,\\ w_{17}=215040,w_{18}=430080,w_{19}=268800,w_{20}=40320,w_{21}=161280,w_{22}=80640,w_{23}=161280,w_{24}=483840,w_{25}=241920,w_{26}=483840,w_{27}=161280,w_{28}=322560,w_{29}=80640,w_{30}=161280,\\ w_{31}=161280,w_{32}=161280,w_{33}=322560,w_{34}=322560\end{array}$. So, we have $W_8={\sum }_{i=1}^{34}{w}_i=5724488$. From Theorem 8, the number of 8-cycles in K₈ is 2520.

Counting the number of cycles in a graph of fixed girth is an important problem in Information theory. By using above Theorem, we give formulas for the number of 8-cycles in a graph G with fixed girth. From the definition of the girth, it is clear that if g is the girth of a graph, then there does not exist any cycle of length less than g in the graph. Therefore, the next corollaries follow immediately from the Theorem 8.

Corollary 10.

Let G be a graph on n vertices with girth 4. Let $A=[a_{ij}]$ be the adjacency matrix of G. Then the number of 8-cycles in G is equal to $\begin{array}{c}[\frac{1}{16}tr(A^8)-2m-28{\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 2\end{array})-4\sum _{i\ne j}[a_{ij}^{(3)}-a_{ij}(d_i+d_j-1)](d_i+3-a_{ij})-72{\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 3\end{array})-66\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^2\\ 2\end{array})-16\sum _{i\ne j}(\begin{array}{c}{d}_i-1-a_{ij}\\ 2\end{array})a_{ij}^{(2)}-\\ 48{\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 4\end{array})-96\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(2)}\\ 2\end{array})(d_i-2-a_{ij})-120\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(2)}\\ 3\end{array})-48\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(2)}\\ 4\end{array})-32\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(2)}\\ 2\end{array})(\begin{array}{c}{d}_i-2-a_{ij}\\ 2\end{array})-16\sum _{i\ne j\ne k}(\begin{array}{c}{a}_{ij}^{(2)}\\ 2\end{array})(\begin{array}{c}{a}_{ik}^{(2)}\\ 2\end{array})-8\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(3)}-a_{ij}(d_i+d_j-1)\\ 2\end{array})(2d_i-3a_{ij}-4)-\\ 8\sum _{i\ne j}[a_{ij}^{(3)}-a_{ij}(d_i+d_j-1)]a_{ij}(d_i-2)(d_j-2)+8\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(2)}\\ 2\end{array})(d_i-2-a_{ij})(d_j-2-a_{ij})].\end{array}$

Corollary 11.

Let G be a graph on n vertices having girth either 5 or 6. Then the number of 8-cycles in G is equal to $\frac{1}{16}\left[tr(A^8)-2m-28{\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 2\end{array})-72{\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 3\end{array})-48{\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 4\end{array})-4\sum _{i\ne j}{a}_{ij}^{(2)}(d_i-1)(4d_i+d_j-1)-16\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(3)}-a_{ij}(d_i+d_j-1)\\ 2\end{array})(d_i-1)\right].$

Proof.

Let G be a graph having girth either 5 or 6. Then, in both cases G does not contain cycles of length 3 and 4. Therefore, we consider the cases from Table 1, in which the subgraphs does not have a 3-cycle or a 4-cycle. Since the girth of the graph is fixed, from Case 5 onwards in Table 2, we are able to simplify the formulas used to calculate the number of subgraphs. The number of closed 8-walks which are not 8-cycles in G will be obtained by adding all w_i’s and $\frac{1}{16}[tr(A^{(8)})-{\sum }_{i=1}^9{w}_i]$ gives the number of 8-cycles in G. □

Table 2 Closed 8-walks which are not 8-cycles.

Case	Subgraph	ni	Fi= Number of such subgraphs in G	$w_i=n_i{F}_i$
1		2	m	$2F_1$
2		28	${\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 2\end{array})$	$28F_2$
3		72	${\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 3\end{array})$	$72F_3$
4		48	${\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 4\end{array})$	$48F_4$
5		32	$\frac{1}{2}\sum _{i\ne j}{a}_{ij}^{(2)}(d_i-1)$	$32F_5$
6		16	$\sum _{i\ne j}{a}_{ij}^{(2)}(\begin{array}{c}{d}_i-1\\ 2\end{array})$	$16F_6$
7		8	$\frac{1}{2}\sum _{i\ne j}{a}_{ij}^{(2)}(d_i-1)(d_j-1)$	$8F_7$
8		96	$\frac{1}{6}\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(3)}-a_{ij}(d_i+d_j-1)\\ 2\end{array})$	$96F_8$
9		16	$\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(3)}-a_{ij}(d_i+d_j-1)\\ 2\end{array})(d_i-2)$	$16F_9$

The next result follows immediately from Corollary 11 by removing Cases 8 and 9.

Corollary 12.

Let G be a graph on n vertices having girth either 7 or 8. Then the number of 8-cycles in G is equal to $\frac{1}{16}\left[tr(A^8)-2m-28{\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 2\end{array})-72{\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 3\end{array})-48{\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 4\end{array})-4\sum _{i\ne j}{a}_{ij}^{(2)}(d_i-1)(4d_i+d_j-1)\right].$

In the proof of Lemma 7, the graphs in Cases 7 and 23 are a 4-cycle and a 6-cycle respectively. Although formulas to determine the number of 4-cycles and 6-cycles in a graph G are provided in [13] and [7], respectively, we were able to find relatively much simpler formulae for the same. We state new formulae for the number of 4-cycles and 6-cycles below.

Observation 13.

Let $A=[a_{ij}]$ be the adjacency matrix of a graph G on n vertices. Then

(i) the number of 4-cycles in G $=\frac{1}{4}\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(2)}\\ 2\end{array})$,

(ii) the number of 6-cycles in G $=\frac{1}{6}\left[\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(3)}-a_{ij}(d_i+d_j-1)\\ 2\end{array})+\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(2)}\\ 2\end{array})(9a_{ij}+4-2d_i)-8{\sum }_{i=1}^n(\begin{array}{c}\frac{1}{2}{a}_{ii}^{(3)}\\ 2\end{array})\right]$.

In 2014, Movarraei and Shikare [22] have given formulae to calculate the number of paths of length 3 and 4 in a graph. While proving Lemma 7, we obtained new formulae for the number of paths of length 3 and 4 in Case 4 and Case 16, respectively. We state formulae for the number of 3-paths and 4-paths below. In addition, we also obtain a new formula for the number of 5-paths in a graph G, which is relatively simpler when compared with the formula given by Boxwala and Movarraei [5]. Even though the two formulas to find the number of 3-paths (Lemma 5(i) and Observation 14(i)) look similar, in the formula given by us, $a_{ij}^{(3)}-a_{ij}(d_i+d_j-1)$ equals to the number of 3-paths from vertex v_i to v_j in G.

Observation 14. Let $A=[a_{ij}]$ be the adjacency matrix of a graph G on n vertices. Then

(i) the number of 3-paths in G is $\sum _{i\ne j}(a_{ij}^{(3)}-a_{ij}(d_i+d_j-1))$,

(ii) the number of 4-paths in G is $\sum _{i\ne j}(a_{ij}^{(3)}-a_{ij}(d_i+d_j-1))(d_i-a_{ij}-1)-{\sum }_{i=1}^n{a}_{ii}^{(3)}(d_i-2)$.

In a similar way, we also find a new formulae for the number of 5-cycles and 5-paths in a graph G in terms of entries of its adjacency matrix.

Theorem 15.

Let G be a graph on n vertices and $A=[a_{ij}]$ be the adjacency matrix of G. Then

(i) the number of 5-cycles in G is $\frac{1}{10}\left[\sum _{i\ne j}(a_{ij}^{(3)}-a_{ij}(d_i+d_j-1))a_{ij}^{(2)}-2{\sum }_{i=1}^n{a}_{ii}^{(3)}(d_i-2)\right]$,

(ii) the number of 5-paths in G is $\sum _{i\ne j}(a_{ij}^{(3)}-a_{ij}(d_i+d_j-1))\left[(d_i-a_{ij}-1)(d_j-a_{ij}-1)-a_{ij}^{(2)}\right]-2\sum _{i\ne j}{a}_{ii}^{(3)}{a}_{ij}^{(2)}-{\sum }_{i=1}^n{a}_{ii}^{(3)}(6d_i-8)+6\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(2)}\\ 2\end{array})a_{ij}$.

Proof.

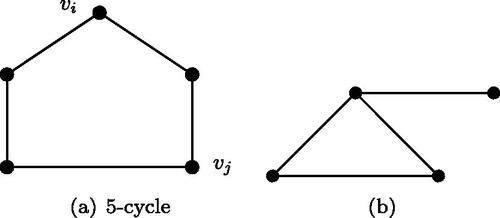
(i) The number of paths of length 3 from vertex v_i to vertex v_j in graph G is $a_{ij}^{(3)}-a_{ij}(d_i+d_j-1)$ and also we know that $a_{ij}^{(2)}$ represents the number of paths of length 2 from vertex v_i to vertex v_j. To find the number of 5-cycles in a graph G we consider the formula $F_1=\frac{1}{10}\sum _{i\ne j}(a_{ij}^{(3)}-a_{ij}(d_i+d_j-1))a_{ij}^{(2)}$.

Other than 5-cycles, each subgraph as shown in Figure 1(b) also contributes $\frac{2}{5}$ to F₁. The number of such subgraphs in a graph G is $F_2=\frac{1}{2}{\sum }_{i=1}^n{a}_{ii}^{(3)}(d_i-2)$. Hence the number of 5-cycles in a graph G is equal to $\frac{1}{10}\left[\sum _{i\ne j}(a_{ij}^{(3)}-a_{ij}(d_i+d_j-1))a_{ij}^{(2)}-2{\sum }_{i=1}^n{a}_{ii}^{(3)}(d_i-2)\right]$.

Fig. 1 Subgraphs of G that contribute to the counting of 5-cycles.

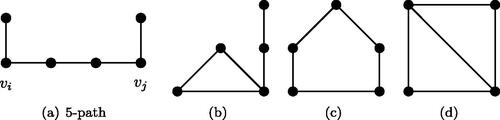
(ii) The number of paths of length 3 from vertex v_i to v_j is $a_{ij}^{(3)}-a_{ij}(d_i+d_j-1)$. To calculate the number of 5-paths in G, we use the formula $P=\sum _{i\ne j}(a_{ij}^{(3)}-a_{ij}(d_i+d_j-1))(d_i-a_{ij}-1)(d_j-a_{ij}-1)$. Each subgraph of G as shown in Figure 2(b) contributes 4 to P. Similarly, each subgraph of G as shown in Figure 2(c,d) contributes 10 and 4, respectively, to P. Let p₁, p₂, and p₃ denote the number of subgraphs as shown in Figure 2(b–d), respectively. Then the number of 5-paths in graph G is $P_5(G)=P-4p_1-10p_2-4p_3$.

Fig. 2 Subgraphs of G that contribute to the counting of 5-paths.

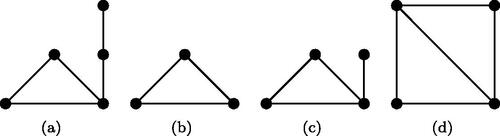
We know that $p_2=\frac{1}{10}\left[\sum _{i\ne j}(a_{ij}^{(3)}-a_{ij}(d_i+d_j-1))a_{ij}^{(2)}-2{\sum }_{i=1}^n{a}_{ii}^{(3)}(d_i-2)\right]$ and $p_3=\frac{1}{2}\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(2)}\\ 2\end{array})a_{ij}$. To calculate p₁, we use the formula $T=\frac{1}{2}\sum _{i\ne j}{a}_{ii}^{(3)}{a}_{ij}^{(2)}$. Each subgraph of G as shown in Figure 3(b–d) contributes 6, 2 and 4, respectively, to T. Let t₁, t₂, and t₃ denote the number of subgraphs as shown in Figure 3(b–d), respectively. Then $p_1=T-6t_1-2t_2-4t_3$. We know that $t_1=\frac{1}{6}tr(A^3)$ and $t_2=\frac{1}{2}{\sum }_{i=1}^n{a}_{ii}^{(3)}(d_i-2)$. Clearly, $t_3=p_3$. Hence, $p_1=\frac{1}{2}\sum _{i\ne j}{a}_{ii}^{(3)}{a}_{ij}^{(2)}-tr(A^3)-{\sum }_{i=1}^n{a}_{ii}^{(3)}(d_i-2)-4p_3$. By substituting $p_1,p_2,$ and p₃ in $P_5(G)$, we get the formula for number of 5-paths in a graph G as $\sum _{i\ne j}(a_{ij}^{(3)}-a_{ij}(d_i+d_j-1))\left[(d_i-a_{ij}-1)(d_j-a_{ij}-1)-a_{ij}^{(2)}\right]-2\sum _{i\ne j}{a}_{ii}^{(3)}{a}_{ij}^{(2)}-{\sum }_{i=1}^n{a}_{ii}^{(3)}(6d_i-8)+6\sum _{i\ne j}(\begin{array}{c}{a}_{ij}^{(2)}\\ 2\end{array})a_{ij}$. □

Fig. 3 Graphs used in calculating p₁.

Example 16.

In K₈, d_i = 7, $a_{ij}^{(2)}=6,a_{ij}^{(3)}=43$, and $a_{ii}^{(3)}=42$. Hence by Theorem 15, the number of 5-cycles in K₈ is equal to 672 and the number of 5-paths in K₈ is equal to 20160.

3 Number of cycles of length 10 and 12 in a graph

In this section, we give an explicit formula for the number of cycles of length 10 (resp. 12) in terms of entries of its adjacency matrix when the girth of G is 10 (resp. 12). If G has girth g, then the graph does not have any cycle of length less than g. To calculate the number of 10-cycles (resp. 12-cycles) in a graph, we follow the same technique used in Theorem 8. That is, the number of k-cycles in a graph G is equal to $\frac{1}{2k}[tr(A^k)-W_k]$, where W_k is the number of closed k-walks which are not k-cycles.

To calculate W_k, we first find all possible subgraphs of G in which there is a closed k-walk that covers each edge of the subgraph at least once. Since the girth g of G is 10 (resp. 12), subgraphs of G in which there is a closed 10-walk (resp. 12-walk) that covers each edge of the subgraph at least once are only the trees. If there is an edge e that is not contained in any cycle, then e occurs at least two times in a closed walk. Hence it is easy to see that, all trees on vertices less than or equal to 6 (resp. 7) are the only subgraphs of G that contains a closed 10-walk (resp. 12-walk) that covers each edge of the subgraph at least once. The number of trees on $2,3,4,5,6,$ and 7 vertices are $1,1,2,3,6,$ and 11, respectively (all trees up to 10 vertices are drawn in [8]). Trees up to 6 and 7 vertices are drawn in Tables 3 and 4, respectively.

Table 3 Closed 10-walks which are not 10-cycles.

Case	Subgraph	ni	Fi= Number of such subgraphs in G	$w_i=n_i{F}_i$
1		2	m	$2F_1$
2		60	${\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 2\end{array})$	$60F_2$
3		120	$\frac{1}{2}\sum _{i\ne j}(a_{ij}^{(3)}-a_{ij}(d_i+d_j-1))$	$120F_3$
4		300	${\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 3\end{array})$	$300F_4$
5		60	$\frac{1}{2}\sum _{i\ne j}{a}_{ij}^{(2)}(d_i-1)(d_j-1)$	$60F_5$
6		140	$\sum _{i\ne j}{a}_{ij}^{(2)}(\begin{array}{c}{d}_i-1\\ 2\end{array})$	$140F_6$
7		480	${\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 4\end{array})$	$480F_7$
8		10	$\frac{1}{2}\sum _{i\ne j}(a_{ij}^{(3)}-a_{ij}(d_i+d_j-1))(d_i-1)(d_j-1)$	$10F_8$
9		20	$\sum _{i\ne j}{a}_{ij}^{(2)}(\begin{array}{c}{d}_i-1\\ 2\end{array})(d_j-1)$	$20F_9$
10		20	$\frac{1}{2}\sum _{i\ne j\ne k}{a}_{ij}{a}_{ik}(d_i-2)(d_j-1)(d_k-1)$	$20F_{10}$
11		40	$\frac{1}{2}\sum _{i\ne j}{a}_{ij}(\begin{array}{c}{d}_i-1\\ 2\end{array})(\begin{array}{c}{d}_j-1\\ 2\end{array})$	$40F_{11}$
12		60	$\sum _{i\ne j}{a}_{ij}^{(2)}(\begin{array}{c}{d}_i-1\\ 3\end{array})$	$60F_{12}$
13		240	${\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 5\end{array})$	$240F_{13}$

Table 4 Closed 12-walks which are not 12-cycles.

Case	Subgraph	ni	Fi= Number of such subgraphs in G	wi
1		2	m	$2F_1$
2		124	${\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 2\end{array})$	$124F_2$
3		390	$\frac{1}{2}\sum _{i\ne j}(a_{ij}^{(3)}-a_{ij}(d_i+d_j-1))$	$390F_3$
4		1080	${\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 3\end{array})$	$1080F_4$
5		300	$\frac{1}{2}\sum _{i\ne j}{a}_{ij}^{(2)}(d_i-1)(d_j-1)$	$300F_5$
6		804	$\sum _{i\ne j}{a}_{ij}^{(2)}(\begin{array}{c}{d}_i-1\\ 2\end{array})$	$804F_6$
7		3120	${\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 4\end{array})$	$3120F_7$
8		96	$\frac{1}{2}\sum _{i\ne j}(a_{ij}^{(3)}-a_{ij}(d_i+d_j-1))(d_i-1)(d_j-1)$	$96F_8$
9		216	$\sum _{i\ne j}{a}_{ij}^{(2)}(\begin{array}{c}{d}_i-1\\ 2\end{array})(d_j-1)$	$216F_9$
10		228	$\frac{1}{2}\sum _{i\ne j\ne k}{a}_{ij}{a}_{ik}(d_i-2)(d_j-1)(d_k-1)$	$228F_{10}$
11		504	$\frac{1}{2}\sum _{i\ne j}{a}_{ij}(\begin{array}{c}{d}_i-1\\ 2\end{array})(\begin{array}{c}{d}_j-1\\ 2\end{array})$	$504F_{11}$
12		792	$\sum _{i\ne j}{a}_{ij}^{(2)}(\begin{array}{c}{d}_i-1\\ 3\end{array})$	$792F_{12}$
13		3600	${\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 5\end{array})$	$3600F_{13}$
14		12	$\frac{1}{2}\sum _{i\ne j\ne k}{a}_{ij}^{(2)}{a}_{ik}^{(2)}(d_j-1)(d_k-1)-F_{10}$	$12F_{14}$
15		24	$\sum _{i\ne j\ne k\ne l}{a}_{ij}{a}_{il}{a}_{jk}(d_i-2)(d_k-1)(d_l-1)$	$24F_{15}$
16		60	$\sum _{i\ne j}{a}_{ij}^{(2)}(\begin{array}{c}{d}_i-1\\ 3\end{array})(d_j-1)$	$60F_{16}$
17		48	$\sum _{i\ne j\ne k}{a}_{ij}{a}_{ik}(d_i-2)(d_j-1)(\begin{array}{c}{d}_k-1\\ 2\end{array})$	$48F_{17}$
18		48	$\frac{1}{2}\sum _{i\ne j}{a}_{ij}^{(2)}(\begin{array}{c}{d}_i-1\\ 2\end{array})(\begin{array}{c}{d}_j-1\\ 2\end{array})$	$48F_{18}$
19		24	$\sum _{i\ne j}(a_{ij}^{(3)}-a_{ij}(d_i+d_j-1))(\begin{array}{c}{d}_i-1\\ 2\end{array})(d_j-1)$	$24F_{19}$
20		24	$\frac{1}{6}\sum _{i\ne j\ne k\ne l}{a}_{ij}{a}_{ik}{a}_{il}(d_j-1)(d_k-1)(d_l-1)$	$24F_{20}$
21		72	$\frac{1}{2}\sum _{i\ne j\ne k}{a}_{ij}{a}_{ik}(\begin{array}{c}{d}_i-2\\ 2\end{array})(d_j-1)(d_k-1)$	$72F_{21}$
22		144	$\sum _{i\ne j}{a}_{ij}(\begin{array}{c}{d}_i-1\\ 3\end{array})(\begin{array}{c}{d}_j-1\\ 2\end{array})$	$144F_{22}$
23		288	$\sum _{i\ne j}{a}_{ij}^{(2)}(\begin{array}{c}{d}_i-1\\ 4\end{array})$	$288F_{23}$
24		1440	${\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 6\end{array})$	$1440F_{24}$

For each tree, we calculate all possible 10-walks (resp. 12-walks), which covers each edge at least once, and denote this number by n_i. The label at each vertex of the graphs in the Tables represents the number of closed 10-walks (resp. 12-walks) from that vertex to itself. For each subgraph, we find a formula that gives the number of such subgraphs in G, and denote it by F_i. We calculate $w_i=n_i{F}_i$. Finally, the number of closed 10-walks (resp. 12-walks) which are not 10-cycles (resp. 12-cycles) are obtained by adding all w_i’s.

For better understanding, we have calculated and kept n_i, F_i and w_i in tablular form, where Table 3 contains closed 10-walks which are not 10-cycles and Table 4 contains closed 12-walks which are not 12-cycles.

Theorem 17.

Let G be a graph having girth 10. Then the number of 10-cycles in G is $\begin{array}{c}\frac{1}{16}[tr(A^{10})-2m-60{\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 2\end{array})-300{\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 3\end{array})-480{\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 4\end{array})-240{\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 5\end{array})-20\sum _{i\ne j}{a}_{ij}(\begin{array}{c}{d}_i-1\\ 2\end{array})(\begin{array}{c}{d}_j-1\\ 2\end{array})-\\ 10\sum _{i\ne j}{a}_{ij}^{(2)}[(d_i-1)(d_j-1)+2(\begin{array}{c}{d}_i-1\\ 2\end{array})(d_j+6)+6(\begin{array}{c}{d}_i-1\\ 3\end{array})]-10\sum _{i\ne j\ne k}{a}_{ij}{a}_{ik}(d_i-2)(d_j-1)(d_k-1)-5\sum _{i\ne j}(a_{ij}^{(3)}-a_{ij}(d_i+d_j-1))(d_i{d}_j-d_i-d_j+13)].\end{array}$

Theorem 18.

Let G be a graph having girth 12. Then the number of 12-cycles in G is $\begin{array}{c}\frac{1}{24}[tr(A^{12})-2m-124{\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 2\end{array})-1080{\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 3\end{array})-3120{\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 4\end{array})-3600{\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 5\end{array})-1440{\sum }_{i=1}^n(\begin{array}{c}{d}_i\\ 6\end{array})-288\sum _{i\ne j}{a}_{ij}^{(2)}(\begin{array}{c}{d}_i-1\\ 4\end{array})-\\ 195\sum _{i\ne j}(a_{ij}^{(3)}-a_{ij}(d_i+d_j-1))-12\sum _{i\ne j}(a_{ij}^{(3)}-a_{ij}(d_i+d_j-1))(d_i+2)(d_i-1)(d_j-1)-150\sum _{i\ne j}{a}_{ij}^{(2)}(d_i-1)(d_j-1)-\\ 12\sum _{i\ne j}{a}_{ij}^{(2)}(\begin{array}{c}{d}_i-1\\ 2\end{array})(18d_j-49)-12\sum _{i\ne j}{a}_{ij}^{(2)}(\begin{array}{c}{d}_i-1\\ 3\end{array})(5d_j-61)-12\sum _{i\ne j}(\begin{array}{c}{d}_i-1\\ 2\end{array})(\begin{array}{c}{d}_j-1\\ 2\end{array})(2a_{ij}^{(2)}+21a_{ij})-\\ 144\sum _{i\ne j}{a}_{ij}(\begin{array}{c}{d}_i-1\\ 3\end{array})(\begin{array}{c}{d}_j-1\\ 2\end{array})-6\sum _{i\ne j\ne k}{a}_{ij}{a}_{ik}(d_i-2)(d_j-1)(d_k-1)(3d_i+4d_k+19)-6\sum _{i\ne j\ne k}{a}_{ij}^{(2)}{a}_{ik}^{(2)}(d_j-2)(d_k-1)-4\sum _{i\ne j\ne k\ne l}{a}_{ij}{a}_{il}(d_k-1)(d_l-1)(24a_{jk}(d_i-2)+a_{ik}(d_j-1))].\end{array}$

Acknowledgments

The authors are thankful to the anonymous referees for a careful reading of the article and the valuable comments made in the report.

Additional information

Funding

The second author acknowledges the financial support from UGC, Government of India.