Descending endomorphism graphs of groups

Abstract

We define a new type of graph of a group with reference to the descending endomorphisms of the group. A descending endomorphism of a group is an endomorphism that induces a corresponding endomorphism in every homomorphic image of the group. We define the undirected (directed) descending endomorphism graph of a group as the undirected (directed) graph whose vertex set is the underlying set of the group, in which there is an undirected (directed) edge from one vertex to another if the group has a descending endomorphism that maps the former element to the latter. We investigate some basic properties of these graphs and show that they are closely related to power graphs. We also determine the descending endomorphism graphs of symmetric, dihedral, and dicyclic groups.

KEYWORDS:

• Graph
• group endomorphism
• power graph

AMS CLASSIFICATION:

• 05C25
• 08A35

1 Introduction

There are several well-known graphs defined from groups, such as the Cayley graph, the commuting graph, the power graph, and other variants of these constructions. In this article, we introduce a graph of a group using the concept of descending endomorphisms, namely the descending endomorphism graph of a group. The definition is motivated by the observation that the descending endomorphisms of an Abelian group are the power maps of the group, and the power graph, which has the elements of the group as its vertices, has edges that join each vertex to its images under all power maps.

The main content of this article is organized into five sections. In Section 2, we define the descending endomorphism graph and make some basic observations. In Section 3, we show that these graphs are closely related to power graphs of groups, by proving some results that parallel ones found in the literature on power graphs. We also show that any Dedekind group is characterized by the property that its descending endomorphism graph is equal to its power graph. In Sections 4–6, we give a complete description of the descending endomorphism graphs of symmetric, dihedral, and dicyclic groups, respectively, and finally show that for certain orders, dihedral and dicyclic groups have isomorphic descending endomorphism graphs.

2 Definition and basic properties

Descending endomorphisms of groups were introduced in [5], and further studied in [6]. We first review the definition and two characterizations of descending endomorphisms that will be used repeatedly throughout this article.

Let G be a group. An endomorphism δ of G is a descending endomorphism if, for any quotient group Q of G, with canonical projection $\phi :G\twoheadrightarrow Q$, the quotient Q has an endomorphism $\overline{\delta }$ such that the diagram in Equation (1) commutes [5].

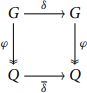
The endomorphism $\overline{\delta }$ of Q is called the descended endomorphism or descent of δ along $\phi$, or the endomorphism induced by δ.

If H is a subgroup (respectively, normal subgroup) of G, we write $H\le G$ (respectively, $H⊴G$). H is invariant under an endomorphism ε of G if $\epsilon (H)\le H$. The conjugate of $x\in G$ by $y\in G$ is $x^y=yx{y}^{-1}$, and the conjugacy class of x is the set of all conjugates of x. The normal closure of an element $x\in G$ is the intersection of all normal subgroups containing x, or equivalently, the subgroup generated by the set of all conjugates of x in G, and is denoted by $〈x^G〉$. Descending endomorphisms are characterized in terms of normal subgroups and normal closures of elements as described in the following results.

Lemma 2.1.

[5, Lemma 2.4] An endomorphism of a group G is a descending endomorphism of G if and only if it leaves every normal subgroup of G invariant. The descent of a descending endomorphism δ of G to any quotient G/N along the canonical projection is given by $\overline{\delta }(xN)=\delta (x)N$ for all $xN\in G/N$.

Corollary 2.2.

[6, Corollary 1] An endomorphism δ of a group G is descending if and only if for every element $x\in G,\delta (x)\in 〈x^G〉$.

The set of all endomorphisms of G forms a monoid, $\text{End}G$, under composition. The set of all descending endomorphisms, $\text{Des}G$, is a submonoid of $\text{End}G$, and by Corollary 2.2, contains $\text{Inn}G$, the inner automorphism group of G, as a subgroup.

Now, we construct a graph of a group by defining a relation on its elements with reference to the descending endomorphisms of the group.

Definition 2.3.

The directed descending endomorphism graph of a group G is the digraph $\overrightarrow{\mathcal{D}\mathcal{G}}(G)$ with vertex set G, in which, for any two vertices x and y, there is a directed edge from x to y, denoted by $x\to y$, if and only if G has a descending endomorphism δ such that $y=\delta (x)$. The undirected descending endomorphism graph of G is the underlying undirected graph of $\overrightarrow{\mathcal{D}\mathcal{G}}(G)$, and is denoted by $\mathcal{D}\mathcal{G}(G)$. We shall write $x\sim y$ to mean that x and y are adjacent in $\mathcal{D}\mathcal{G}(G)$.

Remark 2.4.

In Definition 2.3, it is possible that $x=y$, and as the identity map on G is a descending endomorphism, every vertex x in the (directed or undirected) descending endomorphism graph of G has a self-loop. While this may be uninteresting from the graph theoretical point of view, it will be necessary for other reasons, as will be understood on examining Remark 2.5 and Theorem 2.6 below. Taking this to be known, we will not represent the self-loops in drawings of graphs.

Remark 2.5.

Observe that the relation $\to$ is a preorder on G – i.e., a reflexive and transitive relation. The identity element, 1, is the unique maximal element in this preorder, as no descending endomorphism maps 1 to any other element, implying that there is no element $x\ne 1$ such that $1\to x$. The graph $\overrightarrow{\mathcal{D}\mathcal{G}}(G)$ is the graph of this preorder, and hence, is a transitive digraph. It follows that given any directed path in $\overrightarrow{\mathcal{D}\mathcal{G}}(G)$, its vertices induce a complete subgraph in $\mathcal{D}\mathcal{G}(G)$.

Theorem 2.6.

If $\phi :G\to H$ is an epimorphism from a group G to a group H, then $\phi$ is a surjective digraph (graph) homomorphism from $\overrightarrow{\mathcal{D}\mathcal{G}}(G)$ to $\overrightarrow{\mathcal{D}\mathcal{G}}(H)$ ( $\mathcal{D}\mathcal{G}(G)$ to $\mathcal{D}\mathcal{G}(H)$).

Proof.

Let $x,y\in G$, and suppose that $x\to y$ in $\overrightarrow{\mathcal{D}\mathcal{G}}(G)$. Then there exists $\delta \in \text{Des}G$ such that $y=\delta (x)$. Let $\overline{\delta }$ be the descent of δ to H along $\phi$. Since $\overline{\delta }(\phi (x))=\phi (\delta (x))=\phi (y)$, it follows that $\phi (x)\to \phi (y)$ in $\overrightarrow{\mathcal{D}\mathcal{G}}(H)$. Hence, $\phi$ is a surjective digraph homomorphism from $\overrightarrow{\mathcal{D}\mathcal{G}}(G)$ to $\overrightarrow{\mathcal{D}\mathcal{G}}(H)$. The undirected case is obvious. □

The corollary given below follows immediately from Theorem 2.6.

Corollary 2.7.

The automorphism group of G is a subgroup of the automorphism group of $\overrightarrow{\mathcal{D}\mathcal{G}}(G)$ and of the automorphism group of $\mathcal{D}\mathcal{G}(G)$.

3 Relation with power graphs

The directed power graph of a group G was originally defined in [4] as the graph with vertex set equal to G, in which there is a directed edge from a vertex x to a vertex $y\ne x$ whenever y is an integer power of x in G. We denote the directed power graph of G by $\overrightarrow{\mathcal{P}\mathcal{G}}(G)$ and its underlying undirected graph, the undirected power graph, by $\mathcal{P}\mathcal{G}(G)$. 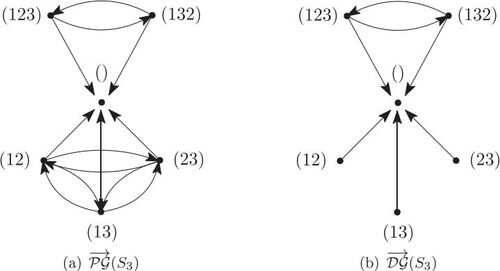In view of Remark 2.4, we shall ignore the condition $y\ne x$ in the definition of power graphs, and therefore $\overrightarrow{\mathcal{P}\mathcal{G}}(G)$ and $\mathcal{P}\mathcal{G}(G)$ will have self-loops on every vertex. Figure 1 shows the directed power graph and the directed descending endomorphism graph of the symmetric group S₃.

Fig. 1 The directed power graph and directed descending endomorphism graph of S₃.

Remark 3.1.

Observe that both power graphs and descending endomorphism graphs can be considered instances of a more general construction, described as follows. Let Ω be a set of functions from a group G to itself. Define a (directed) graph having all the elements of G as its vertices, and with (directed) edges of the form (x, y) whenever $\omega (x)=y$ for some $\omega \in \Omega$. When Ω is taken to be the set of all power maps on G, this graph is the power graph of G, and when $\Omega =\text{Des}G$, it is the descending endomorphism graph of G. Note, however, that in the latter case, $\Omega =\text{Des}G$ is an operator domain on G (i.e., the functions in Ω are endomorphisms of G), whereas in the former case of Ω being the set of power maps of G, it is an operator domain only when G is Abelian.

Interestingly, it has been shown in [2] that any two finite Abelian groups with isomorphic power graphs are themselves isomorphic, while this is not true in the class of all finite groups, nor in the class of infinite Abelian groups. Recall that a Dedekind group is one in which every subgroup is normal. Lemma 2.1 implies that all descending endomorphisms of Dedekind groups are power maps. In the special case of Abelian groups, the converse also holds – i.e., every power map is a descending endomorphism. From this observation, we may conclude that the descending endomorphism graph of a Dedekind group is a subgraph of its power graph. We show that, in fact, the power graph and the descending endomorphism graph of a group are equal exactly when the group is a Dedekind group. First, we list some relevant definitions and results from [6].

Consider the quaternion group $Q_8=\{1,-1,i,-i,j,-j,k,-k\}$. The set {i, j} is a generating set of Q₈, and therefore, any endomorphism of Q₈ can be defined by specifying its action on i and j. For $u,v\in \{0,1,2,3\}$, let ${\tau }^{(uv)}$ denote the unique endomorphism of Q₈ such that ${\tau }^{(uv)}(i)=i^u$ and ${\tau }^{(uv)}(j)=j^v$, provided it is well-defined.

Proposition 3.2.

[6, Proposition 1] The set of descending endomorphisms of Q₈ is $$\text{Des}{Q}_8=\{ {\tau }^{(uv)}|u,v\in \{0,1,2,3\},u\equiv v\hspace{1em}\mathrm{mod}2 \}.$$

A Hamiltonian group is a non-Abelian group in which every subgroup is normal – thus, a Dedekind group is either Abelian or Hamiltonian. It is well-known that a group G is Hamiltonian if and only if it can be written as a direct product $G=G_1\times G_2\times G_3$, where $G_1\cong Q_8$, G₂ is an elementary Abelian 2-group, and G₃ is a torsion Abelian group in which all elements have odd order [10].

Theorem 3.3.

[6, Theorem 8] Let G be a Hamiltonian group with direct decomposition $G=G_1\times G_2\times G_3$, where $G_1\cong Q_8$, G₂ is elementary 2-Abelian, and G₃ is torsion Abelian with all elements having odd order. If ${\text{id}}_{G_2}$ and $0_{G_2}$ denote the identity automorphism and trivial endomorphism, respectively, of G₂, then $$\begin{array}{c}\text{Des}G=\{ {\tau }^{(uv)}\times 0_{G_2}\times {\delta }_3|u,v\in \{0,2\},{\delta }_3\in \text{Des}{G}_3 \}\cup \\ \{ {\tau }^{(uv)}\times {\text{id}}_{G_2}\times {\delta }_3|u,v\in \{1,3\},{\delta }_3\in \text{Des}{G}_3 \}.\end{array}$$

Theorem 3.4.

For any group G, the following are equivalent:

1. G is a Dedekind group.

2. $\overrightarrow{\mathcal{D}\mathcal{G}}(G)=\overrightarrow{\mathcal{P}\mathcal{G}}(G)$.

3. $\mathcal{D}\mathcal{G}(G)=\mathcal{P}\mathcal{G}(G)$.

Proof.

First, let G be a Dedekind group. If G is Abelian, then obviously, (ii) and (iii) hold. So, suppose that G is non-Abelian. Then G is Hamiltonian, and has a direct decomposition $G=G_1\times G_2\times G_3$, as given in Theorem 3.3. Let $(x,y,z)\in G$, where $x\in G_1\cong Q_8,y\in G_2$, which is elementary 2-Abelian, and $z\in G_3$, which is torsion Abelian with all elements having odd order. We need to show that $(x,y,z)\to {(x,y,z)}^k$ in $\overrightarrow{\mathcal{D}\mathcal{G}}(G)$, for any integer k. If k is even, then clearly, there exist $u,v\in \{0,2\}$ such that $x^k={\tau }^{(uv)}(x)$ (in the notation of Proposition 3.2), which is a descending endomorphism of G₁ (by Proposition 3.2), and y^k is the identity element of G₂. Let δ₃ be the kth-power map of G₃, which is a descending endomorphism. Then by Theorem 3.3, ${\tau }^{(uv)}\times 0_{G_2}\times {\delta }_3$ is a descending endomorphism of G. Clearly, $({\tau }^{(uv)}\times 0_{G_2}\times {\delta }_3)(x,y,z)={(x,y,z)}^k$, and therefore, $(x,y,z)\to {(x,y,z)}^k$, as required. The argument is similar when k is odd. Hence, $\overrightarrow{\mathcal{D}\mathcal{G}}(G)=\overrightarrow{\mathcal{P}\mathcal{G}}(G)$, which also implies that $\mathcal{D}\mathcal{G}(G)=\mathcal{P}\mathcal{G}(G)$.

Now we show that (iii) implies (i). Let G be a group such that $\mathcal{D}\mathcal{G}(G)=\mathcal{P}\mathcal{G}(G)$. Then, if x and y are elements of G such that $x\sim y$, either x or y is a power of the other. As observed earlier, all inner automorphisms of G are descending endomorphisms. Therefore, in $\mathcal{D}\mathcal{G}(G)$, every element is adjacent to all its conjugates in G. But this implies that for each element of G, all its conjugates are powers of itself, from which it follows that every subgroup of G is normal. Thus, G is a Dedekind group. □

In [8], Mirzargar et al. prove that the undirected power graph of a finite group G is bipartite if and only if G is an elementary Abelian 2-group. We show that the analogous result holds for the undirected descending endomorphism graph of a group.

Lemma 3.5.

For any non-trivial group G, $\mathcal{D}\mathcal{G}(G)$ is bipartite if and only if G is an elementary Abelian 2-group.

Proof.

Every vertex x of $\mathcal{D}\mathcal{G}(G)$ is adjacent to 1, the identity element of G. Therefore, if any two distinct elements x and y are adjacent, $\mathcal{D}\mathcal{G}(G)$ contains a triangle and hence, would not be bipartite. As inner automorphisms are descending endomorphisms, the conjugacy class of each element induces a complete subgraph of $\mathcal{D}\mathcal{G}(G)$. If $\mathcal{D}\mathcal{G}(G)$ is bipartite, and hence triangle-free, then this implies that no two distinct elements of G can be conjugate to each other, and therefore, G must be Abelian. In that case, every element is adjacent in $\mathcal{D}\mathcal{G}(G)$ to all its powers, and again, as $\mathcal{D}\mathcal{G}(G)$ is triangle-free, this implies that every element has order at most 2. Hence, G is an elementary Abelian 2-group. The converse is obvious. □

Remark 3.6.

Lemma 3.5 also implies that $\mathcal{D}\mathcal{G}(G)$ is a non-trivial tree only if G is an elementary Abelian 2-group, and in that case, it is easily seen to be a star graph.

We will now prove a more general result that characterizes a group G whose descending endomorphism graph is K₄-free.

Remark 3.7.

Let G be a non-Abelian group in which every conjugacy class is of length at most 2. Then observe that the following hold:

1. G is a nilpotent group of class 2, i.e., the commutator subgroup $G\prime$ is contained in the center Z(G).

2. For all $x,y\in G,[x,yz]=[x,y][x,z]$, where $[x,y]=xy{x}^{-1}{y}^{-1}$.

Lemma 3.8.

Let G be a nilpotent group of class 2. Then, for each $y\in G$, the map ${\partial }_y:G\to G$ defined by ${\partial }_y(x)=[y,x]$ is a descending endomorphism of G.

Proof.

For each $y\in G,{\partial }_y$ is an endomorphism since, for all $x,y\in G,[g,xy]=[g,x][g,y]$. If $N⊴G$, then ${\partial }_y(N)=[g,N]\le N$, which implies that ${\partial }_y\in \text{Des}G$. □

Theorem 3.9.

For any non-trivial group G, $\mathcal{D}\mathcal{G}(G)\setminus \left\{1\right\}$ is bipartite, or equivalently, $\mathcal{D}\mathcal{G}(G)$ is K₄-free, if and only if one of the following holds:

1. G is an elementary Abelian 2-group and $\mathcal{D}\mathcal{G}(G)$ is a star graph.

2. G is an elementary Abelian 3-group and $\mathcal{D}\mathcal{G}(G)$ is a friendship graph.

Proof.

Suppose that $\mathcal{D}\mathcal{G}(G)\setminus \left\{1\right\}$ is bipartite, which implies that it is triangle-free and that $\mathcal{D}\mathcal{G}(G)$ is K₄-free. As observed in the proof of Theorem 3.5, every conjugacy class induces a complete subgraph of $\mathcal{D}\mathcal{G}(G)$. Therefore, every element of G has a conjugacy class of length at most 2. As noted in Remark 3.7, this implies that G is either Abelian or is a nilpotent group of class 2. If G is Abelian, then $\mathcal{D}\mathcal{G}(G)$ is the undirected power graph of G. Observe that then, any element x of order greater than 3 would form a triangle in $\mathcal{D}\mathcal{G}(G)\setminus \left\{1\right\}$ together with $x^{-1}$ and x². Thus, G must be an Abelian group in which every element has order 2 or 3, which is possible only if G is an elementary Abelian p-group with p = 2 or 3. If p = 2, then $\mathcal{D}\mathcal{G}(G)$ is a star graph, as noted in Remark 3.6, and if $p=3$, then every nonidentity element of G is adjacent in $\mathcal{D}\mathcal{G}(G)$ only to itself, its inverse, and the identity element, and hence $\mathcal{D}\mathcal{G}(G)$ is a friendship graph. The converse is obvious, in these two cases. Now it remains to prove that G cannot be non-Abelian.

If G is non-Abelian, then it contains non-central elements x and y such that $x^y\ne x$, or equivalently, $[x,y]\ne 1$. Note that $x^y\to x$ in $\overrightarrow{\mathcal{D}\mathcal{G}}(G)$, since inner automorphisms are descending endomorphisms. Also, $x\to [y,x]={\partial }_y(x)$. Thus, x^y, x, and $[y,x]$ are all adjacent to one another and to 1 in $\mathcal{D}\mathcal{G}(G)$, which implies that these four elements cannot be all distinct, as otherwise $\mathcal{D}\mathcal{G}(G)$ would contain a K₄. But if x is non-central, so is x^y, whereas $[y,x]$ is central, since $G\prime \le Z(G)$, and so is 1. Thus, either $x^y=x$, or $[y,x]=1$, both of which contradict our initial assumption. □

Remark 3.10.

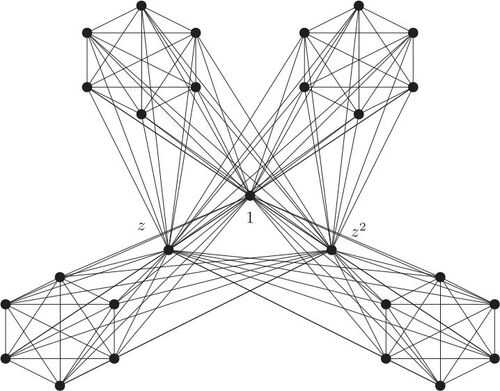
Cameron and Ghosh, in [2], observed that all finite groups of order n and exponent 3 have isomorphic power graphs – namely the friendship graph of order n. For $n=27$, both the elementary Abelian 3-group of order 27 and the Heisenberg group defined by the presentation $〈 x,y,z|x^3=y^3=z^3=[x,z]=[y,z]=1,[x,y]=z 〉$ have exponent 3, and therefore have isomorphic power graphs. We note that by Theorem 3.9, the descending endomorphism graph of the Heisenberg group, which is non-Abelian and non-Hamiltonian, cannot be isomorphic to the descending endomorphism graph of the elementary Abelian 3-group, which is the same as its power graph. The undirected descending endomorphism graph of the Heisenberg group is shown in Figure 2. The central elements, 1, z, and z², are labeled.

Fig. 2 Undirected descending endomorphism graph of the Heisenberg group.

The undirected power graph of a finite group G is complete if and only if G is a cyclic group of prime power order [3, 7]. We now prove that the same result holds for $\mathcal{D}\mathcal{G}(G)$, after stating some preliminary results omitting the evident proofs.

Lemma 3.11.

If $N⊴G$ is such that every normal subgroup of N is normal in G, then the subgraph of $\overrightarrow{\mathcal{D}\mathcal{G}}(G)$ ( $\mathcal{D}\mathcal{G}(G)$) induced by N is a subgraph of $\overrightarrow{\mathcal{D}\mathcal{G}}(N)$ ( $\mathcal{D}\mathcal{G}(N)$).

Corollary 3.12.

The subgraph of the (directed) descending endomorphism graph of a group G induced by the center Z(G) is a subgraph of the (directed) power graph of Z(G).

Lemma 3.13.

For any $x,y\in G$, if $x\to y$ in $\overrightarrow{\mathcal{D}\mathcal{G}}(G)$, then $\left|y\right|$ divides $\left|x\right|$, and any normal subgroup containing y also contains x.

Theorem 3.14.

The undirected descending endomorphism graph of a finite group G is complete if and only if G is trivial or a cyclic p-group for some prime p.

Proof.

The result is obvious if G is the trivial group. If G is a cyclic p-group of order pⁿ, then observe that for each integer k and l, $1\le k\le l\le n$, there is a directed arc $x\to y$ whenever x is an element of order p^l and y is an element of order p^k. Hence, $\mathcal{D}\mathcal{G}(G)$ is a complete graph (with self-loops on every vertex).

We prove the converse by induction on the order of G. Suppose that G is a finite group of order n > 1 and that $\mathcal{D}\mathcal{G}(G)$ is a complete graph. Assume, for the sake of induction, that the result is true for all groups of order less than n, and observe that it holds for the trivial group. Since $\mathcal{D}\mathcal{G}(G)$ is complete, for all $x,y\in G$, either $x\to y$ or $y\to x$, and hence, either $\left|x\right|$ divides $\left|y\right|$, or vice-versa, by Lemma 3.13. Thus, $\left|G\right|$ is divisible by a unique prime p, for otherwise, by Cauchy’s theorem, G would have two elements whose orders are distinct primes. In other words, G is a p-group. Therefore, Z(G) is non-trivial. Let $\phi$ be the canonical epimorphism from G to $G/Z(G)$. By Theorem 2.6, $\phi$ is a surjective homomorphism from $\mathcal{D}\mathcal{G}(G)$ to $\mathcal{D}\mathcal{G}(G/Z(G))$, which implies that $\mathcal{D}\mathcal{G}(G/Z(G))$ is a complete graph. Therefore, by the induction hypothesis, $G/Z(G)$ is a cyclic p-group, which implies that G is Abelian. Then Lemma 3.13 implies that, since $\mathcal{D}\mathcal{G}(G)$ is complete and every subgroup of G is normal, the subgroups of G form a chain under inclusion. Hence, G is cyclic. □

We note that the statement of Theorem 3.14 also holds for any other graph constructed from a group, provided that the construction satisfies Lemma 3.13 and Theorem 2.6. This applies in particular to the power graph of a group.

Now, we apply the results obtained in [6] to describe the structures of the descending endomorphism graphs of the symmetric, dihedral, and dicyclic groups.

4 Symmetric groups

In this section, we describe the descending endomorphism graph of the symmetric group S_n, for $n\ge 3,n\ne 4,6$. Recall that for $n\ne 1,2,4$, S_n has a unique proper, non-trivial subgroup, namely the alternating group A_n, which consists of all even permutations. The index of A_n in S_n is 2. Thus, any non-trivial endomorphism of S_n must have kernel 1 or A_n – i.e., it must be an automorphism, or an endomorphism whose image is a subgroup of order 2 in S_n. For $n\ne 6,\text{Aut}{S}_n=\text{Inn}{S}_n$. Every endomorphism ε with kernel A_n is defined uniquely by the choice of an element $y\in S_n$ having order 2: $$\epsilon (x)=\{\begin{array}{cc}y,\hfill & x\notin A_n\hfill \\ 1,\hfill & x\in A_n\hfill \end{array}$$where 1 denotes the identity element of S_n. It is shown in [6] that every endomorphism of S_n is descending. Combining these observations, we obtain a complete description of $\overrightarrow{\mathcal{D}\mathcal{G}}(S_n)$.

Theorem 4.1.

For $n\ge 3,n\ne 4,6$, the directed descending endomorphism graph $\overrightarrow{\mathcal{D}\mathcal{G}}(S_n)$ has the following structure:

1. Any two permutations in S_n that have the same cycle structure are adjacent to each other.

2. For all $x\notin A_n$, and for all $y\in S_n$ with $\left|y\right|=2,x\to y$.

3. For all $x\in S_n,x\to 1$.

Proof.

Any two permutations with the same cycle structure are mutually conjugate in S_n, which implies that they are adjacent to each other in $\overrightarrow{\mathcal{D}\mathcal{G}}(S_n)$. Let $y\in S_n$ be any element of order 2, and let $\phi$ be the canonical projection from S_n onto the quotient $S_n/A_n$, which is of order 2. Define an embedding $f:S_n/A_n\to S_n$ with image $\{1,y\}$. Then $f°\phi$ is an endomorphism of S_n that maps all elements of A_n to 1 and all elements outside A_n to y. Thus, for each $x\notin A_n,x\to y$ in $\overrightarrow{\mathcal{D}\mathcal{G}}(S_n)$. Finally, all vertices are adjacent to 1 in any directed descending endomorphism graph. □

5 Dihedral groups

In this section, we describe the structure of the descending endomorphism graphs of dihedral groups. Let D_n, $n\ge 3$, denote the dihedral group of order 2n, defined by the presentation $$D_n=〈r,s|r^n=s^2=1,sr=r^{-1}s〉.$$

The cyclic subgroup $〈r〉$ is of index 2 and its elements are called rotations. The elements of the form $r^{k}s$ are called reflections, and have order 2. Now we shall determine the directed descending endomorphism graph of D_n using the description of $\text{Des}{D}_n$ given in [6].

Definition 5.1.

[6, Definition 3] For every pair $i,j\in \{0,\dots ,n-1\}$, we define maps ${\delta }^{(1;ij)}$ and ${\delta }^{(2;ij)}$ on D_n by their action on the generators r and s, as follows:

1. ${\delta }^{(1;ij)}:r\mapsto r^i,s\mapsto r^{2j}s$.

2. ${\delta }^{(2;ij)}:r\mapsto r^i,s\mapsto r^{2j}$.

When ${\delta }^{(1;ij)}$ and ${\delta }^{(2;ij)}$ are well-defined endomorphisms of D_n, we shall call them endomorphisms of the first kind and second kind, respectively.

Theorem 5.2.

[6, Theorem 6] The descending endomorphisms of D_n are completely described by the following:

1. If $n\equiv 1\hspace{1em}\mathrm{mod}2$, then $$\begin{array}{c}\text{Des}{D}_n=\left\{ {\delta }^{(1;ij)} | 0\le i\le n-1, 0\le j\le n-1 \right\}\\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\cup \left\{{\delta }^{(2;00)}=0_{D_n}\right\}.\end{array}$$

2. If $n\equiv 2\hspace{1em}\mathrm{mod}4$, then $$\begin{array}{c}\text{Des}{D}_n=\left\{ {\delta }^{(1;ij)} | i\in \{1,3,\dots ,n-1\}, 0\le j\le \frac{n}{2}-1 \right\}\\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\cup \left\{ {\delta }^{(2;00)}=0_{D_n} \right\}.\end{array}$$

3. If $n\equiv 0\hspace{1em}\mathrm{mod}4$, then $$\begin{array}{c}\text{Des}{D}_n=\left\{ {\delta }^{(1;ij)} | i\in \{1,3,\dots ,n-1\}, 0\le j\le \frac{n}{2}-1 \right\}\\ \cup \left\{ {\delta }^{(2;ij)} | i\in \left\{0,\frac{n}{2}\right\}, j\in \left\{0,\frac{n}{4}\right\} \right\}.\end{array}$$

Theorem 5.3.

The directed descending endomorphism graph $\overrightarrow{\mathcal{D}\mathcal{G}}(D_n)$ has the following structure:

1. If n is odd, then each rotation is adjacent to all its powers, and all reflections are adjacent to one another.

2. If n is even, then each rotation is adjacent to all odd powers of itself and each reflection of the form $r^{k}s$ is adjacent to all reflections of the form $r^{l}s$ where $k\equiv l\hspace{1em}\mathrm{mod}2$. Additionally, if n is a multiple of 4, then all reflections, and all rotations of the form r^k, where k is odd, are adjacent to the rotation $r^{\frac{n}{2}}$.

In both cases, all elements are adjacent to the identity element.

Proof.

First, suppose that n is odd. Then by (i) of Theorem 5.2, the descending endomorphism ${\delta }^{(1;ij)}$ maps each rotation r^k to r^ik for all possible values of i, and maps each reflection $r^{k}s$ to $r^{ik+2j}s$ for all possible values of i and j. As n is odd, $ik+2j$ assumes all values between 0 and $n-1$ as i and j vary between 0 and $n-1$. Hence, in $\overrightarrow{\mathcal{D}\mathcal{G}}(D_n)$, each rotation r^k is adjacent to all its powers, and each reflection $r^{k}s$ is adjacent to all reflections. The only other descending endomorphism of D_n in this case is the trivial one that maps all elements to the identity.

Next, suppose that n is even. Then by (ii) and (iii) of Theorem 5.2, ${\delta }^{(1;ij)}$ maps each rotation r^k to r^ik, for all odd values of i, and maps each reflection $r^{k}s$ to $r^{ik+2j}s$ for all odd values of i and all possible values of j. Since n is even and i is odd, $ik+2j\equiv k\hspace{1em}\mathrm{mod}2$. Therefore, r^k is adjacent to all odd powers of itself, and $r^{k}s$ is adjacent to all elements of the form $r^{l}s$ where $l\equiv k\hspace{1em}\mathrm{mod}2$. If n is not divisible by 4, then the only other descending endomorphism of D_n is the trivial one. But when n is a multiple of 4, ${\delta }^{(2;ij)}$ maps each of r and s to 1 and $r^{\frac{n}{2}}$, independently. It follows that ${\delta }^{(2;ij)}$ also maps each r^k, for odd k, and each $r^{l}s$, for any l, to $r^{\frac{n}{2}}$. □

Example 5.4.

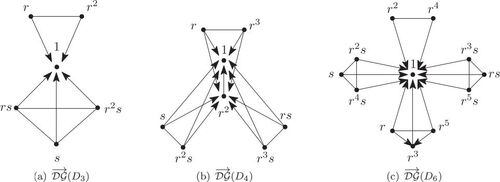
Figure 3 illustrates Theorem 5.3 for three values of n by showing the directed descending endomorphism graphs of D₃, D₄, and D₆. For the sake of simplicity, a pair of directed edges in opposite directions is represented by a single undirected edge.

Fig. 3 The directed descending endomorphism graphs of D₃, D₄, and D₆.

6 Dicyclic groups

In this section, we describe the structure of descending endomorphism graphs of dicyclic groups, and show that for $n=2^k$, $k\ge 1$, dicyclic and dihedral groups of order 2n have isomorphic descending endomorphism graphs.

Let ${\text{Dic}}_n$ denote the dicyclic group of order 4n ([9]), defined by the presentation $${\text{Dic}}_n=〈 x,y|x^{2n}=1,x^n=y^2,yx{y}^{-1}=x^{-1} 〉.$$

Note that each element of ${\text{Dic}}_n$ has a unique representation of the form $x^u{y}^v$, where $0\le u\le 2n-1$, and v = 0 or 1. For $i,j\in \{0,\dots ,2n-1\}$, define maps ${\eta }^{(1;ij)}$ and ${\eta }^{(2;ij)}$ on ${\text{Dic}}_n$ by the prescription $$\begin{array}{c}{\eta }^{(1;ij)}:\hspace{1em}x\mapsto x^i,\hspace{1em}y\mapsto x^{j}y\\ {\eta }^{(2;ij)}:\hspace{1em}x\mapsto x^i,\hspace{1em}y\mapsto x^j.\end{array}$$

Theorem 6.1.

[6, Theorem 9] The descending endomorphisms of ${\text{Dic}}_n$ are characterized as given below:

1. If n is odd, then $$\begin{array}{c}{\text{DesDic}}_n=\{ {\eta }^{(1;ij)}|i\in \{1,3,\dots ,2n-1\},\\ \hspace{1em}0\le j\le 2n-1 \}\cup \{{\eta }^{(2;00)},{\eta }^{(2;0n)}\}.\end{array}$$

2. If n is even, then $$\begin{array}{c}{\text{DesDic}}_n=\{ {\eta }^{(1;ij)}|i\in \{1,3,\dots ,2n-1\},\\ j\in \{0,2,\dots ,2n-2\} \}\cup \\ \hspace{1em}\{ {\eta }^{(2;ij)}|i,j\in \{0,n\} \}.\end{array}$$

The following is easily obtained from Theorem 6.1, and therefore we state only the result and omit the proof, which is obtained along similar lines to that of Theorem 5.3.

Theorem 6.2.

The directed descending endomorphism graph $\Gamma =\overrightarrow{\mathcal{D}\mathcal{G}}({\text{Dic}}_n)$ has edge set as described below:

1. If n is odd, then $$\begin{array}{c}E(\Gamma )=\left\{ (x^u,x^{iu})|0\le u,i\le 2n-1, i\equiv 1\hspace{1em}\mathrm{mod}2 \right\}\cup \\ \left\{ (x^{u}y,x^{t}y)|0\le u,t\le 2n-1 \right\}\cup \\ \left\{ (x^u{y}^v,1)|0\le u\le 2n-1, v\in \{0,1\} \right\}.\end{array}$$

2. If n is even, then $$\begin{array}{c}E(\Gamma )=\left\{ (x^u,x^{iu})|0\le u,i\le 2n-1, i\equiv 1\mathrm{}\hspace{1em}\mathrm{mod}2 \right\}\cup \\ \left\{(x^{u}y,x^{t}y)|0\le u,t\le 2n-1, u\equiv t\mathrm{}\hspace{1em}\mathrm{mod}2 \right\}\cup \\ \left\{(x^u,x^n)|0\le u\le 2n-1, u\equiv 1\mathrm{}\hspace{1em}\mathrm{mod}2 \right\}\cup \\ \left\{(x^{u}y,x^n)|0\le u\le 2n-1 \right\}\cup \\ \left\{(x^u{y}^v,1)|0\le u\le 2n-1, v\in \{0,1\} \right\}\end{array}$$

Example 6.3.

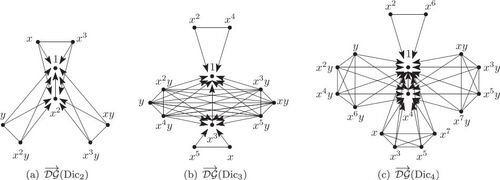
Examples of directed descending endomorphisms graphs of dicyclic groups are shown in Figure 4.

Fig. 4 The directed power descending endomorphism graphs of ${\text{Dic}}_2,{\text{Dic}}_3$, and ${\text{Dic}}_4$

Remark 6.4.

Observe from Examples 5.4 and 6.3 that $\overrightarrow{\mathcal{D}\mathcal{G}}({\text{Dic}}_2) \cong \overrightarrow{\mathcal{D}\mathcal{G}}(D_4)$. However, the dicyclic group ${\text{Dic}}_2$ (which is isomorphic to the quaternion group Q₈) is not isomorphic to the dihedral group D₄. This shows that two finite groups with isomorphic directed or undirected descending endomorphism graphs are not necessarily isomorphic. Theorem 6.5 shows that dihedral and dicyclic 2-groups of the same order have isomorphic descending endomorphism graphs.

Theorem 6.5.

Let $n=2^k,k\ge 1$. Then $\overrightarrow{\mathcal{D}\mathcal{G}}(D_{2n})\cong \overrightarrow{\mathcal{D}\mathcal{G}}({\text{Dic}}_n)$.

Proof.

Define $f:D_{2n}\to {\text{Dic}}_n$ as $f(r^u{s}^v)=x^u{y}^v$, for all u, v, $0\le u\le 2n-1,0\le v\le 1$. Clearly, f is a well-defined bijection. We shall show that it is a directed graph isomorphism from $\overrightarrow{\mathcal{D}\mathcal{G}}(D_{2n})$ to $\overrightarrow{\mathcal{D}\mathcal{G}}({\text{Dic}}_n)$, by considering all possible directed edges in the two graphs.

As n is even, by (ii) of Theorem 5.3, $r^u\to r^{iu}$ in $\overrightarrow{\mathcal{D}\mathcal{G}}(D_{2n})$, for all u and all odd i. By (ii) of Theorem 6.2, $x^u\to x^{iu}$ in $\overrightarrow{\mathcal{D}\mathcal{G}}(Di{c}_n)$, for all u and all odd i. Thus, for each u, $r^u\to g$ in $\overrightarrow{\mathcal{D}\mathcal{G}}(D_{2n})$ if and only if $f(r^u)\to f(g)$ in $\overrightarrow{\mathcal{D}\mathcal{G}}({\text{Dic}}_n)$.

Similarly, $r^{u}s\to r^{t}s$ in $\overrightarrow{\mathcal{D}\mathcal{G}}(D_{2n})$ if and only if $u\equiv t\hspace{1em}\mathrm{mod}2$, and $x^{u}y\to x^{t}y$ if and only if $u\equiv t\hspace{1em}\mathrm{mod}2$. Also, since 2n is a multiple of 4, $r^u\to r^n$ for all odd u, and $r^{u}s\to r^n$ for all u. Correspondingly, $x^u\to x^n$ for all odd u and $x^{u}y\to x^n$ for all u. Finally, all vertices are adjacent to the identity element in both graphs.

These observations show that $g\to h$ in $\overrightarrow{\mathcal{D}\mathcal{G}}(D_{2n})$, for any two vertices g and h, if and only if $f(g)\to f(h)$ in $\overrightarrow{\mathcal{D}\mathcal{G}}({\text{Dic}}_n)$. Hence, f is a graph isomorphism, and $\overrightarrow{\mathcal{D}\mathcal{G}}(D_{2n})\cong \overrightarrow{\mathcal{D}\mathcal{G}}({\text{Dic}}_n)$. □

7 Conclusion

In this article, we have endeavored to develop the basic theory of descending endomorphism graphs, and to demonstrate how this construction helps in the study of groups. We have shown that descending endomorphism graphs are comparable to power graphs of groups in certain respects, and characterized all the groups for which these two constructions produce identical graphs. We have also established that, while the descending endomorphism graph succeeds in distinguishing between certain non-isomorphic groups where power graphs fail to do so (see Remark 3.10), the converse is also true for certain other groups (see Theorem 6.5). The study carried out so far has raised some questions and led to some conjectures, which we list below.

Questions

1. Does there exist a (finite) non-Dedekind group whose undirected (directed) descending endomorphism graph is isomorphic to its undirected (directed) power graph? Note that according to Theorem 3.4, the power graph and descending endomorphism graph are equal only for a Dedekind group, but this does not rule out the possibility of these two graphs being isomorphic.

2. Does there exist a non-isomorphic pair of finite groups whose power graphs are isomorphic to each other, such that their descending endomorphism graphs are also isomorphic to each other?

3. Does the undirected descending endomorphism graph of a finite group determine its directed descending endomorphism graph up to isomorphism?

   Cameron showed, in [1], that two finite groups with isomorphic undirected power graphs have isomorphic directed power graphs. The proof relies heavily on arguments about orders of elements, and in the case of the power graph, there is a close relation between the element orders and the degrees of the vertices. On the other hand, the relation between orders of elements of a group and the degrees of vertices in its descending endomorphism graph is much weaker – the only observation we have been able to make so far is that when two vertices are adjacent in the undirected descending endomorphism graph, the order of one of the elements divides that of the other. This indicates that the analogous result may not hold for descending endomorphism graphs, and that if it does, then a different technique is needed to prove it.

Conjecture 7.1.

If G is a finite group of order n, then $\overrightarrow{\mathcal{D}\mathcal{G}}(G)$ has a vertex of in-degree $n-1$ if and only if one of the following holds:

1. $G\cong {\mathbb{Z}}_p$, for some prime p.

2. G is a non-Abelian 2-group of nilpotency class 2.

Conjecture 7.2.

If G is a finite group such that in $\overrightarrow{\mathcal{D}\mathcal{G}}(G)$, for every pair of non-identity elements $x,y\in G,x\to y$ implies that $y\to x$, then G is a simple group.