Brief survey on divisor graphs and divisor function graphs

Abstract

Number theoretic graphs are one of the emerging fields in Graph theory. This article is a study on existing research results on Number theoretic graphs, especially on Divisor Graphs $(DG)s$, Divisor Function Graphs (DFGs) and Divisor Cayley Graphs (DCGs). We have provided a brief survey on the benchmark findings regarding the above-mentioned graphs.

KEYWORDS:

• Divisor graphs
• divisor function graphs
• divisor Cayley graphs
• matching and covering numbers

1 Introduction

We consider G as a simple connected graph with more than one edge. There are different kinds of graphs available in graph theory. But, number theoretic graphs are one of the emerging fields in Graph theory which involves representing number theoretic functions as graphs. There are many number theoretic graphs like Arithmetic Graphs [2], Divisor graph [31], Relatively Prime Graphs [12], Divisor Function Graphs [19], Möbius Function Graphs [9], Graphs on Numbers [34] and so on. This article is mainly concerned with the survey of divisor graphs, DFGs, and the Divisor Based Cayley and Unitary Cayley graphs. Throughout this survey, we denote divisor graphs, divisor function graphs, Cayley related graphs as DG, DFG, and CG, respectively.

2 Benchmark results on divisor graphs

Melvyn B. Nathanson [26] introduced the concept of the arithmetic graphs.

Definition 2.1.

Let $R\subseteq \{1,2,\dots ,m\}$. Let $G_m(R)$ be the graph with m vertex set $\{1,2,\dots ,m\}$ and edges $ab\in E(G_m(R))$ iff a + b $\equiv$ $r(\mathit{mod}$ $m)$, for some $r\in R$.

These graphs may have loops. For each vertex x and for each $r\in R$ there exists a unique vertex y(r) such that $x+y(r)$ $\equiv$ $r(\mathit{mod}$ $m)$, since $b(r_1)\ne b(r_2)$ if $r_1,r_2\in R$ and $r_1\ne r_2$. The graph $G_m(R)$ is a $\left|R\right|$ - regular graph. The following theorem is used to find the number of connected components in $G_m(R)$. Let $C_m(R)$ denote the number of connected components in $G_m(R)$.

Theorem 2.2.

[26] Let $R\subseteq \{1,2,\dots ,m\}$. Let d be the gcd of m and the numbers $r_i-r_j$ $\forall$ $r_i,r_j\in R$. Let $C_m(R)$ be the number of components of $G_m(R)$. Then $$C_m(R)=\{\begin{array}{cc}\frac{(d+1)}{2}\hfill & ifdis\mathit{odd}\hfill \\ \frac{d}{2}\hfill & ifdis\mathit{even},ris\mathit{odd}\forall r\in R\hfill \\ \frac{d}{2}+1\hfill & ifdis\mathit{even},ris\mathit{even}\forall r\in R\hfill \end{array}$$

Further, Nathanson stated that the graph $G_m(R)$ is connected iff either d = 1 or d = 2 and r is odd, $\forall$ $r\in R$.

Theorem 2.3.

[26] Let $R=\{r_1,r_2\}\subseteq \{1,2,\dots ,m\}$ there exists a permutation of $\{1,2,\dots ,m\}$ such that for each $i=1,2,\dots ,m-1$ there exists an $r\in R$ with $\sigma (i)+\sigma (i+1)$ $\equiv$ $r(\mathit{mod}$ $m)$ iff either $(m,r_2-r_1)=1$ or $(m,r_2-r_1)=2$ and r₁ and r₂ are odd.

[29] dedicated a work to the legendary research person Paul Erdös on his ${70}^{th}$ birthday titled “On the longest simple path in the divisor graph”. For a set $S\subseteq \mathbb{N}$, then the divisor graph on S has vertex set S and the edges are framed as (x, y) either $x|y$ or $y|x$. He denoted the length of the longest simple path in the graph as f(n). He proved that f(n) = O(n), which makes the use of an asymptotic notations. A. D. Pollington [28] proved that for all large n, $$f(n)\ge n{e}^{-(2+e)\sqrt{\mathit{lognlog}(\mathit{logn})}}$$

He considered the graph with vertices as $\{1,2,\dots ,n\}$ and an edge (x, y) is framed iff the lcm of x and y should be less than n. If g(n) is the length of the longest simple path in this graph, then it is clear that $g(n)\ge f(n)$ and he proved that g(n) = O(n). Pomerance further used some supremum and infimum results from the works of [15].

Let $\psi (x,y,z)$ be the function, the number of natural numbers up to x, composed solely of primes in the interval $(z,y]$. With the help of this function and the bounds found by [13, 17], they proposed the following propositions.

Proposition 2.4.

[29] Suppose $0<\alpha <\delta <1$ are fixed. Then $\exists$ an ${ϵ}^{\prime }>0$ such that for each ϵ, $0<ϵ\le ϵ\prime$, there is an n₀ = $n_0(\delta ,\alpha ,ϵ)$ with the property that for each $n\ge n_0$, if $1=a_1<a_2\dots$ are the integers all of whose primes come from $(n^{ϵ},n^{\delta }]$, then $$\sum _{i>2yn}\left[\frac{y}{a_i}\right]>\frac{1}{2}\psi (y,n^{\delta })$$

for any y, $y\in [n^{\alpha },n]$.

Proposition 2.5.

[29] Given $1\ge \delta ,\alpha >0$, then $\exists$ an ${ϵ}^{\prime }>0$ with the property that if $0<ϵ\le ϵ\prime$, there is an n₀ such that if $n\ge n_0$ and $1=b_1<b_2\dots$ are the integers all of whose primes exceed $n^{ϵ}$, then $$\sum _{i>2n^{1-\delta }}\psi (\frac{n}{b_i},n^{ϵ})<\alpha n$$

Proposition 2.6.

[29] Given $1\ge \delta ,\alpha >0$, then $\exists$ an ${ϵ}^{\prime }>0$ with $\delta >ϵ\prime >0$ such that for each ϵ, $ϵ\in (0,ϵ\prime ]$ there is an n₀ with the property that for every $n\ge n_0$, we have $$\sum _{n^{1-ϵ}<D\le n}\frac{1}{D}<\alpha$$

With these three propositions, Pomerance proved the following main result.

Theorem 2.7.

[29] If $m_1,m_2,\dots ,m_{g(n)}$ is the longest sequence of distinct integers from $\{1,2,\dots ,n\}$ such that for each $\upsilon =1,2,\dots ,g(n)-1$ we have $[m_{\upsilon },m_{\upsilon +1}]\le n$ then g(n) = O(n).

Finally, he stated that for each $ϵ>0,\exists$a $\delta >0$ and an n₀ such that if $n\ge n_0$ and $m_1,m_2,m_{h(n)}$ is the longest sequence of distinct numbers from $\{1,2,\dots ,n\}$ such that each $[m_{\upsilon },m_{\upsilon +1}]\le n^{1+\delta }$, then h(n) < n ϵn.

[12] considered S a non-empty finite set of non-negative integers. By relatively prime graph of S, denoted by RP(S), we refer to the graph that has S as its vertex set and two vertices i and j are adjacent iff i and j are co-prime.

[31] defined the concept of graphs based on divisors and named it as divisor graphs. Let S be a nonempty subset of $\mathbb{Z}$, a graph G(V, E) is a divisor graph if V(G) = S and $E(G)=\{ij:$ either $i|j$ or $j|i$; for $i,j\in V$ with $i\ne j\}$.

Theorem 2.8.

[12] Every graph is a relatively prime graph.

Further, Chartrand et al. characterized DGs through the following propositions.

Proposition 2.9.

[12] No DG contains an induced odd cycle of length 5 or more.

Proposition 2.10.

[12] Every induced subgraph of a DG is a DG.

Proposition 2.11.

[12] Let G be a DG then the orientation of the graph induced by any divisor labeling of G is transitive.

Proposition 2.12.

[12] Let G be a DG and f be a divisor labeling of G. Then the oriented graph of G induced by f is acyclic.

Proposition 2.13.

[12] Every complete graph is a DG.

Proposition 2.14.

[12] Every tree is a DG.

Chartrand et al. further gave a conditions for a DG to be a bipartite graph.

Corollary 2.15.

[12] The necessary and sufficient condition for a triangle-free graph G to be a DG is that G is bipartite.

Corollary 2.16.

[12] Every bipartite graph is a DG.

Proposition 2.17.

[12] If G and H are DGs, then G + H is a DG.

Corollary 2.18.

[12] Every complete multi-partite graph is a DG.

In directed graphs, a vertex with indegree 0 is called as transmitter and a vertex with outdegree 0 is called as a receiver.

Theorem 2.19.

[12] The necessary and sufficient condition for a graph G to be a DG is when $\exists$ a direction D such that every vertex of D is either a transmitter or a receiver or a transitive vertex.

Proposition 2.20.

[12] The graph $K_3\times K_2$ is not a DG.

Further, Chartrand generalized the above proposition as

Theorem 2.21.

[12] Let G be a graph. Then $G\times K_2$ is a DG iff G is a bipartite graph.

Christopher Frayer [16]) worked on the properties of DGs.

A vertex-transitive graph is a graph G in which, given any two vertices v₁ and v₂ of G, there is some automorphism $f:G\to G$ such that $f(v_1)=v_2.f(v_1)=v_2.$

Theorem 2.22.

[16] An orientation of a divisor graph, DG, G, contains no transitive vertices iff G is a bipartite graph.

Theorem 2.23.

[16] For a oriented DG, G with a transitive vertex, G × H is a DG iff $E(H)=\varphi$.

Theorem 2.24.

[16] Every bipartite graph is a DG.

Theorem 2.25.

[16] The collection of graphs with order $\le 6$ are DGs except the graph C₅ their complements are DGs.

Theorem 2.26.

[16] $P_m\times P_n$ is a DG.

Theorem 2.27.

[16] Suppose G is a DG. A graph H constructed from G by framing the adjacency between arbitrarily 2 vertices where its distance is a non-odd number $>2$, then H will not be a DG.

Further, Frayer gave results based on the neighborhood and complements of the DGs.

Theorem 2.28.

[16] $K_n\times K_2$ is not a DG, but its complement is a DG, for n > 2.

Le Anh Vinh [35] worked on the order and size of DGs.

Theorem 2.29.

[35] For any $n\ge 1$ and $0\le m\le \frac{n(n-1)}{2}$ $\exists$ a DG of order n and size m.

Theorem 2.30.

[35] G is a DG iff $\exists$ an orientation D such that if $ab,bc\in E(D)$ then $ac\in E(D)$.

The two graphs associated with an arbitrary non-empty subset X of positive integers are defined as follows:

Definition 2.31.

[18] The prime vertex graph $\Delta (X)$ has, as vertex set $\rho (X)$, the set of primes dividing some element of X, and two such primes $p,q$ are joined by an edge iff pq divides some $x\in X$.

Definition 2.32.

[18] The common divisor graph $\Gamma (X)$ has vertex set $X^{*}=X\backslash \left\{1\right\}$, and $x,y\in X^{*}$ form an edge iff $\mathit{gcd}(x,y)>1$.

[18] introduced the bipartite DG $B(X)$, for a nonempty set of positive integers X.

Definition 2.33.

[18] The bipartite divisor graph B(X), for an arbitrary non-empty subset X of positive integers, has as vertex set the disjoint union $\rho (X)\cup X^{*}$, and its edges are the pairs {p, x} where $p\in \rho (X),x\in X^{*}$ and p divides x.

Theorem 2.34.

[18] A bigraph G is isomorphic to $B(X)$, for some non-empty set X iff G is non-empty and has no isolated vertices.

Corollary 2.35.

[18] For a non-empty set X such that $X\ne \left\{1\right\}$, there exists a second non-empty set Y and a graph isomorphism $\varphi$: $B(X)$ → $B(Y)$ that induces isomorphisms $\Delta (X)\cong \Gamma (Y)$ and $\Gamma (X)\cong \Delta (Y)$, where $\Delta (X)$ is the prime vertex graph and $\Gamma (X)$ is the common DG.

Theorem 2.36.

[18] At least one of Δ, Γ contains a triangle iff B contains C₆ or $K_{1,3}$ as an induced subgraph.

Theorem 2.37.

[18] Both the graphs Γ and Δ are acyclic iff each connected component of B is a path or a cycle of length 4.

Corollary 2.38.

[18] Both the graphs Γ and Δ are trees iff either B is a path or $B\cong C_4$.

[4] specified some values of n and k > 1 for which the graphs are DGs.

Corollary 2.39.

[4] Let n, k be 2 integers with k > 1 and $n>2k+2$. If $C_n^k$ is a DG and D be its orientation where $xy\in E(C_n)$ and $xy\in E(D)$, then x and y are the transmitter and receiver in D, respectively.

Theorem 2.40.

[4] For any integer k > 1, the graph $C_n^k$ is a DG iff $n\le 2k+2$.

Yu ping Tsao [33] explored the chromatic number, the maximal complete subgraph number and its cover number along with their independence number and its complement. Here, Yu ping Tsao denote the graph and its complement as D(n) and $\overline{D}(N)$ respectively.

Theorem 2.41.

[33] $\chi (D(n))=\lfloor lo{g}_{2}n\rfloor +1=\omega (D(n))$.

Theorem 2.42.

[33] $\chi (\overline{D}(N))=\lceil \frac{n}{2}\rceil =\omega (\overline{D}(N))$.

Theorem 2.43.

[33]

1. $\theta (D(n))=\lceil \frac{n}{2}\rceil =\alpha (D(n))$

2. $\theta (\overline{D}(N))=\lfloor lo{g}_{2}n\rfloor +1=\alpha (\overline{D}(N))$

Theorem 2.44.

[33] D(n) is a perfect graph.

Corollary 2.45.

[33] A DG is a perfect graph.

Lemma 2.46.

[33] If gcd S = min S, then $B(D(S))\ge \lfloor \frac{\left|S\right|}{2}\rfloor$.

Theorem 2.47.

[33] $B(D(n))$ = $\lfloor \frac{n}{2}\rfloor$.

[5] provided the characterization for the cartesian products of graphs to be a DG.

Lemma 2.48.

[5] A graph G is a DG iff each component of G is DG.

Theorem 2.49.

[5] Let G and H be two graphs. Then G × H is a DG iff either both G and H are bipartite or at least one of them has size zero and the other is a DG.

Corollary 2.50.

[5] Let G and H be two graphs. Then G × H is a DG iff either both G and H has no triangle or at least one of them has size zero.

Lemma 2.51.

[5] If D is a divisor orientation of the antihole $\overline{C_m}$, where m > 4, then every vertex v of D is either a transmitter or a receiver.

Lemma 2.52.

[5] Every antihole of order greater than 4 is not a DG.

Theorem 2.53.

[5] Let G be a DG. Then G has no antihole of order greater than 4.

Theorem 2.54.

[5] Every DG is perfect.

Theorem 2.55.

[5] If G is a DG which has an antihole of order $\ge 6$, then $\overline{G}$ is not a DG.

[1] gave the conditions for the powers of trees to be DGs.

Theorem 2.56.

[1] Let T be a tree with an induced subgraph which is $\cong$ to $T_{k,l}$ with $1\le l\le \lfloor \frac{k-1}{2}\rfloor$ and $k>2$, then T^k is not a DG.

Theorem 2.57.

[1] For the 3 - starlike tree T_s, $T_s^{d-2}$ is not a DG.

Further, Eman A. AbuHijleh et al. characterized the T^k graph for k = 3 and 4.

Theorem 2.58.

[1] Let T be a tree, $\mathit{diam}(T)\le 5$. Then T^k is a DG.

Theorem 2.59.

[1] Suppose T is a tree with diam(T) = 6 or 7. Then T^k is a DG iff the center(s) of T has(have) degree 2.

Lemma 2.60.

[1] Let T be a tree with diam(T) = 6 and T does not contain an induced subgraph that is isomorphic to T_s with $\mathit{diam}(T_s)=6$. Then T⁴ is a DG.

Theorem 2.61.

[1] Suppose T is a tree with diam(T) = 8 or 9. Then T⁴ is a DG iff the center(s) of T has(have) degree 2 and T does not contain an induced subgraph that is isomorphic to T_s with $\mathit{diam}(T_s)=6$.

Finally, Eman A. AbuHijleh et al. concluded that if diam(T) = 10, then T⁴ is not a DG.

[27] gave the condition for a zero DG to be a DG. Here R is a commutative ring and $\Gamma (R)$ the zero DG whose vertices are the non-zero divisors of R with x and y of R adjacent if $x\ne y$ and xy = 0 [7].

Theorem 2.62.

[27] Let R be a local ring. Then $\Gamma (R)$ is a DG.

Lemma 2.63.

[27] If S is a sub-ring of R and $\Gamma (R)$ is a DG, then $\Gamma (S)$ is also a DG when it is non-empty.

Theorem 2.64.

[27] If a ring $R=R_1*R_2*R_3$, where R₁, R₂ and R₃ are nontrivial rings, then $\Gamma (R)$ is not a DG.

Theorem 2.65.

[27] Let $R=R_1\times R_2$ such that $\mathit{diam}(\Gamma (R_2))=3$. Then $\Gamma (R)$ is not a DG.

Theorem 2.66.

[27] Let $R=R_1\times R_2$ such that

• $\mathit{diam}(\Gamma (R_1))$ = $\mathit{diam}(\Gamma (R_2))=0$

• $\mathit{diam}(\Gamma (R_1))=0$ and $\mathit{diam}(\Gamma (R_2))=1$

• $\mathit{diam}(\Gamma (R_1))$ = $\mathit{diam}(\Gamma (R_2))=1$

• $\mathit{diam}(\Gamma (R_1))=0$ and $\mathit{diam}(\Gamma (R_2))=2$

• $\mathit{diam}(\Gamma (R_1))=1$ and $\mathit{diam}(\Gamma (R_2))=2$

Then $\Gamma (R)$ is a DG.

Theorem 2.67.

[27] Let $R=R_1\times R_2$ such that $\mathit{diam}(\Gamma (R_1))$ = $\mathit{diam}(\Gamma (R_2))=2$. Then $\Gamma (R)$ is not a DG.

From all these results, [27] concluded that if R is a finite commutative principal ideal ring with unity then $\Gamma (R)$ is a DG iff R is a local ring or it is a product of 2 local rings with at least one of them having diameter < 2.

Let us denote the finite commutative principal ideal ring as FCPIR.

Theorem 2.68.

[27] Let R be a FCPIR with unity, $T=R[x]$ or $R[[x]]$. Then $\Gamma (R)$ is a DG iff $\Gamma (T)$ is a DG.

[3] proved that the complement of a few bipartite graphs are DGs.

Lemma 2.69.

[3] The complement of a path is a DG.

Lemma 2.70.

[3] The complement of a caterpillar is a DG.

Theorem 2.71.

[3] The complement of a tree is a DG only if the tree is a caterpillar.

Lemma 2.72.

[3] The complement of the power graphs of path, caterpillar and the tree when the tree itself is a caterpillar are DGs.

[6] investigated the conditions for the line graphs L(G) and middle graphs M(G) of some class of graphs to be DGs. Finally, Salah Al-Addasi showed that the line graphs and the middle graphs of the cycle permutation graphs are never DGs.

Proposition 2.73.

[6] $L(C_n)$ is a DG iff either n is even or n = 3.

Theorem 2.74.

[6] Let T be a non trivial tree, then L(T) is a DG iff T is a caterpillar.

Proposition 2.75.

[6] For any graph G, if L(G) is not a DG, then M(G) is also not a DG.

Lemma 2.76.

[6] The $3-$sun is not a DG.

Lemma 2.77.

[6] If M(G) of a graph G is a DG, then G is triangle-free and contains no induced $K_{1,3}$.

Theorem 2.78.

[6] $M(C_n)$ is a DG iff n is even.

Theorem 2.79.

[6] For any arbitrary tree T, M(T) is a DG iff T is a path.

Theorem 2.80.

[6] For n > 1, $L(K_n)$ is a DG iff n < 5.

Theorem 2.81.

[6] $M(K_n)$ is a DG iff n < 3.

Salah Al-Addasi et al. proved that the L(G) and M(G) cannot be a DG if G contains $K_{2,3}$ and the conditions for complete $k-$ partite graphs to be a DG. Let $P_{\alpha }(G)$ denote the cyclic permutation of graph G.

Proposition 2.82.

[6] Let G be a graph containing $K_{2,3}$, then L(G) and M(G) are not a DG.

Lemma 2.83.

[6] $L(K_{m,n})$ is a DG iff either $\min \{m,n\}=1$ or $m=n=2$.

Theorem 2.84.

[6] $L(K_{r_1,r_2,\dots ,r_k})$ is a DG iff any one of the upcoming conditions holds:

1. $k\le 4$ and ri = 1, $\forall$ i.

2. k = 2 and either $r_1=r_2=2$ or $\min \{r_1,r_2\}=1$.

3. k = 3 and rt = 2, for some t with ri = 1, $\forall$ $i\ne t$.

Theorem 2.85.

[6] $M(K_{r_1,r_2,\dots ,r_k})$ is a DG iff k = 2 and $\max \{r_1,r_2\}\le 2$.

Theorem 2.86.

[6] For n > 2, $L(P_{\alpha }(C_n))$ and $M(P_{\alpha }(C_n))$ are not DGs.

Here, we list some open problems given by the authors from the above discussed works.

2.1 Open problems

• Characterization of non-DGs not based up on the cycles of odd length in G [16].

• Characterization of DG but the complement is not a DG [16].

• Characterization of non-DG and their complement is also not a DG [16].

• For a known natural number n > 4, what would be the maximum value m for which there is a non-DG of order and size as n and m, respectively. [16].

• Finding the necessary and sufficient conditions for a non-increasing sequence $n-1\ge d_1\ge \dots \ge d_n\ge 1$ such that there exists a DGs with degree sequence $(d_1,\dots ,d_n)$. [35]

3 Benchmark results on divisor function graphs

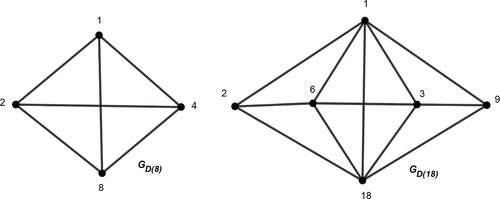
In the previous section, we discussed DGs and their benchmark results. This section deals with the DFGs (Figure 1).

Fig. 1 Divisor Function graphs for n = 8 and 18.

[19] framed the concept of DFG’s and studied its properties.

Definition 3.1.

[19] For all natural integers with k factors f_i, $i=1,2,\dots ,k$ the graph of the divisor function D(n) comprises set of factors as vertices such that two factors (distinct) are adjacent iff either one of them divides the other.

Theorem 3.2.

[19] For any $n\in \mathbb{N}$, the $G_{D(n)}$ is connected.

Theorem 3.3.

[19] For any $n\in \mathbb{N}$, the $G_{D(n)}$ is complete iff no two proper factors of D(n) are co-prime.

Theorem 3.4.

[19] For any composite integer n, the following statements are equivalent.

1. $G_{D(n)}$ is a block.

2. Any 2 vertices of $G_{D(n)}$ lie in a common cycle.

3. Any vertex u and an edge e = uv lie in a common cycle.

4. Any 2 edges of $G_{D(n)}$ lie on a common cycle.

Theorem 3.5.

[19] For any n, $L(G_{D(n)})$ is connected.

Theorem 3.6.

[19] For any $n\in {\mathbb{Z}}^{+},G_{D(n^2)}$ is an Euler graph.

Theorem 3.7.

[19] $G_{D(n)}$ is 3-colorable iff all proper divisors of n are prime.

[20] introduced the difference DG of a finite group ${\mathbb{Z}}_n$. For any $n\in {\mathbb{Z}}^{+}$, D_n the set of proper divisors of n, let us denote the difference DG of a finite group ${\mathbb{Z}}_n$ as $\mathit{Dif}({\mathbb{Z}}_n,D_n)$.

Definition 3.8.

[20] Let $n\in {\mathbb{Z}}^{+}$, the difference DG is defined as $\mathit{Dif}({\mathbb{Z}}_n,D_n)$ associated with a finite group ${\mathbb{Z}}_n$ which is an undirected graph with the vertices $\{0,1,\dots ,n-1\}$ such that any two vertices x and y are adjacent iff either $x-y\in D_n$ or $y-x\in D_n$.

Theorem 3.9.

[20]

• For $n\in {\mathbb{Z}}^{+}$, the graph $\mathit{Dif}({\mathbb{Z}}_n,D_n)$ is connected.

• The graph $\mathit{Dif}({\mathbb{Z}}_n,D_n)$ is a tree iff n is prime.

• The graph $\mathit{Dif}({\mathbb{Z}}_n,D_n)$ is not complete iff n > 2.

Theorem 3.10.

[20]

• If $n\ge 2$ is odd, then $\mathit{Dif}({\mathbb{Z}}_n,D_n)$ is a bipartite graph.

• The graph $\mathit{Dif}({\mathbb{Z}}_n,D_n)$ is not complete iff n > 2.

Theorem 3.11.

[20] For n > 1, we have $$\mathit{diam}(\mathit{Dif}({\mathbb{Z}}_n,D_n))=\{\begin{array}{cc}1\hfill & \mathit{ifn}=2\hfill \\ n-1\hfill & \mathit{ifn}=p,\mathit{anoddprime}\hfill \\ 3\hfill & \mathit{ifn}\ge 4,\mathit{iseven}\hfill \\ 4\hfill & \mathit{ifn}=p^{\alpha },\alpha \in {\mathbb{Z}}^{+}.\hfill \end{array}$$

Theorem 3.12.

[20] The girth of the $\mathit{Dif}({\mathbb{Z}}_n,D_n)$ is given by $$\mathit{gir}(\mathit{Dif}({\mathbb{Z}}_n,D_n))=\{\begin{array}{cc}\infty \hfill & ifnisa\mathit{prime}\mathit{number}\hfill \\ 3\hfill & ifnisan\mathit{even}\mathit{number}\hfill \\ 4\hfill & ifnis\mathit{odd}\mathit{but}\mathit{not}a\mathit{prime}\hfill \end{array}$$

Theorem 3.13.

[20] For any $n\in {\mathbb{Z}}^{+}$, the $\mathit{Dif}({\mathbb{Z}}_n,D_n)$ is not a Cayley graph.

Theorem 3.14.

[20] For any $n\in {\mathbb{Z}}^{+}$, the $\mathit{Dif}({\mathbb{Z}}_n,D_n)$ is not a Eulerian.

Theorem 3.15.

[20]

• For any $n\in {\mathbb{Z}}^{+}$, the $\mathit{Dif}({\mathbb{Z}}_n,D_n)$ is not a Eulerian.

• For any $n\ge 3$ with n as even, the $\mathit{Dif}({\mathbb{Z}}_n,D_n)$ is Hamiltonian.

• For any $n\ge 3$ with n as odd, the $\mathit{Dif}({\mathbb{Z}}_n,D_n)$ is not Hamiltonian.

[24] further worked on the connectivity, independency and colorability for some class of DFG’s.

Theorem 3.16.

[24] $G_{D(n)}$ is $2-$connected iff n is a semi-prime such that n is not a perfect square.

Theorem 3.17.

[24] If n is a sphenic number then $G_{D(n)}$ is $4-$connected.

Theorem 3.18.

[24] If n is a perfect square such that $n=p^2{q}^2$, where $p\ne q$ are primes then $G_{D(n)}$ is $4-$connected.

Theorem 3.19.

[24] $G_{D(n)}$ has a perfect matching iff n is not a perfect square.

Theorem 3.20.

[24] The chromatic number of $G_{D(n)}$ is k if k is the least number of independent sets $S_1,S_2,\dots ,S_k$ such that each S_i is the maximum independent set of $G_{D(n)}^{i-1}$ where $V(G_{D(n)}^i)=V(G_{D(n)})-\underset{i}{\cup }{S}_i$ and $S_k=\left\{1\right\}$ or {n}, $1\le i\le k-1$ and $G_{D(n)}^0=G_{D(n)}$.

Theorem 3.21.

[24] Let $G_{D(n)}$ has r divisors where $n=p^{\alpha }$ and $\alpha \in \mathbb{N}$. Then $${\chi }^{\prime }(G_{D(n)})=\{\begin{array}{cc}r-1\hfill & ifnisa\mathit{perfect}\mathit{square}\hfill \\ r\hfill & \mathit{otherwise}\hfill \end{array}$$

[25] worked on the oriented version of DFG’s and the studied the directed graph properties. When we discuss DFG, the directed version is the most appropriate DFG, since the divisor function satisfies the anti-symmetric property.

Definition 3.22.

[25] For any positive integer $n\ge 1$ with r divisors $d_1,d_2,\dots ,d_r$ the graph of directed divisor function $G_{D_{ij}}(n)$ is a graph whose vertex set $\{d_1,d_2,\dots ,d_r\}$ if $d_i|d_j$ then there is an arc from d_i to d_j for all i, j and $i\ne j$.

Theorem 3.23.

[25]

• The directed DFG $G_{D_{ij}}(n)$ is not strongly connected.

• The directed DFG $G_{D_{ij}}(n)$ is unilaterlly connected iff $n=p^a$, p being prime and $a\in {\mathbb{Z}}^{+}$.

• The directed DFG $G_{D_{ij}}(n)$ is weakly connected.

Theorem 3.24.

[25] For any $n\in {\mathbb{Z}}^{+},G_{D_{ij}}(n)$ is acyclic.

Theorem 3.25.

[25] For any $n\in {\mathbb{Z}}^{+}$ and n is composite $G_{D_{ij}}(n)$ is not a directed bi-graph.

Theorem 3.26.

[25] For any prime p, $G_{D_{ij}}(p)$ is K₂.

Theorem 3.27.

[25] For any $n\in {\mathbb{Z}}^{+},G_{D_{ij}}(n)$ is not a directed complete graph.

Table

Input	A positive integer n
Output	Number of edges m
Complexity	$O(d^2)$

Narasimhan et al. computed the size of $G_{D_{ij}}(n)$, for any $n\in {\mathbb{Z}}^{+}$ with the complexity of $O(d^2)$, d being the number of divisors of n.

Theorem 3.28.

[25]

• Every $G_{D_{ij}}(n)$ has a source and a sink.

• Every $G_{D_{ij}}(n)$ has a topological ordering of divisors.

Definition 3.29.

[25] Let d_i’s $(1\le i\le r)$ be the divisors of $G_{D_{ij}}(n)$ and $(d_i,d_j)\in A(G_{D_{ij}}(n))$ and $(d_j,d_k)\in A(G_{D_{ij}}(n))\iff ((d_i,d_j),(d_j,d_k))\in L(A(G_{D_{ij}}(n)))$, where d_i is a proper divisor of d_j and d_j is a proper divisor of d_k.

Result 3.1.

[25]

• $L(G_{D_{ij}}(n))$ is always disconnected.

• For a prime n, $L(G_{D_{ij}}(n))$ has exactly one component (as isolated point).

• If n has exactly two non-trivial prime divisors then $L(G_{D_{ij}}(n))$ has exactly three components. Otherwise, $L(G_{D_{ij}}(n))$ has exactly two components $\forall n$, but not prime.

• If $G_{D_{ij}}(n)$ has k divisors then $L(G_{D_{ij}}(n))$ has at most $e\le {\sum }_{i=1}^{k}od(d_i).id(d_i)$, where e is the number of edges in $L(G_{D_{ij}}(n))$.

Result 3.2.

[25] Every directed divisor function $G_{D_{ij}}(n)$ is not Eulerian.

Theorem 3.30.

[25] A directed DFG $G_{D_{ij}}(n)$ is said to be a tournament iff $n=p^{\alpha }$, p being prime and $\alpha \in \mathbb{N}$ and let $T_{ij}(n)$ be such tournaments.

Theorem 3.31.

[25] $T_{ij}(n)$ is transitive if and only if the divisor score sequence of $G_{D_{ij}}(n)$ is $0,1,\dots ,r-1$.

Theorem 3.32.

[25] The directed DFG $G_{D_{ij}}(n)$ with $n=p^a$ is directed planar if it has at most 4 divisors in it.

In the year 2021, Shanmugavelan et al. gave a note on the indices of prime power and semiprime divisor function graph [30]. In this work, Shanmugavelan et al. have analyzed the sum of two divisor function graphs and computed several topological indices specially for prime powers and for semi primes along with a result for an independent function.

Theorem 3.33.

[30]

• For any prime power pn, $G_D(p^n)$ has a harmonic index of $\frac{n+1}{2}$.

• The degree distance of $G_D(p^n)$ is $n^2(n+1)$.

• The Wiener index of $G_D(p^n)$ is $\frac{n(n+1)}{2}$.

• The Hyper Wiener index of $G_D(p^n)$ is $\frac{n(n+1)}{2}$.

• The Randić index of $G_D(p^n)$ is $\frac{(n+1)}{2}$.

• The first Zagreb index of $G_D(p^n)$ is $n^2(n+1)$.

• The second Zagreb index of $G_D(p^n)$ is $\frac{n^3(n+1)}{2}$.

• The Gutman index of $G_D(p^n)$ is $\frac{n^3(n+1)}{2}$.

• The Detour Gutman index of $G_D(p^n)$ is $\frac{n^4(n+1)}{2}$.

• The first R index of $G_D(p^n)$ is $n^2(n+1)(n^2+n^{(2n)-2}+2n^n)$.

• The second R index of $G_D(p^n)$ is $\frac{n^3(n+1)(n^2+n^{(2n)-2}+2n^n)}{2}$.

• The third R index of $G_D(p^n)$ is $n(n+1)(n^2+n^n)$.

• The Balaban index of $G_D(p^n)$ is $\frac{n{(n+1)}^2}{2(n^2-n+4)}$.

Theorem 3.34.

[30]

The degree distance of a semiprime divisor function graph is 34.

The Wiener index of a semiprime divisor function graph is 7.

The Hyper Wiener index of a semiprime divisor function graph is 8.

The Randić index of a semiprime divisor function graph is $\frac{2\sqrt{6}+1}{3}$.

The first Zagreb index of a semiprime divisor function graph is 26.

The second Zagreb index of a semiprime divisor function graph is 33.

The Gutman index of a semiprime divisor function graph is 41.

The Detour Gutman index of a semiprime divisor function graph is 90.

Theorem 3.35.

[30] If n₁ or n₂ or both are prime then the sum of divisor function graphs $G_D(n_1)$ and $G_D(n_2)$ is a simple graph, ( $G_D(n_1)$) + $G_D(n_2)$) = $(p_1+p_2;q)$. The number of edges in sum of two divisor function graphs (say) $q=q_1+q_2+p_2+\mathit{jSj}+1$ where $S=V(G_D(n_2))\cap P$ and $P=\left\{x\right|x=n_1.n;n\in \mathbb{N};n\le n_2\}$

Theorem 3.36.

[30]

• If p is prime and $n\in \mathbb{N}$ then Energy of $G_D(p^n)$ is 2n.

• The Energy of a semiprime divisor function graph is $2+\sqrt{17}$.

• If $f:I\to [0,1]$ such that f(v) = 1, $\forall v\in I$, then f becomes an Independent function of $G_{D(n)}$ for some independent I.

[8] derived the results on some distance based and degree-based topological indices of k – d prime divisor function graph. John Rafael M. Antalan et al. defined the k – d prime divisor function graph as Γ_k.

Definition 3.37.

[8] Let $n\ge 1$ be an integer such that $n=p_1{p}_2\dots p_k$, where each p_i are distinct primes for $i=1,2,\dots ,k$. The graph $G_{D(n)}$ with $V(G_{D(n)})=\{u:u|n\}$ and $E(G_{D(n)})=\{uv:$ either $u|v$ or $v|u$ for $u,v\in V(G_{D(n)})$ with $u\ne v\}$ is called a k-dprime divisor function graph.

Theorem 3.38.

[8] The number of vertices in Γ_k is $2^k$.

Theorem 3.39.

[8] The number of edges in Γ_k is $3^k-2^k$.

Theorem 3.40.

[8] If $v\in V({\Gamma }_k)$, then $$de{g}_{{\Gamma }_k}(v)=\{\begin{array}{cc}{2}^k-1\hfill & ifv=1,n\hfill \\ 2^{\omega (v)}+2^{l-\omega (v)}-2\hfill & \mathit{otherwise}\hfill \end{array}$$

where $\omega (v)$ is the number of distinct prime divisors of v.

Theorem 3.41.

[8] Let Γ_k denote k – d prime divisor function graph. If $u,v\in V({\Gamma }_k)$ then $$d_{{\Gamma }_k}(u,v)=\{\begin{array}{cc}0\hfill & ifu=v\hfill \\ 1\hfill & ifuis\mathit{adjacent}tov\hfill \\ 2\hfill & \mathit{otherwise}\hfill \end{array}$$

Corollary 3.42.

[8] Let Γ_k denote k – d prime divisor function graph. The diameter of Γ_k denoted by $\mathit{diam}({\Gamma }_k)$ is 2.

Theorem 3.43.

[8] Let Γ_k denote k – d prime divisor function graph. The Wiener index of Γ_k denoted by $W({\Gamma }_k)$ is given by $2^{2k}-3^k$.

Theorem 3.44.

[8] Let Γ_k denote k – d prime divisor function graph. The hyper-Wiener index of Γ_k denoted by $WW({\Gamma }_k)$ is given by $2^{k-1}(2^{k+1}+2^k+1)-2(3^k)$.

Theorem 3.45.

[8] Let Γ_k denote k – d prime divisor function graph. The Harary index of Γ_k denoted by $H({\Gamma }_k)$ is given by $\frac{2^{k-1}(2^k-3)-3^k}{2}$.

Further, Antalan et al. gave some more results on the various degree based topological indices for some special cases of k – d prime divisor function graphs.

[23] introduced and studied the concept of divisor prime graph. The definition of divisor prime graph is given as

Definition 3.46.

[23] For any $n\in {\mathbb{Z}}^{+}$ with r divisors $d_1,d_2,\dots ,d_r$, then the divisor prime graph $G_{Dp(n)}$ is a graph with vertex set $\{d_1,d_2,\dots ,d_r\}$ such that two vertices d_i and d_j are adjacent iff $\mathit{gcd}(d_i,d_j)=1$.

The immediate observations from the definitions are given as:

• In any divisor prime graph the vertex 1 is adjacent to all other vertices.

• $G_{Dp(n)}$ is connected for all n.

• If $n=p^k$, then $G_{Dp(n)}$ has exactly k edges.

Theorem 3.47.

[23] For any $G_{Dp(n)}$ the maximum degree among the vertices of G, $\Delta (G_{Dp(n)})=(n_1+1)(n_2+1)\dots (n_r+1)-1$, where $n_1,n_2,\dots ,n_r$ are the powers of prime factors of n. The minimum degree among the vertices of G, $\delta (G_{Dp(n)})=1$. For a prime n, $\Delta (G_{Dp(n)})=\delta (G_{Dp(n)})=1$.

Theorem 3.48.

[23]

• $G_{Dp(n)}-1$ is a null graph iff $n=p^k$.

• Divisor prime graph is not an Euler Graph.

• For any $n\ne p^k$, the divisor prime graph $G_{Dp(n)}$ has at least one cycle of length 3.

• If $n=p_1{p}_2\dots p_r$. Then $G_{Dp(n)}-n$ is a complete graph.

• $G_{Dp(n)}$ is a bigraph iff $n=p^k$.

4 Benchmark results on divisor Cayley graphs

In this section, we present results on divisor based Cayley graphs.

[11] introduced a new class of arithmetic CG with the help of divisor function D(n) and studied the properties of it. [14] and [10] also examined the structure of CG along with the arithmetic functions.

Definition 4.1.

[11] Let $n\in {\mathbb{Z}}^{+}$ and let S be the set of divisors of n. The set $S^{*}$ = $\{s,n-s:s\in S\}$ is a symmetric subset of the additive abelian group of integers mod n. Let $G({\mathbb{Z}}_n,S^{*})$ be the divisor Cayley Graph with the vertex set $\{0,1,\dots ,n-1\}$ and the edge set E is the set of all ordered pairs of vertices x, y such that either $x-y\in S^{*}$ or $y-x\in S^{*}$.

Lemma 4.2.

[11] The graph $G({\mathbb{Z}}_n,S^{*})$ is $\left|S^{*}\right|-$ regular and $\left|E\right|$ is $\frac{n\left|S\right|}{2}$.

Lemma 4.3.

[11]

• $\mathrm{deg}(v)\in G({\mathbb{Z}}_n,S^{*})$ is odd iff n is even.

• $\mathrm{deg}(v)\in G({\mathbb{Z}}_n,S^{*})$ is even iff n is odd.

• $G({\mathbb{Z}}_n,S^{*})$ is Eulerian iff n is odd.

Lemma 4.4.

[11]

• The graph $G({\mathbb{Z}}_n,S^{*})$ is connected Hamiltonian but not bipartite.

• If n is prime then $G({\mathbb{Z}}_n,S^{*})$ is the outer Hamiltonian cycle.

Lemma 4.5.

[11] For a given $a\in S^{*}$, the number of fundamental triangles Δ_ab in $G({\mathbb{Z}}_n,S^{*})$ is $\left|S^{*}\right|\cup (a+S^{*})$, where $a+S^{*}$ = $\{a+s:s\in S^{*}\}$.

Lemma 4.6.

[11] The number of fundamental triangles in $G({\mathbb{Z}}_n,S^{*})$ is $\frac{1}{2}\left[\sum _{a\in S}\left|S^{*}\right|\cup (a+S^{*})\right].$

Lemma 4.7.

[11] The number of K₃ in $G({\mathbb{Z}}_n,S^{*})$ is $\frac{1}{6}\left|{\mathbb{Z}}_n\right|\left[\sum _{a\in S}\left|S^{*}\right|\cup (a+S^{*})\right]$.

[21] studied the enumeration process of finding the number of K₃’s in the Cayley graph associated with a finite group or a symmetric subset of a finite group with the help of the results from [11].

[22] investigated the dominating sets of DCG with the help of algorithms.

Theorem 4.8.

[22] If n is prime, then $D=\left\{r{d}_0\right|r\in [0,k)$, where k is the largest non-negative number such that $r{d}_0\le n-1$ and $d_0=3\}$, is a dominating set of $G({\mathbb{Z}}_n,D)$.

Theorem 4.9.

[22] If $n=p^2,p\ne 2$ is prime, then $D=\left\{r{d}_0\right|r\in [0,k)$, where k is the largest non-negative number such that $r{d}_0\le n-1$ and $d_0=3\}$, is a dominating set of $G({\mathbb{Z}}_n,D)$.

Theorem 4.10.

[22] If $n=p^m$, p = 2 and m > 2 is prime, then $D=\left\{r{d}_0\right|r\in [0,k)$, where k is the largest non-negative number such that $r{d}_0\le n-1$ and $d_0=5\}$, is a dominating set of $G({\mathbb{Z}}_n,D)$.

Theorem 4.11.

[22] If $n=p_1^{\alpha }{p}_2^{\beta }$, p₁ and p₂ are primes $\alpha ,\beta \ge 1$, then $D=\left\{r{d}_0\right|r\in [0,k)$, where k is the largest non-negative number such that $r{d}_0\le n-1$ and $d_0=5\}$, is a dominating set of $G({\mathbb{Z}}_n,D)$.

Theorem 4.12.

[22] If $n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}\dots p_m^{{\alpha }_m}$, p₁, $p_2\dots ,p_m$ are primes ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_m\ge 1$, then $D=\left\{r{d}_0\right|r\in [0,k)$, where k is the largest non-negative number such that $r{d}_0\le n-1$ and $d_0=6\}$, is a dominating set of $G({\mathbb{Z}}_n,D)$.

The following results are from the Shodhaganga notes [32]. Here $G({\mathbb{Z}}_n,D)$ is called as the divisor Cayley graph.

Theorem 4.13.

[32] If n > 4 be a prime, then the minimum vertex cover of $G({\mathbb{Z}}_n,D)$ is $\{1,3,5,\dots ,n\}$.

Corollary 4.14.

[32] If n > 4 be a prime, then the vertex covering number of $G({\mathbb{Z}}_n,D)$ is $\frac{n+1}{2}$.

Theorem 4.15.

[32] Let n be non composite number and n > 7. Let d₀ be the smallest positive number which is not a divisor of n.

• The set $V_0=V-U_0$, where $U_0=\left\{k{d}_0\right|k\in [1,r]$ such that $r{d}_0\in S^{*}$ and for t < r, $t{d}_0\notin S^{*}$ $\}$ is a vertex cover of $G({\mathbb{Z}}_n,D)$.

• For any positive number $d>d_0$ that does not divide n. let $U_d=\left\{u\right|u=d+k{d}_0$ if $u\le n$ and $u=d+k{d}_0-n$, if u > n. $k\in [0,r-1]$ $\}$ then the set is also a vertex cover of $G({\mathbb{Z}}_n,D)$.

Theorem 4.16.

[32] Let n = 5 or n > 6 and let d₀ be the smallest positive number that does not divide n. For any integer t > 1, the set of vertices V_t in $G({\mathbb{Z}}_n,D)$, which is of the form $V_t=\{t+n{d}_0|r\in [0,k)$, where k is the least non-negative integer such that $r{d}_0\notin S^{*}$ & $t+r{d}_0<n\}$ is an independent set of $G({\mathbb{Z}}_n,D)$.

Corollary 4.17.

[32] Let n = 5 or n > 6 and let d₀ be the smallest positive number that does not divide n. Then the independence number is k, where k is the least positive integer such that $1+k{d}_0<n$ and either kd₀ divides n, or, $(n-k{d}_0)$ divides n.

Theorem 4.18.

[32] If n > 1, the minimum edge covering of $G({\mathbb{Z}}_n,D)$ is

• $\{(0,1),(2,3),\dots ,(n-2,n-1)\}$, if n is even.

• $\{(0,1),(2,3),\dots ,(n-1,0)\}$, if n is odd.

Corollary 4.19.

[32] If n > 1, the edge covering number of $G({\mathbb{Z}}_n,D)$ is $${\beta }^{\prime }(G({\mathbb{Z}}_n,D))=\{\begin{array}{cc}\frac{n}{2}\hfill & ifnis\mathit{even}\hfill \\ \frac{n+1}{2}\hfill & \mathit{otherwise}\hfill \end{array}$$

Theorem 4.20.

[32] The edge dominating set of $G({\mathbb{Z}}_n,D),n\ge 3$ is

• $\{(0,1),(2,3),\dots ,(n-2,n-1)\}$, if n is even.

• $\{(1,2),(3,4),\dots ,(n-2,n-1)\}$, if n is odd.

Corollary 4.21.

[32] If $n\ge 3$, then ${\gamma }^{\prime }(G({\mathbb{Z}}_n,D))$ is $${\gamma }^{\prime }(G({\mathbb{Z}}_n,D))=\{\begin{array}{cc}\frac{n}{2}\hfill & ifnis\mathit{even}\hfill \\ \frac{n-1}{2}\hfill & \mathit{otherwise}\hfill \end{array}$$

Theorem 4.22.

[32] The matching number of $G({\mathbb{Z}}_n,D)$ is $$M(G({\mathbb{Z}}_n,D))=\{\begin{array}{cc}\frac{n}{2}\hfill & ifnis\mathit{even}\hfill \\ \left[\frac{n-1}{2}\right]\hfill & \mathit{otherwise}\hfill \end{array}$$

The unitary DCG [32] are $\left|S^{*}\right|-$ regular and $\left|E\right|$ of $G({\mathbb{Z}}_n,U_n)$ is $\frac{n\left|S^{*}\right|}{2}$.

Theorem 4.23.

[32]

1. If $n=2k$, where k is odd, then $\left|S^{*}\right|$ is odd.

2. If $n=2^{r}q$, where r > 1 and q is odd, then $\left|S^{*}\right|$ is even.

3. If n is odd, then $\left|S^{*}\right|$ is even.

Corollary 4.24.

[32]

1. If $n=p^a$, where p is prime and $a\in \mathbb{N}$, then $G({\mathbb{Z}}_n,U_n)$ is Eulerian.

2. If $n=2^{r}q$, where r > 1 and q is odd, then $G({\mathbb{Z}}_n,U_n)$ is Eulerian.

3. If n is odd, then $G({\mathbb{Z}}_n,U_n)$ is Eulerian.

Theorem 4.25.

[32] If $n=2^a,a\in \mathbb{N}$, then $G({\mathbb{Z}}_n,U_n)$ is a bipartite graph.

Lemma 4.26.

[32] Let u be a unitary divisor of n. Then $G({\mathbb{Z}}_n,U_n)$ contains exactly u disjoint cycles, each of length $\frac{n}{u}$.

Theorem 4.27.

[32] If $n=2k$, where k is odd, then $G({\mathbb{Z}}_n,U_n)$ cannot be decomposed in to edge disjoint Hamilton cycles.

Theorem 4.28.

[32] If n is odd, then $G({\mathbb{Z}}_n,U_n)$ can be decomposed in to edge disjoint Hamilton cycles.

Theorem 4.29.

[32] Let $n=2^{r}q$, where r > 1 and q is odd. If $u=2^{r}t$, where t is odd is an even unitary divisor of n, then $G({\mathbb{Z}}_n,U_n)$ can be decomposed into $2^{r}t$ edge disjoint cycles of length $\frac{n}{2^{r}t}$, which are not Hamilton cycles.

Theorem 4.30.

[32] Let $n=2^{r}q$, where r > 1 and q is odd. If $n>u_1>u_2>\dots >u_k>1$ are odd unitary divisor of n, then $G({\mathbb{Z}}_n,U_n)$ can be decomposed into k + 1 edge disjoint Hamilton cycle.

Theorem 4.31.

[32] Let $n\ge 4$ be a prime power number, then the minimum vertex cover of $G({\mathbb{Z}}_n,U_n)$ is $\{1,3,5,\dots ,p\}$, where p is an odd integer which is less than n.

Corollary 4.32.

[32] If n > 3 is a prime power number, then the vertex covering number of $G({\mathbb{Z}}_n,U_n)$ is $[\frac{n+1}{2}]$.

5 Conclusion

In this survey, we presented results related to number theoretic graphs and results such as divisor graphs, divisor function graphs and divisor Cayley graphs. There are many number theoretic graphs that have not been presented in this paper and that can be the explored in the future. Further, this survey can be useful to the researchers working on the number theoretic graphs.