Completely positive graphs and entanglement of quantum states

Abstract

We present a short survey on completely positive matrices and on their application to quantum information

KEYWORDS:

• Completely positive matrices
• completely positive graphs
• the separation problem
• entangled states

1 Completely positive matrices and completely positive graphs

Definition 1.1.

A matrix A is completely positive (CP) if it can be decomposed as $A=B{B}^T$, where B is a nonnegative matrix (the elements of B are nonnegative).

Definition 1.2.

A symmetric real matrix A is copositive (COP) if the associated quadratic form $x^{T}Ax$ is nonnegative whenever x is.

A comprehensive source of information on CP matrices and on COP matrices is (Monderer and Berman [14]) which is an extended update of (Berman and Monderer [5]).

Theorem 1.3.

(Hall and Newman [8]) The set $C{P}_n$ of completely positive matrices of order n and the set $CO{P}_n$ of copositive matrices of order n are closed convex cones and one is dual to the other with respect to the inner product $〈X,Y〉=\text{trace} XY$ in the space of $n\times n$ real symmetric matrices.

Definition 1.4.

A matrix is doubly nonnegative (DNN) if it is positive semidefinite (PSD) and nonnegative.

Theorem 1.5.

(Maxfield and Minc [12]) Every doubly nonnegative matrix of order at most 4 is completely positive.

This is not true for larger matrices:

Example 1.6.

Later we will see that $$\left(\begin{array}{ccccc}1& 1& 0& 0& 1\\ 1& 2& 1& 0& 0\\ 0& 1& 2& 1& 0\\ 0& 0& 1& 2& 1\\ 1& 0& 0& 1& 3\end{array}\right)$$is DNN but not CP.

Definition 1.7.

The graph $G(A)$ of a symmetric matrix A of order n has n vertices $1,2,\dots ,n$ and an edge between i and j if and only if $a_{ij}$ is not zero.

A is a matrix realization of $G(A)$.

Definition 1.8.

The comparison matrix $M(A)$ of a symmetric nonnegative matrix A is the matrix obtained from A by multiplying its off-diagonal entries by $-1$.

Theorem 1.9.

(Drew et al. [7]) If $M(A)$ is positive semidefinite then A is completely positive. If A is completely positive and $G(A)$ is triangle free, then $M(A)$ is positive semidefinite.

In the following example $G(A)$ is a triangle:

Example 1.10.

Note that the matrix $A=(\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array})$ is completely positive, but $M(A)$ is not positive semidefinite.

Definition 1.11.

A graph G is completely positive if every DNN matrix realization of G is CP.

Thus, graphs with no more than 4 vertices are CP.

2 Entanglement and separation of quantum states

In quantum theory a state can be entangled or separated. Entanglement is a key resource for quantum information tasks. The separability problem – deciding whether a quantum state is entangled or not, given its description, is in general NP-hard. Asher Peres, (Peres [13]), showed that every state that is not entangled must satisfy the positivity under partial transportation(PPT) criterion. The converse is, in general, not true. There are entangled states that satisfy the PPT criterion. CP matrices should not be confused with CP maps, (Choi [6]), that are very important in quantum theory, but CP matrices also have applications to this theory. (Tura et al. [15]) (see also Yu [16]) studied the separability problem for a special class of quantum states– diagonal symmetric (DS) states. With every DS state $\rho$ they associated a symmetric nonnegative matrix (whose entries sum to 1) $M(\rho )$ and proved:

Theorem 2.1.

$\rho$ is separable if and only if $M(\rho )$ is completely positive.

Theorem 2.2.

$\rho$ satisfies the positivity under partial transformation criterion if and only if $M(\rho )$ is doubly nonnegative.

Corollary 2.3.

If $G(M(\rho ))$ is completely positive, then $\rho$ is entangled if and only if $M(\rho )$ has a negative eigenvalue.

Example 2.4.

If $M(\rho )=1/20(\begin{array}{ccccc}1& 1& 0& 0& 1\\ 1& 2& 1& 0& 0\\ 0& 1& 2& 1& 0\\ 0& 0& 1& 2& 1\\ 1& 0& 0& 1& 3\end{array})$, then $\rho$ is entangled but $M(\rho )$ is PSD.

3 Characterization of completely positive graphs

This section is based on Section 3.5 of (Monderer and Berman [14]). We outline some proofs and refer the readers to (Monderer and Berman [14]) for the other proofs.

Definition 3.1.

A long odd cycle in a graph is a cycle of odd length greater than 4 (a triangle is a short odd cycle).

Theorem 3.2.

(Berman and Hershkowitz [4]) A long odd cycle is not completely positive.

Proof.

Let B be a $k\times (k-1)$ matrix in which $$b_{ii}=1, i=1,2,\dots ,k-1,$$ $$b_{j+1,j}=1, j=1,2,\dots ,k-2\mathrm{\backslash }\mathrm{\backslash }{b}_{kj}={(-1)}^{j+1}, j=1,2,\dots ,k-2,$$ and all other entries are zero.

Let $A=B{B}^T$. A is PSD and for odd k it is also nonnegative. For $k=5$ it is the matrix of Example 1.6. $G(A)$ is a k-cycle so for $k>3$ it is triangle free.

Independent of k, $\mathit{detM}(A)=-4$, so for odd $k>3$, $M(A)$ is not PSD and by Theorem 1.9, the DNN A is not CP. ▪

Theorem 3.3.

(Berman and Hershkowitz [4]) A graph that contains a long odd cycle is not completely positive.

Proof.

Let G be a graph on n vertices that contains a $k-$ cycle, where k is an odd number greater than 4.

Let S be the adjacency matrix of G and let C be an $n\times n$ matrix whose principal submatrix corresponding to the cycle is the matrix A of Theorem 3.2 and all other entries are equal to zero. For every $a>0$ there exists $0<b\le a$ such that $C_a=C+aI+bS$ is DNN. For every a, the graph of $C_a$ is G. When a approaches 0, $C_a$ approaches C which is not CP. Since the cone $C{P}_n$ is closed (Theorem 1.3) there exists some positive a for which $C_a$ is DNN but not CP. ▪

Theorem 3.4.

(Berman and Grone [3]) Bipartite graphs are completely positive.

Definition 3.5.

$T_n$ is a graph that consist of $n-2$ triangles with a common base.

Theorem 3.6.

(Kogan [10]; Kogan and Berman [11] The graph $T_n$ is completely positive.

Definition 3.7.

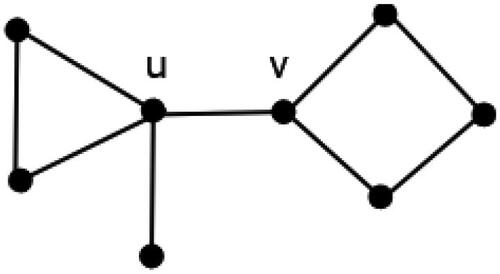
A vertex v of a graph G is a cut vertex if $G-v$ has more components than G. The cut vertices of a graph separate it to blocks.

Example 3.8.

The graph in Figure 1 has two cut vertices and four blocks - a triangle, two single edges, and a 4-cycle.

Figure 1: …

Theorem 3.9.

(Kogan [10]; Kogan and Berman [11]) Let $G=G_1\cup G_2$, where $G_1$ and $G_2$ have only one vertex in common (a cut vertex of G). If $G_1$ and $G_2$ are completely positive, then so is G.

Theorem 3.10.

(Berman [2]; Kogan [10]; Ando [1]; Kogan and Berman [11]) A graph is completely positive if and only if it does not contain a long cycle.

Proof.

Only if: This is Theorem 3.3.

If: If G does not contain a long odd cycle, then the blocks of G (or of its components, if it is not connected) are bipartite or the complete graph on 4 vertices or a $T_k$, so the result follows from Theorems 1.5, 3.4, 3.6, and 3.9. ▪

Corollary 3.11.

Let $\rho$ be a DS state. If $G(M(\rho ))$ does not contain a long odd cycle, then $\rho$ is entangled if and only if $M(\rho )$ has a negative eigenvalue.

Acknowledgments

This article is based on my talk in ICLAA 2021. I am grateful to the organizing committee for the invitation and hope that future talks will be face to face.