Independent k-rainbow bondage number of graphs

Abstract

For an integer $k\ge 1,$ an independent k-rainbow dominating function (IkRDF for short) on a graph G is a function g that assigns to each vertex a set of colors chosen from the subsets of $\{1,2,\dots ,k\}$ satisfying the following conditions: (i) if $g(v)=\varnothing$, then $\underset{u\in N(v)}{\cup }g(u)=\{1,\dots ,k\}$, and (ii) the set $S=\left\{v\right|g(v)\ne \varnothing \}$ is an independent set. The weight of an IkRDF g is the value $w(g)=\sum _{v\in V(G)}|f(v)|$. The independent k-rainbow domination number $i_{rk}(G)$ is the minimum weight of an IkRDF on G. In this paper, we initiate a study of the independent k-rainbow bondage number $b_{\mathit{irk}}(G)$ of a graph G having at least one component of order at least three, defined as the smallest size of set of edges $F\subseteq E(G)$ for which $i_{rk}(G-F)>i_{rk}(G)$. We begin by showing that the decision problem associated with the independent k-rainbow bondage problem is NP-hard for general graphs for $k\ge 2$. Then various upper bounds on $b_{ir2}(G)$ are established as well as exact values on it for some special graphs. In particular, for trees T of order at least three, it is shown that $b_{ir2}(T)\le 2$.

Keywords:

• Independent k-rainbow dominating function
• independent k-rainbow domination number
• independent k-rainbow bondage number

MSC 2010:

• 05C69

1 Introduction

We consider simple graphs G with vertex set $V=V(G)$ and edge set $E=E(G)$. The order of G is $n=n(G)=\left|V\right|$. For a vertex v in V, let $N_G(v)$ denote the set of neighbors of v and let $N_G[v]=N_G(v)\cup \left\{v\right\}.$ The degree of a vertex v is $d_G(v)=|N_G(v)|$. The maximum degree and minimum degree of G are denoted by $\Delta (G)$ and $\delta (G)$, respectively. When no confusion arises, we simply write N, d, δ and $\Delta$ instead of $N_G,$ $d_G,$ $\delta (G)$ and $\Delta (G),$ respectively. A leaf is a vertex of degree one while its neighbor is called a support vertex. If v is a support vertex, then we denote by L(v) the set of leaves adjacent to v. For definitions and notations not given here we refer the reader to [11].

As usual, the path (cycle, complete graph, complete bipartite graph, respectively) of order n is denoted by P_n (C_n, K_n, $K_{p,q}$, respectively). A tree is a connected acyclic graph. A star of order n, with $n\ge 2,$ is the graph $K_{1,n-1}.$ For integers $p,q\ge 1,$a double star $D{S}_{p,q}$ is a tree with exactly two vertices that are not leaves, one of which has p leaf neighbors, and the other has q leaf neighbors.

A set $S\subseteq V(G)$ is a dominating set if every vertex not in S has at least one neighbor in S. The domination number of a graph G is the minimum cardinality of a dominating set of G. In 1990, Fink et al. [8] introduced the bondage number b(G) to measure the vulnerability or the stability of the domination number in an interconnection network G under edge failure. They defined the bondage number of a graph G as the minimum number of edges whose removal from G increases the domination number. Since then the concept of bondage has been studied for several graph parameters, for instance see [7, 14–20, 25].

An independent set of a graph G is a set of vertices, no two of which are adjacent. Given a positive integer k and a graph G, we consider the assignment of a subset of the color set $\{1,2,\dots ,k\}$ to every vertex of G such that every vertex assigned an empty set has all k colors in its neighborhood. Such an assignment is called a k-rainbow dominating function (kRDF) of the graph G. The weight of a kRDF g of a graph G is the value $\omega (g)=\sum _{v\in V(G)}|g(v)|$. If H is a vertex induced subgraph of G, the weight restricted to H is ${\omega }_H(g)=\sum _{v\in H}|g(v)|$. The minimum weight of a kRDFs in G is called the k -rainbow domination number of G, denoted by ${\gamma }_{rk}(G).$ The concept of rainbow domination was introduced by Brešar, Henning and Rall in [5]. An independent k-rainbow dominating function (IkRDF) is a kRDF such that the set of vertices assigned non-empty sets is independent. The independent k-rainbow domination number $i_{rk}(G)$ is the minimum weight of an IkRDFs in G. An IkRDF of G with weight $i_{rk}(G)$ is called an $i_{rk}(G)$-function. It worth mentioning that when $k=1,$ $i_{r1}(G)$ matches with the usual independent domination number $i(G).$ The k-rainbow domination and its variant has been studied extensively [1–3, 9, 13, 21, 23–26]. For more details on rainbow domination we refer the reader to the chapter book [4].

In this paper, we initiate the study of the independent k-rainbow bondage number $b_{\mathit{irk}}(G)$ of a graph G defined as the smallest set of edges $F\subseteq E(G)$ for which $i_{rk}(G-F)>i_{rk}(G)$. Since the independent k-rainbow domination number of a connected graph of order two does not increase after deleting the unique edge, we will therefore assume that $\Delta (G)\ge 2.$ In addition, a subset $F\subseteq E(G)$ is a $b_{\mathit{irk}}(G)$-set if $\left|F\right|=b_{\mathit{irk}}(G)$ and $i_{\mathit{irk}}(G-F)>i_{\mathit{irk}}(G)$. It is worth noting that the independent 1-rainbow bondage number $b_{ir1}(G)$ is the independent bondage number $b_i(G)$ introduced in 2018 by Priddy, Wang and Wei [25] and also recently studied by Pham and Wei [24] for planar graphs with minimum degree at least three. In addition, Jafari Rad and Kamarulhaili [12] have shown that determining the independent 1-rainbow bondage number is NP-hard even for bipartite graphs. We also note that the concept of k-rainbow bondage was first studied by Dehgardi et al. in 2014 for the k-rainbow domination number of a graph G (see [7]), where the corresponding parameter has been denoted by $b_{rk}(G)$ and the NP-hardness of which has been shown in [12].

Among the results established in this paper, we start by showing that the decision problem associated with the independent k-rainbow bondage number is NP-hard for general graphs for any integer $k\ge 2$. Then we focus on the special case $k=2,$ where several upper bounds are given. In particular for trees T of order at least three it is shown that $b_{ir2}(T)\le 2$. Furthermore, exact values of the independent 2-rainbow bondage number are also given for some special graphs including paths, cycles and complete multipartite graphs.

Trivially, for every connected graph G of order $n\ge 2,2\le i_{r2}(G)\le n.$ The characterization of connected graphs G of order n with $i_{r2}(G)\in \{2,n\}$ which will be useful in the sequel, is given by the following result.

Proposition 1

([6]). Let G be a connected graph of order $n\ge 2$. Then

1. $i_{r2}(G)=2$ if and only if $\Delta (G)=n-1$ or $\Delta (G)=n-2$ and there are two non-adjacent vertices of degree n – 2.

2. $i_{r2}(G)=n$ if and only if $G=K_2$.

2 NP-hardness result

In this section, we will show that the decision problem corresponding to the problem of computing the independent k-rainbow bondage domination number for general graphs is NP-hard. Recall that the NP-hardness has been already shown in [12] for bipartite graphs when $k=1.$ In the sequel, k is an integer greater or equal to 2. Let us state the following decision problem.

Independent k-rainbow bondage domination number(Ik RB):

Instance: A graph G and a positive integer q.

Question: Is $b_{\mathit{irk}}(G)\le q$?

We show that the NP-hardness of the IkRB problem by transforming the 3-SAT problem to it in polynomial time. Recall that the 3-SAT problem specified below was proven to be NP-complete in [10].

3-satisfiability problem (3-SAT):

Instance: A collection $\mathcal{C}=\{C_1,C_2,\dots ,C_m\}$ of clauses over a finite set U of variables such that $\left|C_j\right|=3$ for $j=1,2,\dots ,m$.

Question: Is there a truth assignment for U that satisfies all the clauses in $\mathcal{C}$?

Theorem 2.

The IkRB problem is NP-hard for general graphs for $k\ge 2.$

Proof.

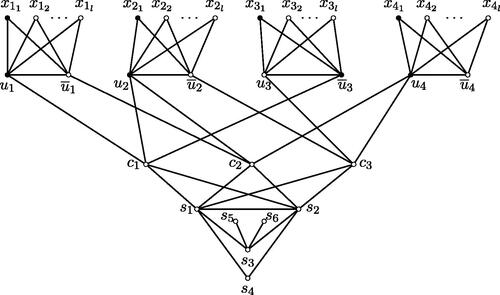
Let $U=\{u_1,u_2,\dots ,u_n\}$ and $\mathcal{C}=\{C_1,C_2,\dots ,C_m\}$ be an arbitrary instance of 3-SAT. We will construct a graph G and choose a positive integer q such that $\mathcal{C}$ is satisfiable if and only if $b_{\mathit{irk}}(G)\le q$. We construct such a graph G as follows. For each $i\in \{1,2,\dots ,n\}$, we associate to each variable $u_i\in U$a graph H_i obtained from a complete bipartite graph $K_{2,\mathcal{l}}$ such that $\mathcal{l}\ge k+1,$ with bipartite sets $X=\{x_{i_1},x_{i_2},\dots ,x_{i_{\mathcal{l}}}\}$ and $Y=\{u_i,{\overline{u}}_i\}$ by adding the edge $u_i\overline{u_i}$. Also for each $j\in \{1,2,\dots ,m\}$, we associate to each clause $C_j=\{p_j,q_j,r_j\}\in \mathcal{C}$a single vertex c_j by adding the edge-set $E_j=\{c_j{p}_j,c_j{q}_j,c_j{r}_j\}$. 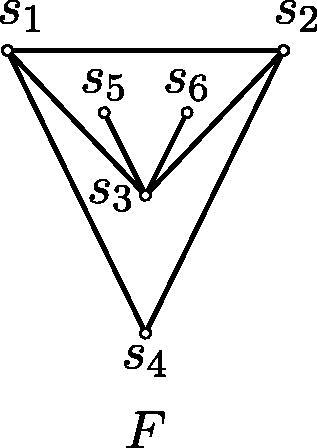Finally, we add a graph F, as depicted in Figure 1, by joining s₁ and s₂ to every vertex $c_j.$ Clearly, G is of order $(\mathcal{l}+2)n+m+6$, and thus the construction can be accomplished in polynomial time. Set $q=1.$ Figure 2 provides an example of the constructed graph when $U=\{u_1,u_2,u_3,u_4\}$ and $\mathcal{C}=\{C_1,C_2,C_3\}$, where $C_1=\{u_1,u_2,\overline{u_3}\},C_2=\{\overline{u_1},u_2,u_3\},C_3=\{\overline{u_2},u_3,u_4\}$. All that remains to be shown is that $\mathcal{C}$ is satisfiable if and only if $b_{\mathit{irk}}(G)=1$. This aim can be fulfilled by proving the following claims. □

Fig. 1 Graph F.

Fig. 2 NP-hardness for general graphs.

Claim 1. $i_{rk}(G)\ge k(n+1)+1$, and for any $i_{rk}(G)$-function f, we have $|f(H_i)|\ge k$. Moreover, if $i_{rk}(G)=k(n+1)+1$, then $f(H_i)=f(s_3)=\{1,2,\dots ,k\},|f(s_4)|=1,f(s_1)=f(s_2)=f(s_5)=f(s_6)=\varnothing$ and $f(u_i)=\{1,2,\dots ,k\},f(\overline{u_i})=\varnothing$ or $f({\overline{u}}_i)=\{1,2,\dots ,k\},f(u_i)=\varnothing$ for each $i\in \{1,2,\dots ,n\},$ while $f(c_j)=\varnothing$ for each $j\in \{1,2,\dots ,m\}$.

Proof

of Claim 1. Let f be a ${\gamma }_{\mathit{irk}}(G)$-function. By the construction of G, we have $|f(V(H_i))|\ge k$ for each $i\in \{1,2,\dots ,n\}.$ Moreover, one can easily see that $|f(V(F))|+{\sum }_{j=1}^m|f(c_j)|\ge k+1,$ and therefore $i_{rk}(G)\ge kn+k+1$.

Suppose now that $i_{rk}(G)=kn+k+1$. Then $|f(V(H_i))|=k$ for each $i\in \{1,2,\dots ,n\}$. Moreover, since u_i is adjacent to $\overline{u_i}$ and $\{x_{i_1},x_{i_2},\dots ,x_{i_{\mathcal{l}}}\}\subseteq N(u_i)\cap N(\overline{u_i}),$ we must have either $f(u_i)=\{1,2,\dots ,k\}$ and $f(\overline{u_i})=\varnothing$ or $f(u_i)=\varnothing$ and $f(\overline{u_i})=\{1,2,\dots ,k\}.$ Now, if $f(s_1)\ne \varnothing$ (the case $f(s_2)\ne \varnothing$ is similar), then $f(s_2)=f(s_4)=f(s_3)=f(c_j)=\varnothing$ for each $j\in \{1,2,\dots ,m\}$ and so need for the other vertices in F that $f(s_1)=\{1,2,\dots ,k\}$ and $|f(s_5)|=|f(s_6)|=1$. But then $\omega (f)=nk+k+2$, a contradiction. Hence $f(s_1)=f(s_2)=\varnothing$ and so $f(s_4)\ne \varnothing$ and $f(s_3)\cup f(s_5)\cup f(s_6)=\{1,2,\dots ,k\}$. The only possibility is ${\cup }_{j=1}^{m}f(c_j)=\varnothing ,$ $|f(s_4)|=1$, and therefore $f(s_3)=\{1,2,\dots ,k\}$. □

Claim 2. $i_{rk}(G)=k(n+1)+1$ if and only if $\mathcal{C}$ is satisfiable.

Proof

of Claim 2. Suppose that $i_{rk}(G)=k(n+1)+1$ and let f be an $i_{rk}(G)$-function of G. By Claim 1, $f(s_3)=\{1,2,\dots ,k\},$ $|f(s_4)|=1,$ $f(s_1)=f(s_2)=f(s_5)=f(s_6)=\varnothing$ and $f(c_j)=\varnothing$ for each $j\in \{1,2,\dots ,m\}$. Also, for each $i\in \{1,2,\dots ,n\}$, either $f(u_i)=\{1,2,\dots ,k\}$ and $f(\overline{u_i})=\varnothing$ or $f({\overline{u}}_i)=\{1,2,\dots ,k\}$ and $f(u_i)=\varnothing .$ Define a mapping $t:\to \{T,F\}$ by (1) $$t(u_i)=\{\begin{array}{cc}T\hfill & \text{if }f(u_i)=\{1,2,\dots ,k\},\hfill \\ F\hfill & \text{otherwise}.\hfill \end{array}i\in \{1,\dots ,n\}$$(1)

We now show that t is a satisfying truth assignment for $\mathcal{C}$. It is sufficient to show that every clause in $\mathcal{C}$ is satisfied by t. Since $f(c_j)=\varnothing$ and the vertex c_j is not adjacent to any member of $\{s_3,s_4\}\cup \{x_{i_1},x_{i_2},\dots ,x_{i_{\mathcal{l}}}\}$, there exists some $i\in \{1,\dots ,n\}$ such that c_j is adjacent to u_i or $\overline{u_i}$ so that it has all k colors in its neighborhood. If c_j is adjacent to u_i and $f(u_i)=\{1,2,\dots ,k\}$, then $t(u_i)=T$. If c_j is adjacent to $\overline{u_i}$ and $f(\overline{u_i})=\{1,2,\dots ,k\},$ then $t(u_i)=F$ and so $t(\overline{u_i})=T$ by (1). Hence, in either case, the clause C_j is satisfied. The arbitrariness of j with $1\le j\le m$ shows that all the clauses in $\mathcal{C}$ are satisfied by t, that is, $\mathcal{C}$ is satisfiable.

Conversely, suppose that $\mathcal{C}$ is satisfiable, and let $t:U\to \{T,F\}$ be a satisfying truth assignment for $\mathcal{C}$. We construct a subset D of vertices of G as follows. If $t(u_i)=T$, then put the vertex u_i in D; if $t(u_i)=F$, then put the vertex $\overline{u_i}$ in D. Hence $\left|D\right|=n$. Define the function h by $h(x)=\{1,2,\dots ,k\}$ for every $x\in D,h(s_3)=\{1,2,\dots ,k\},h(s_4)=\left\{1\right\}$ and $h(y)=\varnothing$ for the remaining vertices. Since t is a satisfying truth assignment for $\mathcal{C}$, the corresponding vertex c_j in G is adjacent to at least one vertex in D. Moreover, one can easy check that h is an IkRDF of G of weight $k(n+1)+1$ and so $i_{rk}(G)\le k(n+1)+1$. The equality follows from Claim 1. □

Claim 3. For any edge $e\in E(G),i_{rk}(G-e)\le k(n+1)+2$.

Proof

of Claim 3. Assume first that $e\in E(H_i)-\left\{u_i\overline{u_i}\right\}.$ Without loss of generality, let $e=x_{i_p}{u}_i$ (the case $e=x_{i_p}\overline{u_i}$ is similar) for some $p\in \{1,2,\dots ,\mathcal{l}\}$ and $i\in \{1,2,\dots ,n\}$. Then the function f defined on G – e by $f(s_2)=\{1,2,\dots ,k\},f(s_5)=f(s_6)=\left\{1\right\},f(\overline{u_i})=\{1,2,\dots ,k\}$ for all $i\in \{1,\dots ,n\}$ and $f(y)=\varnothing$ for the remaining vertices, is an IkRDF of G – e of weight $k(n+1)+2$. One can easily check that the function f previously defined remains an IkRDF of G – e of weight $k(n+1)+2$ even if the removed edge e belongs to $\{s_1{s}_4,s_3{s}_5,s_3{s}_6,s_1{s}_3\}$ or $e=s_1{c}_j$ for some j or e has an endvertex in some $V(H_i)$ and the other endvertex is $c_j$ for some j. Now assume that $e=u_i\overline{u_i}$ for some $i\in \{1,\dots ,n\}.$ Then the function f defined on G – e by $f(s_2)=\{1,2,\dots ,k\},f(s_5)=f(s_6)=\left\{1\right\},f(u_i)=\left\{1\right\},$ $f(\overline{u_i})=\{2,3,\dots ,k\},$ $f(u_t)=\{1,2,\dots ,k\}$ for each $t\in \{1,2,\dots ,n\}-\left\{i\right\}$ and $f(y)=\varnothing$ for the remaining vertices, is an IkRDF of G – e of weight $k(n+1)+2$. If $e=s_1{s}_2$, then the function f defined by $f(\overline{u_i})=\{1,2,\dots ,k\}$ for all $i\in \{1,\dots ,n\}$ and $f(s_1)=\left\{1\right\},f(s_2)=\{2,3,\dots ,k\},f(s_5)=f(s_6)=\left\{1\right\}$ and $f(y)=\varnothing$ for any other vertex y is an IkRDF of G – e of weight $k(n+1)+2$. Finally, if e is an edge incident with vertex s₂ and different from $s_2{s}_1$, then the function f defined by $f(\overline{u_i})=\{1,2,\dots ,k\}$ for all $i\in \{1,\dots ,n\},$ $f(s_1)=\{1,2,\dots ,k\},f(s_5)=f(s_6)=\left\{1\right\}$ and $f(y)=\varnothing$ for any other vertex y is an IkRDF of G – e of weight $k(n+1)+2$. Whatever the edge e that is deleted, we deduce that $i_{rk}(G-e)\le k(n+1)+2.$ □

Claim 4. $i_{rk}(G)=k(n+1)+1$ if and only if $b_{\mathit{irk}}(G)=1$.

Proof

of Claim 4. Assume that $i_{rk}(G)=k(n+1)+1$ and take $e=s_3{s}_6$. Suppose that $i_{rk}(G-e)=i_{rk}(G)$ and let f be an $i_{kr}(G-e)$-function. Since s₆ is a isolated, $\left|f(s_6)\right|=1$. Moreover, since $|f(H_i)|\ge k$ for every i, we deduce that ${\sum }_{i=1}^5\left|f(s_i)\right|+{\sum }_{j=1}^m|f(c_j)|\le k.$ Clearly, it is impossible to assign subsets of $\{1,\dots ,k\}$ over such vertices so that the sum of their sizes is at most k. Consequently $i_{rk}(G-e)>i_{rk}(G)$, and thus $b_{\mathit{irk}}(G)=1$.

Now assume that $b_{\mathit{irk}}(G)=1$ and let e be an edge such that $i_{rk}(G-e)>i_{rk}(G)$. By Claim 1, $i_{rk}(G)\ge k(n+1)+1$ and by Claim 3, $i_{kr}(G-e)\le k(n+1)+1$. Therefore $k(n+1)+1\le i_{rk}(G)<i_{rk}(G-e)\le k(n+1)+2$, which yields $k(n+1)+1=i_{rk}(G)$ .

It follows from Claims 2 and 4, that $b_{\mathit{irk}}(G)=1$ if and only if $\mathcal{C}$ is satisfiable and the desired result follows. □

3 Exact values of $b_{ir2}(G)$

In this section, we are restricting to the particular case $k=2,$ where we determine the independent 2-rainbow bondage number for some special graphs. The proofs of items 1 and 4 of the following proposition are straightforward.

Proposition 3.

1. For $n\ge 2,i_{r2}(K_n)=2$.

2. [22] $i_{r2}(P_n)=\lceil \frac{n+1}{2}\rceil$.

3. [22] For $n\ge 4,i_{r2}(C_n)=\frac{n}{2}$ if $n\equiv 0\hspace{1em}(\mathrm{mod}4)$ and $i_{r2}(C_n)=\lceil \frac{n+2}{2}\rceil$ otherwise.

4. If $G=K_{n_1,n_2,\dots ,n_t}$ is the complete t-partite graph with $t\ge 2$ such that $2\le n_1<n_2\le n_3\le \cdots \le n_t$, then $i_{r2}(G)=n_1$.

Proposition 4.

For $n\ge 3,b_{ir2}(K_n)=\lceil \frac{2n}{3}\rceil .$

Proof.

Let F be a $b_{ir2}(K_n)$-set. Then $i_{r2}(K_n-F)\ge 3$. If the edge-induced subgraph $K_n[F]$ has a components $K_2=uv$, then the function f defined on $K_n-F$ by $f(u)=\left\{1\right\}$, $f(v)=\left\{2\right\}$ and $f(x)=\varnothing$ for $x\in V(K_n)-\{u,v\}$, is an I2RDF of $K_n-F$ which leads to a contradiction. Thus each component of the edge-induced subgraph $K_n[F]$ has at least 3 vertices. Let $H_1,H_2,\dots ,H_t$ be the component of $K_n[F]$. Then $t\le \frac{n}{3}$ and we deduce that $$b_{ir2}(K_n)=\left|F\right|\ge \sum _{i=1}^t(|V(H_i)|-1)=n-t\ge n-\frac{n}{3}=\frac{2n}{3}.$$

This implies that $b_{ir2}(K_n)\ge \lceil \frac{2n}{3}\rceil$.

It is shown in [7] that $b_{r2}(K_n)=\lceil \frac{2n}{3}\rceil$. Hence if F is a $b_{r2}(K_n)$-set, then we have $i_{r2}(K_n-F)\ge {\gamma }_{r2}(K_n-F)>{\gamma }_{r2}(K_n)=i_{r2}(K_n),$ and thus $b_{ir2}(K_n)\le b_{r2}(K_n)=\lceil \frac{2n}{3}\rceil$. Therefore $b_{ir2}(K_n)=\lceil \frac{2n}{3}\rceil$. □

Proposition 5.

For $n\ge 3,b_{ir2}(P_n)=1.$

Proof.

Let $P_n=v_1{v}_2\dots v_n$. Clearly $P_n-v_2{v}_3=P_2\cup P_{n-2}$ and Proposition 3-(2) implies that $i_{r2}(P_n-v_2{v}_3)=2+\lceil \frac{n-1}{2}\rceil =1+\lceil \frac{n+1}{2}\rceil >i_{r2}(P_n)$. Therefore $b_{ir2}(P_n)=1.$ □

Proposition 6.

For $n\ge 3$, $$b_{ir2}(C_n)=\{\begin{array}{ccc}1\hfill & \text{if}\hfill & n\equiv 0\hspace{1em}\left(\mathrm{mod}4\right),\hfill \\ 2\hfill & \text{if}\hfill & n=3\text{or}n\equiv 2\hspace{1em}\left(\mathrm{mod}4\right),\hfill \\ 3\hfill & \hfill & \text{otherwise}.\hfill \end{array}$$

Proof.

The result is immediate for n = 3, and so we assume that $n\ge 4$. If $n\equiv 0\hspace{1em}(\mathrm{mod}4)$, then by Proposition 3-(2,3) it follows that for any edge $e\in E(C_n)$, $i_{r2}(C_n-e)>i_{r2}(C_n)$ leading to $b_{ir2}(C_n)=1$. In the following, we assume that $n\cancel{\equiv }0\hspace{1em}(\mathrm{mod}4)$ and let $C_n=v_1{v}_2\dots v_n{v}_1$. Again, by Proposition 3-(2,3) we see that for any edge $e\in E(C_n)$, $i_{r2}(C_n-e)\le i_{r2}(C_n)$ and so $b_{ir2}(C_n)\ge 2$. Now, if $n\equiv 2\hspace{1em}(\mathrm{mod}4)$, then $C_n-\{v_2{v}_3,v_1{v}_n\}=P_2\cup P_{n-2}$ and Proposition 3-(2,3) yields $i_{r2}(C_n-\{v_2{v}_3,v_1{v}_n\})=2+\lceil \frac{n-1}{2}\rceil >i_{r2}(C_n)$ and so $b_{ir2}(C_n)=2$. Hence we assume that n is odd with $n\ge 5$. Since $C_n-\{v_2{v}_3,v_1{v}_n,v_4{v}_5\}=2P_2\cup P_{n-4}$, we deduce from Proposition 3-(2,3) that $i_{r2}(C_n-\{v_2{v}_3,v_1{v}_n,v_4{v}_5\})=4+\lceil \frac{n-3}{2}\rceil >i_{r2}(C_n)$ and so $b_{ir2}(C_n)\le 3$. To achieve the proof it is enough to show that $b_{ir2}(C_n)\ge 3$ when $n\equiv 1\hspace{1em}(\mathrm{mod}2)$. Hence assume that $n\equiv 1\hspace{1em}(\mathrm{mod}2)$, and let e and $e^{\prime }$ be two arbitrary edges of C_n. Clearly, $C_n-\{e,e^{\prime }\}$ is the union of two disjoint paths P and Q such that $n(P)+n(Q)=n$. Therefore $i_{r2}(C_n-\{e,e^{\prime }\})=i_{r2}(P)+i_{r2}(Q)$. Without loss of generality, we may assume that n(P) is even and thus n(Q) is odd. It follows from Proposition 3-(2) that $i_{r2}(C_n-\{e,e^{\prime }\})=i_{r2}(P)+i_{r2}(Q)=\lceil \frac{n(P)+1}{2}\rceil +\frac{n(Q)+1}{2}=\lceil \frac{n+2}{2}\rceil =i_{r2}(C_n)$ which leads to $b_{ir2}(C_n)\ge 3$, and therefore $b_{ir2}(C_n)=3$ when $n\ge 5$ and $n\equiv 1\hspace{1em}(\mathrm{mod}2)$. □

For an I2RDF f on a graph G, let $V_1=\{v:f(v)=\{1\left\}\right\}$, $V_2=\{v:f(v)=\{2\left\}\right\},V_{12}=\{v:f(v)=\{1,2\left\}\right\}$ and $V_{\varnothing }=\{v:f(v)=\varnothing \}.$ Since these four sets determine f, we can equivalently write $f=(V_{\varnothing },V_1,V_2,V_{12})$ (or $(V_{\varnothing }^f,V_1^f,V_2^f,V_{12}^f)$ to refer to f).

Proposition 7.

Let $G=K_{n_1,n_2,\dots ,n_t}$ be the complete t-partite graph with $t\ge 2$ such that $2\le n_1<n_2\le n_3\le \cdots \le n_t$. Then $b_{ir2}(G)=n_1-1$.

Proof.

Let $X_1,X_2,\dots ,X_t$ be the partite sets of G with $\left|X_i\right|=n_i$ for $1\le i\le t$. In addition, assume that $X_1=\{u_1,u_2,\dots ,u_{n_1}\}$ and $X_2=\{y_1,y_2,\dots ,y_{n_2}\}$. We note that the function h_i defined on V(G) by $h_i(u_i)=\left\{1\right\},h_i(u_j)=\left\{2\right\}$ for each $j\in \{1,2,\dots ,n_1\}-\left\{i\right\}$ and $h_i(x)=\varnothing$ for any $x\in V(G)\setminus X_1$ is an $i_{r2}(G)$-function for every $i\in \{1,\dots ,n_1\}$. Let $F=\left\{u_i{y}_1\right|1\le i\le n_1-1\}$, and let $H=G-F$. Recall that by Proposition 3-4, $i_{r2}(G)=n_1.$ We claim that $i_{r2}(H)=n_1+1>i_{r2}(G)$. To show this, let $f=(V_{\varnothing },V_1,V_2,V_{1,2})$ be an $i_{r2}(H)$-function. We consider three possible situations.

If $y_1\in V_{\varnothing }$, then either $f(u_{n_1})=\{1,2\}$ or $|f(w)|\ge 1$ for some vertex $w\in V(G)\setminus (X_1\cup X_2)$. If $f(u_{n_1})=\{1,2\}$, then the condition that $V(H)-V_{\varnothing }$ is independent implies that $V(H)-X_1\subseteq V_{\varnothing }$ and so $\{u_1,u_2,\dots ,u_{n_1-1}\}\subseteq V_1\cup V_2\cup V_{12}$. This yields to $i_{r2}(H)=\omega (f)\ge n_1+1>i_{r2}(G).$ Now assume that $|f(w)|\ge 1$ for some vertex $w\in V(G)\setminus (X_1\cup X_2)$. If, without loss of generality, $w\in X_3$, then it follows that $|f(x)|\ge 1$ for every vertex $x\in X_3$ and thus $i_{r2}(H)=\omega (f)=n_3\ge n_1+1>i_{r2}(G).$

If $y_1\in V_1$ (the case $y_1\in V_2$ is similar), then $u_{n_1}$ is assigned an empty set as well as any other vertex belonging to X_i with $i\notin \{1,2\}.$ But then we need for $u_{n_1}$ that $\{y_2,y_3,\dots ,y_{n_2}\}\cap (V_1\cup V_2\cup V_{1,2})\ne \varnothing$ and because of the condition $V_1\cup V_2\cup V_{1,2}$ is independent, we deduce that $\{y_2,y_3,\dots ,y_{n_2}\}\subseteq V_1\cup V_2\cup V_{1,2}.$ Therefore $i_{r2}(H)=\omega (f)\ge n_2>i_{r2}(G).$

Finally, assume that $y_1\in V_{1,2}$. Then as before $u_{n_1}$ is assigned an empty set as well as any other vertex belonging to X_i with $i\notin \{1,2\}.$ Since $V_1\cup V_2\cup V_{1,2}$ is independent, we must also have either $\{y_2,y_3,\dots ,y_{n_2}\}\subseteq V_1\cup V_2\cup V_{1,2}$ or $\{u_1,u_2\dots ,u_{n_1-1}\}\subseteq V_1\cup V_2\cup V_{1,2}$. In either case we obtain $i_{r2}(H)=\omega (f)\ge n_1+1>i_{r2}(G).$ Consequently, $b_{ir2}(G)\le n_1-1$.

To prove the inverse inequality, let $F\subseteq E(G)$ be an arbitrary subset of edges with $\left|F\right|<n_1-1$, and let H be the graph obtained from G by removing all edges of F. Then there are two distinct vertices u_i and u_j such that $d_H(u_i)=d_H(u_j)=n_2+n_3+\dots +n_t.$ In this case, define the function g on V(H) by $g(u_i)=\left\{1\right\},g(u_j)=\left\{2\right\}$, $\left|g(u_{\mathcal{l}})\right|=1$ for $\mathcal{l}\in \{1,\dots ,t\}-\{i,j\}$ and $g(x)=\varnothing$ otherwise. Then g is an I2RDF of H of weight n₁, implying that $b_{ir2}(G)\ge n_1-1$. Therefore $b_{ir2}(G)=n_1-1$, and the proof is complete. □

4 Bounds on $b_{ir2}(G)$

In this section, we first present an upper on the independent 2-rainbow bondage number for general graphs and then we will show that this bound is reduced to 2 for trees of order at least three.

Theorem 8.

Let G be a connected graph. If $x_1{x}_2{x}_3$ is a path of length 2 in G and G has no $i_{r2}(G)$-function assigning the set {1, 2} to some neighbor of x_i for each $i\in \{1,2,3\}$, then $$b_{ir2}(G)\le d_G(x_1)+d_G(x_2)+d_G(x_3)-3-\mathcal{l}(x_1,x_3),$$where $\mathcal{l}(x_1,x_3)=1$ if $x_1{x}_3\in E(G)$ and $\mathcal{l}(x_1,x_3)=0$ otherwise.

Proof.

Let B ⊆ E(G) be the set of all edges incident with either x₁, x₂ or x₃ except the edge $x_2{x}_3$. Obviously, $\left|B\right|=d_G(x_1)+d_G(x_2)+d_G(x_3)-3$ when $x_1{x}_3\notin E(G)$ and $\left|B\right|=d_G(x_1)+d_G(x_2)+d_G(x_3)-4$ when $x_1{x}_3\in E(G)$. Let H be the graph obtained from G by removing all edges of B. We claim that $i_{r2}(H)>i_{r2}(G),$ leading to $b_{ir2}(G)\le \left|B\right|$. Let $f=(V_{\varnothing }^f,V_1^f,V_2^f,V_{1,2}^f)$ be an $i_{r2}(H)$-function. Since x₁ is isolated in H and x₂, x₃ induce a path on two vertices in H, we have $|f(x_1)|=1$ and $f(x_2)=\{1,2\}$ or $f(x_3)=\{1,2\}$. Without loss of generality, assume that $f(x_2)=\{1,2\}$ and $f(x_3)=\varnothing$. If $d_G(x_2)=2$ or $|(V_1^f\cup V_2^f\cup V_{1,2}^f)\cap (N_G(x_2)-\left\{x_1\right\})|=0$, then the function h defined on V(G) by $h(x_1)=h(x_3)=\varnothing$ and $h(z)=f(z)$ for any other vertex z, is an I2RDF of G of weight less than $i_{r2}(H)$. Hence we assume $d_G(x_2)\ge 3$ and $|(V_1^f\cup V_2^f\cup V_{1,2}^f)\cap (N_G(x_2)-\left\{x_1\right\})|\ge 1$. We consider the following cases.

Case 1. ${\cup }_{x\in N_G(x_2)-\left\{x_1\right\}}f(x)=\{1,2\}$.

If ${\cup }_{x\in N_G(x_1)-\left\{x_2\right\}}f(x)=\{1,2\}$ and ${\cup }_{x\in N_G(x_3)-\{x_1,x_2\}}f(x)=\{1,2\}$, then the function h defined by $h(x_1)=h(x_2)=h(x_3)=\varnothing$ and $h(z)=f(z)$ for any other vertex z, is an I2RDF of G of weight less than $i_{r2}(H)$. If ${\cup }_{x\in N_G(x_1)-\left\{x_2\right\}}f(x)=\{1,2\}$ and $|{\cup }_{x\in N_G(x_3)-\{x_1,x_2\}}f(x)|=1$, then the function h defined by $h(x_1)=h(x_2)=h(x_3)=\varnothing ,h(w)=\{1,2\}$ for some vertex $w\in ((V_1^f\cup V_2^f)-\{x_1\})\cap N_G(x_3)$ and $h(z)=f(z)$ for any other vertex z, is an I2RDF of G of weight less than $i_{r2}(H)$. If ${\cup }_{x\in N_G(x_1)-\left\{x_2\right\}}f(x)=\{1,2\}$ and ${\cup }_{x\in N_G(x_3)-\{x_1,x_2\}}f(x)=\varnothing$, then the function h defined by $h(x_1)=h(x_2)=\varnothing ,h(x_3)=\left\{1\right\}$ and $h(z)=f(z)$ for any other vertex z, is an I2RDF of G of weight less than $i_{r2}(H)$. Based on the above, we can assume now that ${\cup }_{x\in N_G(x_1)-\left\{x_2\right\}}f(x)⊊\{1,2\}$. Likewise we may assume that ${\cup }_{x\in N_G(x_3)-\{x_1,x_2\}}f(x)⊊\{1,2\}$.

If $|{\cup }_{x\in N_G(x_1)-\left\{x_2\right\}}f(x)|=1$ and $|{\cup }_{x\in N_G(x_3)-\{x_1,x_2\}}f(x)|=1$, then the function h defined by $h(x_1)=h(x_2)=h(x_3)=\varnothing$, $h(u)=\{1,2\}$ for some vertex $u\in (V_1^f\cup V_2^f)\cap N_G(x_1),h(u^{\prime })=\{1,2\}$ for some vertex $u^{\prime }\in ((V_1^f\cup V_2^f)-\{x_1\})\cap N_G(x_3)$ and $h(z)=f(z)$ otherwise, is an I2RDF of G of weight less than $i_{r2}(H)$. If $|{\cup }_{x\in N_G(x_1)-\left\{x_2\right\}}f(x)|=1$ and ${\cup }_{x\in N_G(x_3)-\{x_1,x_2\}}f(x)=\varnothing$, then the function h defined by $h(x_1)=h(x_2)=\varnothing ,h(x_3)=\left\{1\right\}$, $h(u)=\{1,2\}$ for some vertex $u\in (V_1^f\cup V_2^f)\cap N_G(x_1)$ and $h(z)=f(z)$ otherwise, is an I2RDF of G of weight less than $i_{r2}(H)$. Thus we assume that ${\cup }_{x\in N_G(x_1)-\left\{x_2\right\}}f(x)=\varnothing$.

If $|{\cup }_{x\in N_G(x_3)-\{x_1,x_2\}}f(x)|=1$, then the function h defined by $h(x_2)=h(x_3)=\varnothing ,h(u)=${1, 2} for some vertex $u\in (V_1^f\cup V_2^f-\{x_1\})\cap N_G(x_3)$ and $h(z)=f(z)$ otherwise, is an I2RDF of G of weight less than $i_{r2}(H)$. If $(V_1^f\cup V_2^f)\cap N_G(x_3)=\left\{x_1\right\}$, then the function h defined by $h(x_1)=\{1,2\},h(x_2)=h(x_3)=\varnothing$ and $h(z)=f(z)$ otherwise, is an I2RDF of G of weight less than $i_{r2}(H)$.

Finally, if ${\cup }_{x\in N_G(x_1)-\left\{x_2\right\}}f(x)=\varnothing$ and ${\cup }_{x\in N_G(x_3)-\left\{x_2\right\}}f(x)=\varnothing$, then the function h defined by $h(x_3)=\left\{1\right\},h(x_2)=\varnothing$ and $h(z)=h(z)$ for the remaining vertices, is an I2RDF of G of weight less than $i_{r2}(H)$. In any situation previously considered we have shown that $i_{r2}(H)>i_{r2}(G)$.

Case 2. ${\cup }_{x\in N_G(x_2)-\left\{x_1\right\}}f(x)=\left\{1\right\}$ (the case ${\cup }_{x\in N_G(x_2)-\left\{x_1\right\}}f(x)=\left\{2\right\}$ is similar).

Let $y\in V_1^f\cap (N_G(x_2)-\{x_1\})$. If ${\cup }_{u\in N_G(x_1)-\left\{x_2\right\}}f(u)=\{1,2\}$ and ${\cup }_{u\in N_G(x_3)-\{x_1,x_2\}}f(u)=\{1,2\}$, then the function h defined by $h(y)=\{1,2\},f(x_1)=f(x_2)=f(x_3)=\varnothing$ and $h(z)=f(z)$ for any other vertex z, is an I2RDF of G of weight less than $i_{r2}(H)$. If ${\cup }_{x\in N_G(x_1)-\left\{x_2\right\}}f(x)=\{1,2\}$ and $|{\cup }_{x\in N_G(x_3)-\{x_1,x_2\}}f(x)|=1$, then the function h defined by $h(x_1)=h(x_2)=h(x_3)=\varnothing ,h(y)=\{1,2\},h(w)=\{1,2\}$ for some vertex $w\in ((V_1^f\cup V_2^f)-\{x_1\})\cap N_G(x_3)$ and $h(z)=f(z)$ for any other vertex z, is an I2RDF of G of weight less than $i_{r2}(H)$. If ${\cup }_{x\in N_G(x_1)-\left\{x_2\right\}}f(x)=\{1,2\}$ and ${\cup }_{x\in N_G(x_3)-\{x_1,x_2\}}f(x)=\varnothing$, then the function h defined by $h(x_1)=h(x_2)=\varnothing ,h(x_3)=\left\{1\right\},h(y)=\{1,2\}$ and $h(z)=f(z)$ for any other vertex z, is an I2RDF of G of weight less than $i_{r2}(H)$. Based on the above, we can assume now that ${\cup }_{x\in N_G(x_1)-\left\{x_2\right\}}f(x)⊊\{1,2\}$. If $|{\cup }_{u\in N_G(x_1)-\left\{x_2\right\}}f(u)|=1$ and ${\cup }_{u\in N_G(x_3)-\{x_1,x_2\}}f(u)=\{1,2\}$, then the function h defined by $h(x_1)=h(x_2)=h(x_3)=\varnothing ,f(y)=\{1,2\},f(w)=\{1,2\}$ for some vertex $w\in (V_1^f\cup V_2^f)\cap N_G(x_1)$ and $h(z)=f(z)$ otherwise, is an I2RDF of G of weight less than $i_{r2}(H)$. If $|{\cup }_{u\in N_G(x_1)-\left\{x_2\right\}}f(u)|=1$ and $|{\cup }_{u\in N_G(x_3)-\{x_1,x_2\}}f(u)|=1$, then the function h defined by $h(x_1)=h(x_2)=h(x_3)=\varnothing ,h(y)=\{1,2\},h(u)=\{1,2\}$ for some vertex $u\in (V_1^f\cup V_2^f)\cap N_G(x_1),h(u^{\prime })=\{1,2\}$ for some vertex $u^{\prime }\in (V_1^f\cup V_2^f)\cap (N_G(x_3)-\{x_1\})$ and $h(z)=f(z)$ otherwise, is an I2RDF of G of weight $\omega (f)=i_{r2}(H)$ which assigns the set {1, 2} to some neighbor of x_i for each $i\in \{1,2,3\}$, leading by assumption to $i_{r2}(H)=\omega (h)>i_{r2}(G)$. If $|{\cup }_{u\in N_G(x_1)-\left\{x_2\right\}}f(u)|=1$ and $|{\cup }_{u\in N_G(x_3)-\{x_1,x_2\}}f(u)|=0$, then the function h defined by $h(x_1)=h(x_2)=\varnothing ,h(x_3)=\left\{2\right\},h(u)=\{1,2\}$ for some vertex $u\in (V_1^f\cup V_2^f)\cap N_G(x_1)$ and $h(z)=f(z)$ otherwise, is an I2RDF of G of weight less than $i_{r2}(H)$. Hence, we assume that ${\cup }_{u\in N_G(x_1)-\left\{x_2\right\}}f(u)=\varnothing$.

If $\underset{u\in N_G(x_3)-\{x_1,x_2\}}{\cup }f(u)=\{1,2\}$, then the function h defined by $h(x_2)=h(x_3)=\varnothing ,h(x_1)=\left\{2\right\}$, and $h(z)=f(z)$ otherwise, is an I2RDF of G of weight less than $i_{r2}(H)$. If $|{\cup }_{u\in N_G(x_3)-\{x_1,x_2\}}f(u)|=1$, then the function h defined by $h(x_1)=\left\{2\right\}$, $h(x_2)=h(x_3)=\varnothing ,h(u)=\{1,2\}$ for some vertex $u\in (V_1^f\cup V_2^f)\cap N_G(x_3)-\{x_1,x_2\}$ and $h(z)=f(z)$ otherwise, is an I2RDF of G of weight less than $i_{r2}(H)$. If $(V_1^f\cup V_2^f)\cap N_G(x_3)=\left\{x_1\right\}$, then the function h defined by $h(x_1)=\{1,2\},h(x_2)=h(x_3)=\varnothing$ and $h(z)=f(z)$ otherwise, is an I2RDF of G of weight less than $i_{r2}(H)$. Finally, if $|\underset{u\in N_G(x_3)-\{x_1,x_2\}}{\cup }f(u)|=0$, then the function h defined by $h(x_1)=h(x_3)=\left\{2\right\}$, $h(x_2)=\varnothing$ and $h(z)=f(z)$ otherwise, is an I2RDF of G of weight less than $i_{r2}(H)$. In any case considered above we have shown that $i_{r2}(H)>i_{r2}(G)$ which completes the proof. □

Theorem 8 and its proof result the following corollary.

Corollary 9.

Let G be a connected graph. If $x_1{x}_2{x}_3$ is a path of length 2 in G with $d_G(x_1)=1$, then $$b_{ir2}(G)\le d_G(x_2)+d_G(x_3)-2.$$

Proof.

Let f be an $i_{r2}(G)$-function. If $|f(x_2)|=2$, then we must have $f(x)=\varnothing$ for each $x\in N_G(x_2)$, that is f does not assign the set {1, 2} to no neighbor of x₂. On the other hand, if $f(x_2)=\varnothing$, then f does not assign the set {1, 2} to no neighbor of x₁. Hence G satisfies the condition specified in the statement of Theorem 8, and consequently, $b_{ir2}(G)\le d_G(x_1)+d_G(x_2)+d_G(x_3)-3=d_G(x_2)+d_G(x_3)-2$. Thus our corollary is proved. □

A similar argument to that used in the proof of Corollary 9 leads to another consequence of Theorem 8.

Corollary 10.

Let G be a connected graph. If $x_1{x}_2{x}_3$ is a path of length 2 in G with $d_G(x_2)=2$, then $$b_{ir2}(G)\le 2\Delta -1.$$

Dehgardi et al. [7] showed that for any tree T of order at least 3, $b_{r2}(T)\le 2$. The next result shows that this upper bound remains valid for the independent 2-rainbow bondage number. However, unlike the proof given in [7] for $b_{r2}(T),$ the proof for $b_{ir2}(T)$ is quite long where several cases are discussed. Before presenting the result, we give some additional definitions and notations. A path joining two vertices x and y is called a (x, y)-path. The $\mathit{diameter}$ of a connected graph G, denoted diam(G), is the length of the shortest path between the most distanced vertices. A diametral path of a graph G is a shortest path whose length is equal to diam $(G).$ We are also considering rooted trees distinguished by one vertex r called the root. For a vertex $v\ne r$ in a rooted tree T, the parent of v is the neighbor of v on the unique (r, v)-path, while a child of v is any other neighbor of v. A descendant of v is a vertex $w\ne v$ such that the unique(r, w)-path contains v. The set of children of a vertex v is denoted by C(v) while D(v) denotes the set of its descendants. The maximal subtree at v denoted by T_v is the subtree of T induced by v and all its descendants. The depth of v is the largest distance from v to a descendant of v.

Theorem 11.

If T is a tree of order $n\ge 3$, then $$b_{ir2}(T)\le 2.$$Furthermore, this bound is sharp for double star $D{S}_{p,p}$ for $p\ge 2$.

Proof.

Obviously diam $(T)\ge 2$, since $n\ge 3.$ If diam $(T)=2$, then T is a star and for any edge e of T we have $i_{r2}(T-e)=3>i_{r2}(T)=2$ yielding $b_{ir2}(T)=1$. Hence assume that diam $(T)\ge 3,$ and let $x_1{x}_2\dots x_k(k\ge 4)$ be a diametral path in T chosen such that: (i) $d_T(x_2)$ is as large as possible, and (ii) subject to (i) $d_T(x_3)$ is maximized. If $\text{diam}(T)=3$, then T is a double star $D{S}_{p,q}$ for some integers $q\ge p\ge 1$. If p = 1, then $i_{r2}(T-x_2{x}_3)=4>i_{r2}(T)=3$ and thus $b_{ir2}(T)=1.$ Now, if $p\ge 2$, then removing edges $x_1{x}_2$ and $x_3{x}_4$ provides a forest F with three components, two of which are single vertices and the third one is a double star $D{S}_{p-1,q-1}.$ In this case, $i_{r2}(F)=2+(2+(p-1))=3+p>i_{r2}(T)=2+p$ yielding $b_{ir2}(T)\le 2$. In the sequel we may assume that $\text{diam}(T)\ge 4$, and so $k\ge 5$. Root T at $x_k.$

If $d_T(x_3)=2$, then let F be the forest obtained from T by removing edges $x_3{x}_4$ and $x_3{x}_2.$ Clearly any $i_{r2}(F)$-function f such that $|f(x_2)|$ is maximized, assigns {1} or {2} to x₃ and {1, 2} to x₂, and the function h defined on V(T) by $h(x_3)=\varnothing$ and $h(x)=f(x)$ otherwise, is an I2RDF of T of weight less than $\omega (f)$ and thus $b_{ir2}(T)\le 2$. Therefore we may assume that $d_T(x_3)\ge 3$. Similarly, we can assume that each child of x₄ with depth 2 has degree at least 3. Let $N_T(x_3)-\{x_2,x_4\}=\{y_1,\dots ,y_{\mathcal{l}}\}$. We proceed with the following cases.

Case 1. $d_T(x_2)=3$.

Let w be a leaf neighbor of x₂ different from x₁ and let F be the forest obtained from T by removing edges $x_2{x}_1$ and $x_3{x}_2$. Let f be an $i_{r2}(F)$-function. Since x₁ is isolated in F and vertices $x_2$, w induce a P₂ component in F, we must have $|f(x_1)|=1$ and either $f(x_2)=\{1,2\}$ or $f(w)=\{1,2\}$, say $f(w)=\{1,2\}$ and thus $f(x_2)=\varnothing$. Now the function g defined on V(T) by $g(w)=\{1,2\}-f(x_1)$ and $g(x)=f(x)$ otherwise, is an I2RDF of T of weight less than $\omega (f),$ leading to the desired result.

Case 2. $d_T(x_2)\ge 4$ and x₃ has a child of degree 2.

Without loss of generality, let y₁ be a child of x₃ with degree two and let $y_1^{\prime }$ be the leaf neighbor of $y_1.$ Let F be the forest obtained from T by removing edges $x_2{x}_1$ and $x_3{y}_1$. Let f be an $i_{r2}(F)$-function such that $f(x_2)$ is as large as possible. Since x₁ is isolated in F and vertices y₁, $y_1^{\prime }$ induce a P₂ component of F, we must have $|f(x_1)|=1$ and either $f(y_1)=\{1,2\}$ or $f(y_1^{\prime })=\{1,2\}$, say $f(y_1^{\prime })=\{1,2\}$ and thus $f(y_1)=\varnothing$. Now, if $|f(x_3)|\ge 1$, say $2\in f(x_3),$ then the function g defined on V(T) by $g(y_1^{\prime })=\left\{1\right\}$ and $g(x)=f(x)$ otherwise, is an I2RDF of T of weight less than $\omega (f)$. Hence assume that $f(x_3)=\varnothing$. Since x₂ has at least two leaf neighbors in F, by the choice of f we have $f(x_2)=\{1,2\}$ and thus the function g defined on V(T) by $g(x_1)=\varnothing$ and $g(x)=f(x)$ otherwise, is an I2RDF of T of weight less than $\omega (f)$. In either case, $b_{ir2}(T)\le 2.$

Case 3. $d_T(x_2)\ge 4$ and x₃ is a support vertex.

Considering Cases 1 and 2 we may assume that each child of x₃ is either a leaf or has degree at least four. Without loss of generality, let y₁ be a leaf neighbor of x₃. Let F be the forest obtained from T by removing edges $x_1{x}_2$ and $x_3{y}_1,$ and let f be an $i_{r2}(F)$-function. Since x₁ and y₁ are isolated in F, we have $|f(x_1)|=|f(y_1)|=1$. Now, if $f(x_2)=\{1,2\}$, then $f(x_3)=\varnothing$ and the function g defined on V(T) by $g(x_1)=\varnothing$ and $g(x)=f(x)$ for the remaining vertices, is an I2RDF of T of weight less than $\omega (f)$. If $f(x_3)=\{1,2\}$, then $f(x_2)=\varnothing$ and the function g defined on V(T) by $g(y_1)=\varnothing$ and $g(x)=f(x)$ otherwise, is an I2RDF of T of weight less than $\omega (f),$ and both situations lead to $b_{ir2}(T)\le 2$. Hence we can assume that $|f(x_2)|\le 1$ and $|f(x_3)|\le 1$. Then all leaves adjacent to x₂ in F must be assigned non-empty sets under f, and this case it is clear that $f(x_2)=\varnothing$. If $f(x_3)=\varnothing$, then the function g defined on V(T) by $g(x)=\varnothing$ for $x\in N_T(x_2)$, $g(x_2)=\{1,2\}$ and $g(x)=f(x)$ for the remaining vertices, is an I2RDF of T of weight less than $\omega (f)$ and thus $b_{ir2}(T)\le 2$. Hence assume that $|f(x_3)|=1$. Then $f(x_4)=\varnothing$ and y₁ is the only leaf adjacent to x₃. Thus x₄ has a neighbor $w\ne x_3$ such that $f(w)|\ge 1$. Now the function g defined on V(T) by $g(w)=\{1,2\}$, $g(x_3)=\varnothing ,g(x_2)=\{1,2\},g(x)=\varnothing$ for $x\in N_T(x_2)-\left\{x_3\right\}$ and $g(x)=f(x)$ for the remaining vertices, is an I2RDF of T of weight less than $\omega (f)$ and thus $b_{ir2}(T)\le 2$.

Case 4. $d_T(x_2)\ge 4$ and any child of x₃ has degree at least 4.

According to the above cases, every y_i has at least three leaf neighbors, say $y_i^1,$ $y_i^2,$ $y_i^3$. Let F be the forest obtained from T by removing edges $x_2{x}_1$ and $y_1{y}_1^1$ and let $f=(V_0,V_1,V_2)$ be an $i_{r2}(F)$-function such that $f(x_2)+f(y_1)$ is as large as possible. Since x₁ and $y_1^1$ are isolated in F we have $|f(x_1)|=|f(y_1^1)|=1.$ Note that since x₂ and y₁ remains support vertices in F, each with at least two leaf neighbors, these two vertices will be assigned either {1, 2} or $\varnothing$ under f. Now, if $f(x_2)=f(y_1)=\{1,2\}$, then the function g defined on V(T) by $g(x_1)=g(y_1^1)=\varnothing$ and $g(x)=f(x)$ otherwise, is an I2RDF of T of $\omega (f)-2$. Also, if $f(x_2)=\{1,2\}$ and $f(y_1)=\varnothing$ (the case $f(x_2)=\varnothing$ and $f(y_1)=\{1,2\}$ is similar), then the function g defined on V(T) by $g(x_1)=\varnothing$ and $g(x)=f(x)$ otherwise, is an I2RDF of T of weight less than $\omega (f)-1$. Finally, we assume that $f(x_2)=\varnothing$ and $f(y_1)=\varnothing$. The choice of f implies that $|f(x_3)|\ge 1$. It follows that $f(y_i)=\varnothing$ for each $i\in \{1,\dots ,\mathcal{l}\},$ $N_T(x_2)-\left\{x_3\right\}\subseteq V_1\cup V_2$ and $N_T(y_i)-\left\{x_3\right\}\subseteq V_1\cup V_2$ for each $i\in \{1,\dots ,\mathcal{l}\}$. If $(N_T(x_4)-\{x_3\})\cap V_{12}\ne \varnothing$, then the function g defined on V(T) by $g(x_3)=\varnothing ,g(x_2)=g(y_i)=\{1,2\}$ for all $i\in \{1,\dots ,\mathcal{l}\},g(x)=\varnothing$ for $x\in L(x_2)\cup ({\cup }_{i=1}^{\mathcal{l}}L(y_i))$ and $g(x)=f(x)$ otherwise, is an I2RDF of T of weight less than $\omega (f)$. Therefore we may assume that $(N_T(x_4)-\{x_3\})\cap V_{12}=\varnothing$. If $(N_T(x_4)-\{x_3\})\cap V_1\ne \varnothing$ (the case $(N_T(x_4)-\{x_3\})\cap V_2\ne \varnothing$ is similar), say $w\in (N_T(x_4)-\{x_3\})\cap V_1$, then the function g defined on V(T) by $g(w)=\{1,2\},g(x_3)=\varnothing ,g(x_2)=g(y_i)=\{1,2\}$ for all $i\in \{1,\dots ,\mathcal{l}\}$, $g(x)=\varnothing$ for $x\in L(x_2)\cup ({\cup }_{i=1}^{\mathcal{l}}L(y_i))$ and $g(x)=f(x)$ otherwise, is an I2RDF of T of weight less than $\omega (f)$. Hence let $(N(x_4)-\{x_3\})\cap V_1=\varnothing$ and $(N(x_4)-\{x_3\})\cap V_2=\varnothing$. In this case, define an I2RDF g on V(T) by $g(x_4)=\left\{1\right\},g(x_3)=\varnothing ,g(x_2)=g(y_i)=\{1,2\}$ for all $i\in \{1,\dots ,\mathcal{l}\},g(x)=\varnothing$ for $x\in L(x_2)\cup ({\cup }_{i=1}^{\mathcal{l}}L(y_i))$ and $g(x)=f(x)$ otherwise. Clearly, g is an I2RDF of T of weight less than $\omega (f).$ In either case, we have shown that $i_{r2}(T)<i_{r2}(F)$ and thus $b_{ir2}(T)\le 2.$

Case 5. $d_T(x_2)=2$.

It follows from the choice of the diametral path that each child of x₃ with depth one has degree 2. Thus the maximal subtree rooted at x₃ is a spider. Similarly, we may assume that the maximal subtree rooted at any child of x₄ with depth 2 is a spider. Let us examine the following situations.

Subcase 5.1. $d_T(x_3)=3$ and x₃ has a leaf neighbor.

Let y₁ be the leaf neighbor of x₃ and let F be the forest obtained from T by removing edges $x_3{x}_2,x_3{x}_4.$ Let f be an $i_{r2}(F)$-function such that $|f(x_2)|+|f(y_1)|$ is maximized. Since x₃, y₁ induce a P₂ component of F and the same for x₁ and x₂, by the choice of f we have $f(x_2)=f(y_1)=\{1,2\}$. In this case, the function g defined on V(T) by $g(y_1)=\left\{1\right\}$ and $g(x)=f(x)$ otherwise, is an I2RDF of T of weight $i_{r2}(F)-1,$ implying that $b_{ir2}(T)\le 2.$

By Subcase 5.1, we may assume that $d_T(x_3)\ge 4$ or $d_T(x_3)=3$ and x₃ has two children with depth 1 and degree 2.

Subcase 5.2. $d_T(x_4)=2$.

Let F be the forest obtained from T by removing edges $x_3{x}_2,x_4{x}_5,$ and let f be an $i_{r2}(F)$-function such that $|f(x_3)|$ is maximized. Clearly $\left|f(x_1)\right|+\left|f(x_2)\right|=2$ and by the choice of f we must have $|f(x_3)|\ge 1$. Without loss of generality, assume that $1\in f(x_3)$, and consider the function g defined on V(T) by $g(x_2)=\varnothing$ and $g(x_1)=\left\{2\right\}$ and $g(x)=f(x)$ otherwise. Then g is an I2RDF of T of weight $i_{r2}(F)-1,$ yielding $b_{ir2}(T)\le 2.$

Subcase 5.3. $d_T(x_4)\ge 3$ and x₄ has a child w of degree two which is a support vertex.

Let $w^{\prime }$ be a leaf neighbor of w and consider the forest F obtained from T by removing edges $w{x}_4,x_3{x}_2$. Let f be an $i_{r2}$-function of F such that $|f(x_1)|+|f(w^{\prime })|$ is maximized. Then we must have $f(x_1)=f(w^{\prime })=\{1,2\}$. Now if $|f(x_4)|\ge 1$ and $1\in f(x_4)$ (the case $2\in f(x_4)$ is similar), then reassigning the set {2} to $w^{\prime }$ provides an I2RDF T of weight smaller than $i_{r2}(F)$. Likewise, if $|f(x_3)|\ge 1$ and $1\in f(x_3)$ (the case $2\in f(x_3)$ is similar), then reassigning the set {2} to x₁ provides an I2RDF of T of weight smaller than $i_{r2}(F)$. Hence we can assume that $f(x_4)=f(x_3)=\varnothing$. Thus the function g defined on V(T) by $g(x_3)=\left\{1\right\},g(x)=\varnothing$ for $x\in N_T(x_3),g(x)=\left\{2\right\}$ for $x\in D(x_3)-C(x_3)$ and $g(x)=f(x)$ otherwise, when x₃ is not a support vertex, and by $g(x_3)=\{1,2\},g(x)=\varnothing$ for $x\in N_T(x_3),g(x)=\left\{1\right\}$ for $x\in D(x_3)-C(x_3)$ and $g(x)=f(x)$ otherwise, when x₃ is a support vertex, is an I2RDF of T of weight less than $\omega (f)$, and therefore in any case $b_{ir2}(T)\le 2$.

Subcase 5.4. $d_T(x_4)\ge 3$ and v₄ is a support vertex.

Let w be a leaf neighbor of x₄ and consider the forest F obtained from T by removing edges $w{x}_4,x_3{x}_2$. Let f be an $i_{r2}(F)$-function such that $|f(x_1)|$ is maximized. Obviously, $|f(w)|=1$ and $f(x_1)=\{1,2\}$. Now if $f(x_4)=\{1,2\}$, then reassigning an empty set to w we get an I2RDF T of weight $i_{r2}(F)-1$. Hence let $|f(x_4)|\le 1$. If $|f(x_3)|\ge 1$ and $1\in f(x_3)$, then reassigning the set {2} to x₁ provides again an I2RDF of T of weight $i_{r2}(F)-1$. Hence we assume that $|f(x_4)|\le 1$ and $f(x_3)=\varnothing$. Then $\left|f(z)\right|=1$ for each leaf neighbor z of x₃ and $f(a)+f(a^{\prime })=2$ for each child a of x₃ with depth 1 and degree 2, where $a^{\prime }$ is the leaf adjacent to a. If $f(x_4)=\varnothing$, then define the function g on V(T) by $g(x_3)=\{1,2\}$, $g(x)=\varnothing$ for $x\in N(v_3),g(x)=\left\{1\right\}$ for $x\in D(x_3)-C(x_3)$ and $g(x)=f(x)$ otherwise, when x₃ is a support vertex, and $g(x_3)=\left\{1\right\},g(x)=\varnothing$ for $x\in N(v_3),g(x)=\left\{2\right\}$ for $x\in D(x_3)-C(x_3)$ and $g(x)=f(x)$ otherwise when x₃ is not a support vertex. Clearly since by assumption $d_T(x_3)\ge 4$ or $d_T(x_3)=3$ and x₃ is not a support vertex, the function g is an I2RDF of T of weight less than $i_{r2}(F).$ Finally we can assume that $|f(x_4)|=1,$ say $f(x_4)=\left\{1\right\}$. Then w is the only leaf neighbor of x₄. Also by considering Subcase 5.3, we may assume that any child of x₄ with depth 1 has degree at least three. On the other hand, we may assume that the maximal subtree rooted at each child of x₄ with depth 2 is either a P₅ whose center vertex is adjacent to x₄ or a spider with maximum degree at least three. Thus f can be chosen such that each child of x₄ with depth 2 is 2-rainbow dominated by its children. Now, if x₅ has a neighbor in $V_{1,2}$, then define the function g on V(T) by $g(x_4)=\varnothing$, $g(x_3)=\{1,2\},g(x)=\varnothing$ for $x\in N(v_3),g(x)=\left\{1\right\}$ for $x\in D(x_3)-C(x_3)$ and $g(x)=f(x)$ otherwise when x₃ is a support vertex, and $g(x_3)=\left\{1\right\},g(x)=\varnothing$ for $x\in N(v_3)$, $g(x)=\left\{2\right\}$ for $x\in D(x_3)-C(x_3)$ and $g(x)=f(x)$ otherwise, when x₃ is not a support vertex. Clearly whatever the case, g is an I2RDF of T of weight less than $i_{r2}(F).$ Hence we can assume that x₅ has a neighbor z in $(V_1\cup V_2)-\left\{x_4\right\}$. Define the function g on V(T) by $g(z)=\{1,2\},g(x_4)=\varnothing ,g(x_3)=\{1,2\}$, $g(x)=\varnothing$ for $x\in N(v_3),g(x)=\left\{1\right\}$ for $x\in D(x_3)-C(x_3)$ and $g(x)=f(x)$ otherwise when x₃ is a support vertex, and $g(x_3)=\left\{1\right\},g(x)=\varnothing$ for $x\in N(v_3),g(x)=\left\{2\right\}$ for $x\in D(x_3)-C(x_3)$ and $g(x)=f(x)$ otherwise, when x₃ is not a support vertex. Again whatever the case, g is an I2RDF of T of weight less than $i_{r2}(F).$ In any case seen before, we conclude that $b_{ir2}(T)\le 2.$

By Subcases 5.1, 5.2, 5.3, and 5.4 we may assume that the maximal subtree at each child of x₄ (which is also the center vertex of such a subtree) is either a star of order at least three or a path P₅ or a spider with maximum degree at least 3. Consider the forest F obtained from T by removing edges $x_3{x}_2$ and let f be an $i_{r2}(F)$-function such that each child of x₄ is either assigned a non-empty set under f or 2-rainbowly dominated by its neighbors. Clearly $\left|f(x_1)\right|+\left|f(x_2)\right|=2$. If $|f(x_3)|\ge 1$ and $1\in f(x_3)$, then the function g defined on V(T) by $g(x_1)=\left\{2\right\}$, $g(x_2)=\varnothing$ and $g(x)=f(x)$ otherwise, is an I2RDF of T of weight less than $\omega (f)$. Hence we assume that $f(x_3)=\varnothing$. If $f(x_4)=\varnothing$, then the function g on V(T) by $g(x_3)=\{1,2\}$, $g(x)=\varnothing$ for $x\in N(v_3),g(x)=\left\{1\right\}$ for $x\in D(x_3)-C(x_3)$ and $g(x)=f(x)$ otherwise, when x₃ is a support vertex, and $g(x_3)=\left\{1\right\},g(x)=\varnothing$ for $x\in N(v_3)$, $g(x)=\left\{2\right\}$ for $x\in D(x_3)-C(x_3)$ and $g(x)=f(x)$ otherwise, when x₃ is not a support vertex, is an I2RDF of T of weight less than $i_{r2}(F).$ Hence we can assume that $|f(x_4)|\ge 1$. If x₅ has a neighbor in $V_{1,2}$, then define the function g defined on V(T) by $g(x_4)=\varnothing ,g(u)=\{1,2\}$ for each $u\in C(x_4),g(x)=\varnothing$ for $x\in {\cup }_{u\in C(x_4)}{N}_T(u),g(x)=\left\{1\right\}$ for $x\in {\cup }_{u\in C(x_4)}(D(u)-C(u))$ and $g(x)=f(x)$ otherwise, is an I2RD-function of T of weight less than $i_{r2}(F).$ Finally, suppose that x₅ has a neighbor z in $(V_1\cup V_2)-\left\{x_4\right\}$. Define the function g on V(T) by $g(z)=\{1,2\}$, $g(x_4)=\varnothing ,g(x_3)=\{1,2\},g(x)=\varnothing$ for $x\in N(v_3),g(x)=\left\{1\right\}$ for $x\in D(x_3)-C(x_3)$ and $g(x)=f(x)$ otherwise when x₃ is a support vertex, and $g(x_3)=\left\{1\right\},g(x)=\varnothing$ for $x\in N(v_3),g(x)=\left\{2\right\}$ for $x\in D(x_3)-C(x_3)$ and $g(x)=f(x)$ otherwise, when x₃ is not a support vertex. Clearly, whatever the case, g is an I2RDF of T of weight less than $i_{r2}(F).$ Therefore in either case we have $b_{ir2}(T)\le 2,$ and the proof is complete. □

Disclosure statement

The authors declare that they have no conflict of interest.

Data availability statement

Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.

Additional information

Funding

This research was financially supported by fund from Hubei Province Key Laboratory of Intelligent Information Processing and Real-time Industrial System (Wuhan University of Science and Technology) (under grant 622274).