Euler dynamic H-trails in edge-colored graphs

Abstract

Alternating Euler trails has been extensively studied for its diverse practical and theoretical applications. Let H be a graph possibly with loops and G be a multigraph without loops. In this paper we deal with any fixed coloration of E(G) with V(H) (H-coloring of G). A sequence $W=(v_0,e_0^1,\dots ,e_0^{k_0},v_1,e_1^1,\dots ,e_{n-1}^{k_{n-1}},v_n)$ in G, where for each $i\in \{0,\dots ,n-1\},k_i\ge 1$ and $e_i^j=v_i{v}_{i+1}$ is an edge in G, for every $j\in \{1,\dots ,k_i\}$, is a dynamic H-trail if W does not repeat edges and $c(e_i^{k_i})c(e_{i+1}^1)$ is an edge in H, for each $i\in \{0,\dots ,n-2\}$. In particular, a dynamic H-trail is an alternating trail when H is a complete graph without loops and k_i = 1, for every $i\in \{1,\dots ,n-1\}$. In this paper, we introduce the concept of dynamic H-trail, which arises in a natural way in the modeling of many practical problems, in particular, in theoretical computer science.

We provide necessary and sufficient conditions for the existence of closed Euler dynamic H-trail in H-colored multigraphs. Also we provide polynomial time algorithms that allows us to convert a cycle in an auxiliary graph, $L_2^H(G)$, in a closed dynamic H-trail in G, and vice versa, where $L_2^H(G)$ is a non-colored simple graph obtained from G in a polynomial time.

Keywords:

• Edge colored graph
• dynamic H-trail
• Euler dynamic H-trails
• Hamiltonian cycles

1 Introduction

For basic concepts, terminology and notation not defined here, we refer the reader to [3] and [5]. Throughout this work, we will consider graphs, multigraphs (graphs allowing parallel edges) and simple graphs (graphs with no parallel edges nor loops). Let V(G) and E(G) the sets of vertices and edges of a multigraph G, respectively.

A spanning circuit in a graph G is defined as a closed trail that contains each vertex of G. We will say that a graph is supereulerian if it contains a spanning circuit. Let T be a spanning circuit in G: if T visits each vertex of G exactly once, then T will be called Hamilton cycle; and if T visits each edge of G, then T will be called Euler trail. We will say that a graph is hamiltonian if it has a Hamilton cycle and eulerian if it contains an Euler trail.

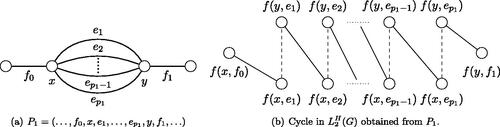
In [15], Harary and Nash-Williams introduced the following graphs. Let G be a graph with p vertices and q edges. For $n\ge 2$, let $L_n(G)$ the graph with nq vertices that are obtained as follows: for each edge e = uv of G, we take two vertices f(u, e) and f(v, e) in $L_n(G)$ and adding a path with n – 2 new intermediate vertices connecting f(u, e) and f(v, e); finally, for each vertex u of G, we add an edge joining f(u, e) and f(u, g), whenever e and g are distinct edges with end point u. They also proved the followings relationships between eulerian graphs and hamiltonian cycles of $L_n(G)$.

Theorem 1

(Harary and Nash-Williams [15]). Let G be a graph. The following assertions holds:

1. If G is eulerian, then $L_n(G)$ is hamiltonian, for every $n\ge 2$.

2. If $L_n(G)$ is hamiltonian, for some $n\ge 3$, then G is eulerian.

3. G is superulerian if and only if $L_2(G)$ is hamiltonian.

An edge-coloring of a graph G is defined as a mapping $c:E(G)\to \mathbb{N}$, where $\mathbb{N}$ is the set of natural numbers. We will say that G is an edge-colored graph whenever we are taking a fixed edge-coloring of G. A properly colored spanning circuit is a spanning circuit with no consecutive edges having the same color, including the first and the last in a closed spanning circuit. An edge-colored graph is supereulerian, if G contains a properly colored spanning circuit. Several authors have worked with this concept, for example, Bang-Jensen et al. [2]; Guo et al. [13]; Guo et al. [14]. Properly colored walks are of interest as a generalization of walk in undirected and directed graphs, see [3], as well as, in graph theory application, for example, in genetic and molecular biology [9, 10, 20], social science [6], channel assignment is wireless networks [1, 18]. For more details on properly colored walks, we refer the reader to Chapter 16 of [3].

Kotzig [16] gave the following characterization of edge-colored multigraphs containing properly colored closed Euler trail.

Theorem 2

(Kotzig [16]). Let G be an edge-colored eulerian multigraph. Then G has a properly colored closed Euler trail if and only if ${\delta }_i(x)\le \sum _{j\ne i}{\delta }_j(x)$, where ${\delta }_i(x)$ is the number of edges with color i incident with x, for each vertex x of G.

Different kinds of edge-coloring in undirected and directed graphs have been studied, for example, in [17] the arcs of a tournament were colored with the vertices of a poset. In this paper we will consider the following edge-coloring. Let H be a graph possibly with loops and G be a graph without loops. An H-coloring of G is a function $c:E(G)\to V(H)$. We will say that G is an H-colored graph, whenever we are taking a fixed H-coloring of G. A walk $W=(v_0,e_0,v_1,e_1,v_2,\dots ,v_{k-1},e_{k-1},v_k)$ in G, where $e_i=v_i{v}_{i+1}$ for every i in $\{0,\dots ,k-1\}$, is an H-walk if $(c(e_0),a_0,c(e_1),\dots ,c(e_{k-2}),a_{k-2},c(e_{k-1}))$ is a walk in H, with $a_i=c(e_i)c(e_{i+1})$ for every $i\in \{0,\dots ,k-2\}$. We will say that W is closed if $v_0=v_k$ and $c(e_{k-1})c(e_0)\in E(H)$. Let W be an H-walk, if W is a trail then W will be called H-trail. Notice that if H is a complete graph without loops, then an H-walk is a properly colored walk.

Since, properly colored walks have been very useful for modeling and solving different problems, as we mentioned above, H-colored graphs and H-walks can also model interesting problems, for example, routing problems or in communications networks were some transitions are restricted because of natural phenomenon, external attack or failure. More applications of colored walks with restrictions in color’s succession can be found in [19].

The concepts of H-coloring and H-walks were introduced, for the first time by Linek and Sands in [17], and have been worked mainly in the context of kernel theory and related topics, see [7, 8, 12].

Galeana-Sánchez et al. [11] defined the graph G_u as follows: Let u be a vertex of G; G_u is the graph such that $V(G_u)=\{e\in E(G):e\text{isincidentwith}u\}$, and two different vertices a and b are joining by only one edge in G_u if and only if c(a) and c(b) are adjacent in H.

They also showed necessary and sufficient conditions for the existence of closed Euler H-trails, as follows.

Theorem 3

(Galeana-Sánchez et al. [11]). Let H be a graph possibly with loops and G be an H-colored multigraph without loops. Suppose that G is Eulerian and G_u is a complete k_u -partite graph, for every u in V(G) and for some k_u in $\mathbb{N}$. Then G has a closed Euler H-trail if and only if $\left|C_i^u\right|\le \sum _{j\ne i}\left|C_j^u\right|$ for every u in V(G), where $\{C_1^u,\dots ,C_{k_u}^u\}$ is the partition of $V(G_u)$ into independent sets.

Benítez-Bobadilla et al. [4] introduced a generalization of H-walk as follows. They allowed “lane changes”, i.e., they allowed concatenation of two H-walks as long as, the last edge of the first one and the first edge of the second one satisfy that $x_{k-1}=y_0$ and $x_k=y_1$. As a result, they defined the following new concept: Let G be an H-colored multigraph, a dynamic H-walk in G is a sequence of vertices $W=(x_0,x_1,\dots ,x_k)$ in G such that for each $i\in \{0,\dots ,k-2\}$ there exists an edge $f_i=x_i{x}_{i+1}$ and there exists an edge $f_{i+1}=x_{i+1}{x}_{i+2}$ such that $c(f_i)c(f_{i+1})$ is an edge in H.

For the purpose of this paper, we need a definition and notation that will allows us to know the edges that belong to a dynamic H-walk. So, we will say that $W=(v_0,e_0^1,\dots ,e_0^{k_0},v_1,e_1^1,\dots ,e_1^{k_1},v_2,\dots ,v_{n-1},e_{n-1}^{k_{n-1}},\dots ,e_{n-1}^{k_{n-1}},v_n)$, where for each $i\in \{0,\dots ,n-1\},k_i\ge 1$ and $e_i^j=v_i{v}_{i+1}$ for every $j\in \{1,\dots ,k_i\}$, is a dynamic H-walk if $c(e_i^{k_i})c(e_{i+1}^1)$ is an edge in H, for each $i\in \{0,\dots ,n-2\}$. If W is a dynamic H-walk that does not repeat edges, then W will be called dynamic H-trail. We will say that a dynamic H-trail, W, is an Euler dynamic H-trail if $E(G)=E(W)$. We will say that a dynamic H-trail is a closed dynamic H-trail whenever a) $v_0=v_n$ and $c(e_{n-1}^{k_{n-1}})c(e_0^1)$ is an edge in H; or b) $v_1=v_n$ and $e_{n-1}^{k_{n-1}}$ and $e_0^1$ are parallel in G. Notice that if W is a closed dynamic H-walk that satisfies condition b, then W can be rewrite as $W=(v_1,e_1^1,\dots ,v_{n-1}=v_0,e_{n-1}^1,\dots ,e_{n-1}^{k_{n-1}},e_0^1,\dots ,e_0^{k_0},v_n=v_1)$, and W satisfies condition (a) (unless n = 1, i.e., W is of the form $(x,e_0,\dots ,e_k,y)$, where $k\ge 1$).

It follows from the definition of dynamic H-trail that every H-trail in G is a dynamic H-trail in G. Moreover, if G has no parallel edges, then every dynamic H-trail is an H-trail.

A motivation for the study of dynamic H-walks are their possibles applications. For example, suppose that it is require to send a message from point A to point B through communication network which can have faults in its links (such as damage, attack, virus or blockage), where each one of its edge has an assigned color depending on the probability that the message is delivered correctly (in time, complete, unchanged or virus-free). In this case, the vertices of H are the colors assigned to the edges of the network and the set of edges of H will depend on the transitions that are convenient (for example, if transition with the same probability of failure are forbidden, then H will have no loops). In practice, it is possible to send messages simultaneously over two or more connections. In these cases, the use of dynamic H-walks can improve message delivery.

Motivated by Theorem 3 and its proof, we think that it is possible to give conditions, similar to those of Theorem 3, on an H-colored multigraph that guarantee the existence of closed Euler dynamic H-trail. In the process, we find an auxiliary graph, we call it $L_3^H(G)$, that allows us to link the closed dynamic H-trails with hamiltonian graphs. As a result, we will prove that G contains a closed Euler dynamic H-trails if and only if $L_n^H(G)$ is hamiltonian, for every $n\ge 3$.

2 Main results

In what follows, H will be a graph possibly with loops, and G will be a multigraph without loops.

First of all, we will introduce an auxiliary graph, denoted by $L_n^H(G)$, which is defined as follows.

Definition 1.

Let G be an H-colored multigraph with $|E(G)|=q$. For $n\ge 2,L_n^H(G)$ is the graph with nq vertices, obtained as follows: for each edge e = uv of G, we take two vertices f(u, e) and f(v, e) in $L_n^H(G)$, and adding a path with n – 2 new intermediate vertices connecting f(u, e) and f(v, e). And the rest of the edges of $L_n^H(G)$ are defined as follows: a) f(u, e) and f(u, g) are adjacent iff $e\ne g$ and $c(e)c(g)\in E(H)$; b) f(u, e) and f(v, g) are adjacent iff $u\ne v$ and e and g are parallel in G.

Notice that $L_n^H(G)$ is a simple graph.

Before giving a new way to construct the graph $L_n^H(G)$, we first introduce some additional notation.

Recall that G_u is the graph such that $V(G_u)=\{e\in E(G):e\text{isincidentwith}u\}$, and two different vertices a and b are joining by only one edge in G_u if and only if c(a) and c(b) are adjacent in H. Notice that $V(G_u)$ can also be denoted as $\{f(u,e):e\text{ is incident in }u\}$.

For each e = xy in E(G), by the definition of G_x and G_y , we have that $e\in V(G_x)$ and $e\in V(G_y)$. So, we will say that f(x, e) and f(y, e) are the copies of e seen as a vertex in G_x and G_y , respectively; and if E_xy is the set of all the edges with end vertices x and y, then we will say that $E_{xy}^x=\{f(x,e):e\in E_{xy}\}$.

Notice that $L_n^H(G)$ can be constructed as follows. First take the disjoint union of G_x , for every x in V(G). Then, for every pair of distinct vertices, x and y in V(G), such that $\left|E_{xy}\right|=m\ge 1$, we will have a complete bipartite graph $K_{m,m}$ between $E_{xy}^x$ and $E_{xy}^y$. Finally, for every $e=xy\in E(G)$, we change the edge joining f(x, e) and f(y, e) by a path with n – 2 new intermediate vertices. The construction of $L_3^H(G)$ is illustrated in Figure 1.

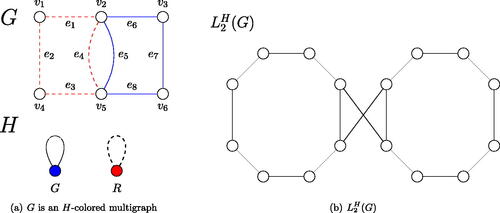
Fig. 1 The sequence $P=(v_1,e_1,v_2,e_6,e_5,v_4,e_4,v_3,e_3,e_2,v_1)$ is a closed Euler dynamic H-trail in G but there is no closed Euler H-trail in G.

It follows from the definition of $L_2^H(G)$ that $M_J=\{f(x,e)f(y,e)\in E(L_2^H(G)):e=xy\in E(G)\}$ is a perfect matching, that we will called it joint matching of $L_2^H(G)$.

The following two lemmas show how to construct a cycle in $L_2^H(G)$, based on the order of the edges in a closed dynamic H-trail in G, and vice versa.

Lemma 4.

Let G be an H-colored multigraph. If $P=(x_0,e_1,\dots ,e_{p_0},x_1,e_{p_0+1},\dots ,e_{p_0+\dots +p_1},x_2,\dots ,x_{n-1},e_{p_0+\dots +p_{n-2}+1},\dots ,e_{p_0+\cdots +p_{n-1}},x_n)$ is a closed dynamic H-trail in G, then $C=(f(x_0,e_1),f(x_1,e_1),\dots ,f(x_0,e_{p_0}),f(x_1,e_{p_0}),f(x_1,e_{p_0+1}),f(x_2,e_{p_0+1}),\dots ,f(x_n,e_{p_0+\dots +p_{n-1}}),f(x_0,e_1))$ is a cycle in $L_2^H(G)$.

Proof.

It follows from the definition of $L_2^H(G)$ that $f(x_i,e)f(x_{i+1},e)$ is an edge of $L_2^H(G)$, for every $e=x_i{x}_{i+1}\in E(P)$.

Let e_i and $e_{i+1}$ be consecutive edges in P (if $i=p_0+\cdots +p_{n-1}$, then $e_{i+1}=e_1$). If e_i and $e_{i+1}$ are parallel, such that x_j and $x_{j+1}$ are the ends of both edges, then $f(x_{j+1},e_i)$ and $f(x_j,e_{i+1})$ are adjacent in $L_2^H(G)$, by the definition of $L_2^H(G)$. Otherwise, e_i and $e_{i+1}$ are incident with x_j , for some x_j in V(P). Since P is a closed dynamic H-trail, then $c(e_i)c(e_{i+1})$ is an edge in H and $f(x_j,e_i)f(x_j,e_{i+1})\in E(L_2^H(G))$. Hence, C is a walk in $L_2^H(G)$. Since, P is a closed dynamic H-trail, then C does not repeat vertices and, so C is a cycle. Moreover, C alternate edges between $E(L_2^H(G))\setminus M_J$ and M_J . □

Lemma 5.

Let G be an H-colored multigraph and M_J be the joint matching of $L_2^H(G)$. If $C=(f(x_1,e_1),f(y_1,e_1),f(x_2,e_2),f(y_2,e_2)\dots ,f(y_q,e_q),f(x_1,e_1))$, where $e_i=x_i{y}_i\in E(G)$, is a cycle in $L_2^H(G)$ that alternate edges between $E(L_2^H(G))\setminus M_J$ and M_J , then the following steps produces a closed dynamic H-trail in G.

1. Star with $P=(x_1,e_1,y_1)$ and k = 2.

2. Let e_k , with end vertices x_k and y_k . If $e_{k-1}$ and e_k are parallel, $x_k=x_{k-1}$ and $y_k=y_{k-1}$, then we change lanes from the edge $e_{k-1}$ to e_k in P. Otherwise, continue P by the edge e_k .

3. $k=k+1$.

4. If $k=q+1$, finish. Otherwise, go to step 2.

Proof.

First, we will prove that P is a dynamic H-trail in G.

Let $e_{k-1}$ and e_k , with $2\le k\le q$.

Since $f(y_{k-1},e_{k-1})f(x_k,e_k)\in E(C)$, we have that $f(y_{k-1},e_{k-1})f(x_k,e_k)$ is in $E(L_2^H(G))$. Hence, $y_{k-1}=x_k$ and $c(e_{k-1})c(e_k)\in E(H)$ or $y_{k-1}\ne x_k$ and $e_{k-1}$ and e_k are parallel in G.

If $y_{k-1}=x_k$ and $c(e_{k-1})c(e_k)\in E(H)$, then $e_{k-1}$ and e_k are incident in $y_{k-1}=x_k$ and $(x_1,e_1,P,x_{k-1},e_{k-1},y_{k-1}=x_k,e_k,y_k)$ is a dynamic H-walk in G.

Otherwise, $y_{k-1}\ne x_k$ and $e_{k-1}$ and e_k are parallel edges in G, and $(x_1,e_1,P,x_{k-1}=x_k,e_{k-1},e_k,y_{k-1}=y_k)$ is a dynamic H-walk in G.

Hence, P is a dynamic H-walk in G.

On the other hand, since C is a cycle, then e_i appears exactly once in P, for every $i\in \{1,\dots ,q\}$, and so P is a dynamic H-trail.

Now, we prove that P is closed.

Recall that $e_i=x_i{y}_i$, for every $i\in \{1,\dots ,q\}$, and $y_i=x_{i+1}$ or $x_i=x_{i+1}$ and $y_i=y_{i+1}$ (if $i=q+1$, then $x_{i+1}=x_1$ and $y_{i+1}=y_1$). We will consider two cases.

Case 1. x_i = x_j and y_i = y_j , for every pair of distinct elements, i and j, in $\{1,\dots ,q\}$.

It follows from the construction of P that $P=(x_1,e_1,\dots ,e_q,y_1)$. Since C is a cycle in $L_2^H(G)$, then $q\ge 2$ and, so P is closed.

Case 2. There exists i in $\{1,\dots ,q\}$ such that $y_i=x_{i+1}$.

If $y_q=x_1$, then $c(e_q)c(e_1)\in E(H)$. Therefore, P is closed.

Otherwise, e_q and e₁ are parallel and, so P is closed.

Therefore, P is a closed dynamic H-trail in G. □

It follows from Lemmas 4 and 5 the following result.

Theorem 6.

Let G be an H-colored multigraph and M_J be the joint matching. Then, there is a bijection between the set of closed dynamic H-trails in G and the set of cycles in $L_2^H(G)$ that alternate edges between $E(L_2^H(G))\setminus M_J$ and M_J .

Proof.

Let G be an H-colored multigraph and M_J the joint matching of $L_2^H(G)$. We will denote by $\mathcal{P}$ the set of closed dynamic H-trails in G and by $\mathcal{C}$ the set of cycles in $L_2^H(G)$ that alternate edges between $E(L_2^H(G))\setminus M_J$ and M_J .

Let $T:\mathcal{P}\to \mathcal{C}$ defined by T(P) = C, where $P=(x_0,e_1,\dots ,e_{p_0},x_1,e_{p_0+1},\dots ,e_{p_1},x_2,e_{p_1+1},\dots ,x_{n-1},e_{p_0+\dots +p_{n-2}+1},\dots ,e_{p_0+\cdots +p_{n-1}},x_n)$, and $C=(f(x_0,e_1),f(x_1,e_1),\dots ,f(x_0,e_{p_0}),f(x_1,e_{p_0}),f(x_1,e_{p_0+1}),\dots ,f(x_n,e_{p_0+\cdots +p_{n-1}}),f(x_0,e_1))$.

Claim 1. T is well-defined.

It follows from Lemma 4 that $T(P)\in \mathcal{C}$.

Let $P_1=(x_0,e_0,\dots ,e_{p_0},x_1,e_{p_0+1},\dots ,e_{p_0+p_1},x_2,\dots ,x_{n-1},e_{p_0+\dots +p_{n-2}+1},\dots ,e_{p_0+\cdots +p_{n-1}},x_n)$ and $P_2=(y_0,f_0,\dots ,f_{q_0},y_1,f_{q_0+1},\dots ,f_{q_0+q_1},y_2,\dots ,y_{n-1},f_{q_0+\dots +q_{n-2}+1},\dots ,f_{q_0+\dots +q_{n-1}},y_n)$ in $\mathcal{P}$ such that P₁ = P₂.

Since P₁ = P₂, then $E(P_1)=E(P_2)$ and there exists $k\in \mathbb{N}$ such that $e_i=f_{i+k(\mathit{mod}\mathrm{ }{p}_0+\dots +p_{n-1})}$ (since the edges are traversed in the same order but the first edge is not the same). It follows from the definition of T that $V(T(P_1))=V(T(P_2))$ and the order of the vertices are the same. Then, we have that $T(P_1)=T(P_2)$. Therefore, T is well-defined.

Claim 2. T is injective.

Let P₁ and P₂ in $\mathcal{P}$ such that $P_1\ne P_2$.

If $E(P_1)\ne E(P_2)$, then $V(T(P_1))\ne V(T(P_2))$ and, so $T(P_1)\ne T(P_2)$. Otherwise, since $P_1\ne P_2$, then there exists $\{e_i,e_{i+1}\}\subseteq E(P_1)=E(P_2)$ such that e_i is the edge preceding $e_{i+1}$ in P₁ and e_i is not the edge preceding $e_{i+1}$ in P₂. Therefore, $T(P_1)\ne T(P_2)$ and T is injective.

Claim 3. T is surjective.

Let C be a cycle in $\mathcal{C}$. Since C alternate edges between $E(L_2^H(G))\setminus M_J$ and M_J , C must be of the form $C=(f(x_1,e_1),f(y_1,e_1),\dots ,f(x_q,e_q),f(y_q,e_q),f(x_1,e_1))$, where $e_i=x_i{y}_i\in E(G)$.

It follows from the definition of T that T(P) = C, where P be the closed dynamic H-trail obtained by applying the Lemma 5 to the cycle C. Hence, T is surjective.

Therefore, T is a bijection. □

Recall the following classical lemma, which will be useful for what follows.

Lemma 7.

Let M and $M\prime$ be two perfect matching of a graph G. If $M\cap M\prime =\varnothing$, then there exists a partition of the vertices of G into even cycles. Moreover, every cycle alternate edges between M and $M\prime$.

Theorem 8.

Let G be an H-colored multigraph and M_J be the joint matching of $L_2^H(G)$. There exists a perfect matching M in $L_2^H(G)\setminus M_J$ if and only if there exists a partition of the edges of G into closed dynamic H-trails. (Notice that some of the closed dynamic H-trails can be of the form $(x,e_0,\dots ,e_k,y)$, where $k\ge 1$).

Proof.

Let G be an H-colored multigraph and M_J be the joint matching of $L_2^H(G)$.

Suppose that there exists a perfect matching M in $L_2^H(G)\setminus M_J$.

It follows by Lemma 7, that there exists a partition of the vertices of $L_2^H(G)$ into vertex-disjoint cycles, say $\mathfrak{C}=\{C_1,\dots ,C_n\}$. Moreover, each cycle in $\mathfrak{C}$ alternate edges between M_J and M.

Let $\mathfrak{P}=\{P_1,\dots ,P_n\}$ be the set of closed dynamic H-trails in G such that $T(P_i)=C_i$, for every $i\in \{1,\dots ,n\}$.

Claim 1 $E(P_i)\cap E(P_j)=\varnothing$, for every $\{i,j\}\subseteq \{1,\dots ,n\}$.

Proceeding by contradiction, suppose that there exists a pair of distinct elements, i and j in $\{1,\dots ,n\}$, such that $E(P_i)\cap E(P_j)\ne \varnothing$.

Let $e=xy\in E(P_i)\cap E(P_j)$, it follows from the definition of T that f(x, e) and f(y, e) are vertices in $V(C_i)\cap V(C_j)$, a contradiction.

Claim 2 ${\cup }_{i=1}^{n}E(P_i)=E(G)$.

By the definition of T, we have that ${\cup }_{i=1}^{n}E(P_i)\subseteq E(G)$.

On the other hand, let $e\in E(G)$ join x and y. Since, $\mathfrak{C}$ is a partition of the vertices of $L_2^H(G)$, then there exists a cycle in $\mathfrak{C}$, say C_j , such that $f(x,e)f(y,e)\in E(C_j)$. It follows from the construction of P_j that $e\in E(P_j)$. Therefore, $e\in {\cup }_{i=1}^{n}E(P_i)$ and $E(G)\subseteq {\cup }_{i=1}^{n}E(P_i)$.

Therefore, $\mathfrak{P}=\{P_1,\dots ,P_n\}$ is a partition of the edges of G into closed dynamic H-trails.

Conversely, suppose that there exists a partition of the edges of G into closed dynamic H-trails, say $\mathfrak{P}=\{P_1,\dots ,P_k\}$.

Let $\mathfrak{C}=\{C_1,\dots ,C_k\}$a set of cycles in $L_2^H(G)$ such that $T(P_i)=C_i$, for every $i\in \{1,\dots ,k\}$.

Claim 3 If $i\ne j$, then $V(C_i)\cap V(C_j)=\varnothing$.

Suppose, to the contrary, that there exists i and j in $\{1,\dots ,k\}$, such that $V(C_i)\cap V(C_j)\ne \varnothing$. Let $f(x,e)\in V(C_i)\cap V(C_j)$, for some $e\in E(G)$ and $x\in V(G)$, such that e is incident with x.

It follows from the construction of C_i and C_j that $e\in E(P_i)$ and $e\in E(P_j)$, a contradiction.

Claim 4 ${\cup }_{i=1}^{k}V(C_i)=V(L_2^H(G))$.

By the construction of C_i , we have that ${\cup }_{i=1}^{k}V(C_i)\subseteq V(L_2^H(G))$.

Let $f(x,e)\in V(L_2^H(G))$, with $e\in E(G)$ and $x\in V(G)$, such that e is incident with x.

Since $\mathfrak{P}$ is a partition of the edges of G, then there exists $P_i\in \mathfrak{P}$ such that $e\in E(P_i)$. It follows from the construction of C_i that $f(x,e)\in V(C_i)\subseteq {\cup }_{j=1}^{k}V(C_j)$. Hence, $V(L_2^H(G))\subseteq {\cup }_{j=1}^{k}V(C_j)$.

Therefore, ${\cup }_{i=1}^{k}V(C_i)=V(L_2^H(G))$.

Claim 5 $M={\cup }_{i=1}^{k}E(C_i)\setminus M_J$ is a perfect matching in $L_2^H(G)$.

Recall $M_J=\{f(x,e)f(y,e)\in E(L_2^H(G)):e=xy\in E(G)\}$.

It follows from the construction of C_i and claims 3 and 4 that M is a perfect matching in $L_2^H(G)$.

Therefore, M is a perfect matching in $L_2^H(G)$, such that $M\cap M_J=\varnothing$. □

Theorem 9.

Let G be an H-colored multigraph. Then:

1. If G has a closed Euler dynamic H-trail, then $L_n^H(G)$ is hamiltonian, for every $n\ge 2$.

2. If $L_n^H(G)$ is hamiltonian, for some $n\ge 3$, then G has a closed Euler dynamic H-trail.

3. G has a closed Euler dynamic H-trail if and only if $L_n^H(G)$ is hamiltonian, for every $n\ge 3$.

Proof.

Let G be an H-colored multigraph.

1. It follows from Theorems 6 and 8 and definition of $L_n^H(G)$.

2. b. Suppose that there exist $n\ge 3$, such that $L_n^H(G)$ is hamiltonian. Let $C\prime$ be a hamiltonian cycle in $L_n^H(G)$.

Then, every path from f(x, e) to f(y, e) is in $V(C\prime )$ in some order, for every e = xy in E(G), by the definition of $L_n^H(G)$. Hence, we replace the path for the edge $f(x,e)f(y,e)$ to $C\prime$, and we get a hamiltonian cycle in $L_2^H(G)$, say C.

Since C is a hamiltonian cycle, then $P=T^{-1}(C)$ is a closed Euler dynamic H-trail in G, by Theorem 8.

1. It follows from a and b. □

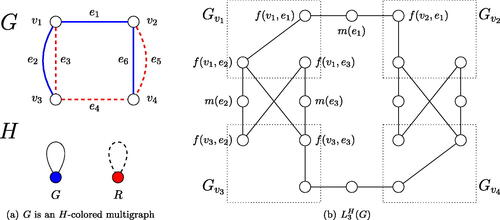
In Theorem 9, we cannot change $n\ge 3$ by $n\ge 2$ because there are H-colored multigraphs without closed Euler dynamic H-trail and $L_2^H(G)$ is hamiltonian, see Figure 2.

Fig. 2 The graph $L_2^H(G)$ is hamiltonian but there is no closed Euler dynamic H-trail in G.

Recall that E_xy is the set of all the edges with end vertices x and y.

Definition 2.

Let G be an H-colored multigraph and M be a matching in $L_2^H(G)$. For each x in V(G), we will say that $M_x=\{f(x,e)f(x,g)\in M\}$, i.e., M_x consists of the edges in G_x that are in M. And, for every pair of vertices x and y in V(G), such that $E_{xy}\ne \varnothing$, we will define the following sets: $A_{xy}^M=\{e\in E_{xy}:f(x,e)$ is M_x -saturate and f(y, e) is not M_y -saturate $\}$; $B_{xy}^M=\{e\in E_{xy}:f(y,e)$ is M_y -saturate and f(x, e) is not M_x -saturate $\}$; $C_{xy}^M=\{e\in E_{xy}:f(x,e)$ is M_x -saturate and f(y, e) is M_y -saturate $\}$; and $D_{xy}^M=\{e\in E_{xy}:f(x,e)$ is not M_x -saturate and f(y, e) is not M_y -saturate $\}$.

Theorem 10.

Let G be an H-colored multigraph. There exists a partition of the edges of G into closed dynamic H-trails, none of them in the form $(x,a_1,\dots ,a_l,y),l\ge 2$, if and only if there exists a non empty matching, say M, in $L_2^H(G)$, such that for each set $E_{xy}\ne \varnothing$ one of the following conditions hold: a) $C_{xy}^M=E_{xy}$; b) $\left|C_{xy}^M\right|<\left|E_{xy}\right|$ and $1\le \left|A_{xy}^M\right|=\left|B_{xy}^M\right|$.

Proof.

Let G be an H-colored multigraph and M_J be the joint matching of $L_2^H(G)$.

Suppose that $\mathfrak{P}=\{P_1,\dots ,P_k\}$ is a partition of the edges of G into closed dynamic H-trails, such that none of them have the form $(x,a_1,\dots ,a_l,y),l\ge 2$.

By Theorem 8, there exists a perfect matching in $L_2^H(G)\setminus M_J$. Let M be the perfect matching obtained as in the proof of Theorem 8, i.e., $M={\cup }_{i=1}^{k}E(T(P_i))\setminus M_J$.

Let x and y be a pair of vertices in G, such that $E_{xy}=\{e_1,\dots ,e_q\}$, with $q\ge 1$. Since $\mathfrak{P}$ is a partition of the edges of G into closed dynamic H-trails, then there exists $P_i\in \mathfrak{P}$ such that $E_{xy}\cap E(P_i)\ne \varnothing$, say $P_i=P_1$.

Since P₁ is not of the form $(x,a_1,\dots ,a_l,y),l\ge 2$, and $E_{xy}\cap E(P_1)\ne \varnothing$, then $P_1=(\dots ,f_0,x,e_{t_1},\dots ,e_{t_{p_1}},y,f_1,\dots )$, where $p_1\le q$ and $\{f_0,f_1\}\subset E(G)$. (Recall that M_x consists of the edges in G_x that are in M).

If $p_1=1$, then $P_1=(\dots ,f_0,x,e_{t_1},y,f_1,\dots )$. Hence, $f(x,f_0)f(x,e_{t_1})$ and $f(y,e_{t_1})f(y,f_1)$ are in M.

Therefore, $f(x,f_0)f(x,e_{t_1})\in M_x,f(y,e_{t_1})f(y,f_1)\in M_y$ and $e_{t_1}\in C_{xy}^M$.

On the other hand, if $p_1\ge 2$, then $f(x,f_0)f(x,e_{t_1})$, $f(y,e_{t_{p_1}})f(y,f_1)$ and $f(y,e_{t_i})f(x,e_{t_{i+1}})$ are in M, for every $i\in \{1,\dots ,p_1-1\}$, see Figure 3. Hence, $e_{t_1}\in A_{xy}^M$, $e_{t_{p_1}}\in B_{xy}^M$ and $e_{t_i}\in D_{xy}^M$, for every $i\in \{2,\dots ,p_1-1\}$.

Fig. 3 In b, the continued edges are in M and the dashed edges are in M_J .

If $E_{xy}\setminus \{e_{t_1},\dots ,e_{t_{p_1}}\}=\varnothing$, then $C_{xy}^M=E_{xy}$ (when $p_1=1$ occurs) or $\left|C_{xy}^M\right|<\left|E_{xy}\right|$ and $1\le \left|A_{xy}^M\right|=\left|B_{xy}^M\right|$ (when $p_1\ge 2$). So, suppose that $E_1=E_{xy}\setminus \{e_{t_1},\dots ,e_{t_{p_1}}\}\ne \varnothing$, then there exists $P\in \mathfrak{P}$, such that $E(P)\cap E_1\ne \varnothing$.

Since P is not of the form $(x,a_1,\dots ,a_l,y),l\ge 2$, and $E_1\cap E(P)\ne \varnothing$, then $P=(\dots ,f_2,x,e_{s_1},\dots ,e_{s_{p_2}},y,f_3,\dots )$, where $\{f_2,f_3\}\subset E(G)$. We will consider two cases.

If $p_2=1$, then $P=(\dots ,f_2,x,e_{s_1},y,f_3,\dots )$. By the construction of M we have that the edges $f(x,f_2)f(x,e_{s_1})$ and $f(y,e_{s_1})f(y,f_3)$ are in M. Thus, $f(x,f_2)f(x,e_{s_1})\in M_x,f(y,e_{s_1})f(y,s_1)\in M_y$ and $e_{s_1}\in C_{xy}^M$.

On the other hand, if $p_2\ge 2$, then $f(x,f_2)f(x,e_{s_1}),f(y,e_{s_{p_2}})f(y,f_3)$ and $f(y,e_{s_i})f(x,e_{s_{i+1}})$ are in M, for every $i\in \{1,\dots ,s_2-1\}$. Hence, $e_{s_1}\in A_{xy}^M,e_{s_{p_2}}\in B_{xy}^M$ and $e_{s_i}\in D_{xy}^M$, for every $i\in \{2,\dots ,p_2-1\}$.

If $E_2=E_1\setminus \{e_{s_1},\dots ,e_{s_{p_2}}\}=\varnothing$, then $C_{xy}^M=E_{xy}$ (when $p_1=p_2=1$) or $\left|C_{xy}^M\right|<\left|E_{xy}\right|$ and $1\le \left|A_{xy}^M\right|=\left|B_{xy}^M\right|$ (when $p_1\ge 2$ or $p_2\ge 2$). Otherwise, there exists $P\prime \in \mathfrak{P}$, such that $E_2\cap E(P\prime )\ne \varnothing$ and we can repeat this procedure and after a finite number of steps we obtain that $C_{xy}^M=E_{xy}$ or $\left|C_{xy}^M\right|<\left|E_{xy}\right|$ and $1\le \left|A_{xy}^M\right|=\left|B_{xy}^M\right|$.

Now, suppose that there exists M, a matching in $L_2^H(G)$, such that for every set $E_{xy}\ne \varnothing$, it holds that: $C_{xy}^M=E_{xy}$ or $\left|C_{xy}^M\right|<\left|E_{xy}\right|$ and $1\le \left|A_{xy}^M\right|=\left|B_{xy}^M\right|$.

If M is a perfect matching in $L_2^H(G)\setminus M_J$, then there exists a partition of E(G) into closed dynamic H-trails, by Theorem 8. So, suppose that M is not a perfect matching in $L_2^H(G)\setminus M_J$. Recall that $M_x=M\cap E(G_x)$, for every $x\in V(G)$.

Since $C_{xy}^M=E_{xy}\ne \varnothing$ or $1\le \left|A_{xy}^M\right|$, then for every $x\in V(G),M_x\ne \varnothing$.

Let $N=\underset{x\in V(G)}{\cup }{M}_x$. Notice that N is a matching in $L_2^H(G)\setminus M_J,A_{xy}^M=A_{xy}^N,B_{xy}^M=B_{xy}^N,C_{xy}^M=C_{xy}^N$ and $D_{xy}^M=D_{xy}^N$. So, for every set $E_{xy}\ne \varnothing$, it holds that: $C_{xy}^N=E_{xy}$ or $\left|C_{xy}^N\right|<\left|E_{xy}\right|$ and $1\le \left|A_{xy}^N\right|=\left|B_{xy}^N\right|$.

Let x and y be two different vertices in V(G), such that $E_{xy}\ne \varnothing$.

If $C_{xy}^N=E_{xy}$, then f(x, e) and f(y, e) are N-saturate, for every $e\in E_{xy}$. So, we do not add any edge to N.

On the other hand, if $\left|C_{xy}^N\right|<\left|E_{xy}\right|$ and $1\le \left|A_{xy}^N\right|=\left|B_{xy}^N\right|$, then we will consider G_xy , the subgraph of $L_2^H(G)$ induced by the set $\{f(x,e):e\in E_{xy}\setminus C_{xy}^N\}\cup \{f(y,e):e\in E_{xy}\setminus C_{xy}^N\}$.

Since $\left|C_{xy}^N\right|<\left|E_{xy}\right|$, then $V(G_{xy})\ne \varnothing$. Let $A_{xy}^N=\{e_1,\dots ,e_t\}$ and $B_{xy}^N=\{f_1,\dots ,f_t\}$, since $1\le \left|A_{xy}^N\right|=\left|B_{xy}^N\right|$ we have that $t\ge 1$.

If $D_{xy}^N=\varnothing$, then we add the edges $f(y,e_i)f(x,f_i)$ to N, for every $i\in \{1,\dots ,t\}$. By the definition of the edges of $L_2^H(G)$ (point b) and the definition of G_xy , we have that $f(y,e_i)f(x,f_i)\in E(G_{xy})$. Moreover, $N\cup \{f(y,e_i)f(x,f_i):i\in \{1,\dots ,t\left\}\right\}$ is still a matching.

On the other hand, when $D_{xy}^N\ne \varnothing$, let $D_{xy}^N=\{g_1,\dots ,g_s\}$. We add the edges $f(y,e_1)f(x,g_1)$, $f(x,f_1)f(y,g_s),f(y,e_i)f(x,f_i)$ and $f(y,g_j)f(x,g_{j+1})$ to N, for every $i\in \{2,\dots ,t\}$ and $j\in \{1,\dots ,s-1\}$.

By the definition of the edges of $L_2^H(G)$ and the definition of G_xy , we have that all the edges we add to N are in $E(G_{xy})$ and N is still a matching.

Thus, we add edges to N in such a way every vertex in G_xy is N-saturate.

So, we repeat the same process for x and y in V(G) such that $E_{xy}\ne \varnothing$.

Therefore, N is a perfect matching in $L_2^H(G)\setminus M_J$ and there exists a partition of E(G) into closed dynamic H-trails, by Theorem 8 and, by the construction of N, none of them is of the form $(x,a_1,\dots ,a_l,y)$, with $l\ge 2$. □

The following result shows a condition on the graph G_x that guarantees the existence of closed Euler dynamic H-trail.

Theorem 11.

Let G be a connected H-colored multigraph, such that G_u is a complete k_u -partite graph for every $u\in V(G)$ and for some k_u in $\mathbb{N}\setminus \left\{1\right\}$. Then G has a closed Euler dynamic H-trail if and only if there exists a matching M in $L_2^H(G)$, such that for every set $E_{xy}\ne \varnothing$ one of the following conditions hold: a) $C_{xy}^M=E_{xy}$; or b) $\left|C_{xy}^M\right|<\left|E_{xy}\right|$ and $1\le \left|A_{xy}^M\right|=\left|B_{xy}^M\right|$.

Proof.

Let G be a connected H-colored multigraph, such that G_u is a complete k_u -partite graph for every $u\in V(G)$ and for some k_u in $\mathbb{N}\setminus \left\{1\right\}$.

Suppose that G has a closed Euler dynamic H-trail, say P.

Case 1. P is not of the form $(x,e_1,\dots ,e_k,y)$, with $k\ge 2$.

In this case there exists a matching, say M, in $L_2^H(G)$, such that for every set $E_{xy}\ne \varnothing$ one of the following conditions hold: $C_{xy}^M=E_{xy}$ or $\left|C_{xy}^M\right|<\left|E_{xy}\right|$ and $1\le \left|A_{xy}^M\right|=\left|B_{xy}^M\right|$.

Case 2. $P=(x,e_1,\dots ,e_k,y)$, with $k\ge 2$.

In this case, since G_x is a complete k_x -partite graph, for some $k_x\ge 2$, then there exists two edges e and f in $E(G)=E(P)$, such that $c(e)c(f)\in E(H)$. Suppose, without loss of generality, that $c(e_1)c(e_2)\in E(H)$.

If k = 2, then $P\prime =(x,e_1,y,e_2,x)$ is a closed Euler dynamic H-trail. Otherwise, since G_x is k_x -partite graph, we have that $c(e_1)c(e_k)\in E(H)$ or $c(e_2)c(e_k)\in E(H)$.

Hence, $P\prime =(x,e_1,y,e_2,\dots ,e_k,x)$ or $P\prime =(x,e_1,e_3,\dots ,e_k,y,e_2,x)$ is a closed Euler dynamic H-trail. By Theorem 10, there exists a matching M in $L_2^H(G)$, such that for every set $E_{xy}\ne \varnothing ,C_{xy}^M=E_{xy}$ or $\left|C_{xy}^M\right|<\left|E_{xy}\right|$ and $1\le \left|A_{xy}^M\right|=\left|B_{xy}^M\right|$.

Conversely, suppose that there exists a matching M in $L_2^H(G)$, such that for every set $E_{xy}\ne \varnothing$ one of the following conditions hold: $C_{xy}^M=E_{xy}$ or $\left|C_{xy}^M\right|<\left|E_{xy}\right|$ and $1\le \left|A_{xy}^M\right|=\left|B_{xy}^M\right|$.

It follows from Theorem 10 that there exists a partition of E(G) into closed dynamic H-trails, none of them in the form $(x,e_1,\dots ,e_l,y)$, with $l\ge 2$, say $\mathcal{P}=\{P_1,\dots ,P_k\}$.

If k = 1, then $E(P_1)=E(G)$ and P₁ is a closed Euler dynamic H-trail. Otherwise, since G is connected it follows that there exists $P_i\in \mathcal{P}\setminus \left\{P_1\right\}$, say P₂, such that $V(P_1)\cap V(P_2)\ne \varnothing$. Since P₁ and P₂ are closed, we can suppose that $P_1=(x_0,e_1,\dots ,e_m,x_0)$, where $e_1=x_0{x}_1$ and $e_m=x_{k_1}{x}_0$, and $P_2=(y_0,f_1,\dots ,f_n,y_0)$, where $f_1=y_0{y}_1$ and $f_n=y_{k_2}{y}_0$, such that x₀ = y₀. By the definition of dynamic H-trail, we have that $c(e_1)c(e_m)$ and $c(f_1)c(f_n)$ are in E(H). Furthermore, $e_1,f_1,e_m$ and f_n are incident with x₀ = y₀. Hence, $e_1{e}_m$ and $f_1{f}_n$ are in $E(G_{x_0})$.

We will consider the following: if $\{e_1,f_1\}\subseteq E_j^{x_0}$ or $\{e_m,f_n\}\subseteq E_j^{x_0}$, for some $j\in \{1,\dots ,k_{x_0}\}$, it follows that $e_1{f}_n$ and $e_m{f}_1$ are in $E(G_{x_0})$, because $G_{x_0}$ is a complete $k_{x_0}$-partite graph. In other case, $e_1{f}_1$ and $e_m{f}_n$ are in $E(G_{x_0})$.

By the definition of $G_{x_0}$, we have that $c(e_1)c(f_n)$ and $c(e_m)c(f_1)$ are edges of H or $c(e_1)c(f_1)$ and $c(e_m)c(f_n)$ are edges of H.

If $c(e_1)c(f_n)$ and $c(e_m)c(f_1)$ are edges of H, we have that $Q_1=P_1\cup P_2$ is a closed dynamic H-trail. And, if $c(e_1)c(f_1)$ and $c(e_m)c(f_n)$ are edges of H, we have that $Q_1=P_1\cup P_2^{-1}$ is a closed dynamic H-trail.

If $E(Q_1)=E(G)$, then Q₁ is a closed Euler dynamic H-trail. Otherwise, since G is connected it follows that there exists $P_i\in \mathcal{P}\setminus \{P_1,P_2\}$, say P₃, such that $V(Q_1)\cap V(P_3)\ne \varnothing$. Since Q₁ and P₃ are closed, we can suppose that $P_1=(v_1,a_1,\dots ,a_s,v_0)$, where $a_1=v_0{v}_1$ and $a_s=v_{k_3}{v}_0$, and $P_3=(u_0,g_1,\dots ,g_t,u_0)$, where $g_1=u_0{u}_1$ and $g_t=u_{k_3}{u}_0$, such that v₀ = u₀. By the definition of dynamic H-trail, we have that $c(a_1)c(a_s)$ and $c(g_1)c(g_t)$ are in E(H). Furthermore, $a_1,g_1,a_s$ and g_t are incident with u₀ = v₀. Hence, $a_1{a}_s$ and $g_1{g}_t$ are in $E(G_{v_0})$.

We will consider the following: if $\{a_1,g_1\}\subseteq E_j^{v_0}$ or $\{a_s,g_t\}\subseteq E_j^{v_0}$, for some $j\in \{1,\dots ,k_{v_0}\}$, it follows that $a_1{g}_t$ and $a_s{g}_1$ are in $E(G_{v_0})$, because $G_{v_0}$ is a complete $k_{v_0}$-partite graph. In other case, $a_1{g}_1$ and $a_s{g}_t$ are in $E(G_{v_0})$.

By the definition of $G_{v_0}$, we have that $c(a_1)c(g_t)$ and $c(a_s)c(g_1)$ are edges of H or $c(a_1)c(g_1)$ and $c(a_s)c(g_t)$ are edges of H.

If $c(a_1)c(g_t)$ and $c(a_s)c(g_1)$ are edges of H, we have that $Q_2=Q_1\cup P_3$ is a closed dynamic H-trail. And, if $c(a_1)c(g_1)$ and $c(a_s)c(g_t)$ are edges of H, we have that $Q_2=Q_1\cup P_3^{-1}$ is a closed dynamic H-trail.

If $E(Q_2)=E(G)$, then Q₂ is a closed Euler dynamic H-trail. Otherwise, we repeat the procedure until we get the desired closed Euler dynamic H-trail. □

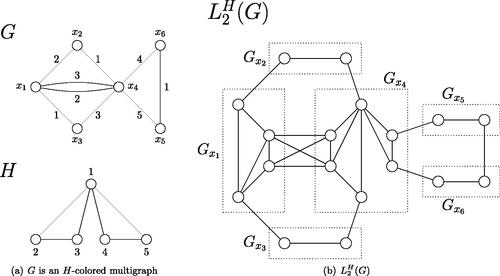
In Theorem 11 we cannot change the hypothesis “G_u is a complete k_u -partite for every $u\in V(G)$” to “G_u has a complete k_u -partite spanning subgraph”, as Figure 4 shows.

Fig. 4 G_u is a complete k_u -partite graph, for $u\in V(G)\setminus \left\{x_4\right\}$, and $G_{x_4}$ has a bipartite spanning subgraph but there is no closed Euler dynamic H-trail in G.

Corollary 12.

Let G be an H-colored multigraph. Then G_x has a perfect matching, for every $x\in V(G)$, if and only if there exists a partition of E(G) into closed H-trails.

Proof.

Let G be an H-colored multigraph and M_J be the joint matching of $L_2^H(G)$.

Suppose that G_x has a perfect matching, for every $x\in V(G)$, say M_x . Let $M=\underset{x\in V(G)}{\cup }{M}_x$.

It follows from the definition of M_J that $M\cap M_J=\varnothing$. Hence, G has a partition of its edges into closed dynamic H-trails, by Theorem 8.

Let $\mathcal{P}$ be the partition that is obtained as in the proof of Theorem 8. It follows, from the construction of each dynamic H-trail in $\mathcal{P}$, that there is no lane change. So, $\mathcal{P}$ is a partition of E(G) into closed H-trails.

Now, suppose that there exists a partition of E(G) into closed H-trails, say $\mathcal{P}$. By Theorem 8, there exists a perfect matching in $L_2^H(G)\setminus M_J$. Let M be the perfect matching that is obtained as in the proof of Theorem 8.

Let $f(x,e)\in V(L_2^H(G))$. Then, there exists $P\in \mathcal{P}$ such that $e\in E(P)$. Since P is an H-trail and by the construction of M, it follows that $P=(u,g,x,e,v,\dots )$ and $f(x,g)f(x,e)\in M$. Moreover, $f(x,g)f(x,e)\in M\cap E(G_x)$.

Therefore, $M\cap E(G_x)$ is a perfect matching of G_x . □

Recall the following classical theorem, which will be useful.

Theorem 13

(Tutte [21]). G has a perfect matching if and only if $o(G\setminus S)\le \left|S\right|$ for all proper subset S of V(G).

Notice that if H is a complete graph without loops and G is an H-colored multigraph. Then P is a properly colored closed trail if and only if P is a closed H-trail.

Corollary 14

(Kotzig). Let G be an edge-colored eulerian multigraph. Then G has a properly colored closed Euler trail if and only if ${\delta }_i(x)\le \sum _{j\ne i}{\delta }_j(x)$, where ${\delta }_i(x)$ is the number of edges with color i incident with x, for each vertex x of G.

Proof.

Let G be an H-colored multigraph, where H is a complete graph without loops and $|V(H)|=c$.

Let G_u , with $u\in V(G)$. It follows from the definition of G_u and H is a complete graph that G_u is a complete k_u -paritite graph with independent sets $E_i^u=\{e\in E(G) : e=ux\text{forsome}x\in V(G)\text{and}c(e)=i\}$, with $i\in \{1,\dots ,c\}$. Moreover, $\left|E_i^u\right|={\delta }_i(u)$.

Suppose that G has a closed Euler H-trail. By Corollary 12 G_u has a perfect matching, for every $u\in V(G)$.

Hence, ${\delta }_i(u)=\left|E_i^u\right|=o(G\setminus S)\le \left|S\right|=\sum _{j\ne i}\left|E_j^u\right|=\sum _{j\ne i}{\delta }_i(u)$, where $S=V(G_u)\setminus E_i^u$, by Theorem 13.

Suppose that $\left|E_i^u\right|={\delta }_i(x)\le \sum _{j\ne i}{\delta }_j(x)=\sum _{j\ne i}\left|E_j^u\right|$, for each vertex x of G.

Claim 1. G_u has a perfect matching.

Let S be a proper subset of $V(G_u)$. Consider $G_u\setminus S$.

Case 1. $G_u\setminus S$ is connected.

Then $o(G_u\setminus S)\le 1\le \left|S\right|$.

Case 2. $G_u\setminus S$ is disconnected.

Since G_u is a complete k_u -partite graph, then $V(G_u\setminus S)\subseteq E_i^u$, for some $i\in \{1,\dots ,c\}$. Hence $o(G_u\setminus S)=|V(G_u\setminus S)|\le \left|E_i^u\right|\le \sum _{j\ne i}\left|E_j^u\right|\le \left|S\right|$.

Therefore, it follows from Theorem 13 that G_u has a perfect matching.

Let $M=\underset{u\in V(G)}{\cup }{M}_u$, where M_u is a perfect matching in G_u . So, M is a perfect matching in $L_2^H(G)$ and $C_{xy}^M=E_{xy}$, for every $E_{xy}\ne \varnothing$.

It follows from Theorem 11 and Corollary 12 that G has a closed Euler H-trail. □

Corollary 15

(Galeana-Sánchez et al.). Let H be a graph possibly with loops and G be an H-colored multigraph without loops. Suppose that G is Eulerian and G_u is a complete k_u -partite graph, for every u in V(G) and for some k_u in $\mathbb{N}$. Then G has a closed Euler H-trail if and only if $\left|C_i^u\right|\le \sum _{j\ne i}\left|C_j^u\right|$ for every u in V(G), where $\{C_1^u,\dots ,C_{k_u}^u\}$ is the partition of $V(G_u)$ into independent sets.

Acknowledgments

The authors wish to thank the anonymous referees for many suggestions which improved the rewriting of this paper.

Disclosure statement

The authors report there are no competing interests to declare

Additional information

Funding

This research was supported by CONACYT FORDECYT-PRONACES/39570/2020; UNAM DGAPA-PAPIIT IN102320. The second author received a fellowship from CONACYT under Grant 782239.