Integral sum graphs G_n and G_-r,n are perfect graphs

Abstract

A graph G is an integral sum graph (sum graph) if its vertices can be labeled with distinct integers (positive integers) so that e = uv is an edge of G if and only if the sum of the labels on vertices u and v is also a label in G. A graph G is perfect if the chromatic number of each of its induced subgraphs is equal to the clique number of the same. A simple graph G is of class 1 if its edge chromatic number and maximum degree are same. In this paper, we prove that integral sum graphs G_n, $G_{0,n}$ and $G_{-r,n}$ over the label sets $[1,n],[0,n]$ and $[-r,n]$, respectively, are perfect graphs as well as of class 1 for $r,n\in \mathbb{N}$. We also obtain a few structural properties of these graphs.

Keywords:

• Integral sum graph
• covering number
• independence number
• chromatic number
• clique number
• perfect graphs

2010MATHEMATICS SUBJECT CLASSIFICATION:

• 05C78
• 05C15
• 05C17
• 05C99

1 Introduction

Harary [6, 7] introduced the concepts of sum graphs and integral sum graphs. A graph G is called as an integral sum graph (sum graph) if the vertices of G can be labeled with distinct integers (positive integers) so that e = uv is an edge of G if and only if the sum of the labels on vertices u and v is also a label of a vertex in G. An anti-sum graph is defined [11] as a graph G in which there exist a labeling $f:V(G)\to \mathbb{N}$ such that two vertices are adjacent in G if and only if the sum of their labels is not a label of any vertex in G.

Different notations are used for integral sum graphs by different authors. For any non-empty set S of integers, let $G^{+}(S)$ denote the integral sum graph on the vertex label set S, G_n denote the sum graph for $S=\{1,2,\dots ,n\}$ = $[1,n],G_{-r}$ denote the integral sum graph for S = $[-r,-1]$, the integral sum graph with respect to $S=[-n,n]$ is denoted by $G_{-n,n}$ [6, 7] which is generalized to $G_{-r,n}$ and $G_{0,n}$ denote the integral sum graph for S = $[0,n],r,n\in \mathbb{N}$ [12]. Throughout this paper, for integral sum graph $G^{+}(S)$, we consider v_i as the vertex with integral sum labeling i, $i\in S$.

The order of a graph G is $\left|G\right|$, the number of vertices in G. The join of two graphs A and B denoted by A + B is the graph $A\cup B$ together with edges joining each vertex of A with all the vertices of B [14].

Theorem 1.1.

[12] For positive integers r and n, $G_{-r,n}\cong K_1+(G_{-r}+G_n)$.

An assignment of colors to the vertices of a graph so that adjacent vertices have the distinct colors is called a proper coloring of the graph. A color class is the set of all vertices with any one color and that is an independent set. The chromatic number $\chi (G)$ of a graph G is the minimum number of colors required to color the vertices of G for which G has a proper coloring [5]. Similarly, an assignment of colors to the edges of a graph G in such a way that adjacent edges have distinct colors is termed as proper edge coloring. An edge color class is the set of all edges of G with any single color and it is an independent set of edges. The edge chromatic number ${\chi }^{\prime }(G)$ is defined as the minimum number of colors required to color the edges of G for which G has a proper edge coloring [5]. A simple graph G is class 1 if ${\chi }^{\prime }(G)$ = $\Delta (G)$. It is class 2 if ${\chi }^{\prime }(G)$ = $\Delta (G)+1$.

The clique of a graph G is the maximal complete subgraph in G and its order is the clique number of G, denoted by $\omega (G)$ [5]. Clearly $\omega (K_n)$ = n. Here we denote the clique of the graph G by C_G.

A graph G is perfect if for every induced subgraph of G, the clique number and the chromatic number have the same value. Equivalently, for every $A\subseteq V(G),\chi (G[A])$ = $\omega (G[A])$ [14]. A graph G is 1-perfect if $\chi (G)$ = $\omega (G)$ [14]. It is also proved that graph G is perfect if and only if every induced subgraph of G is 1-perfect [3].

Theorem 1.2.

[8] The complement of a perfect graph is perfect as well.

Several graphs are proved as perfect [1, 4, 14]. They include bipartite graphs and their line graphs, chordal graphs, comparability graphs, triangulated graphs, etc. Perfect graphs arise in the statistical competition of block designs and in graph coloring problems. Another application of perfect graphs is the optimal routing of garbage trucks related to urban science problems. The perfect graph is also closely related to perfect channels in communication theory [9].

This paper contains 4 sections. Section 1 contains an introduction and some basic definitions and Section 2 presents a few structural properties which are required to prove results on integral sum graphs G_n, $G_{0,n}$ and $G_{-r,n}$ in the subsequent sections, $n,r\in \mathbb{N}$. In Section 3, we prove that sum graphs G_n and integral sum graphs $G_{0,n}$ are perfect and in Section 4, we show that integral sum graphs $G_{-r,n}$ are perfect and graphs G_n, $G_{0,n}$ and $G_{-r,n}$ are of class 1 for $r,n\in \mathbb{N}$.

While studying proper edge coloring of integral sum graphs, we felt that graphs G_n, $G_{0,n}$ and $G_{-r,n}$ must be perfect graphs and that is the motivation for this study.

All graphs we consider in this paper are simple and finite, and we follow Harary [5] for all graph-theoretic notions which are not mentioned here.

2 Preliminaries

In this section, we present a few structural properties of integral sum graphs G_n, $G_{0,n}$ and $G_{-r,n}$ that are required to prove results in the subsequent sections, $n,r\in \mathbb{N}$.

Theorem 2.1.

[5] (Vizing’s Theorem) For any graph G, the edge chromatic number satisfies the inequalities, $\Delta (G)\le {\chi }^{\prime }(G)\le \Delta (G)+1$.

A vertex and an edge of a graph are said to cover each other if they are incident [5].

A set of vertices (edges) which covers all the edges (vertices) of a graph G is called a vertex cover (edge cover) for G. Vertex covering number (edge covering number) is the minimum cardinality among all the vertex covers (edge covers) for G and is denoted by ${\alpha }_0(G)$ or α₀ (${\alpha }_1(G)$ or α₁) [5].

A set of vertices (edges) in G is independent if none of them are adjacent. The maximum cardinality among all the vertex (edge) independent set is called its vertex independence number (edge independence number) and is denoted by ${\beta }_0(G)$ or β₀ (${\beta }_1(G)$ or β₁) [5]. We denote the independent set of the graph G by I_G.

Theorem 2.2.

[5] For any connected nontrivial graph G of order n, ${\alpha }_0(G)+{\beta }_0(G)$ = n = ${\alpha }_1(G)+{\beta }_1(G)$.

Lemmas 2.3

and 2.4 are related to clique, minimum vertex cover, minimum edge cover, maximum independent set and maximum matching and are given without proof since the proofs are obvious.

Lemma 2.3.

For every $n\in \mathbb{N}$, the integral sum graph G_n has

1. Clique of G_n, $C_{G_n}$ = $\left\{v_i\in V(G_n):i=1,2,3,\dots ,\lceil \frac{n}{2}\rceil \right\}$

and $\omega (G_n)$ = $\lceil \frac{n}{2}\rceil$.

1. Minimum vertex cover of G_n $$=\; \{v_i\in V(G_n):i=1,2,3,\dots ,\lceil \frac{n}{2}\rceil -1\}$$

and ${\alpha }_0(G_n)$ = $\lceil \frac{n}{2}\rceil -1$.

1. Maximum independent set of G_n, $I_{G_n}$ = $\left\{v_i\in V(G_n):i=\lceil \frac{n}{2}\rceil ,\lceil \frac{n}{2}\rceil +1,\lceil \frac{n}{2}\rceil +2,\dots ,n\right\}$

and ${\beta }_0(G_n)$ = $\lfloor \frac{n}{2}\rfloor +1.$

1. Maximum matching of G_n $$=\; \{v_i{v}_j\in E(G_n):(i,j)=\left(1,n-1\right),\left(2,n-2\right),\dots ,$$ $$\left(\lceil \frac{n}{2}\rceil -1,\lceil \frac{n}{2}\rceil \right)\}$$

and ${\beta }_1(G_n)$ = $\lceil \frac{n}{2}\rceil -1$.

1. Any sum graph $G^{+}(S)$ has no edge cover since the vertex corresponding to the biggest label which is a natural number is an isolated vertex in $G^{+}(S)$. In particular, G_n has no edge cover, $n\in \mathbb{N}$.

Lemma 2.4.

For every integral sum graph $G_{-r,n},r,n\in \mathbb{N}$, we have

1. Clique of $G_{-r,n}$,

$C_{G_{-r,n}}=\{v_i\in V(G_{-r,n}):i=-\lceil \frac{r}{2}\rceil ,\dots ,-2,-1,0,1,2,\dots ,\lceil \frac{n}{2}\rceil \}$ and $\omega (G_{-r,n})=1+\lceil \frac{r}{2}\rceil +\lceil \frac{n}{2}\rceil$.

1. Minimum vertex cover of $G_{-r,n}=\{\begin{array}{cc}\left\{v_i\in V(G_{-r,n}):i=-r,\dots ,-1,0,1,\dots ,\lceil \frac{n}{2}\rceil -1\right\}\hfill & \text{if}r\le n.\hfill \\ \left\{v_i\in V(G_{-r,n}):i=-\lceil \frac{r}{2}\rceil +1,\dots ,-1,0,1,\dots ,n\right\}\hfill & \text{if}r\ge n.\hfill \end{array}$

and ${\alpha }_0(G_{-r,n})$ = $\min \{r,n\}+\lceil \frac{\max \{r,n\}}{2}\rceil$.

1. Maximum independent set of $G_{-r,n}$ $$=\; \{\begin{array}{cc}\left\{v_i\in V(G_{-r,n}):i=\lceil \frac{n}{2}\rceil ,\lceil \frac{n}{2}\rceil +1,\dots ,n-1,n\right\}\hfill & \text{if}r\le n.\hfill \\ \left\{v_i\in V(G_{-r,n}):i=-r,-r+1,\dots ,-\lceil \frac{r}{2}\rceil \right\}\hfill & \text{if}r\ge n.\hfill \end{array}$$

and ${\beta }_0(G_{-r,n})$ = $\lfloor \frac{\max \{r,n\}}{2}\rfloor +1$.

1. Minimum edge cover of $G_{-r,n}$ $$=\; \{\begin{array}{c}\left\{v_i{v}_j\in E(G_{-r,n}):i+j=n-r\right\}\hspace{1em}\text{if}k\text{is even}.\hfill \\ \left\{v_i{v}_j\in E(G_{-r,n}):i+j=n-r \& \left(i,j\right)=\left(0,\frac{n-r}{2}\right)\right\}\hspace{1em}\text{if }k\text{is odd}.\hfill \end{array}$$ $$=\; \{\begin{array}{c}\left\{v_i{v}_j\in E(G_{-r,n}):(i,j)=(-r,n),(-r+1,n-1),\dots ,(0,n-r)\right\}\hfill \\ \text{if}k\text{is even}.\hfill \\ \left\{v_i{v}_j\in E(G_{-r,n}):(i,j)=(-r,n),(-r+1,n-1),\dots ,(0,n-r)\&\left(0,\frac{n-r}{2}\right)\right\}\hfill \\ \text{ if}k\text{is odd}.\hfill \end{array}$$

and ${\alpha }_1(G_{-r,n})$ = $\lceil \frac{r+n+1}{2}\rceil$ where k = $r+n+1$.

1. Maximum matching of $G_{-r,n}$ $$=\; \{v_i{v}_j\in E(G_{-r,n}):i+j=n-r\}$$

and ${\beta }_1(G_{-r,n})$ = $\lfloor \frac{r+n+1}{2}\rfloor$.

Note 2.5. By putting r = 0 in Lemma 2.4, we obtain the corresponding properties of $G_{0,n},n\in \mathbb{N}$.

Note 2.6. In the integral sum graph $G_{-r,n}$ of even order, every maximum matching is a perfect matching for $r,n\in \mathbb{N}\cup \left\{0\right\}$.

For any integral sum graph G_n, $G_{0,n}$ or $G_{-r,n}$, maximum independent set, minimum vertex cover, minimum edge cover, and maximum matching need not be unique but clique is unique, $r,n\in \mathbb{N}$.

3 Sum graphs G_n and Integral sum graphs $G_{0,n}$ are perfect

In this section, we prove that for $n\in \mathbb{N}$, sum graphs G_n and integral sum graphs $G_{0,n}$ are perfect.

Theorem 3.1.

For a positive integer n, the sum graph G_n is perfect.

Proof.

Let G_n be the sum graph of order n obtained by the labeling $f:V(G_n)\to \mathbb{N}$ defined by $f(v_i)=i,1\le i\le n$. Let H be any induced subgraph of G_n. Our aim is to prove that $\chi (H)$= $\omega (H)$ for all subgraphs H of G_n where $\chi (H)$ is the chromatic number of H and $\omega (H)$ is its clique number.

G_n is a split graph with clique $C_{G_n}$ = $\left\{v_i\in V(G_n):i=1,2,\dots ,\lceil \frac{n}{2}\rceil \right\}$ and the independent set $I_{G_n}=\left\{v_i\in V(G_n):i=\lceil \frac{n}{2}\rceil ,\lceil \frac{n}{2}\rceil +1,\lceil \frac{n}{2}\rceil +2,\dots ,n\right\}$. To prove the theorem we consider the following three cases of H.

Case 1. $V(H)\subseteq V(C_{G_n})$.

Every induced subgraph of a clique is another clique of order fewer than or equal to the maximal clique. And thereby H itself a clique and $\chi (H)$= $\omega (H)$.

Case 2. $V(H)\subseteq V(I_{G_n})$.

Induced subgraph of an independent set is also an independent set and the clique number of any induced subgraph of an independent set is 1. This implies, $\chi (H)$= $\omega (H)$ = 1 for every $V(H)\subseteq V(I_{G_n})$.

Case 3. $V(H)\subseteq V(C_{G_n})\cup V(I_{G_n})$.

In this case, vertices of H belong to either $C_{G_n}$ or $I_{G_n}$. Let V(H) = $V(C_H)\cup V(I_H)$ where $V(C_H)\subseteq C_{G_n}$ and $V(I_H)\subseteq I_{G_n},V(C_H),V(I_H)\ne \varnothing$. Let $\omega (H)=k$. This implies that $\left|C_H\right|$ = k = $\chi (C_H)$ where C_H is the clique in H. If H itself is a clique, then H = C_H and thereby $\chi (H)$ = $\omega (H)$ = k. Hence the result is true in this case. If H is not a clique, let $\omega (H)$ = k. This implies, $\chi (C_H)$ = $\left|C_H\right|$ = k.

For each vertex $v_j\in V(I_H)$, there exists atleast one $v_i\in V(C_H)$ such that $v_i{v}_j\notin E(H)$ (since $i+j>n$) so that there will not be a clique of higher order than that of $C_H$ and thus v_i and v_j can be assigned with the same color. That is, the colors used in $C_H$ are enough for coloring $V(I_H)$. This implies, $\chi (H)$= $\chi (C_H)$ = k. Hence we get $\chi (H)$ = k = $\omega (H)$.

Thus in all the three cases we obtain $\chi (H)$ = $\omega (H)$ for every induced subgraph H of G_n and thereby graph G_n is perfect for $n\in \mathbb{N}$. □

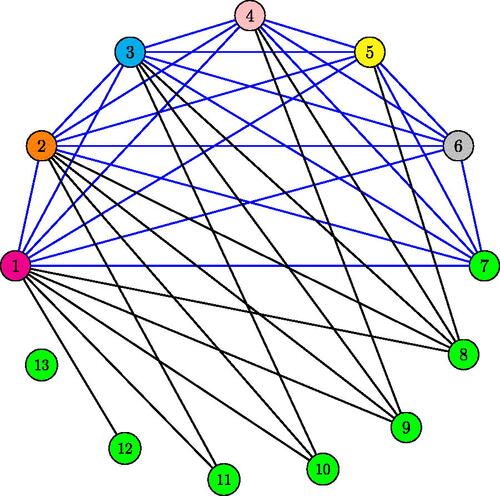
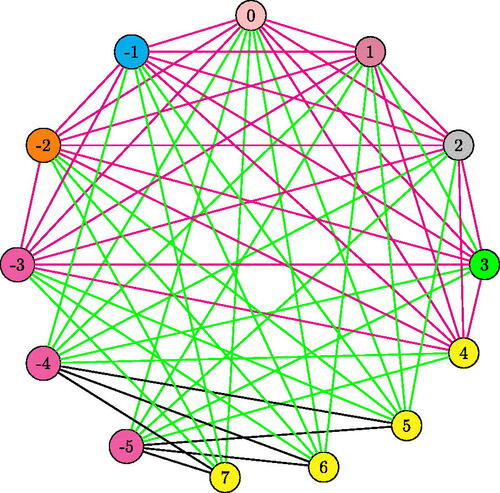
Illustration 3.2. Consider the sum graph G₁₃ as given in Figure 1. Vertices v₁,v₂,v₃,v₄,v₅,v₆ and v₇ (vertices joined by edges with blue color) form a clique in G₁₃ and $\omega (G_{13})=7$. These vertices are colored by the colors $c_1,c_2,\dots ,c_7$. All the remaining vertices are nonadjacent to v₇ and so, they can be colored by c₇. Or, the vertices v₈,v₉,v₁₀, v₁₁,v₁₂ and v₁₃ are nonadjacent to the vertices v₆,v₅,v₄,v₃,v₂ and v₁ respectively, and can be colored by the corresponding colors $c_1,c_2,\dots ,c_6$. Therefore, the chromatic number of the sum graph G₁₃ is 7. i.e., $\chi (G_{13})$ = 7 = $\omega (G_{13})$. Thus G₁₃ is 1-perfect. Clearly every pair of nonadjacent vertices in G₁₃ are also nonadjacent in any of its induced subgraphs. This shows that every induced subgraph of G₁₃ is 1-perfect. This implies, graph G₁₃ is 1-perfect and thereby G₁₃ is perfect.

Fig. 1 $G_{13}:$ vertex coloring and clique.

Corollary 3.3.

For every positive integer n, graph $G_n^c$ is perfect.

Proof.

The proof follows from Theorems 3.1 and 1.2. □

Theorem 3.4.

For every $n\in \mathbb{N}$,

1. the chromatic number of G_n is $\lfloor \frac{n}{2}\rfloor$;

2. the edge chromatic number of G₁ is 0 and for $n\ge 2$, the edge chromatic number of G_n is n – 2.

i.e., ${\chi }^{\prime }(G_1)$ = 0 and for $n\ge 2,{\chi }^{\prime }(G_n)$ = n – 2.

Proof.

The sum graph G_n is obtained by the labeling $f:V(G_n)\to \mathbb{N}$ defined by $f(v_i)=i$, i = 1 to n.

1. From Theorem 3.1, G_n is perfect and thereby the chromatic number of G_n is equal to its clique number. This implies, $\chi (G_n)$ = $\omega (G_n)$ = $\lceil \frac{n}{2}\rceil$. Hence we get the result (i). Vertex coloring and clique of G₁₃ are shown in Figure 1.

2. For n = 1, G_n is an empty graph and thus the edge chromatic number ${\chi }^{\prime }(G_1)$ = 0.

For $n\ge 2$, the maximum degree of sum graph G_n is $\Delta (G_n)$ = n – 2. Using Theorem 2.1, we have, $\Delta (G_n)\le {\chi }^{\prime }(G_n)\le \Delta (G_n)+1$. Here, we present the edge coloring of the sum graph G_n with exactly n – 2 colors so that ${\chi }^{\prime }(G_n)=n-2,n\ge 2$.

Let c_k denote k^th color assigned to an edge and C_k denote the color class of edges each with color c_k in G_n, $n\ge 2$. Color the set of edges $\{v_i{v}_j\in E(G_n):i+j=k+2,1\le i,j\le n,i\ne j\}$ of G_n with the color c_k.

It is clear from the above edge coloring that colors c₁ to $c_{n-2}$ are assigned to the edges of G_n and no more edge colors are required. And all the colors of edges incident at each vertex v_i of sum graph G_n are all distinct since there are exactly n – 2 possibilities of j, $i\ne j,1\le j\le n$ for which $i+j=k+2$ in G_n, $1\le k\le n-2$. This implies, ${\chi }^{\prime }(G_n)$ = n – 2 for $n\ge 2$. Hence we get the result (ii). □

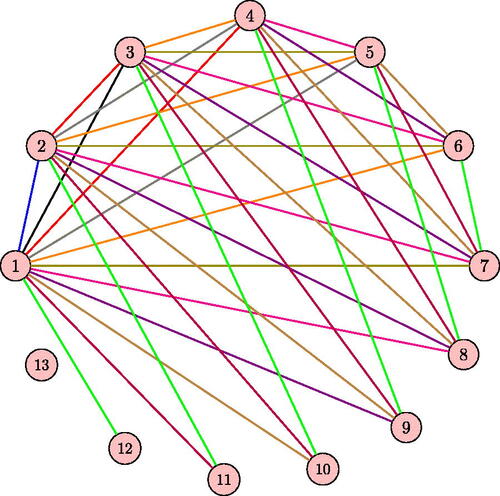
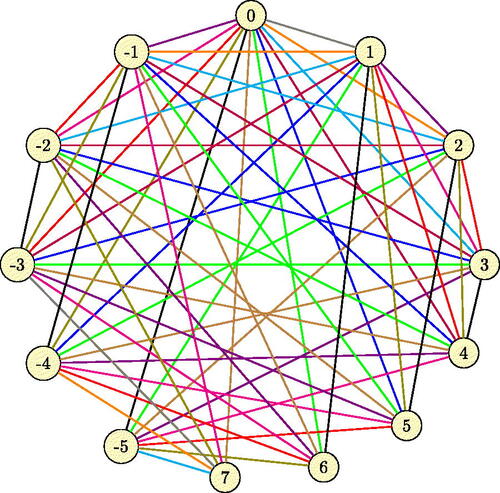
Illustration 3.5. Consider the sum graph G₁₃. The vertices v₁,v₂,v₃,v₄,v₅,v₆ and v₇ in G₁₃ (vertices joined by edges with blue color) form a clique, $\omega (G_{13})$ = 7 and $\Delta (G_{13})$ = 11. Since G₁₃ is perfect, $\chi (G_n)$ = $\omega (G_{13})$ which implies, $\chi (G_n)$ = 7 = $\lceil \frac{13}{2}\rceil$. As in the proof, color the set of edges $\{v_i,v_j\in E(G_n):i+j=k+2,1\le i,j\le n, i\ne j\}$ of G_n with the color c_k. The colors of each edge of G₁₃ is given as follows. $$c_1\to v_1{v}_{\mathrm{2;}}$$ $$c_2\to v_1{v}_{\mathrm{3;}}$$ $$c_3\to v_1{v}_4,v_2{v}_{\mathrm{3;}}$$ $$c_4\to v_1{v}_5,v_2{v}_{\mathrm{4;}}$$ $$c_5\to v_1{v}_6,v_2{v}_5,v_3{v}_{\mathrm{4;}}$$ $$c_6\to v_1{v}_7,v_2{v}_6,v_3{v}_{\mathrm{5;}}$$ $$c_7\to v_1{v}_8,v_2{v}_7,v_3{v}_6,v_4{v}_{\mathrm{5;}}$$ $$c_8\to v_1{v}_9,v_2{v}_8,v_3{v}_7,v_4{v}_{\mathrm{6;}}$$ $$c_9\to v_1{v}_{10},v_2{v}_9,v_3{v}_8,v_4{v}_7,v_5{v}_{\mathrm{6;}}$$ $$c_{10}\to v_1{v}_{11},v_2{v}_{10},v_3{v}_9,v_4{v}_8,v_5{v}_{\mathrm{7;}}$$ $$c_{11}\to v_1{v}_{12},v_2{v}_{11},v_3{v}_{10},v_4{v}_9,v_5{v}_8,v_6{v}_7.$$

See Figure 2 with the edge coloring of G₁₃ with 11 colors using the method given in the proof of Theorem 3.4. Here, ${\chi }^{\prime }(G_{13})=11=13-2$.

Fig. 2 $G_{13}:$ edge coloring.

Results are available for the composition of perfect graphs which allows different types of graph operations [2]. But the graph operation join is not available yet. Following is the result corresponding to join of two perfect graphs.

Theorem 3.6.

Join of two perfect graphs is also perfect.

Proof.

Let G and F be two perfect graphs with $\chi (G)$ = $\omega (G)$ = p and $\chi (F)$ = $\omega (F)$ = q. Also let J = G + F, the join of the graphs G and F. When we take the join of two graphs G and F, the clique in G together with clique in F form a higher clique of order p + q. i.e., $\omega (J)$ = p + q. Let H be any induced subgraph of J. We have to prove that $\chi (H)$= $\omega (H)$.

Let $\omega (H)$ = k and let C_H be the clique in H of order k. Then $\omega (H)$ = |C_H| = k = $\chi (C_H)$. That is C_H can be colored using k colors.

Let $D=V(H)\setminus V(C_H)$. For each v_j $\in D\cap V(G)$ and v_y $\in D\cap V(F)$, there exist v_i $\in V(C_H)\cap V(G)$ and v_x $\in V(C_H)\cap V(F)$ such that $v_i{v}_j,v_x{v}_y\notin E(H)$ so that there does not exist a clique of higher order than that of $C_H$. Hence, the colors of v_i and v_x can be assigned to v_j and v_y, respectively. And thereby the vertices of D can be colored using the colors of vertices of C_H. This implies, $\chi (H)$ = $\chi (C_H)$ = $\omega (H)$. Thus, for every induced subgraph H of J, $\chi (H)$ = $\omega (H)$. Thus the graph J is perfect. □

Theorem 3.7.

For every $n\in \mathbb{N}$, the integral sum graph $G_{0,n}$ is perfect.

Proof.

The integral sum graph $G_{0,n}$ = K₁ + G_n where K₁ = G₁ is labeled with 0. Then using Theorems 3.1 and 3.6, the graph $G_{0,n}$ is perfect, $n\in \mathbb{N}$. □

Figure 3 shows the clique in $G_{0,12}$ and its vertex coloring.

Fig. 3 $G_{0,12}:$ vertex coloring and clique.

Theorem 3.8.

For every $n\in \mathbb{N}$, the integral sum graph $G_{0,n}$ has

1. the chromatic number $\chi (G_{0,n})$ = $\lceil \frac{n}{2}\rceil +1$;

2. the edge chromatic number ${\chi }^{\prime }(G_{0,n})$ = n.

Proof.

The integral sum graph $G_{0,n}$ is obtained by the labeling $f:V(G_{0,n})\to \mathbb{N}\cup \left\{0\right\}$ defined by $f(v_i)=i$, i = 0 to n.

1. Using Theorem 1.1, $G_{0,n}\cong K_1+G_n$ which implies, $\chi (G_{0,n})$ = $\chi (K_1)$ + $\chi (G_n)$ = 1+$\lceil \frac{n}{2}\rceil$ using Theorem 3.4

2. For $n\in \mathbb{N}$, the maximum degree of integral sum graph $G_{0,n}$ is $\Delta (G_{0,n})$ = n. Using Theorem 2.1, we get, $\Delta (G_{0,n})\le {\chi }^{\prime }(G_{0,n})\le \Delta (G_{0,n})+1$. Now, we present a proper edge coloring of $G_{0,n}$ with n colors so that ${\chi }^{\prime }(G_{0,n})$ = n.

Let c_k denote k^th color assigned to an edge and C_k denote the color class of edges, each with color c_k in $G_{0,n},n\in \mathbb{N}$. Color all the edges in the set $\{v_i{v}_j\in E(G_{0,n}):i+j=k, 0\le i,j\le n, i\ne j,1\le k\le n\}$ with the same color c_k. Clearly, the edges of $G_{0,n}$ take at the most n colors since $1\le i+j\le n$. Also, there are n edges incident at the vertex v₀, and all these n edges take n distinct colors. That is, ${\chi }^{\prime }(G_{0,n})$ = n, $n\in \mathbb{N}$. See Figure 4 for the edge coloring of $G_{0,12}$ and it can be done as the illustration 3.5 for G₁₃. □

Fig. 4 $G_{0,12}:$ edge coloring.

4 Integral sum graphs $G_{-r,n}$ are perfect

In this section, we prove that for $r,n\in \mathbb{N}$, (i) integral sum graphs $G_{-r,n}$ are perfect; (ii) the chromatic number of $G_{-r,n}$ = $1+\lceil \frac{r}{2}\rceil +\lceil \frac{n}{2}\rceil$ and (iii) the edge chromatic number of $G_{-r,n}$ = r + n. These results are illustrated by examples.

Theorem 4.1.

For $r,n\in \mathbb{N}$, the integral sum graph $G_{-r,n}$ is perfect.

Proof.

Using Theorem 1.1, $G_{-r,n}\cong K_1+(G_{-r}+G_n)\cong K_1+(G_n+G_{-r})\cong (K_1+G_n)+G_{-r}\cong G_{o,n}+G_{-r}$ since join operation is associative as well as commutative among undirected graphs. Graphs G_r and $G_{-r}$ are isomorphic without vertex labeling and so both are perfect by Theorems 3.1 whereas $G_{0,n}$ is perfect by Theorem 3.7 for $r,n\in \mathbb{N}$. Therefore using Theorem 3.6, graph $G_{o,n}+G_{-r}$ is perfect for $r,n\in \mathbb{N}$. This implies, graph $G_{-r,n}\cong G_{o,n}+G_{-r}$ is perfect for $r,n\in \mathbb{N}$. □

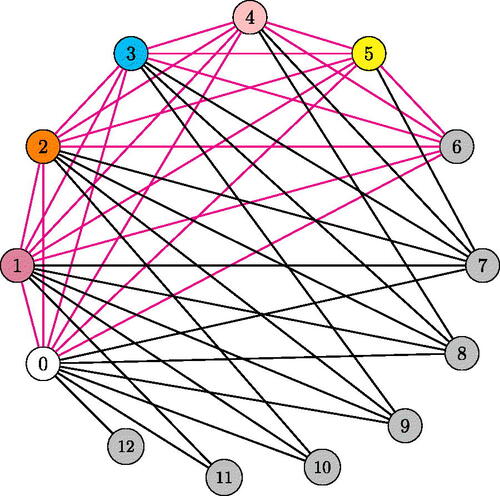
Illustration 4.2. Consider the integral sum graph $G_{-5,7}$ given in Figure 5. Vertices $v_1,v_2,v_3,v_4,v_0,v_{-1},v_{-2},v_{-3}$ (Vertices joined by the edges with magenta color) in $G_{-5,7}$ form a clique. Thus, $\omega (G_{-5,7})$ = 8. These vertices can be colored by 8 distinct colors, say $c_1,c_2,c_3,c_4,c_5,c_6,c_7,c_8$, respectively. Vertices $v_{-4}$ and $v_{-5}$ are nonadjacent to $v_{-3}$ and can be colored by c₈, the color of $v_{-3}$. Vertices v₇, v₆ and v₅ are nonadjacent to v₄ and can be colored by c₄. Therefore, $\chi (G_{-5,7})$ = 8. This implies, $G_{-5,7}$ is 1-perfect. Likewise we can show that every induced subgraph of $G_{-5,7}$ is 1-perfect. This implies, graph $G_{-5,7}$ is perfect.

Fig. 5 $G_{-5,7}:$ vertex coloring.

Theorem 4.3.

[13] For $n\in \mathbb{N}$,

1. ${\chi }^{\prime }(G_{-1,1})$ = 3.

2. ${\chi }^{\prime }(G_{-1,n})$ = n + 1 for $n\ge 2$.

3. ${\chi }^{\prime }(G_{-n,n})$ = 2n for $2\le n\le 6$.

In [13] (also see [10]), Vilfred proposed Theorem 4.4 (ii) as a conjecture and here we provide a proof.

Theorem 4.4.

For $r,n\in \mathbb{N}$,

1. the chromatic number of $G_{-r,n}$ is $\chi (G_{-r,n})$ = $1+\lceil \frac{r}{2}\rceil +\lceil \frac{n}{2}\rceil$;

2. the edge chromatic number of $G_{-r,n}$ is ${\chi }^{\prime }(G_{-r,n})$ = r + n.

Proof.

For $-r\le i\le n$ and $r,n\in \mathbb{N}$, let $f:V(G_{-r,n})\to \mathbb{Z}$ defined by $f(v_i)=i$ be the integral sum labeling of the graph $G_{-r,n}$.

1. For $r,n\in \mathbb{N}$, integral sum graph $G_{-r,n}$ is perfect by Theorem 4.1. Therefore $\chi (G_{-r,n})$ = $\omega (G_{-r,n})$ = $1+\lceil \frac{r}{2}\rceil +\lceil \frac{n}{2}\rceil$ follows from Lemma 2.4. Hence the result is true in this case. Figure 5 shows the vertex coloring and clique in $G_{-5,7}$.

2. For $r,n\in \mathbb{N}$, the maximum degree of integral sum graph $G_{-r,n}$ is $\Delta (G_{-r,n})$ = r + n. And using Theorem 2.1, we get, $\Delta (G_{-r,n})\le {\chi }^{\prime }(G_{-r,n})\le \Delta (G_{-r,n})+1$. Here we present a proper edge coloring of the integral sum graph $G_{-r,n}$ with r + n colors so ${\chi }^{\prime }(G_{-r,n})=r+n$ for $r,n\in \mathbb{N}$.

Let c_k denote k^th color assigned to an edge and C_k denote the color class of edges, each with color c_k in $G_{-r,n},r,n\in \mathbb{N}$. For $r,n\in \mathbb{N}$, color the edges of $G_{-r,n}$ as follows.

$v_0{v}_j\mapsto$ c_j, $1\le j\le n$; i.e., edge $v_0{v}_j$ is taking color c_j, $1\le j\le n$; $$v_0{v}_{-i}\mapsto c_{i+n},1\le i\le \mathrm{r;}$$

$v_{-i}{v}_j\mapsto c_{i+j}$, $1\le i\le r$ and $1\le j\le n-1$;

$v_{-i}{v}_n\mapsto c_{2i+n}$, $1\le i\le \lfloor \frac{r}{2}\rfloor$;

$v_{-i}{v}_n\mapsto c_{i-\lfloor \frac{r}{2}\rfloor }$, $\lfloor \frac{r}{2}\rfloor <i\le r,n>\lceil \frac{r}{2}\rceil$;

$v_{-i}{v}_n\mapsto c_{i-\lfloor \frac{r}{2}\rfloor }$, $\lfloor \frac{r}{2}\rfloor <i\le \lfloor \frac{r}{2}\rfloor +n-1,n\le \lceil \frac{r}{2}\rceil$;

$v_{-i}{v}_n\mapsto c_{2(i-\lfloor \frac{r}{2}\rfloor )-n+1}$, $\lfloor \frac{r}{2}\rfloor +n\le i\le r,n\le \lceil \frac{r}{2}\rceil$;

$v_i{v}_j\mapsto c_{i+j+r}$, $1\le i,j,i+j\le n$ and i < j and

$v_{-i}{v}_{-j}\mapsto c_{i+j+n}$, $1\le i,j,i+j\le r$ and i < j.

It is clear from the above edge coloring that colors c₁ to $c_{n+r}$ are assigned to the edges of $G_{-r,n}$ and no more edge colors are required. And also colors of edges at each vertex of $G_{-r,n}$ are all distinct by the following. By Theorem 1.1, we have $G_{-r,n}\cong K_1+(G_{-r}+G_n)$. Also, $G_{-r}+G_n\cong G_{-r}\cup G_n\cup K_{-r,n}$.

In $G_{-r,n}$, colors c₁, c₂, …, $c_{n+r}$ are assigned to the n + r edges incident at the vertex v₀.

In $K_{-r,n}$, we get the following possible colors taken by its edges incident at each of its vertices under the coloring already assigned to the edges of $G_{-r,n}$.

1. For $1\le j\le n-1$, distinct colors $c_{j+1},c_{j+2}$, …, $c_{j+r}$ are assigned to the r edges incident at v_j. And these colors are also different from color c_j of the edge $v_0{v}_j$ at v₀.

2. For $n>\lceil \frac{r}{2}\rceil$, distinct colors $c_{2+n},c_{4+n}$, …, $c_{2(\lfloor \frac{r}{2}\rfloor -1)+n},c_{2\lfloor \frac{r}{2}\rfloor +n},c_1,c_2,\dots ,c_{r-\lfloor \frac{r}{2}\rfloor }$ are assigned to the r edges incident at v_n and these colors are different from color c_n of the edge $v_0{v}_n$ at v_n. Clearly, $2\lfloor \frac{r}{2}\rfloor +n\le$ r + n and thus the colors assigned are from the r + n colors only.

3. For $n\le \lceil \frac{r}{2}\rceil$, distinct colors $c_{2+n},c_{4+n}$, …, $c_{2(\lfloor \frac{r}{2}\rfloor -1)+n},c_{2\lfloor \frac{r}{2}\rfloor +n},c_1,c_2,\dots ,c_{\lfloor \frac{r}{2}\rfloor +n-1},c_{n+1},c_{n+3},\dots ,c_{2\lceil \frac{r}{2}\rceil -n+1}$ are assigned to the r edges incident at v_n and these colors are different from color c_n of the edge $v_0{v}_n$ at v_n. Clearly, $2\lfloor \frac{r}{2}\rfloor +n,2\lceil \frac{r}{2}\rceil -n+1\le$ r + n and atmost r + n colors are assigned.

4. For $1\le i\le \lfloor \frac{r}{2}\rfloor$, distinct colors $c_{i+1},c_{i+2}$, …, $c_{i+n-1},c_{2i+n}$ are assigned to the n edges incident at $v_{-i}$. And all these colors are different from color $c_{i+n}$ of the edge $v_0{v}_{-i}$ at $v_{-i}$.

5. For $n>\lceil \frac{r}{2}\rceil$ and $\lfloor \frac{r}{2}\rfloor <i\le r$, distinct colors $c_{i+1},c_{i+2}$, …, $c_{i+n-1},c_{i-\lfloor \frac{r}{2}\rfloor }$ are assigned to the n edges incident at $v_{-i}$ and all these colors are different from color $c_{i+n}$ of the edge $v_0{v}_{-i}$ at $v_{-i}$.

6. For $n\le \lceil \frac{r}{2}\rceil$ and $\lfloor \frac{r}{2}\rfloor <i\le \lfloor \frac{r}{2}\rfloor +n-1$, distinct colors $c_{i+1},c_{i+2}$, …, $c_{i+n-1},c_{i-\lfloor \frac{r}{2}\rfloor }$ are assigned to the n edges incident at $v_{-i}$ and all these colors are different from color $c_{i+n}$ of the edge $v_0{v}_{-i}$ at $v_{-i}$.

7. For $n\le \lceil \frac{r}{2}\rceil$ and $\lfloor \frac{r}{2}\rfloor +n\le i\le r$, distinct colors $c_{i+1},c_{i+2}$, …, $c_{i+n-1},c_{2(i-\lfloor \frac{r}{2}\rfloor )-n+1}$ are assigned to the n edges incident at $v_{-i}$ and all these colors are different from color $c_{i+n}$ of the edge $v_0{v}_{-i}$ at $v_{-i}$.

Thus, in the above edge coloring of $G_{-r,n}$, edges of $K_{-r,n}$ take colors from the r + n colors and colors of edges incident at each vertex of $K_{-r,n}$ are all distinct.

In G_n, for $1\le i,j\le n,i\ne j$ and $3\le i+j\le n$, color of edge $v_i{v}_j$ is $c_{i+j+r}$ and thereby edges of G_n are taking colors only from the colors $c_{3+r},c_{4+r}$, …, $c_{n+r}$; edge colors $c_{i+j+r}$ at v_i are all distinct and also different from c_i of the edge $v_0{v}_i$ at v_i as well as that of other possible colors of edges which incident at v_i in $G_{-r,n}$ where $i\ne j$ and $3\le i+j\le n$. The same arguments also hold when i and j are interchanged.

In $G_{-r}$, for $1\le i,j\le r,i\ne j$ and $3\le i+j\le r$, color of edge $v_{-i}{v}_{-j}$ is $c_{i+j+n}$ and thereby edges of $G_{-r}$ are taking colors only from the colors $c_{3+n},c_{4+n}$, …, $c_{r+n}$; edge colors $c_{i+j+n}$ at $v_{-i}$ are all distinct and also different from $c_{i+n}$ of the edge $v_0{v}_{-i}$ at $v_{-i}$ as well as that of other possible colors of edges which incident at $v_{-i}$ in $G_{-r,n}$ where $i\ne j$ and $3\le i+j\le r$. The same arguments also hold when i and j are interchanged in this case.

Thus, in the above edge coloring, edges of $G_{-r,n}$ takes only r + n number of colors and colors of edges incident at each vertex of $G_{-r,n}$ are all distinct and thereby ${\chi }^{\prime }(G_{-r,n})$ = $r+n$ since $\Delta (G_{-r,n})\le {\chi }^{\prime }(G_{-r,n})\le \Delta (G_{-r,n})+1$ by Theorem 2.1. □

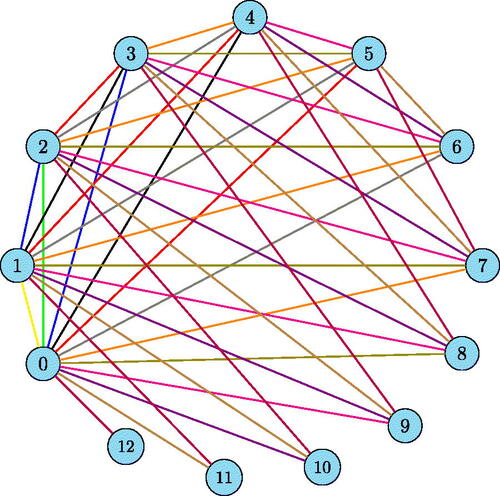
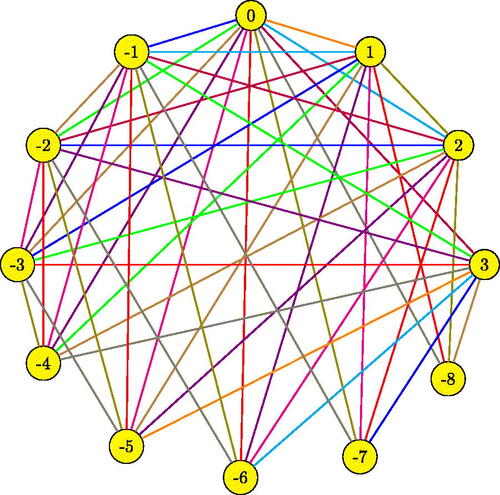
Illustration 4.5. Consider the integral sum graph $G_{-8,3}$, the case where $n\le \lceil \frac{r}{2}\rceil$. We know $\Delta (G_{-8,3})$ = 11. Using the algorithm given in the above proof, we can color the edges of $G_{-8,3}$ as follows. $$c_1\to v_0{v}_1,v_{-5}{v}_{\mathrm{3;}}$$ $$c_2\to v_0{v}_2,v_{-1}{v}_1,v_{-6}{v}_{\mathrm{3;}}$$ $$c_3\to v_0{v}_3,v_{-1}{v}_2,v_{-2}{v}_{\mathrm{1;}}$$ $$c_4\to v_0{v}_{-1},v_{-2}{v}_2,v_{-3}{v}_1,v_{-7}{v}_{\mathrm{3;}}$$ $$c_5\to v_0{v}_{-2},v_{-1}{v}_3,v_{-3}{v}_2,v_{-4}{v}_{\mathrm{1;}}$$ $$c_6\to v_0{v}_{-3},v_{-1}{v}_{-2},v_{-4}{v}_2,v_{-5}{v}_1,v_{-8}{v}_{\mathrm{3;}}$$ $$c_7\to v_0{v}_{-4},v_{-1}{v}_{-3},v_{-2}{v}_3,v_{-5}{v}_2,v_{-6}{v}_{\mathrm{1;}}$$ $$c_8\to v_0{v}_{-5},v_{-1}{v}_{-4},v_{-2}{v}_{-3},v_{-6}{v}_2,v_{-7}{v}_{\mathrm{1;}}$$ $$c_9\to v_0{v}_{-6},v_{-1}{v}_{-5},v_{-2}{v}_{-4},v_{-3}{v}_3,v_{-7}{v}_2,v_{-8}{v}_{\mathrm{1;}}$$ $$c_{10}\to v_0{v}_{-7},v_{-1}{v}_{-6},v_{-2}{v}_{-5},v_{-3}{v}_{-4},v_{-8}{v}_{\mathrm{2;}}$$ $$c_{11}\to v_0{v}_{-8},v_{-1}{v}_{-7},v_{-2}{v}_{-6},v_{-3}{v}_{-5},v_{-4}{v}_3,v_1{v}_2.$$

See Figure 7 for the edge coloring of $G_{-8,3}$. Here we colored the integral sum graph $G_{-8,3}$ using 11 colors. That is, ${\chi }^{\prime }(G_{-8,3})$ = 11 = 8 + 3. Similarly the integral sum graph $G_{-5,7}$, the case where $n>\lceil \frac{r}{2}\rceil$, can be colored using 12 colors by the algorithm given in the above proof. That is ${\chi }^{\prime }(G_{-5,7})$ = 12 = 5 + 7. See Figure 6 for the edge coloring of $G_{-5,7}$.

Fig. 6 $G_{-5,7}$ with edge coloring.

Fig. 7 $G_{-8,3}$ with edge coloring.

Theorem 4.6.

For positive integers r and n, integral sum graphs G_n, $G_{0,n}$ and $G_{-r,n}$ are of class 1.

Proof.

Using Theorems 3.4, 3.8 and 4.4, we get ${\chi }^{\prime }(G_n)$ = n – 2 = $\Delta (G_n)$ = degree of the vertex with label 1, ${\chi }^{\prime }(G_{0,n})$ = n = $\Delta (G_{0,n})$ = degree of the vertex with label 0 and ${\chi }^{\prime }(G_{-r,n})$ = r + n = $\Delta (G_{-r,n})$ = degree of the vertex with label 0. □

Acknowledgments

The first, second and fourth authors express their sincere gratitude to the Central University of Kerala, Periye, Kasaragod - 671316, Kerala, India for providing facilities to carry out this research work. Also, the authors are thankul to the anonymous reviewers for their valuable comments and suggestions to improve the presentation of the paper.

Disclosure statement

The authors declare that there is no conflict of interests regarding the publication of this paper.

Additional information

Funding

The first author would like to acknowledge her gratitude to the University Grants Commission (UGC), India, for providing financial support in the form of Junior Research fellowship (Ref. No.: 19/06/2016(i)EU-V). The second author would like to acknowledge her gratitude to the Council of Scientific and Industrial Research (CSIR), India, for the financial support under the CSIR Junior Research Fellowship scheme.