On local distance antimagic labeling of graphs

Abstract

Let $G=(V,E)$ be a graph of order n and let $f:V\to \{1,2\dots ,n\}$ be a bijection. For every vertex $v\in V$, we define the weight of the vertex v as $w(v)=\sum _{x\in N(v)}f(x)$ where N(v) is the open neighborhood of the vertex v. The bijection f is said to be a local distance antimagic labeling of G if $w(u)\ne w(v)$ for every pair of adjacent vertices $u,v\in V$. The local distance antimagic labeling f defines a proper vertex coloring of the graph G, where the vertex v is assigned the color w(v). We define the local distance antimagic chromatic number ${\chi }_{ld}(G)$ to be the minimum number of colors taken over all colorings induced by local distance antimagic labelings of G. In this paper we obtain the local distance antimagic labelings for several families of graphs including the path P_n, the cycle C_n, the wheel graph W_n, friendship graph F_n, the corona product of graphs $G°\overline{K_m}$, complete multipartite graph and some special types of the caterpillars. We also find upper bounds for the local distance antimagic chromatic number for these families of graphs.

Keywords:

• Distance magic graphs
• local distance antimagic labeling
• local distance antimagic chromatic number

2010 MATHEMATICS SUBJECT CLASSIFICATION:

• 05C 78

1 Introduction

By a graph $G=(V,E)$, we mean a finite, undirected and connected graph with neither loops nor multiple edges. The order $\left|V\right|$ and the size $\left|E\right|$ are denoted by n and m, respectively. For graph theoretic terminology and notation we refer to Chartrand and Lesniak [3].

The notion of antimagic labeling was introduced by Hartsfield and Ringel [8] in 1990. A graph G is antimagic if the edges of G can be labeled by the numbers $\{1,2,\dots ,m\}$ such that the sums of the labels of the edges incident to each vertex (called weight of a vertex) are distinct. Also they conjectured that every connected graph different from K₂ is antimagic. This conjecture is still open.

Arumugam and Kamatchi [2] considered a vertex version of antimagic labeling of a graph. Let $G=(V,E)$ be a graph of order n and let f be a bijection from V onto $\{1,2,\dots ,n\}$. Given such a bijection f, the weight of a vertex is defined as: $w(v)=\sum _{x\in N(v)}f(x)$, where N(v) is the open neighborhood of the vertex v, which is defined as the set of all vertices of the graph G which are adjacent to v. The bijection f is called distance antimagic labeling if all vertices have distinct vertex-weights. A graph is called distance antimagic if it admits a distance antimagic labeling (see [9]). A distance antimagic labeling is said to be an $(a,d)-$ distance antimagic labeling if the set of vertex weights is $\{a,a+d,a+2d,\dots ,a+(n-1)d\}$.

In [1] Arumugam et al. introduced a local version of antimatic labeling as follows: let $G=(V,E)$ be a connected graph with $\left|V\right|=n$ and $\left|E\right|=m$. A bijection $f:E\to \{1,2,\dots ,m\}$ is called a local antimagic labeling if for any two adjacent vertices u and v, $w(u)\ne w(v)$, where $w(u)=\sum _{e\in E(u)}f(e)$, and E(u) is the set of edges incident to u. Thus any local antimagic labeling induces a proper vertex coloring of G where the vertex v is assigned the color w(v). The local antimagic chromatic number ${\chi }_{la}(G)$ is the minimum number of colors taken over all colorings induced by local antimagic labelings of G.

Motivated by this concept, in 2018 Handa et al. [6] introduced the notion of a local distance antimagic labeling as follows: let $G=(V,E)$ be a graph of order n and let $f:V\to \{1,2\dots ,n\}$ be a bijection. For every vertex $v\in V$, define the weight of v as $w(v)=\sum _{x\in N(v)}f(x)$. The labeling f is said to be a local distance antimagic labeling of G if $w(u)\ne w(v)$ for every pair of adjacent vertices $u,v\in V$. A graph which admits such a labeling is called a local distance antimagic graph. A local distance antimagic labeling induces a proper vertex coloring of the graph, with the vertex v assigned the color w(v). The local distance antimagic chromatic number ${\chi }_{ld}(G)$ is the minimum number of colors taken over all colorings induced by local distance antimagic labelings of G (see [7]). 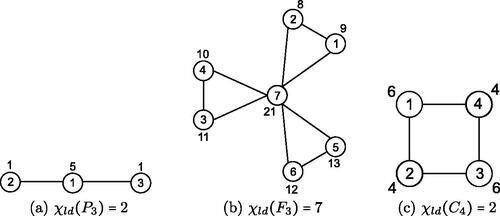An illustration of a local distance antimagic labeling of $P_3,F_3$, and C₄ are shown in Figure 1.

Fig. 1 Local distance antimagic labelings of P₃, F₃, and C₄.

Remark 1.1.

Every distance antimagic graph is local distance antimagic, but the converse is not true. For example, the graph P₃ is local distance antimagic however it is not distance antimagic. Furthermore for every local distance antimagic graph G of order n, $\chi (G)\le {\chi }_{ld}(G)$, where $\chi (G)$ is the chromatic number of the graph G.

The wheel graph W_n is the graph $C_n+K_1$, formed by joining an isolated vertex to every vertex of a cycle C_n. The friendship graph F_n is a graph which consists of n triangles C₃ with a common vertex (see Figure 7). A vertex v in a graph G is called a support vertex if it is adjacent to a vertex of degree 1 in G. A vertex of degree 1 is called a pendent vertex or a leaf.

The corona product of two graphs G and H is the graph obtained by taking one copy of G and $|V(G)|$ copies of H and joining the ith vertex of G to every vertex in the ith copy of H. The corona product of G and H is denoted by $G°H$.

We now present an important result on magic rectangles which will be useful in our subsequent investigation. A magic rectangle $R_{a,b}$ is an a × b array with entries $1,2,\dots ,ab$, each appearing once, such that the sum of entries in each row is equal to $b\left(\frac{ab+1}{2}\right)$ and the sum of each column is equal to $a\left(\frac{ab+1}{2}\right)$. The following theorem gives the necessary and sufficient condition for existence of a magic rectangle $R_{a,b}$.

Theorem 1.2.

[5] For $a,b>1$, there is a magic rectangle $R_{a,b}$ if and only if $a\equiv b(\mathrm{mod}2)$ and $(a,b)\ne (2,2)$.

1.1 Local distance antimagic chromatic number of some graphs

For two sets A and B the symmetric difference $A\Delta B$ is defined to be the set $(A\cup B)-(A\cap B)$.

Proposition 1.3.

Let G be a local distance antimagic graph of order n. If u, v are vertices such that $|N(u)\Delta N(v)|=1or2$, then $w(u)\ne w(v)$.

Proof.

Let $f:V(G)\to \{1,2,\dots ,n\}$ be a local distance antimagic labeling of G. We consider the following two cases:

Case 1: Suppose $|N(u)\Delta N(v)|=1$. Let $x\in V$ such that $N(u)\Delta N(v)=\left\{x\right\}$. Then $|w(u)-w(v)|=|f(x)|\ne 0$. Therefore, $w(u)\ne w(v)$.

Case 2: Suppose $|N(u)\Delta N(v)|=2$. Let $x,y\in V$ such that $N(u)\Delta N(v)=\{x,y\}$. Without loss of generality suppose that $x\in N(u)$, then either $y\in N(u)$ or $y\in N(v)$. If $y\in N(u)$, then $|w(u)-w(v)|=|f(x)+f(y)|$. On the other hand if $y\in N(v)$, then $|w(u)-w(v)|=|f(x)-f(y)|$. In both cases $|w(u)-w(v)|\ne 0$, hence $w(u)\ne w(v)$. □

We begin our investigation of a local distance antimagic coloring of graphs with a path P_n. It is easy to see that ${\chi }_{ld}(P_2)=2$ and ${\chi }_{ld}(P_3)=2$ (see Figure 1). For $n\ge 4$ we have the following result.

Proposition 1.4.

For a path P_n with $n\ge 4,{\chi }_{ld}(P_n)\ge 3$.

Proof.

Let $P_n=v_0{v}_1\dots v_{n-1}$ be a path on n vertices with $n\ge 4$. Let f be a local distance antimagic labeling of P_n. We first calculate the weights of the vertices v₀, v₁ and v₂. We shall show that these vertices have distinct weights, hence proving the result. Suppose $w(v_0)=w_0,w(v_1)=w_1$ and $w(v_2)=w_2$. Now, since v₀ and v₁ are adjacent vertices, therefore $w_0\ne w_1$. In the same way since v₁ and v₂ are adjacent, therefore $w_1\ne w_2$. Now, since $|N(v_0)\Delta N(v_2)|=1$, therefore by Proposition 1.3, $w_0\ne w_2$. Therefore the vertices $v_0,v_1,v_2$ have distinct weights and hence ${\chi }_{ld}(P_n)\ge 3$. Examples of local distance antimagic labeling of P₅ and P₁₁ are shown in Figures 2 and 3 respectively. □

Fig. 2 A local distance antimagic labeling of P₅ proving that ${\chi }_{ld}(P_5)=3$.

Fig. 3 A local distance antimagic labeling of P₁₁ proving that ${\chi }_{ld}(P_{11})=3$.

Proposition 1.5.

For $n\ge 5$ and $n\equiv 0\text{or}1(\mathrm{mod}3)$, ${\chi }_{ld}(P_n) \ge 4$.

Proof.

Let $P_n=v_0{v}_1\dots v_{n-1}$ be a path on n vertices with $n\ge 5$ and $n\equiv 0\text{or}1(\mathrm{mod}3)$. Let f be a local distance antimagic labeling of P_n. Since ${\chi }_{ld}(P_n)\ge 3$, the labeling f admits at least three distinct vertex weights. Suppose that f admits exactly three distinct weights. Let $w(v_i)=w_i$ where $0\le i\le n-1$. From the previous proof we have seen that the weights $w_0,w_1,w_2$ are distinct. Now we consider the following two cases:

Case 1: $n\equiv 1(\mathrm{mod}3)$. Consider the weight of the vertex v₃. Since v₃ and v₂ are adjacent, therefore $w_3\ne w_2$. Moreover, since $|N(v_1)\Delta N(v_3)|=2$, therefore by Proposition 1.3, $w(v_1)\ne w(v_3)$. Now since the labeling f admits exactly 3 colors, it follows that $w(v_3)=w_0$. Using the same argument we can show that $w(v_4)=w_1$, $w(v_5)=w_2$ and so on. Hence $w(v_i)=w_{i(\text{mod}3)}$. Now, since $n\equiv 1(\mathrm{mod}3)$, it follows that $w(v_{n-1})=w_0$. However, $w_0=w(v_0)=f(v_1)$ and $w_0=w(v_{n-1})=f(v_{n-2})$. Therefore $f(v_{n-2})=f(v_1)$ which contradicts the fact that f is a bijection. Hence the labeling f must admit at least 4 colors.

Case 2: $n\equiv 0(\mathrm{mod}3)$. Now for each $0\le i\le n-1$, $w(v_i)=w_{i(\text{mod}3)}$ and since $n\equiv 0(\mathrm{mod}3)$ it follows that $w(v_{n-1})=w_2$. Now $w_0=w(v_0)=f(v_1)$ and $w_2=w(v_2)=f(v_1)+f(v_3)$. Therefore, $w_2>w_0$. Similarly $w_2=w(v_{n-1})=f(v_{n-2})$ and $w_0=w(v_{n-3})=f(v_{n-2})+f(v_{n-4})$. Therefore, $w_0>w_2$. This is a contradiction. Hence for $n\ge 4$ and $n\equiv 0\text{or}1(\mathrm{mod}3),{\chi }_{ld}(P_n)\ge 4$. □

Lemma 1.6.

The path P_n is local distance antimagic with ${\chi }_{ld}(P_n)\le 6$.

Proof.

Let $V=\{v_0,v_1,\dots ,v_{n-1}\}$ be the vertex set of P_n. We define a local distance antimagic labeling f of P_n, which admits at most 6 distinct colors. We consider the following four cases:

Case 1: $n\equiv 0(\mathrm{mod}4)$.

In this case, we define the vertex labels as follows: $$f(v_i)=\{\begin{array}{cc}\frac{3n}{4}-\frac{i}{4}\hfill & \text{ if }i\equiv 0(\mathrm{mod}4)\hfill \\ \frac{n}{2}-\frac{i-1}{4}\hfill & \text{ if }i\equiv 1(\mathrm{mod}4)\hfill \\ \frac{3n}{4}+\frac{i+2}{4}\hfill & \text{ if }i\equiv 2(\mathrm{mod}4)\hfill \\ \frac{i+1}{4}\hfill & \text{ if }i\equiv 3(\mathrm{mod}4).\hfill \end{array}$$

Now the weight of vertices are as follows: $w(v_{n-1})=n$ and for $i\ne n-1$ we have; $$w(v_i)=\{\begin{array}{cc}\frac{n}{2}\hfill & \text{ if }i\equiv 0(\mathrm{mod}4)\hfill \\ \frac{3n}{2}+1\hfill & \text{ if }i\equiv 1(\mathrm{mod}4)\hfill \\ \frac{n}{2}+1\hfill & \text{ if }i\equiv 2(\mathrm{mod}4)\hfill \\ \frac{3n}{2}\hfill & \text{ if }i\equiv 3(\mathrm{mod}4).\hfill \end{array}$$

Case 2: $n\equiv 1(\mathrm{mod}4)$.

Define the vertex labels as follows: $$f(v_i)=\{\begin{array}{cc}\frac{n+1}{2}-\frac{i}{4}\hfill & \text{ if }i\equiv 0(\mathrm{mod}4)\hfill \\ \frac{3n+1}{4}+\frac{i+3}{4}\hfill & \text{ if }i\equiv 1(\mathrm{mod}4)\hfill \\ \frac{i+2}{4}\hfill & \text{ if }i\equiv 2(\mathrm{mod}4)\hfill \\ \frac{3n+1}{4}-\frac{i-3}{4}\hfill & \text{ if }i\equiv 3(\mathrm{mod}4).\hfill \end{array}$$

Following are the resulting vertex weights: $w(v_0)=\frac{3n+5}{4}$ and $w(v_{n-1})=\frac{n+3}{2}$.

For $i\ne 0$ and n – 1, $$w(v_i)=\{\begin{array}{cc}\frac{3n+5}{2}\hfill & \text{ if }i\equiv 0(\mathrm{mod}4)\hfill \\ \frac{n+3}{2}\hfill & \text{ if }i\equiv 1(\mathrm{mod}4)\hfill \\ \frac{3n+3}{2}\hfill & \text{ if }i\equiv 2(\mathrm{mod}4)\hfill \\ \frac{n+1}{2}\hfill & \text{ if }i\equiv 3(\mathrm{mod}4).\hfill \end{array}$$

Case 3: $n\equiv 2(\mathrm{mod}4)$.

Define the vertex labels as follows: $$f(v_i)=\{\begin{array}{cc}\frac{3n+2}{4}+\frac{i}{4}\hfill & \text{ if }i\equiv 0(\mathrm{mod}4)\hfill \\ \frac{n}{2}-\frac{i-1}{4}\hfill & \text{ if }i\equiv 1(\mathrm{mod}4)\hfill \\ \frac{3n-2}{4}-\frac{i-2}{4}\hfill & \text{ if }i\equiv 2(\mathrm{mod}4)\hfill \\ \frac{i+1}{4}\hfill & \text{ if }i\equiv 3(\mathrm{mod}4).\hfill \end{array}$$

Following are the resulting vertex weights.

For $i\ne n-1$ $$w(v_i)=\{\begin{array}{cc}\frac{n}{2}\hfill & \text{ if }i\equiv 0(\mathrm{mod}4)\hfill \\ \frac{3n}{2}\hfill & \text{ if }i\equiv 1(\mathrm{mod}4)\hfill \\ \frac{n}{2}+1\hfill & \text{ if }i\equiv 2(\mathrm{mod}4)\hfill \\ \frac{3n}{2}+1\hfill & \text{ if }i\equiv 3(\mathrm{mod}4).\hfill \end{array}$$and $w(v_{n-1})=n$.

Case 4: $n\equiv 3(\mathrm{mod}4)$.

Define the vertex labels as follows: $$f(v_i)=\{\begin{array}{cc}\frac{n+1}{2}-\frac{i}{4}\hfill & \text{ if }i\equiv 0(\mathrm{mod}4)\hfill \\ \frac{3n+3}{4}+\frac{i-1}{4}\hfill & \text{ if }i\equiv 1(\mathrm{mod}4)\hfill \\ \frac{i+2}{4}\hfill & \text{ if }i\equiv 2(\mathrm{mod}4)\hfill \\ \frac{3n-1}{4}-\frac{i-3}{4}\hfill & \text{ if }i\equiv 3(\mathrm{mod}4).\hfill \end{array}$$

Resulting vertex weights are as follows: $w(v_{n-1})=n$, $w(v_0)=\frac{3n+3}{4}$.

For $i\ne 0,n-1$. $$w(v_i)=\{\begin{array}{cc}\frac{3n+3}{2}\hfill & \text{ if }i\equiv 0(\mathrm{mod}4)\hfill \\ \frac{n+3}{2}\hfill & \text{ if }i\equiv 1(\mathrm{mod}4)\hfill \\ \frac{3n+1}{2}\hfill & \text{ if }i\equiv 2(\mathrm{mod}4)\hfill \\ \frac{n+1}{2}\hfill & \text{ if }i\equiv 3(\mathrm{mod}4).\hfill \end{array}$$

In each of these cases, there are either five or six distinct weights (colors) of the vertices with respect to the labeling f, hence ${\chi }_{ld}(P_n)\le 6$. This completes the proof. □

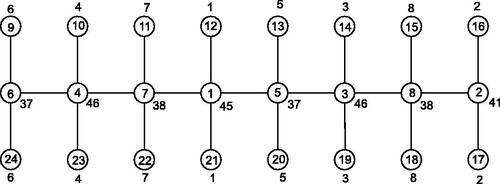
An illustration of a local distance antimagic labeling of P₁₀ is shown in Figure 4. A local distance antimagic labeling of P₁₃ is shown in Figure 5.

Fig. 4 A local distance antimagic labeling of P₁₀.

Fig. 5 A local distance antimagic labeling of P₁₃.

Theorem 1.7.

For the path P_n, $n\ge 5$ and $n\equiv 0\text{ or }1(\mathrm{mod}3),4\le {\chi }_{ld}(P_n)\le 6$.

Proof.

The proof follows from Proposition 1.5 and Lemma 1.6. □

Theorem 1.8.

For the path P_n, $n\ge 4$ and $n\equiv 2(\mathrm{mod}3),3\le {\chi }_{ld}(P_n)\le 6$.

Proof.

The proof follows from Proposition 1.4 and Lemma 1.6. □

We now study the local distance antimagic coloring for the cycle C_n. For n = 3, the graph $C_3\cong K_3$, hence ${\chi }_{ld}(C_3)=3$. For n = 4, ${\chi }_{ld}(C_4)=2$ (see Figure 1). For $n\ge 5$ we have the following result.

Proposition 1.9.

For the cycle C_n, $n\ge 5,{\chi }_{ld}(C_n)\ge 3$.

Proof.

Let $C_n=v_0{v}_1\dots v_{n-1}{v}_0$ be a cycle on n vertices with $n\ge 5$. Let f be a local distance antimagic labeling of C_n. We first calculate the weights of the vertices v₀, v₁ and v₂. We shall show that these weights are distinct, hence proving the result. Let $w(v_0)=w_0,w(v_1)=w_1$ and $w(v_2)=w_2$. Now, since v₀ and v₁ are adjacent vertices, therefore $w_0\ne w_1$. Similarly since v₁ and v₂ are adjacent, therefore $w_1\ne w_2$ and since $|N(v_0)\Delta N(v_2)|=2$, therefore by Proposition 1.3, $w_0\ne w_2$. Hence the weights $w_1,w_2,w_3$ are distinct. Therefore, ${\chi }_{ld}(C_n)\ge 3$. □

Proposition 1.10.

For $n\ge 5$ and $n\cancel{\equiv }0(\mathrm{mod}3),{\chi }_{ld}(C_n)\ge 4$.

Proof.

Let $C_n=v_0{v}_1\dots v_{n-1}{v}_0$ be a cycle on n vertices with $n\ge 5$ and $n\cancel{\equiv }0(\mathrm{mod}3)$. Let f be a local distance antimagic labeling of C_n. By Proposition 1.9 the labeling f admits at least three distinct vertex weights. Suppose that f admits exactly three distinct weights. Let $w(v_i)=w_i$. From the previous proof, the weights $w_0,w_1,w_2$ are distinct. Now consider the weight of the vertex v₃. Since v₃ and v₂ are adjacent, therefore $w_3\ne w_2$ and since $|N(v_3)\Delta N(v_1)|=2$, therefore by Proposition 1.3, $w_3\ne w_1$. Now since the labeling f admits exactly three distinct weights, it follows that w₃ = w₀. Using the same argument we can show that $w(v_4)=w_1,w(v_5)=w_2$ and so on. Therefore $w(v_i)=w_{i(\text{mod}3)}$. Next consider the weight of the vertex $v_{n-1}$. Since $v_{n-1}$ and v₀ are adjacent, therefore $w_{n-1}\ne w_0$ and since $|N(v_{n-1})\Delta N(v_1)|=2$, therefore by Proposition 1.3, $w_{n-1}\ne w_1$. Hence $w_{n-1}=w_2$, therefore $n-1\equiv 2(\mathrm{mod}3)$. Hence $n\equiv 0(\mathrm{mod}3)$ which is a contradiction. Therefore for $n\ge 5$ and $n\cancel{\equiv }0(\mathrm{mod}3),{\chi }_{ld}(C_n)\ge 4$. □

Lemma 1.11.

The cycle $C_n,n\ge 3$ is a local distance antimagic graph with ${\chi }_{ld}(C_n)\le 6$.

Proof.

Let $V=\{v_0,\dots ,v_{n-1}\}$ be the vertex set of C_n. We define a local distance antimagic labeling $f:V\to \{1,2,\dots ,n\}$ as follows:

Case 1: n is even. $$f(v_i)=\{\begin{array}{cc}\frac{i}{4}+1\hfill & \text{ if }i\equiv 0(\mathrm{mod}4)\hfill \\ \frac{n}{2}+\frac{i+3}{4}\hfill & \text{ if }i\equiv 1(\mathrm{mod}4)\hfill \\ \frac{n}{2}-\frac{i-2}{4}\hfill & \text{ if }i\equiv 2(\mathrm{mod}4)\hfill \\ n-\frac{i-3}{4}\hfill & \text{ if }i\equiv 3(\mathrm{mod}4).\hfill \end{array}$$

Now the weight of vertices are as follows: $w(v_0)=\frac{5n+8}{4},w(v_{n-1})=\frac{n+8}{4}$, when $n\equiv 0(\mathrm{mod}4)$ and $w(v_0)=\frac{5n+6}{4},w(v_{n-1})=\frac{n+6}{4}$, when $n\equiv 2(\mathrm{mod}4)$.

For $i\ne 0,n-1$ the vertex weights are $$w(v_i)=\{\begin{array}{cc}\frac{3n+4}{2}\hfill & \text{ if }i\equiv 0(\mathrm{mod}4)\hfill \\ \frac{n+2}{2}\hfill & \text{ if }i\equiv 1(\mathrm{mod}4)\hfill \\ \frac{3n+2}{2}\hfill & \text{ if }i\equiv 2(\mathrm{mod}4)\hfill \\ \frac{n+4}{2}\hfill & \text{ if }i\equiv 3(\mathrm{mod}4).\hfill \end{array}$$

Case 2: n is odd. $$f(v_i)=\{\begin{array}{cc}\frac{4+i}{4}\hfill & \text{ if }i\equiv 0(\mathrm{mod}4)\hfill \\ \frac{4n-i+1}{4}\hfill & \text{ if }i\equiv 1(\mathrm{mod}4)\hfill \\ \frac{n+1}{2}-\frac{i-2}{4}\hfill & \text{ if }i\equiv 2(\mathrm{mod}4)\hfill \\ \frac{n+1}{2}+\frac{i+1}{4}\hfill & \text{ if }i\equiv 3(\mathrm{mod}4).\hfill \end{array}$$

Now the vertex weights are as follows: $w(v_0)=\frac{5n+5}{4},w(v_{n-1})=\frac{3n+7}{4}$ for $n\equiv 3(\mathrm{mod}4)$ and $w(v_0)=\frac{5n+3}{4},w(v_{n-1})=\frac{3n+5}{4}$ when $n\equiv 1(\mathrm{mod}4)$,

For $i\ne 0,n-1$ the vertex weights are $$w(v_i)=\{\begin{array}{cc}\frac{3n+1}{2}\hfill & \text{ if }i\equiv 0(\mathrm{mod}4)\hfill \\ \frac{n+3}{2}\hfill & \text{ if }ı\equiv 1(\mathrm{mod}4)\hfill \\ \frac{3n+3}{2}\hfill & \text{ if }i\equiv 2(\mathrm{mod}4)\hfill \\ \frac{n+5}{2}\hfill & \text{ if }i\equiv 3(\mathrm{mod}4).\hfill \end{array}$$

In each of the above cases, there are only six distinct weights, whenever $n\ge 6$. Hence ${\chi }_{ld}(C_n)\le 6$. This completes the proof. □

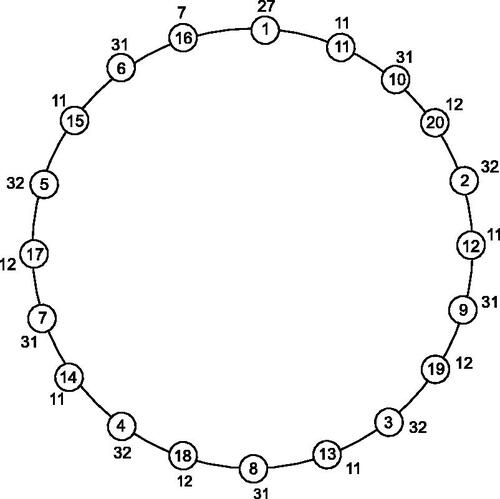
The illustration of a local distance antimagic labeling of C₂₀ is shown in Figure 6.

Fig. 6 A local distance antimagic labeling of C₂₀.

Theorem 1.12.

For the cycle C_n, $n\ge 5,3\le {\chi }_{ld}(C_n)\le 6$.

Proof.

The proof follows from Proposition 1.9 and Lemma 1.11. □

Theorem 1.13.

For the cycle C_n, $n\ge 5,n\cancel{\equiv }0(\mathrm{mod}3),4\le {\chi }_{ld}(C_n)\le 6$.

Proof.

The proof follows from Proposition 1.10 and Lemma 1.11. □

Proposition 1.14.

Let G be a local distance antimagic graph with m support vertices, then ${\chi }_{ld}(G)\ge m$.

Proof.

Let $v_1,v_2,\dots ,v_m$ be m support vertices of G. Let $u_1,u_2,\dots ,u_m$ be pendent vertices such that for $1\le i\le m$ the vertex u_i adjacent to v_i. Then for any local distance antimagic labeling f of G, $w_f(u_i)=f(v_i)$. Therefore the vertices u_i receive distinct weights under f. Hence ${\chi }_{ld}(G)\ge m$. □

Lemma 1.15.

For a local distance antimagic graph G, ${\chi }_{ld}(G)\ge \omega (G)$, where $\omega (G)$ is the clique number of G.

Proof.

Let $G\prime \subset G$ be a clique of order $\omega (G)$. Then for every local distance antimagic labeling f of G, each vertex in $G\prime$ receives a distinct weight under f. Hence it follows that ${\chi }_{ld}(G)$ $\ge \omega (G)$. □

Remark 1.16.

The complete graph K_n is local distance antimagic with ${\chi }_{ld}(K_n)=n$.

Lemma 1.17.

The wheel graph W_n, $n\ge 3$ is local distance antimagic with $3\le {\chi }_{ld}(W_n)\le 7$.

Proof.

Let $V=\{u,v_0,v_1,\dots ,v_{n-1}\}$ be the vertex set of W_n such that the vertices $v_0,v_1,\dots ,v_{n-1}$ form a cycle of length n and u is the central vertex of the wheel. We label the cycle using the labeling described in Lemma 1.11, and the vertex u is assigned the highest label n + 1. The resulting labeling is a local distance antimagic labeling of W_n which admits at most 7 distinct colors. By Lemma 1.15, ${\chi }_{ld}(W_n)\ge 3$. Hence, $3\le {\chi }_{ld}$ $(W_n)\le 7$. □

Theorem 1.18.

Let G be a local distance antimagic graph of order n with ${\chi }_{ld}(G)=r$, then for $n\equiv m(\mathrm{mod}2)$, ${\chi }_{ld}(G°\overline{K_m})\le n+r$.

Proof.

Let $u_1,u_2,\dots ,u_n$ be the vertices of graph G and let $v_{i,1},v_{i,2},\dots ,v_{i,m}$ be the m pendant vertices adjacent to u_i, in the graph $G°\overline{K_m}$. By Theorem 1.2, for $n\equiv m(\mathrm{mod}2)$, there exists a magic rectangle $R_{m,n}$ of order m × n. Let $C_1,C_2,\dots ,C_n$ be the n columns of the magic rectangle $R_{m,n}$. Define $C_i^{\prime }=C_i+n\overrightarrow{1}$, where $\overrightarrow{1}={[1,1,1\dots ,1]}^T$. The sum of entries in $C_i^{\prime }$ is $\frac{m(nm+2n+1)}{2}$. Let $f:V(G)\to \{1,2,\dots ,n\}$, be a local distance antimagic labeling of G which admits r distinct vertex weights. Let $w_f(u_i)$ be the vertex weights under the labeling f. We define a local distance antimagic labeling $f^{\prime }$ of $G°\overline{K_m}$ as follows: for each i, define $f^{\prime }(u_i):=f(u_i)$ and the vertices $v_{i,1},v_{i,2},\dots ,v_{i,m}$ are labeled with the elements of the column vector $C_i^{\prime }$. The resulting vertex weights under the labeling $f^{\prime }$ are as follows: $w_{f^{\prime }}(v_{i,j})=f(u_i)$, and $w_{f^{\prime }}(u_i)=w_f(u_i)+\frac{m(nm+2n+1)}{2}$. The labeling $f^{\prime }$ is a local distance antimagic labeling which admits at most n + r distinct colors. Hence ${\chi }_{ld}(G°\overline{K_m})\le n+r$. This completes the proof. □

Theorem 1.19.

Let F_n be a friendship graph and r be a positive integer, then the graph rF_n is local distance antimagic with $2n\le {\chi }_{ld}(r{F}_n)\le 2n+r$.

Proof.

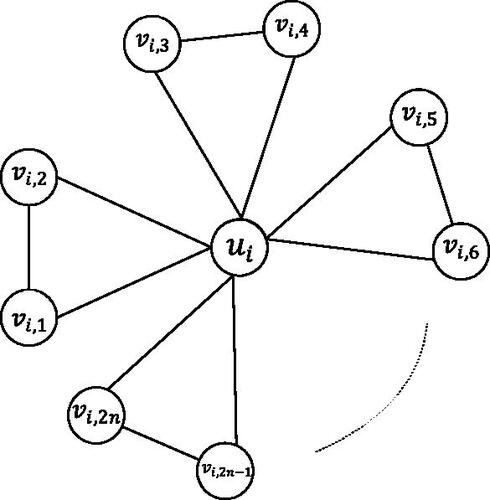
Let $V=\{c_i,v_{i,j}:1\le i\le r,1\le j\le 2n\}$ be the vertex set of rF_n such that for a fixed i the set of vertices $\{c_i,v_{i,j}:1\le j\le 2n\}$ forms one copy of F_n with the vertices $v_{i,j}$ arranged as shown in Figure 7. For every vertex $v_{i,j}\in V(r{F}_n),N(v_{i,j})=\{c_i,v_{i,j+1}\}$ if j is odd and $N(v_{i,j})=\{c_i,v_{i,j-1}\}$ if j is even. Let f be a local distance antimagic labeling of rF_n. Consider the 2n vertices $v_{i,1},v_{i,2},\dots ,v_{i,2n}$ in ith copy of F_n. Now for $1\le j_1,j_2\le 2n,|N(v_{i,j_1})\Delta N(v_{i,j_2})|=2$, therefore by Proposition 1.3, $w(v_{i,j_1})\ne w(v_{i,j_2})$. Therefore the vertices $v_{i,1},v_{i,2},\dots ,v_{i,2n}$ admit distinct vertex weights, hence ${\chi }_{ld}(r{F}_n)\ge 2n$. Next we prove that ${\chi }_{ld}(r{F}_n)\le 2n+r$. We define a local distance antimagic labeling f of rF_n as follows: $f(v_{i,j})=(i-1)(2n+1)+j$ and $f(c_i)=(r-i+1)(2n+1)$. The resulting vertex weights are $$w(c_i)=(2i-1)n(2n+1)$$

Fig. 7 Arrangement of vertices $v_{i,j}$ in the ith copy of F_n .

and $$w(v_{i,j})=\{\begin{array}{cc}\hfill & (i-1)(2n+1)+j+1+(r-i+1)(2n+1)\hfill \\ \hfill & \text{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} if }j\equiv 1(\mathrm{mod}2)\hfill \\ \hfill & (i-1)(2n+1)+j-1+(r-i+1)(2n+1)\hfill \\ \hfill & \text{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} if }j\equiv 0(\mathrm{mod}2).\hfill \end{array}$$

The labeling f is a local distance antimagic labeling which produces $2n+r$ distinct vertex weights. Hence ${\chi }_{ld}(r{F}_n)\le 2n+r$. □

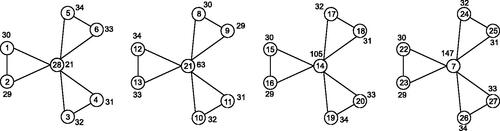
The illustration of a local distance antimagic labeling of $4F_3$ is shown in Figure 8.

Fig. 8 A local distance antimagic labeling of $4F_3$ inducing 10 distinct vertex colors.

Theorem 1.20.

The complete multipartite graph $G=K_{m_1,m_2,\dots ,m_r}$ is local distance antimagic with ${\chi }_{ld}(G)=r$.

Proof.

Let $V_1,V_2,\dots ,V_r$ be the partite sets of $K_{m_1,m_2,\dots ,m_r}$ with $\left|V_i\right|=m_i$, and $m_1\le m_2\le \cdots \le m_r$. Furthermore, let $m_1+m_2+\cdots +m_r=n$. Now since $\omega (K_{m_1,m_2,\dots ,m_r})=r$, it follows that ${\chi }_{ld}(K_{m_1,m_2,\dots ,m_r})\ge r$. We define a local distance antimagic labeling f of $K_{m_1,m_2,\dots ,m_r}$ which admits exactly r distinct vertex weights. We first label the vertices of V₁ with the lowest m₁ labels, followed by next higher m₂ labels assigned to the vertices of V₂. We continue in this manner until the vertices of V_r are labeled with the set of labels $\{n-m_r+1,n-m_r+2,\dots ,n\}$. The labeling f is a local distance antimagic labeling which admits r distinct vertex weights. Therefore ${\chi }_{ld}(K_{m_1,m_2,\dots ,m_r})\le r$. This completes the proof. □

Theorem 1.21.

Let G be a caterpillar with the central path of order n and m pendant vertices on each central vertex, then for $m\equiv n(\mathrm{mod}2),n\le {\chi }_{ld}(G)\le n+6$.

Proof.

Let P_n denote the central path, let $V(P_n)=\{u_0,u_1,\dots ,$ $u_{n-1}\}$ be the vertices on the central path and $v_{i,1},v_{i,2},\dots ,$ $v_{i,m}$ are the m pendant vertices adjacent to u_i. Then $G\cong P_n°{\overline{K}}_m$, hence the proof follows from the Lemma 1.6 and Theorem 1.18. □

The illustration of a local distance antimagic labeling of a caterpillar with central path P₈ is shown in Figure 9.

Fig. 9 A local distance antimagic labeling of a caterpillar with central path P₈.

2 Conclusion and scope

In this paper, we have introduced the concept of local distance antimagic chromatic number of a graph. We found local distance antimagic labelings for several families of graphs including the path P_n, the cycle C_n, the wheel graph W_n, friendship graph F_n, the corona product of graphs $G°\overline{K_m}$, the complete multipartite graph and some special types of the caterpillars. We also obtain upper bounds for the local distance antimagic chromatic number for these families of graphs. Obtaining the exact value of the local distance antimagic chromatic number for these classes of graphs is a problem for further investigation. The concept of local distance antimagic labeling is also independently introduced and studied by Divya et al. [4].