Characterization of rings with planar, toroidal or projective planar prime ideal sum graphs

Abstract

Let R be a commutative ring with unity. The prime ideal sum graph $\text{PIS}(R)$ of the ring R is the simple undirected graph whose vertex set is the set of all nonzero proper ideals of R and two distinct vertices I and J are adjacent if and only if I + J is a prime ideal of R. In this paper, we study some interplay between algebraic properties of rings and graph-theoretic properties of their prime ideal sum graphs. In this connection, we classify non-local commutative Artinian rings R such that $\text{PIS}(R)$ is of crosscap at most two. We prove that there does not exist a non-local commutative Artinian ring whose prime ideal sum graph is projective planar. Further, we classify non-local commutative Artinian rings of genus one prime ideal sum graphs.

KEYWORDS:

• Non-local ring
• ideals
• genus and crosscap of a graph
• prime ideal

2020 MATHEMATICS SUBJECT CLASSIFICATION:

• 05C25

1 Introduction

The investigation of algebraic structures through graph-theoretic properties of the associated graphs has become a fascinating research subject over the past few decades. Numerous graphs attached with ring structures have been studied in the literature (see, [2, 4, 6–8, 14, 15, 17, 27]). Because of the crucial role of ideals in the theory of rings, many authors have explored the graphs attached to the ideals of rings also, for example, inclusion ideal graph [3], intersection graphs of ideals [18], ideal-relation graph [26], co-maximal ideal graph [44], prime ideal sum graph [34] etc. Topological graph theory is principally related to the embedding of a graph on a surface without edge crossing. Its applications lie in electronic printing circuits where the purpose is to embed a circuit, that is, the graph on a circuit board (the surface) without two connections crossing each other, resulting in a short circuit. To determine the genus and crosscap of a graph is a fundamental but highly complex problem. Indeed, it is NP-complete. Many authors have investigated the problem of finding the genus of zero divisor graphs of rings in [5, 12, 16, 38, 42, 43]. Genus and crosscap of the total graph of the ring were investigated in [11, 23, 28, 36]. Asir et al. [10] determined all isomorphic classes of commutative rings whose ideal based total graph has genus at most two. Pucanović et al. [30] classified the planar and toroidal graphs that are intersection ideal graphs of Artinian commutative rings. In [31], all the graphs of genus two that are intersection graphs of ideals of some commutative rings are characterized. Ramanathan [32] determined all Artinian commutative rings whose intersection ideal graphs have crosscap at most two. Work related to the embedding of graphs associated with other algebraic structures on a surface can be found in [1, 9, 19–22, 24, 25, 33, 35, 37].

Recently, Saha et al. [34] introduced and studied the prime ideal sum graph of a commutative ring. The prime ideal sum graph $\text{PIS}(R)$ of the ring R is the simple undirected graph whose vertex set is the set of all nonzero proper ideals of R and two distinct vertices I and J are adjacent if and only if I + J is a prime ideal of R. Authors of [34] studied the interplay between graph-theoretic properties of $\text{PIS}(R)$ and algebraic properties of ring R. In this connection, they investigated the clique number, the chromatic number and the domination number of prime ideal sum graph $\text{PIS}(R)$. The purpose of this article is to investigate the prime ideal sum graph $\text{PIS}(R)$ to a greater extent. In this connection, we discuss the question of embedding of $\text{PIS}(R)$ on various surfaces without edge crossing. This paper aims to characterize all commutative non-local Artinian rings for which $\text{PIS}(R)$ has crosscap at most two. We also characterize all the non-local commutative Artinian rings whose prime ideal sum graph is toroidal. Moreover, we classify all the non-local commutative Artinian rings for which $\text{PIS}(R)$ is planar and outerplanar, respectively. The paper is arranged as follows. Section 2 comprises basic definitions and necessary results. In Section 3, we classify all the non-local commutative Artinian rings R for which $\text{PIS}(R)$ has genus one. Also, we determine all the non-local commutative Artinian rings for which $\text{PIS}(R)$ has crosscap at most two.

2 Preliminaries

A graph Γ is a pair $(V(\Gamma ),E(\Gamma ))$, where $V(\Gamma )$ and $E(\Gamma )$ are the set of vertices and edges of Γ, respectively. Two distinct vertices u₁ and u₂ are $\mathit{\text{adjacent}}$, denoted by $u_1\sim u_2$ (or $(u_1,u_2)$), if there is an edge between u₁ and u₂. Otherwise, we write as $u_1\nsim u_2$. If $X\subseteq V(\Gamma )$ then the subgraph $\Gamma (X)$ induced by X is the graph with vertex set X and two vertices of $\Gamma (X)$ are adjacent if and only if they are adjacent in Γ. For other basic graph theoretic definitions and concepts, we refer the reader to [39, 40]. A graph Γ is outerplanar if it can be embedded in the plane such that all vertices lie on the outer face of Γ. In a graph Γ, the subdivision of an edge (u, v) is the deletion of (u, v) from Γ and the addition of two edges (u, w) and (w, v) along with a new vertex w. A graph obtained from Γ by a sequence of edge subdivision is called a subdivision of Γ. Two graphs are said to be homeomorphic if both can be obtained from the same graph by subdivisions of edges. A graph Γ is planar if it can be drawn on a plane without edge crossing. It is well known that every outerplanar graph is a planar graph. The following results will be useful for later use.

Theorem 2.1.

[39] A graph Γ is outerplanar if and only if it does not contain a subdivision of K₄ or $K_{2,3}$.

Theorem 2.2.

[39] A graph Γ is planar if and only if it does not contain a subdivision of K₅ or $K_{3,3}$.

A compact connected topological space such that each point has a neighborhood homeomorphic to an open disc is called a surface. For a nonnegative integer g, let ${\mathbb{S}}_g$ be the orientable surface with g handles. The genus $g(\Gamma )$ of a graph Γ is the minimum integer g such that the graph can be embedded in ${\mathbb{S}}_g$, i.e. the graph Γ can be drawn into a surface ${\mathbb{S}}_g$ with no edge crossing. Note that the graphs having genus 0 are planar and the graphs having genus one are toroidal. The following results are useful in the sequel.

Proposition 2.3.

[40, Ringel and Youngs] Let m, n be positive integers.

1. If $n\ge 3$, then $g(K_n)=\lceil \frac{(n-3)(n-4)}{12}\rceil$.

2. If $m,n\ge 2$, then $g(K_{m,n})=\lceil \frac{(m-2)(n-2)}{4}\rceil$.

Lemma 2.4.

[40, Theorem 5.14] Let Γ be a connected graph with a 2-cell embedding in ${\mathbb{S}}_g$. Then $v-e+f=2-2g$, where v, e and f are the number of vertices, edges and faces embedded in ${\mathbb{S}}_g$, respectively and g is the genus of the graph Γ.

Lemma 2.5.

[41] The genus of a connected graph Γ is the sum of the genera of its blocks.

Let ${\mathbb{N}}_k$ denote the non-orientable surface formed by the connected sum of k projective planes, that is, ${\mathbb{N}}_k$ is a non-orientable surface with k crosscap. The crosscap of a graph Γ, denoted by $\mathit{\text{cr}}(\Gamma )$, is the minimum nonnegative integer k such that Γ can be embedded in ${\mathbb{N}}_k$. For instance, a graph Γ is planar if $\mathit{\text{cr}}(\Gamma )=0$ and the Γ is projective if $\mathit{\text{cr}}(\Gamma )=1$. The following results are useful to obtain the crosscap of a graph.

Proposition 2.6.

[29, Ringel and Youngs] Let m, n be positive integers. Then

1. $\mathit{\text{cr}}(K_n)=\{\begin{array}{cc}\lceil \frac{(n-3)(n-4)}{6}\rceil \hfill & \mathit{\text{if}} n\ge 3\hfill \\ 3\hfill & \mathit{\text{if}} n=7\hfill \end{array}$

2. $\mathit{\text{cr}}(K_{m,n})=\lceil \frac{(m-2)(n-2)}{2}\rceil \mathit{\text{if}} m,n\ge 2$

Lemma 2.7.

[29, Lemma 3.1.4] Let $\varphi :\Gamma \to {\mathbb{N}}_k$ be a 2-cell embedding of a connected graph Γ to the non-orientable surface ${\mathbb{N}}_k$. Then $v-e+f=2-k$, where v, e and f are the number of vertices, edges and faces of $\varphi (\Gamma )$, respectively, and k is the crosscap of ${\mathbb{N}}_k$.

Fig. 1 A subgraph of $\text{PIS}(R_1\times R_2\times R_3\times R_4)$ homeomorphic to $K_{3,3}$

Fig. 2 A subgraph of $\text{PIS}(R_1\times F_2\times F_3)$ homeomorphic to K₅

Fig. 3 Subgraph of $\text{PIS}(R_1\times R_2)$, where R₁ is not a principal ring

Fig. 4 Subgraph of $\text{PIS}(R_1\times R_2)$, where $\eta ({\mathcal{M}}_1)\ge 3$ and $\eta ({\mathcal{M}}_2)\ge 2$

Definition 2.8.

[41] A graph Γ is orientably simple if $\mu (\Gamma )\ne 2-\mathit{\text{cr}}(\Gamma )$, where $\mu (\Gamma )=\mathrm{\text{max}}\{2-2g(\Gamma ),2-\mathit{\text{cr}}(\Gamma )\}$.

Lemma 2.9.

[41] Let Γ be a graph with blocks ${\Gamma }_1,{\Gamma }_2,\dots ,{\Gamma }_k$. Then $\mathit{\text{cr}}(\Gamma )=$ $\{\begin{array}{cc}1-k+{\sum }_{i=1}^k\mathit{\text{cr}}({\Gamma }_i),\hfill & \mathit{\text{if}} \Gamma \mathit{\text{is orientably simple}}\hfill \\ 2k-{\sum }_{i=1}^k\mu ({\Gamma }_i),\hfill & \mathit{\text{otherwise}}.\hfill \end{array}$

We use the following remark frequently in this paper.

Remark 2.10.

For a simple graph Γ, we have $2e\ge 3f$.

A ring R is called local if it has a unique maximal ideal $\mathcal{M}$ and it is abbreviated by $(R,\mathcal{M})$. For an ideal I of R, the smallest positive integer n such that $I^n=0$ is called the nilpotency index $\eta (I)$ of the ideal I. Let R be a non-local commutative Artinian ring. By the structural theorem (see [13]), R is uniquely (up to isomorphism) a finite direct product of local rings R_i that is $R\cong R_1\times R_2\times \cdots \times R_n$, where $n\ge 2$. Note that for any commutative Artinian ring, every prime ideal is a maximal ideal (see [13, Proposition 8.1]). Hence, we use the maximal ideal for the adjacency between the two vertices of the prime ideal sum graph. The following remark specifies maximal ideals in a non-local Artinian commutative ring, where $\mathrm{\text{Max}}(R)$ denotes the set of all maximal ideals of R. The set of nonzero proper ideals of R is denoted by ${\mathcal{I}}^{*}(R)$. Throughout the paper, F_i denotes a field. For other basic definitions of ring theory, we refer the reader to [13].

Remark 2.11.

Let $R\cong R_1\times R_2\times \cdots \times R_n$ $(n\ge 2)$ be a non-local commutative ring, where each R_i is a local ring with maximal ideal ${\mathcal{M}}_i$. Then $\mathrm{\text{Max}}(R)=\{J_1,J_2,\dots ,J_n\}$, where $J_i=R_1\times R_2\times \cdots \times R_{i-1}\times {\mathcal{M}}_i\times R_{i+1}\times \cdots \times R_n$.

3 Embedding of $\text{PIS}(R)$ on surfaces

In this section, we study the embedding of the prime ideal sum graph $\text{PIS}(R)$ on a surface without edge crossing. We begin with the investigation of an embedding of $\text{PIS}(R)$ on a plane.

3.1 Planarity of $\text{PIS}(R)$

In this subsection, we classify all the non-local commutative Artinian rings with unity for which the graph $\text{PIS}(R)$ is planar and outerplanar, respectively.

Theorem 3.1.

Let $R\cong R_1\times R_2\times \cdots \times R_n$ $(n\ge 2)$ be a non-local commutative ring, where each R_i is a local ring with maximal ideal ${\mathcal{M}}_i$ and let F₁, F₂, F₃ be fields. Then the graph $\text{PIS}(R)$ is planar if and only if one of the following holds:

1. $R\cong F_1\times F_2\times F_3$.

2. $R\cong F_1\times F_2$.

3. $R\cong R_1\times R_2$ such that both R₁ and R₂ are principal ideal rings with $\eta ({\mathcal{M}}_1)=\eta ({\mathcal{M}}_2)=2$.

4. $R\cong F_1\times R_2$, where the local ring R₂ is principal ideal ring.

Proof.

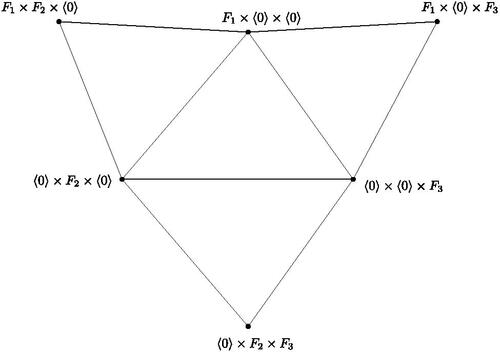
First suppose that the graph $\text{PIS}(R)$ is planar and $R\cong R_1\times R_2\times \cdots \times R_n$, where $n\ge 5$. Then the set $X=\{{\mathcal{M}}_1\times R_2\times \cdots \times R_n,{\mathcal{M}}_1\times 〈0〉\times R_3\times \cdots \times R_n,{\mathcal{M}}_1\times R_2\times 〈0〉\times R_4\times \cdots \times R_n,{\mathcal{M}}_1\times R_2\times R_3\times 〈0〉\times R_5\times \cdots \times R_n,{\mathcal{M}}_1\times R_2\times R_3\times R_4\times 〈0〉\times R_6\times \cdots \times R_n\}$ induces a subgraph isomorphic to K₅, a contradiction. Therefore, $n\in \{2,3,4\}$. If $R\cong R_1\times R_2\times R_3\times R_4$, then by Figure 1 and Theorem 2.2, the graph $\text{PIS}(R)$ is not planar, a contradiction. Consequently, $n\in \{2,3\}$.

Now assume that $R\cong R_1\times R_2\times R_3$ such that one of $R_i(1\le i\le 3)$ is not a field. Without loss of generality, we assume that R₁ is not a field. By Figure 2, note that $\text{PIS}(R)$ contains a subgraph homeomorphic to K₅, which is not possible. Thus, $R\cong F_1\times F_2\times F_3$.

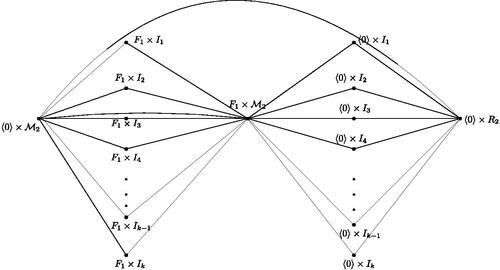
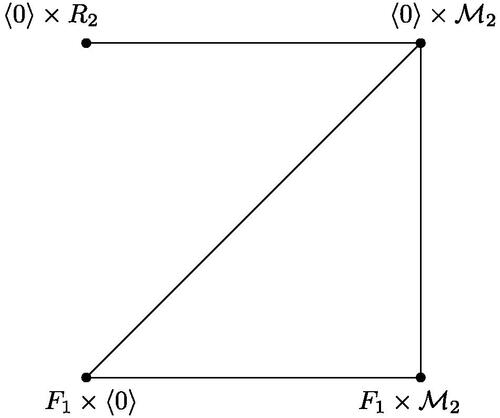
We may now suppose that $R\cong R_1\times R_2$. First note that both R₁ and R₂ are principal rings. On contrary, if one of them is not principal say R₁. Then R₁ has atleast two nontrivial ideals J₁ and J₂ different from ${\mathcal{M}}_1$ such that $J_1+J_2={\mathcal{M}}_1$. By Figure 3, note that $\text{PIS}(R_1\times R_2)$ contains a subgraph homeomorphic to $K_{3,3}$, which is not possible.

Consequently, $R\cong R_1\times R_2$ such that both the rings R₁ and R₂ are principal. If at least one of R_i $(1\le i\le 2)$ is a field, then R is isomorphic to $F_1\times F_2$ or $F_1\times R_2$, where R₂ is a principal ideal ring. Now let $R\cong R_1\times R_2$ such that both R₁ and R₂ are principal ideal rings which are not fields. If $\eta ({\mathcal{M}}_1)\ge 3$ and $\eta ({\mathcal{M}}_2)\ge 2$, then there exists a nonzero proper ideal ${\mathcal{M}}_1^2(\ne {\mathcal{M}}_1)$ of R₁. By Figure 4, the graph $\text{PIS}(R_1\times R_2)$ contains a subgraph homeomorphic to $K_{3,3}$, a contradiction. Consequently, for $R\cong R_1\times R_2$, where both R₁ and R₂ are not fields, we have $\eta ({\mathcal{M}}_1)=\eta ({\mathcal{M}}_2)=2$.

The converse follows from Figures 5–8. □

Fig. 5 The prime ideal sum graph of $F_1\times F_2$

Fig. 6 The graph $\text{PIS}(F_1\times F_2\times F_3)$

Fig. 7 The graph $\text{PIS}(F_1\times R_2)$, where R₂ is a principal ideal ring

Fig. 8 The graph $\text{PIS}(R_1\times R_2)$, where $\eta ({\mathcal{M}}_1)=\eta ({\mathcal{M}}_2)=2$

Theorem 3.2.

Let $R\cong R_1\times R_2\times \cdots \times R_n$ $(n\ge 2)$ be a non-local commutative ring, where each R_i is a local ring with maximal ideal ${\mathcal{M}}_i$. Then the graph $\text{PIS}(R)$ is outerplanar if and only if R is isomorphic to one of the following rings: $F_1\times F_2\times F_3,F_1\times F_2,F_1\times R_2$, where F₁, F₂, F₃ are fields and R₂ is a principal ideal ring with $\eta ({\mathcal{M}}_2)=2$.

Proof.

Suppose that $\text{PIS}(R)$ is an outerplanar graph. Since every outerplanar graph is planar, we get R is isomorphic to the following rings: $F_1\times F_2\times F_3,F_1\times F_2,F_1\times R_2^{\prime },R_1\times R_2$, where $R_2^{\prime }$ is any principal ideal ring and R₁, R₂ are principal ideal rings with $\eta ({\mathcal{M}}_1)=\eta ({\mathcal{M}}_2)=2$.

Let $R\cong R_1\times R_2$, where R₁ and R₂ are principal rings. First suppose that both R₁ and R₂ are not fields together with ${\mathcal{I}}^{*}(R_1)=\left\{{\mathcal{M}}_1\right\}$ and ${\mathcal{I}}^{*}(R_2)=\left\{{\mathcal{M}}_2\right\}$. Consider $J_1={\mathcal{M}}_1\times R_2,J_2=R_1\times {\mathcal{M}}_2,J_3=〈0〉\times R_2,J_1^{\prime }={\mathcal{M}}_1\times {\mathcal{M}}_2,J_2^{\prime }={\mathcal{M}}_1\times 〈0〉$. Notice that the subgraph induced by the set $\{J_1,J_2,J_3,J_1^{\prime },J_2^{\prime }\}$ of vertices of $\text{PIS}(R)$ contains $K_{3,2}$ as a subgraph, a contradiction. Without loss of generality, we may now assume that R₁ is a field. Further, let R₂ is a principal ideal ring with $\eta ({\mathcal{M}}_2)\ge 3$. By Figure 9, the graph $\text{PIS}(F_1\times R_2)$ contains a subgraph homeomorphic to $K_{2,3}$, a contradiction. Therefore, either $R\cong F_1\times F_2$ or $R\cong F_1\times R_2$, where R₂ is a principal ideal ring with $\eta ({\mathcal{M}}_2)=2$.

Fig. 9 Subgraph of $\text{PIS}(F_1\times R_2)$, where $\eta ({\mathcal{M}}_2)\ge 3$

The converse follows from Figures 5, 6, and 10. □

Fig. 10 The graph $\text{PIS}(F_1\times R_2)$, where $\eta ({\mathcal{M}}_2)=2$

3.2 Genus of $\text{PIS}(R)$

In this subsection, we classify all the non-local commutative Artinian rings with unity R such that $\text{PIS}(R)$ has toroidal embedding. By $F_{123\dots n}$, we mean $F_1\times F_2\times \cdots \times F_n$. We begin with the following lemma.

Lemma 3.3.

Let $R\cong F_1\times F_2\times F_3\times F_4\times F_5$, where each F_i $(1\le i\le 5)$ is a field. Then $g(\text{PIS}(R))\ge 3$.

Proof.

Let $R\cong F_1\times F_2\times F_3\times F_4\times F_5$. Consider the subset $$\begin{array}{c}X=\{F_{145},F_{24},F_{45},F_{14},F_{15},F_{345},F_{1245},F_{13},F_{135},F_{12},\\ F_{134},F_{1345},F_{1235},F_{234},F_{35},F_{245},F_{235}\}\end{array}$$of vertices of $\text{PIS}(R)$. Note that the subgraph induced by X contains a subgraph homeomorphic to $K_{5,5}$ (see Figure 11). By Proposition 2.3, we have $g(\text{PIS}(R))\ge 3$. □

Fig. 11 Subgraph of $\text{PIS}(F_1\times F_2\times F_3\times F_4\times F_5)$

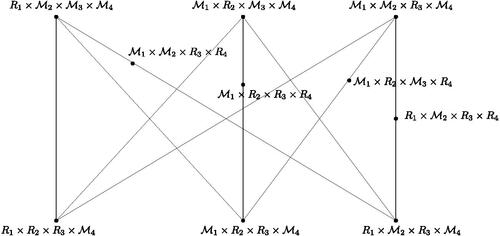
Theorem 3.4.

Let $R\cong R_1\times R_2\times \cdots \times R_n$ $(n\ge 3)$ be a non-local commutative ring, where each R_i is a local ring with maximal ideal ${\mathcal{M}}_i$. Then $g(\text{PIS}(R))=1$ if and only if $R\cong R_1\times F_2\times F_3$, where R₁ is a principal ideal ring with $\eta ({\mathcal{M}}_1)=2$ and F₂, F₃ are fields.

Proof.

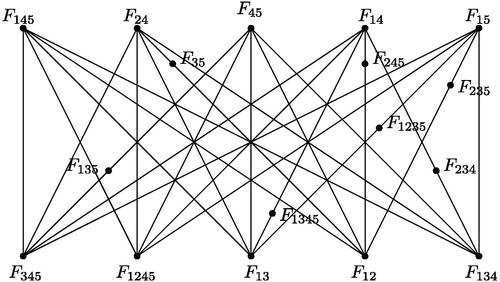
First suppose that $g(\text{PIS}(R))=1$. By Lemma 3.3, we have $n\le 4$. Let $R\cong R_1\times R_2\times R_3\times R_4$. Assume that each R_i ($1\le i\le 4$) is a field. Notice that v = 14 and e = 48. By Lemma 2.4, we obtain f = 34. It follows that $2e<3f$, a contradiction. Consequently, $R\cong R_1\times R_2\times R_3$. If each R_i is a field, then by Figure 6, $\text{PIS}(R)$ is a planar graph, which is not possible. Next, assume that R₁ and R₂ are not fields. Then by Figure 12, the graph $\text{PIS}(R_1\times R_2\times F_3)$ contains a subgraph homeomorphic to $K_{5,4}$, a contradiction.

Fig. 12 Subgraph of $\text{PIS}(R_1\times R_2\times F_3)$

It follows that R₁ is not a field but R₂ and R₃ are fields. Now assume that either R₁ is not a principal ideal ring or R₁ is a principal ideal ring with $\eta ({\mathcal{M}}_1)\ge 3$. Then $|{\mathcal{I}}^{*}(R_1)|\ge 2$. Let K $(\ne {\mathcal{M}}_1)$ be a nonzero proper ideal of R₁. Then by Figure 13 and Lemma 2.5, we get $g(\text{PIS}(R))>1$, a contradiction.

Fig. 13 Subgraph of $\text{PIS}(R_1\times F_2\times F_3)$, where ${\mathcal{I}}^{*}(R_1)=\{K,{\mathcal{M}}_1\}$

Therefore, $R\cong R_1\times F_2\times F_3$, where R₁ is a principal ideal ring with $\eta ({\mathcal{M}}_1)=2$. The converse follows from Figure 14. □

Fig. 14 Embedding of $\text{PIS}(R_1\times F_2\times F_3)$ in ${\mathbb{S}}_1$, where $\eta ({\mathcal{M}}_1)=2$

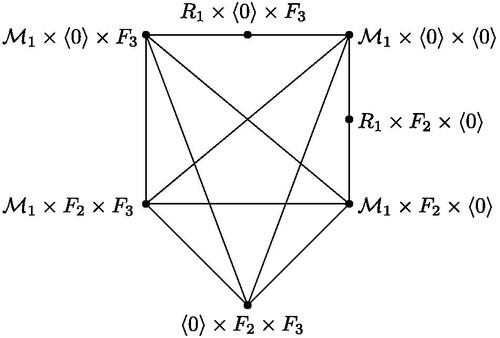
Theorem 3.5.

Let $R\cong R_1\times R_2$, where R₁ and R₂ are local rings with maximal ideals ${\mathcal{M}}_1$ and ${\mathcal{M}}_2$, respectively. Then $g(\text{PIS}(R))=1$ if and only if R₁ and R₂ are principal ideal rings with $\eta ({\mathcal{M}}_1)=3$ and $\eta ({\mathcal{M}}_2)=2$.

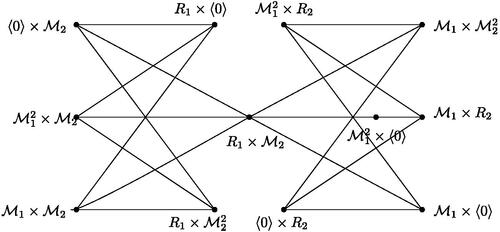
Proof.

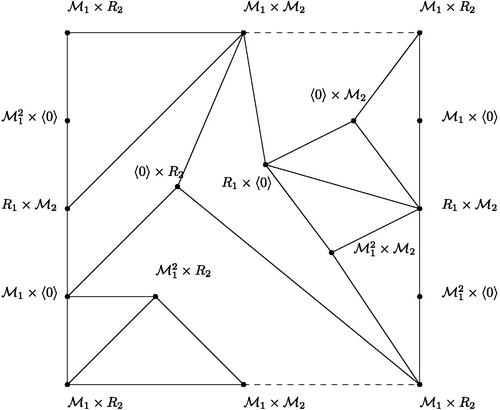
Suppose that $g(\text{PIS}(R))=1$. Assume that one of R_i $(1\le i\le 2)$ is not a principal ideal ring. Without loss of generality, let R₁ is not a principal ideal ring. Then ${\mathcal{M}}_1=〈x_1,x_2,\dots ,x_r〉$, where $r\ge 2$. Let r = 2 i.e., ${\mathcal{M}}_1=〈x,y〉$ for some $x,y\in R_1$. Now let ${\mathcal{I}}^{*}(R_2)=\left\{{\mathcal{M}}_2\right\}$. Consider the vertices $I_1=〈x〉\times 〈0〉,I_2=〈x+y〉\times 〈0〉,I_3=R_1\times {\mathcal{M}}_2,I_4=〈x〉\times R_2,I_5=〈y〉\times R_2,I_6=〈x+y〉\times R_2,I_7={\mathcal{M}}_1\times R_2,I_8={\mathcal{M}}_1\times {\mathcal{M}}_2,I_9=〈x+y〉\times {\mathcal{M}}_2$ and $I_{10}={\mathcal{M}}_1\times 〈0〉$. Note that the subgraph induced by these vertices contains a subgraph homeomorphic to $K_{5,4}$ (see Figure 15).

Fig. 15 Subgraph of $\text{PIS}(R_1\times R_2)$, where ${\mathcal{M}}_1=〈x,y〉$ and ${\mathcal{I}}^{*}(R_2)=\left\{{\mathcal{M}}_2\right\}$

It follows that $g(\text{PIS}(R))>1$, a contradiction. Next let, R₂ be a field. Let $x^2\ne 0$. Then consider the ideals $J_1=〈x〉\times F_2,J_2=〈x^2,x+y〉\times F_2,J_3=〈x+y〉\times F_2,J_4={\mathcal{M}}_1\times F_2,J_5=R_1\times 〈0〉,J_1^{\prime }=〈y〉\times F_2,J_2^{\prime }=〈x^2,y〉\times 〈0〉,J_3^{\prime }={\mathcal{M}}_1\times 〈0〉,J_4^{\prime }=〈y〉\times 〈0〉$ and $K_1=〈x〉\times 〈0〉$. Then the subgraph induced by these vertices contains a subgraph homeomorphic to $K_{5,4}$, where $\{J_1,J_2,J_3,J_4,J_5\}$ and $\{J_1^{\prime },J_2^{\prime },J_3^{\prime },J_4^{\prime }\}$ are partition sets and K₁ join the vertices J₅ and $J_1^{\prime }$. By Proposition 2.3, we get a contradiction. Consequently, $x^2=0=y^2$ and so ${\mathcal{M}}_1^2=〈\mathit{\text{xy}}〉$. Next, we find all the nontrivial ideals of the ring R₁. Let $I=〈a_{1}x+a_{2}y〉$, for some $a_1,a_2\in R_1$, be the principal ideal of R₁ except $〈x〉,〈y〉$ and $〈\mathit{\text{xy}}〉$. Clearly both $a_1,a_2\notin {\mathcal{M}}_1$. If $a_1\in U(R_1)$, then $I=〈x+a_{3}y〉$ for some $a_3\in R_1$. Suppose that $a_3\in {\mathcal{M}}_1$, then we have $I=〈x〉$. Therefore, principal ideals of R₁ are of the form $〈\mathit{\text{xy}}〉,〈y〉,〈x+a_{3}y〉$ where $a_3\in U(R_1)\cup \left\{0\right\}$. Note that ${\mathcal{M}}_1$ is the only ideal which is not principal. Therefore, all the nontrivial ideals of R₁ are $〈\mathit{\text{xy}}〉,〈x,y〉,〈y〉,〈x+a_{3}y〉$, where $a_3\in U(R_1)\cup \left\{0\right\}$. If $|R_1/{\mathcal{M}}_1|\ge 3$, then there exists $a\in U(R_1)\setminus \left\{1\right\}$ and $1-a\notin {\mathcal{M}}_1$. Now, we show that $〈x+y〉+〈x+\mathit{\text{ay}}〉={\mathcal{M}}_1$. Clearly, $〈x+y〉+〈x+\mathit{\text{ay}}〉\subseteq {\mathcal{M}}_1$. Since $1-a\notin {\mathcal{M}}_1$, we have $1-a$ is a unit of R₁ and so $x={(1-a)}^{-1}(x+\mathit{\text{ay}})+[1-{(1-a)}^{-1}](x+y)$. It follows that $x\in 〈x+\mathit{\text{ay}}〉+〈x+y〉$. Similarly, $y\in 〈x+\mathit{\text{ay}}〉+〈x+y〉$. Consequently, ${\mathcal{M}}_1\subseteq 〈x+\mathit{\text{uy}}〉+〈x+\mathit{\text{vy}}〉$. Let $|R_1/{\mathcal{M}}_1|=2$. It follows that $\text{PIS}(R_1)$ has excatly 5 vertices $〈x〉,〈y〉,〈\mathit{\text{xy}}〉,〈x,y〉$ and $〈x+y〉$. Thus, $J_1=〈x〉\times 〈0〉,J_2=〈y〉\times 〈0〉,J_3=〈x+y〉\times 〈0〉,J_4=R_1\times 〈0〉,J_5=〈\mathit{\text{xy}}〉\times 〈0〉,J_6=〈0〉\times F_2,J_7=〈x〉\times F_2,J_8=〈y〉\times F_2,J_9=〈x+y〉\times F_2,J_{10}={\mathcal{M}}_1\times F_2,J_{11}={\mathcal{M}}_1\times 〈0〉,J_{12}=〈\mathit{\text{xy}}〉\times F_2$ are the vertices of $\text{PIS}(R_1\times F_2)$.

Now, consider $X=\{J_1,J_3,J_4,J_7,J_8,J_{10},J_{11}\}$. Note that the subgraph $\Omega =\text{PIS}(X)-\{(J_1,J_8),(J_7,J_8),(J_3,J_{10}),(J_{10},J_{11})\}$ is homeomorphic to $K_{3,3}$. By Proposition 2.3, we have $g(\Omega )=1$ and by Lemma 2.4, we get three faces in any embedding of $K_{3,3}$ in ${\mathbb{S}}_1$. Consequently, any embedding of Ω has at least one face of length 6. If we insert the adjacent vertices J₂, J₉ and the respective edges incident to J₂ and J₉ to the embedding of Ω, then (J₂, J₉) must be embedded in a face of length 6. To embed the graph $\text{PIS}(R)$ in ${\mathbb{S}}_1$, we need to add the edges $\{(J_1,J_8),(J_7,J_8),(J_3,J_{10}),(J_{10},J_{11})\}$ and remaining vertices to the embedding of $K_{3,3}$. Observe that this is not possible without edge crossings. It follows that $g(\text{PIS}(R))>1$, a contradiction. If $x^2=0=y^2=\mathit{\text{xy}}$, then by the similar argument, we get a contradiction. 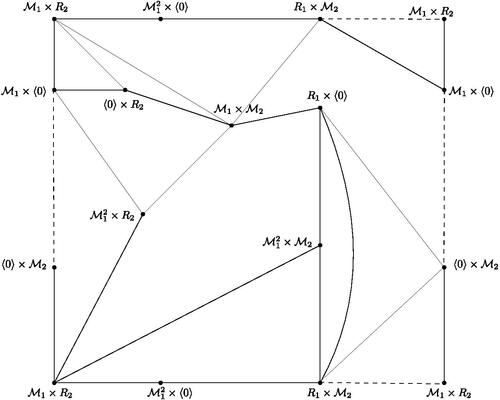Similarly, if $|R_1/{\mathcal{M}}_1|\ge 3$, we get a contradiction. Therefore, the local rings R₁ and R₂ are principal.

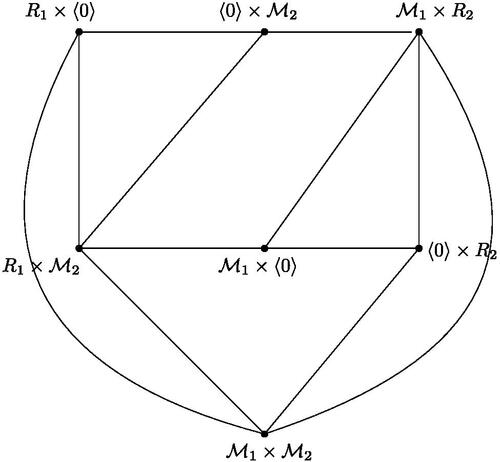
Let $R\cong R_1\times R_2$, where both R₁ and R₂ are principal ideal rings. If $\eta ({\mathcal{M}}_1)=\eta ({\mathcal{M}}_2)=2$, then by Theorem 3.1, we get a contradiction. Next, let $\eta ({\mathcal{M}}_1),\eta ({\mathcal{M}}_2)\ge 3$. Then $\text{PIS}(R)$ contains a subgraph with two blocks of $K_{3,3}$ (see Figure 16). By Proposition 2.3 and Lemma 2.5, we have $g(\text{PIS}(R))>1$, a contradiction.

Fig. 16 Subgraph of $\text{PIS}(R_1\times R_2)$, where $\eta ({\mathcal{M}}_1),\eta ({\mathcal{M}}_2)\ge 3$

Now assume that R₁ is a principal ideal ring and R₂ is a field. By Theorem 3.1, we get $\text{PIS}(R_1\times F_2)$ is a planar graph, a contradiction. If $\eta ({\mathcal{M}}_1)\ge 4$ and $\eta ({\mathcal{M}}_2)=2$, then by Figure 17 and Lemma 2.5, we obtain $g(\text{PIS}(R))\ge 2$, a contradiction.

Fig. 17 Subgraph of $\text{PIS}(R_1\times R_2)$, where $\eta ({\mathcal{M}}_1)\ge 4$ and $\eta ({\mathcal{M}}_2)=2$

Therefore, $R\cong R_1\times R_2$, where R₁ and R₂ are principal ideal rings with $\eta ({\mathcal{M}}_1)=3$ and $\eta ({\mathcal{M}}_2)=2$. The converse follows from Figure 18. □

Fig. 18 Embedding of $\text{PIS}(R_1\times R_2)$ in ${\mathbb{S}}_1$, where $\eta ({\mathcal{M}}_1)=3$ and $\eta ({\mathcal{M}}_2)=2$

3.3 Crosscap of $\text{PIS}(R)$

In this subsection, we classify all the non-local commutative Artinian rings R with unity such that the crosscap of $\text{PIS}(R)$ is at most two. The following theorem asserts that for a non-local commutative ring R its prime ideal sum graph $\text{PIS}(R)$ cannot be of crosscap one.

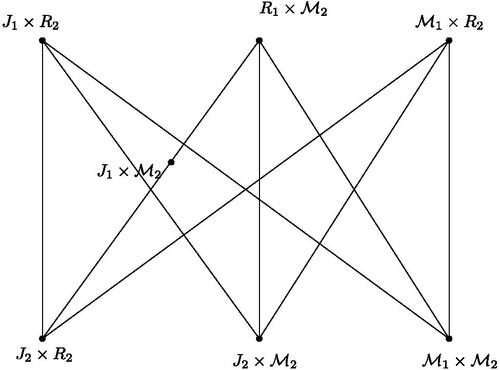
Theorem 3.6.

For any non-local commutative Artinian ring R with unity, the prime ideal sum graph $\text{PIS}(R)$ can not be projective planar.

Proof.

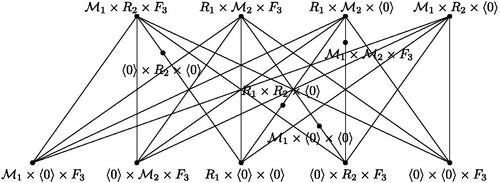
Let $R\cong R_1\times R_2\times \cdots \times R_n$ ($n\ge 2$), where each R_i is local ring with maximal ideal ${\mathcal{M}}_i$. Suppose that $\mathit{\text{cr}}(\text{PIS}(R))=1$. Let $n\ge 5$. By the proof of Lemma 3.3, we get a subgraph of $\text{PIS}(R)$ which is homeomorphic to $K_{5,5}$. By Proposition 2.6, we get $n\le 4$. Now suppose that $R\cong F_1\times F_2\times F_3\times F_4$. Then we get v = 14 and e = 48. Lemma 2.7 yields f = 35. It follows that $2e<3f$, a contradiction. Thus, $n\le 3$. We may now suppose that $R\cong R_1\times R_2\times R_3$. If each R_i is a field, then by Theorem 3.1, we get a contradiction. Next, assume that both R₁ and R₂ are not fields but R₃ is a field. By Figure 12, the graph $\text{PIS}(R_1\times R_2\times F_3)$ contains a subgraph homeomorphic to $K_{5,4}$, a contradiction. Now suppose that R₁ is not a field but both R₂ and R₃ are fields. If ${\mathcal{I}}^{*}(R_1)=\{K,{\mathcal{M}}_1\}$, then by Figure 13 and Lemma 2.9, we get $\mathit{\text{cr}}(\text{PIS}(R))>1$, a contradiction. Therefore, $R\cong R_1\times F_2\times F_3$, where ${\mathcal{I}}^{*}(R_1)=\left\{{\mathcal{M}}_1\right\}$. Now consider the set $X=\{{\mathcal{M}}_1\times F_2\times 〈0〉,{\mathcal{M}}_1\times 〈0〉\times 〈0〉,{\mathcal{M}}_1\times F_2\times F_3,R_1\times F_2\times 〈0〉,{\mathcal{M}}_1\times 〈0〉\times F_3,〈0〉\times F_2\times F_3,〈0〉\times F_2\times 〈0〉,R_1\times 〈0〉\times F_3\}$ and the subgraph $G=\text{PIS}(X)-\{({\mathcal{M}}_1\times 〈0〉\times 〈0〉,{\mathcal{M}}_1\times F_2\times F_3),(〈0〉\times F_2\times 〈0〉,{\mathcal{M}}_1\times 〈0〉\times F_3),({\mathcal{M}}_1\times F_2\times 〈0〉,{\mathcal{M}}_1\times F_2\times F_3),({\mathcal{M}}_1\times 〈0〉\times F_3,〈0〉\times F_2\times F_3)\}$. Then G is homeomorphic to $K_{3,3}$. By Lemma 2.6, we have cr(G) = 1. Moreover, by Lemma 2.7, we get four faces in any embedding of G in ${\mathbb{N}}_1$. Consequently, any embedding of G in ${\mathbb{N}}_1$ has three faces of length 4 and one face of length 6. To embed $\text{PIS}(R)$ from G in ${\mathbb{N}}_1$, first we insert vertex $R_1\times 〈0〉\times 〈0〉$ in an embedding of G in ${\mathbb{N}}_1$. Both the adjacent vertices $R_1\times 〈0〉\times 〈0〉$ and $〈0〉\times 〈0〉\times F_3$ must be inserted in the same face $F\prime$. Note that $R_1\times 〈0〉\times 〈0〉$ is adjacent to ${\mathcal{M}}_1\times F_2\times 〈0〉,R_1\times F_2\times 〈0〉,{\mathcal{M}}_1\times 〈0〉\times F_3$. Also, $〈0〉\times 〈0〉\times F_3\sim {\mathcal{M}}_1\times F_2\times F_3$. Moreover, $〈0〉\times 〈0〉\times F_3\sim R_1\times 〈0〉\times F_3\sim M_1\times 〈0〉\times 〈0〉$. Consequently, the face $F\prime$ should be of length 6. After inserting $R_1\times 〈0〉\times 〈0〉$ in $F\prime$, we need to add the edges $(〈0〉\times 〈0〉\times F_3,R_1\times 〈0〉\times 〈0〉),(〈0〉\times 〈0〉\times F_3,{\mathcal{M}}_1\times F_2\times F_3),(〈0〉\times 〈0〉\times F_3,R_1\times 〈0〉\times F_3),(〈0〉\times 〈0〉\times F_3,{\mathcal{M}}_1\times F_2\times 〈0〉)$, which is not possible without edge crossing (see Figure 19), a contradiction. Thus, $R\cong R_1\times R_2$.

Fig. 19 The face $F\prime$ of $\text{PIS}(R_1\times F_2\times F_3)$

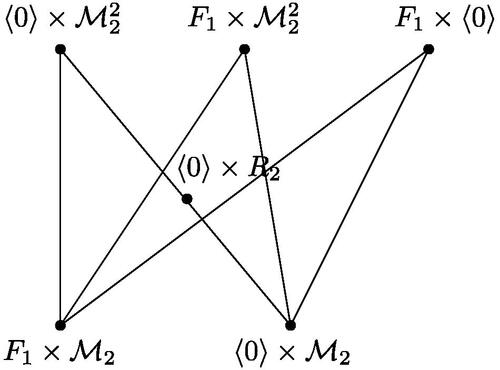
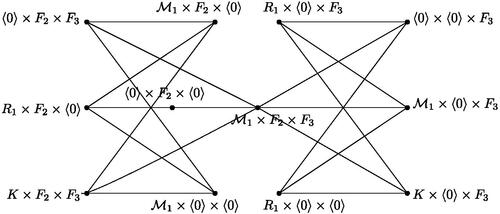
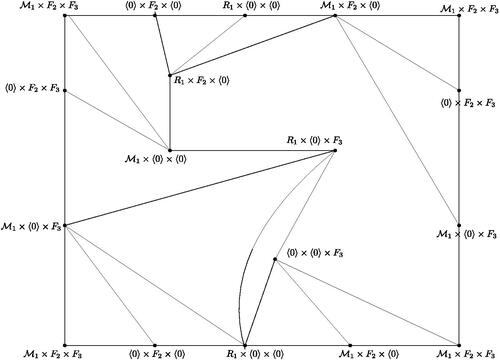
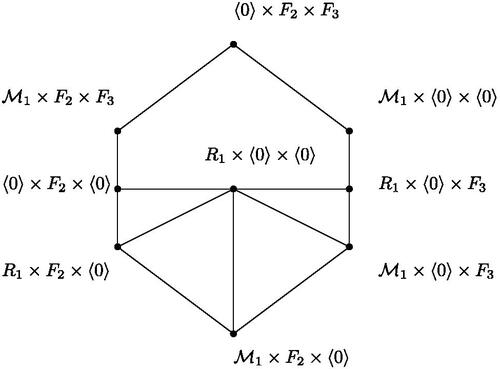
Now let $R\cong R_1\times R_2$. Assume that one of R_i $(1\le i\le 2)$ is not a principal ideal ring. Without loss of generality, let R₁ is not a principal ideal ring. In the similar lines of the proof of Theorem 3.5, we get $\mathit{\text{cr}}(\text{PIS}(R))>1$. Therefore, $R\cong R_1\times R_2$, where the local rings R₁ and R₂ are principal. If both R₁ and R₂ are fields, then the graph $\text{PIS}(R_1\times R_2)$ is planar, a contradiction. If $\eta ({\mathcal{M}}_1)=\eta ({\mathcal{M}}_2)=2$, then by Theorem 3.1, the graph $\text{PIS}(R_1\times R_2)$ is planar, again a contradiction. Next, let $\eta ({\mathcal{M}}_1),\eta ({\mathcal{M}}_2)\ge 3$. Then $\text{PIS}(R)$ contains a subgraph which has two $K_{3,3}$ blocks (see Figure 16). By Proposition 2.6 and Lemma 2.9, we get $\mathit{\text{cr}}(\text{PIS}(R))>1$, a contradiction. Now assume that R₁ is a principal ideal ring and R₂ is a field. By Theorem 3.1, the graph $\text{PIS}(R)$ is planar, a contradiction. Next, let $\eta ({\mathcal{M}}_1)\ge 4$ and $\eta ({\mathcal{M}}_2)=2$. Then by Figure 17 and Lemma 2.9, we obtain $\mathit{\text{cr}}(\text{PIS}(R))\ge 2$, a contradiction. Now, let $R\cong R_1\times R_2$, where R₁, R₂ are principal ideal rings with $\eta ({\mathcal{M}}_1)=3$ and $\eta ({\mathcal{M}}_2)=2$. Then consider the set $$\begin{array}{c}Y=\{R_1\times 〈0〉,{\mathcal{M}}_1\times R_2,R_1\times {\mathcal{M}}_2,{\mathcal{M}}_1^2\times {\mathcal{M}}_2,〈0〉\\ \times {\mathcal{M}}_2,{\mathcal{M}}_1\times {\mathcal{M}}_2\}\end{array}$$and the subgraph $G\prime =\text{PIS}(Y)-\{(R_1\times 〈0〉,R_1\times {\mathcal{M}}_2)\}$. Then the subgraph $G\prime$ is homeomorphic to $K_{3,3}$. It follows that any embedding of $G\prime$ in ${\mathbb{N}}_1$ has 4 faces. Now to embed $\text{PIS}(R)$ in ${\mathbb{N}}_1$ through $G\prime$, first we insert the vertex ${\mathcal{M}}_1\times 〈0〉$. Since ${\mathcal{M}}_1\times 〈0〉$ is adjacent to $〈0〉\times R_2$ and ${\mathcal{M}}_1^2\times R_2$, we must have ${\mathcal{M}}_1\times 〈0〉,〈0〉\times R_2$ and ${\mathcal{M}}_1^2\times R_2$ in the same face $F″$. Note that ${\mathcal{M}}_1\times 〈0〉$ is adjacent to ${\mathcal{M}}_1\times R_2,R_1\times {\mathcal{M}}_2$ and $〈0〉\times R_2$. Also ${\mathcal{M}}_1^2\times R_2$ is adjacent to ${\mathcal{M}}_1\times {\mathcal{M}}_2$. Therefore, the face $F″$ contains the vertices ${\mathcal{M}}_1\times R_2,R_1\times {\mathcal{M}}_2$ and ${\mathcal{M}}_1\times {\mathcal{M}}_2$. Now after inserting the edges $({\mathcal{M}}_1\times 〈0〉,{\mathcal{M}}_1\times R_2),({\mathcal{M}}_1\times 〈0〉,R_1\times {\mathcal{M}}_2),(〈0〉\times R_2,{\mathcal{M}}_1\times {\mathcal{M}}_2),(〈0〉\times R_2,{\mathcal{M}}_1\times 〈0〉)$ and $(〈0〉\times R_2,{\mathcal{M}}_1\times R_2)$, the insertion of the edges $({\mathcal{M}}_1^2\times R_2,{\mathcal{M}}_1\times {\mathcal{M}}_2),({\mathcal{M}}_1^2\times R_2,{\mathcal{M}}_1\times 〈0〉),({\mathcal{M}}_1^2\times R_2,{\mathcal{M}}_1\times R_2)$ without edge crossing is not possible. Hence, $\mathit{\text{cr}}(\text{PIS}(R))\ge 2$. □

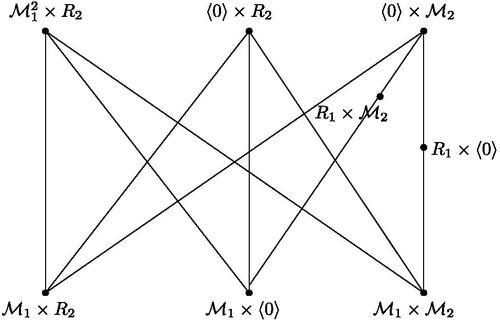
Theorem 3.7.

Let R be a non-local commutative ring such that $R\cong R_1\times R_2\times \cdots \times R_n$ $(n\ge 2)$, where each R_i is a local ring with maximal ideal ${\mathcal{M}}_i$. Then $\mathit{\text{cr}}(\text{PIS}(R))=2$ if and only if

1. $R\cong R_1\times F_2\times F_3$, where R₁ is a principal ideal ring with $\eta ({\mathcal{M}}_1)=2$ and F₂, F₃ are fields.

2. $R\cong R_1\times R_2$, where both R₁ and R₂ are principal ideal rings with $\eta ({\mathcal{M}}_1)=3$ and $\eta ({\mathcal{M}}_2)=2$.

Proof.

Suppose that $\mathit{\text{cr}}(\text{PIS}(R))=2$. If $n\ge 5$, then by the proof of the Lemma 3.3, we get a subgraph of $\text{PIS}(R)$ homeomorphic to $K_{5,5}$. By the Proposition 2.6, we get $n\le 4$. Now let $R\cong F_1\times F_2\times F_3\times F_4$. Then we get v = 14 and e = 48. By Lemma 2.7, we have f = 34. It implies that $2e<3f$, a contradiction. Thus, $n\le 3$. Let $R\cong R_1\times R_2\times R_3$. Suppose that both R₁ and R₂ are not fields but R₃ is a field. Then by Figure 12, $\text{PIS}(R)$ contains a subgraph homeomorphic to $K_{5,4}$, a contradiction. Next, let $R\cong R_1\times F_2\times F_3$ such that ${\mathcal{I}}^{*}(R_1)=\{{\mathcal{M}}_1,K\}$. Then by Figure 13, note that $\text{PIS}(R)$ contains a subgraph G, which has two $K_{3,3}$ blocks. Then $\mathit{\text{cr}}(\text{PIS}(G))=2$. To embed $\text{PIS}(R)$ in ${\mathbb{N}}_2$ from G, first we insert the edges $e_1=(〈0〉\times F_2\times F_3,{\mathcal{M}}_1\times 〈0〉\times F_3),e_2=(K\times F_2\times F_3,{\mathcal{M}}_1\times 〈0〉\times F_3)$ and $e_3=({\mathcal{M}}_1\times F_2\times F_3,{\mathcal{M}}_1\times F_2\times 〈0〉)$. After adding the edges e₁ and e₂, note that we have two triangles: (i) $〈0〉\times F_2\times F_3\sim {\mathcal{M}}_1\times F_2\times F_3\sim {\mathcal{M}}_1\times 〈0〉\times F_3\sim 〈0〉\times F_2\times F_3$, and (ii) $K\times F_2\times F_3\sim {\mathcal{M}}_1\times F_2\times F_3\sim {\mathcal{M}}_1\times 〈0〉\times F_3\sim K\times F_2\times F_3$. Also ${\mathcal{M}}_1\times F_2\times 〈0〉$ is adjacent to $〈0〉\times F_2\times F_3,{\mathcal{M}}_1\times 〈0〉\times F_3$ and $K\times F_2\times F_3$. Since the vertex ${\mathcal{M}}_1\times 〈0〉\times 〈0〉$ is adjacent to $〈0〉\times F_2\times F_3$ and $K\times F_2\times F_3$, we cannot insert the edge e₃ without edge crossing. It implies that $|{\mathcal{I}}^{*}(R_1)|=1$. Note that if R₁ is not a principal ideal ring, then $|{\mathcal{I}}^{*}(R_1)|\ge 2$. Therefore, $R\cong R_1\times F_2\times F_3$ such that R₁ is a principal ideal ring with $\eta ({\mathcal{M}}_1)=2$.

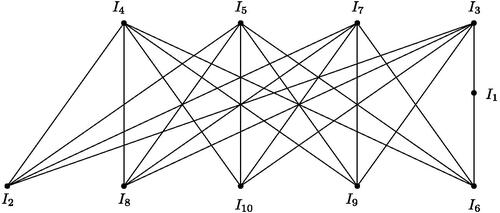
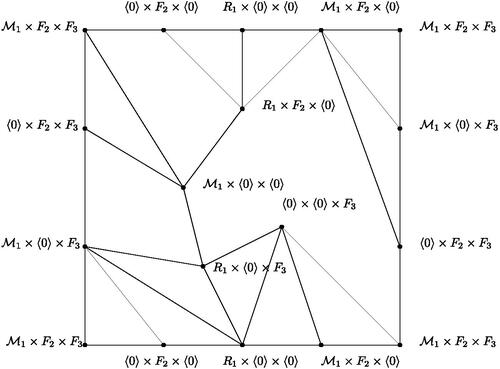
Next, let $R\cong R_1\times R_2$. First, assume that one of R_i $(1\le i\le 2)$ is not a principal ideal ring. Without loss of generality, let R₁ is not a principal ideal ring. Then ${\mathcal{M}}_1=〈x_1,x_2,\dots ,x_r〉$, where $r\ge 2$. Let r = 2 i.e., ${\mathcal{M}}_1=〈x,y〉$ for some $x,y\in R_1$. Now let ${\mathcal{I}}^{*}(R_2)=\left\{{\mathcal{M}}_2\right\}$. By the proof of Theorem 3.5, $\text{PIS}(R)$ contains a subgraph homeomorphic to $K_{5,4}$, a contradiction. Let $R\cong R_1\times F_2$ and ${\mathcal{M}}_1=〈x,y〉$. If $x^2\ne 0$, then by the proof of Theorem 3.5, $\text{PIS}(R)$ contains a subgraph homeomorphic to $K_{5,4}$, which is not possible. Therefore, $R\cong R_1\times F_2$ and ${\mathcal{M}}_1=〈x,y〉$ such that $x^2=y^2=0$. Let $J_1=〈x〉\times 〈0〉,J_2=〈y〉\times 〈0〉,J_3=〈x+y〉\times 〈0〉,J_4=R_1\times 〈0〉,J_5=〈\mathit{\text{xy}}〉\times 〈0〉,J_6=〈0〉\times F_2,J_7=〈x〉\times F_2,J_8=〈y〉\times F_2,J_9=〈x+y〉\times F_2,J_{10}={\mathcal{M}}_1\times F_2,J_{11}={\mathcal{M}}_1\times 〈0〉,J_{12}=〈\mathit{\text{xy}}〉\times F_2$ be the vertices of $\text{PIS}(R_1\times F_2)$. Consider the set $X=\{J_1,J_7,J_8,J_9,J_{10},J_{11}\}$. Then the subgraph induced the set $X\setminus \left\{J_1\right\}$ is isomorphic to K₅. Thus, $\mathit{\text{cr}}(\text{PIS}(X))\ge 1$. Observe that the subgraph $\text{PIS}(X)$ is isomorphic to a subgraph of K₆ and all the faces of K₆ in ${\mathbb{N}}_1$ are triangles. Thus, $\mathit{\text{cr}}(\text{PIS}(X))=1$. Note that $\text{PIS}(X)$ has 6 vertices and 13 edges. By Lemma 2.7, it follows that f = 8 in any embedding of $\text{PIS}(X)$ in ${\mathbb{N}}_1$. Therefore, $\text{PIS}(X)$ has either seven faces of length 3 and one face of length 5, or six faces of length 3 and two faces of length 4. Notice that the 5-length face of $\text{PIS}(X)$ contains the vertices $J_1,J_7,J_8,J_{10}$, and J₁₁. Now first we insert J₂ and J₄ in an embedding of $\text{PIS}(X)$ in ${\mathbb{N}}_1$. Since $J_2\sim J_4$, they must be inserted in the same face. Note that J₂ is adjacent to $J_7,J_9,J_{10}$, and $J_4\sim J_{11}$. Also, J₁₁ is adjacent to $J_7,J_8,J_9$, and J₁₀. Moreover, $J_9\sim J_{10},J_7\sim J_9$, and $J_7\sim J_{10}$. It follows that both J₂ and J₄ must be inserted in a face of length 5 containing the vertices $J_7,J_9,J_{10},J_{11}$ which is not possible. Consequently, $\mathit{\text{cr}}(\text{PIS}(X\cup \{J_2,J_4\}))\ge 2$. Next, consider the set $Y=V(\text{PIS}(R))\setminus \left\{J_3\right\}$. Since $(X\cup \{J_2,J_4\})⊊Y$, we have $\mathit{\text{cr}}(\text{PIS}(Y))\ge 2$. For the subgraph $\text{PIS}(Y)$, note that v = 9 and e = 21. It implies that f = 12 in any embedding of $\text{PIS}(Y)$ in ${\mathbb{N}}_2$. Thus, $\text{PIS}(Y)$ have seven faces of length 3, two faces of length 4 and one face of length 5 in any embedding of $\text{PIS}(Y)$ in ${\mathbb{N}}_2$. Now to embed $\text{PIS}(R)$ in ${\mathbb{N}}_2$, we insert J₃ in a face F of an embedding of $\text{PIS}(Y)$. Then F must contain J₄, J₇, J₈ and J₁₀, but J₄ is not adjacent to J₇, J₈ and J₁₀. Thus, F must contain at least 6 vertices, which is not possible. It follows that $\mathit{\text{cr}}(\text{PIS}(R))\ge 3$.

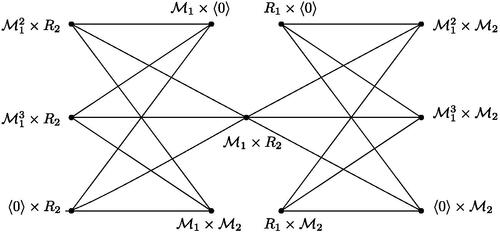
Consequently, $R\cong R_1\times R_2$, where R₁ and R₂ are principal local rings. If both R₁ and R₂ have at most one nontrivial ideal i.e., $\eta ({\mathcal{M}}_1),\eta ({\mathcal{M}}_2)\le 2$, then by Theorem 3.1, we get a contradiction. Next, let $\eta ({\mathcal{M}}_1),\eta ({\mathcal{M}}_2)\ge 3$. Note that $\text{PIS}(R)$ contains a subgraph G₁ as two blocks of $K_{3,3}$ (see Figure 16). By Lemma 2.9, $\mathit{\text{cr}}(\text{PIS}(G_1))=2$. To embed $\text{PIS}(R)$ in ${\mathbb{N}}_2$ from G₁, first we insert the edges $e_1^{\prime }=(〈0〉\times R_2,{\mathcal{M}}_1\times {\mathcal{M}}_2),e_2^{\prime }=({\mathcal{M}}_1^2\times R_2,{\mathcal{M}}_1\times {\mathcal{M}}_2),e_3^{\prime }=({\mathcal{M}}_1\times R_2,{\mathcal{M}}_1\times {\mathcal{M}}_2)$ and $e_4^{\prime }=({\mathcal{M}}_1\times R_2,{\mathcal{M}}_1\times 〈0〉)$. After inserting the edges $e_1^{\prime },e_2^{\prime }$ and $e_3^{\prime }$, note that we have two triangles: (i) $〈0〉\times R_2\sim {\mathcal{M}}_1\times {\mathcal{M}}_2\sim {\mathcal{M}}_1\times R_2\sim 〈0〉\times R_2$, and (ii) ${\mathcal{M}}_1\times {\mathcal{M}}_2\sim {\mathcal{M}}_1^2\times R_2\sim {\mathcal{M}}_1\times R_2\sim {\mathcal{M}}_1\times {\mathcal{M}}_2$. Also, ${\mathcal{M}}_1\times 〈0〉$ is adjacent to $〈0〉\times R_2,{\mathcal{M}}_1^2\times R_2,R_1\times {\mathcal{M}}_2$. Moreover, $R_1\times {\mathcal{M}}_2\sim {\mathcal{M}}_1\times {\mathcal{M}}_2$. Since $〈0〉\times R_2\sim {\mathcal{M}}_1\times {\mathcal{M}}_2^2\sim {\mathcal{M}}_1^2\times R_2$, we cannot insert the edge $e_4^{\prime }$ without edge crossing. Now, let $\eta ({\mathcal{M}}_1)\ge 4$ and $\eta ({\mathcal{M}}_2)=2$. Then $\text{PIS}(R)$ contains a subgraph $G″$ which has two blocks of $K_{3,3}$ (see Figure 17). Then by Lemma 2.9, $\mathit{\text{cr}}(\text{PIS}(G″))=2$. To embed $\text{PIS}(R)$ in ${\mathbb{N}}_2$ through $G″$, first we insert the edges $e_1^{\prime }\prime =(R_1\times {\mathcal{M}}_2,{\mathcal{M}}_1\times {\mathcal{M}}_2),e_2^{\prime }\prime =({\mathcal{M}}_1\times 〈0〉,{\mathcal{M}}_1\times R_2),e_3^{\prime }\prime =(R_1\times {\mathcal{M}}_2,{\mathcal{M}}_1^2\times 〈0〉),e_4^{\prime }\prime =({\mathcal{M}}_1^2\times 〈0〉,{\mathcal{M}}_1\times R_2)$ and $e_5^{\prime }\prime =(R_1\times {\mathcal{M}}_2,{\mathcal{M}}_1\times 〈0〉)$. Note that ${\mathcal{M}}_1\times {\mathcal{M}}_2\sim 〈0〉\times R_2\sim {\mathcal{M}}_1\times 〈0〉\sim {\mathcal{M}}_1^2\times R_2\sim {\mathcal{M}}_1\times {\mathcal{M}}_2$. Also, $〈0〉\times R_2\sim {\mathcal{M}}_1\times R_2\sim {\mathcal{M}}_1^2\times R_2$. Then after inserting the edges $e_1^{\prime }\prime ,e_2^{\prime }\prime ,e_3^{\prime }\prime$, and $e_4^{\prime }\prime$, we can not insert the edge $e_5^{\prime }\prime$ without edge crossing in an embedding of $G″$ in ${\mathbb{N}}_2$. Hence, $R\cong R_1\times R_2$, where R₁, R₂ are principal ideal rings with $\eta ({\mathcal{M}}_1)=3$ and $\eta ({\mathcal{M}}_2)=2$.

Converse follows from Figures 20 and 21. □

Fig. 20 Embedding of $\text{PIS}(R_1\times F_2\times F_3)$ in ${\mathbb{N}}_2$, where $\eta ({\mathcal{M}}_1)=2$

Fig. 21 Embedding of $\text{PIS}(R_1\times R_2)$ in ${\mathbb{N}}_2$, where $\eta ({\mathcal{M}}_1)=3$ and $\eta ({\mathcal{M}}_2)=2$

Code availability (software application or custom code)

Not applicable.

Acknowledgments

We would like to thank the referees for their valuable suggestions which helped us to improve the presentation of the paper.

Disclosure statement

There is no conflict of interest regarding the publishing of this paper.

Data availability statement

Not applicable.

Additional information

Funding

The first author gratefully acknowledges Birla Institute of Technology and Science (BITS) Pilani, India, for providing financial support.