A-vertex magicness of product of graphs

Abstract

In this paper, we discuss the A-vertex magicness of some products of graphs, where A is a non-trivial additive Abelian group with identity 0. We characterize A-vertex magicness of the Cartesian product of P_n and P_m, where A has at least three elements, and we also discuss the A -vertex magicness of co-normal and tensor product of two graphs. Finally, we give a new method to construct an infinite number of A-vertex magic graphs from existing ones using the join operation. As a consequence we obtain an earlier result in [Balamoorthy et al. in AKCE Int. J. Graphs Comb. (2022) 19 (3), 268–275]

KEYWORDS:

• A-vertex magic
• cartesian product
• co-normal product
• tensor product
• perfect matching

AMS SUBJECT CLASSIFICATION:

• 05C78
• 05C76
• 05C25

1 Introduction

All the graphs considered in this paper are finite, simple, connected and undirected. Let $G=(V(G),E(G))$ be a graph, we denote by V(G) the vertex set of graph G. The neighbourhood of a vertex u, is defined as $N_G(u)=\{v\in V(G):v\text{ and }u\text{ are adjacent in }G\}$. A subset M of E(G) is said to be a matching if no two edges in M are adjacent. A matching M of a graph of order n is said to be perfect (or nearly perfect) if $\left|M\right|=\frac{n}{2}$ (or $\frac{n}{2}-1)$.

In [5], Kamatchi et al. introduced the concept of group vertex magic graphs and they also studied some properties of V₄-vertex magic trees with diameter at most 4. In [6] Lee at el. introduced the concept of group magic graph, this is the main motivation to study group vertex magic graphs and this work was further studied by Lee et al. [7], Low and Lee [8]. In [1] and [2] the authors obtained a necessary condition for a graph to be A-vertex magic and they obtained results for the magicness of product graphs. In [9], Sabeel et al. have completely studied A-vertex magic trees of diameter at most 5.

In this paper, we use group elements to label the vertices of a graph and we have extended the study of the A-vertex magicness of a graph by considering an arbitrary Abelian group. We use the following important results in group theory namely Cauchy’s theorem, Sylow’s first theorem and Fundamental theorem of finite Abelian groups. We refer to Bondy and Murty [3], for basic terminology on graph theory. Let R be a commutative ring with unity, U(R) denotes the multiplicative group of units in R. For group theoretic terminology and notations, we refer to Herstien [4].

Here, we recall some basic definitions. In [5], Kamatchi et al. introduced the concept of group vertex magic graphs.

Definition 1.

Let A be any non-trivial Abelian group. A mapping $l:V(G)\to A\setminus \left\{0\right\}$ is said to be an A-vertex magic labeling of G if there exists an element μ in A such that $w(u)=\sum _{v\in N(u)}l(v)=\mu$ for any vertex u of G. The element μ is called the magic constant of the labeling l. A graph G that admits such a labeling is called an A-vertex magic graph. If G is A-vertex magic graph for any non-trivial Abelian group A, then G is called a group vertex magic graph.

Definition 2.

The cartesian product $G\square H$ of graphs G and H is a graph such that the vertex set of $G\square H$ is the product $V(G)\times V(H)$. Two vertices (g, h) and $(g\prime ,h\prime )$ are adjacent in $G\square H$ if and only if either $g=g\prime$ and h is adjacent to $h\prime$ in H or $h=h\prime$ and g is adjacent to $g\prime$ in G.

Definition 3.

The Ladder graph L_n is defined as $P_2\square P_n$, where $n\ge 2$.

Definition 4.

The Book graph is defined as $P_2\square S_n$, where S_n is a star graph on n + 1 vertices and $n\ge 1$. It is denoted by B_n.

Definition 5.

The co-normal product $H\ast G$ of graphs H and G is a graph such that the vertex set of $H\ast G$ is the product $V(H)\times V(G)$ and vertices (h, g) and $(h\prime ,g\prime )$ are adjacent in $H\ast G$ if and only if h is adjacent to $h\prime$ in H or g is adjacent to $g\prime$ in G.

Definition 6.

The tensor product of two graphs G and H is the graph, denoted by $G\otimes H$, with the vertex set of $G\otimes H$ is the product $V(G)\times V(H)$ and vertices (g₁, h₁) and (g₂, h₂) are adjacent in $G\otimes H$, whenever g₁ is adjacent to g₂ in G and h₁ is adjacent to h₂ in H.

We state the following results from [1], which are used in this paper.

Proposition 1

([1]). A graph G is ${\mathbb{Z}}_2$ magic if and only if degree of every vertex in G is of same parity.

Theorem 1

([1]). Let G₁ and G₂ be graphs. If the graph $G_1+G_2$ is A-vertex magic, then G₁ and G₂ are A-vertex magic.

2 Main results

In this section, first we obtain the A-vertex magicness of $P_n\square P_m$, where $\left|A\right|>2$. Further, we prove some main results for A-vertex magicness of co-normal product of graphs, where A is an Abelian group underlying a commutative ring and we discuss the A-vertex magicness of the tensor product of graphs. Finally, we construct an infinite number of A-vertex magic graphs from existing ones using join operation.

Lemma 1.

Let G be a graph and G has two adjacent vertices v₁, v₂ such that $\mathrm{\text{deg}}(v_1)=1$ and $\mathrm{\text{deg}}(v_2)=2$. Then the graph $G\square P_2$ is not A-vertex magic, where A is any non-trivial Abelian group.

Proof.

Let $v_1,v_2,\dots ,v_n$ are the vertices of G. Let $V(P_2)=\{u_1,u_2\}$ and $N_G(v_2)=\{v_1,v_3\}$. Assume that $G\square P_2$ is A-vertex magic with labeling l. Since $w((v_1,u_1))=w((v_2,u_2))$, which implies $l((v_3,u_2))=0$, which leads to a contradiction. □

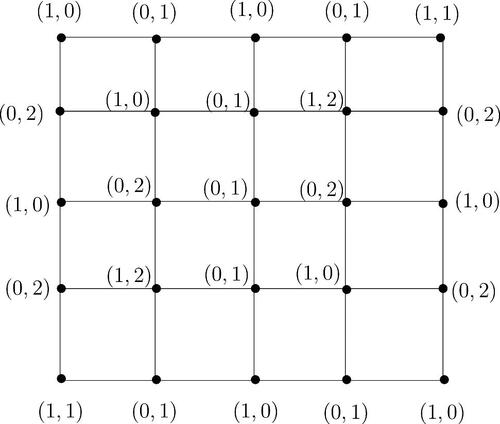
Theorem 2.

The graph $G=P_n\square P_m$ is A-vertex magic, where A has at least three elements if and only if n = m and $n\le 4$.

Proof.

Let P_n and P_m be two paths with vertices $v_1,v_2,\dots ,v_n$ and $u_1,u_2,\dots ,u_m$, respectively. To prove this theorem it is enough to prove the following Lemmas 2–5. □

Lemma 2.

The graph $G=P_2\square P_m$ is A-vertex magic if and only if m = 2.

Proof.

By Lemma 1, $P_2\square P_m$ is not A-vertex magic, where m > 2.

Conversely, assume that m = 2. Then the graph $P_2\square P_2$ is regular and hence it is A-vertex magic. □

Lemma 3.

The graph $G=P_3\square P_m$ is A-vertex magic, where $\left|A\right|>2$ if and only if m = 3.

Proof.

By Lemma 2, we have $P_3\square P_2$ is not A-vertex magic. Assume that $P_3\square P_m$ is A-vertex magic, where m > 3. Since $w((v_3,u_2))=w((v_2,u_3))$, which implies (2.1) $$l((v_3,u_1))=l((v_2,u_4))+l((v_1,u_3)).$$(2.1)

Also $w((v_2,u_1))=w((v_1,u_2))$, we have (2.2) $$l((v_3,u_1))=l((v_1,u_3)).$$(2.2)

By Equations (2.1)(2.1) $$l((v_3,u_1))=l((v_2,u_4))+l((v_1,u_3)).$$(2.1) and (2.2)(2.2) $$l((v_3,u_1))=l((v_1,u_3)).$$(2.2) , we have $l((v_2,u_4))=0$, which is a contradiction.

Conversely, assume that m = 3.

Case 1. p is an odd prime and p divides o(A).

By Cauchy’s theorem A has an element of order p. Define $l:V(G)\to A\setminus \left\{0\right\}$ by $$l((v_i,u_j))=\{\begin{array}{cc}-2a\hfill & \hspace{1em}\text{if }j=2\hfill \\ 2a\hfill & \hspace{1em}\text{if }i=2\text{ and }j=1,3\hfill \\ a\hfill & \hspace{1em}\text{otherwise,}\hfill \end{array}$$where o(a) = p. Thus w(v) = 0, for all $v\in V(G)$.

Case 2. 4 divides o(A).

By Sylow’s first theorem and Fundamental theorem of finite Abelian groups, A has a subgroup isomorphic to either V₄ or ${\mathbb{Z}}_4$. If A has a subgroup isomorphic to ${\mathbb{Z}}_4$, then define $l:V(G)\to {\mathbb{Z}}_4\setminus \left\{0\right\}$ by $$l((v_i,u_j))=\{\begin{array}{cc}2a\hfill & \hspace{1em}\text{if }i=2\text{ or }j=2\hfill \\ a\hfill & \hspace{1em}\text{otherwise,}\hfill \end{array}$$where o(a) = 4. Thus w(v) = 0, for all $v\in V(G)$.

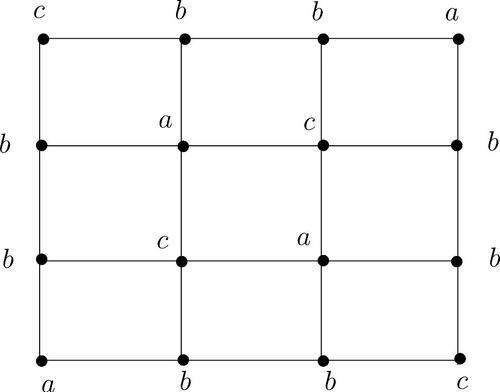
If A has a subgroup isomorphic to V₄, then define $l:V(G)\to V_4\setminus \left\{0\right\}$ by $$l((v_i,u_j))=\{\begin{array}{cc}a\hfill & \hspace{1em}\text{if }i=2\text{ or }j=2\hfill \\ c\hfill & \hspace{1em}\text{if }i=j\text{ and }i,j\in \{1,3\}\hfill \\ b\hfill & \hspace{1em}\text{otherwise,}\hfill \end{array}$$where $a,b,c\in V_4\setminus \left\{0\right\}$ and a, b, c are distinct. Thus w(v) = 0, for all $v\in V(G)$.

Case 3. o(A) is infinite.

In this case, either A has a subgroup isomorphic to $\mathbb{Z}$ or A contains an element of finite order. Hence, the labeling defined in Case 1 or Case 2 is a magic labeling. □

Lemma 4.

The graph $G=P_4\square P_m$ is A-vertex magic, where $\left|A\right|>2$ if and only if m = 4.

Proof.

By Lemmas 2 and 3, we have $P_4\square P_m$ is not A-vertex magic, where m < 4. Assume that $P_4\square P_m$ is A-vertex magic, where m > 4. Since $w((v_1,u_1))=w((v_2,u_2))$, which implies (2.3) $$l((v_2,u_3))+l((v_3,u_2))=0.$$(2.3)

Then by Equation (2.3)(2.3) $$l((v_2,u_3))+l((v_3,u_2))=0.$$(2.3) , we have $w((v_3,u_3))=l((v_3,u_4))+l((v_4,u_3)).$ Now, $w((v_3,u_3))=w((v_4,u_4))$, which implies $l((v_4,u_5))=0$, which is a contradiction.

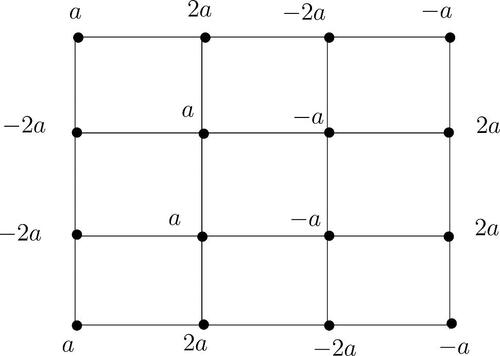
Conversely, assume that m = 4. If p is an odd prime and p divides o(A) then the labeling is given in Figure 1, where o(a) = p. Thus G is A-vertex magic and the magic constant is 0.

Fig. 1 ${\mathbb{Z}}_p$-vertex magic of $P_4\square P_4$.

If 4 divides o(A), then A has a subgroup isomorphic to ${\mathbb{Z}}_4$ or V₄. If A has a subgroup isomorphic to ${\mathbb{Z}}_4$, then the labeling is given in Figure 1, where o(a) = 4. If A has a subgroup isomorphic to V₄, then the labeling is given in Figure 2, where $a,b,c\in V_4\setminus \left\{0\right\}$ and a, b, c are distinct. Thus G is A-vertex magic and the magic constant is 0. □

Fig. 2 V₄-vertex magic of $P_4\square P_4$.

Lemma 5.

If $m\ne 5$, then the graph $P_5\square P_m$ is not A-vertex magic.

Proof.

By Lemmas 2, 3, and 4, we have $P_5\square P_m$ is not A-vertex magic, where m < 5. Assume that $P_5\square P_m$ is A-vertex magic with magic constant $a\in A$, where m > 5. Since $w((v_1,u_2))=w((v_1,u_4))=a$, which implies (2.4) $$l((v_2,u_2))=a-l((v_1,u_1))-l((v_1,u_3))$$(2.4) (2.5) $$l((v_2,u_4))=a-l((v_1,u_3))-l((v_1,u_5)).$$(2.5)

Using $w((v_2,u_3))=a$, Equations (2.4)(2.4) $$l((v_2,u_2))=a-l((v_1,u_1))-l((v_1,u_3))$$(2.4) and (2.5)(2.5) $$l((v_2,u_4))=a-l((v_1,u_3))-l((v_1,u_5)).$$(2.5) , we have (2.6) $$l((v_3,u_3))=-a+l((v_1,u_1))+l((v_1,u_3))+l((v_1,u_5)).$$(2.6)

Applying Equation (2.4)(2.4) $$l((v_2,u_2))=a-l((v_1,u_1))-l((v_1,u_3))$$(2.4) in $w((v_2,u_1))=a$, we have (2.7) $$l((v_3,u_1))=l((v_1,u_3)).$$(2.7)

Using $w((v_3,u_2))=a$, Equations (2.4)(2.4) $$l((v_2,u_2))=a-l((v_1,u_1))-l((v_1,u_3))$$(2.4) , (2.6)(2.6) $$l((v_3,u_3))=-a+l((v_1,u_1))+l((v_1,u_3))+l((v_1,u_5)).$$(2.6) and (2.7)(2.7) $$l((v_3,u_1))=l((v_1,u_3)).$$(2.7) , we have (2.8) $$l((v_4,u_2))=a-l((v_1,u_3))-l((v_1,u_5)).$$(2.8)

Using $w((v_4,u_1))=a$, Equations (2.7)(2.7) $$l((v_3,u_1))=l((v_1,u_3)).$$(2.7) and (2.8)(2.8) $$l((v_4,u_2))=a-l((v_1,u_3))-l((v_1,u_5)).$$(2.8) , we have (2.9) $$l((v_5,u_1))=l((v_1,u_5)).$$(2.9)

From $w((v_5,u_2))=a$, Equations (2.8)(2.8) $$l((v_4,u_2))=a-l((v_1,u_3))-l((v_1,u_5)).$$(2.8) and (2.9)(2.9) $$l((v_5,u_1))=l((v_1,u_5)).$$(2.9) , we have (2.10) $$l((v_5,u_3))=l((v_1,u_3)).$$(2.10)

From $w((v_4,u_3))=a$, Equations (2.6)(2.6) $$l((v_3,u_3))=-a+l((v_1,u_1))+l((v_1,u_3))+l((v_1,u_5)).$$(2.6) , (2.8)(2.8) $$l((v_4,u_2))=a-l((v_1,u_3))-l((v_1,u_5)).$$(2.8) , and (2.10), we have (2.11) $$l((v_4,u_4))=a-l((v_1,u_3))-l((v_1,u_1)).$$(2.11)

Using $w((v_3,u_4))=a$, Equations (2.5)(2.5) $$l((v_2,u_4))=a-l((v_1,u_3))-l((v_1,u_5)).$$(2.5) , (2.6)(2.6) $$l((v_3,u_3))=-a+l((v_1,u_1))+l((v_1,u_3))+l((v_1,u_5)).$$(2.6) , and (2.11), we have (2.12) $$l((v_3,u_5))=l((v_1,u_3)).$$(2.12)

Applying Equations (2.5)(2.5) $$l((v_2,u_4))=a-l((v_1,u_3))-l((v_1,u_5)).$$(2.5) and (2.12)(2.12) $$l((v_3,u_5))=l((v_1,u_3)).$$(2.12) in $w((v_2,u_5))=a$, we have $l((v_2,u_6))=0$ which is a contradiction. □

Lemma 6.

The graph $P_5\square P_5$ is not ${\mathbb{Z}}_3$-vertex magic.

Proof.

Let us assume that $P_5\square P_5$ is ${\mathbb{Z}}_3$-vertex magic with magic constant $a\in {\mathbb{Z}}_3$.

Case 1. Magic constant a = 0.

Since $w((v_1,u_2))=0$, which implies (2.13) $$l((v_2,u_2))=-(l((v_1,u_1))+l((v_1,u_3))).$$(2.13)

If $l((v_1,u_1))\ne l((v_1,u_3))$, then $l((v_2,u_2))=0$, therefore (2.14) $$l((v_1,u_1))=l((v_1,u_3)).$$(2.14)

Since $w(v_1,u_4)=0$, which implies (2.15) $$\begin{array}{c}l((v_2,u_4))=-(l((v_1,u_3))+l((v_1,u_5)))\hspace{1em}\text{ and }\\ l((v_1,u_3))=l((v_1,u_5)).\end{array}$$(2.15)

Therefore (2.16) $$l((v_1,u_1))=l((v_1,u_3))=l((v_1,u_5)).$$(2.16)

Using $w((v_2,u_3))=0$ and Equations (2.13)(2.13) $$l((v_2,u_2))=-(l((v_1,u_1))+l((v_1,u_3))).$$(2.13) , (2.15)(2.15) $$\begin{array}{c}l((v_2,u_4))=-(l((v_1,u_3))+l((v_1,u_5)))\hspace{1em}\text{ and }\\ l((v_1,u_3))=l((v_1,u_5)).\end{array}$$(2.15) , (2.16)(2.16) $$l((v_1,u_1))=l((v_1,u_3))=l((v_1,u_5)).$$(2.16) , we have $l((v_3,u_3))=0$, which leads to contradiction.

Case 2. Magic constant $a\ne 0$.

Since $w((v_1,u_1))=w((v_2,u_2))$, which implies (2.17) $$l((v_3,u_2))+l((v_2,u_3))=0.$$(2.17)

Since $w((v_1,u_5))=w((v_3,u_5))$, which implies (2.18) $$l((v_4,u_5))=l((v_1,u_4))-l((v_3,u_4)).$$(2.18)

Applying Equation (2.17)(2.17) $$l((v_3,u_2))+l((v_2,u_3))=0.$$(2.17) in $w((v_3,u_3))=a$, we have (2.19) $$l((v_4,u_3))=a-l((v_3,u_4)).$$(2.19)

Since $w((v_1,u_5))=a$, which implies (2.20) $$l((v_2,u_5))=a-l((v_1,u_4)).$$(2.20)

Suppose a = 1, then by Equation (2.20)(2.20) $$l((v_2,u_5))=a-l((v_1,u_4)).$$(2.20) we have $l((v_1,u_4))=2$ and also by Equations (2.18)(2.18) $$l((v_4,u_5))=l((v_1,u_4))-l((v_3,u_4)).$$(2.18) and (2.19)(2.19) $$l((v_4,u_3))=a-l((v_3,u_4)).$$(2.19) we have (2.21) $$l((v_4,u_5))=2-l((v_3,u_4))\text{ and }l((v_4,u_3))=1-l(v_3,u_4)).$$(2.21)

If $l((v_3,u_4))=1$ or 2, then by Equation (2.21)(2.21) $$l((v_4,u_5))=2-l((v_3,u_4))\text{ and }l((v_4,u_3))=1-l(v_3,u_4)).$$(2.21) , we have $l((v_4,u_3))=0$ or $l((v_4,u_5))=0$, which leads to a contradiction.

By a similar argument for a = 2, we get a contradiction, therefore $P_5\square P_5$ is not ${\mathbb{Z}}_3$-vertex magic. □

Lemma 7.

If $n,m\ge 6$, then the graph $P_n\square P_m$ is not ${\mathbb{Z}}_3$-vertex magic.

Proof.

Suppose, for the sake of contradiction, the graph $P_n\square P_m$ is ${\mathbb{Z}}_3$-vertex magic with magic constant $a\in {\mathbb{Z}}_3$.

Case 1. Magic constant a = 0

Since $w((v_1,u_1))=0$, which implies (2.22) $$l((v_2,u_1))=-l((v_1,u_2)).$$(2.22)

Applying Equation (2.22)(2.22) $$l((v_2,u_1))=-l((v_1,u_2)).$$(2.22) in $w((v_1,u_3))=0$, we have (2.23) $$l((v_2,u_3))=l((v_2,u_1))-l((v_1,u_4)).$$(2.23)

By Equation (2.23)(2.23) $$l((v_2,u_3))=l((v_2,u_1))-l((v_1,u_4)).$$(2.23) , we have (2.24) $$l((v_2,u_1))\ne l((v_1,u_4)).$$(2.24)

Since $w((v_1,u_5))=0$, which implies (2.25) $$l((v_2,u_5))=-l((v_1,u_4))-l((v_1,u_6)).$$(2.25)

Suppose $l((v_2,u_1))=l((v_1,u_6))$, by using Equations (2.24)(2.24) $$l((v_2,u_1))\ne l((v_1,u_4)).$$(2.24) and (2.25)(2.25) $$l((v_2,u_5))=-l((v_1,u_4))-l((v_1,u_6)).$$(2.25) , we have $l((v_1,u_6))\ne l((v_1,u_4))$. By Equation (2.25)(2.25) $$l((v_2,u_5))=-l((v_1,u_4))-l((v_1,u_6)).$$(2.25) , we have $l((v_2,u_5))=0$, which is a contradiction.

Suppose $l((v_2,u_1))\ne l((v_1,u_6))$, by Equation (2.24)(2.24) $$l((v_2,u_1))\ne l((v_1,u_4)).$$(2.24) we have (2.26) $$l((v_1,u_6))=l((v_1,u_4)).$$(2.26)

Since G is ${\mathbb{Z}}_3$-vertex magic, (2.27) $$l((v_1,u_6))=-l((v_2,u_1)).$$(2.27)

Using $w((v_2,u_4))=0$, Equations (2.23)(2.23) $$l((v_2,u_3))=l((v_2,u_1))-l((v_1,u_4)).$$(2.23) , (2.25)(2.25) $$l((v_2,u_5))=-l((v_1,u_4))-l((v_1,u_6)).$$(2.25) , (2.26)(2.26) $$l((v_1,u_6))=l((v_1,u_4)).$$(2.26) , and (2.27), we have $l((v_3,u_4))=3·l((v_1,u_6)=0$, as G is ${\mathbb{Z}}_3$-vertex magic, which is a contradiction.

Case 2. Magic constant $a\ne 0$.

Since $w((v_1,u_1))=a$, which implies (2.28) $$l((v_1,u_2))=a-l((v_2,u_1)).$$(2.28)

Applying Equation (2.28)(2.28) $$l((v_1,u_2))=a-l((v_2,u_1)).$$(2.28) in $w((v_1,u_3))=a$, we have (2.29) $$l((v_2,u_3))=l((v_2,u_1))-l((v_1,u_4)).$$(2.29)

From $w((v_2,u_2))=a$, equations (2.28)(2.28) $$l((v_1,u_2))=a-l((v_2,u_1)).$$(2.28) and (2.29)(2.29) $$l((v_2,u_3))=l((v_2,u_1))-l((v_1,u_4)).$$(2.29) (2.30) $$l((v_3,u_2))=l((v_1,u_4))-l((v_2,u_1)).$$(2.30)

Applying Equation (2.30)(2.30) $$l((v_3,u_2))=l((v_1,u_4))-l((v_2,u_1)).$$(2.30) in $w((v_3,u_1))=a$, we have (2.31) $$l((v_4,u_1))=a-l((v_1,u_4)).$$(2.31)

Suppose a = 1. By Equation (2.28)(2.28) $$l((v_1,u_2))=a-l((v_2,u_1)).$$(2.28) , we have $l((v_2,u_1))=2$ and by Equation (2.30)(2.30) $$l((v_3,u_2))=l((v_1,u_4))-l((v_2,u_1)).$$(2.30) , we have $l((v_1,u_4))=1$. By Equation (2.31)(2.31) $$l((v_4,u_1))=a-l((v_1,u_4)).$$(2.31) , $l((v_4,u_1))=0$, which leads to a contradiction. By a similar argument for a = 2, we get a contradiction, therefore $P_n\square P_m$ is not ${\mathbb{Z}}_3$-vertex magic. □

As an immediate consequence of Theorem 2, we get the following.

Corollary 1.

The Ladder graph L_n is A-vertex magic, where $\left|A\right|>2$ if and only if n = 2.

Theorem 3.

The graph $G=P_5\square P_5$ is A-vertex magic if and only if A has at least four elements.

Proof.

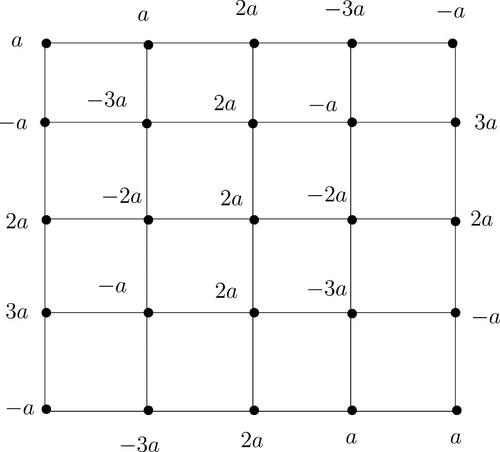
The necessity follows from Proposition 1 and Lemma 6. Now, let us prove the sufficiency. Let m be a positive integer and m > 3. If m divides o(A), then the labeling is given in Figure 3, where $a\in A$ and o(a) = m. Thus G is A-vertex magic and the magic constant is 0.

Fig. 3 ${\mathbb{Z}}_m$-vertex magic of $P_5\square P_5$.

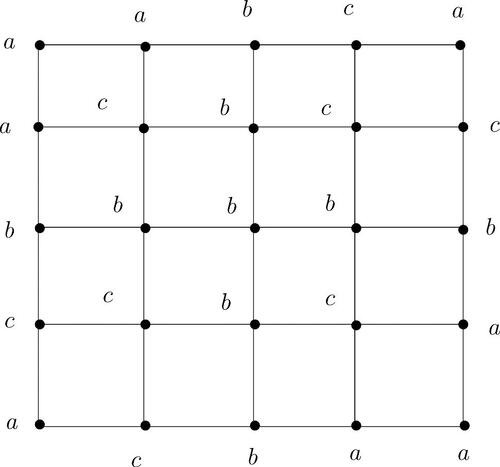
Suppose 4 divides o(A). If A has a subgroup isomorphic to ${\mathbb{Z}}_4$, then the labeling is given in Figure 3, where $a\in {\mathbb{Z}}_4$ and o(a) = 4. If A has a subgroup isomorphic to V₄, then the labeling is given in Figure 4, where $a,b,c\in V_4\setminus \left\{0\right\}$ and a, b, c are distinct. Thus G is A-vertex magic and the magic constant is 0.

Fig. 4 V₄-vertex magic of $P_5\square P_5$.

If A has a subgroup isomorphic to ${\mathbb{Z}}_3\times {\mathbb{Z}}_3$, then the labeling is given in Figure 5, G is A-vertex magic and the magic constant is (0, 0). □

Fig. 5 ${\mathbb{Z}}_3\times {\mathbb{Z}}_3$-vertex magic of $P_5\square P_5$.

Theorem 4.

Let n be a natural number and $n\ge 3$. The Book graph B_n is A-vertex magic if and only if A has a subgroup isomorphic to ${\mathbb{Z}}_p$, where p is prime number and $p|n-1$.

Proof.

Let $V(B_n)=V(P_2)\times V(S_n)$, be the vertex set of B_n, where $V(P_2)=\{v_1,v_2\},V(S_n)=\{u_1,u_2,\dots ,u_n,u_{n+1}\}$ and $\mathrm{\text{deg}}(u_{n+1})=n$. Assume that B_n is A-vertex magic and corresponding magic labeling is l. Since $w((v_1,u_i))=w((v_1,u_j))$, for any $i,j\in \{1,2,\dots ,n\}$, which implies $l((v_2,u_i))=l((v_2,u_j))$. By a similar argument for $w((v_2,u_i))=w((v_2,u_j))$, we get $l((v_1,u_i))=l((v_1,u_j))$. Assume that $l((v_1,u_i))=a,l((v_2,u_i))=b,l((v_1,u_{n+1}))=c$ and $l((v_2,u_{n+i}))=d$, where $a,b,c,d\in A\setminus \left\{0\right\}$. Since $w((v_1,u_1))=w((v_2,u_{n+1}))$, which implies $(n-1)b=0$. Now, applying Cauchy’s theorem to the subgroup generated by b, we get A has a subgroup isomorphic to ${\mathbb{Z}}_p$, where $p|o(b)$.

Let us prove the converse part. Assume that A has a subgroup isomorphic to ${\mathbb{Z}}_p$, where p is prime number and $p|n-1$. Define $l:V(B_n)\to A\setminus \left\{0\right\}$ by $$l((v_i,u_j))=\{\begin{array}{cc}(p-1)a\hfill & \hspace{1em}\text{if }j=n+1\hfill \\ a\hfill & \hspace{1em}\text{otherwise,}\hfill \end{array}$$

where o(a) = p. Thus w(v) = 0, for all $v\in V(B_n)$. □

Next, we discuss the A -vertex magicness of co-normal and tensor product of two graphs.

Theorem 5.

Let A be an Abelian group, underlying a commutative ring R. If there exists an A-vertex magic labeling $l_1:V(H)\to A\cap U(R)$ and $l_2:V(G)\to A\cap U(R)$ for graphs G and H, respectively, then $H\ast G$ is A-vertex magic.

Proof.

Let us assume that μ₁ and μ₂ are the magic constant of H and G, under the labeling l₁ and l₂ respectively. Let $h\in V(H)$ and $g\in V(G)$. Now, define $l:V(H\ast G)\to A\cap U(R)$ by $l(h,g)=l_1(h)·l_2(g)$. Then $N((h,g))=N(h)\times V(G)\cup {(N(h))}^c\times N(g)$, where ${(N(h))}^c=V(H)\setminus N(h)$. Now $$\begin{array}{c}w((h,g))=\sum _{\stackrel{u\in N(h)}{v\in V(G)}}l((u,v))+\sum _{\stackrel{u\in {(N(h))}^c}{v\in N(g)}}l((u,v))\\ =\sum _{\stackrel{u\in N(h)}{v\in V(G)}}(l_1(u)·l_2(v))+\sum _{\stackrel{u\in {(N(h))}^c}{v\in N(g)}}(l_1(u)·l_2(v))\\ ={\mu }_1·a_1+a_2·{\mu }_2,\end{array}$$

where $a_1=\sum _{v\in V(G)}{l}_2(v)$ and $a_2=\sum _{u\in V(H)}{l}_1(u)-{\mu }_1$. Since (h, g) is arbitrary, $w((h,g))={\mu }_1·a_1+a_2·{\mu }_2$, for all $(h,g)\in V(H\ast G)$. □

Theorem 6.

Let H be any k-regular graph and G be an A-vertex magic graph, where $\left|A\right|>2$. Then the graph $H\ast G$ is A-vertex magic.

Proof.

Assume that μ is the magic constant of G under the labeling l. Define $l\prime :V(H\ast G)\to A\setminus \left\{0\right\}$ by $l\prime (h,g)=l(g)$. Then $$\begin{array}{c}w((h,g))=\sum _{\stackrel{u\in N(h)}{v\in V(G)}}l\prime ((u,v))+\sum _{\stackrel{u\in {(N(h))}^c}{v\in N(g)}}l\prime ((u,v))\\ =k\sum _{v\in V(G)}l(v)+(n-k)\sum _{v\in N(g)}l(v)\\ =\mathit{\text{ka}}+(n-k)\mu ,\end{array}$$

where $a=\sum _{v\in V(G)}l(v)$. Since (h, g) is arbitrary, $w((h,g))=\mathit{\text{ka}}+(n-k)\mu$, for all $(h,g)\in V(H\ast G)$. □

Theorem 7.

Let G be an A-vertex magic graph, where $\left|A\right|>2$ and H be any r-regular graph. Then the graph $G\otimes H$ is A-vertex magic.

Proof.

Assume that l is an A-vertex magic labeling of G with magic constant μ. Now, define $l\prime :V(G\otimes H)\to A\setminus \left\{0\right\}$ by $l\prime ((g,h))=l(g)$. Let $g\in V(G)$ and $h\in V(H)$. Assume that $N_G(g)=\{g_1,g_2,\dots ,g_t\}$ and $N_H(h)=\{h_1,h_2,\dots ,h_r\}$. Then $N((g,h))=\{(g_i,h_j):i=1,2,\dots ,t\text{ and }j=1,2,\dots ,r\}$. Then $$\begin{array}{c}w((g,h))=\sum _{j=1}^r\sum _{i=1}^{t}l\prime ((v_i,u_j))\\ =r\sum _{i=1}^{t}l(v_i)\\ =\mathit{r\mu }.\end{array}$$

Since (g, h) is arbitrary, $w((g,h))=\mathit{r\mu }$, for all $(g,h)\in V(G\otimes H)$.□

Remark 1.

From the above two theorems we see that the co-normal and tensor product of a regular graph and an A-vertex magic graph is A-vertex magic.

Theorem 8.

Let G be a graph of order n and $u\prime v\prime \in E(G)$, where $\mathrm{\text{deg}}(u\prime )=\mathrm{\text{deg}}(v\prime )=n-1$. If G is A-vertex magic, where $\left|A\right|>2$, then the graph $G-u\prime v\prime$ is A-vertex magic.

Proof.

Let us assume that G is A-vertex magic and corresponding magic constant is μ. Since $w(u\prime )=w(v\prime )$, which implies $l(u\prime )=l(v\prime )$. Assume that $l(v\prime )=a$, where $a\in A\setminus \left\{0\right\}$. Let $v\in V(G)$, where $v\ne u\prime$ and $v\ne v\prime$. Since $w(v)=\mu$, which implies (2.32) $$\mu -2a=\sum _{u\in N(v)\setminus \{u\prime ,v\prime \}}l(u).$$(2.32)

Also, $w(v\prime )=\mu$, which implies (2.33) $$\mu -a=\sum _{u\in V(G)\setminus \{u\prime ,v\prime \}}l(u).$$(2.33)

Now, define $l\prime :V(G-u\prime v\prime )\to A\setminus \left\{0\right\}$ by $$l\prime (v)=\{\begin{array}{cc}b\hfill & \hspace{1em}\text{if }v=u\prime \hfill \\ a-b\hfill & \hspace{1em}\text{if }v=v\prime \hfill \\ l(v)\hfill & \hspace{1em}\text{otherwise,}\hfill \end{array}$$where $a,b\in A\setminus \left\{0\right\}$ and $a\ne b$. By Equation (2.33)(2.33) $$\mu -a=\sum _{u\in V(G)\setminus \{u\prime ,v\prime \}}l(u).$$(2.33) , we have $w(v\prime )=w(u\prime )=\sum _{u\in V(G)\setminus \{u\prime ,v\prime \}}l\prime (u)=\mu -a$. Let $v\in V(G)\setminus \{u\prime ,v\prime \}$. Now, $w(v)=\sum _{u\in N(v)\setminus \{u\prime ,v\prime \}}l(u)+l\prime (u\prime )+l\prime (v\prime )$. By Equation (2.32)(2.32) $$\mu -2a=\sum _{u\in N(v)\setminus \{u\prime ,v\prime \}}l(u).$$(2.32) , we have $w(v)=\mu -a$. Thus $w(u)=\mu -a$, for all $u\in V(G)$. □

Corollary 2.

For an Abelian group containing at least three elements, $K_n-F$ is A-vertex magic, where F is perfect matching if n is even, otherwise F is nearly perfect matching.

Remark 2.

The following theorem provides a new technique to construct infinite class of A-vertex magic graphs from existing ones, where A contains at least three elements.

Theorem 9.

Let H be an A-vertex magic graph, where $\left|A\right|>2$. Then the graph $G=H+K_m{}^c$ is A-vertex magic, where m > 1.

Proof.

Let $V(G)=V(H)\cup V(K_m{}^c)$ be a partition of the vertex set of G, where $V(H)=\{v_1,v_2,\dots ,v_n\}$ and $V(K_m{}^c)=\{u_1,u_2,\dots ,u_m\}$. Assume that l is A-vertex magic labeling of H with magic constant a. Let $b=\sum _{v\in V(H)}l(v)$.

Case 1. a = b.

Assume that m is odd and define $l\prime :V(G)\to A\setminus \left\{0\right\}$ by $$l\prime (v)=\{\begin{array}{cc}l(v)\hfill & \hspace{1em}\text{if }v\in V(H)\hfill \\ c-d\hfill & \hspace{1em}\text{if }v=u_1\hfill \\ d\hfill & \hspace{1em}\text{if }v=u_2\hfill \\ -c\hfill & \hspace{1em}\text{if }v=u_i,i>2\text{ and }i\text{ is odd}\hfill \\ c\hfill & \hspace{1em}\text{if }v=u_i,i>2\text{ and }i\text{ is even,}\hfill \end{array}$$where $c,d\in A\setminus \left\{0\right\}$ and $c\ne d$. Thus w(v) = a, for all $v\in V(G)$.

Suppose m is even. Define $l\prime :V(G)\to A\setminus \left\{0\right\}$ by $$l\prime (v)=\{\begin{array}{cc}l(v)\hfill & \hspace{1em}\text{if }v\in V(H)\hfill \\ -c\hfill & \hspace{1em}\text{if }v=u_i\text{ and }i\text{ is odd}\hfill \\ c\hfill & \hspace{1em}\text{if }v=u_i\text{ and }i\text{iseven}.\hfill \end{array}$$

Thus w(v) = a, for all $v\in V(G)$.

Case 2. $a\ne b$

Subcase 2.1 a = 0.

Suppose m is odd. Now, define $l\prime :V(G)\to A\setminus \left\{0\right\}$ by $$l\prime (v)=\{\begin{array}{cc}l(v)\hfill & \hspace{1em}\text{if }v\in V(H)\hfill \\ b\hfill & \hspace{1em}\text{if }v=u_i\text{ and }i\text{ is odd}\hfill \\ -b\hfill & \hspace{1em}\text{if }v=u_i\text{ and }i\text{ is even}\hfill \end{array}$$

Thus w(v) = b, for all $v\in V(G)$.

Suppose m is even, then define $l\prime :V(G)\to A\setminus \left\{0\right\}$ by $$l\prime (v)=\{\begin{array}{cc}l(v)\hfill & \hspace{1em}\text{if }v\in V(H)\hfill \\ b-c\hfill & \hspace{1em}\text{if }v=u_1\hfill \\ c\hfill & \hspace{1em}\text{if }v=u_i\text{ and }i\text{ is even}\hfill \\ -c\hfill & \hspace{1em}\text{if }v=u_i,i>2\text{ and }i\text{ is odd,}\hfill \end{array}$$where $c,b\in A\setminus \left\{0\right\}$ and $c\ne b$. Thus w(v) = b, for all $v\in V(G)$.

Subcase 2.2 b = 0.

By a similar argument of subcase 2.1, we get the result.

Subcase 2.3 $a\ne 0$ and $b\ne 0$.

If m is odd, then define $$l\prime (v)=\{\begin{array}{cc}l(v)\hfill & \hspace{1em}\text{if }v\in V(H)\hfill \\ b-a\hfill & \hspace{1em}\text{if }v=u_1\hfill \\ b\hfill & \hspace{1em}\text{if }v=u_i\text{ and }i\text{ is even}\hfill \\ -b\hfill & \hspace{1em}\text{if }v=u_i,i>2\text{ and }i\text{isodd}.\hfill \end{array}$$

Thus w(v) = b, for all $v\in V(G)$.

Suppose m is even. Define $$l\prime (v)=\{\begin{array}{cc}l(v)\hfill & \hspace{1em}\text{if }v\in V(H)\hfill \\ b\hfill & \hspace{1em}\text{if }v=u_1\hfill \\ -a\hfill & \hspace{1em}\text{if }v=u_2\hfill \\ -b\hfill & \hspace{1em}\text{if }v=u_i,i>2\text{ and }i\text{ is odd}\hfill \\ b\hfill & \hspace{1em}\text{if }v=u_i,i>2\text{ and }i\text{iseven}.\hfill \end{array}$$

Thus w(v) = b, for all $v\in V(G)$. □

The following results are a consequence of Theorem 9.

Corollary 3.

Let $G=K_{1,1,n_3,\dots ,n_k}$ be a complete k-partite graph with $k\ge 3$. Then G is A-vertex magic, where $\left|A\right|>2$.

Proof.

Clearly, G = K₂ is A-vertex magic. The complete k-partite graph can be written as $K_{1,1,n_3,\dots ,n_k}$ such that $n_3\le n_4\le \cdots \le n_k$. By induction on k we write $K_{1,1,n_3,\dots ,n_k}\cong H+{(K_{n_k})}^c$. Let r be non-negative integer such that $n_3=n_4=\cdots =n_r=1$ and $n_i\ge 2$, for all $i\in \{r+1,\dots ,k\}$. Let $H_1=K_r$. Then we have $K_{1,1,n_3,\dots ,n_r,n_{r+1}}=H_1+{(K_{r+1})}^c$, by Theorem 9 which is A-vertex magic. Continuing this way we have $K_{1,1,n_3,\dots ,n_k}=H+{(K_{n_k})}^c$, where $H=K_{1,1,n_3,\dots ,n_{k-1}}$ is A-vertex magic. □

As an immediate consequence of Theorem 9, we deduce the following result in [1].

Corollary 4

(Theorem 5 in [1]). Let G be an arbitrary r-regular graph with n vertices. Then the graph $G+K_m{}^c$ is A-vertex magic, where $\left|A\right|>2$ and m > 1.

Theorem 10.

Let H be a graph of order n and A be an Abelian group with at least three elements. Then the graph $G=H+K_1$ is A-vertex magic if and only if H has A-vertex magic labeling with the magic constant not equal to the label sum of all the vertices of H.

Proof.

Let $V(H)=\{v_1,v_2,\dots ,v_n\}$ and u be the vertex of K₁. Assume that G is A-vertex magic with labeling l. Since $w(v_1)=w(u)$, which implies (2.34) $$l(u)+\sum _{v\in N_H(v_1)}l(v)=\sum _{v\in V(H)}l(v).$$(2.34)

By the proof of Theorem 1, we have H is A-vertex magic under the same labeling l restricted to H. Now, $w(v_1)$ in H is equal to $\sum _{v\in N_H(v_1)}l(v)$. From Equation (2.34)(2.34) $$l(u)+\sum _{v\in N_H(v_1)}l(v)=\sum _{v\in V(H)}l(v).$$(2.34) , $\sum _{v\in N_H(v_1)}l(v)=\sum _{v\in V(H)}l(v)-l(u)$. By definition of A-vertex magic $l(u)\ne 0$, therefore we get the required result.

Conversely, assume that the graph H satisfies the sufficient condition, a equal to magic constant and b equal to the label sum of all the vertices of H. Now, we extend the labeling of H to G, define $$l(u)=\{\begin{array}{cc}b\hfill & \hspace{1em}\text{if }a=0\hfill \\ -a\hfill & \hspace{1em}\text{if }b=0\hfill \\ b-a\hfill & \hspace{1em}\text{if }a\ne 0\text{ and }b\ne 0.\hfill \end{array}$$

Thus w(v) = b, for all $v\in V(G)$. □

Acknowledgments

The author would like to thank Dr. S.V. Bharanedhar and Dr. T. Kavaskar, Central University of Tamil Nadu, Thiruvarur for their support and fruitful discussions.

Additional information

Funding

The work of S. Balamoorthy is supported by a Junior Research Fellowship from CSIR-UGC, India (UGC-Ref.No.:1085/(CSIR-UGC NET JUNE 2019)).