Signed total double Roman dominating functions in graphs

Abstract

A signed total double Roman dominating function (STDRDF) on an isolated-free graph $G=(V,E)$ is a function $f:V(G)\to \{-1,1,2,3\}$ such that (i) every vertex v with $f(v)=-1$ has at least two neighbors assigned 2 under f or one neighbor w with f(w) = 3, (ii) every vertex v with f(v) = 1 has at least one neighbor w with $f(w)\ge 2$ and (iii) $\sum _{u\in N(v)}f(u)\ge 1$ holds for any vertex v. The weight of a STDRDF is the value $f(V(G))=\sum _{u\in V(G)}f(u).$ The signed total double Roman domination number ${\gamma }_{\mathit{\text{sdR}}}^t(G)$ is the minimum weight of a STDRDF on G. In this article, we provide various bounds on ${\gamma }_{\mathit{\text{sdR}}}^t(G)$ and we show that the corresponding decision problem is NP-complete for bipartite and chordal graphs. In addition, we determine the signed total double Roman domination number of some classes of graphs including cycles, complete graphs and complete bipartite graphs.

Keywords:

• Roman domination
• signed double Roman domination
• signed total double Roman domination

2010 MATHEMATICS SUBJECT CLASSIFICATION:

• 05C69
• 05C05

1 Introduction

In this paper, G is a simple isolated-free graph with vertex set $V=V(G)$ and edge set $E=E(G)$. The order $\left|V\right|$ of G is denoted by $n=n(G)$. For every vertex $v\in V$, the open neighborhood N(v) is the set $\{u\in V(G):\mathit{\text{uv}}\in E(G)\}$ and the closed neighborhood of v is the set $N[v]=N(v)\cup \left\{v\right\}$. The degree of a vertex $v\in V$ is ${\mathrm{\text{deg}}}_G(v)=|N(v)|$. The minimum and maximum degree of a graph G are denoted by $\delta =\delta (G)$ and $\Delta =\Delta (G)$, respectively. A leaf of G is a vertex of degree one, while a support vertex of G is a vertex adjacent to a leaf. An edge of a graph is said to be pendant edge if one of its vertices is a leaf. We write P_n for the path of order n, C_n for the cycle of order n, K_n for the complete graph of order n and $K_{m,n}$ for the complete bipartite graph.

A set $S\subseteq V$ in a graph G is called a (total) dominating set if every vertex of $V\setminus S$ (V) is adjacent to a vertex of S. The (total) domination number $\gamma (G)({\gamma }_t(G))$ equals the minimum cardinality of a (total) dominating set in G.

A function $f:V(G)\to \{0,1,2\}$ is a Roman dominating function (RDF) on G if every vertex $u\in V$ for which f(u) = 0 is adjacent to at least one vertex v for which f(v) = 2. The weight of an RDF is the value $f(V(G))=\sum _{u\in V(G)}f(u).$ The Roman domination number ${\gamma }_R(G)$ is the minimum weight of an RDF on G. Roman domination was introduced by Cockayne et al. in [11]. Since 2004, several papers have been published on this topic and its variations.

In 2016, Beeler et al. [10] introduced the double Roman domination defined as follows. A function $f:V\to \{0,1,2,3\}$ is a double Roman dominating function (DRDF) on a graph G if the following conditions hold:

1. If f(v) = 0, then v has at least two neighbors assigned 2 under f or one neighbor assigned 3 under f.

2. If f(v) = 1, then v has at least one neighbor w with $f(w)\ge 2$.

The double Roman domination number ${\gamma }_{\mathit{\text{dR}}}(G)$ equals the minimum weight of a double Roman dominating function on G. For further results on double Roman domination see [1, 4].

In 2014 Abdollahzadeh Ahangar et al. [7] introduced the concept of Signed Roman domination. Also, the other variations of this concept have been introduced in [2, 3, 18, 19].

Abdollahzadeh Ahangar et al. [5] introduced the concept of a variation of double Roman domination as signed double Roman domination. A signed double Roman dominating function (SDRDF) on a graph $G=(V,E)$ is a function $f:V(G)\to \{-1,1,2,3\}$ such that (i)every vertex v with $f(v)=-1$ is adjacent to at least two vertices assigned a 2 or to at least one vertex w with $f(w)=3,$ (ii) every vertex v with f(v) = 1 is adjacent to at least one vertex w with $f(w)\ge 2$ and (iii) $f(v)=\sum _{u\in N[v]}f(u)\ge 1$ holds for any vertex v. The weight of a SDRDF f is the value $\omega (f)=\sum _{u\in V(G)}f(u).$ The signed double Roman domination number ${\gamma }_{\mathit{\text{sdR}}}(G)$ is the minimum weight of a SDRDF on G. For a SDRDF f, let $V_i(f)=\{v\in V:f(v)=i\}$. In the context of a fixed SDRDF, we suppress the argument and simply write $V_{-1}$, V₁, V₂, and V₃. Since this partition determines f, we can equivalently write $f=(V_{-1},V_1,V_2,V_3)$. For further results on signed double Roman domination see [6, 9, 20].

A signed total double Roman dominating function (STDRDF) on a graph $G=(V,E)$ is a function $f:V(G)\to \{-1,1,2,3\}$ such that (i) every vertex v with $f(v)=-1$ is adjacent to at least two vertices assigned a 2 or to at least one vertex w with $f(w)=3,$ (ii) every vertex v with f(v) = 1 is adjacent to at least one vertex w with $f(w)\ge 2$ and (iii) $f(v)=\sum _{u\in N(v)}f(u)\ge 1$ holds for any vertex v. The weight of a STDRDF f is the value $\omega (f)=\sum _{u\in V(G)}f(u).$ The signed total double Roman domination number ${\gamma }_{\mathit{\text{sdR}}}^t(G)$ is the minimum weight of a STDRDF on G. This parameter and its variants have been studied in [8, 15, 17].

In this article, we provide various bounds on ${\gamma }_{\mathit{\text{sdR}}}^t(G)$ and we show that the corresponding decision problem is NP-complete for bipartite and chordal graphs. In addition, we determine the signed total double Roman domination number of some classes of graphs including cycles, complete graphs and complete bipartite graphs.

We end this section by recalling the well-known upper bound due to Ore that $\gamma (G)\le n/2$ for graphs G of order n and minimum degree $\delta (G)\ge 1.$ Moreover, the graphs G of even order and without isolated vertices with $\gamma (G)=n/2$ have been characterized independently by Payan and Xuong [16] and Fink et al. [12], as follows.

Theorem 1.

[12, 16] Let G be a graph of even order n without isolated vertices. Then $\gamma (G)=n/2$ if and only if each component of G is either a cycle C₄ or the corona $H°K_1$ of a connected graph H.

2 Basic properties and preliminary bounds

In this section we investigate some basic properties of STDRDF.

Observation 2.

Let $f=(V_{-1},V_1,V_2,V_3)$ be a STDRDF in a graph G without isolated vertices. Then the following holds.

1. Every vertex in $V_{-1}\cup V_1$ is dominated by a vertex in $V_2\cup V_3$.

2. $w(f)=\left|V_1\right|+2\left|V_2\right|+3\left|V_3\right|-\left|V_{-1}\right|$.

3. $n=\left|V_1\right|+\left|V_2\right|+\left|V_3\right|+\left|V_{-1}\right|$.

4. $V_1\cup V_2\cup V_3$ is a total dominating set in G.

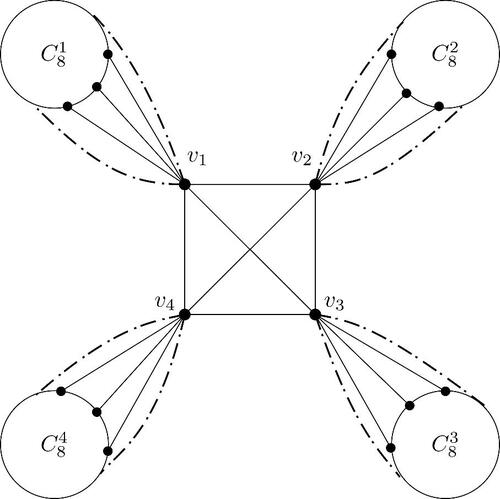
Let $k\ge 1$ be an integer and $K_{4k}$a complete graph with vertex set $\{v_1,v_2,\dots ,v_{4k}\}$. Assume G_k is the graph obtained from $K_{4k}$ by adding 4k disjoint cycles $C^1,C^2,\dots ,C^{4k}$ each of order $(12k-4)$ and joining v_j to the vertices of the cycle C^j for each j, see Figure 1. It is easy to verify that G_k is a graph of order $4k(12k-3)$ with minimum degree 3 and maximum degree $\Delta (G_k)=16k-5$. Clearly, the function $f=(V(G_k)\setminus V(K_{4k}),\varnothing ,\varnothing ,V(K_{4k}))$ is a signed total double Roman dominating function of G_k .

Fig. 1 The graph G₁.

Proposition 3.

Let G be a graph of order n, minimum degree $\delta \ge 1$ and maximum degree Δ, and let $f=(V_{-1},V_1,V_2,V_3)$ be a STDRDF in G. Then the following holds.

1. $(3\Delta -1)\left|V_3\right|+(2\Delta -1)\left|V_2\right|+(\Delta -1)\left|V_1\right|\ge (\delta +1)\left|V_{-1}\right|$.

2. $(3\Delta +\delta )\left|V_3\right|+(2\Delta +\delta )\left|V_2\right|+(\Delta +\delta )\left|V_1\right|\ge (\delta +1)n$.

3. $(\Delta +\delta )w(f)\ge (\delta -\Delta +2)n+(\delta -\Delta )\left|V_2\right|+2(\delta -\Delta )\left|V_3\right|$.

4. $w(f)\ge (\delta -3\Delta +2)n/(3\Delta +\delta )+\left|V_2\right|+2\left|V_3\right|$.

Furthermore, the bounds in (i), (ii), (iii), and (iv) are sharp for the graph $G_k(k\ge 1)$

Proof.

(i) By Observation 2 (Item (iii)) and definition, we have $$\begin{array}{cc}\left|V_{-1}\right|+\sum _{i=1}^3\left|V_i\right|& =n\\ & \le \sum _{v\in V}f(N(v))\\ & =\sum _{v\in V}d(v)f(v)\\ & =\sum _{v\in V_3}3d(v)+\sum _{v\in V_2}2d(v)+\sum _{v\in V_1}d(v)\\ & -\sum _{v\in V_{-1}}d(v)\\ & \le 3\Delta \left|V_3\right|+2\Delta \left|V_2\right|+\Delta \left|V_1\right|-\delta \left|V_{-1}\right|,\end{array}$$ and this leads to the desired result.

(ii) This follows by substituting $\left|V_{-1}\right|=n-{\sum }_{i=1}^3\left|V_i\right|$ in Item (i).

(iii) By Observation 2, we have that $$\begin{array}{cccc}(\Delta +\delta )w(f)& =& (\Delta +\delta )\left(2(\sum _{i=1}^3|V_i|)-n+\left|V_2\right|+2\left|V_3\right|\right)& \\ & \ge & 2(\delta +1)n-2\Delta \left|V_2\right|-4\Delta \left|V_3\right|& \\ & & +(\Delta +\delta )(|V_2|+2|V_3|-n)(\text{by Part }(\text{ii}))& \\ & =& (\delta -\Delta +2)n+(\delta -\Delta )\left|V_2\right|+2(\delta -\Delta )\left|V_3\right|.& \\ & & & \end{array}$$

(iv) By Item (i), we have $$\begin{array}{c}n\le 3\Delta \left|V_3\right|+2\Delta \left|V_2\right|+\Delta \left|V_1\right|-\delta \left|V_{-1}\right|\\ \le 3\Delta \left|{\cup }_{i=1}^3{V}_i\right|-\delta \left|V_{-1}\right|\\ \le 3\Delta \left|{\cup }_{i=1}^3{V}_i\right|-\delta (n-|{\cup }_{i=1}^3{V}_i|)\\ =(3\Delta +\delta )\left|{\cup }_{i=1}^3{V}_i\right|-\delta n.\end{array}$$

And so $\left|{\cup }_{i=1}^3{V}_i\right|\ge n(\delta +1)/(3\Delta +\delta )$. Therefore, $w(f)=2\left|{\cup }_{i=1}^3{V}_i\right|-n+\left|V_2\right|+2\left|V_3\right|\ge (\delta -3\Delta +2)n/(3\Delta +\delta )+\left|V_2\right|+2\left|V_3\right|$. □

Using Proposition 3 (Item (iii)), we obtain the following lower bound on the signed total double Roman domination number of regular graphs.

Corollary 4.

If G is an r-regular graph of order n with $r\ge 1$, then ${\gamma }_{\mathit{\text{sdR}}}^t(G)\ge \frac{n}{r}$.

If G is not a regular graph, then as a consequence of Proposition 3 (Items (iii) and (iv)), we have the following result.

Corollary 5.

If G is a non-regular graph of order n, minimum degree $\delta \ge 1$ and maximum degree Δ, then $${\gamma }_{\mathit{\text{sdR}}}^t(G)\ge \lceil \frac{(3\delta -3\Delta +4)n}{3\Delta +\delta }\rceil .$$

This bound is sharp for all graphs $G_k(k\ge 1)$ illustrated before Proposition 3.

Proof.

Multiplying both sides of the inequality in Proposition 3 (Item (iv)) by $\Delta -\delta$ and adding the resulting inequality to the inequality in Proposition 3 (Item (iii)) leads to the desired result. □

Next we present a so-called Nordhaus-Gaddum type inequality for the signed total double Roman domination number of regular graphs.

Theorem 6.

If G is an r-regular graph of order n such that $r\ge 1$ and $n-r-1\ge 1$, then $${\gamma }_{\mathit{\text{sdR}}}^t(G)+{\gamma }_{\mathit{\text{sdR}}}^t(\overline{G})\ge \frac{4n}{n-1}.$$

If n is even, then ${\gamma }_{\mathit{\text{sdR}}}^k(G)+{\gamma }_{\mathit{\text{sdR}}}^k(\overline{G})\ge \frac{4(n-1)}{n-2}$.

Proof.

Since G is an r-regular, the complement $\overline{G}$ is $(n-r-1)$-regular. By Corollary 4 $${\gamma }_{\mathit{\text{sdR}}}^t(G)+{\gamma }_{\mathit{\text{sdR}}}^t(\overline{G})\ge n(\frac{1}{r}+\frac{1}{n-r-1}).$$

The conditions $r\ge 1,n-r-1\ge 1$ imply that $1\le r\le n-2$. Since the function $g(x)=1/x+1/(n-x-1)$ takes its minimum at $x=(n-1)/2$ when $1\le x\le n-2$, we obtain $${\gamma }_{\mathit{\text{sdR}}}^t(G)+{\gamma }_{\mathit{\text{sdR}}}^t(\overline{G})\ge n(\frac{2}{n-1}+\frac{2}{n-1})=\frac{4n}{n-1},$$ and this is the desired bound. If n is even, then the function g takes its minimum at $r=x=(n-2)/2$ or $r=x=n/2$, since r is an integer. This implies that $$\begin{array}{c}{\gamma }_{\mathit{\text{sdR}}}^t(G)+{\gamma }_{\mathit{\text{sdR}}}^t(\overline{G})\ge n(\frac{1}{r}+\frac{1}{n-r-1})\\ \ge n(\frac{2}{n}+\frac{2}{n-2})=\frac{4(n-1)}{n-2},\end{array}$$ and the proof is complete. □

3 Complexity result

Our aim in this section is to establish the NP-complete result for the signed total double Roman domination problem in bipartite and chordal graphs.

Signed total double Roman dominating function(signed TDTRF):

Instance: Graph $G=(V,E)$, positive integer $k\le \left|V\right|$.

Question: Does G have a signed total double Roman dominating function of weight at most k?

We will show that this problem is NP-complete by reducing the special case of Exact Cover by 3-sets (X3C) to which we refer as X3C3. The NP-completeness of X3C3 was proven in 2008 by Hickey et al. [14]

X3C3

Instance: A set of elements X with $\left|X\right|=3q$, and a collection C of $m=3q$ 3-element subsets of X, such that each element occurs in exactly, 3 members of C.

Question: Does C contain an exact cover for X, i.e. does there exist a subcollection $C^{\prime }\subset C$ such that every element of X occurs in exactly one member of $C^{\prime }$?

Theorem 7.

Problem signed-TDRDF is NP-Complete for bipartite and chordal graphs.

Proof.

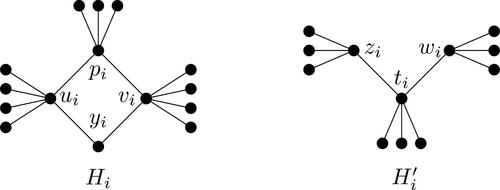
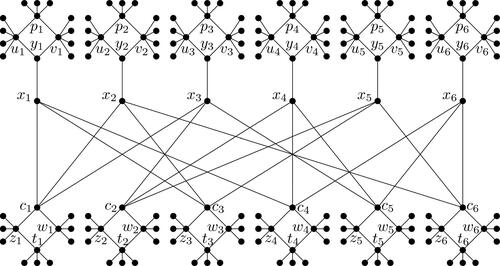
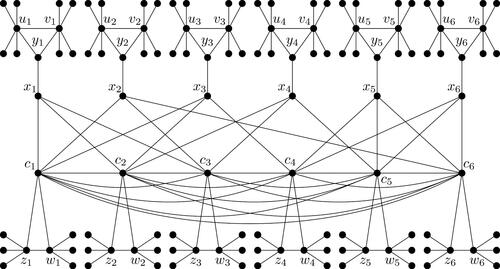
Clearly signed-TDRDF is a member of $\mathcal{N}\mathcal{P}$ since we can check in polynomial time that a function $f:V\to \{-1,1,2,3\}$ has weight at most k and is a signed total double Roman dominating function. Now let us how to transform any instance of X3C3 into an instance G of signed-TDRDF so that one of them has a solution if and only if the other one has a solution. Let $X=\{x_1,x_2,\dots ,x_{3q}\}$ and $C=\{C_1,C_2,\dots ,C_{3q}\}$ be an arbitrary instance of X3C3. We now construct the bipartite graph G₁ (respectively, the chordal graph $G_2$). Let $G\in \{G_1,G_2\}.$

For each $x_i\in X,$ we create a single vertex x_i to which we associate a copy of the graph H_i as shown in Figure 2 (respectively, $F_i$ when G₂ is considered) by adding the edge $y_i{x}_i.$ For each $C_j,$ we create a vertex c_j to which we associate a copy of the graph $H_j^{\prime }$ as shown in Figure 2 (respectively, $F_j^{\prime }$ when G₂ is considered) by adding the edges $c_j{z}_j$ and $c_j{w}_j.$ Now to obtain the graph G, we add edges $c_j{x}_j$ if $x_i\in C_j.$ In addition, for the graph $G_2,$ we add all edges between vertices c_j ’s. Let $A=\{c_1,c_2,\dots ,c_{3q}\}$, and set $k=q.$ Figures 3 and 5 give examples of G₁ and G₂, respectively.

Fig. 2 The graphs H_i and $H_i^{\prime }$.

Fig. 3 The graphs F_i and $F_i^{\prime }$.

Fig. 4 NP-completeness of signed total double Roman for bipartite graphs.

Fig. 5 NP-completeness of signed total double Roman for chordal graphs.

Suppose that $C^{\prime }$ is a solution of X3C3. Define two signed total double Roman dominating functions f and g on G₁ and $G_2,$ respectively, of weight k as follows: $f(u_i)=f(v_i)=f(p_i)=f(z_i)=f(w_i)=f(t_i)=3,f(y_i)=2$ for $1\le i\le 3q,f(c_j)=2$ for every c_j if $C_j\in C^{\prime }$, and $f(c_j)=1$ if $C_j\notin C^{\prime }$, every x_i and every leaf is assigned a –1 under f. Also, $g(u_i)=g(v_i)=g(z_i)=g(w_i)=3,g(y_i)=2$ for $1\le i\le 3q,g(c_j)=2$ for every c_j if $C_j\in C^{\prime }$, and $g(c_j)=1$ if $C_j\notin C^{\prime }$, every x_i and every leaf is assigned a –1 under g. Clearly, since $C^{\prime }$ exists, $\left|C^{\prime }\right|=q$, and so the number of c_j ’s with weight 2 is q, having disjoint neighborhoods in $\{x_1,x_2,\dots ,x_{3q}\}$. It is straightforward to see that f and $g$ are signed total double Roman dominating functions on G with weight $f(V)=q=k$ and $g(V)=q=k$.

Since the proof does not differ and uses the same principle for the two graphs G₁ and G₂, the graph G designates the two graphs G₁ or G₂.

Conversely, assume that G has a signed total Roman dominating function with weight at most k = q. Among all such functions, let f be one chosen so that:

(C1) f assigns small values to the leaves of G.

(C2) Subject to Condition (C1): f assigns small values to y_j’s.

According to (C1), one can easily see that $f(x)=-1$ for every leaf if G. Hence every support vertex of G is assigned a 3.

Now, since $\sum _{u\in N(u_i)-\left\{y_i\right\}}f(u)=-1$ and $\sum _{u\in N(v_i)-\left\{y_i\right\}}f(u)=-1$, we deduce that $f(y_i)\ge 2$ for every i. Likewise, $f(c_j)\ge 1$ for every j, since $\sum _{u\in N(z_i)-\left\{c_j\right\}}f(u)=\sum _{u\in N(w_i)-\left\{c_j\right\}}f(u)=0$. It follows that no x_i needs to be assigned a positive value, that is $f(x_i)=-1$ for each i. Moreover, according to the choice of f, Condition (C2) implies that $f(y_i)=2$ for each i. Since each x_i must have two neighbors assigned a 2 under f and since f has weight at most k = q, we deduced that exactly q vertices of A must be assigned a 2 and the remaining vertices of A are assigned a 1. But since each c_j has exactly three neighbors in X, we conclude that $C^{\prime }=\{C_j:f(c_j)=2\}$ is an exact cover for C. □

4 Upper bounds

In this section we present some sharp bounds on the signed total double Roman domination number in graphs.

Theorem 8.

For any graph G of order $n\ge 2$ with $\delta (G)\ge 1,$ $${\gamma }_{\mathit{\text{sdR}}}^t(G)\le n+\alpha \prime (G)$$ where $\alpha \prime (G)$ is the matching number of G. This bound is sharp for $G=m{K}_2(m\ge 1)$.

Proof.

Let $M=\{u_1{v}_1,u_2{v}_2,\dots ,u_{\alpha \prime }{v}_{\alpha \prime }\}$ be a maximum matching of G and let X be the independent set of M-unsaturated vertices. If y and z are vertices of X and $y{u}_i\in E(G)$, then since the matching M is maximum, $z{v}_i\notin E(G)$. Therefore, for all $i\in \{1,2,\dots ,\alpha \prime \}$ there are at most two edges between the sets $\{u_i,v_i\}$ and {y, z}. If there exists a vertex $v\in X$ such that $v{u}_i,v{v}_i\in E(G)$ for some i, say i = 1, then $y{u}_1,y{v}_1\notin E(G)$ for each $y\in X\setminus \left\{v\right\}$ because M is a maximum matching. Let B be the set of all vertices $v\in X$ such that $v{u}_i,v{v}_i\in E(G)$ for some i. Then $v{u}_i\notin E(G)$ or $v{v}_i\notin E(G)$ for each $v\in X-B$ and each $i\in \{1,2,\dots ,\alpha \prime \}$. Thus we may assume that $N(x)\subseteq \{u_1,u_2,\dots ,u_{\alpha \prime }\}$ for each $x\in X-B$. Define the function $f:V(G)\to \{-1,1,2,3\}$ by $f(u_i)=2$ and $f(v_i)=1$ for $i\in \{1,2,\dots ,\alpha \prime \}$ and f(x) = 1 for $x\in X$. Clearly, f is a STDRDF of G of weight $n+\alpha \prime$ and thus ${\gamma }_{\mathit{\text{sdR}}}^t(G)\le n+\alpha \prime (G)$. □

Next result is an immediate consequence of Theorem 8.

Corollary 9.

For any connected graph G of order $n\ge 2,{\gamma }_{\mathit{\text{sdR}}}^t(G)\le \frac{3n}{2}$. The equality holds if and only if G = K₂.

Proof.

The bound is immediate from Theorem 8 because $\alpha (G)\le \frac{n}{2}$. If G = K₂, then clearly ${\gamma }_{\mathit{\text{sdR}}}^t(K_2)=3=\frac{3n}{2}$.

Conversely, let ${\gamma }_{\mathit{\text{sdR}}}^t(G)=\frac{3n}{2}$. Let D be a $\gamma (G)$-set and define the function f on G by f(x) = 2 for every $x\in D$ and f(x) = 0 for any other vertex. One can easily see that f is a STDRDF of G and using Ore’s theorem we have (1) $$\frac{3n}{2}={\gamma }_{\mathit{\text{sdR}}}^t(G)\le \omega (f)=n+\gamma (G)\le \frac{3n}{2}.$$(1)

It follows from (1) and Theorem 1 that G is either a cycle C₄ or the corona $H°K_1$ of a connected graph H. If G = C₄, then certainly ${\gamma }_{\mathit{\text{sdR}}}^t(C_4)=4<\frac{3n}{2}$ which is a contradiction. Henceforth, we may assume that G is the corona $H°K_1$ of a connected graph H. If $n(H)\ge 2$, then define the function f on G by f(v) = 3 for every $v\in V(H)$ and $f(x)=-1$ for any other vertex. It is easy to see that f is a STDRDF of G of weight n leading to a contradiction. Thus n(H) = 1 and so G = K₂. This completes the proof. □

Next we present a bound on the signed total double Roman domination number in terms of the order and signed total domination number.

Theorem 10.

For any graph G of order $n\ge 2$ with $\delta (G)\ge 1$, $${\gamma }_{\mathit{\text{sdR}}}^t(G)\le \mathrm{\text{min}}\{n+{\gamma }_{\mathit{\text{st}}}(G),\frac{5n}{4}+\frac{{\gamma }_{\mathit{\text{st}}}(G)}{4}\}.$$

Proof.

Let f be a ${\gamma }_{\mathit{\text{st}}}(G)$-function and let $P=\{v⏧f(v)=1\}$ and $M=\{v⏧f(v)=-1\}$. Clearly, $P=\frac{n+{\gamma }_{\mathit{\text{st}}}(G)}{2}$ and $M=\frac{n-{\gamma }_{\mathit{\text{st}}}(G)}{2}$.

Define $g:V(G)\to \{-1,1,2,3\}$ by g(v) = 3 for $v\in P$ and $g(v)=-1$ for $v\in M$. It is easy to see that g is a STDRDF of G and hence ${\gamma }_{\mathit{\text{sdR}}}^t(G)\le 3\left|P\right|-\left|M\right|\le n+{\gamma }_{\mathit{\text{st}}}(G)$.

Let $M=\{x_1,x_2,\dots ,x_r\}$. By definition each x_i is adjacent to a vertex $x_i^{\prime }\in P$. Let S be a minimum dominating set for the induced subgraph $G[P]$. Since $G[P]$ is isolated free, we have $\left|S\right|\le \frac{\left|P\right|}{2}$ (Ore’s theorem). Define $g:V(G)\to \{-1,1,2,3\}$ by $g(x_i^{\prime })=3$ for $i\in \{1,2,\dots ,r\}$, g(x) = 2 for $x\in S-\{x_1,x_2,\dots ,x_r^{\prime }\}$ and $g(v)=f(x)$ otherwise. Clearly, g is a STDRDF of G and hence ${\gamma }_{\mathit{\text{sdR}}}^t(G)\le \left|P\right|-\left|M\right|+2\left|M\right|+\left|P\right|/2\le \frac{5n}{4}+\frac{{\gamma }_{\mathit{\text{st}}}(G)}{4}$. This completes the proof. □

In [13] Henning and Slater studied the concept of open packing in graphs. A set $L\subseteq V$ is an open packing set if for every vertex $v\in V,|N(v)\cap L|\le 1$. The open packing number ${\rho }_0(G)$ is the maximum cardinality of an open packing set.

Here, we present an upper bound on the signed total double Roman domination number in terms of the order and open packing number.

Theorem 11.

For any graph G of order $n\ge 2$ with $\delta (G)\ge 3,{\gamma }_{\mathit{\text{sdR}}}^t(G)\le 2n-3{\rho }_0(G).$

Proof.

Let S be an open packing set of G with $\left|S\right|={\rho }_0(G)$. Define $g:V(G)\to \{-1,1,2,3\}$ by g(x) = 2 for $x\in V-S$ and $g(x)=-1$ for $x\in S$. Clearly, g is a STDRDF of G of weight $2n-3{\rho }_0(G)$ and thus ${\gamma }_{\mathit{\text{sdR}}}^t(G)\le 2n-3{\rho }_0(G)$. □

Let H be a bipartite graph with partite sets $\mathcal{L}$ and $\mathcal{R}$ (standing for “left” and “right”). We define a left dominating set of H to be a set of vertices in $\mathcal{R}$ that dominate $\mathcal{L}$. The minimum cardinality of a left dominating set in H is called the left domination number, denoted ${\gamma }_{\mathcal{L}}(H)$, of H. Let ${\delta }_{\mathcal{L}}(H)$ and ${\Delta }_{\mathcal{L}}(H)$ denote minimum and maximum degree, respectively, of a vertex of $\mathcal{L}$ in H.

Abdollahzadeh Ahangar et al. [7] established the following upper bound on the left domination number of a bipartite graph.

Theorem 12.

Let H be a bipartite graph of order n with partite sets $\mathcal{L}$ and $\mathcal{R}$. If ${\delta }_{\mathcal{L}}(H)\ge 2$, then ${\gamma }_{\mathcal{L}}(H)\le \frac{n}{3}$, with equality if and only if every component of H is isomorphic to P₃ or C₆.

Theorem 13.

Let G be a graph of order n and $\delta \ge 3$. Then $${\gamma }_{\mathit{\text{sdR}}}^t(G)\le \frac{3n}{4}+\frac{5{\gamma }_{\mathit{\text{sT}}}(G)}{4}.$$

Proof.

Let f be a ${\gamma }_{\mathit{\text{st}}}(G)$-function. Let $\mathcal{L}$ and $\mathcal{R}$ denote the sets of those vertices in G which are assigned under f the values –1 and +1, respectively. Then $\left|\mathcal{L}\right|+\left|\mathcal{R}\right|=n,\left|\mathcal{R}\right|-\left|\mathcal{L}\right|={\gamma }_s(G)$ and so $\left|\mathcal{L}\right|=(n-{\gamma }_s(G))/2$. Let H be the bipartite spanning subgraph of G with partite sets $\mathcal{L}$ and $\mathcal{R}$, where $E(H)=[\mathcal{L},\mathcal{R}]$, that is, E(H) consists of all edges in G between $\mathcal{L}$ and $\mathcal{R}$. Suppose $S\subseteq \mathcal{R}$ is a minimum left dominating set in H and $S_1\subset \mathcal{R}-S$ is a minimum dominating set of induced subgraph $G[\mathcal{R}-S]$. Define the function $g:V(G)\to \{-1,1,2,3\}$ by $g(x)=-1$ for $x\in \mathcal{L}$, g(x) = 3 for $x\in S$, g(x) = 2 for $x\in S_1$ and g(x) = 1 otherwise. Clearly, g is a STDRDF of f. Using Theorem 12 and Ore’s theorem, we obtain $$\begin{array}{ccc}{\gamma }_{\mathit{\text{sdR}}}^t(G)\hfill & =\hfill & 3\left|S\right|+2\left|S_1\right|+(n-|\mathcal{L}|-|S|-|S_1|)-\left|\mathcal{L}\right|\hfill \\ \hfill & \le \hfill & 2\left|S\right|+\left|S_1\right|+n-2\left|\mathcal{L}\right|\hfill \\ \hfill & \le \hfill & 2\left|S\right|+(n-|\mathcal{L}|-|S|)/2+n-2\left|\mathcal{L}\right|\hfill \\ \hfill & \le \hfill & (3|S|)/2+(3n)/2-(5|\mathcal{L}|)/2\hfill \\ \hfill & \le \hfill & 2n-\frac{5\left|\mathcal{L}\right|}{2}\hfill \\ \hfill & =\hfill & \frac{3n}{4}+\frac{5{\gamma }_{\mathit{\text{st}}}(G)}{4}.\hfill \end{array}$$

□

5 Special classes of graphs

In this section, we determine the signed total double Roman domination number of some classes of graphs including paths complete graphs, cycles and complete bipartite graphs.

Theorem 14.

Let $n\ge 2$ be an integer. Then $${\gamma }_{\mathit{\text{sdR}}}^t(P_n)=\{\begin{array}{ccc}n+1\hfill & \text{if}\hfill & n\in \{2,3,5,6,9\}\hfill \\ n\hfill & \hfill & \text{otherwise}.\hfill \end{array}$$

Proof.

First we show that ${\gamma }_{\mathit{\text{sdR}}}^t(P_n)\ge n$. Let $P_n=x_1{x}_2\dots x_n$. The proof is by induction on n. The result is trivial for $n\le 5$. Let $n\ge 6$ and the result holds for any path $P_{n^{\prime }}$ for $n^{\prime }<n$. Let f be a ${\gamma }_{\mathit{\text{sdR}}}^t(P_n)$-function. If $V_{-1}=\varnothing$, then by definition $\omega (f)\ge n+1$. Suppose $V_{-1}\ne \varnothing$. We have $f(x_2)=f(N(x_1))\ge 1$ and $f(x_{n-1})=f(N(x_n))\ge 1$. If $f(x_i)=f(x_{i+1})=-1$ for some i, then clearly the function f restricted to the paths $P_i=x_1{x}_2\dots x_i$ and $P_{n-i}=x_{i+1}{x}_{i+2}\dots x_n$ is a STDRDF on P_i and $P_{n-i}$ and by the induction hypothesis we obtain $$\omega (f)=\omega (f{|}_{P_i})+\omega (f{|}_{P_{n-i}})\ge i+(n-i)=n.$$

Suppose there is no i such that $f(x_i)=f(x_{i+1})=-1$. Consider the following cases.

Case 1. $x_1\in V_{-1}$ (the case $x_n\in V_{-1}$ is similar).

By definition we have $f(x_2)=3$ and $f(x_3)\ge 2$. If $f(x_4)\ge 1$, then the function f restricted to $P_{n-2}=x_3{x}_4\dots x_n$ is a STDRDF of $P_{n-2}$ and by the induction hypothesis we have $$\omega (f)=2+\omega (f{|}_{P_{n-2}})\ge n.$$

Let $f(x_4)=-1$. Then by assumption $f(x_5)\ge 1$. If $f(x_3)=3$, then the function f restricted to $P_{n-4}=x_5{x}_6\dots x_n$ is a STDRDF and it follows from the induction hypothesis that $$\omega (f)=4+\omega (f{|}_{P_{n-4}})\ge n.$$

If $f(x_3)=2$, then we must have $f(x_5)\ge 2$. Define the function $g:V(P_n-\{x_1,x_2,x_3\})\to \{-1,1,2,3\}$ by $g(x_5)=3$ and $g(x)=f(x)$ otherwise. Obviously g is a STDRDF of $P_{n-3}$ and by the induction hypothesis we obtain $$\omega (f)=3+\omega (g)\ge 3+(n-3)=n.$$

Case 2. $x_i\in V_{-1}$ for some $i\in \{3,4,\dots ,n-2\}$.

Since $f(x_i)+f(x_{i+2})\ge 1$ and $f(x_i)+f(x_{i-2})\ge 1$, we must have $f(x_{i+2})\ge 2$ and $f(x_{i-2})\ge 2$. By assumption, we have $f(x_{i+1})\ge 1$ and $f(x_{i-1})\ge 1$. Since each vertex in $V_{-1}$, is adjacent to a vertex in V₃ or adjacent to two vertices in V₂, we have $f(x_{i-1})+f(x_{i+1})\ge 4$. Let $P_{n-3}$ be a path obtain from $P_n-\{x_{i-1},x_i,x_{i+1}\}$ by adding the edge $x_{i-2}{x}_{i+2}$. Clearly the function f restricted to $P_{n-3}$ is a STDRDF and by the induction hypothesis we have $$\omega (f)\ge 3+\omega (f{|}_{P_{n-3}})\ge 3+(n-3)=n.$$

Thus ${\gamma }_{\mathit{\text{sdR}}}^t(P_n)\ge n$.

It is not hard to see that ${\gamma }_{\mathit{\text{sdR}}}^t(P_n)=n+1$ for $n\in \{2,3,5,6,9\}$. Let $n\notin \{2,3,5,6,9\}$. Now we show that ${\gamma }_{\mathit{\text{sdR}}}^t(P_n)\le n$.

If $n=4k$, define $f:V(P_n)\to \{-1,1,2,3\}$ by $f(x_{4i+2})=f(x_{4i+3})=3$ for $0\le i\le \frac{n}{4}-1$ and $f(x)=-1$ otherwise.

If $n=4k+1$ where $k\ge 3$, define $f:V(P_n)\to \{-1,1,2,3\}$ by $f(x_2)=f(x_{n-1})=3,f(x_{3i})=f(x_{3i+2})=2$ for $1\le i\le \frac{n-4}{3}$ and $f(x)=-1$ otherwise.

If $n=4k+2$ where $k\ge 2$, define $f:V(P_n)\to \{-1,1,2,3\}$ by $f(x_2)=f(x_9)=3,f(x_{3i})=f(x_{3i+2})=2$ for i = 1, 2 and $f(x_{4i+8})=f(x_{4i+9})=3$ for $1\le i\le \frac{n-10}{4}$ and $f(x)=-1$ otherwise.

If $n=4k+3$ where $k\ge 1$, define $f:V(P_n)\to \{-1,1,2,3\}$ by $f(x_2)=f(x_6)=3,f(x_3)=f(x_5)=2$ and $f(x_{4i+5})=f(x_{4i+6})=3$ for $1\le i\le \frac{n-7}{4}$ and $f(x)=-1$ otherwise.

Clearly, f is a STDRDF of P_n and so ${\gamma }_{\mathit{\text{sdR}}}^t(P_n)\le n$. Thus ${\gamma }_{\mathit{\text{sdR}}}^t(P_n)=n$. □

Theorem 15.

If $n\ne 5$, then ${\gamma }_{\mathit{\text{sdR}}}^t(C_n)=n$ and ${\gamma }_{\mathit{\text{sdR}}}^t(C_5)=6$.

Proof.

It is not hard to see that ${\gamma }_{\mathit{\text{sdR}}}^t(C_5)=6$. Assume that $n\ne 5$ and $C_n=(x_1{x}_2\dots x_n)$. First we show that ${\gamma }_{\mathit{\text{sdR}}}^t(C_n)\ge n$. Let f be a ${\gamma }_{\mathit{\text{sdR}}}^t(C_n)$-function. If $V_{-1}=\varnothing$, then clearly ${\gamma }_{\mathit{\text{sdR}}}^t(C_n)=\omega (f)\ge n+1$. Let $V_{-1}\ne \varnothing$. If $f(x_i)=f(x_{i+1})=-1$ for some i, then clearly the function f restricted to the path $P_n=x_{i+1}{x}_{i+2}\dots x_n{x}_1\dots x_i$ is a STDRDF and it follows from Theorem 14 that $\omega (f)=\omega (f{|}_{P_n})\ge n.$

Suppose now that there is no i such that $f(x_i)=f(x_{i+1})=-1$. Suppose without loss of generality that $f(x_2)=-1$. By assumption, we have $f(x_1)\ge 1$ and $f(x_3)\ge 1$. Since f is a STDRDF on C_n , we must have $\mathrm{\text{min}}\{f(x_1),f(x_3)\}\ge 2$ or $\mathrm{\text{min}}\{f(x_1),f(x_3)\}=1$ and $\mathrm{\text{max}}\{f(x_1),f(x_3)\}=3$. It follows from $f(N(x_1))\ge 1$ and $f(N(x_3))\ge 1$ that $f(x_n)\ge 2$ and $f(x_4)\ge 2$. Let $C_{n-3}$ is a cycle obtained from $C_n-\{x_1,x_2,x_3\}$ by joining x_n to x₄. Then the function f restricted to $C_{n-3}$ is a STDRDF of $C_{n-3}$ and by the induction hypothesis and the fact ${\gamma }_{\mathit{\text{sdR}}}^t(C_5)=6$, we have $\omega (f)\ge 3+\omega (f{|}_{C_{n-3}})\ge 3+n-3=n$.

To prove the inverse inequality, define $f:V(C_n)\to \{-1,1,2,3\}$ by $f(v_{3i+1})=f(v_{3i+2})=2$ for $0\le i\le \frac{n-3}{3}$ and $f(x)=-1$ otherwise, where $n\equiv 0\hspace{1em}(\mathrm{\text{mod}}3),f(v_1)=f(v_4)=3$ and $f(v_{3i+2})=(v_{3i+4})=2$ for $1\le i\le \frac{n-4}{3}$ and $f(x)=-1$ otherwise, where $n\equiv 1\hspace{1em}(\mathrm{\text{mod}}3)$ and $f(v_1)=f(v_4)=f(v_5)=f(v_8)=3$ and $f(v_{3i})=(v_{3i+2})=2$ for $3\le i\le \frac{n-8}{3}$ and $f(x)=-1$ otherwise, if $n\equiv 2\hspace{1em}(\mathrm{\text{mod}}3)$. Clearly, f is a STDRDF of C_n yielding ${\gamma }_{\mathit{\text{sdR}}}^t(C_n)\le n$. Thus ${\gamma }_{\mathit{\text{sdR}}}^t(C_n)=n$. □

Next we determine the exact value for complete bipartite graphs.

Proposition 16.

For $n\ge m\ge 1$, $${\gamma }_{\mathit{\text{sdR}}}^t(K_{m,n})=\{\begin{array}{ccc}4,& & (m=n=2,4),(m=2,n=4),\\ & & \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\text{or }(m=1,n\ge 2)\\ 2,& & (m=3,n\ne 4)\text{ or }m\ge 5\\ 3& & \mathit{\text{otherwise}}.\end{array}$$

Proof.

Let $X=\{x_1,x_2,\dots ,x_m\}$ and $Y=\{y_1,y_2,\dots ,y_n\}$ be the bipartite sets of $K_{m,n}$. We consider the following cases.

Case 1. m = 1.

The result is immediate for $m=n=1$. Let $n\ge 2$. Define $g:V(K_{1,n})\to \{-1,1,2,3\}$ by $g(x_1)=3,g(y_1)=2,g(y_2)=-1$ and $g(y_i)={(-1)}^i$ for $3\le i\le n$ when n is even, and $g(x_1)=3,g(y_1)=1$ and $g(y_i)={(-1)}^i$ for $2\le i\le n$ when n is odd. It is easy to see that g is a STDRDF of $K_{1,n}$ of weight 4, and so ${\gamma }_{\mathit{\text{sdR}}}^t(K_{1,n})\le 4$.

Now we show that ${\gamma }_{\mathit{\text{sdR}}}^t(K_{1,n})\ge 4$. Clearly, ${\gamma }_{\mathit{\text{sdR}}}^t(K_{1,2})={\gamma }_{\mathit{\text{sdR}}}^t(P_3)=4$. Let $n\ge 3$ and f be a ${\gamma }_{\mathit{\text{sdR}}}^t(K_{1,n})$-function. Since f is a ${\gamma }_{\mathit{\text{sdR}}}^t(K_{1,n})$-function, we have $f(x_1)\ge 1$. If $f(x_1)=3$, then we have ${\gamma }_{\mathit{\text{sdR}}}^t(K_{1,n})=f(x_1)+f(N(x_1))\ge 4$ as desired. Suppose that $f(x_1)=1\text{ or }2$. Since f is a ${\gamma }_{\mathit{\text{sdR}}}^t(K_{1,n})$-function, we must have $f(v_i)\ge 1$ for each i. This implies that $\omega (f)\ge 1+{\sum }_{i=1}^{n}f(v_i)\ge 4$ and so $\omega (f)\ge 4$. Thus ${\gamma }_{\mathit{\text{sdR}}}^t(K_{1,n})=4$.

Case 2. $m\ge 5$.

For any ${\gamma }_{\mathit{\text{sdR}}}^t(K_{m,n})$-function f, we have $$\begin{array}{ccc}{\gamma }_{\mathit{\text{sdR}}}^t(K_{m,n})& =& \sum _{i=1}^{m}f(x_i)+\sum _{i=1}^{n}f(y_i)\\ & =& f(N(x_i))+f(N(y_i))\\ & \ge & 2.\end{array}$$

Now define $g:V(K_{m,n})\to \{-1,1,2,3\}$ as follows:

$g(x_1)=g(y_1)=3,g(x_2)=g(y_2)=2$, $g(x_i)=g(y_i)=-1$ for $i\in \{3,4,5,6\}$ and $g(x_i)=g(y_i)={(-1)}^i$ for $i\ge 7$, when m, n are both even,

$g(x_1)=g(y_1)=3,g(x_2)=g(y_2)=1$, $g(x_i)=g(y_i)=-1$ for $i\in \{3,4,5\}$ and $g(x_i)=g(y_i)={(-1)}^i$ for $i\ge 6$, when m, n are both odd,

$g(x_1)=g(y_1)=3,g(x_2)=2,g(y_2)=1,g(x_i)=g(y_j)=-1$ for $i\in \{3,4,5,6\},j\in \{3,4,5\}$ and $g(x_i)={(-1)}^i$ for $i\ge 7$ and $g(y_j)={(-1)}^j$ for $j\ge 6$, when m is even and n is odd.

It is easy to see that g is a STDRDF of $K_{m,n}$ and so $\omega (g)\le 2$. Thus ${\gamma }_{\mathit{\text{sdR}}}^t(K_{m,n})=2$.

Case 3. m = 4.

Clearly, ${\gamma }_{\mathit{\text{sdR}}}^t(K_{4,4})=4$. Let $n\ge 5$. First we show that ${\gamma }_{\mathit{\text{sdR}}}^t(K_{4,n})\le 4$. Define $g:V(K_{4,n})\to \{-1,1,2,3\}$ as follows:

$g(x_1)=g(x_2)=2,g(x_3)=g(x_4)=-1,g(y_1)=3,g(y_2)=2$, $g(y_i)=-1$ for $i\in \{3,4,5,6\}$ and $g(y_i)={(-1)}^i$ for $i\ge 7$, when n is even,

$g(x_1)=g(x_2)=2,g(x_3)=g(x_4)=-1,g(y_1)=3,g(y_2)=1$, $g(y_i)=-1$ for $i\in \{3,4,5\}$ and $g(y_i)={(-1)}^i$ for $i\ge 6$, when n is odd.

It is easy to see that g is a STDRDF of $K_{4,n}$ and so ${\gamma }_{\mathit{\text{sdR}}}^t(K_{4,n})\le 3$ for $n\ge 5$.

Now we show that ${\gamma }_{\mathit{\text{sdR}}}^t(K_{4,n})\ge 4$. Let f be a ${\gamma }_{\mathit{\text{sdR}}}^t(K_{4,n})$-function. As in the Case 2, we have ${\sum }_{i=1}^{n}f(y_i)\ge 1$ and ${\sum }_{i=1}^{4}f(x_i)\ge 1.$ We claim that ${\sum }_{i=1}^{4}f(x_i)\ge 2$. If $|V_{-1}\cap X|\le 1$, then the claim is trivial. Let $|V_{-1}\cap X|\ge 2.$ It follow from ${\sum }_{i=1}^{4}f(x_i)\ge 1$ that $|V_{-1}\cap X|=2$. Suppose $f(x_3)=f(x_4)=-1$. If $f(x_i)=3$ for some $i\in \{1,2\}$ or $f(x_1)=f(x_2)=2$, then clearly ${\sum }_{i=1}^{4}f(x_i)\ge 2$ as desired. Suppose that $f(x_1)=2,f(x_2)=1$. Since f is a ${\gamma }_{\mathit{\text{sdR}}}^t$-function, we must have $f(y_i)\ge 1$ for each i. This implies that $\omega (f)={\sum }_{i=1}^{4}f(x_i)+{\sum }_{i=1}^{n}f(y_i)\ge 1+n\ge 6$ which is a contradiction. So ${\sum }_{i=1}^{4}f(x_i)\ge 2$ and this implies that ${\gamma }_{\mathit{\text{sdR}}}^t(K_{4,n})\ge 3$. Thus ${\gamma }_{\mathit{\text{sdR}}}^t(K_{m,n})=3$.

Case 4. m = 3.

It is not hard to see that ${\gamma }_{\mathit{\text{tsdR}}}(K_{3,3})=2$ and ${\gamma }_{\mathit{\text{tsdR}}}(K_{3,4})=3$. Let $n\ge 5$. As in the Case 1, we have ${\gamma }_{\mathit{\text{sdR}}}^t(K_{3,n})\ge 2$. Define $g:V(K_{3,n})\to \{-1,1,2,3\}$ as follows:

$g(x_1)=3,g(x_2)=g(x_3)=-1,g(y_1)=3,g(y_2)=2$, $g(y_i)=-1$ for $i\in \{3,4,5,6\}$ and $g(y_i)={(-1)}^i$ for $i\ge 7$, when n is even,

$g(x_1)=3,g(x_2)=g(x_3)=-1,g(y_1)=3,g(y_2)=1$, $g(y_i)=-1$ for $i\in \{3,4,5\}$ and $g(y_i)={(-1)}^i$ for $i\ge 6$, when n is odd.

Clearly, g is a STDRDF of $K_{3,n}$ of weight 2 and so ${\gamma }_{\mathit{\text{sdR}}}^t(K_{3,n})\le 2$ for $n\ge 5$. Thus ${\gamma }_{\mathit{\text{sdR}}}^t(K_{3,n})=2$ when $n\ge 5$.

Case 5. m = 2.

It is not hard to see that ${\gamma }_{\mathit{\text{sdR}}}^t(K_{2,2})=4,{\gamma }_{\mathit{\text{tsdR}}}(K_{2,3})=3$ and ${\gamma }_{\mathit{\text{tsdR}}}(K_{2,4})=4$. Let $n\ge 5$. Define $g:V(K_{2,n})\to \{-1,1,2,3\}$ as follows:

$g(x_1)=3,g(x_2)=-1,g(y_1)=3,g(y_2)=2$, $g(y_i)=-1$ for $i\in \{3,4,5,6\}$ and $g(y_i)={(-1)}^i$ for $i\ge 7$, when n is even,

$g(x_1)=3,g(x_2)=-1,g(y_1)=3,g(y_2)=1$, $g(y_i)=-1$ for $i\in \{3,4,5\}$ and $g(y_i)={(-1)}^i$ for $i\ge 6$, when n is odd.

Clearly, g is a STDRDF of $K_{2,n}$ of weight 2 and so ${\gamma }_{\mathit{\text{sdR}}}^t(K_{2,n})\le 3$ for $n\ge 5$.

To prove the inverse inequality, let f be a ${\gamma }_{\mathit{\text{sdR}}}^t(K_{2,n})$-function. As in the Case 2, ${\sum }_{i=1}^{n}f(y_i)\ge 1$ and $f(x_1)+f(x_2)\ge 1$. Using a similar argument that described in Case 3, we can see that $f(x_1)+f(x_2)\ge 2$. This implies that $\omega (f)\ge 3$ yielding ${\gamma }_{\mathit{\text{sdR}}}^t(K_{2,n})\ge 3$. Thus ${\gamma }_{\mathit{\text{sdR}}}^t(K_{2,n})=3$ and the proof is complete. □

Proposition 17.

For $n\ge 5,{\gamma }_{\mathit{\text{sdR}}}^t(K_n)=3$.

Proof.

Let $n\ge 5$ and let $V(K_n)=\{v_1,v_2,\dots ,v_n\}$ be the vertex set of K_n . Define the function $g:V(K_n)\to \{-1,1,2,3\}$ by $g(v_1)=g(v_2)=2$ and $g(v_3)=-1$ and $g(v_i)={(-1)}^i$ for $4\le i\le n$ when n is odd, and $g(v_1)=g(v_2)=g(v_3)=2$, $g(v_4)=g(v_5)=g(v_6)=-1$ and $g(v_i)={(-1)}^i$ for $7\le i\le n$ when n is even. Clearly, g is a STDRDF and so ${\gamma }_{\mathit{\text{sdR}}}^t(K_n)\le 3$.

To show that ${\gamma }_{\mathit{\text{sdR}}}^t(K_n)\ge 3$, let f be a ${\gamma }_{\mathit{\text{sdR}}}^t(K_n)$-function. By definition we have $V_2\cup V_3\ne \varnothing$. Suppose $v\in V_2\cup V_3$. Then ${\gamma }_{\mathit{\text{sdR}}}^t(K_n)=\omega (f)=f(v)+f(N(v))\ge 2+1=3$ and so ${\gamma }_{\mathit{\text{sdR}}}^t(K_n)=3$. □

6 Conclusion

The concepts of Roman domination has been recognized in the field of domination theory since 2004. In this research, we study a variation of Roman domination called signed total double Roman domination number and we provide several sharp bounds for this parameter. We also show that the corresponding decision problem is NP-complete for bipartite and chordal graphs. In addition, we determine the signed total double Roman domination number of some classes of graphs including paths, cycles, complete graphs and complete bipartite graphs. There is still potential for further research. For instance, progress could be made by determining the signed total double Roman domination number for other classes of graphs and characterizing the graphs attaining the bounds of Theorems 8 and 11.

Additional information

Funding

H. Abdollahzadeh Ahangar was supported by the Babol Noshirvani University of Technology under research Grant Number BNUT/385001/1403.