Randić spectrum of the weakly zero-divisor graph of the ring ℤ_n

Abstract

In this article, we find the Randić spectrum of the weakly zero-divisor graph of a finite commutative ring $\mathfrak{R}$ with identity $1\ne 0$, denoted as $W\Gamma (\mathfrak{R})$, where $\mathfrak{R}$ is taken as the ring of integers modulo $\mathfrak{n}$. The weakly zero-divisor graph of the ring $\mathfrak{R}$ is a simple undirected graph with vertices representing non-zero zero-divisors in $\mathfrak{R}$. Two vertices, denoted as a and b, are connected if there are elements x in the annihilator of a and y in the annihilator of b such that their product xy equals zero. In particular, we examine the Randić spectrum of $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$ for specific values of $\mathfrak{n}$, which are products of prime numbers and their powers.

Keywords:

• Weakly zero-divisor graph
• Randić spectrum
• Euler totient function
• ring of integers modulo $\mathfrak{n}$

2020 Mathematics Subject Classification:

• 05C25
• 05C50
• 15A18

1 Introduction

In this research, we focus on connected, undirected, simple, and finite graphs. These graphs are denoted as $\mathcal{C}(\nu ,e)$, where ν and e represents the sets of vertices and edges in $\mathcal{C}$, respectively. An edge between two vertices a and b in $\mathcal{C}$ is indicated by $a\sim b$. The neighborhood of a vertex a in $\mathcal{C}$, symbolized as $N_{\mathcal{C}}(a)$, refers to the set of vertices directly connected to a. The degree of a vertexa, denoted asdeg(a), is the number of adjacent edges to a. A graph is termed r-regular if each vertex has the same degree r. Complete graphs with vertices a and complete bipartite graphs with vertex sets of sizes, (a, b) are represented as K_a and $K_{a,b},$ respectively. It is also essential to point out that the sources referenced in [6, 10, 16] may contain additional symbols and terms that have not been defined or discussed in this text.

This study also involves a finite commutative ring $\mathfrak{R}$ with a non-zero multiplicative identity. Within, $\mathfrak{R}$a non-zero element a is a zero-divisor if it satisfies ab = 0 for some non-zero $b\in \mathfrak{R}$. The set of these zero-divisors is denoted as $\mathbb{Z}(\mathfrak{R})$, and $\mathbb{Z}{(\mathfrak{R})}^{*}=\mathbb{Z}(\mathfrak{R})\setminus \left\{0\right\}$. The ring of integers modulo a positive integer $\mathfrak{n}$ is denoted as ${\mathbb{Z}}_{\mathfrak{n}}$. The adjacency matrix A of a graph $\mathcal{C}$ is a (0, 1) matrix reflecting the connections between vertices. The Randić matrix ${\mathcal{R}}_{\mathcal{C}}$ of $\mathcal{C}$ is defined based on the degrees of the vertices as follows: $${\mathcal{R}}_{\mathcal{C}}=(r_{\mathit{\text{ij}}})=\{\begin{array}{cc}\frac{1}{\sqrt{d_{\mathcal{C}}(v_i)d_{\mathcal{C}}(v_j)}},\hfill & v_i\sim v_j,\hfill \\ 0,\hfill & \mathit{\text{otherwise}}.\hfill \end{array}$$

This matrix is symmetric with real eigenvalues, ordered as ${\chi }_1\ge {\chi }_2\ge \dots \ge {\chi }_k.$ More about the Randić matrix can be found in [1, 2]. Various aspects of zero-divisor graphs have been explored in previous studies, as documented in prior works such as [3, 5, 7, 12, 13]. Rather et al. [11] conducted a study focusing on the Randić spectrum of the zero-divisor graph for the ring ${\mathbb{Z}}_{\mathfrak{n}}$. Their research provided evidence indicating that the zero-divisor graph $\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$ exhibits Randić integral. Nazim et al. [8] examined normalized Laplacian spectra of the weakly zero-divisor graph of the ring ${\mathbb{Z}}_{\mathfrak{n}}$ for different values of $\mathfrak{n}.$

This paper extends the research on the Randić spectrum of the weakly zero-divisor graphs. Nikmehr et al. [9], first introduce the concept of a weakly zero-divisor graph. The weakly zero-divisor graph $W\Gamma (\mathfrak{R})$ is an undirected graph whose vertices are non-zero zero-divisors of $\mathfrak{R}$ with a unique adjacency condition. Additional details regarding the weakly zero-divisor graphs can be located in the references cited as [14, 15]. We investigate the Randić spectrum of $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$ for specific values of $\mathfrak{n}$, which are products of prime numbers and their powers.

We examine the Randić spectrum of the weakly zero-divisor graph $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$ for some values of $\mathfrak{n}\in \{\alpha \beta ,{\alpha }^2\beta ,\alpha \beta \gamma ,{\alpha }^{\mathfrak{m}}\beta \}$, where α, β, and γ are prime numbers with $\alpha <\beta <\gamma$, and $\mathfrak{m}\ge 2$ is a positive integer. Also for $\mathfrak{n}={\alpha }_1{\alpha }_2\cdots {\alpha }_{\mathfrak{m}}{\beta }_1^{k_1}{\beta }_2^{k_2}\cdots {\beta }_r^{k_r}(k_i\ge 2,\mathfrak{m}\ge 1,r\ge 0)$, where α_i ’s and β_i ’s are distinct primes. Computational tools like Wolfram Mathematica are employed for approximating eigenvalues and characteristic polynomials of various matrices.

2 Preliminaries

We begin by introducing the fundamental definitions and existing research results that will be used to form the main conclusions.

Definition 2.1.

Let $\mathcal{C}(\nu ,e)$ be a graph of order $\mathfrak{n}$ having vertex set $\{1,2,\dots ,\mathfrak{n}\}$ and ${\mathcal{C}}_i({\nu }_i,e_i)$ be disjoint graphs of order ${\mathfrak{n}}_i,1\le i\le \mathfrak{n}$. The graph $\mathcal{C}[{\mathcal{C}}_1,{\mathcal{C}}_2,\dots ,{\mathcal{C}}_{\mathfrak{n}}]$ is formed by taking the graphs ${\mathcal{C}}_1,{\mathcal{C}}_2,\dots ,{\mathcal{C}}_{\mathfrak{n}}$ and joining each vertex of ${\mathcal{C}}_i$ to every vertex of ${\mathcal{C}}_j$ whenever i and j are adjacent in $\mathcal{C}$.

This operation $\mathcal{C}[{\mathcal{C}}_1,{\mathcal{C}}_2,\dots ,{\mathcal{C}}_{\mathfrak{m}}]$ is also known as generalized join graph operation as defined in [4], and it is also referred to as the $\mathcal{C}$-join operation. If $\mathcal{C}=K_2$, the K₂-join is the usual join operation, namely ${\mathcal{C}}_1\nabla {\mathcal{C}}_2$. In this context, we will continue to use the notation $\mathcal{C}[{\mathcal{C}}_1,{\mathcal{C}}_2,\dots ,{\mathcal{C}}_{\mathfrak{m}}]$ and call it a $\mathcal{C}$-join.

Let us explore the set of integers modulo $\mathfrak{n}$, which we denote as ${\mathbb{Z}}_{\mathfrak{n}}$. The order of the ${\mathbb{Z}}^{*}({\mathbb{Z}}_{\mathfrak{n}})$ is $\mathfrak{n}-\varphi (\mathfrak{n})-1$, where $\varphi (\mathfrak{n})$ represents the Euler totient function. An integer u, where $1<u<\mathfrak{n}$, is called a proper divisor of $\mathfrak{n}$ if $u|\mathfrak{n}$. The number of all the divisors of $\mathfrak{n}$ is denoted by $\tau (n)$. Now, suppose we have proper divisors of $\mathfrak{n}$, which we will denote as $u_1,u_2,\dots ,u_k$. For each integer r in the range of 1 to k, let us consider sets of elements given by the following: $$A_{u_r}=\{x\in {\mathbb{Z}}_{\mathfrak{n}}:(x,\mathfrak{n})=u_r\},$$ where $(x,\mathfrak{n})$ signifies the largest common divisor between the values x and $\mathfrak{n}$. Furthermore, it is evident that $A_{u_r}\cap A_{u_x}=\varphi$ whenever $r\ne x$. This fact implies that the sets $A_{u_1},A_{u_2},\dots ,A_{u_k}$ are distinct from each other and they collectively divide and organize the vertex set of $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$ in the following manner: $$V(W\Gamma ({\mathbb{Z}}_{\mathfrak{n}}))=A_{u_1}\cup A_{u_2}\cup \cdots \cup A_{u_k}.$$

The subsequent lemma provides insight into the size of $A_{u_r}$.

Lemma 2.2.

[16] If u_r as a divisor of $\mathfrak{n}$, then $\left|A_{u_r}\right|=\varphi \left(\frac{\mathfrak{n}}{u_r}\right),1\le r\le k$.

Lemma 2.3.

[15] Let us consider the set of proper divisors of $\mathfrak{n}$, which we can represent as $u_1,u_2,\dots ,u_k$. Also, express the number $\mathfrak{n}$ as $\mathfrak{n}=p_1{p}_2\dots p_m{q}_1^{k_1}{q}_2^{k_2}\dots q_i^{k_i}$, where $k_i\ge 2,m\ge 1$, and $i\ge 0$. If a proper divisor u_r is one of the prime factors $\{p_1,p_2,\dots ,p_m\}$, then the sub-graph induced in $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$ by the set of elements $A_{u_r}$ forms ${\overline{K}}_{\varphi \left(\frac{\mathfrak{n}}{u_r}\right)}$.

Corollary 2.4.

[15] Consider u_r is a proper divisor of the positive integer $\mathfrak{n}$. The following statements hold:

1. The sub-graph $W\Gamma (A_{u_r})$ of $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$, formed by the vertices in the set $A_{u_r}$, can take one of two forms: it’s either the complete graph $K_{\varphi \left(\frac{\mathfrak{n}}{u_r}\right)}$, or it’s complement graph ${\overline{K}}_{\varphi \left(\frac{\mathfrak{n}}{u_r}\right)}$, where r is in the set $\{1,2,\dots ,k\}$.

2. If r is not equal to x, where both r and x belong to the set $\{1,2,\dots ,k\}$, then a vertex within $A_{u_r}$ is either connected to all vertices in $A_{u_x}$ or not connected to any vertex in $A_{u_x}$ within the graph $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$.

Corollary 2.4, mentioned above shown that the sub-graphs $W\Gamma (A_{u_r})$, which are formed within the structure of $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$, can be categorized as either complete graphs or empty graphs. The subsequent lemma asserts that $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$ can be described as a composite structure comprising complete graphs and their corresponding complementary graphs. We define ${{\rm Y}}_{\mathfrak{n}}^{*}$ by a complete graph on the set $\{u_1,u_2,\dots ,u_k\}$ of all proper divisors of $\mathfrak{n}$.

Lemma 2.5.

[15] Let the induced sub-graph $W\Gamma (A_{u_r})$ of $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$ formed by the vertices in the set $A_{u_r}$, where $1\le r\le k$. Then $$W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})={{\rm Y}}_{\mathfrak{n}}^{*}[W\Gamma (A_{u_1}),W\Gamma (A_{u_2}),\dots ,W\Gamma (A_{u_k})].$$

Theorem 2.6.

[1] Consider a graph denoted as $\mathcal{C}$, where the vertex set $\nu (\mathcal{C})$ consists of elements from 1 to t. Let ${\mathcal{C}}_i$’s represent r_i -regular graphs of size ${\mathfrak{n}}_i$ for i ranging from 1 to t. If we express $\mathcal{C}$ as a combination of these graphs, denoted as $\mathcal{C}[{\mathcal{C}}_1,{\mathcal{C}}_2,\dots ,{\mathcal{C}}_t]$, then the Randić spectrum of $\mathcal{C}$ can be determined as follows: $${\sigma }_R(\mathcal{C})=(\underset{i=1}{\overset{t}{\cup }}(\frac{\rho }{{\mathcal{N}}_i+r_i}):\rho \in {\sigma }_R({\mathcal{C}}_i)\setminus \{r_i\})\cup \sigma (C_R(\mathcal{C})),$$ where $${\mathcal{N}}_i=\{\begin{array}{cc}\sum _{j\in {\mathcal{N}}_{\mathcal{C}}(i)}{\mathfrak{n}}_j,\hfill & {\mathcal{N}}_{\mathcal{C}}(i)\ne \varphi ,\hfill \\ 0,\hfill & \mathit{\text{otherwise}}\hfill \end{array}$$

and (2.1) $$C_R(\mathcal{C})={(c_{\mathit{\text{ij}}})}_{t\times t}=\{\begin{array}{cc}\frac{r_i}{{\mathcal{N}}_i+r_i},\hfill & i=j,\hfill \\ \hfill & \hfill \\ \sqrt{\frac{{\mathfrak{n}}_i{\mathfrak{n}}_j}{({\mathcal{N}}_i+r_i)({\mathcal{N}}_j+r_j)}},\hfill & \mathit{\text{ij}}\in e(\mathcal{C}),\hfill \\ \hfill & \hfill \\ 0\hfill & \mathit{\text{otherwise}}.\hfill \end{array}$$(2.1)

ρ is the adjacency eigenvalue of ${\mathcal{C}}_i$.

A graph, denoted as $\mathcal{C}$ is considered to be a Randić integral graph if all its Randić eigenvalues are integer. The following statement provides a condition for a $\mathcal{C}$-join graph to possess this integral attribute, and the proof of this condition can be readily deduced from Theorem 2.6.

Proposition 2.7.

The $\mathcal{C}$-join graph $\mathcal{C}[{\mathcal{C}}_1,{\mathcal{C}}_2,\dots ,{\mathcal{C}}_t]$ is Randić integral if and only if $\frac{\rho }{{\mathcal{N}}_i+r_i}\in \mathbb{Z},$ for $i=1,2,\dots ,t$ and matrix $C_R(\mathcal{C})$ is integral.

From Theorem 2.6, if ${\mathcal{C}}_i$ is isomorphic to ${\overline{K}}_i$, then we have $\frac{\rho }{{\mathcal{N}}_i+r_i}=0$. In this scenario, the graph $\mathcal{C}$, which is constructed as $\mathcal{C}[{\mathcal{C}}_1,{\mathcal{C}}_2,\dots ,{\mathcal{C}}_t]$ exhibits a Randić integral characteristic if and only if the matrix $C_R(\mathcal{C})$ has integral values.

3 Randić spectrum of $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$

In this section, we determine the Randić spectrum of $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$ for any arbitrary $\mathfrak{n}$. Let us denote the proper divisors of $\mathfrak{n}$ as $u_1,u_2,\dots ,u_k$. For each $1\le r\le k$, we assign a weight of $\left|A_{u_k}\right|=\varphi \left(\frac{\mathfrak{n}}{u_k}\right)$ to the vertex u_k within the graph ${{\rm Y}}_{\mathfrak{n}}^{*}$. The kth order weighted Randić matrix of ${{\rm Y}}_{\mathfrak{n}}^{*}$, denoted as $\mathbb{L}({{\rm Y}}_{\mathfrak{n}}^{*})$ and defined in Theorem 2.6, is represented as: (3.1) $$\mathbb{L}({{\rm Y}}_{\mathfrak{n}}^{*})=\left[\begin{array}{cccc}{t}_{1,1}& t_{1,2}& \dots & t_{1,k}\\ t_{2,1}& t_{2,2}& \dots & t_{2,k}\\ ⋮& ⋮& \ddots & ⋮\\ t_{k,1}& t_{k,2}& \dots & t_{k,k}\end{array}\right],$$(3.1) where $$t_{i,j}=\{\begin{array}{cc}\frac{r_{u_i}}{r_{u_i}+M_{u_i}},\hfill & i=j,\hfill \\ \sqrt{\frac{\varphi \left(\frac{\mathfrak{n}}{u_i}\right)\varphi \left(\frac{\mathfrak{n}}{u_j}\right)}{(r_{u_i}+M_{u_i})(r_{u_j}+M_{u_j})}},\hfill & u_i\sim u_j\in {{\rm Y}}_{\mathfrak{n}}^{*},\hfill \\ 0,\hfill & \mathit{\text{otherwise}}.\hfill \end{array}$$

For $1\le i\ne j\le k$ and $M_{u_j}=\sum _{u_i\in N_{{{\rm Y}}_{\mathfrak{n}}^{*}}(u_j)}\varphi \left(\frac{\mathfrak{n}}{u_i}\right)$.

The matrix known as $\mathbb{L}({{\rm Y}}_{\mathfrak{n}}^{*})$ is termed the weighted Randić matrix associated with ${{\rm Y}}_{\mathfrak{n}}^{*}$. An essential observation can be made when we compare the matrices $C_R(\mathcal{C})$ and $\mathbb{L}({{\rm Y}}_{\mathfrak{n}}^{*})$.

Remark 3.1.

$C_R(\mathcal{C})=\mathbb{L}({{\rm Y}}_{\mathfrak{n}}^{*})$

The primary finding in this research paper involves the presentation and demonstration of the Randić spectrum for the weakly zero-divisor graph of $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$.

Theorem 3.2.

Consider the proper divisors of $\mathfrak{n}$ are $u_1,u_2,\dots ,u_k$. Then the Randić spectrum of $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$ is given by $$\begin{array}{c}{\sigma }_R(W\Gamma ({\mathbb{Z}}_{\mathfrak{n}}))=\mathrm{}(\underset{i=1}{\overset{k}{\cup }}(\frac{\rho }{M_{u_i}+r_{u_i}}):\rho \in {\sigma }_R(W\Gamma (A_{u_i}))\setminus \{r_{u_i}\}\mathrm{})\\ \mathrm{\hspace{1em}\hspace{1em}}\cup {\sigma }_R(\mathbb{L}({{\rm Y}}_{\mathfrak{n}}^{*})),\end{array}$$ where $W\Gamma (A_{u_i})$ are r_i -regular graph and ρ is the adjacency eigenvalue of $W\Gamma (A_{u_i})$.

Proof.

Based on Lemma 2.5, we can observe that $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})={{\rm Y}}_{\mathfrak{n}}^{*}[W\Gamma (A_{u_1}),W\Gamma (A_{u_2}),\dots ,W\Gamma (A_{u_k})].$ This implies that by utilizing the relationship $C_R(\mathcal{C})=\mathbb{L}({{\rm Y}}_{\mathfrak{n}}^{*})$ and utilizing the implications of Theorem 2.6, the outcome is established. □

Remember that the adjacency spectrum of complete graph $K_{\mathfrak{m}}$ and its complement graph ${\overline{K}}_{\mathfrak{m}}$ with $\mathfrak{m}$ vertices, including multiplicity, is as follows: $$\left\{\begin{array}{cc}-1& \mathfrak{m}-1\\ \mathfrak{m}-1& 1\end{array}\right\} \text{and} \left\{\begin{array}{c}0\\ \mathfrak{m}\end{array}\right\},\text{respectively}.$$

From Corollary 2.4, $W\Gamma (A_{u_i})$ is isomorphic to either $K_{\varphi \left(\frac{\mathfrak{n}}{u_i}\right)}$ or ${\overline{K}}_{\varphi \left(\frac{\mathfrak{n}}{u_i}\right)}$. Consequently, as outlined in Theorem 3.2, there exists a total of $\mathfrak{n}-\varphi (\mathfrak{n})-1$ Randić eigenvalues associated with $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$. Out of these, the value $\mathfrak{n}-\varphi (\mathfrak{n})-1-t$ has already been calculated. The remaining t Randić eigenvalues of $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$ can be derived from the solutions to the characteristic polynomial of the matrix $\mathbb{L}({{\rm Y}}_{\mathfrak{n}}^{*})$, as depicted in equation (3.1)(3.1) $$\mathbb{L}({{\rm Y}}_{\mathfrak{n}}^{*})=\left[\begin{array}{cccc}{t}_{1,1}& t_{1,2}& \dots & t_{1,k}\\ t_{2,1}& t_{2,2}& \dots & t_{2,k}\\ ⋮& ⋮& \ddots & ⋮\\ t_{k,1}& t_{k,2}& \dots & t_{k,k}\end{array}\right],$$(3.1) .

Utilizing Theorem 3.2, we can examine the provided diagram below to compute the Randić spectrum.

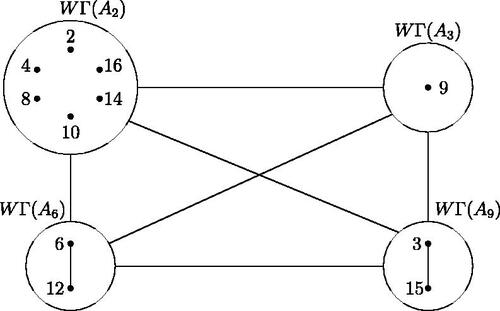
Example 3.3.

The Randić spectrum of the weakly zero-divisor graph $W\Gamma ({\mathbb{Z}}_{18})$. (See Figure 1).

Fig. 1 The graph G₁.

Let $\mathfrak{n}=18=3^2\times 2$. First, we can observe that ${{\rm Y}}_{18}^{*}$ is the complete graph on 4 vertices. i.e., $\{2,3,6,9\}.$ Then by Lemma 2.5, we have $$W\Gamma ({\mathbb{Z}}_{18})={{\rm Y}}_{18}^{*}[W\Gamma (A_2),W\Gamma (A_3),W\Gamma (A_6),W\Gamma (A_9)].$$

By using Lemma 2.3, also we can observe that $W\Gamma ({\mathbb{Z}}_{18})={{\rm Y}}_{18}^{*}[{\overline{K}}_6,K_2,K_2,K_1].$ The cardinality $\left|V\right|$ of the vertex set V of $W\Gamma ({\mathbb{Z}}_{18})$ is given by $\varphi (2)+\varphi (3)+\varphi (6)+\varphi (9)=11$. It follows that $M_2=\varphi (2)+\varphi (3)+\varphi (6)=\left|V\right|-\varphi (9)=5,M_3=\left|V\right|-\varphi (6)=9,M_6=\left|V\right|-\varphi (3)=9,M_9=\left|V\right|-\varphi (2)=10.$ Also, we see that $r_2=r_9=0$ and $r_3=r_6=1$. Therefore, by Theorem 3.2, the Randić spectrum of $W\Gamma ({\mathbb{Z}}_{18})$ is $$\begin{array}{c}{\sigma }_R(W\Gamma ({\mathbb{Z}}_{18}))=(\underset{i=1}{\overset{4}{\cup }}(\frac{\rho }{r_{u_i}+M_{u_i}}:\rho \in {\sigma }_R(W\Gamma (A_{u_i}))\setminus \left\{r_{u_i}\right\})\mathrm{})\\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\cup {\sigma }_R(\mathbb{L}({{\rm Y}}_{18}^{*}))=\\ \left\{\begin{array}{cc}-1& 0\\ 2& 5\end{array}\right\}\cup {\sigma }_R(\mathbb{L}({{\rm Y}}_{18}^{*})).\end{array}$$

Thus, the remaining 4 Randić eigenvalues are the eigenvalues of the matrix $$\mathbb{L}({{\rm Y}}_{18}^{*})=\left[\begin{array}{cccc}\frac{1}{10}& \frac{\sqrt{6}}{5}& \frac{2}{5}& \frac{2}{5}\\ \frac{\sqrt{6}}{5}& 0& \frac{\sqrt{3}}{5}& \frac{\sqrt{6}}{5}\\ \frac{2}{5}& \frac{\sqrt{3}}{5}& 0& \frac{\sqrt{2}}{10}\\ \frac{2}{5}& \frac{\sqrt{6}}{5}& \frac{\sqrt{2}}{10}& \frac{1}{10}\end{array}\right].$$

The estimated eigenvalues of the above matrix are $$\{-0.5096,-0.4165,-0.0822,1.2083\}.$$

Now, we explore the Randić spectrum of $\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$ for various values of $\mathfrak{n}$: when $\mathfrak{n}=\alpha \beta ,{\alpha }^2\beta ,\alpha \beta \gamma$ and ${\alpha }^{\mathfrak{m}}\beta$, where α, β, and γ are prime numbers with $\alpha <\beta <\gamma$, and $\mathfrak{m}\ge 2$ is a positive integer.

Proposition 3.4.

The Randić spectrum of $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}}),$ for $\mathfrak{n}=\alpha \beta$ is given by $$\left\{\begin{array}{ccc}-1& 0& 1\\ 1& \alpha +\beta -4& 1\end{array}\right\},$$ where α, β are distinct primes.

Proof.

Let $\mathfrak{n}=\alpha \beta$, with $\alpha <\beta$ and α, β are distinct primes. First, we can observe that ${{\rm Y}}_{\alpha \beta }^{*}$ is the complete graph on 2 vertices so that ${{\rm Y}}_{\alpha \beta }^{*}$ is K₂. Since $r_{\alpha }=r_{\beta }=0$ and $(M_{\alpha },M_{\beta })=(\alpha -1,\beta -1)$. Therefore, by Theorem 3.2, the Randić spectrum of $W\Gamma ({\mathbb{Z}}_{\alpha \beta })$ consists of the eigenvalue 0 with multiplicity $\alpha +\beta -4$ and the matrix $\mathbb{L}({{\rm Y}}_{\alpha \beta }^{*})$ is given by $$\mathbb{L}({{\rm Y}}_{\alpha \beta }^{*})=\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right],$$ which has eigenvalues 1 and –1. □

Proposition 3.5.

The Randić spectrum of $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}}),$ for $\mathfrak{n}={\alpha }^2\beta$, where α, β are distinct primes, is given by $$\left\{\begin{array}{cccccc}\frac{-1}{\left|V\right|-1}& 0& x_1& x_2& x_3& x_4\\ \varphi (\alpha \beta )+\varphi (\alpha )+\varphi (\beta )-3& \varphi ({\alpha }^2)-1& 1& 1& 1& 1\end{array}\right\},$$ where $x_1,x_2,x_3$, and x₄ represent the non-zero roots of the characteristic polynomial of matrix (3.2), and V denotes the set of vertices in $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$.

Proof.

Let $\mathfrak{n}={\alpha }^2\beta$, with $\alpha <\beta$ and α, β are distinct primes. First, we can observe that ${{\rm Y}}_{{\alpha }^2\beta }^{*}$ is the complete graph on 4 vertices $\{\alpha ,\beta ,{\alpha }^2,\alpha \beta \}$. Then by Lemma 2.5, we have $$W\Gamma ({\mathbb{Z}}_{{\alpha }^2\beta })={{\rm Y}}_{{\alpha }^2\beta }^{*}[W\Gamma (A_{\alpha }),W\Gamma (A_{\beta }),W\Gamma (A_{{\alpha }^2}),W\Gamma (A_{\alpha \beta })].$$

By using Lemma 2.3, also we can observe that $$W\Gamma ({\mathbb{Z}}_{{\alpha }^2\beta })={{\rm Y}}_{{\alpha }^2\beta }^{*}[K_{\varphi (\alpha \beta )},{\overline{K}}_{\varphi ({\alpha }^2)},K_{\varphi (\beta )},K_{\varphi (\alpha )}].$$

Cardinality $\left|V\right|$ of the vertex set V of $W\Gamma ({\mathbb{Z}}_{{\alpha }^2\beta })$ is given by $\varphi (\alpha \beta )+\varphi ({\alpha }^2)+\varphi (\beta )+\varphi (\alpha )$. It follows that $M_{\alpha }=\varphi ({\alpha }^2)+\varphi (\beta )+\varphi (\alpha )=\left|V\right|-\varphi (\alpha \beta ),M_{\beta }=\left|V\right|-\varphi ({\alpha }^2),M_{{\alpha }^2}=\left|V\right|-\varphi (\beta )$ and $M_{\alpha \beta }=\left|V\right|-\varphi (\alpha )$. Also, we have $r_{\alpha }=\varphi (\alpha \beta )-1,r_{{\alpha }^2}=\varphi (\beta )-1,r_{\alpha \beta }=\varphi (\alpha )-1$ and $r_{\beta }=0.$ Therefore, by Theorem 3.2, the Randić spectrum of $W\Gamma ({\mathbb{Z}}_{{\alpha }^2\beta })$ is $$\begin{array}{c}{\sigma }_R(W\Gamma ({\mathbb{Z}}_{{\alpha }^2\beta }))=(\underset{i=1}{\overset{4}{\cup }}(\frac{\rho }{r_{u_i}+M_{u_i}}:\rho \in {\sigma }_R(W\Gamma (A_{u_i}))\setminus \left\{r_{u_i}\right\})\mathrm{})\\ \hspace{1em}\cup {\sigma }_R(\mathbb{L}({{\rm Y}}_{{\alpha }^2\beta }^{*}))\\ =\left\{\begin{array}{cc}\frac{-1}{\left|V\right|-1}& 0\\ \varphi (\alpha \beta )+\varphi (\alpha )+\varphi (\beta )-3& \varphi ({\alpha }^2)-1\end{array}\right\}\\ \hspace{1em}\cup {\sigma }_R(\mathbb{L}({{\rm Y}}_{{\alpha }^2\beta }^{*})).\end{array}$$

Thus, the remaining 4 Randić eigenvalues are the eigenvalues of the matrix (3.2) $$\mathbb{L}({{\rm Y}}_{{\alpha }^2\beta }^{*})=\left[\begin{array}{cccc}\frac{\varphi (\alpha \beta )-1}{\left|V\right|-1}& A& B& C\\ A& 0& D& E\\ B& D& \frac{\varphi (\beta )-1}{\left|V\right|-1}& F\\ C& E& F& \frac{\varphi (\alpha )-1}{\left|V\right|-1}\end{array}\right].$$(3.2)

Where $A=\sqrt{\frac{\varphi (\alpha \beta )\varphi ({\alpha }^2)}{(|V|-1)(|V|-\varphi ({\alpha }^2))}}$, $B=\frac{\sqrt{\varphi (\alpha \beta )\varphi (\beta )}}{\left|V\right|-1}$, $C=\frac{\sqrt{\varphi (\alpha \beta )\varphi (\alpha )}}{\left|V\right|-1}$, $D=\sqrt{\frac{\varphi ({\alpha }^2)\varphi (\beta )}{(|V|-1)(|V|-\varphi ({\alpha }^2))}}$, $E=\sqrt{\frac{\varphi ({\alpha }^2)\varphi (\alpha )}{(|V|-1)(|V|-\varphi ({\alpha }^2))}}$, and $F=\frac{\sqrt{\varphi (\alpha )\varphi (\beta )}}{\left|V\right|-1}$. □

Proposition 3.6.

The Randić spectrum of $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$, for $\mathfrak{n}=\alpha \beta \gamma$, with $\alpha <\beta <\gamma$ and α, β, γ are distinct primes, is given by $$\begin{array}{c}{\sigma }_R(W\Gamma ({\mathbb{Z}}_{\alpha \beta \gamma }))\\ \hspace{1em}=\left\{\begin{array}{cc}0& \frac{-1}{\left|V\right|-1}\\ \varphi (\alpha \beta )+\varphi (\alpha \gamma )+\varphi (\beta \gamma )-3& \varphi (\alpha )+\varphi (\beta )+\varphi (\gamma )-3\end{array}\right\},\end{array}$$ where V represents the set of vertices in $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$. The remaining Randić eigenvalues of $W\Gamma ({\mathbb{Z}}_{\alpha \beta \gamma })$ can be determined from the solutions to the characteristic polynomial of matrix (3.3).

Proof.

Let $\mathfrak{n}=\alpha \beta \gamma$, with $\alpha <\beta <\gamma$ and α, β, γ are distinct primes. First, we can observe that ${{\rm Y}}_{\alpha \beta \gamma }^{*}$ is the complete graph on 6 vertices. i.e., $\alpha ,\beta ,\gamma ,\alpha \beta ,\alpha \gamma$, and $\beta \gamma$. Then by using Lemma 2.5, we have $$\begin{array}{c}W\Gamma ({\mathbb{Z}}_{\alpha \beta \gamma })={{\rm Y}}_{\alpha \beta \gamma }^{*}[W\Gamma (A_{\alpha }),W\Gamma (A_{\beta }),W\Gamma (A_{\gamma }),W\Gamma (A_{\alpha \beta }),\\ \mathrm{\hspace{1em}\hspace{1em}}W\Gamma (A_{\alpha \gamma }),W\Gamma (A_{\beta \gamma })].\end{array}$$

By using Lemma 2.3, we can observe that $$\begin{array}{c}W\Gamma ({\mathbb{Z}}_{\alpha \beta \gamma })={{\rm Y}}_{\alpha \beta \gamma }^{*}[{\overline{K}}_{\varphi (\beta \gamma )},{\overline{K}}_{\varphi (\alpha \gamma )},{\overline{K}}_{\varphi (\alpha \beta )},K_{\varphi (\gamma )},\\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}{K}_{\varphi (\beta )},K_{\varphi (\alpha )}].\end{array}$$

The cardinality $\left|V\right|$ of the vertex set V of $W\Gamma ({\mathbb{Z}}_{\alpha \beta \gamma })$ is given by $\varphi (\alpha )+\varphi (\beta )+\varphi (\gamma )+\varphi (\alpha \beta )+\varphi (\alpha \gamma )+\varphi (\beta \gamma )$. It follows that $M_{\alpha }=\varphi (\alpha )+\varphi (\beta )+\varphi (\gamma )+\varphi (\alpha \beta )+\varphi (\alpha \gamma )=\left|V\right|-\varphi (\beta \gamma ),M_{\beta }=\left|V\right|-\varphi (\alpha \gamma ),M_{\gamma }=\left|V\right|-\varphi (\alpha \beta ),M_{\alpha \beta }=\left|V\right|-\varphi (\gamma ),M_{\alpha \gamma }=\left|V\right|-\varphi (\beta )$ and $M_{\beta \gamma }=\left|V\right|-\varphi (\alpha )$. Also, we see that $r_{\alpha }=r_{\beta }=r_{\gamma }=0$ and $r_{\alpha \beta }=\varphi (\gamma )-1,r_{\alpha \gamma }=\varphi (\beta )-1$ and $r_{\beta \gamma }=\varphi (\alpha )-1$. Therefore, by Theorem 3.2, the Randić spectrum of $W\Gamma ({\mathbb{Z}}_{\alpha \beta \gamma })$ is $$\begin{array}{c}\hspace{1em}{\sigma }_R(W\Gamma ({\mathbb{Z}}_{\alpha \beta \gamma }))=(\underset{i=1}{\overset{6}{\cup }}(\frac{\rho }{r_{u_i}+M_{u_i}}:\rho \in {\sigma }_R(W\Gamma (A_{u_i}))\setminus \left\{r_{u_i}\right\}))\\ \cup {\sigma }_R(\mathbb{L}({{\rm Y}}_{\alpha \beta \gamma }^{*}))\\ =\left\{\begin{array}{cc}0& \frac{-1}{\left|V\right|-1}\\ \varphi (\alpha \beta )+\varphi (\alpha \gamma )+\varphi (\beta \gamma )-3& \varphi (\alpha )+\varphi (\beta )+\varphi (\gamma )-3\end{array}\right\}\\ \hspace{1em}\cup {\sigma }_R(\mathbb{L}({{\rm Y}}_{\alpha \beta \gamma }^{*})).\end{array}$$

Thus, the remaining 6 Randić eigenvalues are the eigenvalues of the matrix (3.3) $$\mathbb{L}({{\rm Y}}_{\alpha \beta \gamma }^{*})=\left[\begin{array}{cccccc}0& A_{12}& A_{13}& A_{14}& A_{15}& A_{16}\\ A_{12}& 0& B_{23}& B_{24}& B_{25}& B_{26}\\ A_{13}& B_{23}& 0& C_{34}& C_{35}& C_{36}\\ A_{14}& B_{24}& C_{34}& \frac{\varphi (\gamma )-1}{\left|V\right|-1}& D_{45}& D_{46}\\ A_{15}& B_{25}& C_{35}& D_{45}& \frac{\varphi (\beta )-1}{\left|V\right|-1}& E_{56}\\ A_{16}& B_{26}& C_{36}& D_{46}& E_{56}& \frac{\varphi (\alpha )-1}{\left|V\right|-1}\end{array}\right].$$(3.3)

Where $A_{12}=\sqrt{\frac{\varphi (\beta \gamma )\varphi (\alpha \gamma )}{(|V|-\varphi (\beta \gamma ))(|V|-\varphi (\alpha \gamma ))}}$, $A_{13}=\sqrt{\frac{\varphi (\beta \gamma )\varphi (\alpha \beta )}{(|V|-\varphi (\beta \gamma ))(|V|-\varphi (\alpha \beta ))}},A_{14}=\sqrt{\frac{\varphi (\beta \gamma )\varphi (\gamma )}{(|V|-\varphi (\beta \gamma ))(|V|-1)}}$, $$A_{15}=\sqrt{\frac{\varphi (\beta \gamma )\varphi (\beta )}{(|V|-\varphi (\beta \gamma ))(|V|-1)}},A_{16}=\sqrt{\frac{\varphi (\beta \gamma )\varphi (\alpha )}{(|V|-\varphi (\beta \gamma ))(|V|-1)}},$$ $$B_{23}=\sqrt{\frac{\varphi (\alpha \gamma )\varphi (\alpha \beta )}{(|V|-\varphi (\alpha \gamma ))(|V|-\varphi (\alpha \beta ))}},B_{24}=\sqrt{\frac{\varphi (\alpha \gamma )\varphi (\gamma )}{(|V|-\varphi (\alpha \gamma ))(|V|-1}},$$ $$B_{25}=\sqrt{\frac{\varphi (\alpha \gamma )\varphi (\beta )}{(|V|-\varphi (\alpha \gamma ))(|V|-1)}},B_{26}=\sqrt{\frac{\varphi (\alpha \gamma )\varphi (\alpha )}{(|V|-\varphi (\alpha \gamma ))(|V|-1)}},$$ $$C_{34}=\sqrt{\frac{\varphi (\alpha \beta )\varphi (\gamma )}{(|V|-\varphi (\alpha \beta ))(|V|-1)}},C_{35}=\sqrt{\frac{\varphi (\alpha \beta )\varphi (\beta )}{(|V|-\varphi (\alpha \beta ))(|V|-1)}},$$ $$C_{36}=\sqrt{\frac{\varphi (\alpha \beta )\varphi (\alpha )}{(|V|-\varphi (\alpha \beta ))(|V|-1)}},D_{45}=\frac{\sqrt{\varphi (\gamma )\varphi (\beta )}}{(|V|-1)},$$

$D_{46}=\frac{\sqrt{\varphi (\gamma )\varphi (\alpha )}}{(|V|-1)}$, and $E_{56}=\frac{\sqrt{\varphi (\beta )\varphi (\alpha )}}{(|V|-1)}$. □

Theorem 3.7.

The Randić spectrum of $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$, for $\mathfrak{n}={\alpha }^{\mathfrak{m}}\beta$ $(\mathfrak{m}\ge 2)$, where α, β are distinct primes is given by $$\begin{array}{c}{\sigma }_R(W\Gamma ({\mathbb{Z}}_{{\alpha }^{\mathfrak{m}}\beta }))\\ \hspace{1em}=\left\{\begin{array}{cc}\frac{-1}{\left|V\right|-1}& 0\\ (\sum _{i=1}^{\mathfrak{m}}\varphi ({\alpha }^{\mathfrak{m}-i}\beta )+\sum _{i=1}^{\mathfrak{m}-1}\varphi ({\alpha }^{\mathfrak{m}-i}))-(2\mathfrak{m}-1)& \varphi ({\alpha }^{\mathfrak{m}})-1\end{array}\right\},\end{array}$$ where V represents the set of vertices in $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$. The remaining Randić eigenvalues of $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$ can be found from the solutions to the characteristic polynomial of matrix (3.4).

Proof.

Let $\mathfrak{n}={\alpha }^{\mathfrak{m}}\beta (\mathfrak{m}\ge 2)$. The vertex set of the graph ${{\rm Y}}_{{\alpha }^{\mathfrak{m}}\beta }^{*}$ comprises the elements from the set $\{\alpha ,{\alpha }^2,\dots ,{\alpha }^{\mathfrak{m}},$ $\beta ,\alpha \beta ,{\alpha }^2\beta ,\dots ,{\alpha }^{\mathfrak{m}-1}\beta \}$. Then by using Lemma 2.5, we have $$\begin{array}{c}W\Gamma ({\mathbb{Z}}_{{\alpha }^{\mathfrak{m}}\beta })={{\rm Y}}_{{\alpha }^{\mathfrak{m}}\beta }^{*}[W\Gamma (A_{\alpha }),W\Gamma (A_{{\alpha }^2}),\dots ,W\Gamma (A_{{\alpha }^{\mathfrak{m}}}),W\Gamma (A_{\beta }),\\ \mathrm{\hspace{1em}\hspace{1em}}W\Gamma (A_{\alpha \beta }),W\Gamma (A_{{\alpha }^2\beta }),\dots ,W\Gamma (A_{{\alpha }^{\mathfrak{m}-1}\beta })].\end{array}$$

By Lemma 2.3, also we can observe that $$\begin{array}{c}W\Gamma ({\mathbb{Z}}_{{\alpha }^{\mathfrak{m}}\beta })={{\rm Y}}_{{\alpha }^{\mathfrak{m}}\beta }^{*}[K_{\varphi ({\alpha }^{\mathfrak{m}-1}\beta )},K_{\varphi ({\alpha }^{\mathfrak{m}-2}\beta )},\dots ,K_{\varphi (\beta )},{\overline{K}}_{\varphi ({\alpha }^{\mathfrak{m}})},\\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}{K}_{\varphi ({\alpha }^{\mathfrak{m}-1})},\dots ,K_{\varphi (\alpha )}].\end{array}$$

Cardinality $\left|V\right|$ of the vertex set V of $W\Gamma ({\mathbb{Z}}_{{\alpha }^{\mathfrak{m}}\beta })$ is given by $\varphi ({\alpha }^{\mathfrak{m}-1}\beta )+\varphi ({\alpha }^{\mathfrak{m}-2}\beta )+\varphi ({\alpha }^{\mathfrak{m}-3}\beta )+\cdots +\varphi (\beta )+\varphi ({\alpha }^{\mathfrak{m}-1})+\varphi ({\alpha }^{\mathfrak{m}-2})+\varphi ({\alpha }^{\mathfrak{m}-3})+\cdots +\varphi (\alpha )+\varphi ({\alpha }^{\mathfrak{m}})$. It follows that $M_{\alpha }=\varphi ({\alpha }^{\mathfrak{m}})+\varphi ({\alpha }^{\mathfrak{m}-2}\beta )+\varphi ({\alpha }^{\mathfrak{m}-3}\beta )+\cdots +\varphi (\beta )+\varphi ({\alpha }^{\mathfrak{m}-1})+\varphi ({\alpha }^{\mathfrak{m}-2})+\varphi ({\alpha }^{\mathfrak{m}-3})+\cdots +\varphi (\alpha )=\left|V\right|-\varphi ({\alpha }^{\mathfrak{m}-1}\beta ),M_{{\alpha }^2}=\left|V\right|-\varphi ({\alpha }^{\mathfrak{m}-2}\beta ),\dots ,M_{{\alpha }^{\mathfrak{m}}}=\left|V\right|-\varphi (\beta ),M_{\alpha \beta }=\left|V\right|-\varphi ({\alpha }^{\mathfrak{m}-1}),\dots ,M_{{\alpha }^r\beta }=\left|V\right|-\varphi ({\alpha }^{\mathfrak{m}-r}),\dots ,M_{{\alpha }^{\mathfrak{m}-1}\beta }=\left|V\right|-\varphi (\alpha ),M_{\beta }=\left|V\right|-\varphi ({\alpha }^{\mathfrak{m}}).$ Also, $r_{\alpha }=\varphi ({\alpha }^{\mathfrak{m}-1}\beta )-1,r_{{\alpha }^2}=\varphi ({\alpha }^{\mathfrak{m}-2}\beta )-1,\dots ,r_{{\alpha }^{\mathfrak{m}}}=\varphi (\beta )-1,r_{\alpha \beta }=\varphi ({\alpha }^{\mathfrak{m}-1})-1,\dots ,r_{{\alpha }^k\beta }=\varphi ({\alpha }^{\mathfrak{m}-k})-1,\dots ,r_{{\alpha }^{\mathfrak{m}-1}\beta }=\varphi (\alpha )-1$ and $r_{\beta }=0.$ Therefore, by Theorem 3.2, the Randić spectrum of $W\Gamma ({\mathbb{Z}}_{{\alpha }^{\mathfrak{m}}\beta })$ is given by $$\begin{array}{c}{\sigma }_R(W\Gamma ({\mathbb{Z}}_{{\alpha }^{\mathfrak{m}}\beta }))\\ \hspace{1em}=(\frac{\rho }{r_{\alpha }+M_{\alpha }}:\rho \in {\sigma }_R(W\Gamma (A_{\alpha }))\setminus \{r_{\alpha }\})\\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\cup (\frac{\rho }{r_{{\alpha }^2}+M_{{\alpha }^2}}:\rho \in {\sigma }_R(W\Gamma (A_{{\alpha }^2}))\setminus \{r_{{\alpha }^2}\})\\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\cup \cdots \cup (\frac{\rho }{r_{{\alpha }^m}+M_{{\alpha }^m}}:\rho \in {\sigma }_R(W\Gamma (A_{{\alpha }^m}))\setminus \{r_{{\alpha }^m}\})\\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\cup (\frac{\rho }{r_{\beta }+M_{\beta }}:\rho \in {\sigma }_R(W\Gamma (A_{\beta }))\setminus \{r_{\beta }\})\\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\cup (\frac{\rho }{r_{\alpha \beta }+M_{\alpha \beta }}:\rho \in {\sigma }_R(W\Gamma (A_{\alpha \beta }))\setminus \{r_{\alpha \beta }\})\\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\cup \cdots \cup (\frac{\rho }{r_{{\alpha }^{m-1}\beta }+M_{{\alpha }^{m-1}\beta }}:\rho \in {\sigma }_R(W\Gamma (A_{{\alpha }^{m-1}\beta }))\setminus \{r_{{\alpha }^{m-1}\beta }\})\\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\cup {\sigma }_R(\mathbb{L}({{\rm Y}}_{{\alpha }^{\mathfrak{m}}\beta }^{*}))\\ \hspace{1em}=\left\{\begin{array}{cc}\frac{-1}{\left|V\right|-1}& 0\\ (\sum _{i=1}^{\mathfrak{m}}\varphi ({\alpha }^{\mathfrak{m}-i}\beta )+\sum _{i=1}^{\mathfrak{m}-1}\varphi ({\alpha }^{\mathfrak{m}-i}))-(2\mathfrak{m}-1)& \varphi ({\alpha }^{\mathfrak{m}})-1\end{array}\right\}\\ \mathrm{\hspace{1em}}\mathrm{\hspace{1em}}\cup {\sigma }_R(\mathbb{L}({{\rm Y}}_{{\alpha }^{\mathfrak{m}}\beta }^{*})).\end{array}$$

□

The remaining $2\mathfrak{m}$ Randić eigenvalues are the eigenvalues of this matrix $\mathbb{L}({{\rm Y}}_{{\alpha }^{\mathfrak{m}}\beta }^{*})=$ (3.4) $$\begin{array}{c}\left[\begin{array}{c}\begin{array}{ccccccccc}& \frac{\sqrt{\varphi ({\alpha }^{\mathfrak{m}-1}\beta )\varphi ({\alpha }^{\mathfrak{m}-2}\beta )}}{\left|V\right|-1}& \cdots & -\frac{\sqrt{\varphi ({\alpha }^{\mathfrak{m}-1}\beta )\varphi (\beta )}}{\left|V\right|-1}& \sqrt{\frac{\varphi ({\alpha }^{\mathfrak{m}-1}\beta )\varphi ({\alpha }^{\mathfrak{m}})}{(|V|-1)(|V|-\varphi ({\alpha }^{\mathfrak{m}}))}}& \frac{\sqrt{\varphi ({\alpha }^{\mathfrak{m}-1}\beta )\varphi ({\alpha }^{\mathfrak{m}-1})}}{\left|V\right|-1}& \cdots & \frac{\sqrt{\varphi ({\alpha }^{\mathfrak{m}-1}\beta )\varphi ({\alpha }^2)}}{\left|V\right|-1}& \frac{\sqrt{\varphi ({\alpha }^{\mathfrak{m}-1}\beta )\varphi (\alpha )}}{\left|V\right|-1}\\ \frac{\sqrt{\varphi ({\alpha }^{\mathfrak{m}-1}\beta )\varphi ({\alpha }^{\mathfrak{m}-2}\beta )}}{\left|V\right|-1}& \frac{\varphi ({\alpha }^{\mathfrak{m}-2}\beta )-1}{\left|V\right|-1}& \cdots & \frac{\sqrt{\varphi ({\alpha }^{\mathfrak{m}-2}\beta )\varphi (\beta )}}{\left|V\right|-1}& \sqrt{\frac{\varphi ({\alpha }^{\mathfrak{m}-2}\beta )\varphi ({\alpha }^{\mathfrak{m}})}{(|V|-1)(|V|-\varphi ({\alpha }^{\mathfrak{m}}))}}& \frac{\sqrt{\varphi ({\alpha }^{\mathfrak{m}-2}\beta )\varphi ({\alpha }^{\mathfrak{m}-1})}}{\left|V\right|-1}& \cdots & \frac{\sqrt{\varphi ({\alpha }^{\mathfrak{m}-2}\beta )\varphi ({\alpha }^2)}}{\left|V\right|-1}& \frac{\sqrt{\varphi ({\alpha }^{\mathfrak{m}-2}\beta )\varphi (\alpha )}}{\left|V\right|-1}\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ \frac{\sqrt{\varphi ({\alpha }^{\mathfrak{m}-1}\beta )\varphi (\beta )}}{\left|V\right|-1}& \frac{\sqrt{\varphi ({\alpha }^{\mathfrak{m}-2}\beta )\varphi (\beta )}}{\left|V\right|-1}& \cdots & \frac{\varphi (\beta )-1}{\left|V\right|-1}& \sqrt{\frac{\varphi (\beta )\varphi ({\alpha }^{\mathfrak{m}})}{(|V|-1)(|V|-\varphi ({\alpha }^{\mathfrak{m}}))}}& \frac{\sqrt{\varphi (\beta )\varphi ({\alpha }^{\mathfrak{m}-1})}}{\left|V\right|-1}& \cdots & \frac{\sqrt{\varphi (\beta )\varphi ({\alpha }^2)}}{\left|V\right|-1}& \frac{\sqrt{\varphi (\beta )\varphi (\alpha )}}{\left|V\right|-1}\end{array}\\ \begin{array}{ccccccccc}& \sqrt{\frac{\varphi ({\alpha }^{\mathfrak{m}-2}\beta )\varphi ({\alpha }^{\mathfrak{m}})}{(|V|-1)(|V|-\varphi ({\alpha }^{\mathfrak{m}}))}}& \cdots & -\sqrt{\frac{\varphi ({\alpha }^{\mathfrak{m}-2}\beta )\varphi ({\alpha }^{\mathfrak{m}})}{(|V|-1)(|V|-\varphi ({\alpha }^{\mathfrak{m}}))}}& 0& \sqrt{\frac{\varphi ({\alpha }^{\mathfrak{m}-1})\varphi ({\alpha }^{\mathfrak{m}})}{(|V|-1)(|V|-\varphi ({\alpha }^{\mathfrak{m}}))}}& \cdots & \sqrt{\frac{\varphi ({\alpha }^2)\varphi ({\alpha }^{\mathfrak{m}})}{(|V|-1)(|V|-\varphi ({\alpha }^{\mathfrak{m}}))}}& \sqrt{\frac{\varphi (\alpha )\varphi ({\alpha }^{\mathfrak{m}})}{(|V|-1)(|V|-\varphi ({\alpha }^{\mathfrak{m}}))}}\\ \frac{\sqrt{\varphi ({\alpha }^{\mathfrak{m}-1}\beta )\varphi ({\alpha }^{\mathfrak{m}-1})}}{\left|V\right|-1}& \frac{\sqrt{\varphi ({\alpha }^{\mathfrak{m}-2}\beta )\varphi ({\alpha }^{\mathfrak{m}-1})}}{\left|V\right|-1}& \cdots & \frac{\sqrt{\varphi (\beta )\varphi ({\alpha }^{\mathfrak{m}-1})}}{\left|V\right|-1}& \sqrt{\frac{\varphi ({\alpha }^{\mathfrak{m}-1})\varphi ({\alpha }^{\mathfrak{m}})}{(|V|-1)(|V|-\varphi ({\alpha }^{\mathfrak{m}}))}}& \frac{\varphi ({\alpha }^{\mathfrak{m}-1})-1}{\left|V\right|-1}& \cdots & \frac{\sqrt{\varphi ({\alpha }^{\mathfrak{m}-1})\varphi ({\alpha }^2)}}{\left|V\right|-1}& \frac{\sqrt{\varphi ({\alpha }^{\mathfrak{m}-1})\varphi (\alpha )}}{\left|V\right|-1}\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\end{array}\\ \begin{array}{ccccccccc}& ⋮& ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ \frac{\sqrt{\varphi ({\alpha }^{\mathfrak{m}-1}\beta )\varphi ({\alpha }^2)}}{\left|V\right|-1}& \frac{\sqrt{\varphi ({\alpha }^{\mathfrak{m}-2}\beta )\varphi ({\alpha }^2)}}{\left|V\right|-1}& \cdots & \frac{\sqrt{\varphi (\beta )\varphi ({\alpha }^2)}}{\left|V\right|-1}& \sqrt{\frac{\varphi ({\alpha }^2)\varphi ({\alpha }^{\mathfrak{m}})}{(|V|-1)(|V|-\varphi ({\alpha }^{\mathfrak{m}}))}}& \frac{\sqrt{\varphi ({\alpha }^{\mathfrak{m}-1})\varphi ({\alpha }^2)}}{\left|V\right|-1}& \cdots & \frac{\varphi ({\alpha }^2)-1}{\left|V\right|-1}& \frac{\sqrt{\varphi ({\alpha }^2)\varphi (\alpha )}}{\left|V\right|-1}\\ \frac{\sqrt{\varphi ({\alpha }^{\mathfrak{m}-1}\beta )\varphi (\alpha )}}{\left|V\right|-1}& \frac{\sqrt{\varphi ({\alpha }^{\mathfrak{m}-2}\beta )\varphi (\alpha )}}{\left|V\right|-1}& \cdots & \frac{\sqrt{\varphi (\beta )\varphi (\alpha )}}{\left|V\right|-1}& \sqrt{\frac{\varphi (\alpha )\varphi ({\alpha }^{\mathfrak{m}})}{(|V|-1)(|V|-\varphi ({\alpha }^{\mathfrak{m}}))}}& \frac{\sqrt{\varphi ({\alpha }^{\mathfrak{m}-1})\varphi (\alpha )}}{\left|V\right|-1}& \cdots & \frac{\sqrt{\varphi ({\alpha }^2)\varphi (\alpha )}}{\left|V\right|-1}& \frac{\varphi (\alpha )-1}{\left|V\right|-1}\end{array}\end{array}\right].\\ \end{array}$$(3.4)

Theorem 3.8.

Let $\mathfrak{n}={\alpha }_1{\alpha }_2\cdots {\alpha }_{\mathfrak{m}}{\beta }_1^{k_1}{\beta }_2^{k_2}\cdots {\beta }_r^{k_r}(k_i\ge 2,\mathfrak{m}\ge 1,r\ge 0)$, where α_i ’s and β_i ’s are distinct primes. Suppose $\{u_1,u_2,\dots ,u_{\tau (\mathfrak{n})-2}\}$ represents the collection of all proper divisors of $\mathfrak{n}$. Then the Randić spectrum of $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$ is determined as follows: $$\left\{\begin{array}{cc}0& \frac{-1}{\left|V\right|-1}\\ \sum _{i=1}^{\mathfrak{m}}\varphi \left(\frac{\mathfrak{n}}{{\alpha }_i}\right)-\mathfrak{m}& \sum _{u_i\ne {\alpha }_i}\varphi \left(\frac{\mathfrak{n}}{u_i}\right)-(\tau (\mathfrak{n})-2-\mathfrak{m})\end{array}\right\},$$ where V represents the set of vertices in $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$. The remaining Randić eigenvalues of $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$ can be determined from the solutions to the characteristic polynomial of matrix (3.5).

Proof.

Suppose that $\mathfrak{n}={\alpha }_1{\alpha }_2\cdots {\alpha }_{\mathfrak{m}}{\beta }_1^{k_1}{\beta }_2^{k_2}\cdots {\beta }_r^{k_r}(k_i\ge 2,\mathfrak{m}\ge 1,r\ge 0)$, where α_i ’s and β_i ’s are distinct primes. Let $\mathfrak{D}=\{{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_{\mathfrak{m}}\}$, then by using Theorem 3.2, the Randić spectrum of $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$ is $$\begin{array}{c}{\sigma }_R(W\Gamma ({\mathbb{Z}}_{\mathfrak{n}}))=\underset{u_i\in \mathfrak{D}}{\cup }(\frac{\rho }{r_{u_i}+r_{u_i}}:\rho \in {\sigma }_R(W\Gamma (A_{u_i}))\setminus \{r_{u_i}\})\cup \\ \underset{u_i\notin \mathfrak{D}}{\cup }(\frac{\rho }{r_{u_i}+r_{u_i}}:\rho \in {\sigma }_R(W\Gamma (A_{u_i}))\setminus \{r_{u_i}\})\\ \cup {\sigma }_R(\mathbb{L}({{\rm Y}}_{\mathfrak{n}}^{*})).\end{array}$$

Using Lemmas 2.2, 2.3, and Corollary 2.4, we can deduce the following outcomes for each $u_i\in \mathfrak{D}$. Specifically, we establish that $W\Gamma (A_{u_i})$ is a complement of a complete graph ${\overline{K}}_{\varphi \left(\frac{\mathfrak{n}}{u_i}\right)}$, and for $u_j\notin \mathfrak{D}$, we find that $W\Gamma (A_{u_j})$ is a complete graph $K_{\varphi \left(\frac{\mathfrak{n}}{u_j}\right)}$. It is worth noting that the size, denoted as $\left|V\right|$, of the vertex set V within the graph $W\Gamma ({\mathbb{Z}}_{\mathfrak{n}})$ equals the sum of $\varphi \left(\frac{\mathfrak{n}}{u_i}\right)$ for i ranging from 1 to $\tau (n)-2$. In other words, $\left|V\right|$ can be expressed as $({\sum }_{i=1}^{\tau (n)-2}\varphi (\frac{\mathfrak{n}}{u_i}))$. Additionally, it should be observed that for values of i within the range of 1 to $\tau (n)-2$, the following relationship holds: $$M_{u_i}=\sum _{j=1,j\ne i}^{\tau (n)-2}\varphi \left(\frac{\mathfrak{n}}{u_j}\right)=\left|V\right|-\varphi \left(\frac{\mathfrak{n}}{u_i}\right).$$

Also, $r_{u_i}=0$, for $u_i\in \mathfrak{D}$ and $r_{u_j}=\varphi \left(\frac{\mathfrak{n}}{u_j}\right)-1$, for $u_j\notin \mathfrak{D}$. Thus, we obtain $$\begin{array}{c}{\sigma }_R(W\Gamma ({\mathbb{Z}}_{\mathfrak{n}}))\\ =\underset{u_i\in \mathfrak{D}}{\cup }(0:\rho \in {\sigma }_R({\overline{K}}_{\varphi \left(\frac{\mathfrak{n}}{u_i}\right)}))\setminus \left\{r_{u_i}\right\})\\ \underset{u_j\notin \mathfrak{D}}{\cup }(\frac{\rho }{\left|V\right|-1}:\rho \in {\sigma }_R(K_{\varphi \left(\frac{\mathfrak{n}}{u_j}\right)}))\setminus \left\{r_{u_j}\right\})\\ \cup {\sigma }_R(\mathbb{L}({{\rm Y}}_{\mathfrak{n}}^{*}))\\ =\underset{u_i\in \mathfrak{D}}{\cup }(\begin{array}{c}0\\ \varphi \left(\frac{\mathfrak{n}}{u_i}\right)-1\end{array})\underset{u_j\notin \mathfrak{D}}{\cup }(\begin{array}{c}\frac{-1}{\left|V\right|-1}\\ \varphi \left(\frac{\mathfrak{n}}{u_j}\right)-1\end{array})\\ \cup {\sigma }_R(\mathbb{L}({{\rm Y}}_{\mathfrak{n}}^{*}))=(\begin{array}{cc}0& \frac{-1}{\left|V\right|-1}\\ \sum _{i=1}^{\mathfrak{m}}\varphi \left(\frac{\mathfrak{n}}{{\alpha }_i}\right)-\mathfrak{m}& \sum _{u_i\ne {\alpha }_i}\varphi \left(\frac{\mathfrak{n}}{u_i}\right)-(\tau (\mathfrak{n})-2-\mathfrak{m})\end{array})\\ \cup {\sigma }_R(\mathbb{L}({{\rm Y}}_{\mathfrak{n}}^{*})).\end{array}$$

□

Thus, the remaining Randić eigenvalues are the eigenvalues of the matrix $\mathbb{L}({{\rm Y}}_{\mathfrak{n}}^{*})=$ (3.5) $$\left[\begin{array}{c}\begin{array}{cccccccc}0& \sqrt{\frac{\varphi \left(\frac{\mathfrak{n}}{u_1}\right)\varphi \left(\frac{\mathfrak{n}}{u_2}\right)}{(|V|-\varphi (\frac{\mathfrak{n}}{u_1}))(|V|-\varphi (\frac{\mathfrak{n}}{u_2}))}}& \cdots & \sqrt{\frac{\varphi \left(\frac{\mathfrak{n}}{u_1}\right)\varphi \left(\frac{\mathfrak{n}}{u_{\mathfrak{m}}}\right)}{(|V|-\varphi (\frac{\mathfrak{n}}{u_1}))(|V|-\varphi (\frac{\mathfrak{n}}{u_{\mathfrak{m}}}))}}& \sqrt{\frac{\varphi \left(\frac{\mathfrak{n}}{u_1}\right)\varphi \left(\frac{\mathfrak{n}}{u_{\mathfrak{m}+1}}\right)}{(|V|-\varphi (\frac{\mathfrak{n}}{u_1}))(|V|-1)}}& \cdots & \sqrt{\frac{\varphi \left(\frac{\mathfrak{n}}{u_1}\right)\varphi \left(\frac{\mathfrak{n}}{u_{\tau (\mathfrak{n})-2}}\right)}{(|V|-\varphi (\frac{\mathfrak{n}}{u_1}))(|V|-1)}}& \\ \sqrt{\frac{\varphi \left(\frac{\mathfrak{n}}{u_1}\right)\varphi \left(\frac{\mathfrak{n}}{u_2}\right)}{(|V|-\varphi (\frac{\mathfrak{n}}{u_1}))(|V|-\varphi (\frac{\mathfrak{n}}{u_2}))}}& 0& \cdots & \sqrt{\frac{\varphi \left(\frac{\mathfrak{n}}{u_2}\right)\varphi \left(\frac{\mathfrak{n}}{u_{\mathfrak{m}}}\right)}{(|V|-\varphi (\frac{\mathfrak{n}}{u_2}))(|V|-\varphi (\frac{\mathfrak{n}}{u_{\mathfrak{m}}}))}}& \sqrt{\frac{\varphi \left(\frac{\mathfrak{n}}{u_2}\right)\varphi \left(\frac{\mathfrak{n}}{u_{\mathfrak{m}+1}}\right)}{(|V|-\varphi (\frac{\mathfrak{n}}{u_2}))(|V|-1)}}& \cdots & \sqrt{\frac{\varphi \left(\frac{\mathfrak{n}}{u_2}\right)\varphi \left(\frac{\mathfrak{n}}{u_{\tau (\mathfrak{n})-2}}\right)}{(|V|-\varphi (\frac{\mathfrak{n}}{u_2}))(|V|-1)}}& \\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& ⋮& \\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& ⋮& \\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& ⋮& \end{array}\\ \begin{array}{ccccccc}& \sqrt{\frac{\varphi \left(\frac{\mathfrak{n}}{u_2}\right)\varphi \left(\frac{\mathfrak{n}}{u_{\mathfrak{m}}}\right)}{(|V|-\varphi (\frac{\mathfrak{n}}{u_2}))(|V|-\varphi (\frac{\mathfrak{n}}{u_{\mathfrak{m}}}))}}& \cdots & 0& \sqrt{\frac{\varphi \left(\frac{\mathfrak{n}}{u_{\mathfrak{m}}}\right)\varphi \left(\frac{\mathfrak{n}}{u_{\mathfrak{m}+1}}\right)}{(|V|-\varphi (\frac{\mathfrak{n}}{u_{\mathfrak{m}}}))(|V|-1)}}& \cdots & \sqrt{\frac{\varphi \left(\frac{\mathfrak{n}}{u_{\mathfrak{m}}}\right)\varphi \left(\frac{\mathfrak{n}}{u_{\tau (\mathfrak{n})-2}}\right)}{(|V|-\varphi (\frac{\mathfrak{n}}{u_{\mathfrak{m}}}))(|V|-1)}}\\ \sqrt{\frac{\varphi \left(\frac{\mathfrak{n}}{u_1}\right)\varphi \left(\frac{\mathfrak{n}}{u_{\mathfrak{m}+1}}\right)}{(|V|-\varphi (\frac{\mathfrak{n}}{u_1}))(|V|-1)}}& \sqrt{\frac{\varphi \left(\frac{\mathfrak{n}}{u_2}\right)\varphi \left(\frac{\mathfrak{n}}{u_{\mathfrak{m}+1}}\right)}{(|V|-\varphi (\frac{\mathfrak{n}}{u_2}))(|V|-1)}}& \cdots & \sqrt{\frac{\varphi \left(\frac{\mathfrak{n}}{u_{\mathfrak{m}}}\right)\varphi \left(\frac{\mathfrak{n}}{u_{\mathfrak{m}+1}}\right)}{(|V|-\varphi (\frac{\mathfrak{n}}{u_{\mathfrak{m}}}))(|V|-1)}}& \frac{\varphi \left(\frac{\mathfrak{n}}{u_{\mathfrak{m}+1}}\right)-1}{\left|V\right|-1}& \cdots & \frac{\sqrt{\varphi \left(\frac{\mathfrak{n}}{u_{\mathfrak{m}+1}}\right)\varphi \left(\frac{\mathfrak{n}}{u_{\tau (\mathfrak{n})-2}}\right)}}{\left|V\right|-1}\end{array}\\ \begin{array}{ccccccc}& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ \sqrt{\frac{\varphi \left(\frac{\mathfrak{n}}{u_1}\right)\varphi \left(\frac{\mathfrak{n}}{u_{\tau (\mathfrak{n})-2}}\right)}{(|V|-\varphi (\frac{\mathfrak{n}}{u_1}))(|V|-1)}}& \sqrt{\frac{\varphi \left(\frac{\mathfrak{n}}{u_2}\right)\varphi \left(\frac{\mathfrak{n}}{u_{\tau (\mathfrak{n})-2}}\right)}{(|V|-\varphi (\frac{\mathfrak{n}}{u_2}))(|V|-1)}}& \cdots & \sqrt{\frac{\varphi \left(\frac{\mathfrak{n}}{u_{\mathfrak{m}}}\right)\varphi \left(\frac{\mathfrak{n}}{u_{\tau (\mathfrak{n})-2}}\right)}{(|V|-\varphi (\frac{\mathfrak{n}}{u_{\mathfrak{m}}}))(|V|-1)}}& \frac{\sqrt{\varphi \left(\frac{\mathfrak{n}}{u_{\mathfrak{m}+1}}\right)\varphi \left(\frac{\mathfrak{n}}{u_{\tau (\mathfrak{n})-2}}\right)}}{\left|V\right|-1}& \cdots & \frac{\varphi \left(\frac{\mathfrak{n}}{u_{\tau (\mathfrak{n})-2}}\right)-1}{\left|V\right|-1}\end{array}\end{array}\right].$$(3.5)

Acknowledgments

The authors are deeply grateful to the anonymous reviewers for their thorough review and constructive feedback, which greatly enriched the quality and depth of this manuscript.

Disclosure statement

The authors confirm that there are no conflicts of interest pertaining to this paper. The decision to publish in this journal was solely determined by the authors independent judgment.