Optimal L(3,2,1)-labeling of trees

Abstract

Given a graph G, an $L(3,2,1)$-labeling of G is an assignment f of non-negative integers (labels) to the vertices of G such that $\left|f(u)-f(v)\right|\ge 4-i$ if $\text{dist}(u,v)=i$ (i = 1, 2, 3). For a non-negative integer k, a k-$L(3,2,1)$-labeling is an $L(3,2,1)$-labeling such that no label is greater than k. The $L(3,2,1)$-labeling number of G, denoted by ${\lambda }_{3,2,1}(G)$, is the smallest number k such that G has a k-$L(3,2,1)$-labeling. Chia proved that the $L(3,2,1)$-labeling number of a tree T with maximum degree Δ can have one of three values: $2\Delta +1,2\Delta +2$ and $2\Delta +3$. This paper gives some sufficient conditions for ${\lambda }_{3,2,1}(T)\ge 2\Delta +2$ and ${\lambda }_{3,2,1}(T)=2\Delta +3$, respectively. As a result, the $L(3,2,1)$-labeling numbers of complete m-ary trees, spiders and banana trees are completely determined.

KEYWORDS:

• Channel assignment
• $L(3,2,1)$-labeling
• trees

MATHEMATICS SUBJECT CLASSIFICATION:

• 05C78
• 05C15

1 Introduction

One of the practical interests on channel assignment problem in a radio communication network is to assign channels (represented by non-negative integers) to the transmitters in a way such that no transmitters interfere with each other. Hale [6] formulated this problem in terms of so-called T-coloring of graphs. Furthermore, Griggs and Yeh [5] proposed a modification of this problem, namely the L(2, 1)-labeling problem, and they generalized it to p-levels of interference, specifically for given positive integers $k_1,k_2,\dots ,k_p$, an $L(k_1,k_2,\dots ,k_p)$-labeling of a graph G is an assignment f of non-negative integers (labels) to the vertices of G such that $\left|f(u)-f(v)\right|\ge k_t$ if $\text{dist}(u,v)=t$, where $\text{dist}(u,v)$ is the distance between u and v. For a non-negative integer k, a k- $L(k_1,k_2,\dots ,k_p)$-labeling is an $L(k_1,k_2,\dots ,k_p)$-labeling such that no label is greater than k. The $L(k_1,k_2,\dots ,k_p)$-labeling number of G, denoted by ${\lambda }_{k_1,k_2,\dots ,k_p}(G)$, is the smallest number k such that G has a k-$L(k_1,k_2,\dots ,k_p)$-labeling.

The $L(k_1,k_2,\dots ,k_p)$-labeling problem mentioned above is interesting in both theoretical and practical applications. For instance, when p = 1 and $k_1=1$, it becomes the ordinary vertex-coloring problem. When p = 2, many interesting results (see [2, 5, 10]) have been obtained for various families of finite graphs, especially for the case $(k_1,k_2)=(2,1)$. For more details, one may refer to the surveys [1, 11].

For p = 3 and $(k_1,k_2,k_3)=(3,2,1)$, Shao [8] studied the $L(3,2,1)$-labeling of Kneser graphs, extremely irregular graphs, Halin graphs, and gave bounds for the $L(3,2,1)$-labeling numbers of these classes of graphs. Shao and Liu [9] studied the $L(3,2,1)$-labeling of planar graphs, and showed that ${\lambda }_{3,2,1}(G)\le 15({\Delta }^2-\Delta +1)$ if G is a planar graph of maximum degree Δ. Clipperton [4] determined the $L(3,2,1)$-labeling numbers for paths, cycles, caterpillars, m-ary trees, complete graphs and complete bipartite graphs, and showed that ${\lambda }_{3,2,1}(G)\le {\Delta }^3+{\Delta }^2+3\Delta$ for any graph G with maximum degree Δ. Chia [3] proved that the $L(3,2,1)$-labeling number of a tree T with maximum degree Δ can have one of three values: $2\Delta +1,2\Delta +2$ and $2\Delta +3$. Furthermore, providing some sufficient conditions for the bounds or giving a characterization result for trees becomes a meaningful topic.

Based on the above topics, this paper gives some sufficient conditions for ${\lambda }_{3,2,1}(T)\ge 2\Delta +2$ and ${\lambda }_{3,2,1}(T)=2\Delta +3$, respectively. As a result, the $L(3,2,1)$-labeling numbers of complete m-ary trees, spiders and banana trees are completely determined.

2 Some sufficient conditions for the bounds

In this article, we always suppose that T is a tree with diameter at least 3. For an $L(3,2,1)$-labeling f of T and $S\subseteq V(T)$, we define $f(S)=\{f(v):v\in S\}$. A vertex u is said to be k-vertex if d(u) = k, where d(u) is the degree of u. Let $N_{\Delta }(u)=\{w\in N(u):w\text{ is }\Delta$-vertex $\}$ and $d_{\Delta }(u)$ be the cardinality of $N_{\Delta }(u)$.

For integers i and j with $i\le j$, we denote $[i,j]$ as the set $\{i,i+1,\dots ,j-1,j\}$. Let $O_{[i,j]}$ and $E_{[i,j]}$ be the set of all odd numbers and all even numbers in $[i,j]$, respectively.

A rooted tree T_u rooted at u is a tree in which one of the vertices (say u) is distinguished from the others. For a rooted tree T_u, define $L_i(u)=\{w\in V(T_u):\text{dist}(u,w)=i\}$ for $i=0,1,\dots$. In particular, $L_0(u)=\left\{u\right\}$.

Chia [3] studied the $L(3,2,1)$-labeling of trees and gave the following result.

Theorem 2.1.

[3] For any tree T, $2\Delta +1\le {\lambda }_{3,2,1}(T)\le 2\Delta +3$. Moreover, if ${\lambda }_{3,2,1}(T)=2\Delta +1$ and f is a $(2\Delta +1)$-$L(3,2,1)$-labeling of T, then $f(v)\in \{0,2\Delta +1\}$ for each Δ-vertex v. Furthermore, $f(N(v))=O_{[3,2\Delta +1]}$ if f(v) = 0 and $f(N(v))=E_{[0,2\Delta -2]}$ if $f(v)=2\Delta +1$.

Let $M(T)=\{u\in V(T):d(u)=\Delta \}$ and m(T) be the cardinality of M(T). It is not difficult to find that the $L(3,2,1)$-labeling number of a tree T is closely related to m(T) and the distance between any two vertices in M(T). In fact, we have the following result.

Theorem 2.2.

Let T be a tree with $m(T)\le 2$ and $d_{\Delta }(v)\le 1$ for all $v\in N(u)$, where $u\in M(T)$. Then ${\lambda }_{3,2,1}(T)=2\Delta +1$.

Proof.

Let $u\in M(T)$ and we think of T as a rooted tree T_u rooted at u. Firstly, ${\lambda }_{3,2,1}(T)\ge 2\Delta +1$ by Theorem 2.1. To prove the upper bound, a $(2\Delta +1)$-$L(3,2,1)$-labeling f of T is defined as follows.

1. f(u) = 0;

2. $f(N(x))\subseteq O_{[1,2\Delta +1]}\setminus \{f(x)\pm 1\}$ for each $x\in L_{2k}(u),k=0,1,2,\dots$;

3. $f(N(y))\subseteq E_{[0,2\Delta ]}\setminus \{f(y)\pm 1\}$ for each $y\in L_{2k-1}(u),k=1,2,\dots$.

Based on the above labeling f, the label 0 or $2\Delta +1$ is assigned to the Δ-vertex except u (if exists). This can be done since $m(T)\le 2$ and $d_{\Delta }(v)\le 1$ for all $v\in N(u)$, where $u\in M(T)$.

It is clear that any pair of vertices of distance at most 3 have different labels. Secondly, ${\mathrm{\text{min}}}_{\mathit{\text{xy}}\in E(T)}\left|f(x)-f(y)\right|\ge 3$. Finally, ${\mathrm{\text{min}}}_{x,y\in V(T),\mathit{\text{dist}}(x,y)=2}\left|f(x)-f(y)\right|\ge 2$. Therefore, f is a $(2\Delta +1)$-$L(3,2,1)$-labeling of T, which implies ${\lambda }_{3,2,1}(T)\le 2\Delta +1$. □

In the following, we provide some sufficient conditions for ${\lambda }_{3,2,1}(T)\ge 2\Delta +2$ based on the value of d(u) and $d_{\Delta }(u)$. It is proved in [12] that ${\lambda }_{3,2,1}(T)\ge 2\Delta +2$ if T contains a vertex u₀ satisfying that $d_{\Delta }(u_0)\ge 2$. Hence, the sufficient conditions for ${\lambda }_{3,2,1}(T)\ge 2\Delta +2$ we given below, always suppose $d_{\Delta }(u)\le 1$ for all $u\in V(T)$.

Theorem 2.3.

Let T_u be a rooted tree with $\Delta \ge 4$. If T_u contains one of the following configurations, then ${\lambda }_{3,2,1}(T_u)\ge 2\Delta +2$.

• (C1) $d(u)=\Delta ,d_{\Delta }(u)=0$ and $d_{\Delta }(w)=1$ for all $w\in L_1(u)\cup L_2(u)$.

• (C2) $d(u)=\Delta ,d(w)=\Delta -1$ for all $w\in L_1(u)\cup L_2(u)$ and $d_{\Delta }(w)=1$ for all $w\in L_3(u)$.

• (C3) $d(w)\ge \Delta -1$ for all $w\in L_0(u)\cup L_1(u)$ and $d_{\Delta }(w)=1$ for all $w\in L_0(u)\cup L_1(u)\cup L_2(u)$.

Proof.

Suppose for the contrary that ${\lambda }_{3,2,1}(T_u)=2\Delta +1$ and f is a $(2\Delta +1)$-$L(3,2,1)$-labeling of T_u. Now we will draw contradictions for different configurations (C1)–(C3), as shown in Figure 1.

Fig. 1 (a) for (C1), (b) for (C2), (c1) and (c2) for (C3) of Theorem 2.3. Throughout, the black dots represent Δ-vertices, the white dots represent $(\Delta -1)$-vertices and the rectangular dots represent any type of vertices.

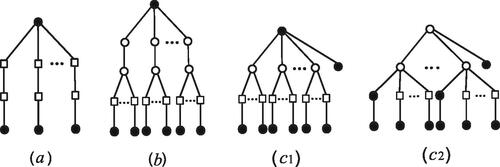
(C1) By Theorem 2.1, we have $f(u)\in \{0,2\Delta +1\}$ since $d(u)=\Delta$. If f(u) = 0, then $f(N(u))=O_{[3,2\Delta +1]}$ again by Theorem 2.1. Particularly, there must exist some $u_1\in N(u)$ satisfying that $f(u_1)=2\Delta +1$. But now no proper label can be assigned to $N_{\Delta }(w)$ for all $w\in N(u_1)\setminus \left\{u\right\}$. The case for $f(u)=2\Delta +1$ can be discussed similarly.

(C2) Without loss of generality, let f(u) = 0 and $f(N(u))=O_{[3,2\Delta +1]}$ by Theorem 2.1. Thus, for all $w\in L_1(u),f(N(w))=E_{[0,2\Delta ]}\setminus \{f(w)\pm 1\}$ if $f(w)\in O_{[3,2\Delta -1]}$ and $f(N(w))\subseteq E_{[0,2\Delta -2]}$ if $f(w)=2\Delta +1$ since $d(w)=\Delta -1$. This implies for all $w\in L_2(u),f(N(w))=O_{[1,2\Delta +1]}\setminus \{f(w)\pm 1\}$ in view of $d(w)=\Delta -1$. In particular, there must exist some $w_0\in L_3(u)$ such that $f(w_0)=1$. However, no label is available for $N_{\Delta }(w_0)$ since $f(N(w))=O_{[1,2\Delta +1]}\setminus \{f(w)\pm 1\}$ for all $w\in L_2(u)$.

(C3) In this case, we treat the following two cases to prove.

Case 1. $d(u)=\Delta$.

Let f(u) = 0 and $f(N(u))=O_{[3,2\Delta +1]}$ by Theorem 2.1. Then there must exist some $u_1\in L_1(u)$ such that $f(u_1)=3$. This implies $f(N(u_1)\setminus \{u\})=E_{[6,2\Delta ]}$ because of $d(u_1)=\Delta -1$. Assume $f(w_0)=2\Delta$ for some $w_0\in N(u_1)\setminus \left\{u\right\}$. But now there is no proper label for $N_{\Delta }(w_0)$.

Case 2. $d(u)=\Delta -1$.

Let $N_{\Delta }(u)=\left\{u_1\right\}$ since $d_{\Delta }(u)=1$. We may assume that $f(u_1)=0$, which implies $f(N(u_1))=O_{[3,2\Delta +1]}$ and $f(N_{\Delta }(u_1))=\{2\Delta +1\}$ by Theorem 2.1. So $f(u)\in O_{[3,2\Delta -1]}$ owing to $u\in N(u_1)$ and $d(u)=\Delta -1$. Next, if $f(u)\in O_{[3,2\Delta -3]}$, then $f(N(u))=E_{[0,2\Delta ]}\setminus \{f(u)\pm 1\}$. It means that there must exist some $w_0\in L_1(u)$ such that $f(w_0)=2\Delta$. But now there is no proper label for $N_{\Delta }(w_0)$. So $f(u)=2\Delta -1$ and $f(N(u))=E_{[0,2\Delta -4]}$. Hence $f(N(w))=O_{[1,2\Delta +1]}\setminus \{f(w)\pm 1\}$ for all $w\in L_1(u)\setminus \left\{u_1\right\}$. In particular, there must exist some $w_0\in L_2(u)$ such that $f(w_0)=1$. However, no feasible label is available for $N_{\Delta }(w_0)$ since $f(N(w))=O_{[1,2\Delta +1]}\setminus \{f(w)\pm 1\}$ for all $w\in L_1(u)$. □

The following lemma proved in [12] is useful.

Lemma 2.4.

[12] Let f be a $(2\Delta +2)$-$L(3,2,1)$-labeling of T. Then $f(v)\in O_{[1,2\Delta +1]}\cup \{0,2\Delta +2\}$ for each Δ-vertex v. Moreover, if v is a Δ-vertex and $f(v)\in O_{[1,2\Delta +1]}$, then $f(N(v))=E_{[0,2\Delta +2]}\setminus \{f(v)\pm 1\}$.

Based on Lemma 2.4, we now prove the following lemmas.

Lemma 2.5.

Let f be a $(2\Delta +2)$-$L(3,2,1)$-labeling of T. Then for any $u\in V(T),f(u)\notin \{1,2\Delta +1\}$ if $d_{\Delta }(u)\ge 2$. Furthermore, $f(u)\in E_{[0,2\Delta +2]}$ and $f(N(u))\subseteq O_{[1,2\Delta +1]}$ if $d_{\Delta }(u)\ge 3$.

Proof.

Suppose otherwise. Let $d_{\Delta }(u)\ge 2$ and $f(u)\in \{1,2\Delta +1\}$. Then $0\notin f(N_{\Delta }(u))$ or $2\Delta +2\notin f(N_{\Delta }(u))$. By Lemma 2.4, there must exist some $w_0\in N_{\Delta }(u)$ such that $f(w_0)\in O_{[1,2\Delta +1]}$ since $d_{\Delta }(u)\ge 2$. This implies $f(N(w_0))=E_{[0,2\Delta +2]}\setminus \{f(w_0)\pm 1\}$ again by Lemma 2.4. Note that $u\in N(w_0)$. So $f(u)\in E_{[0,2\Delta +2]}\setminus \{f(w_0)\pm 1\}$, which is impossible since $f(u)\in \{1,2\Delta +1\}$. Therefore, $f(u)\notin \{1,2\Delta +1\}$ if $d_{\Delta }(u)\ge 2$.

If $d_{\Delta }(u)\ge 3$, then there must exist some $w_0\in N_{\Delta }(u)$ such that $f(w_0)\in O_{[1,2\Delta +1]}$. So $f(N(w_0))=E_{[0,2\Delta +2]}\setminus \{f(w_0)\pm 1\}$. Thus $f(u)\in E_{[0,2\Delta +2]}$. This implies $f(N(u))\subseteq O_{[1,2\Delta +1]}$ owing to $f(N(w_0))=E_{[0,2\Delta +2]}\setminus \{f(w_0)\pm 1\}$. □

Lemma 2.6.

Let f be a $(2\Delta +2)$-$L(3,2,1)$-labeling of T. Let $\mathit{\text{uv}}\in E(T),d(u_1)=d(v_1)=\Delta -1$ and $\mathrm{\text{min}}\{d_{\Delta }(u_1),d_{\Delta }(v_1)\}\ge 3$, where $u_1\in N(u)\setminus \left\{v\right\},v_1\in N(v)\setminus \left\{u\right\}$. Then $d_{\Delta }(u)=d_{\Delta }(v)=0$ and $d(u)+d(v)\le \Delta$. Furthermore, for any $w\in N(u)\setminus \{v,u_1\},d(w)\le \Delta -2$ when $d_{\Delta }(w)\ge 3$.

Proof.

According to Lemma 2.5, we have $f(u_1),f(v_1)\in E_{[0,2\Delta +2]}$ and $f(N(u_1))\subseteq O_{[1,2\Delta +1]}$ and $f(N(v_1))\subseteq O_{[1,2\Delta +1]}$ by the fact that $\mathrm{\text{min}}\{d_{\Delta }(u_1),d_{\Delta }(v_1)\}\ge 3$. Thus $f(u),f(v)\in O_{[1,2\Delta +1]}$ owing to $u\in N(u_1),v\in N(v_1)$. Secondly, if $f(u_1)\in E_{[2,2\Delta ]}$, then $f(N(u_1))=O_{[1,2\Delta +1]}\setminus \{f(u_1)\pm 1\}$ since $d(u_1)=\Delta -1$. But no label is available for v, a contradiction. So $f(u_1)\in \{0,2\Delta +2\}$. A similar argument can be made for $f(v_1)$. Thus $\{f(u_1),f(v_1)\}=\{0,2\Delta +2\}$. This implies $f(N(u_1))=O_{[1,2\Delta +1]}\setminus \{f(u_1)\pm 1,f(v)\}$ and $f(N(v_1))=O_{[1,2\Delta +1]}\setminus \{f(v_1)\pm 1,f(u)\}$ in view of $d(u_1)=d(v_1)=\Delta -1$. From this one can see that $f(N(u)\setminus \{v\})\subseteq E_{[2,2\Delta ]}$ and $f(N(v)\setminus \{u\})\subseteq E_{[2,2\Delta ]}$. So $d_{\Delta }(u)=d_{\Delta }(v)=0$ by Lemma 2.4. On the other hand, $f((N(u)\cup N(v))\setminus \{u,v\})\subseteq E_{[0,2\Delta +2]}\setminus \{f(u)\pm 1,f(v)\pm 1\}$ since $f(N(u_1))=O_{[1,2\Delta +1]}\setminus \{f(u_1)\pm 1,f(v)\}$ and $f(N(v_1))=O_{[1,2\Delta +1]}\setminus \{f(v_1)\pm 1,f(u)\}$. So $d(u)+d(v)-2\le (\Delta +2)-4$. Therefore, $d(u)+d(v)\le \Delta$.

Finally, suppose for the contrary that $d_{\Delta }(w_0)\ge 3$ and $d(w_0)\ge \Delta -1$ for some $w_0\in N(u)\setminus \{v,u_1\}$. In the same fashion, one can prove that $f(w_0)\in \{0,2\Delta +2\}$. It is a contraction to $\{f(u_1),f(v_1)\}=\{0,2\Delta +2\}$. Thus, for any $w\in N(u)\setminus \{v,u_1\},d(w)\le \Delta -2$ when $d_{\Delta }(w)\ge 3$. □

Inspired by the similar results proved for the L(2, 1)-labeling numbers of trees by Griggs and Yeh in [5], we give some sufficient conditions for ${\lambda }_{3,2,1}(T)=2\Delta +3$. The methods used in proofs, although elementary, give a deeper understanding what forces the $L(3,2,1)$-labeling number to be equal to $2\Delta +3$.

Theorem 2.7.

[12] Let $u\in V(T)$ and $\mathit{\text{uv}}\in E(T)$.

1. If $\mathrm{\text{min}}\{d_{\Delta }(u),d_{\Delta }(v)\}\ge 3$, then ${\lambda }_{3,2,1}(T)=2\Delta +3$.

2. If $d(u)\ge \Delta -1,d_{\Delta }(u)\ge 3$ and $d_{\Delta }(u_i)=2$ for all $u_i\in N(u)$, then ${\lambda }_{3,2,1}(T)=2\Delta +3$.

Theorem 2.8.

Let $\mathit{\text{uv}}\in E(T)$. If $\mathrm{\text{min}}\{d(u),d(v)\}\ge \Delta -1$ and $d_{\Delta }(w)\ge 2$ for all $w\in N(u)\cup N(v)$, then ${\lambda }_{3,2,1}(T)=2\Delta +3$.

Proof.

Assume that T admits a $(2\Delta +2)$-$L(3,2,1)$ -labeling f. Now we treat the following three cases, as shown in Figure 2, to prove.

Fig. 2 (a1), (a2), and (a3) for the three cases of Theorem 2.8.

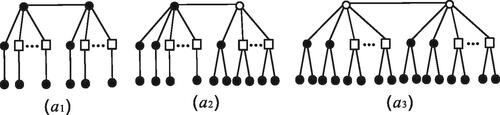
Case 1. $d(u)=d(v)=\Delta$.

Let $\{v,u_1\}\subseteq N_{\Delta }(u)$. By Lemma 2.5, we have $f(u)\notin \{1,2\Delta +1\}$ since $d_{\Delta }(u)\ge 2$. Now we assume that $f(u)\in O_{[3,2\Delta -1]}$. Then $f(N(u))=E_{[0,2\Delta +2]}\setminus \{f(u)\pm 1\}$ and $f(N_{\Delta }(u))=\{0,2\Delta +2\}$ by Lemma 2.4. Without loss of generality, let $f(v)=0,f(u_1)=2\Delta +2$. Then $f(N(v))=O_{[3,2\Delta +1]}$ since $f(N(u))=E_{[0,2\Delta +2]}\setminus \{f(u)\pm 1\}$. Particularly, there must exist some $w_0\in N(v)\setminus \left\{u\right\}$ such that $f(w_0)=2\Delta +1$. This contradicts to $d_{\Delta }(w_0)\ge 2$. Therefore, $f(u)\in \{0,2\Delta +2\}$. Similarly, $f(v)\in \{0,2\Delta +2\}$. Next, we suppose that $f(u)=0,f(v)=2\Delta +2$. This implies $f(u_1)\in O_{[3,2\Delta -1]}$ by Lemma 2.4. Then $f(N_{\Delta }(u_1))=\{0,2\Delta +2\}$, which contradicts to $f(v)=2\Delta +2$.

Case 2. $d(u)=\Delta ,d(v)=\Delta -1$ or $d(u)=\Delta -1,d(v)=\Delta$.

It suffices to prove this for $d(u)=\Delta ,d(v)=\Delta -1$ due to the symmetry. Let $\{u_1,u_2\}\subseteq N_{\Delta }(u),\{u,v_1\}\subseteq N_{\Delta }(v)$. Note that $f(u)\notin \{1,2\Delta +1\}$. If $f(u)\in O_{[3,2\Delta -1]}$, then $f(N(u))=E_{[0,2\Delta +2]}\setminus \{f(u)\pm 1\}$ and $f(N_{\Delta }(u))=\{0,2\Delta +2\}$ by Lemma 2.4. So $f(v)\in E_{[2,2\Delta ]}$ since $v\in N(u)$ and $d(v)=\Delta -1$. Thus $f(N(v))\subseteq [0,2\Delta +2]\setminus \{f(v),f(v)\pm 1,f(v)\pm 2\}$. On the other hand, $0,2\Delta +2\notin f(N(v))$ since $f(N_{\Delta }(u))=\{0,2\Delta +2\}$. Therefore, $f(N(v))=O_{[1,2\Delta +1]}\setminus \{f(v)\pm 1\}$ since $d(v)=\Delta -1$. In particular, there must exist some $w_0\in N(v)\setminus \left\{u\right\}$ such that $f(w_0)=1$ or $2\Delta +1$. This contradicts to $d_{\Delta }(w_0)\ge 2$. Therefore, $f(u)\in \left\{0,2\Delta +2\right\}$. Similarly, we can prove that $f(v_1)\in \{0,2\Delta +2\}$. Let f(u) = 0 and $f(v_1)=2\Delta +2$. This means $f(u_1)\in O_{[1,2\Delta +1]}$ and $f(N(u_1))=E_{[0,2\Delta +2]}\setminus \{f(u_1)\pm 1\}$. It follows that $f(N(u))=O_{[3,2\Delta +1]}$. Clearly, there must exist some $w_0\in N(u)\setminus \left\{v\right\}$ such that $f(w_0)=2\Delta +1$, again a contradiction to $d_{\Delta }(w_0)\ge 2$.

Case 3. $d(u)=d(v)=\Delta -1$.

Let $\{u_1,u_2\}\subseteq N_{\Delta }(u),\{v_1,v_2\}\subseteq N_{\Delta }(v)$. Firstly, note that $f(u_i),f(v_i)\notin \{1,2\Delta +1\}$ for i = 1, 2. Secondly, suppose $f(u_1)\in O_{[3,2\Delta -1]}$, then $f(N(u_1))=E_{[0,2\Delta +2]}\setminus \{f(u_1)\pm 1\}$ and $f(N_{\Delta }(u_1))=\{0,2\Delta +2\}$ by Lemma 2.4. So $f(u_2)\in O_{[3,2\Delta -1]}$. By a similar argument, if $f(v_1)\in O_{[3,2\Delta -1]}$, then $f(v_2)\in O_{[3,2\Delta -1]}$. We now treat the following two subcases.

Case 3.1. $f(u_1),f(u_2)\in O_{[3,2\Delta -1]}$ and $f(v_1),f(v_2)\in O_{[3,2\Delta -1]}$.

In this case, $f(N_{\Delta }(u_i))=\{0,2\Delta +2\}$ and $f(N_{\Delta }(v_i))=\{0,2\Delta +2\}$ since $f(N(u_i))=E_{[0,2\Delta +2]}\setminus \{f(u_i)\pm 1\}$ and $f(N(v_i))=E_{[0,2\Delta +2]}\setminus \{f(v_i)\pm 1\}$ for i = 1, 2. So $f(N(u)\cup N(v))\subseteq [0,2\Delta +2]\setminus \{0,2\Delta +2,f(u)\pm 1,f(v)\pm 1\}$. Thus $\left|f(N(u)\cup N(v))\right|\le (2\Delta +3)-6=2\Delta -3$, a contradiction to $d(u)=d(v)=\Delta -1$.

Case 3.2. $f(u_1),f(u_2)\in \{0,2\Delta +2\}$ and $f(v_1),f(v_2)\in O_{[3,2\Delta -1]}$.

Notice that $f(N(v_1))=E_{[0,2\Delta +2]}\setminus \{f(v_1)\pm 1\}$ in view of $f(v_1)\in O_{[3,2\Delta -1]}$. So $f(v)\in E_{[2,2\Delta ]}$ owing to $v\in N(v_1)$ and $f(u_1),f(u_2)\in \{0,2\Delta +2\}$. Then $f(N(v))\subseteq [0,2\Delta +2]\setminus \{f(v),f(v)\pm 1,f(v)\pm 2\}$. On the other hand, $0,2\Delta +2\notin f(N(v))$ since $\{f(u_1),f(u_2)\}=\{0,2\Delta +2\}$. Therefore, $f(N(v))=O_{[1,2\Delta +1]}\setminus \{f(v)\pm 1\}$ since $d(v)=\Delta -1$. Particularly, there must exist some $w_0\in N(v)\setminus \left\{u\right\}$ such that $f(w_0)=1$ or $2\Delta +1$. This contradicts to $d_{\Delta }(w_0)\ge 2$. □

Theorem 2.9.

Let $\mathit{\text{uv}}\in E(T)$. If $d(u)\ge \Delta -1$ and $d_{\Delta }(v_1)\ge 3,d_{\Delta }(u_i)\ge 2$ for some $v_1\in N(v)\setminus \left\{u\right\}$ and all $u_i\in N(u)$, then ${\lambda }_{3,2,1}(T)=2\Delta +3$.

Proof.

On the contrary, that f is a $(2\Delta +2)$-$L(3,2,1)$-labeling of T. By Lemma 2.5, $f(N(v_1))\subseteq O_{[1,2\Delta +1]}$ since $d_{\Delta }(v_1)\ge 3$. So $f(v)\in O_{[1,2\Delta +1]}$ in view of $v\in N(v_1)$. Thus $f(N_{\Delta }(v))=\{0,2\Delta +2\}$ by Lemma 2.4. We treat the following two cases.

Case 1. $d(u)=\Delta$.

As $u\in N_{\Delta }(v),f(u)\in \{0,2\Delta +2\}$. If f(u) = 0, then $f(N(u))=O_{[3,2\Delta +1]}$ in view of $f(v)\in O_{[1,2\Delta +1]}$. Particularly, there must exist some $w_0\in N(u)\setminus \left\{v\right\}$ such that $f(w_0)=2\Delta +1$, a contradiction to $d_{\Delta }(w_0)\ge 2$. The case for $f(u)=2\Delta +2$ can be discussed similarly.

Case 2. $d(u)=\Delta -1$.

In this case, $f(u)\in [2,2\Delta ]$. Now if $f(u)\in O_{[3,2\Delta -1]}$, then $f(N(u))\subseteq [1,2\Delta +1]\setminus \{f(u),f(u)\pm 1,f(u)\pm 2\}$. So $\left|f(N(u))\right|\le \frac{2\Delta +1-5}{2}=\Delta -2$, a contradiction to $d(u)=\Delta -1$. Thus $f(u)\in E_{[2,2\Delta ]}$ and $f(N(u))\subseteq [0,2\Delta +2]\setminus \{f(u),f(u)\pm 1,f(u)\pm 2\}$. On the other hand, $0,2\Delta +2\notin f(N(u))$ since $f(N_{\Delta }(v))=\{0,2\Delta +2\}$. Hence $f(N(u))=O_{[1,2\Delta +1]}\setminus \{f(u)\pm 1\}$ since $d(u)=\Delta -1$. Particularly, there must exist some $w_0\in N(u)\setminus \left\{v\right\}$ such that $f(w_0)=1$ or $2\Delta +1$. This contradicts to $d_{\Delta }(w_0)\ge 2$. □

Theorem 2.10.

Let $\mathit{\text{uv}}\in E(T)$ and $\mathrm{\text{min}}\{d_{\Delta }(u_1),d_{\Delta }(v_1)\}\ge 3$, where $u_1\in N(u)\setminus \left\{v\right\},v_1\in N(v)\setminus \left\{u\right\}$. If T contains the following configurations, then ${\lambda }_{3,2,1}(T)=2\Delta +3$.

• (C1) $\mathrm{\text{max}}\{d(u),d(v)\}=\Delta$ or $\mathrm{\text{max}}\{d(u_1),d(v_1)\}=\Delta$.

• (C2) $d(u_1)=d(u_2)=d(v_1)=\Delta -1$ and $d_{\Delta }(u_2)\ge 3$ for some $u_2\in N(u)\setminus \{v,u_1\}$.

• (C3) $d(u_1)=d(v_1)=\Delta -1,d(u)+d(v)\ge \Delta +1$.

• (C4) $d(u)=d(v)=\Delta -1,d(u_1)+d(v_1)\ge \Delta +3$.

Proof.

Suppose f is a $(2\Delta +2)$-$L(3,2,1)$-labeling of T. By Lemma 2.5, we have $f(u),f(v)\in O_{[1,2\Delta +1]}$ owing to $\mathrm{\text{min}}\{d_{\Delta }(u_1),d_{\Delta }(v_1)\}\ge 3$.

(C1) We may assume that $d(u)=\Delta$ when $\mathrm{\text{max}}\{d(u),d(v)\}=\Delta$. Thus we have $f(N(u))=E_{[0,2\Delta +2]}\setminus \{f(u)\pm 1\}$ by Lemma 2.4. But this is impossible since $v\in N(u)$ and $f(v)\in O_{[1,2\Delta +1]}$. Secondly, suppose $d(u_1)=\Delta$ when $\mathrm{\text{max}}\{d(u_1),d(v_1)\}=\Delta$. Then $f(u_1)\in \{0,2\Delta +2\}$ by Lemmas 2.4 and 2.5. Without loss of generality, let $f(u_1)=0$. Hence $f(N(u_1))=O_{[3,2\Delta +1]}$. This implies $f(v)\in E_{[0,2\Delta +2]}$. But it contradicts to $f(v)\in O_{[1,2\Delta +1]}$.

(C2) By Lemma 2.6, we have $d(u_2)\le \Delta -2$ owing to $d_{\Delta }(u_2)\ge 3$ for some $u_2\in N(u)\setminus \{v,u_1\}$. But this contradicts to $d(u_2)=\Delta -1$.

(C3) This is a direct consequence of Lemma 2.6.

(C4) Firstly, $f(u)\pm 1,f(v)\pm 1\notin f(N(u)\cup N(v))$. Let $a=\left|\{f(x)\in O_{[1,2\Delta +1]}:x\in N(u)\}\right|$ and $b=\left|\{f(x)\in O_{[1,2\Delta +1]}:x\in N(v)\}\right|$. Hence $a+b\ge d(u)+d(v)-(\Delta +2-4)=\Delta$. On the other hand, $d(u_1)\le \Delta +1-a$ and $d(v_1)\le \Delta +1-b$ since $f(N(u_1))\subseteq O_{[1,2\Delta +1]}$ and $f(N(v_1))\subseteq O_{[1,2\Delta +1]}$. So $d(u_1)+d(v_1)\le 2\Delta +2-(a+b)\le \Delta +2$. This contradicts to $d(u_1)+d(v_1)\ge \Delta +3$. □

3 $L(3,2,1)$-labeling of complete m-ary trees, spiders and banana trees

Motivated by the sufficient conditions shown in Section 2, the $L(3,2,1)$-labeling numbers of complete m-ary trees, spiders and banana trees are completely determined in this section.

Theorem 3.1.

[4] For a path P_n on n vertices with $n\ge 8,{\lambda }_{3,2,1}(P_n)=7$.

The above result is known, but it can be easily derived from Theorem 2.8.

A complete m-ary tree $(m\ge 2)$ is a rooted tree such that each vertex of degree greater than one has exactly m children and all degree-one vertices are of equal distance (height) to the root. Denote by $T_{m,h}$a complete m-ary tree of the height h. It can be seen that $T_{m,h}$ has the maximum degree $\Delta =m+1$ for $h\ge 2$.

Clipperton [4] studied the $L(3,2,1)$-labeling of complete m-ary trees and obtained ${\lambda }_{3,2,1}(T_{m,h})=2m+5$ for any complete m-ary tree $T_{m,h}$. In fact, ${\lambda }_{3,2,1}(T_{m,h})\ne 2m+5$ when m = 2 and h = 3. Next, we correct and prove it in the following.

Theorem 3.2.

Let $T_{m,h}$ be a complete m-ary tree of height $h\ge 3$. Then $${\lambda }_{3,2,1}(T_{m,h})=\{\begin{array}{ccc}8,\hfill & \hfill & \text{if }m=2\text{ and }h=3,\hfill \\ 2m+5,\hfill & \hfill & \text{otherwise}.\hfill \end{array}$$

Proof.

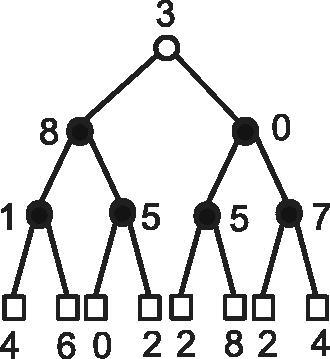
For the case m = 2 and h = 3, we have ${\lambda }_{3,2,1}(T_{2,3})\ge 2(2+1)+2=8$ since T contains a vertex u with $d_{\Delta }(u)=2$. Secondly, a 8-$L(3,2,1)$-labeling is given in Figure 3, which means ${\lambda }_{3,2,1}(T_{2,3})\le 8$. So ${\lambda }_{3,2,1}(T_{2,3})=8$.

Fig. 3 A 8-$L(3,2,1)$-labeling of $T_{2,3}$.

For m = 2 and $h\ge 4$, there exists $\mathit{\text{uv}}\in E(T_{2,h})$ such that $d(u)=\Delta -1$ and $d_{\Delta }(v_1)=3,d_{\Delta }(u_i)=2$ for some $v_1\in N(v)\setminus \left\{u\right\}$ and all $u_i\in N(u)$. Hence ${\lambda }_{3,2,1}(T_{2,h})=2(2+1)+3=9$ by Theorem 2.9.

When $m\ge 3$, there exists $\mathit{\text{uv}}\in E(T_{m,h})$ such that $d_{\Delta }(u)=d_{\Delta }(v)=3$. Therefore, ${\lambda }_{3,2,1}(T_{m,h})=2(m+1)+3=2m+5$ by Theorem 2.7. □

A spider is a tree with at most one vertex of degree more than two, called the center of spider (if no vertex of degree more than two, then any vertex can be the center). Thus a spider with Δ = 2 is a path. If $\Delta \ge 3$, then m(T) = 1. By Theorem 2.2, we have the following result.

Theorem 3.3.

Let T be a spider with $\Delta \ge 3$. Then ${\lambda }_{3,2,1}(T)=2\Delta +1$.

A banana tree is a tree obtained by connecting a new vertex u to one leaf of each of any number of stars (u is not in any of the stars). Murugan [7] considered the $L(3,2,1)$-labeling numbers of banana trees and obtained ${\lambda }_{3,2,1}(B_{n,t})=2n+1$ when t < n and ${\lambda }_{3,2,1}(B_{n,t})=2t+3$ when $t\ge n$ for any banana tree $B_{n,t}$ with t copies of $K_{1,n}$. Actually, ${\lambda }_{3,2,1}(B_{n,t})\ne 2t+3$ when $t\ge n$. Now we correct and prove it in the following.

Theorem 3.4.

Let $B_{n,t}$ be a banana tree with t copies of $K_{1,n}$. Then $${\lambda }_{3,2,1}(B_{n,t})=\{\begin{array}{ccc}2\mathrm{\text{max}}\{n,t\}+1,\hfill & \hfill & \text{if }n\ne t,\hfill \\ 2n+2,\hfill & \hfill & \text{otherwise}.\hfill \end{array}$$

Proof.

Let u be the new vertex. For n < t, we have $M(B_{n,t})=\left\{u\right\}$. Hence ${\lambda }_{3,2,1}(B_{n,t})=2t+1$ by Theorem 2.2. For n > t, ${\lambda }_{3,2,1}(B_{n,t})\ge 2n+1$ by Theorem 2.1. Next, consider the following labeling f:

1. f(u) = 2;

2. $f(N(u))=O_{[5,2t+3]}$;

3. $f(N(x)\setminus \{u\})=\left\{0\right\}$ for each $x\in L_1(u)$;

4. $f(N(y))=O_{[3,2n+1]}$ for each $y\in L_2(u)$.

It is straightforward to check that f is a $(2n+1)$-$L(3,2,1)$-labeling of $B_{n,t}$. Thus ${\lambda }_{3,2,1}(B_{n,t})=2n+1$.

For the case n = t. There exists $u\in V(B_{n,t})$ such that $d_{\Delta }(u)=2$. Hence ${\lambda }_{3,2,1}(B_{n,t})\ge 2n+2$. On the other hand, a $(2n+2)$-$L(3,2,1)$-labeling f of $B_{n,t}$ is defined as follows.

1. f(u) = 1;

2. $f(N(u))=E_{[4,2n+2]}$;

3. $f(N(x)\setminus \{u\})=\{2n+5-f(x)\}$ for each $x\in L_1(u)$;

4. $f(N(y))=E_{[0,2n+2]}\setminus \{f(y)\pm 1\}$ for each $y\in L_2(u)$.

It is evident that f is a $(2n+2)$-$L(3,2,1)$-labeling of $B_{n,t}$, which implies ${\lambda }_{3,2,1}(B_{n,t})=2n+2$. □

4 Concluding remarks

Motivated by channel assignment problem, the graph labeling problem, especially the $L(3,2,1)$-labeling problem has attracted much attention. It was known in [3] that the $L(3,2,1)$-labeling number of a tree T with maximum degree Δ can have one of three values: $2\Delta +1,2\Delta +2$ and $2\Delta +3$. Furthermore, providing some sufficient conditions for the bounds or giving a characterization result for trees becomes a meaningful topic. Based on the above topics, this paper gives some sufficient conditions for ${\lambda }_{3,2,1}(T)\ge 2\Delta +2$ and ${\lambda }_{3,2,1}(T)=2\Delta +3$, respectively. As a result, the $L(3,2,1)$-labeling numbers of complete m-ary trees, spiders and banana trees are completely determined.

Acknowledgments

The authors would like to thank the anonymous referees for careful reading and comments.

Code availability

Not applicable.

Disclosure statement

The authors declare that they have no conflict of interest.

Data availability statement

Not applicable.

Additional information

Funding

This research is supported by the National Natural Science Foundation of China (Grant No. 11601265, 12271210) and Scientific Research Foundation of Jimei University (Grant No. Q202201).