On the maximum atom-bond sum-connectivity index of molecular trees

Abstract

Let G be a graph with V(G) and E(G), as vertex set and edge set, respectively. The atom-bond sum-connectivity (ABS) index is a vertex-based topological index which is defined as $\mathit{\text{ABS}}(G)=\sum _{\mathit{\text{ab}}\in E(G)}\sqrt{\frac{{\varrho }_a+{\varrho }_b-2}{{\varrho }_a+{\varrho }_b}},$ where ${\varrho }_a$ is the degree of the vertex a. In this paper, we obtain sharp upper bounds for the ABS index of molecular trees in terms of order and number of branching vertices and vertices of degree two.

Keywords:

• The atom-bond sum-connectivity index
• molecular trees

AMS Subject Classification:

• 05C07
• 05C90
• 05C92

1 Introduction

In this article, we are only concerned with a simple, connected, and undirected graph denoted by G that has a vertex set denoted by V(G) and an edge set denoted by E(G). Degree of a vertex u is the number of edges adjacent to the vertex u, denoted by ${\varrho }_u$.

Let ${\varrho }_1\ge {\varrho }_2\ge \dots \ge {\varrho }_n>0$, be the degree sequence of G. A vertex a is called a pendent vertex or a branching vertex if ${\varrho }_a=1$ or ${\varrho }_a\ge 3$, respectively.

Let t_j denotes the count of vertices having degree j in the graph G. Denote by $h_{r,s}$ the cardinality of the set consisting of the edges connecting the vertex of degree i with the vertex of degree j in the graph G.

Let $P:x_1{x}_2\dots x_l(l\ge 3)$ be a path, denoted by vertices $x_2,x_3,\dots ,x_{l-1}$ internal vertex of P. A path from a branching vertex of degree a to a branching vertex of degree b in a molecular tree M, denoted by P(a, b), such that all the internal vertices (if exist) of P(a, b) have degree two.

Topological indices are numerical variables that describe the topology of a graph and are typically graph invariant. It may be analytically deduced directly from a molecule’s structural layout.

An alternative to the atom-bond connectivity index (6(6) $$\sum _{1\le k\le 4,l\ne k}{h}_{k,l}(M)+2h_{k,k}(M)=k{t}_k,\text{with} k=1,2,3,4.$$(6) ) that incorporates the basic idea of the sum-connectivity index (11(11) $$t_1(M_b)-2t_4(M_b)=2.$$(11) ) is the atom-bond sum-connectivity (ABS) index (1(1) $$M_p=\{M\in M(n,t_b):t_2(M)=0 \text{and} t_3(M)\ge 0\},$$(1) ). The definition of the ABS index is $$\mathit{\text{ABS}}(G)=\sum _{\mathit{\text{uv}}\in E(G)}\sqrt{\frac{{\varrho }_u+{\varrho }_v-2}{{\varrho }_u+{\varrho }_v}}=\sum _{\mathit{\text{uv}}\in E(G)}\sqrt{1-\frac{2}{{\varrho }_u+{\varrho }_v}}.$$

The ABS index is a topological index that is based on the degree of the vertices, but it can also be thought of as a topological index that is based on the degree of the edges due to the fact that the degree of the edge $\mathit{\text{uv}}\in E(G)$ is represented by the number ${\varrho }_u+{\varrho }_v-2$. Due to the fact that this index has recently been introduced, it has attracted the attention of many researchers and many articles have been published.

In (13(13) $$h_{4,4}(M_b)=0.$$(13) ), presented the extremal ABS index of chemical trees, unicyclic, bicyclic, and tricyclic graphs. Unicyclic graphs as one of the great classes can exhibit various chemical structures as well, extremal unicyclic graphs graphs have been found in (3(3) $$n=t_1(M)+t_2(M)+t_3(M)+t_4(M),$$(3) ). Studied ABS index general graphs and trees in terms of a fixed order have been found in (1(1) $$M_p=\{M\in M(n,t_b):t_2(M)=0 \text{and} t_3(M)\ge 0\},$$(1) ). Extremal ABS index of graphs with givwn the number of pendent vertices have been studied in (5(5) $$t_b=t_3(M)+t_4(M).$$(5) ). In (9(9) $$t_4(M_b)\le t_2(M_b).$$(9) ), presented the minimum ABS index of trees in terms of number of pendent vertices. For the recent results on the mathematical properties of ABS index can be seen in (4, 7, 8, 10, 12).

In this paper, we will obtain the sharp upper bounds for the ABS index of molecular trees with given branching vertices or vertices of degree two.

2 Auxiliary results

In this section, we state and prove some lemmas that will help us in proving the main results.

The proof of the following result is obvious using derivation, so we omit it from the proof here.

Lemma 1.

Suppose a and b are positive numbers, then for a > b, the following function is strictly decreasing on t and for b > a is strictly increasing on t. $$l(t)=\sqrt{1-\frac{2}{t+b}}-\sqrt{1-\frac{2}{t+a}}.$$

It should be noted that throughout this section the molecular trees M and $M\prime$ have the same degree sequence.

Lemma 2.

Suppose M be a molecular tree that is contains a path $P(4,4):b_1{b}_2\dots b_s$ and an edge xy with ${\varrho }_x=1$ and ${\varrho }_y=3$ such that b₁ lies on the path $y-b_s$. Let $M\prime$ be a molecular tree that obtained from M by removing the edges $b_1{b}_2,\mathit{\text{xy}}$ and create the new edges $b_{2}y,b_{1}x$. Then, $\mathit{\text{ABS}}(M)<\mathit{\text{ABS}}(M\prime )$.

Proof.

By the definition ABS index, we have $$\begin{array}{c}\mathit{\text{ABS}}(M)-\mathit{\text{ABS}}(M\prime )=\sqrt{1-\frac{2}{4}}-\sqrt{1-\frac{2}{5}}\\ \hspace{1em}+\sqrt{1-\frac{2}{2+{\varrho }_{b_2}}}-\sqrt{1-\frac{2}{3+{\varrho }_{b_2}}}<0.\end{array}$$

□

Lemma 3.

Suppose M be a molecular tree with $h_{1,3}(M)>0$, such that M contains the paths $P(4,3):a_1{a}_2\dots a_k$ and $P\prime (4,3):a_k{a}_{k+1}\dots a_{l-1}{a}_l$, with $k\ge 2,l\ge 3$, and k < l. Let $M\prime$ is obtained with $h_{1,3}(M\prime )<h_{1,3}(M)$. Then $\mathit{\text{ABS}}(M)<\mathit{\text{ABS}}(M\prime )$.

Proof.

If $\mathit{\text{ab}}\in E(M)$ with ${\varrho }_a=1$ and ${\varrho }_b=3$. Therefore, to complete the proof, we need to check the following cases.

Case 1. $l\le 4$.

We know that one of two ways paths P(4, 3) and $P\prime (4,3)$ have exactly one internal vertex while the other does not internal vertex. Here, we let k = 2, when l = 3, then by taking $M\prime =M-\{\mathit{\text{ab}},a_1{a}_2,a_2{a}_3\}+\{a_1{a}_3,a{a}_2,a_{2}b\}$, and when $l=4$, we setting $M\prime =M-\{a_1{a}_2,a_3{a}_4,\mathit{\text{ab}}\}+\{a_1{a}_4,a{a}_2,a_{3}b\}$. It can be easily seen that in both cases, M and $M\prime$ have the same degree sequence with $h_{1,3}(M\prime )<h_{1,3}(M)$, and $$\begin{array}{c}\mathit{\text{ABS}}(M)-\mathit{\text{ABS}}(M\prime )=\sqrt{1-\frac{2}{7}}+\sqrt{1-\frac{2}{4}}\\ \hspace{1em}-\sqrt{1-\frac{2}{6}}-\sqrt{1-\frac{2}{5}}<0\end{array}$$ as required.

Case 2. l > 4.

When k = 2 or $k=l-1$, with an argument similar to Case 1, the results are obtained. So, we let that $2<k<l-2$. If l = 5 then (k = 3 and) we setting $M\prime =M-\{a_2{a}_3,a_4{a}_5,\mathit{\text{ab}}\}+\{a_2{a}_5,a_{3}a,a_{4}b\}$, and otherwise (that is, if $l\ge 6$) then, we let $M\prime =M-\{a_2{a}_3,a_{k-1}{a}_k,a_{l-1}{a}_l,\mathit{\text{ab}}\}+\{a_2{a}_l,a{a}_k,a_{l-1}{a}_3,a_{k-1}b\}$. It can be easily seen that in both cases, M and $M\prime$ have the same degree sequence, such that $h_{1,3}(M\prime )<h_{1,3}(M)$, and $$\mathit{\text{ABS}}(M)-\mathit{\text{ABS}}(M\prime )=\sqrt{1-\frac{2}{4}}+\sqrt{1-\frac{2}{6}}-2\sqrt{1-\frac{2}{5}}<0.$$

□

By using the definition and by direct calculation, we arrive at the proof of the following lemma, so here we state this lemma without proof.

Lemma 4.

Suppose M be a molecular tree such that $\mathit{\text{ef}},\mathit{\text{ab}},\mathit{\text{yc}}\in E(M)$ with ${\varrho }_a=1,{\varrho }_e=3={\varrho }_f,{\varrho }_b={\varrho }_f={\varrho }_c=4$, and y lies on one of the three paths $a-c,e-c,f-c$, and also, $h_{1,3}(M)=0$. When $N_M(c)=\{w,c_1,c_2,c_3\}$ and $M\prime =M-\{\mathit{\text{ef}},c_{1}c,c_{2}c,c_{3}c,\mathit{\text{ab}}\}+\{\mathit{\text{ea}},\mathit{\text{af}},c_{1}a,c_{2}a,c_{3}b\}$. Then, $\mathit{\text{ABS}}(M)<\mathit{\text{ABS}}(M\prime )$.

Lemma 5.

Suppose M be a molecular tree such that $\mathit{\text{ab}},c\prime y,\mathit{\text{yc}}\in E(M)$ with ${\varrho }_y=2,\mathrm{\text{min}}\{{\varrho }_a,{\varrho }_b,{\varrho }_c,{\varrho }_{c\prime }\}\ge 3$ and ${\varrho }_a+{\varrho }_b>{\varrho }_c+{\varrho }_{c\prime }$. If $M\prime =M-\{\mathit{\text{ab}},c\prime y,\mathit{\text{yc}}\}+\{c\prime c,\mathit{\text{ay}},\mathit{\text{yb}}\}$, then, $\mathit{\text{ABS}}(M)<\mathit{\text{ABS}}(M\prime )$.

Proof.

Since two trees M and $M\prime$ have the same degree sequence, then using the definition ABS index, we have $$\begin{array}{c}\mathit{\text{ABS}}(M)-\mathit{\text{ABS}}(M\prime )=\sqrt{1-\frac{2}{{\varrho }_a+{\varrho }_b}}+\sqrt{1-\frac{2}{2+{\varrho }_{c\prime }}}\\ \hspace{1em}+\sqrt{1-\frac{2}{2+{\varrho }_c}}-\sqrt{1-\frac{2}{2+{\varrho }_b}}\\ \hspace{1em}-\sqrt{1-\frac{2}{2+{\varrho }_a}}-\sqrt{1-\frac{2}{{\varrho }_c+{\varrho }_{c\prime }}}\\ =Y.\end{array}$$

We know that ${\varrho }_a+{\varrho }_b\in \{7,8\}$, hence, there are two cases.

1. When ${\varrho }_a+{\varrho }_b=8$, we have ${\varrho }_a=4={\varrho }_b$ and hence ${\varrho }_c+{\varrho }_{c\prime }\in \{6,7\}$, it is easy to see that Y < 0.

2. When ${\varrho }_a+{\varrho }_b=7$, we have ${\varrho }_a=3$ and ${\varrho }_b=4$ (or ${\varrho }_a=4$ and ${\varrho }_b=3$) and also, ${\varrho }_c=3={\varrho }_{c\prime }$ and therefore, we get Y < 0. □

Lemma 6.

Suppose M be a molecular tree with $\mathit{\text{ab}},\mathit{\text{by}},\mathit{\text{ef}}\in E(M)$ with ${\varrho }_a=2={\varrho }_b,{\varrho }_y\ge 2$, and $\mathrm{\text{min}}\{{\varrho }_e,{\varrho }_f\}\ge 3$. We define $M\prime =M-\{\mathit{\text{ab}},\mathit{\text{by}},\mathit{\text{ef}}\}+\{\mathit{\text{ay}},\mathit{\text{eb}},\mathit{\text{bf}}\}$. Then $\mathit{\text{ABS}}(M)<\mathit{\text{ABS}}(M\prime )$.

Proof.

By the definition ABS index and ${\varrho }_e,{\varrho }_f\in \{3,4\}$, we have $$\begin{array}{c}\mathit{\text{ABS}}(M)-\mathit{\text{ABS}}(M\prime )=\sqrt{1-\frac{2}{4}}+\sqrt{1-\frac{2}{{\varrho }_e+{\varrho }_f}}\\ \hspace{1em}-\sqrt{1-\frac{2}{{\varrho }_e+2}}-\sqrt{1-\frac{2}{{\varrho }_f+2}}<0.\end{array}$$

□

3 Main results

In this section, we obtain sharp upper bounds for the ABS index of molecular trees in terms of order and number of branching vertices and vertices of degree two.

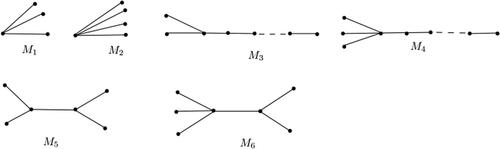
For $n\ge 4$, let $M(n,t_b)$ be the set of molecular trees of order n and branching vertices t_b with $t_b\le \frac{n-2}{2}$. We know that $M(n,0)$ is the path P_n , hence, we have $\mathit{\text{ABS}}(P_n)=\frac{\sqrt{2}(n-2)}{2}+\frac{2\sqrt{3}}{3}$ and M(4, 1) is the graph M₁ in Figure 1 and the value of ABS is shown in Table 1. Therefore, in the following we let n > 4 and $t_b\ge 1$. Now, we will remind the following two families of $M(n,t_b)$: (1) $$M_p=\{M\in M(n,t_b):t_2(M)=0 \text{and} t_3(M)\ge 0\},$$(1) (2) $$M\prime {\prime }_q=\{M\in M(n,t_b):t_3(M)=0 \text{and} t_2(M)\ge 0\}.$$(2)

Fig. 1 Molecular trees M_i for $i=1,2,\dots ,6$.

Table 1 The ABS index of the trees M_i for $i=1,\dots ,6$.

	$\mathit{\text{ABS}}(M_i)$
M1	$\frac{3\sqrt{2}}{2}$
M2	$\frac{4\sqrt{15}}{5}$
M3	$\frac{\sqrt{2}(n-5)}{2}+\sqrt{2}+\frac{\sqrt{15}}{5}+\frac{\sqrt{3}}{3}$
M4	$\frac{\sqrt{2}(n-6)}{2}+\frac{3\sqrt{15}}{5}+\frac{\sqrt{6}}{3}+\frac{\sqrt{3}}{3}$
M5	$2\sqrt{2}+\frac{\sqrt{6}}{3}$
M6	$\sqrt{2}+\frac{3\sqrt{15}}{5}+\frac{\sqrt{35}}{7}$

Now here we present a lemma related to the maximum value of ABS index of molecular tree that will help us in obtaining the main results.

Lemma 7.

Suppose M_b be the molecular tree that attain the maximum value of ABS index over the class $M(n,t_b)$, then $M_b\in M_p$ or $M_b\in M\prime {\prime }_q$.

Proof.

Suppose it is not so, in other words $M_b\in M(n,t_b)\setminus (M_p\cup M\prime {\prime }_q)$. Therefore, there must be vertices a and b in M_b such that ${\varrho }_a=3$ and ${\varrho }_b=2$. Now, we let $N_a(M_b)=\{a_1,a_2,a_3\}$ and $N_b(M_b)=\{b_1,b_2\}$ with b₂ and a₃ lie on the path a–b. Note that $\mathit{\text{ab}}\in E(M)$ hence, we set $b_2=a$ and $a_3=b$, and also it possible that a₃ = b₂. If $M\prime$ be a tree obtained from M by removing the edges aa₁, aa₂ and create the new edges ba₁, ba₂ in M, it can be easily seen that $M\prime \in M(n,t_b)$ and using Lemma 1, we have $$\begin{array}{c}\mathit{\text{ABS}}(M_b)-\mathit{\text{ABS}}(M\prime )\\ =\sum _{i=1}^3\sqrt{1-\frac{2}{3+{\varrho }_{a_i}}}+\sum _{j=1}^2\sqrt{1-\frac{2}{2+{\varrho }_{b_j}}}-\sqrt{1-\frac{2}{1+{\varrho }_{a_3}}}\\ \hspace{1em}-\sum _{i=1}^2\sqrt{1-\frac{2}{4+{\varrho }_{a_i}}}-\sum _{j=1}^2\sqrt{1-\frac{2}{4+{\varrho }_{b_j}}}\\ =\sum _{j=1}^2\left(\sqrt{1-\frac{2}{2+{\varrho }_{b_j}}}-\sqrt{1-\frac{2}{4+{\varrho }_{b_j}}}\right)\\ \hspace{1em}+\sum _{i=1}^2\left(\sqrt{1-\frac{2}{3+{\varrho }_{a_i}}}-\sqrt{1-\frac{2}{4+{\varrho }_{a_i}}}\right)\\ \hspace{1em}+\sqrt{1-\frac{2}{3+{\varrho }_{a_3}}}-\sqrt{1-\frac{2}{1+{\varrho }_{a_3}}}\\ \le \sum _{j=1}^2\left(\sqrt{1-\frac{2}{2+{\varrho }_{b_j}}}-\sqrt{1-\frac{2}{4+{\varrho }_{b_j}}}\right)\\ \hspace{1em}+\sum _{i=1}^2\left(\sqrt{1-\frac{2}{3+{\varrho }_{a_i}}}-\sqrt{1-\frac{2}{4+{\varrho }_{a_i}}}\right)\\ \hspace{1em}+\sqrt{1-\frac{2}{5}}-\sqrt{1-\frac{2}{3}}\\ \le \sum _{i=1}^2\left(\sqrt{1-\frac{2}{3+{\varrho }_{a_i}}}-\sqrt{1-\frac{2}{4+{\varrho }_{a_i}}}\right)\\ \hspace{1em}+\frac{\sqrt{15}}{5}+\frac{2\sqrt{6}}{3}-\frac{4\sqrt{3}}{3}\\ \le 2\left(\sqrt{1-\frac{2}{7}}-\sqrt{1-\frac{2}{8}}\right)+\frac{\sqrt{15}}{5}+\frac{2\sqrt{6}}{3}-\frac{4\sqrt{3}}{3}\\ <0\end{array}$$ that is contradicting with the choice of M_b . □

The next lemma shows the relationship between the maximum value of ABS index and the number of edges $h_{1,2}$.

Lemma 8.

Suppose $t_b>1$ and $M_b\in M(n,t_b)$ be a molecular tree that possessing the maximum value of ABS index, then $h_{1,2}(M_b)=0$.

Proof.

On the contrary, suppose that there is a path $P:b_1{b}_2\dots b_t$ in M_b with $t\ge 3,{\varrho }_{b_1}=1,{\varrho }_{b_t}>2$ and ${\varrho }_{b_j}=2$ for $2\le j\le t-1$. Since, $t_2(M_b)\ge 1$, applying Lemma 7 we get ${\varrho }_{b_t}=4$. Moreover, we know that at least one of the neighbors of $b_t\ne b_{t-1}$ is non-pendent vertex, since $t_b>1$. Setting $y\in N_{M_b}(b_t)\setminus \left\{b_{t-1}\right\}$ with ${\varrho }_y\ge 2$. We know that $t_3(M_b)=0$, applying Lemma 7, we get ${\varrho }_y\in \{2,4\}$. Now, we define $M\prime =M_b-\{b_1{b}_2,b_{t-1}{b}_1,\mathit{\text{ay}}\}+\{b_1{b}_t,a{b}_2,b_{t-1}y\}$, hence, $M\prime \in M(n,t_b)$ and $$\begin{array}{c}\mathit{\text{ABS}}(M_b)-\mathit{\text{ABS}}(M\prime )=\sqrt{1-\frac{2}{3}}-\sqrt{1-\frac{2}{5}}\\ \hspace{1em}+\sqrt{1-\frac{2}{4+{\varrho }_y}}-\sqrt{1-\frac{2}{2+{\varrho }_y}}<0,\end{array}$$ that is a contradiction. □

Note that if M be molecular tree with n > 1, we have the following results (2(2) $$M\prime {\prime }_q=\{M\in M(n,t_b):t_3(M)=0 \text{and} t_2(M)\ge 0\}.$$(2) ): (3) $$n=t_1(M)+t_2(M)+t_3(M)+t_4(M),$$(3) (4) $$t_1(M)+2t_2(M)+3t_3(M)+4t_4(M)=2(n-1),$$(4) (5) $$t_b=t_3(M)+t_4(M).$$(5)

The next lemma is a direct consequence of Eqs (3)–(5).

Lemma 9.

(2(2) $$M\prime {\prime }_q=\{M\in M(n,t_b):t_3(M)=0 \text{and} t_2(M)\ge 0\}.$$(2) ) Suppose $M\in M(n,t_b)$ be a molecular tree, then

1. If $M\in M_p$, we have $t_1(M)=n-t_b,t_3(M)=3t_b-n+2$ and $t_4(M)=n-2t_b-2$.

2. If $M\in M\prime {\prime }_q$, we have $t_1(M)=2t_b+2,t_2(M)=n-3t_b-2$ and $t_4(M)=t_b$.

3. $M\in M_p\cap M\prime {\prime }_q$ if and only if $t_b=\frac{n-2}{3}$.

The next lemma shows the relationship between the maximum value of ABS index and the number of vertices of degree 2.

Lemma 10.

Suppose M be the molecular tree that attain the maximum value of ABS index over the class $M(n,t_b)$, then $t_2(M)\ge 1$ if and only if $0\le t_b<\frac{n-2}{3}$ or $n\ge 3t_b+3.$

Proof.

When $t_2(M)\ge 1$, then from Lemma 7, we have $t_3(M)=0$, therefore, $M\in M\prime {\prime }_q$, using Lemma 9, we have $t_2(M)=n-3t_b-2$, hence, we get $t_b<\frac{n-2}{3}$ or $n\ge 3t_b+3$. On the contrary, let $0\le t_b<\frac{n-2}{3}$ or $n\ge 3t_b+3$ such that $t_b\ge 0$ and $t_2(M)=0$. Applying Eqs. (3)–(5), we get $2t_b+t_4(M)=n-2$, the fact $n\ge 3t_b+3$ meaning $t_4(M)\ge t_b+1$, that is a contradiction. □

Now here we need to introduce several families of chemical trees that will help us to continue the proofs.

We know that M₂ and M₃ of orders n = 5 (see Figure 1) are the only molecular trees in M(1, 5), from Table 1 it is clear $\mathit{\text{ABS}}(M_2)>\mathit{\text{ABS}}(M_3)$.

For $n\ge 5$, the following families of molecular trees introduced in (2(2) $$M\prime {\prime }_q=\{M\in M(n,t_b):t_3(M)=0 \text{and} t_2(M)\ge 0\}.$$(2) ): $$\begin{array}{c}{X}_0=\{M\in M\prime {\prime }_q:t_b=1 \text{ and} h_{1,2}(M)=1\},\\ X_1=\{M\in M\prime {\prime }_q:1<t_b<\frac{n-1}{4} \text{ and} h_{1,2}(M)=0=h_{4,4}(M)\},\\ X_2=\{M\in M\prime {\prime }_q:\frac{n-1}{4}\le t_b<\frac{n-2}{3} \text{ and}\\ \hspace{1em} h_{1,2}(M)=0=h_{2,2}(M)\},\\ X_3=\{M\in M_p:\frac{n-2}{3}<t_b\le \frac{3n-7}{8} \text{ and}\\ \hspace{1em}{h}_{1,3}(M)=0=h_{3,3}(M)\},\\ X_4=\{M\in M_p:\frac{3n-7}{8}<t_b\le \frac{2n-6}{5} \text{ and}\\ \hspace{1em}{h}_{1,3}(M)=0=h_{4,4}(M)\text{ and} h_{3,3}\ne 0\},\\ X_5=\{M\in M_p:\frac{2n-6}{5}<t_b\le \frac{n-2}{2} \text{ and}\\ \hspace{1em}{h}_{4,4}=0 \text{ and} h_{3,3}=t_3(M)-1\},\end{array}$$ where M_p and $M\prime {\prime }_q$ are defined in (1(1) $$M_p=\{M\in M(n,t_b):t_2(M)=0 \text{and} t_3(M)\ge 0\},$$(1) ) and (2(2) $$M\prime {\prime }_q=\{M\in M(n,t_b):t_3(M)=0 \text{and} t_2(M)\ge 0\}.$$(2) ). Hence, we have (6) $$\sum _{1\le k\le 4,l\ne k}{h}_{k,l}(M)+2h_{k,k}(M)=k{t}_k,\text{with} k=1,2,3,4.$$(6)

In the next theorem we give an upper bound for the ABS index.

Theorem 1.

Suppose $n\ge 6$ and $M\in M(n,1)$, then, we have $$\mathit{\text{ABS}}(M)\le \frac{\sqrt{2}(n-6)}{2}+\frac{3\sqrt{15}}{5}+\frac{\sqrt{6}}{3}+\frac{\sqrt{3}}{3}$$ with equality if and only if $C\cong X_0$.

Proof.

Let $M_1\in M(n,1)$ be a molecular tree that possessing the maximum value of ABS index. Let $b\in V(M_1)$ be the unique branching, then we have the following two situations.

Claim 1. ${\varrho }_b=4$.

On the contrary, if ${\varrho }_b=3$ for $n\ge 6$, there is a vertex $a\in V(M_1)$ such that ${\varrho }_a=2$ and is adjacent to a pendent vertex, we called y. Here, we let $M\prime$ be a tree obtained from M₁ by removing the edge ay and adding the new edge by. It is easy to see that $M\prime \in M(n,1)$. Then, we have $$\begin{array}{c}\mathit{\text{ABS}}(M_1)-\mathit{\text{ABS}}(M\prime )=\sum _{c\in N_{M_1}(b)}\sqrt{1-\frac{2}{3+{\varrho }_c}}\\ \hspace{1em}+E-\sum _{c\in N_{M_1}(c)}\sqrt{1-\frac{2}{4+{\varrho }_c}}\\ \hspace{1em}-\sqrt{1-\frac{2}{5}}<0,\end{array}$$

where, $E=\sqrt{1-\frac{2}{3}}$ if $\mathit{\text{ab}}\in V(M_1),$ and $E=\sqrt{1-\frac{2}{4}}$ if $\mathit{\text{ab}}\notin V(M_1).$

Claim 2. b has exactly one non pendent neighbor.

Note that $n\ge 6$, the vertex b has at least one non pendent neighbor. Assume the opposite $P_1:b_1{b}_2\dots b_{r}b$ and $P_2:y_1{y}_2\dots y_{s}b$ be two paths in M₁ such that ${\varrho }_{b_1}=1={\varrho }_{y_1}$ and ${\varrho }_{b_i}=2={\varrho }_{y_j}$ for $2\le i\le r$ and $2\le j\le s$. We define $M\prime =M_1-\{b_2{b}_1,b_{r}b\}+\{b_{1}b,b_r{y}_1\}$, we can see that $M\prime \in M(n,1)$ and $$\begin{array}{c}\mathit{\text{ABS}}(M_1)-\mathit{\text{ABS}}(M\prime )=\sqrt{1-\frac{2}{2+{\varrho }_b}}-\sqrt{1-\frac{2}{1+{\varrho }_b}}\\ \hspace{1em}+\sqrt{1-\frac{2}{3}}-\sqrt{1-\frac{2}{4}}<0,\end{array}$$

applying Claim 1 for ${\varrho }_b=4$, we get a contradiction. By combining these two claims, we will prove the desired result. □

In the following theorem, we present an upper bound on the ABS index based on the number of branching vertices.

Theorem 2.

For $M\in M(n,t_b)$ with $1<t_b<\frac{n-1}{4}$, we have $$\mathit{\text{ABS}}(M)\le \frac{\sqrt{2}(n-4t_b-1)}{2}+\frac{2\sqrt{6}(t_b-1)}{3}+\frac{2\sqrt{15}(t_b+1)}{5}$$ with equality if and only if $M\cong X_1$.

Proof.

Let $M_b\in M(n,t_b)$ be a molecular tree that possessing the maximum value of ABS index, when $1<t_b<\frac{n-1}{4}$. Note that $t_b<\frac{n-1}{4}<\frac{n-2}{3}$, using Lemma 10, we get $t_2(M_b)>0$ and with combination Lemma 7, we get $M_b\in M\prime {\prime }_q$, and applying Lemma 9(b), we have $t_1(M_b)=2t_b+2,t_2(M_b)=n3t_b-2$ and $t_4(M_b)=t_b$. Since, $t_b>1$, by Lemma 8, we get guaranties that (7) $$h_{1,2}(M_b)=0$$(7) taking in (6(6) $$\sum _{1\le k\le 4,l\ne k}{h}_{k,l}(M)+2h_{k,k}(M)=k{t}_k,\text{with} k=1,2,3,4.$$(6) ) for i = 1, we have (8) $$h_{1,4}(M_b)=t_1(M_b)=2t_b+2.$$(8)

Since $t_b<\frac{n-1}{4}$ or $4t_b<n-1$, we have $t_4(M_b)-1=t_b-1<n-3t_b-2=t_2(M_b)$, therefore, we get (9) $$t_4(M_b)\le t_2(M_b).$$(9)

Now here we claim that $h_{2,2}(M_b)\ne 0$. Contrarily, assume that $h_{2,2}(M_b)=0$. From, (6(6) $$\sum _{1\le k\le 4,l\ne k}{h}_{k,l}(M)+2h_{k,k}(M)=k{t}_k,\text{with} k=1,2,3,4.$$(6) ) with i = 2, we obtain that (10) $$h_{2,4}(M_b)=2t_2(M_b).$$(10)

Using (3(3) $$n=t_1(M)+t_2(M)+t_3(M)+t_4(M),$$(3) ) and (4(4) $$t_1(M)+2t_2(M)+3t_3(M)+4t_4(M)=2(n-1),$$(4) ), we get (11) $$t_1(M_b)-2t_4(M_b)=2.$$(11)

For (6(6) $$\sum _{1\le k\le 4,l\ne k}{h}_{k,l}(M)+2h_{k,k}(M)=k{t}_k,\text{with} k=1,2,3,4.$$(6) ) if i = 4, we have (12) $$2h_{4,4}(M_b)=4t_4(M_b)-h_{1,4}(M_b)-h_{2,4}(M_b).$$(12)

Applying (8(8) $$h_{1,4}(M_b)=t_1(M_b)=2t_b+2.$$(8) )–(11(11) $$t_1(M_b)-2t_4(M_b)=2.$$(11) ) in (12(12) $$2h_{4,4}(M_b)=4t_4(M_b)-h_{1,4}(M_b)-h_{2,4}(M_b).$$(12) ), we get $$\begin{array}{c}2h_{4,4}(M_b)=4t_4(M_b)-t_1(M_b)-2t_2(M_b)\le 4t_4(M_b)\\ \hspace{1em}-t_1(M_b)-2t_4(M_b)=-2,\end{array}$$

that is a contradiction. Therefore, the claim $h_{2,2}(M_b)\ne 0$ is true. Now, we claim that (13) $$h_{4,4}(M_b)=0.$$(13)

Assume the opposite $h_{4,4}(M_b)\ne 0$. Setting $\mathit{\text{ef}}\in E(M_b)$ with ${\varrho }_e={\varrho }_f=4$. Note that $h_{2,2}(M_b)\ne 0$, by setting $\mathit{\text{ab}},\mathit{\text{bc}}\in E(M_b)$ with ${\varrho }_a={\varrho }_b=2$ and ${\varrho }_c\ge 2$. Let $M\prime$ be a tree that obtained by applying the transformation mentioned in the statement of Lemma 6, hence, by Lemma 6 we get, $\mathit{\text{ABS}}(M_b)<\mathit{\text{ABS}}(M\prime )$, that is a contradiction to the definition of M_b . Hence, $h_{4,4}(M_b)=0$. Applying (6(6) $$\sum _{1\le k\le 4,l\ne k}{h}_{k,l}(M)+2h_{k,k}(M)=k{t}_k,\text{with} k=1,2,3,4.$$(6) )-(8(8) $$h_{1,4}(M_b)=t_1(M_b)=2t_b+2.$$(8) ) and (13(13) $$h_{4,4}(M_b)=0.$$(13) ), we have $h_{2,4}(M_b)=2t_b-2$ and $h_{2,2}(M_b)=n-4t_b-1$. Then, $\mathit{\text{ABS}}(M_b)=\frac{\sqrt{2}(n-4t_b-1)}{2}+\frac{2\sqrt{6}(t_b-1)}{3}+\frac{2\sqrt{15}(t_b+1)}{5}.$ □

The next theorem is related to the relationship between ABS index branching vertices.

Theorem 3.

For $M\in M(n,t_b)$ with $\frac{n-1}{4}\le t_b<\frac{n-2}{3}$, we have $$\begin{array}{c}\mathit{\text{ABS}}(M)\le \frac{2\sqrt{6}(n-3t_b-2)}{3}\\ \hspace{1em}+\frac{\sqrt{3}(4t_b-n+1)}{2}+\frac{2\sqrt{15}(t_b+1)}{5}\end{array}$$ the equality occurs if and only if $M\cong X_2$.

Proof.

Let $M_b\in M(n,t_b)$ be a molecular tree that possessing the maximum value of ABS index, when $\frac{n-1}{4}\le t_b<\frac{n-2}{3}$. Applying Lemma 10, we get $t_2(M_b)>0$ with $t_b<\frac{n-2}{3}$ and using Lemma 7 we have $M_b\in M\prime {\prime }_q$ or $t_3(M_b)=0$. Applying part (b) of Lemma 9, we have $t_1(M_b)=2t_b+2,t_2(M_b)=n-3t_b-2$ and $t_4(M_b)=t_b$ and by Lemma 8, equations (7)(7) $$h_{1,2}(M_b)=0$$(7) and (8)(8) $$h_{1,4}(M_b)=t_1(M_b)=2t_b+2.$$(8) are hold. We know that $t_2(M_b)\le t_4(M_b)-1$ is obtained from $\frac{n-1}{4}\le t_b.$ With an argument similar to the proof of Theorem 2, we have that $h_{2,2}(M_b)=0,h_{2,4}(M_b)=2t_2(M_b)=2n-6t_b-4$ and $h_{4,4}(M_b)=t_b-1-t_2(M_b)=4t_b-n+1$. Therefore, we have $\mathit{\text{ABS}}(M_b)=\frac{2\sqrt{6}(n-3t_b-2)}{3}+\frac{\sqrt{3}(4t_b-n+1)}{2}+\frac{2\sqrt{15}(t_b+1)}{5}.$ □

Theorem 4.

For $M\in M(n,t_b)$ with $t_b=\frac{n-2}{3}$, we have $$\mathit{\text{ABS}}(M)=\frac{2\sqrt{15}(n+1)}{15}+\frac{\sqrt{3}(n-5)}{6}.$$

Proof.

Applying Lemma 9 part (c), we get $M\in M_p\cap M\prime {\prime }_q$, this meaning $t_3(M)=0=t_2(M)$. Hence, $h_{1,4}(M)=n-t_b=\frac{2}{3}$ and $h_{4,4}(M)=t_b-1=\frac{(n-5)}{3}$. □

The next result is related to ABS index and branching vertices such that $\frac{n-2}{3}<t_b\le \frac{3n-7}{8}$.

Theorem 5.

For $M\in M(n,t_b)$ with $\frac{n-2}{3}<t_b\le \frac{3n-7}{8}$, we have $$\begin{array}{c}\mathit{\text{ABS}}(M)\le \frac{\sqrt{3}(3n-8t_b-7)}{2}\\ \hspace{1em}+\frac{3\sqrt{35}(3t_b-n+2)}{7}+\frac{\sqrt{15}(n-t_b)}{5}\end{array}$$ and the equality occurs if and only if $M\cong X_3$.

Proof.

Let $M_b\in M(n,t_b)$ be a molecular tree that possessing the maximum value of ABS index, when $\frac{n-2}{3}<t_b\le \frac{3n-7}{8}$. Applying Lemma 10, we get $t_2(M_b)=0$ (as $\frac{n-2}{3}<t_b$), that is $M_b\in M_p$. From Lemma 9(a), we have $t_1(M_b)=n-t_b,t_3(M_b)=3t_b-n+2$ and $t_4(M_b)=n-2t_b-2$. Note that $t_b\le \frac{3n-7}{8}$ is equal to $6t_b-2n+5<n-2t_b-2$, and this means that $2t_3(M_b)+1\le t_4(M_b)$. Applying Lemmas 2–4 and using the fact $t_4(M_b)\ge 2t_3(M_b)+1$, we get (14) $$h_{1,3}(M_b)=0$$(14) and (15) $$h_{1,4}(M_b)=n-t_b.$$(15)

Applying Lemmas 2–4 and (6, 14), and (15(15) $$h_{1,4}(M_b)=n-t_b.$$(15) ), we get $h_{3,3}(M_b)=0,h_{3,4}(M_b)=3t_3(M_b)=9t_b-3n+6,h_{4,4}(M_b)=t_4(M_b)-2t_3(M_b)-1=3n-8t_b-7$. Therefore, we obtain that $\mathit{\text{ABS}}(M_b)=\frac{\sqrt{3}(3n-8t_b-7)}{2}+\frac{3\sqrt{35}(3t_b-n+2)}{7}+\frac{\sqrt{15}(n-t_b)}{5}.$ □

The next theorem is related to ABS index and branching vertices such that $\frac{3n-7}{8}<t_b\le \frac{2n-6}{5}$.

Theorem 6.

For $M\in M(n,t_b)$ with $\frac{3n-7}{8}<t_b\le \frac{2n-6}{5}$, we have $$\begin{array}{c}\mathit{\text{ABS}}(M)\le \frac{\sqrt{35}(3n-7t_b-8)}{7}+\frac{\sqrt{15}(n-t_b)}{5}\\ \hspace{1em}+\frac{\sqrt{6}(8t_b-3n+7)}{3}\end{array}$$ and the equality occur if and only if $M\cong X_4$.

Proof.

Let $M_b\in M(n,t_b)$ be a molecular tree that possessing the maximum value of ABS index, when $\frac{3n-7}{8}<t_b-\frac{2n-6}{5}$. Applying Lemma 10, we can obtain that $t_2(M_b)=0$ as $\frac{n-2}{3}<\frac{3n-7}{8}<t_b$, this is what it means $M_b\in M_p$ and applying Lemma 9(a), we have $t_1(M_b)=n-t_b,t_3(M_b)=3t_b-n+2$ and $t_4(M_b)=n-2t_b-2$. We know that $t_b\le \frac{2n-6}{5}$, hence, $3t_b-n+4\le n-2t_b-2$, this means $t_3(M_b)+2\le t_4(M_b)$.

Using Lemmas 2–4 it is clear that we have to place the vertices as described in the proof of Theorem 5. We know that $2t_3(M_b)+1>t_4(M_b)\ge t_3(M_b)+2$ and using (6, 14), and (15(15) $$h_{1,4}(M_b)=n-t_b.$$(15) ), we get $h_{3,3}(M_b)=2t_3(M_b)+1-t_4(M_b)=8t_b-3n+7,h_{3,4}(M_b)=t_3(M_b)+2+2(t_4(M_b)-(t_3(M_b)+2))=3n-7t_b-8$ and $h_{4,4}(M_b)=0$. Therefore, we have $\mathit{\text{ABS}}(M)=\frac{\sqrt{35}(3n-7t_b-8)}{7}+\frac{\sqrt{15}(n-t_b)}{5}+\frac{\sqrt{6}(8t_b-3n+7)}{3}$. □

The next theorem gives an upper bound for ABS index with the condition $\frac{2n-6}{5}<t_b\le \frac{n-2}{2}$.

Theorem 7.

For $M\in M(n,t_b)$ with $\frac{2n-6}{5}<t_b\le \frac{n-2}{2}$, we have $$\begin{array}{c}\mathit{\text{ABS}}(M)\le \frac{3\sqrt{15}(n-2t_b-2)}{5}+\frac{\sqrt{2}(5t_b-2n+6)}{2}\\ \hspace{1em}+\frac{\sqrt{35}(n-2t_b-2)}{7}+\frac{\sqrt{6}(3t_b-n+1)}{3}\end{array}$$ and the equality occurs if and only if $M\cong X_5$.

Proof.

Let $M_b\in M(n,t_b)$ be a molecular tree that possessing the maximum value of ABS index, when $\frac{2n-6}{5}<t_b\le \frac{n-2}{2}$. Applying Lemma 10, we have $t_2(M_b)=0$ as $\frac{n-2}{3}<\frac{2n-6}{5}<t_b$, that is $M_b\in M_p$ and from Lemma 9 (a), we have $t_1(M_b)=n-t_b,t_3(M)=3t_b-n+2$ and $t_4(M_b)=n-2t_b-2$. Since, $t_b>\frac{2n-6}{5}$, we can write that $3t_b-n+4>n-2t_b-2$, that is $t_3(M_b)+2>t_4(M_b)$. Applying Lemmas 2–4 it is clear that we have to place the vertices of degree 4 between the pendent vertices and the vertices of degree 3. We know that $t_3(M_b)+2>t_4(M_b)$, hence, we have (16) $$h_{1,4}(M_b)=3t_4(M_b)=3n-6t_b-6,$$(16) and (17) $$h_{1,3}(M_b)=5t_b-2n+6.$$(17)

Applying (6, 16), and (17(17) $$h_{1,3}(M_b)=5t_b-2n+6.$$(17) ), we get $h_{3,3}(M_b)=t_3(M_b)-1=3t_b-n+1,h_{3,4}(M_b)=t_4(M_b)=n-2t_b-2$ and $h_{4,4}(M_b)=0$. Therefore, we have $\mathit{\text{ABS}}(M_b)=\frac{3\sqrt{15}(n-2t_b-2)}{5}+\frac{\sqrt{2}(5t_b-2n+6)}{2}+\frac{\sqrt{35}(n-2t_b-2)}{7}+\frac{\sqrt{6}(3t_b-n+1)}{3}.$ □

Suppose that $M″(n,r)$ be the trees with n vertices, from which r vertices have degree 2.

It is obvious that $M″(n,n-2)$ is the path graph and there is no graph with value $r=n-3$ in the class $M″(n,r)$. Therefore, we suppose that $0\le r\le n-4$.

Lemma 11.

(2(2) $$M\prime {\prime }_q=\{M\in M(n,t_b):t_3(M)=0 \text{and} t_2(M)\ge 0\}.$$(2) ) Let $M\in M″(n,r)$, then

1. $t_3(M)=0$ if and only if $n-r-2\equiv 0(\mathit{\text{mod}} 3),t_4(M)=\frac{n-r-2}{3}$ and $t_1(M)=\frac{2(n-r+1)}{3}$

2. $t_3(M)=1$ if and only if $n-r-1\equiv 0(\mathit{\text{mod}} 3),t_4(M)=\frac{n-r-4}{3}$ and $t_1(M)=\frac{2(n-r-1)+1}{3}$,

3. $t_3(M)=2$ if and only if $n-r\equiv 0(\mathit{\text{mod}} 3),t_4(M)=\frac{n-r-6}{3}$ and $t_1(M)=\frac{2(n-r)}{3}.$

The next theorem examines the relationship between the maximum value of ABS index and the number of vertices of degree 2.

Lemma 12.

Let $M\in M″(n,r)$ be a tree that possessing the maximum value of ABS index and $n-4\le r\le n-5$, then, $h_{1,2}(M)\le 1$.

Proof.

Since there is a unique branching vertex $a\in V(M)$ with ${\varrho }_a=3$ if $r=n-4$, and ${\varrho }_a=4$ if $r=n-5$. Suppose that for $l,m\ge 3$, there are paths $a_1{a}_2\dots a_{l}a$ and $a{\prime }_{1}a{\prime }_2\dots a{\prime }_m$ in M with ${\varrho }_{a_i}=2={\varrho }_{a{\prime }_j}$ for all $2\le i\le l$ and $2\le j\le m$, and ${\varrho }_{a_1}=1={\varrho }_{a{\prime }_1}$. Let $M\prime \in M″(n,r)$ be a tree with $M\prime =M-\left\{a_{l-1}{a}_l\right\}+\left\{a_{l-1}a{\prime }_1\right\}$, hence, $$\begin{array}{c}\mathit{\text{ABS}}(M)-\mathit{\text{ABS}}(M\prime )=\sqrt{1-\frac{2}{2+{\varrho }_a}}-\sqrt{1-\frac{2}{1+{\varrho }_a}}\\ \hspace{1em}+\sqrt{1-\frac{2}{3}}-\sqrt{1-\frac{2}{4}}\end{array}$$ taking ${\varrho }_a=3$ or ${\varrho }_a=4$ in the above inequality, we get $\mathit{\text{ABS}}(M)<\mathit{\text{ABS}}(M\prime )$, that is a contradiction. □

The proof of the next lemma is similar to Lemma 8, so here we omit the proof of this lemma.

Lemma 13.

Let $M\in M″(n,r)$ be a tree that possessing the maximum value of ABS index and $r\le n-6$, then $h_{1,2}(M)=0$.

Since $M″(4,0)$ and $M″(5,0)$ contain unique trees M₁ and M₂, respectively, with the ABS index values in Table 1. Moreover, from Lemma 12, we know that M₅ and M₆ are the molecular trees with maximum ABS index values among the graphs in $M″(6,0)$ and $M″(7,0)$, respectively. Among all the molecular trees $M″(n,r)$ with $r\ge 1$, if we defined $M_3=\{M\in M″(n,r):h_{1,3}(M)=2,h_{1,2}(M)=1,h_{2,3}(M)=1,h_{2,2}(M)=n-5\}$ and $M_4=\{M\in M″(n,r):h_{1,4}(M)=3,h_{1,2}(M)=1,h_{2,4}(M)=1,h_{2,2}(M)=n-6\}$ (given in Figure 1), the next result is obtained.

Theorem 8.

Let $M\in M″(n,r)$ be a molecular tree with $n\ge 5$, then:

1. If $M\in M\prime {\prime }_{n,n-4}\setminus M_3$, then $\mathit{\text{ABS}}(M)<\mathit{\text{ABS}}(M_3)$.

2. If $M\in M\prime {\prime }_{n,n-5}\setminus M_4$, then $\mathit{\text{ABS}}(M)<\mathit{\text{ABS}}(M_4)$.

Proof.

Applying Lemma 12, we get that M₃ attains the maximum value of ABS index among the class $M″(n,n-4)$ and M₄ attain the maximum value of ABS index among the class $M″(n,n-5)$ (see Table 1), which completes the proof. □

Next, we need to remember the families of subsets of $M″(n,r)$ as:

$A_0=\{M\in M″(n,r):r<n-5$ and $t_3(M)=0$ with $h_{1,4}(M)=\frac{2(n-q+1)}{3}$ and $h_{2,2}(M)=0 \mathit{\text{whenever}} h_{4,4}(M)\ne 0\},A_1=\{M\in M″(n,r):r<n-5$ and $t_3(M)=1$ with $h_{1,2}(M)=0$ and $h_{1,3}(M)\ne 0$ this means that $P(4,4)\notin M,$ moreover if $h_{2,j}(M)\ne 0$ for $2\le j\le 3,$ then $h_{4,4}(M)=0\},A_2=\{M\in M″(n,r):t_3(M)=2$ with $h_{1,2}(M)=0,h_{1,3}(M)\ne 0,$ so $P(4,4)=0$ and $P(3,3)\ne 0,$ and whenever $h_{1,3}(M)=0$ along with $P(3,3)\ne 0,$ hence, $P(4,4)=0,$ moreover $h_{2,i}(M)\ne 0\Rightarrow h_{j,k}=0,$ where $2\le i\le 3$ and $3\le j,k\le 4\}$.

The next theorem gives two upper bounds for ABS index based on the number of vertices with degree two.

Theorem 9.

For $r<n-5$ and $M\in M″(n,r)$ with $t_3(M)=0$, we have $$\mathit{\text{ABS}}(M)\le \{\begin{array}{cc}\frac{2\sqrt{15}((n-r+1))}{15}+\frac{2\sqrt{6}r}{3}+\frac{\sqrt{3}(n-4r-5)}{6}\hfill & \text{when }r<\frac{n-5}{4},\hfill \\ \frac{2\sqrt{15}((n-r+1))}{15}+\frac{\sqrt{2}(4r-n+5)}{6}+\frac{2\sqrt{6}(n-r-5)}{9}\hfill & \text{when }r\ge \frac{n-5}{4}.\hfill \end{array}$$

Equalities hold if and only if $M\in A_0$.

Proof.

Let $M_{a_0}\in M″(n,r)$ be a molecular tree that attains the maximum value of ABS index with $t_3(M_{a_0})=0$. Applying Lemma 11, we have $n-r-2\equiv 0$ (mod 3), $t_4(M_{a_0})=\frac{n-r-2}{3}$ and $t_1(M_{a_0})=\frac{2(n-r+1)}{3}$. Therefore, vertices of degree two were placed according to the conditions of proof of Lemmas 6 and 13, this means that all the vertices of degree 1 are connected to vertices of degree four, i.e., by Lemma 13, we have (18) $$h_{1,2}(M_{a_0})=0,$$(18)

this means that (19) $$h_{1,4}(M_{a_0})=\frac{2(n-r+1)}{3}.$$(19)

Moreover, the vertices of degree 2 are to be placed between the vertices of degree 4 in such a way that if there is an edge connecting the vertices of degree 4, then no two vertices of degree 2 are adjacent. Therefore, $M_{a_0}\in A_0$. Here, we need to check the following two cases as:

Case i. $t_2(M_{a_0})<t_4(M_{a_0})-1$ or $r<\frac{n-5}{4}$. Using Lemma 6, we have (20) $$h_{2,2}(M_{a_0})=0.$$(20)

Applying (6, 18–20), we have $h_{2,4}(M_{a_0})=2r$ and $h_{4,4}(M_{a_0})=\frac{n-4r-5}{3}$. Therefore, we have $\mathit{\text{ABS}}(M_{a_0})=\frac{2\sqrt{15}((n-r+1))}{15}+\frac{2\sqrt{6}r}{3}+\frac{\sqrt{3}(n-4r-5)}{6}$.

Case ii. $t_2(M_{a_0})\ge t_4(M_{a_0})-1$ or $r\ge \frac{n-5}{4}$. Again by using Lemma 6, we get (21) $$h_{4,4}(M_{a_0})=0.$$(21)

Applying (6, 18–21), we obtain that $h_{2,2}(M_{a_0})=\frac{4r-n+5}{3}$ and $h_{2,4}(M_{a_0})=2(t_4(M_{a_0})-1)=\frac{2(n-r-5)}{3}$. Hence, we have $\mathit{\text{ABS}}(M_{a_0})=\frac{2\sqrt{15}((n-r+1))}{15}+\frac{\sqrt{2}(4r-n+5)}{6}+\frac{2\sqrt{6}(n-r-5)}{9}$. □

In the next results, we present upper bounds for ABS index which has the number of vertices of degree 3 equal to one.

Theorem 10.

For $M\in M″(n,r)$ with $t_3(M)=1$, we have $$\text{\&}\mathit{\text{ABS}}(M)\text{ \&}\le \{\begin{array}{cc}\frac{3\sqrt{15}}{5}+\frac{\sqrt{35}}{7}+\sqrt{2}\hfill & \text{when} r=0,\text{and } n=7,\hfill \\ \frac{\sqrt{2}(r+1)}{2}+\frac{4\sqrt{15}}{15}+\frac{\sqrt{6}}{3}\hfill & \text{when} r=n-7\ge 1,\hfill \\ \frac{2\sqrt{35}}{7}+\frac{\sqrt{2}}{2}+\frac{6\sqrt{15}}{15}\hfill & \text{when} r=0,\text{and } n=10,\hfill \\ \frac{\sqrt{2}}{2}+\frac{7\sqrt{15}}{15}+\frac{\sqrt{35}}{7}+\frac{\sqrt{6}}{3}\hfill & \text{when} r=0,\text{and } n=11,\hfill \\ \frac{\sqrt{2}(r-1)}{2}+\frac{8\sqrt{15}}{15}+\frac{2\sqrt{6}}{3}\hfill & \text{when} r\ge 2,\text{and } n-r=10,\hfill \\ \frac{\sqrt{15}(r+9)}{15}+\frac{\sqrt{6}r}{3}-\frac{\sqrt{35}(r-3)}{7}\hfill & \text{when} r\le 2,\text{and } n-r=13,\hfill \\ \frac{\sqrt{2}(r-3)}{2}+\frac{12\sqrt{15}}{15}+\sqrt{6}\hfill & \text{when} r>2,\text{and } n-r=13,\hfill \\ \frac{\sqrt{3}(n-4r-13)}{6}+\frac{\sqrt{15}(2n-2r+1)}{15}\hfill & \hfill \\ \hspace{1em}+\frac{2\sqrt{6}r}{3}+\frac{3\sqrt{35}}{7}\hfill & \text{when} r<\frac{n-13}{4},\hfill \\ \frac{\sqrt{15}(2r+n+14)}{15}+\frac{\sqrt{6}(n+2r-13)}{9}\hfill & \hfill \\ \hspace{1em}+\frac{\sqrt{35}(n-4r-4)}{21}\hfill & \text{when} \frac{n-13}{4}<r\le \frac{n-4}{3},\hfill \\ \frac{\sqrt{15}(2n-2r+1)}{15}+\frac{\sqrt{2}(4r-n+4)}{6}\hfill & \hfill \\ \hspace{1em}+\frac{\sqrt{6}(2n-2r-15)}{9}+\frac{3\sqrt{15}}{5}\hfill & \text{when} r\ge \frac{n-4}{3}.\hfill \end{array}$$

Equalities hold if and only if $M\in A_1$.

Proof.

Let $M_{a_1}\in M″(n,r)$ be a molecular tree that possessing the maximum value of ABS index with $t_3(M_{a_1})=1$, then applying Lemma 11 we get $n-r-1\equiv 0$ (mod 3), $t_1(M_{a_1})=\frac{2n-2r+1}{3},t_4(M_{a_1})=\frac{n-r-4}{3}$. Using Lemmas 2, 13, and 5 we know that $M_{a_1}\in A_1$. This means (22) $$h_{1,2}(M_{a_1})=0,$$(22) and the vertices of degree 4 are to be placed in the three neighbors of the vertex of degree 3 in such a way that if a pendent vertex is present in $M_{a_1}$ which is adjacent to the vertex of degree 3, then $P(4,4)\notin M_{a_1}$. To continue the proof, we need to check the following cases:

Case 1. $t_4(M_{a_1})=1$

Subcase 1.1. r = 0.

Here, we let $n=7,h_{2,j}(M_{a_1})=0$ for all $1\le j\le 4,h_{3,4}(M_{a_1})=1,h_{1,3}(M_{a_1})=2$ and $h_{1,4}(M_{a_1})=3$. Therefore, the desired graph is M₆, which is described in Figure 1, and its ABS index value is also shown in Table 1.

Subcase 1.2. r > 0.

Here, for $n\ge 8$, from Lemmas 5 and 6, and equations (6)(6) $$\sum _{1\le k\le 4,l\ne k}{h}_{k,l}(M)+2h_{k,k}(M)=k{t}_k,\text{with} k=1,2,3,4.$$(6) and (22)(22) $$h_{1,2}(M_{a_1})=0,$$(22) , we get $h_{3,4}(M_{a_1})=0,h_{2,3}(M_{a_1})=1=h_{2,4}(M_{a_1}),h_{1,3}(M_{a_1})=2,h_{1,4}(M_{a_1})=3$ and $h_{2,2}(M_{a_1})=r-1$. Therefore, we get $\mathit{\text{ABS}}(M_{a_1})=\frac{\sqrt{2}(r+1)}{2}+\frac{4\sqrt{15}}{15}+\frac{\sqrt{6}}{3}$.

Case 2. $t_4(M_{a_1})=2$.

Subcase 2.1. r = 0.

For n = 10 and using Lemma 2, we have (23) $$h_{3,4}(M_{a_1})=2.$$(23)

Applying (6, 22), and (23(23) $$h_{3,4}(M_{a_1})=2.$$(23) ), we get $h_{1,3}(M_{a_1})=1$ and $h_{1,4}(M_{a_1})=6$, hence, by the definition ABS index, we have $\mathit{\text{ABS}}(M_{a_1})=\frac{2\sqrt{35}}{7}+\frac{\sqrt{2}}{2}+\frac{6\sqrt{15}}{15}$.

Subcase 2.2. r = 1

Now, for n = 11, from (6, 22), we get $h_{1,3}(M_{a_1})=1,h_{1,4}(M_{a_1})=6$ and $h_{3,4}(M_{a_1})=1=h_{2,3}(M_{a_1})=h_{2,4}(M_{a_1})$, hence, we have $\mathit{\text{ABS}}(M_{a_1})=\frac{\sqrt{2}}{2}+\frac{7\sqrt{15}}{15}+\frac{\sqrt{35}}{7}+\frac{\sqrt{6}}{3}$.

Subcase 2.3. $r\ge 2$.

Here, when $n\ge 12$, and from Lemmas 5, 6 and equations (6)(6) $$\sum _{1\le k\le 4,l\ne k}{h}_{k,l}(M)+2h_{k,k}(M)=k{t}_k,\text{with} k=1,2,3,4.$$(6) and (22)(22) $$h_{1,2}(M_{a_1})=0,$$(22) , we obtain that $h_{1,3}(M_{a_1})=1,h_{1,4}(M_{a_1})=6,h_{2,4}(M_{a_1})=2=h_{2,3}(M_{a_1})$ and $h_{2,2}(M_{a_1})=r-2$. Therefore, $\mathit{\text{ABS}}(M_{a_1})=\frac{\sqrt{2}(r-1)}{2}+\frac{8\sqrt{15}}{15}+\frac{2\sqrt{6}}{3}$.

Case 3. $t_4(M_{a_1})=3$

Using Lemma 2, we have (24) $$h_{1,3}(M_{a_1})=0.$$(24)

Subcase 3.1. $r\le 2$

Applying Lemmas 5, 6 and equations (6)(6) $$\sum _{1\le k\le 4,l\ne k}{h}_{k,l}(M)+2h_{k,k}(M)=k{t}_k,\text{with} k=1,2,3,4.$$(6) , (22)(22) $$h_{1,2}(M_{a_1})=0,$$(22) , and (24)(24) $$h_{1,3}(M_{a_1})=0.$$(24) , we get $h_{1,4}(M_{a_1})=9,h_{2,3}(M_{a_1})=h_{2,4}(M_{a_1})=r,h_{2,2}(M_{a_1})=0=h_{4,4}(M_{a_1})$ and $h_{3,4}(M_{a_1})=3-r$. Therefore, we have $\mathit{\text{ABS}}(M_{a_1})=\frac{\sqrt{15}(r+9)}{15}+\frac{\sqrt{6}r}{3}-\frac{\sqrt{35}(r-3)}{7}$.

Subcase 3.2. r > 2.

Applying Lemmas 5, 6 and equations (6)(6) $$\sum _{1\le k\le 4,l\ne k}{h}_{k,l}(M)+2h_{k,k}(M)=k{t}_k,\text{with} k=1,2,3,4.$$(6) , (22)(22) $$h_{1,2}(M_{a_1})=0,$$(22) , and (24)(24) $$h_{1,3}(M_{a_1})=0.$$(24) , we get $h_{1,4}(M_{a_1})=9,h_{2,3}(M_{a_1})=h_{2,4}(M_{a_1})=3,h_{2,2}(M_{a_1})=r-3$ and $h_{3,4}(M_{a_1})=0$. Then, we have, $\mathit{\text{ABS}}(M_{a_1})=\frac{\sqrt{2}(r-3)}{2}+\frac{12\sqrt{15}}{15}+\sqrt{6}$.

Case 4. $t_4(M_{a_1})>3$

Subcase 4.1. $r<\frac{n-13}{4}$.

It is easy to see that $r<\frac{n-13}{4}$ this means $r<t_4(M_{a_1})-3$ or $r<h_{4,4}(M_{a_1})$. Applying Lemmas 5, 6 and equations (6)(6) $$\sum _{1\le k\le 4,l\ne k}{h}_{k,l}(M)+2h_{k,k}(M)=k{t}_k,\text{with} k=1,2,3,4.$$(6) , (22)(22) $$h_{1,2}(M_{a_1})=0,$$(22) and (23)(23) $$h_{3,4}(M_{a_1})=2.$$(23) , we get $h_{2,2}(M_{a_1})=0=h_{2,3}(M_{a_1}),h_{2,4}(M_{a_1})=2r,h_{3,4}(M_{a_1})=3,h_{1,4}(M_{a_1})=\frac{2n-2r+1}{3}$ and $h_{4,4}(M_{a_1})=\frac{n-4r-13}{3}$. Therefore, we have $\mathit{\text{ABS}}(M_{a_1})=\frac{\sqrt{3}(n-4r-13)}{6}+\frac{\sqrt{15}(2n-2r+1)}{15}+\frac{2\sqrt{6}r}{3}+\frac{3\sqrt{35}}{7}$.

Subcase 4.2. $\frac{n-13}{4}\le r<\frac{n-4}{3}$.

We have, $t_4(M_{a_1})-3\le r<t_4$, this means (25) $$h_{4,4}(M_{a_1})=0.$$(25)

Applying Lemmas 5, 6 and taking equations (22)(22) $$h_{1,2}(M_{a_1})=0,$$(22) , (24)(24) $$h_{1,3}(M_{a_1})=0.$$(24) , and (25)(25) $$h_{4,4}(M_{a_1})=0.$$(25) in (6(6) $$\sum _{1\le k\le 4,l\ne k}{h}_{k,l}(M)+2h_{k,k}(M)=k{t}_k,\text{with} k=1,2,3,4.$$(6) ), we get $h_{2,2}(M_{a_1})=0,h_{2,3}(M_{a_1})=\frac{4r-n+13}{3},h_{2,4}(M_{a_1})=\frac{n+2r-13}{3},h_{1,4}(M_{a_1})=\frac{2n-2r+1}{3}$ and $h_{3,4}(M_{a_1})=\frac{n-4r-4}{3}$. Therefore, $\mathit{\text{ABS}}(M_{a_1})=\frac{\sqrt{15}(2r+n+14)}{15}+\frac{\sqrt{6}(n+2r-13)}{9}+\frac{\sqrt{35}(n-4r-4)}{21}$.

Subcase 4.3. $r\ge \frac{n-4}{3}$.

This means $r\ge t_4(M)$, and applying Lemmas 5 and 6, we get (26) $$h_{3,4}(M_{a_1})=0,$$(26)

taking (22, 24–26) in (6(6) $$\sum _{1\le k\le 4,l\ne k}{h}_{k,l}(M)+2h_{k,k}(M)=k{t}_k,\text{with} k=1,2,3,4.$$(6) ), we obtain that $h_{1,4}(M_{a_1})=\frac{2n-2r+1}{3},h_{2,2}(M_{a_1})=\frac{4r-n+4}{3},h_{2,3}(M_{a_1})=3$ and $h_{2,4}(M_{a_1})=\frac{2n-2r-15}{3}$. Therefore, $\mathit{\text{ABS}}(M_{a_1})=\frac{\sqrt{15}(2n-2r+1)}{15}+\frac{\sqrt{2}(4r-n+4)}{6}+\frac{\sqrt{6}(2n-2r-15)}{9}+\frac{3\sqrt{15}}{5}.$ □

In the next results, we present upper bounds for ABS index which has the number of vertices of degree 3 equal to two.

Theorem 11.

Let $M\in M″(n,r)$ such that $t_3(M)=2$. Then $$\begin{array}{c}\mathit{\text{ABS}}(M)\\ \le \{\begin{array}{cc}2\sqrt{2}+\frac{\sqrt{6}}{3}\hfill & \text{when} n-r=6,\text{and } r=0,\hfill \\ \frac{\sqrt{2}(r+3)}{2}+\frac{2\sqrt{15}}{5}\hfill & n-r=6,\text{and } r>0,\hfill \\ \frac{\sqrt{2}(18-n+r)}{6}+\frac{\sqrt{15}(n-r-6)}{5}\hfill & \hfill \\ \hspace{1em}+\frac{\sqrt{35}(n-r-6)}{21}+\frac{\sqrt{6}}{3}\hfill & \text{when} 9\le n-r\le 15,\text{and } r=0,\hfill \\ \frac{\sqrt{2}(18-n+r)}{6}+\frac{\sqrt{15}(n-6)}{5}\hfill & \hfill \\ \hspace{1em}+\frac{\sqrt{6}(r+1)}{3}+\frac{\sqrt{35}(3-r)}{7}\hfill & \text{when} 9\le n-r\le 15,\text{and } 1\le r\le \frac{n-6}{4},\hfill \\ \frac{\sqrt{2}(5r-2n+21)}{6}+\frac{2\sqrt{15}(2n-2r-9)}{15}\hfill & \hfill \\ \hspace{1em}+\frac{\sqrt{6}(n-r-6)}{9}\hfill & \text{when} 9\le n-r\le 15,\text{and } r>\frac{n-6}{4},\hfill \\ \frac{\sqrt{15}(2n+r)}{15}+\frac{\sqrt{6}(r+1)}{3}\hfill & \hfill \\ \hspace{1em}-\frac{\sqrt{35}(r-4)}{7}\hfill & \text{when} n-r=18,\text{and } 1\le r\le 4,\hfill \\ \frac{2\sqrt{15}(n-r+9)}{15}+\frac{\sqrt{2}(r-5)}{2}+\frac{4\sqrt{6}}{3}\hfill & \text{when} n-r=18,\text{and } r>4,\hfill \\ \frac{2\sqrt{15}(2n+r)}{15}+\frac{\sqrt{6}r}{3}-\frac{\sqrt{35}(r-6)}{7}\hfill & \text{when} n-r=21,\text{and } 0\le r\le 6,\hfill \\ \frac{2\sqrt{15}(n-r+9)}{15}+\frac{\sqrt{2}(r-6)}{2}+2\sqrt{6}\hfill & \text{when} n-r=21,\text{and } r>6,\hfill \\ \frac{2\sqrt{15}(n-r)}{15}+\frac{2\sqrt{6}r}{3}\hfill & \hfill \\ \hspace{1em}+\frac{\sqrt{3}(n-4r-21)}{6}\hfill & \hfill \\ \hspace{1em}+\frac{6\sqrt{35}}{7}\hfill & \text{when} n-r>21,\text{and } r\le \frac{n-21}{4},\hfill \\ \frac{\sqrt{15}(2r+n+21)}{15}+\frac{\sqrt{6}(n+2r-21)}{9}\hfill & \hfill \\ \hspace{1em}+\frac{\sqrt{35}(n-4r-3)}{21}\hfill & \text{when} n-r>21,\text{and } \frac{n-21}{4}<r\le \frac{n-3}{4},\hfill \\ \frac{2\sqrt{15}(n-r+9)}{15}+\frac{\sqrt{2}(4r-n+3)}{6}\hfill & \hfill \\ \hspace{1em}+\frac{2\sqrt{6}(n-r-12)}{9}\hfill & \text{when} n-r>21,\text{and } r>\frac{n-3}{4}.\hfill \end{array}\end{array}$$

Equalities hold if and only if $M\in A_2$.

Proof.

Let $M_{a_2}\in M″(n,r)$ be a molecular tree that possessing the maximum value of ABS index with $t_3(M_{a_2})=2$, hence, applying Lemma 11, we get $n-r-1\equiv 0$ (mod 3), $t_1(M_{a_2})=\frac{2n-2r}{3},t_4(M_{a_2})=\frac{n-r-6}{3}$. From Lemma 13, we have (27) $$h_{1,2}(M_{a_2})=0.$$(27)

Using Lemmas 2–6, we know that $M_{a_2}\in A_2$. Now, to continue the proof, we need to check the following cases:

Case 1. $t_4(M_{a_2})=0$ or $n-r=6$.

Subcase 1.1. r = 0

Applying (6(6) $$\sum _{1\le k\le 4,l\ne k}{h}_{k,l}(M)+2h_{k,k}(M)=k{t}_k,\text{with} k=1,2,3,4.$$(6) ), we get $h_{1,3}(M_{a_2})=4$ and $h_{3,3}(M_{a_2})=1$, that is $\mathit{\text{ABS}}(M_{a_2})=2\sqrt{2}+\frac{\sqrt{6}}{3}.$

Subcase 1.2. r > 0.

Applying (27) in (6(6) $$\sum _{1\le k\le 4,l\ne k}{h}_{k,l}(M)+2h_{k,k}(M)=k{t}_k,\text{with} k=1,2,3,4.$$(6) ), we obtain that $h_{1,3}(M_{a_2})=4,h_{2,2}(M_{a_2})=r-1,h_{2,3}(M_{a_2})=2$ and $h_{3,3}(M_{a_2})=0$, that is $\mathit{\text{ABS}}(M_{a_2})=\frac{\sqrt{2}(r+3)}{2}+\frac{2\sqrt{15}}{5}$.

Case 2. $1\le t_4(M_{a_2})\le 3$ or $9\le n-r\le 15$.

From Lemmas 2–4 and (27), we get (28) $$h_{1,3}(M_{a_2})=4-t_4(M_{a_2})=\frac{18-n+r}{3},$$(28) (29) $$h_{1,4}(M_{a_2})=t_1(M_{a_2})-h_{1,3}(M_{a_2})=n-r-6,$$(29) and (30) $$h_{4,4}(M_{a_2})=0.$$(30)

Subcase 2.1. r = 0.

Applying (27)–(30) in (6(6) $$\sum _{1\le k\le 4,l\ne k}{h}_{k,l}(M)+2h_{k,k}(M)=k{t}_k,\text{with} k=1,2,3,4.$$(6) ), we get that $h_{3,3}(M_{a_2})=1$ and $h_{3,4}(M_{a_2})=\frac{n-r-6}{3}$, that is $\mathit{\text{ABS}}(M_{a_2})=\frac{\sqrt{2}(18-n+r)}{6}+\frac{\sqrt{15}(n-r-6)}{5}+\frac{\sqrt{35}(n-r-6)}{21}+\frac{\sqrt{6}}{3}.$

Subcase 2.2. $1\le r\le \frac{n-6}{4}$.

Note that here, we have $r\le t_4(M_{a_2})$, therefore, using Lemmas 5 and 6 and taking equations (27)(27) $$h_{1,2}(M_{a_2})=0.$$(27) , (30)(30) $$h_{4,4}(M_{a_2})=0.$$(30) in (6(6) $$\sum _{1\le k\le 4,l\ne k}{h}_{k,l}(M)+2h_{k,k}(M)=k{t}_k,\text{with} k=1,2,3,4.$$(6) ), we will arrive $h_{3,3}(M_{a_2})=1,h_{3,4}(M_{a_2})=3-q,h_{2,3}(M_{a_2})=r=h_{2,4}(M_{a_2})$ and $h_{2,2}(M_{a_2})=0$, this means $\mathit{\text{ABS}}(M_{a_2})=\frac{\sqrt{2}(18-n+r)}{6}+\frac{\sqrt{15}(n-6)}{5}+\frac{\sqrt{6}(r+1)}{3}+\frac{\sqrt{35}(3-r)}{7}$.

Subcase 2.3. $r>\frac{n-6}{4}$.

Now, when $r>t_4(M_{a_2})$, and using Subcase 2.2, we have, $h_{3,3}(M_{a_2})=0=h_{3,4}(M_{a_2}),h_{2,3}(M_{a_2})=\frac{n-r}{3},h_{2,4}(M_{a_2})=\frac{n-r-6}{3}$ and $h_{2,2}(M_{a_2})=\frac{4r-n+3}{3}$. Hence, $\mathit{\text{ABS}}(M_{a_2})=\frac{\sqrt{2}(5r-2n+21)}{6}+\frac{2\sqrt{15}(2n-2r-9)}{15}+\frac{\sqrt{6}(n-r-6)}{9}.$

Case 3. $n-r=18$ or $t_4(M_{a_2})=4$.

Applying Lemmas 2–4 and (27) show that (30) holds and (31) $$h_{1,3}(M_{a_2})=0,$$(31) also (32) $$h_{1,4}(M_{a_2})=\frac{2n-2r}{3}.$$(32)

Now we consider the following subcases:

Subcase 3.1. $0\le r\le 4$.

From Lemmas 5 and 6, and (6(6) $$\sum _{1\le k\le 4,l\ne k}{h}_{k,l}(M)+2h_{k,k}(M)=k{t}_k,\text{with} k=1,2,3,4.$$(6) ), (27) and (30)–(32), we get that $h_{2,2}(M_{a_2})=0,h_{2,3}(M_{a_2})=r=h_{2,4}(M_{a_2}),h_{3,3}(M_{a_2})=1$ and $h_{3,4}(M_{a_2})=4-r$. Therefore, $\mathit{\text{ABS}}(M_{a_2})=\frac{\sqrt{15}(2n+r)}{15}+\frac{\sqrt{6}(r+1)}{3}-\frac{\sqrt{35}(r-4)}{7}.$

Subcase 3.2. r > 4.

With a similar argument Subcase 3.1, we reach $h_{2,2}(M_{a_2})=r-5,h_{2,3}(M_{a_2})=6,h_{2,4}(M_{a_2})=4$ and $h_{3,3}(M_{a_2})=0=h_{3,4}(M_{a_2})$. Therefore, $\mathit{\text{ABS}}(M_{a_2})=\frac{2\sqrt{15}(n-r+9)}{15}+\frac{\sqrt{2}(r-5)}{2}+\frac{4\sqrt{6}}{3}.$

Case 4. $n-r>18$ or $t_4(M_{a_2})>4$.

From Lemmas 2–4 we know that (31) and (32) hold, hence, we have (33) $$h_{3,3}(M_{a_2})=0.$$(33)

Subcase 4.1. $n-r=21$ and $0\le r\le 6.$

Since, (30) holds in this case, applying Lemmas 5, 6 and equations (6)(6) $$\sum _{1\le k\le 4,l\ne k}{h}_{k,l}(M)+2h_{k,k}(M)=k{t}_k,\text{with} k=1,2,3,4.$$(6) , (27)(27) $$h_{1,2}(M_{a_2})=0.$$(27) , (30)(30) $$h_{4,4}(M_{a_2})=0.$$(30) and (31)–(33), we get $h_{2,2}(M_{a_2})=0,h_{2,3}(M_{a_2})=r=h_{2,4}(M_{a_2})$ and $h_{3,4}(M_{a_2})=6-r$. Then, $\mathit{\text{ABS}}(M_{a_2})=\frac{2\sqrt{15}(2n+r)}{15}+\frac{\sqrt{6}r}{3}-\frac{\sqrt{35}(r-6)}{7}.$

Subcase 4.2. $n-r=21$ and r > 6.

With a similar argument Subcase 3.1, we reach $h_{2,2}(M_{a_2})=r-6,h_{2,3}(M_{a_2})=6=h_{2,4}(M_{a_2})$ and $h_{3,4}(M_{a_2})=0$. Then, $\mathit{\text{ABS}}(M_{a_2})=\frac{2\sqrt{15}(n-r+9)}{15}+\frac{\sqrt{2}(r-6)}{2}+2\sqrt{6}.$

Subcase 4.3. $n-r>21$ and $r\le \frac{n-21}{4}$.

This case means $r\le t_4(M_{a_2})-5$, using Lemma 5, we have $h_{2,3}(M_{a_2})=0$. Applying Lemma 6 and (6(6) $$\sum _{1\le k\le 4,l\ne k}{h}_{k,l}(M)+2h_{k,k}(M)=k{t}_k,\text{with} k=1,2,3,4.$$(6) ), (27) and (31)–(33), we get $h_{2,2}(M_{a_2})=0,h_{2,4}(M_{a_2})=2r,h_{4,4}(M_{a_2})=\frac{n-4r-21}{3}$ and $h_{3,4}(M_{a_2})=6$. Therefore, $\mathit{\text{ABS}}(M_{a_2})=\frac{2\sqrt{15}(n-r)}{15}+\frac{2\sqrt{6}r}{3}+\frac{\sqrt{3}(n-4r-21)}{6}+\frac{6\sqrt{35}}{7}$.

Subcase 4.4. $n-r>21$ and $\frac{n-21}{4}<r\le \frac{n-3}{4}$.

Since (30) holds in this case and applying (6(6) $$\sum _{1\le k\le 4,l\ne k}{h}_{k,l}(M)+2h_{k,k}(M)=k{t}_k,\text{with} k=1,2,3,4.$$(6) ), (27), and (31)–(33), we will arrive $h_{2,2}(M_{a_2})=0,h_{2,3}(M_{a_2})=\frac{4r-n+21}{3},h_{2,4}(M_{a_2})=\frac{n+2r-21}{3}$ and $h_{3,4}(M_{a_2})=\frac{n-4r-3}{3}$. Therefore, $\mathit{\text{ABS}}(M_{a_2})=\frac{\sqrt{15}(2r+n+21)}{15}+\frac{\sqrt{6}(n+2r-21)}{9}+\frac{\sqrt{35}(n-4r-3)}{21}$.

Subcase 4.5. $n-r>21$ and $r>\frac{n-3}{4}$.

Applying Lemmas 5, 6, and (6(6) $$\sum _{1\le k\le 4,l\ne k}{h}_{k,l}(M)+2h_{k,k}(M)=k{t}_k,\text{with} k=1,2,3,4.$$(6) ), (27), (30), and (31)–(33), we get $h_{2,2}(M_{a_2})=\frac{4r-n+3}{3},h_{2,3}(M_{a_2})=6,h_{2,4}(M_{a_2})=\frac{2(n-r-12)}{3}$ and $h_{3,4}(M_{a_2})=0$. Therefore, $\mathit{\text{ABS}}(M_{a_2})=\frac{2\sqrt{15}(n-r+9)}{15}+\frac{\sqrt{2}(4r-n+3)}{6}+\frac{2\sqrt{6}(n-r-12)}{9}.$

□

4 Conclusions

In the paper, we determined the maximum value of the atom-bond sum-connectivity (ABS) index among molecular trees of a given order and a fixed number of (i) vertices of degree greater than 2. (ii) vertices of degree 2. But the problem of minimum values of the ABS index among the considered classes of molecular trees has not been investigated yet, so we present the following problem.

Problem 1. Characterize graphs that attain the minimum atom-bond sum-connectivity index among molecular trees of a given order and a fixed number of (i) vertices of degree greater than 2. (ii) vertices of degree 2.

Acknowledgments

The authors are grateful to the anonymous referee for his insightful comments.

Disclosure statement

The authors declare that they have no competing interests.

Additional information

Funding

The first author is supported by the Natural Science Foundation of Anhui Province(No 2022AH052810).