On the structure of spikes II

Abstract

The class spike is an important class of 3-connected matroids. For an integer $r\ge 3$, each matroid that is obtained by relaxing one of the circuit-hyperplanes of an r-spike (spike with rank r) is isomorphic to another r-spike and repeating this procedure will produce other r-spikes. So it will be useful to characterize the collection of circuit-hyperplanes of a spike. In this paper, we first introduce a technique to characterize the only two ternary r-spikes in terms of their matrix representations, circuit-hyperplanes, and $(r+1)$-circuits and then we generalize this technique to characterize the class of r-spikes that is representable over the field GF(p), for all primes p. Moreover, we pose a conjecture which would characterize the class of all r-spikes by using all GF(p)-representable r-spikes.

KEYWORDS:

• Matroid
• spike
• circuit-hyperplane
• relaxing

2000 MSC:

• 05B35

1 Introduction

Spikes play an important role in matroid theory. They have been used as a counterexample for many conjectures. So one needs to find the structure of all $\mathbb{F}$-representable spikes with rank r (It is denoted by r-spike and $r\ge 3$) in terms of matrix representation and, in particular, circuit-hyperplanes. Wu [6] evaluated the number of GF(p)-representable r-spikes, for p in $\{3,4,5,7\}$. He also found the asymptotic value of the number of distinct r-spikes that are representable over GF(p) when p is prime. Moreover, Wu [7] showed that a GF(p)-representable r-spike M is only representable over fields with characteristic p provided that $r\ge 2p-1$ and M is uniquely representable over GF(p). In our first paper about spikes [2], we showed that all binary spikes and many non-binary spikes of each rank can be derived from the Fano matroid by a sequence of es-splitting operations and circuit-hyperplane relaxations. In this paper, our main goal is to find the structure of all GF(p)-representable r-spikes in terms of their collections of circuits and matrix representations.

Let $E=\{x_1,x_2,\dots ,x_r,y_1,y_2,\dots ,y_r,t\}$ for some $r\ge 3$. Let ${\mathcal{C}}_1=\left\{\right\{t,x_i,y_i\}:1\le i\le r\}$ and ${\mathcal{C}}_2=\left\{\right\{x_i,y_i,x_j,y_j:1\le i<j\le r\}$. The set of circuits of every spike on E includes ${\mathcal{C}}_1\cup {\mathcal{C}}_2$. Let ${\mathcal{C}}_3$ be a, possibly empty, subset of $\left\{\right\{z_1,z_2,\dots ,z_r\}:z_i\text{ is in }\{x_i,y_i\left\}\text{ for all }i\right\}$ such that no two members of ${\mathcal{C}}_3$ have more than r – 2 common elements. Finally, let ${\mathcal{C}}_4$ be the collection of all $(r+1)$-element subsets of E that contain no member of ${\mathcal{C}}_1\cup {\mathcal{C}}_2\cup {\mathcal{C}}_3$. There is a rank-r matroid M on E whose collection $\mathcal{C}$ of circuits is ${\mathcal{C}}_1\cup {\mathcal{C}}_2\cup {\mathcal{C}}_3\cup {\mathcal{C}}_4$ [4] and the matroid M is called an r-spike with tip t and legs $L_1,L_2,\dots ,L_r$ where $L_i=\{t,x_i,y_i\}$ for all i. In an arbitrary spike M, each circuit in ${\mathcal{C}}_3$ is also a hyperplane of M and when such a circuit-hyperplane is relaxed, we obtain another spike. If ${\mathcal{C}}_3$ is empty, the corresponding spike is called the free r-spike with tip t.

For $r\ge 3$, let $[I_r|J_r-I_r|\mathbf{1}]$ be an $r\times (2r+1)$ matrix over GF(2) whose columns are labeled, in order, $x_1,x_2,\dots ,x_r,y_1,y_2,\dots ,y_r,t$ where J_r and $\mathbf{1}$ are the r × r and $r\times 1$ matrices of all ones, respectively. This matrix represents the unique binary r-spike. Moreover, if we interchange GF(2) and GF(p), for p prime, then we obtain a matrix representation for one of GF(p)-representable r-spikes. But we cannot apply the es-splitting operation on such r-spikes to construct other $(r+1)$-spikes since this operation is only defined for binary matroids.

Let E be the ground set of a GF(p)-representable spike M. We wish to determine what subsets of E are members of ${\mathcal{C}}_3$ or ${\mathcal{C}}_4$ and how we can obtain a matrix representing M. This leads to computing the number of circuit-hyperplanes of M and producing many spikes from M which are not GF(p)-representable, by relaxing operation.

Let $\mathbb{F}$ be a field and ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_r$ be non-zero elements of $\mathbb{F}$. Let $\mathbf{1}$ be the $r\times 1$ matrix of all ones, and let (1) $$\begin{array}{cc}& \begin{array}{ccccccc}& y_1& y_2& y_3& \dots & y_{r-1}& y_r\end{array}\\ A_r=& \left[\begin{array}{ccccccc}& 1+{\alpha }_1{}^{-1}& 1& 1& \dots & 1& 1\\ & 1& 1+{\alpha }_2{}^{-1}& 1& \dots & 1& 1\\ & 1& 1& 1+{\alpha }_3{}^{-1}& \dots & 1& 1\\ & ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ & 1& 1& 1& \dots & 1+{\alpha }_{r-1}{}^{-1}& 1\\ & 1& 1& 1& \dots & 1& 1+{\alpha }_r{}^{-1}\end{array}\right]\end{array}.$$(1)

Geelen, Gerards, and Whittle [1] described the following key result for the representability of spikes.

Proposition 1.

Suppose that $r\ge 3$ and $\mathbb{F}$ is a field. Let M be an $\mathbb{F}$-representable r-spike with legs $\{t,x_1,y_1\},\{t,x_2,y_2\},\dots ,\{t,x_r,y_r\}$ such that $\{x_1,x_2,\dots ,x_r\}$ is independent. Then every $\mathbb{F}$-representation of M is projectively equivalent to a matrix of the form $[I_r|A_r|1]$ whose columns are labeled, in order, $x_1,x_2,\dots ,x_r,y_1,y_2,\dots ,y_r,t$, where A_r is as in (1). Moreover, for $K\subseteq \{1,2,\dots ,r\}$, the set $\{x_k:k\notin K\}\cup \{y_k:k\in K\}$ is a circuit of M if and only if $\sum _{k\in K}{\alpha }_k=-1$.

The following result of Oxley and Whittle [5] gives a necessary and sufficient condition for a matroid that is obtained by relaxing operation to be ternary.

Proposition 2.

Let M be a matroid that is obtained by relaxing a circuit-hyperplane H in a ternary matroid N. Then M is ternary if and only if N is isomorphic to the cycle matroid of a graph that is obtained from a cycle with edge set H by adjoining an extra vertex v and then adding some non-zero number of edges from v to the vertices of H.

Proposition 3.

[6] For each integer $r\ge 3$, there are exactly two distinct ternary r-spikes.

We refer to Oxley [4] for basic definitions not given in this paper such as matrix representations of matroids, properties of circuits and hyperplanes of matroids and good information about spikes.

2 Characterization of ternary spikes

Let r be an integer exceeding two. Let M be the vector matroid of the matrix $[I_r|A_r|1]$ over GF(p) for p prime where the columns of this matrix are labeled, in order, $x_1,x_2,\dots ,x_r,y_1,y_2,\dots ,y_r,t$ and A_r is as in (1). Then, by Proposition 1, M is a GF(p)-representable r-spike. We denote this matroid by M_r and call it the r-spike with respect to A_r over GF(p).

Now let p = 3. By Proposition 2 and the fact that there is no graphic spike, we conclude that all spikes that are obtained from an M_r by relaxing operation are non-ternary. Thus we can find the two non-isomorphic ternary r-spikes by changing some of the diagonal entries of A_r from 0 to –1 and vice versa. In this section, we introduce one way to find all members of ${\mathcal{C}}_3\cup {\mathcal{C}}_4$ for M_r. Moreover, if N_r is the r-spike with respect to $A{\prime }_r$ over GF(3) such that $A{\prime }_r$ is as in (1) with diagonal entries different from A_r, then, by counting the number of circuit-hyperplanes of M_r and N_r, we can determine whether M_r and N_r are isomorphic or not. This will lead to characterize the two ternary r-spikes.

For this section, we let X and Y be disjoint r-element sets $\{x_1,x_2,\dots ,x_r\}$ and $\{y_1,y_2,\dots ,y_r\}$, respectively. We also let i in $\{1,2,\dots ,r\}$, j in {1, 2}, and for p prime, two integers k and $k\prime$ are in $\{1,2,\dots ,p\}$.

Definition 4.

Let $\mathbb{F}$ be a prime field GF(p) and r be an integer exceeding two. For each $k\in \mathbb{N}$, with $k\le p$ we define (2) $${\mathcal{P}}_k=\{\mathit{\text{pn}}-k:n\in \mathbb{N} \text{and} n\le \frac{k+r}{p}\}.$$(2)

For all distinct k and $k\prime$, we have ${\mathcal{P}}_k\cap {\mathcal{P}}_{k\prime }=\varnothing$ and ${\cup }_{k=1}^p{\mathcal{P}}_k=\{0,1,\dots ,r\}$. So $({\mathcal{P}}_1,{\mathcal{P}}_2,\dots ,{\mathcal{P}}_p)$ is a partition of $\{0,1,\dots ,r\}$. We say that such partition is a GF(p)-partition of r.

Definition 5.

Let ${\mathcal{P}}_k$ be the set defined in Definition 4. For all primes p, the field GF(p) coincides with ${\mathbb{Z}}_p$, the ring of integers modulo p. Thus, all members of ${\mathcal{P}}_k$ are congruent to p – k modulo p. We denote this value by $t{r}_p({\mathcal{P}}_k)$ and call it GF(p)-trace of ${\mathcal{P}}_k$.

Let M_r be an r-spike with respect to A_r over GF(3). Then $E(M)=X\cup Y\cup t$. Let $B=({\beta }_1,{\beta }_2,\dots ,{\beta }_r)$ be the ordered r-tuples of diagonal entries of A_r such that β_i is a corresponding entry in the ith row and column of A_r. Then, for all i, we have ${\beta }_i=1+{\alpha }_i^{-1}$, so ${\beta }_i\in \{0,-1\}$. We denote by $\mathcal{D}(A_r)$ the set of non-zero elements of B.

Let $(Y_1,Y_2)$ be a partition of Y such that if ${\beta }_i=0$, then $y_i\in Y_1$, otherwise $y_i\in Y_2$ where Y₁ or Y₂ may be empty. This partition is unique and we call it GF(3)-partition of Y. Now the GF(3)-partition of r is $({\mathcal{P}}_1,{\mathcal{P}}_2,{\mathcal{P}}_3)$ where (3) $${\mathcal{P}}_k=\{3n-k:n\in \mathbb{N} \text{and} n\le \frac{k+r}{3}\}.$$(3)

For an r-spike M_r with respect to A_r over GF(p), we denote by $\ddot{r}$-element set the subset of $E(M_r)$ that has cardinality r and contains at most one element of each $\{x_i,y_i\}$ for all i.

Theorem 6.

Let M_r be an r-spike with respect to A_r over GF(3). Let $(Y_1,Y_2)$ be the GF(3)-partition of Y. An $\ddot{r}$-element set is a circuit-hyperplane of M_r if and only if it is a member of one of the following sets:

1. $\{Z:|Z\cap Y_1|\in {\mathcal{P}}_3 \text{and}|Z\cap Y_2|\in {\mathcal{P}}_1\}$;

2. $\{Z:|Z\cap Y_1|\in {\mathcal{P}}_2 \text{and}|Z\cap Y_2|\in {\mathcal{P}}_3\}$; or

3. $\{Z:|Z\cap Y_1|\in {\mathcal{P}}_1 \text{and}|Z\cap Y_2|\in {\mathcal{P}}_2\}$.

Proof.

Let M_r be an r-spike with respect to A_r over GF(3). Let $(Y_1,Y_2)$ be the GF(3)-partition of Y where $Y=\{y_1,y_2,\dots ,y_r\}$. For $r\ge 3$, consider the GF(3)-partition of r which is $({\mathcal{P}}_1,{\mathcal{P}}_2,{\mathcal{P}}_3)$ so that the GF(3)-trace of ${\mathcal{P}}_k$ is (4) $$t{r}_3({\mathcal{P}}_k)=\{\begin{array}{cc}-1,\hfill & \text{k = 1;}\hfill \\ 1,\hfill & \text{k = 2;}\hfill \\ 0,\hfill & \text{k = 3}.\hfill \end{array}$$(4)

Let ${\beta }_i=1+{\alpha }_i^{-1}$ for all i, if ${\beta }_i=0$, then $y_i\in Y_1$ and ${\alpha }_i=-1$, and if ${\beta }_i=-1$, then $y_i\in Y_2$ and ${\alpha }_i=1$ where β_i is a corresponding entry in the ith row and column of A_r. Hence $\left|Y_1\right|$ is the number of α_i whose values are –1 and $\left|Y_2\right|$ is the number of α_i whose values are 1.

Let Z be an $\ddot{r}$-element set and let I be the set of all indexes of $Z\cap Y$. Suppose that $|Z\cap Y_1|\in {\mathcal{P}}_3$ and $|Z\cap Y_2|\in {\mathcal{P}}_1$. Then, By (4), The numbers $\left|Y_1\right|$ and $\left|Y_2\right|$ are congruent to 0 and –1 modulo 3, respectively. Therefore (5) $$\sum _{i\in I}{\alpha }_i=\left|Y_1\right|(-1)+\left|Y_2\right|(1)=-1.$$(5)

Moreover, the columns of the matrix $[I_r|A_r|1]$ are labeled, in order, $x_1,x_2,\dots ,x_r,y_1,y_2,\dots ,y_r,t$. Hence, the set $\{x_1,x_2,\dots ,x_r\}$ is an independent set of M_r and so, by Proposition 1, Z is a circuit of M_r. Also, as M_r is an r-spike, the set Z is a hyperplane of M_r. Now let Z be a member of one of the sets listed in (ii) or (iii). Then, a similar argument establishes that Z is a circuit-hyperplane of M_r.

To complete the proof, we need to show that if $Z\prime$ is an $\ddot{r}$-element set that is not in $(i)-(\mathit{\text{iii}})$, then $Z\prime$ is not a circuit-hyperplane of M_r. Assume the contrary and let $|\mathcal{D}(A_r)|=m$. Then the number of α_i in diagonal entries of A_r with values 1 and –1 are m and r – m, respectively. Therefore $\left|Y_1\right|=r-m$ and $\left|Y_2\right|=m$. Suppose that $Z\prime =X\prime \cup Y{\prime }_1\cup Y{\prime }_2$ such that $Y{\prime }_j\subseteq Y_j$ and $X\prime \subseteq X$, and let $\left|Y{\prime }_j\right|=m{\prime }_j$. Then $m{\prime }_j$ is a member of one of ${\mathcal{P}}_k$ such that $m{\prime }_1\le r-m$, and $m{\prime }_2\le m$. Thus, (6) $$\sum _{i\in I\prime }{\alpha }_i=\{\begin{array}{cc}1,\hfill & m{\prime }_1\in {\mathcal{P}}_3\text{ and }m{\prime }_2\in {\mathcal{P}}_2;\hfill \\ 1,\hfill & m{\prime }_1\in {\mathcal{P}}_1\text{ and }m{\prime }_2\in {\mathcal{P}}_3;\hfill \\ 1,\hfill & m{\prime }_1\in {\mathcal{P}}_2\text{ and }m{\prime }_2\in {\mathcal{P}}_1;\hfill \\ 0,\hfill & m{\prime }_1\in {\mathcal{P}}_3\text{ and }m{\prime }_2\in {\mathcal{P}}_3;\hfill \\ 0,\hfill & m{\prime }_1\in {\mathcal{P}}_2\text{ and }m{\prime }_2\in {\mathcal{P}}_2;\hfill \\ 0,\hfill & m{\prime }_1\in {\mathcal{P}}_1\text{ and }m{\prime }_2\in {\mathcal{P}}_1.\hfill \end{array}$$(6)

Where $I\prime$ is the set of all indexes of $Z\prime \cap Y$. By Proposition 1, The set $Z\prime$ can not be a circuit-hyperplane of M_r; a contradiction. □

Note that, if $|\mathcal{D}(A_r)|=r$, then $Y_1=\varnothing$ and so the sets of all circuit-hyperplanes of M_r is $\{Z:|Z\cap Y_2|\in {\mathcal{P}}_1\}$, and if $|\mathcal{D}(A_r)|=0$, then $Y_2=\varnothing$ and therefore the sets of all circuit-hyperplanes of M_r is $\{Z:|Z\cap Y_1|\in {\mathcal{P}}_2\}$.

Corollary 7.

Let M_r be an r-spike with respect to A_r over GF(3). Let $|\mathcal{D}(A_r)|=m$. Then the number of circuit-hyperplanes of M is (7) $$\sum _{l\in {\mathcal{P}}_3}\sum _{h\in {\mathcal{P}}_1}\left(\begin{array}{c}m\\ h\end{array}\right)\left(\begin{array}{c}r-m\\ l\end{array}\right)+\sum _{l\in {\mathcal{P}}_2}\sum _{h\in {\mathcal{P}}_3}\left(\begin{array}{c}m\\ h\end{array}\right)\left(\begin{array}{c}r-m\\ l\end{array}\right)+\sum _{l\in {\mathcal{P}}_1}\sum _{h\in {\mathcal{P}}_2}\left(\begin{array}{c}m\\ h\end{array}\right)\left(\begin{array}{c}r-m\\ l\end{array}\right).$$(7)

Proof.

Since $|\mathcal{D}(A_r)|=m$, It follows that $\left|Y_2\right|=m$ and $\left|Y_1\right|=r-m$. Thus by Theorem 6, Part (i), the number of h-combinations from m such that $h\in {\mathcal{P}}_1$ is $(\begin{array}{c}m\\ h\end{array})$ and the number of l-combinations from r – m such that $l\in {\mathcal{P}}_3$ is $(\begin{array}{c}r-m\\ l\end{array})$. Now, the number of all circuit-hyperplanes in Part (i) is equal to the sum over all combinations $(h,l)\in ({\mathcal{P}}_1,{\mathcal{P}}_3)$ which is $\sum _{l\in {\mathcal{P}}_3}\sum _{h\in {\mathcal{P}}_1}(\begin{array}{c}m\\ h\end{array})(\begin{array}{c}r-m\\ l\end{array})$. For a similar reason, the number of circuit-hyperplanes of M in Parts (ii) and (iii) are $\sum _{l\in {\mathcal{P}}_2}\sum _{h\in {\mathcal{P}}_3}(\begin{array}{c}m\\ h\end{array})(\begin{array}{c}r-m\\ l\end{array})$ and $\sum _{l\in {\mathcal{P}}_1}\sum _{h\in {\mathcal{P}}_2}(\begin{array}{c}m\\ h\end{array})(\begin{array}{c}r-m\\ l\end{array})$, respectively. □

Theorem 8.

Let M_r be an r-spike with respect to A_r over GF(3). Let $(Y_1,Y_2)$ be the GF(3)-partition of Y. A union of an $\ddot{r}$-element set which is not a circuit-hyperplane and one element of $E(M_r)$ is an $(r+1)$-circuit of M_r if and only if it is a member of one of the following sets:

1. $\{Z\cup z:|Z\cap Y_j|\in {\mathcal{P}}_k$ for all $\mathit{\text{jin}}\{1,2\}\text{ and }z\in ((Y_2-Z)\cup t)\}$; or

2. $\{Z\cup z:|Z\cap Y_1|\in {\mathcal{P}}_k \text{and}|Z\cap Y_2|\in {\mathcal{P}}_{k\prime },k\ne k\prime \text{and} z\in ((Y_1-Z)\cup t)\}$.

Proof.

Let M_r be an r-spike with respect to A_r over GF(3). Let $(Y_1,Y_2)$ be the GF(3)-partition of Y where $Y=\{y_1,y_2,\dots ,y_r\}$. Consider the GF(3)-partition of r which is $({\mathcal{P}}_1,{\mathcal{P}}_2,{\mathcal{P}}_3)$ and let Z be an $\ddot{r}$-element set. Suppose that $Z\cup z$ where $|Z\cap Y_j|\in {\mathcal{P}}_k$ for all j in {1, 2} and $z\in ((Y_2-Z)\cup t)$. By (6), Z is not a circuit-hyperplane of M_r and, by the fact that $|Z\cap \{x_i,y_i\left\}\right|=1$, the set Z does not contain any leg and circuit of the form $\{x_i,y_i,x_l,y_l\}$ for $1\le i<l\le r$. We conclude that Z is an independent set and M_r has a unique circuit contained in $Z\cup z$, and this circuit contains z. If z = t, then clearly $Z\cup t$ is an $(r+1)$-circuit of M_r. Now suppose that $|Z\cap Y_j|\in {\mathcal{P}}_1$ and $z=y_i$ such that $y_i\in (Y_2-Z)$ and let $Z\prime =((Z-x_i)\cup y_i)$. Then $|Z\prime \cap Y_1|\in {\mathcal{P}}_1$ and $|Z\prime \cap Y_2|\in {\mathcal{P}}_3$. Clearly, the set $Z\prime$ does not contain any leg and circuit of the form $\{x_i,y_i,x_l,y_l\}$ for $1\le i<l\le r$ and, by (6), the set $Z\prime$ is not a circuit-hyperplane of M_r. Therefore $Z\prime \cup x_i$ is an $(r+1)$-circuit of M_r. To complete the proof we must show that when $z\notin ((Y_2-Z)\cup t)$, the set $Z\cup z$ is not a circuit of M_r. To see this, assume the contrary and let $z=y_i$ such that $y_i\in (Y_1-Z)$. Then $|((Z-x_i)\cup y_i)\cap Y_1|\in {\mathcal{P}}_3$ and $|((Z-x_i)\cup y_i)\cap Y_2|\in {\mathcal{P}}_1$. Thus, by Theorem 6, $((Z-x_i)\cup y_i)$ is a circuit-hyperplane of M_r; a contradiction. Moreover, if $z=x_i$ such that $y_i\in Y_2\cap Z$, then $|((Z-y_i)\cup x_i)\cap Y_1|\in {\mathcal{P}}_1$ and $|((Z-y_i)\cup x_i)\cap Y_2|\in {\mathcal{P}}_2$ and so, by Theorem 6 again, $((Z-y_i)\cup x_i)$ is a circuit-hyperplane of M_r; a contradiction.

Finally, suppose $z=x_i$ and $Z\prime =((Z-y_i)\cup x_i)$ where $y_i\in Y_1\cap Z$, then $|Z\prime \cap Y_1|\in {\mathcal{P}}_2$ and $|Z\prime \cap Y_2|\in {\mathcal{P}}_1$. Therefore, the set $Z\prime \cup y_i$ is a member of one of the sets listed in (ii) and one can continue this process to prove that all members of the set in (ii) are $(r+1)$-circuits of M_r. □

Note that, if $|\mathcal{D}(A_r)|=r$, then $Y_1=\varnothing$ and so the sets of all $(r+1)$-circuit of M_r is the union of the sets consists of

1. $\{Z\cup z:|Z\cap Y_2|\in {\mathcal{P}}_3 \text{and} z\in ((Y_2-Z)\cup t\}$;

2. $\{Z\cup t:|Z\cap Y_2|\in {\mathcal{P}}_2\}\cup \{Z\cup t:|Z\cap Y_2|\in {\mathcal{P}}_1\}$.

Moreover, if $|\mathcal{D}(A_r)|=0$, then $Y_2=\varnothing$ and therefore the sets of all $(r+1)$-circuits of M_r is the union of the sets consists of

1. $\{Z\cup t:|Z\cap Y_1|\in {\mathcal{P}}_3\}$;

2. $\{Z\cup z:|Z\cap Y_1|\in {\mathcal{P}}_2 \text{and} z\in ((Y_1-Z)\cup t\}$

3. $\{Z\cup z:|Z\cap Y_2|\in {\mathcal{P}}_1 \text{and} z\in ((Y_1-Z)\cup t\}$.

The proof of the following result can be done using an argument similar to Corollary 7, on Parts (i) and (ii) of Theorem 8.

Corollary 9.

Let M_r be an r-spike with respect to A_r over GF(3). Let $|\mathcal{D}(A_r)|=m$ and $(k,k\prime )$ be a pair of numbers such that $(k,k\prime )\notin \{(3,1),(2,3),(1,2)\}$. Then the number of $(r+1)$-circuits of M is (8) $$\begin{array}{c}\sum _{k=1}^3(\sum _{l\in {\mathcal{P}}_k}\sum _{h\in {\mathcal{P}}_k}\left(\begin{array}{c}m\\ h\end{array}\right)\left(\begin{array}{c}r-m\\ l\end{array}\right)(m-h+1))\\ +\sum _{k\ne k^{\prime }}(\sum _{l\in {\mathcal{P}}_k}\sum _{h\in {\mathcal{P}}_{k^{\prime }}}\left(\begin{array}{c}m\\ h\end{array}\right)\left(\begin{array}{c}r-m\\ l\end{array}\right)(r-m-l+1)).\end{array}$$(8)

By the fact that there are exactly two ternary r-spikes, any of the summation formulae (7) and (8) has exactly two different values. Next, we establish a characterization of these two ternary spikes.

Definition 10.

[3] For integers q and d such that $0\le d\le q$, the following identity is the sum of binomial coefficients with step c and is called the series multisection. (9) $$\left(\begin{array}{c}q\\ d\end{array}\right)+\left(\begin{array}{c}q\\ d+c\end{array}\right)+\left(\begin{array}{c}q\\ d+2c\end{array}\right)+\cdots =\frac{1}{c}\sum _{k=0}^{c-1}{(2\hspace{0.17em}\mathrm{\text{cos}}\hspace{0.17em}\frac{\pi k}{c})}^q.\hspace{0.17em}\mathrm{\text{cos}}\hspace{0.17em}\frac{\pi (q-2d)k}{c}.$$(9)

By Definition 10, one can find the following relations. (10) $$\sum _{h\in {\mathcal{P}}_1}\left(\begin{array}{c}r\\ h\end{array}\right)=\frac{1}{3}(2^r+2\hspace{0.17em}\mathrm{\text{cos}}\hspace{0.17em}\frac{(n-4)\pi }{3}),$$(10) (11) $$\sum _{h\in {\mathcal{P}}_2}\left(\begin{array}{c}r\\ h\end{array}\right)=\frac{1}{3}(2^r+2\hspace{0.17em}\mathrm{\text{cos}}\hspace{0.17em}\frac{(n-2)\pi }{3}),$$(11)

and (12) $$\sum _{h\in {\mathcal{P}}_3}\left(\begin{array}{c}r\\ h\end{array}\right)=\frac{1}{3}(2^r+2\hspace{0.17em}\mathrm{\text{cos}}\hspace{0.17em}\frac{n\pi }{3}).$$(12)

For an r-spike M_r with respect to A_r, we denote by $n_H(M_r)$ the number of circuit-hyperplanes of M_r.

Theorem 11.

Let M_r and N_r be two r-spikes with respect to two matrices A_r and B_r over GF(3), respectively, where $|\mathcal{D}(A_r)|=r$ and $|\mathcal{D}(B_r)|=0$. Suppose 3 does not divide r. Then $M_r\ncong N_r$.

Proof.

Since 3 does not divide r, we have $r=3n-1$ or $r=3n-2$, for $n\in \mathbb{N}$. First let $r=3n-1$. As $|\mathcal{D}(A_r)|=r$ and $|\mathcal{D}(B_r)|=0$, On combining Corollary 7 with (10) and (11), we obtain the following. (13) $$n_H(M_r)=\sum _{h\in {\mathcal{P}}_1}\left(\begin{array}{c}r\\ h\end{array}\right)=\{\begin{array}{cc}\frac{1}{3}(2^{3n-1}+1),\hfill & n\text{ is even };\hfill \\ \hfill & \hfill \\ \frac{1}{3}(2^{3n-1}-1),\hfill & n\text{ is odd};\hfill \end{array}$$(13) and (14) $$n_H(N_r)=\sum _{h\in {\mathcal{P}}_2}\left(\begin{array}{c}r\\ h\end{array}\right)=\{\begin{array}{cc}\frac{1}{3}(2^{3n-1}-2),\hfill & n\text{ is even};\hfill \\ \hfill & \hfill \\ \frac{1}{3}(2^{3n-1}+2),\hfill & n\text{ is odd};\hfill \end{array}$$(14)

Therefore (15) $$n_H(M_r)-n_H(N_r)=\{\begin{array}{cc}1,\hfill & \text{if }r=6n-1;\hfill \\ -1,\hfill & \text{if }r=6n-4;\hfill \end{array}$$(15)

A similar argument establishes the following result when $r=3n-2$. (16) $$n_H(M_r)-n_H(N_r)=\{\begin{array}{cc}1,\hfill & \text{if }r=6n-2;\hfill \\ -1,\hfill & \text{if }r=6n-5;\hfill \end{array}$$(16)

We conclude that $n_H(M_r)\ne n_H(N_r)$, so $M_r\ncong N_r$. □

Theorem 12.

Let M_r, N_r and O_r be three r-spikes with respect to three matrices A_r, B_r, and C_r over GF(3), respectively. Let $|\mathcal{D}(A_r)|=r,|\mathcal{D}(B_r)|=0$ and $|\mathcal{D}(C_r)|=2$ and let 3 divide r. Then $M_r\cong N_r\ncong O_r$.

Proof.

Since 3 divides r, we have $r=3n$, for $n\in \mathbb{N}$. Moreover, as $|\mathcal{D}(A_r)|=r$ and $|\mathcal{D}(B_r)|=0$, by Corollary 7, (17) $$n_H(M_r)=\sum _{h\in {\mathcal{P}}_1}\left(\begin{array}{c}r\\ h\end{array}\right)=\left(\begin{array}{c}3n\\ 2\end{array}\right)+\left(\begin{array}{c}3n\\ 5\end{array}\right)+\cdots +\left(\begin{array}{c}3n\\ 3n-1\end{array}\right).$$(17) and (18) $$n_H(N_r)=\sum _{h\in {\mathcal{P}}_2}\left(\begin{array}{c}r\\ h\end{array}\right)=\left(\begin{array}{c}3n\\ 1\end{array}\right)+\left(\begin{array}{c}3n\\ 4\end{array}\right)+\cdots +\left(\begin{array}{c}3n\\ 3n-2\end{array}\right),$$(18)

and (19) $$\begin{array}{c}{n}_H(O_r)=\sum _{h\in {\mathcal{P}}_3}\left(\begin{array}{c}r-2\\ h\end{array}\right)+\sum _{h\in {\mathcal{P}}_2}\left(\begin{array}{c}r-2\\ h\end{array}\right)+2\sum _{h\in {\mathcal{P}}_1}\left(\begin{array}{c}r-2\\ h\end{array}\right).\hfill \end{array}$$(19)

Clearly, $n_H(M_r)=n_H(N_r)$. To complete the proof, it suffices to show that, $n_H(M_r)-n_H(O_r)\ne 0$. By applying the argument in the proof of the Theorem 11, we have (20) $$n_H(M_r)-n_H(O_r)=\{\begin{array}{cc}1,\hfill & \text{if }r=6n-3;\hfill \\ -1,\hfill & \text{if }r=6n;\hfill \end{array}$$(20) and this completes the proof of the theorem. □

As an immediate consequence of the two last theorems, we have the following result

Corollary 13.

Let M_r and N_r be two non-isomorphic ternary spikes. Then $|n_H(M_r)-n_H(N_r)|=1$.

Proof.

Let M_r, N_r be two non-isomorphic ternary r-spikes with respect to two matrices A_r, B_r. We now distinguish two cases:

1. The number 3 divides r. In this case, by Theorem 11, we let two matrices A_r and B_r with $|\mathcal{D}(A_r)|=r$ and $|\mathcal{D}(B_r)|=0$. Thus, by (15) and (16), we have $|n_H(M_r)-n_H(N_r)|=1$.

2. The number 3 does not divide r over GF(3). In this case, by Theorem 12, we let two matrices A_r and B_r with $|\mathcal{D}(A_r)|=r$ or 0 and $|\mathcal{D}(B_r)|=2$. Thus, by (20), we have $|n_H(M_r)-n_H(N_r)|=1$.

Finally, suppose that $M{\prime }_r,N{\prime }_r$ be two ternary r-spikes with respect to two matrices $A{\prime }_r,B{\prime }_r$ such that $|\mathcal{D}(A_r)|\ne |\mathcal{D}(B{\prime }_r)|\ne t$ where $t\in \{0,1,2\}$. Then, by applying the argument in Theorems 11, 12, and using Corollary 7 and the series multisection, one can check whether or not two spikes are isomorphic. Now, if $M{\prime }_r\ncong N{\prime }_r$, Then $A{\prime }_r$ and $B{\prime }_r$ are projectively equivalent to one of A_r and B_r in cases (a) and (b). This means $|n_H(M{\prime }_r)-n_H(N{\prime }_r)|=1$. □

3 On GF(p)-representable spikes

In this section, we investigate GF(p)-representable r-spikes for p prime, focusing particularly on the question of whether the algorithm on Section (2) can be generalized to such spikes. In other words, for an r-spike M_r with respect to A_r over GF(p), can we find all circuit-hyperplanes and all $(r+1)$-circuits of M_r? Moreover, for $p\ne q$, if N_r is another r-spike with respect to A_r over GF(q), then, for which values of r and q, two spikes M_r and N_r are the same matroid?

Let M_r be an r-spike with respect to A_r over GF(p). Then M_r is the vector matroid of the matrix $[I_r|A_r|1]$ whose columns are labeled, in order, $x_1,x_2,\dots ,x_r,y_1,y_2,\dots ,y_r,t$ and $B=({\beta }_1,{\beta }_2,\dots ,{\beta }_r)$ is the ordered r-tuples of diagonal entries of A_r such that β_i is a corresponding entry in the ith row and column of A_r. Thus, B is an r-tuples of distinct non-unit elements of GF(p). Let $Y=\{y_1,y_2,\dots ,y_r\}$ and $(Y_1,Y_2,\dots ,Y_{p-1})$ be the GF(p)-partition of Y, either of which may be empty, such that if ${\beta }_i=0$ for $i\in \{1,2,\dots ,r\}$, then $y_i\in Y_1$, and if ${\beta }_i=q$, then $y_i\in Y_q$, where $q\in \{2,3,\dots ,p-1\}$. We denote by ${\mathcal{D}}_0(A_r)$ the set of elements of B whose values are 0 and ${\mathcal{D}}_q(A_r)$ the set of non-zero elements of B whose values are q. Now consider the GF(p)-partition of r which is $({\mathcal{P}}_1,{\mathcal{P}}_2,\dots ,{\mathcal{P}}_p)$ where (21) $${\mathcal{P}}_k=\{\mathit{\text{pn}}-k:n\in \mathbb{N} \text{and} n\le \frac{k+r}{p}\}.$$(21)

The following lemmas will be useful to answer our questions about the r-spike M_r with the notation defined above. Note that, every circuit-hyperplane of a spike M is an $\ddot{r}$-element set and every $(r+1)$-circuit of M is also the union of an $\ddot{r}$-element set Z and one element of $E(M)-Z$. Therefore, we expect readers to identify the $\ddot{r}$-element sets in the following.

Lemma 14.

If $|{\mathcal{D}}_0(A_r)|=r$, then the collection of all circuit-hyperplanes of M_r is (22) $$\{Z:|Z\cap Y|\in {\mathcal{P}}_{(p-1)}\}.$$(22)

Proof.

Let Z be a member of (22) and I be the set of all indexes of $Z\cap Y$ and let $|{\mathcal{D}}_0(A_r)|=r$. Then, $Y_2=Y_3=\cdots =Y_{p-1}=\varnothing$ and $Y_1=Y$. Thus, (23) $$\begin{array}{cc}1+{\alpha }_i^{-1}\hfill & =0\hfill \\ {\alpha }_i\hfill & =p-1\hfill \end{array}$$(23)

Since ${\mathcal{P}}_{(p-1)}=\{\mathit{\text{pn}}-p+1:n\in \mathbb{N}\}$ and $t{r}_p({\mathcal{P}}_{(p-1)})=1$, we deduce that $\sum _{i\in I}{\alpha }_i=p-1=-1$ modulo p. It is easy to see that $(p-1)q\ne -1$ modulo p, for non-unit element q of GF(p). Hence, by Proposition 1, the collection of all circuit-hyperplanes of M_r is (22). □

Lemma 15.

If $|{\mathcal{D}}_0(A_r)|=r$, then the collection of all $(r+1)$-circuit of M_r is (24) $$\begin{array}{cc}\{\hfill & Z\cup z:|Z\cap Y|\in {\mathcal{P}}_k,\text{for all }k\text{ in}\{1,2,\dots ,(p-2)\}\text{and}\hfill \\ \hfill & z\in ((Y-Z)\cup t)\}\cup \{Z\cup t:|Z\cap Y|\in {\mathcal{P}}_p\}.\hfill \end{array}$$(24)

Proof.

Let Z be an $\ddot{r}$-element set such that $|Z\cap Y|\in {\mathcal{P}}_k$, for $k\in \{1,2,\dots ,(p-2),p\}$ and let I be the set of all indexes of $|Z\cap Y|$. Then $t{r}_p({\mathcal{P}}_k)\ne 1$ and therefore $\sum _{i\in I}{\alpha }_i\ne -1$ modulo p. Hence, by Proposition 1, the set Z is not a circuit-hyperplane of M_r. Moreover, Z is an independent set since $|Z\cap \{x_i,y_i\left\}\right|=1$ for all i and $t\notin Z$. Therefore M_r has a unique circuit contained in $Z\cup z$, and this circuit contains z where $z\in (E(M_r)-Z)$. Clearly $Z\cup t$ is an $(r+1)$-circuit of M_r. Now suppose that $|Z\cap Y|\in {\mathcal{P}}_k$ for $k\in \{1,2,\dots ,(p-2)\}$ and $z=y_i$ where $y_i\in (Y-Z)$, for $i\in \{1,2,\dots ,r\}$. Let $Z\prime =((Z-x_i)\cup y_i)$. Then $|Z\prime \cap Y|\in {\mathcal{P}}_{k-1}$. By Lemma 14, the set $Z\prime$ is not a circuit-hyperplane of M_r and does not contain any leg and circuit of the form $\{x_i,y_i,x_l,y_l\}$ for $1\le i<l\le r$. Thus, $Z\prime \cup x_i$ is an $(r+1)$-circuit of M_r.

To complete the proof, let $|Z\cap Y|\in {\mathcal{P}}_p$ and $z\in (Y-Z)$. Then, for all y_j in $(Y-Z)$, we have $|((Z-x_j)\cup y_j)\cap Y|\in {\mathcal{P}}_{(p-1)}$ and therefore $Z\cup z$ contains a circuit-hyperplane of M_r; a contradiction. We conclude that in this case $z\notin (Y-Z)$. Moreover, for $k\in \{1,2,\dots ,(p-2),p\}$, if $z=x_i$ be in X – Z where $X=\{x_1,x_2,\dots ,x_r\}$, then $|(Z-y_i)\cup x_i)\cap Y|\in {\mathcal{P}}_{(k+1)}$ and so Z is a circuit-hyperplane of M_r or we get a repetitive member of collection in (24). □

On combining the last two lemmas, we obtain the following result to answer the second question that is stated in the first paragraph of this section.

Theorem 16.

Let $P=\{p_1,p_2,p_3,\dots \}$ be the ordered set of prime numbers. Let $p_i\in P$ for some i. Then, for all $q\ge p_i$, the matrix $[I_r|A_r|1]$ with $|{\mathcal{D}}_0(A_r)|=r$ over GF(q) represents the same matroid if and only if $p_{i-1}<r\le p_i$ where q, $p_{i-1}$ and p_i are in P.

Proof.

Let p_i be a member of P. Let $M_r^{(1)},M_r^{(2)},M_r^{(3)},\dots$ be the r-spikes with respect to A_r over $\mathit{\text{GF}}(p_i),\mathit{\text{GF}}(q_1),\mathit{\text{GF}}(q_2),\dots$, respectively, such that $q_j\ge p_i$ and $|{\mathcal{D}}_0(A_r)|=r$. For all q in $\{p_i,q_1,q_2,q_3,\dots \}$, we have (25) $${\mathcal{P}}_{(q-1)}=\{1,1+q,1+2q,\dots \}.$$(25)

Suppose that $p_{i-1}$ is the greatest prime number such that $p_{i-1}<p_i$ and let $p_{i-1}<r\le p_i$. Then $|Z\cap Y|<1+q$. Thus, by Lemma 14, for all l in $\{1,2,3,\dots \}$, the collection of all circuit-hyperplanes of $M_r^{(l)}$ is (26) $$\{Z:|Z\cap Y|=1\}.$$(26)

Moreover, by using Lemma 15 and applying the above argument, the collection of all $(r+1)$-circuits of $M_r^{(l)}$ is (27) $$\{Z\cup z:2\le |Z\cap Y|\le r \text{such that} z\in (Y-Z)\cup t\}\cup \{Z\cup t:|Z\cap Y|=0\}.$$(27)

We deduce that $M_r^{(1)}=M_r^{(2)}=M_r^{(3)}=\cdots$. □

Next, we show how Lemmas 14 and 15 can be extended to give a characterization of the circuit-hyperplanes and $(r+1)$-circuits of an r-spike M_r with respect to A_r when $|{\mathcal{D}}_q(A_r)|=r$ for $q\in \{2,3,\dots ,p-1\}$.

Lemma 17.

If $|{\mathcal{D}}_q(A_r)|=r$ for $q\in \{2,3,\dots ,p-1\}$, then the collection of all circuit-hyperplanes of M_r is (28) $$\{Z:|Z\cap Y|\in {\mathcal{P}}_{(q-1)}\}.$$(28)

Proof.

Clearly, $Y_1=Y_2=\cdots =Y_{q-1}=Y_{q+1}=\cdots =Y_p=\varnothing$ and $Y_q=Y$. For all i in $\{1,2,\dots ,r\}$, we have ${\alpha }_i={(q-1)}^{-1}$. The set ${\mathcal{P}}_{(q-1)}$ is $\{\mathit{\text{pn}}-(q-1):n\in \mathbb{N}\}$ and so $t{r}_p({\mathcal{P}}_{(q-1)})=p-(q-1)$. Let Z be a member of (28) and I be the set of all indexes of $Z\cap Y$. Then (29) $$\sum _{i\in I}{\alpha }_i=(p-(q-1)){(q-1)}^{-1}=-1 \text{modulop}.$$(29)

Since the inverse of q is unique, by Proposition 1, we conclude that the collection of all circuit-hyperplanes of M_r is (28) □

Lemma 18.

If $|{\mathcal{D}}_q(A_r)|=r$ for $q\in \{2,3,\dots ,p-1\}$, then the collection of all $(r+1)$-circuits of M_r is (30) $$\begin{array}{cc}\{\hfill & Z\cup z:|Z\cap Y|\in {\mathcal{P}}_k,\text{for all }k\text{ in}\{1,2,\dots ,q-2,q+1,\dots ,\hfill \\ \hfill & (p-1),p\},z\in (Y-Z)\cup t\}\cup \{Z\cup t:|Z\cap Y|\in {\mathcal{P}}_q\}.\hfill \end{array}$$(30)

Proof.

Let $Z\cup z$ be a member of (30). Then, by Lemma 17, Z is not a circuit-hyperplane of M_r and by the fact that $|Z\cap \{x_i,y_i\left\}\right|=1$, for $i\in \{1,2,\dots ,r\}$, Z contains no legs and 4-circuits of M_r. So Z is an independent set and $Z\cup z$ contains a circuit of M_r. Clearly $Z\cup t$ is an $(r+1)$-circuit of M_r. Now suppose that $|Z\cap Y|\in {\mathcal{P}}_k$ for $k\notin \{q-1,q\}$ and $z=y_i$ such that $y_i\in Y-Z$. Then $|((Z-x_i)\cup y_i)\cap Y|\in {\mathcal{P}}_{k\prime }$ with $k\prime \ne q-1$. By Lemma 17, the set $((Z-x_i)\cup y_i)$ is not a circuit-hyperplane of M_r and so $Z\cup z$ is an $(r+1)$-circuit. Moreover, if $|Z\cap Y|\in {\mathcal{P}}_q$ and $z=y_i$ such that $y_i\in Y-Z$. Then $|((Z-x_i)\cup y_i)\cap Y|\in {\mathcal{P}}_{(q-1)}$ and so $Z\cup z$ is not an $(r+1)$-circuit of M_r. □

Now suppose that M_r is an r-spike with respect to A_r over GF(p) for some prime number p. Let the columns of the matrix $[I_r|A_r|1]$ are indexed by $x_1,x_2,\dots ,x_r,y_1,y_2,\dots ,y_r,t$. The GF(p)-partitions of r and Y where $Y=\{y_1,y_2,\dots ,y_r\}$ are $({\mathcal{P}}_1,{\mathcal{P}}_2,\dots ,{\mathcal{P}}_p)$ and $(Y_1,Y_2,\dots ,Y_{p-1})$, respectively. Let $|{\mathcal{D}}_0(A_r)|=h_1$ and $|{\mathcal{D}}_q(A_r)|=h_q$ for all q in $\{2,3,\dots ,p-1\}$. Then (31) $$h_1+h_2+\cdots +h_{p-1}=r.$$(31)

Let $({\underset{¯}{v}}_1,{\underset{¯}{v}}_2,\dots ,{\underset{¯}{v}}_{p-1})$ be ordered $(p-1)$-tuples of distinct members of GF(p) such that ${\underset{¯}{v}}_j\le h_j$ for j in $\{1,2,\dots ,p-1\}$. We define $\phi$ as a collection of $\ddot{r}$-element sets of $E(M_r)$ as follows. (32) $$\phi =\{Z:|Z\cap Y_j|\in {\mathcal{P}}_k \mathit{\text{such}} \mathit{\text{that}} t{r}_p({\mathcal{P}}_k)={\underset{¯}{v}}_j \mathit{\text{for}} \mathit{\text{all}} j\}.$$(32)

Note that, for all k in $\{1,2,\dots ,p\}$, the GF(p)-trace of ${\mathcal{P}}_k$ is $(p-k)$. So (33) $$\phi =\{Z:|Z\cap Y_j|\in {\mathcal{P}}_k \mathit{\text{such}} \mathit{\text{that}} k=p-{\underset{¯}{v}}_j \mathit{\text{for}} \mathit{\text{all}} j\}.$$(33)

Summarizing the above discussion, we have the following theorem, one of the main result of this section about M_r.

Theorem 19.

Let Z be a member of $\phi$. Then it is a circuit-hyperplane of M_r if and only if (34) $${\underset{¯}{v}}_1(p-1)+\sum _{j=2}^{p-1} {\underset{¯}{v}}_j{(j-1)}^{-1}=-1 (\mathit{\text{modulo}} p).$$(34)

Proof.

Let Z be a member of $\phi$. Then $\left|Z\right|=r$ and there is a $K\subseteq \{1,2,\dots ,r\}$ such that $Z=\{x_k:k\notin K\}\cup \{y_k:k\in K\}$. By Proposition 1, the set Z is a circuit of M_r if and only if $\sum _{k\in K}{\alpha }_k=-1$. Consider $B=({\beta }_1,{\beta }_2,\dots ,{\beta }_r)$ is the ordered r-tuples of diagonal entries of A_r such that β_i is a corresponding entry in the ith row and column of A_r. By using the fact ${\beta }_i=1+{\alpha }_i^{-1}$, we have ${\alpha }_i=p-1$ when ${\beta }_i=0$ and ${\alpha }_i={(j-1)}^{-1}$ when ${\beta }_i=j$, for $j\in \{2,3,\dots ,p-1\}$ (finding α_i in this case will depend on choice of P). Suppose ${\underset{¯}{v}}_1$ and ${\underset{¯}{v}}_j$ be the numbers of β_i which is equal to 0 and j, respectively. Then it is straightforward to check that (35) $$\sum _{k\in K}{\alpha }_k={\underset{¯}{v}}_1(p-1)+\sum _{j=2}^{p-1} {\underset{¯}{v}}_j{(j-1)}^{-1} (\mathit{\text{modulo}} p).$$(35)

Moreover, since M_r is an r-spike, the set Z is a circuit-hyperplane. □

The next example illustrates the use of the last theorem to find all circuit-hyperplane of an r-spike with respect to A_r over GF(p).

Example 20.

Let M be a 6-spike with matrix representation $[I_6|A_6|1]$ over GF(5), whose columns are indexed $x_1,x_2,\dots ,x_6,y_1,y_2,\dots ,y_6,t$ and let the ordered 6-tuples of diagonal entries of A₆ be $(0,2,4,2,4,2)$. Then the GF(5)-partitions of Y with $Y=\{y_1,y_2,\dots ,y_6\}$ is (36) $$(Y_1,Y_2,Y_3,Y_4)=(\{y_1\},\{y_2,y_4,y_6\},\varnothing ,\{y_3,y_5\}).$$(36)

This means (37) $$|{\mathcal{D}}_q(A_6)|=\{\begin{array}{cc}1,\hfill & q=0;\hfill \\ 3,\hfill & q=2;\hfill \\ 0,\hfill & q=3;\hfill \\ 2,\hfill & q=4.\hfill \end{array}$$(37)

Now consider the GF(5)-partitions $({\mathcal{P}}_1,{\mathcal{P}}_2,\dots ,{\mathcal{P}}_5)$ of r and let $({\underset{¯}{v}}_1,{\underset{¯}{v}}_2,{\underset{¯}{v}}_3,{\underset{¯}{v}}_4)$ be ordered 4-tuples such that $\underset{¯}{v_j}\le h_j$ where $h_1=1,h_2=3,h_3=0$, and $h_4=2$. Thus, by (35), (38) $${\underset{¯}{v}}_1(4)+{\underset{¯}{v}}_2(1)+{\underset{¯}{v}}_3(3)+{\underset{¯}{v}}_4(2)=-1 (\text{modulo} p).$$(38)

Since $h_3=0$, we have ${\underset{¯}{v}}_3=0$. The following table is obtained by combining (38) and (33).

Table

$({\underset{¯}{v}}_1,{\underset{¯}{v}}_2,{\underset{¯}{v}}_3,{\underset{¯}{v}}_4)$	All possible members of $\phi$ under (38)
$(1,0,0,0)$	$\{Z:|Z\cap Y_1|\in {\mathcal{P}}_4,|Z\cap Y_2|\in {\mathcal{P}}_5 \mathit{\text{and}}|Z\cap Y_4|\in {\mathcal{P}}_5\}$
$(0,0,0,2)$	$\{Z:|Z\cap Y_1|\in {\mathcal{P}}_5,|Z\cap Y_2|\in {\mathcal{P}}_5 \mathit{\text{and}}|Z\cap Y_4|\in {\mathcal{P}}_3\}$
$(0,2,0,1)$	$\{Z:|Z\cap Y_1|\in {\mathcal{P}}_5,|Z\cap Y_2|\in {\mathcal{P}}_3 \mathit{\text{and}}|Z\cap Y_4|\in {\mathcal{P}}_4\}$
$(1,1,0,2)$	$\{Z:|Z\cap Y_1|\in {\mathcal{P}}_4,|Z\cap Y_2|\in {\mathcal{P}}_4 \mathit{\text{and}}|Z\cap Y_4|\in {\mathcal{P}}_3\}$
$(1,3,0,1)$	$\{Z:|Z\cap Y_1|\in {\mathcal{P}}_4,|Z\cap Y_2|\in {\mathcal{P}}_2 \mathit{\text{and}}|Z\cap Y_4|\in {\mathcal{P}}_4\}$

Therefore all circuit-hyperplanes of M are $$\begin{array}{c}\{x_2,x_3,x_4,x_5,x_6,y_1\},\{x_1,x_2,x_4,x_6,y_3,y_5\},\{x_1,x_5,x_6,y_2,y_3,y_4\},\{x_1,x_3,x_6,y_2,y_4,y_5\},\{x_1,x_4,x_5,y_2,y_3,y_6\},\\ \{x_1,x_3,x_4,y_2,y_5,y_6\},\{x_1,x_2,x_5,y_3,y_4,y_6\},\{x_1,x_2,x_3,y_4,y_5,y_6\},\{x_4,x_6,y_1,y_2,y_3,y_5\},\{x_2,x_6,y_1,y_3,y_4,y_5\},\\ \{x_2,x_4,y_1,y_3,y_5,y_6\},\{x_3,y_1,y_2,y_3,y_4,y_6\},\{x_3,y_1,y_2,y_4,y_5,y_6\}.\end{array}$$

An interesting application of the existing algorithm in this article for identifying the structure of GF(p)-representable spikes is that we may be able to establish it in the SageMath program, for p prime. For example, one can investigate the structure of a GF(p)-representable r-spike by type the first command as S = matroids.Spike(r,p).

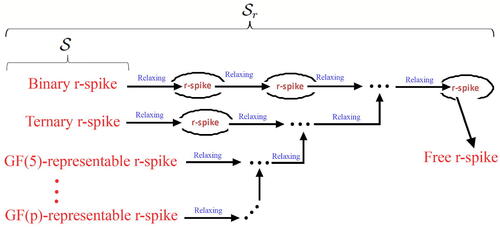
We end this article by proposing a conjecture and a problem that may enable us to prove the conjecture. We know that when a circuit–hyperplane of a spike is relaxed, we obtain another spike and repeating this procedure until all of the circuit–hyperplanes of a spike have been relaxed will produce the free spike. For $r\ge 3$ and some prime p, let $\mathcal{S}$ be the class of all GF(p)-representable r-spikes such that no members of it are not obtained from another r-spike by a sequence of the relaxing operations. In the following conjecture, we claim that all members of the class of all r-spikes can be constructed from all members of $\mathcal{S}$.

Conjecture 21. Let ${\mathcal{S}}_r$ be the class of all r-spikes. Then, by applying a sequence of relaxing operations on circuit-hyperplanes of each member of $\mathcal{S}$ until we arrive at the free r-spike, we can find all members of ${\mathcal{S}}_r-\mathcal{S}$.

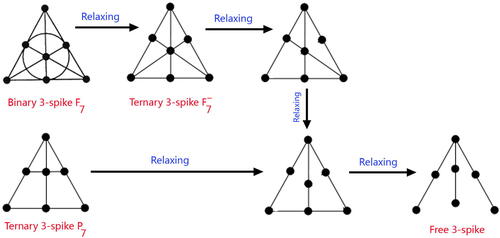
As an example to illustrate this guess, let r = 3. Then $\mathcal{S}=\{F_7,P_7\}$ and in Figure 1, you can see the diagram of the geometric representations of the only six 3-spikes that are obtained by sequences of relaxing operations with starting from the binary 3-spike F₇ and ternary 3-spike P₇.

Fig. 1 Geometric Representations of the only Six 3-Spikes.

The following diagram provides another illustration of Conjecture 21 for finding all r-spike by applying sequences of relaxing operation on members of $\mathcal{S}$.

We end this paper with the following problem and we think that this conjecture can be proved if we can solve the following problem about relaxing operation (Figure 2).

Fig. 2 Illustrating Conjecture 21 to characterize the class ${\mathcal{S}}_r$.

Problem 22.

For p prime, let M be a GF(p)-representable matroid and let H be a circuit-hyperplane of M. Let N be a matroid that is obtained from M by relaxing H. For which filed $\mathbb{F}$ the matroid N is $\mathbb{F}$-representable?